Skip to main content
PMC home page
Protein Science : A Publication of the Protein Society logoLink to Protein Science : A Publication of the Protein Society
. 2007 Aug;16(8):1667–1675. doi: 10.1110/ps.072867007

The role of protein homochirality in shaping the energy landscape of folding

Vikas Nanda 1, Aina Andrianarijaona 1, Chitra Narayanan 1
PMCID: PMC2203351  PMID: 17600146

Abstract

The homochirality, or isotacticity, of the natural amino acids facilitates the formation of regular secondary structures such as α-helices and β-sheets. However, many examples exist in nature where novel polypeptide topologies use both l- and d-amino acids. In this study, we explore how stereochemistry of the polypeptide backbone influences basic properties such as compactness and the size of fold space by simulating both lattice and all-atom polypeptide chains. We formulate a rectangular lattice chain model in both two and three dimensions, where monomers are chiral, having the effect of restricting local conformation. Syndiotactic chains with alternating chirality of adjacent monomers have a very large ensemble of accessible conformations characterized predominantly by extended structures. Isotactic chains on the other hand, have far fewer possible conformations and a significant fraction of these are compact. Syndiotactic chains are often unable to access maximally compact states available to their isotactic counterparts of the same length. Similar features are observed in all-atom models of isotactic versus syndiotactic polyalanine. Our results suggest that protein isotacticity has evolved to increase the enthalpy of chain collapse by facilitating compact helical states and to reduce the entropic cost of folding by restricting the size of the unfolded ensemble of competing states.

Keywords: lattice chain model, tacticity, folding funnel, protein design

How proteins transition to a well-defined three-dimensional structure from an unfolded ensemble has been a defining problem in biology for many decades. Proposed resolutions to the Levinthal paradox emphasize the role of hydrophobic collapse and rapid nucleation of local secondary structure in reducing the size of conformational space to be searched during a folding trajectory. These two mechanisms are coupled: Compact structures stabilize secondary structure and vice versa (Hunt et al. 1994; Yee et al. 1994). The contributions of backbone and side-chain components of a protein to its folding can be ascribed, perhaps oversimplistically, as local versus long-range stability and specificity (Honig and Cohen 1996). The backbone promotes rapid formation of helices and sheets that can assemble through side-chain interactions to stabilize and specify the tertiary structure.

An obvious, but underemphasized feature of protein backbones is their homochirality. What is the role of backbone stereochemistry in protein folding? In the case of glycine, the only amino acid lacking a chiral center at the Cα atom, a significant increase in chain flexibility is possible, which can entropically destabilize the folded state of proteins (O'Neil and DeGrado 1990; Maity et al. 2003). The chemical substitution of glycine that occupies an αL conformation (ϕ ≈ + 65°, ψ ≈ + 40°) by the nonnatural alanine stereoisomer, d-alanine, can stabilize a protein by reducing this inherent flexibility (Schneider and DeGrado 1998; Anil et al. 2004; Bang et al. 2006). For amino acids other than glycine, the stereochemistry at the Cα atom directly influences secondary and tertiary structure. An α-helix composed of l-amino acids will have the opposite sense to one constructed from d-amino acids. Furthermore, insertion of a d-alanine into the middle of an αR-helix can destabilize folding by ∼1 kcal/mol (Fairman et al. 1992). In a dramatic example, HIV-1 protease, which was chemically synthesized using d-amino acids, exhibited a mirror-image structure and an inverse substrate stereospecificity to the natural protein (Milton et al. 1992).

Homochirality is also a feature of other biological polymers such as DNA and RNA. The importance of a single nucleotide enantiomer is at the heart of the RNA-world theory of prebiotic evolution (Joyce 2002). Racemic mixtures of D and L monomers can prevent facile polymerization of nucleotides (Joyce et al. 1984), and it has been proposed that the first self-replicating prebiotic molecules may have been acyclic, prochiral precursors to the extant nucleotides (Joyce et al. 1987). Similarly, the stereochemical rules for abiotic polymer structure are currently being worked out. Probably the best understood example is the β-amino acid, which contains an extra methylene group in the backbone that can accommodate a second side chain. Various stereoregular β-peptide repeats facilitate the formation of helical secondary structures (Cheng et al. 2001).

Despite the prevalent homochirality, or isotacticity 1 of natural proteins, there are numerous cases where mixtures of l and d-amino acids in the same chain facilitate new secondary structures. A classic example is the β-helix of gramicidin, which is formed by a syndiotactic (alternating L and D) polypeptide chain (Urry et al. 1971; Veatch et al. 1974). The cell goes through great biochemical effort to synthesize these small, heterochiral peptides, often serving as antimicrobials or toxins. Because the ribosome is dedicated to synthesizing natural proteins, the cell instead, expresses large biosynthetic protein complexes for directing the synthesis of heterochiral peptides. Although this process is taxing on cellular resources, combining l and d amino acids confers a functional advantage because of the increased chemical diversity available. Heterochiral peptides also are potentially useful as therapeutics, because they are resistant to proteolytic degradation and generally not toxic, enhancing their pharmacological properties (Guichard et al. 1994).

Heterochiral molecular designs, such as self-assembling organic nanotubes, make use of short cyclic peptides with alternating l and d amino acids (Ghadiri et al. 1993). Using stereochemically constrained nonnatural amino acids, it is possible to stabilize secondary structures or design new conformations (Aravinda et al. 2003). Similarly, in β-peptides, chains made of alternating stereoisomers can stably form regular secondary structures (Cheng et al. 2001; Martinek et al. 2006). It is important to explore the basic physical properties of heterochiral chains. We want to understand why heterochirality is the exception rather than the norm in most biological systems. Also, we hope to determine whether many of the lessons learned from protein folding and structure can be applied to the design of heterochiral molecules.

We present a simulation study of two types of chain models—the rectangular lattice chain and an all-atom polyalanine polypeptide. The lattice model allows complete enumeration of all possible structures, permitting us to study the role of tacticity in modulating the size and nature of fold space. It also allows us to study the effects of chirality in isolation from the other chemical properties of a given polymer. In the second set of simulations, Monte Carlo sampling of an all-atom polypeptide chain, we can test whether the observations found in lattice models bear out in a more realistic representation of proteins. Overall, varying chain tacticity has a significant influence on the number of conformations and the mean compactness of folds. We propose that isotacticity has prevailed in proteins because it promotes rapid folding into compact helical conformations.

Results

Chiral lattice chains

To model the effect of chirality on a polymer chain in the absence of other chemical information, we carry out simulations on two-dimensional rectangular lattices. Using the first two rules (see Materials and Methods), we enumerate all possible conformations of an isotactic and syndiotactic chain. The number of structures that obey the excluded volume constraint increase more quickly for syndiotactic chains as a function of length than do isotactic chains (Fig. 1A). Chains that do not have any chiral constraint have even more possible structures. Logistically, this makes it possible to enumerate conformations of a longer chain when it is isotactic than when it is syndiotactic or achiral. Isotactic chains occupy a very small subset of the total available fold space. Relatively more folds are available to syndiotactic chains.

Figure 1.

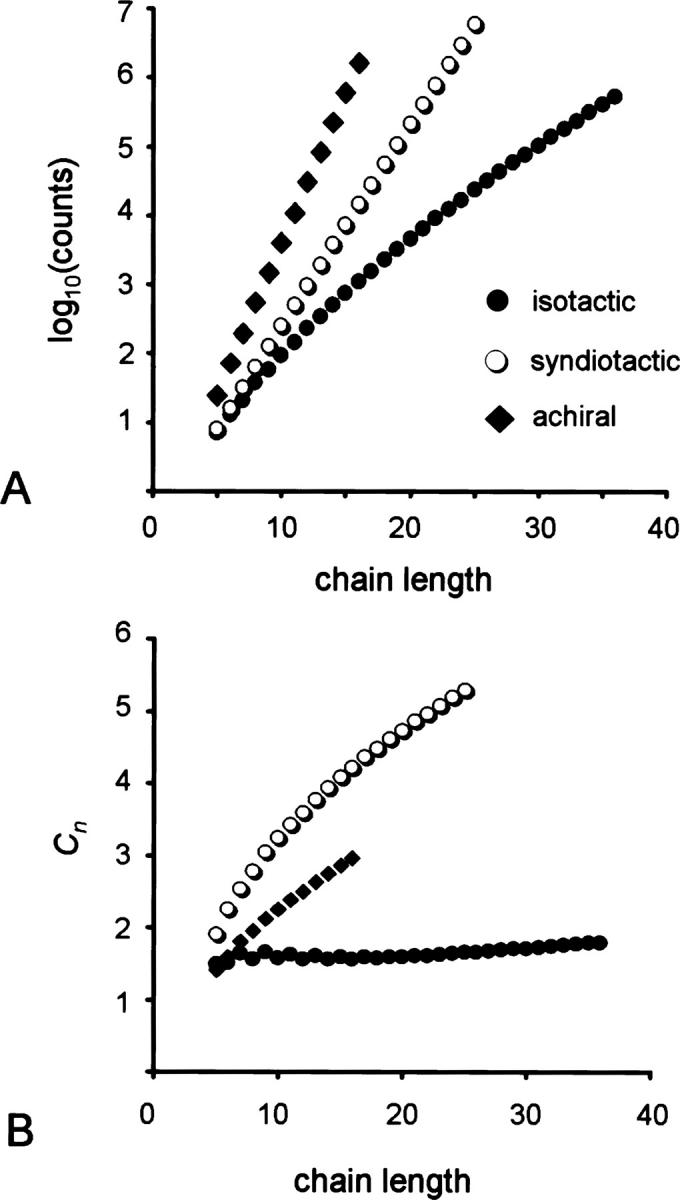
Figure 1.

Open in a new tab

(A) Number of distinct conformations in a two-dimensional lattice that obey the excluded volume constraint for isotactic, syndiotactic, and achiral chains of different lengths. (B) Characteristic ratio of the enumerated ensemble of isotactic, syndiotactic, and achiral chains as a function of length (Equation 1).

We characterize the mean dimension of the ensemble of chain conformations for a given length and tacticity using the characteristic ratio, Cn, defined as:

graphic file with name 1667equ1.jpg

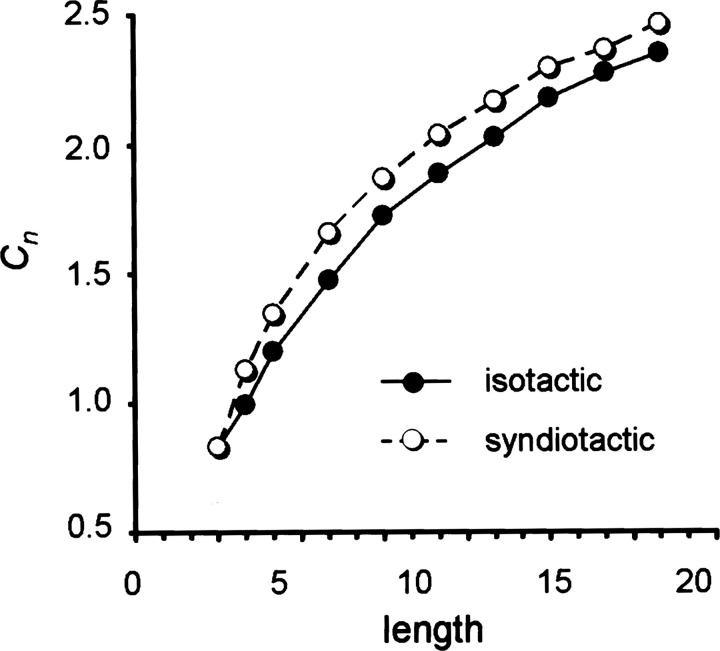
where r is the end-to-end distance of a given chain and ℓ is the length of one monomer (equal to unity). Cn reflects the compactness of the ensemble, with larger values reflecting a higher propensity for extended conformations. In the case of two-dimensional chains, we find that Cn increases as a function of length more rapidly for syndiotactic chains than for isotactic ones (Fig. 1B). The ensemble of conformations for syndiotactic chains has a higher Cn than for isotactic chains, indicating that it is less compact. Similarly, the ensemble of syndiotactic chains is less compact than that of all achiral chain conformations.

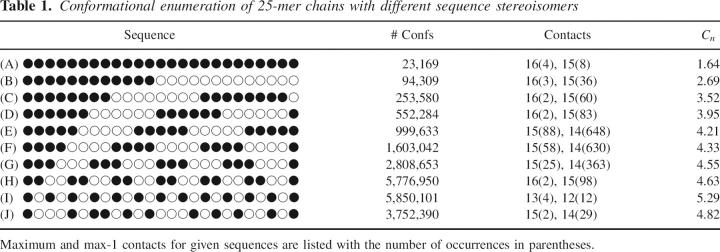
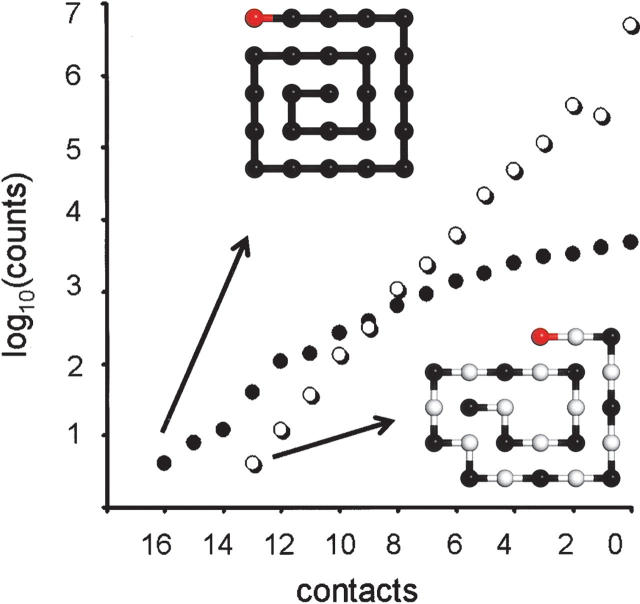
We can also measure compactness by examining the distribution of contacts for a chain of given length when the sequence is isotactic or syndiotactic. The maximum number of contacts for a chain of n = 25 is 16 in a 5 × 5 square. For an achiral chain, there are a total of 5.78 billion self-avoiding conformations, of which 1081 form a 5 × 5 square (Chan and Dill 1991; Irback and Troein 2002). As expected, enumerating all possible conformations of an isotactic chain reveals a very small number of self-avoiding walks (23,169), whereas for the syndiotactic 25-mer, there are just under 6,000,000 allowed conformations (Table 1, sequences A and I). When these two ensembles are plotted as a distribution of number of contacts (Fig. 2), it becomes clear that the isotactic chains, though fewer in number, are more likely to form compact structures than the syndiotactic chains. The maximally compact syndiotactic chains have three fewer contacts than the isotactic chains.

Table 1.

Conformational enumeration of 25-mer chains with different sequence stereoisomers

graphic file with name 1667tbl1.jpg

Open in a new tab

Figure 2.

Figure 2.

Open in a new tab

Number of structures in the enumerated ensemble of 25-mer as a function of number of contacts for an isotactic chain (•) and a syndiotactic chain (○). One conformation is pictured for an isotactic chain (16 contacts) and for a syndiotactic chain (13 contacts). The red monomer corresponds to the first position.

A series of 25-mer sequences are enumerated with varying numbers of reversals (or size of internal isotactic domains) (Table 1). The number of allowed conformations and the characteristic ratio, Cn, increase with the number of reversals in the sequence. Furthermore, the number of maximally compact structures goes down with increasing numbers of reversals. Thus, isotactic and syndiotactic chains (sequences A and I) represent extreme cases of the effect of chirality on chain properties, and a range of intermediate properties are possible. A randomly specified sequence, J, falls somewhere between G and H, consistent with the physical properties scaling approximately with the number of reversals. Some sequence-specific idiosyncrasies of the lattice are evident, such as the ability for sequence H to form two maximally compact conformations.

In extending the treatment to a three-dimensional lattice, we find similar behavior to that observed in two dimensions (Fig. 3). The relative difference in counts between isotactic and syndiotactic chains is less pronounced, i.e., a 16-mer has fivefold more syndiotactic structures than isotactic ones, whereas in two dimensions, this difference is just over 50-fold. Likewise, the mean compactness of the ensemble, as measured by the characteristic ratio, is tighter for isotactic sequences. Cn for the enumerated ensemble of isotactic 16-mers is 15.0, whereas for syndiotactic chains of the same length, it is 62.5.

Figure 3.

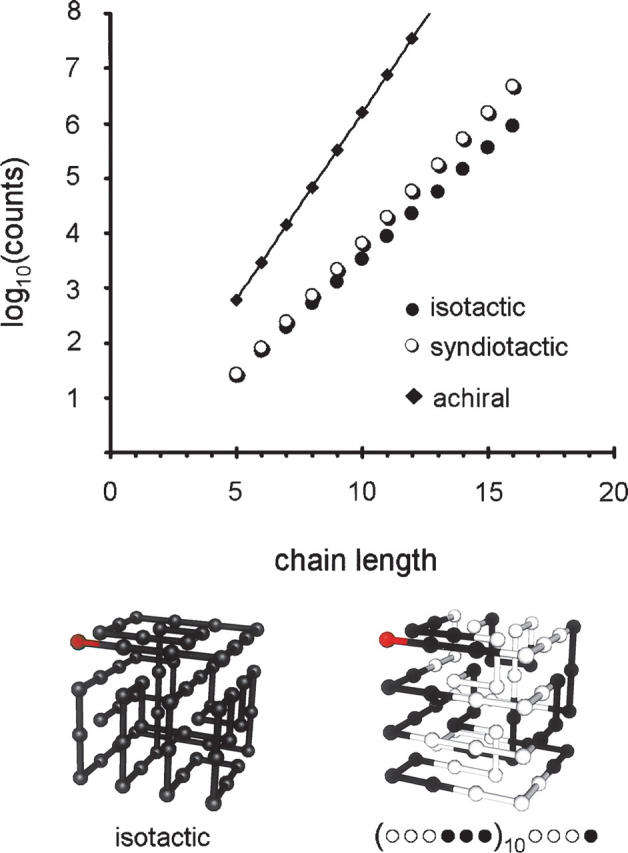
Figure 3.

Open in a new tab

Enumeration of conformations for isotactic and syndiotactic cubic lattice chains. The number of unique conformations that obey the excluded volume constraint are plotted as a function of chain length. The number of achiral conformations are estimated using a continuous approximation (Hiley and Sykes 1961). At bottom are two examples of maximally compact 64-mers, one from an isotactic sequence, the other from a stereoregular sequence that reverses chirality every three monomers. The red monomer corresponds to the first position.

The relationship holds for very long chains. A 64-mer can form a 4 × 4 × 4 cube that satisfies the maximum number of contacts. While a full enumeration was not computationally feasible, we are able to find 165,004 distinct cubic solutions for an isotactic 64-mer in a several-week-long search (one example is pictured in Fig. 3). By comparison, no syndiotactic solutions are found. A stereoregular sequence with pairs of monomers of the same chirality, (○○••)16, gives only two solutions during this time. As the number of adjacent monomers of the same chirality is increased to three, we find 371 structures (example in Fig. 3). For the sequence (○○○○••••)8, there are 3107 examples. Thus, sampling suggests a very similar trend in three dimensions to that observed with the two-dimensional 25-mer. Increasing the number of reversals reduces the number of accessible, maximally compact conformations.

All atom model of polyalanine

Lattice models can be useful as tools to provide a basic chemical intuition, but there is always the risk that one is characterizing idiosyncrasies of the lattice rather than real polymer properties. From the simulations presented thus far, it appears that homochirality facilitates the formation of maximally compact structures and reduces the size of accessible fold space. To see whether these observations are true for proteins, we generate an ensemble of polyalanine chains and compute steric overlap using a van der Waals energy, Evdw. Although there are other forces relevant to protein structure, such as electrostatics and hydrogen bonding, we choose to focus on sterics as a measure of the allowable conformational space available to a given stereochemical sequence of polyalanine.

We compute 106 conformations each for all possible stereochemical permutations of a six-residue polyalanine. The results for three sequences are shown in Figure 4A. A large, negative Evdw represents a well-packed structure with minimal steric overlap. The greatest number of well-packed structures is found in the ensemble of isotactic polyalanine (56 conformations with an Evdw between −15 and −13 kcal/mol, and 1598 conformations between −13 and −11 kcal/mol). Syndiotactic polyalanine gives no structures below −13 kcal/mol and only eight between −13 and −11 kcal/mol. Similar to the 25-mer lattice previously described (Fig. 2), isotactic polyalanine has an increased propensity to form maximally compact structures relative to a syndiotactic chain.

Figure 4.

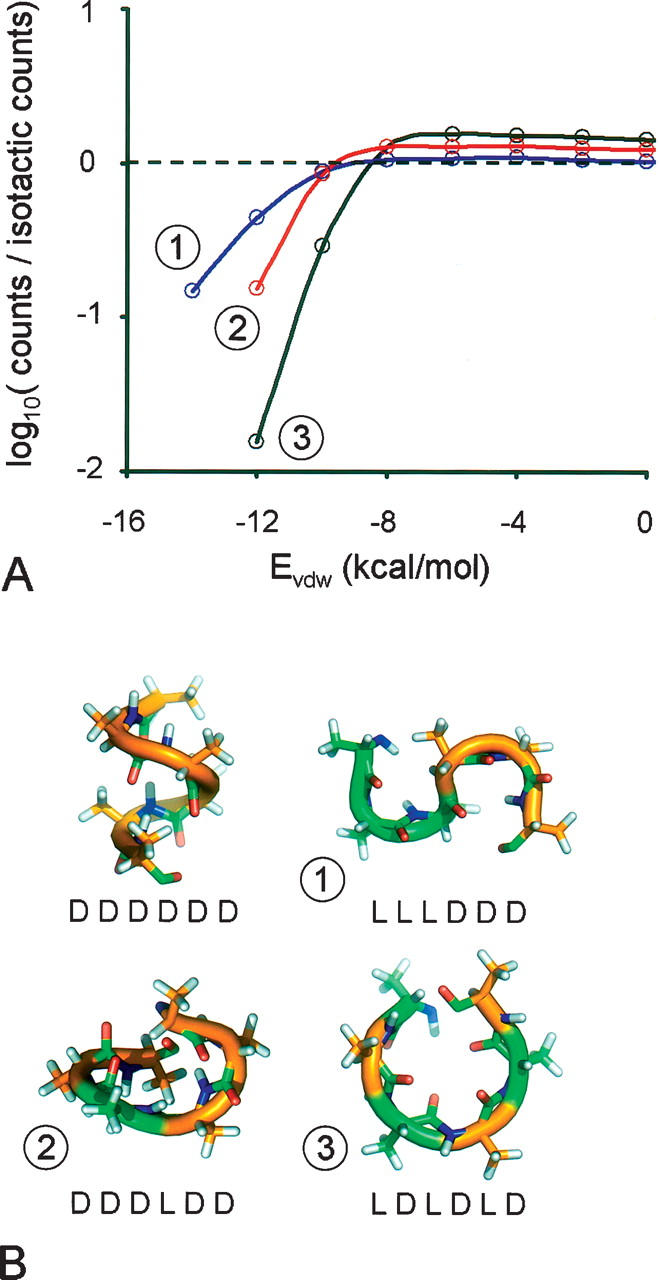
Figure 4.

Open in a new tab

(A) Number of conformations for 6-mer polyalanine sequences 1–3 that had a particular van der Waals energy (Evdw) of 2,000,000 structures. Counts are summed over the given sequence and its sequence stereoisomer. The results are plotted as a ratio of the number of conformations for a given sequence over the number of conformations within a similar 2 kcal/mol interval in the isotactic sequence. (B) Lowest energy conformations for isotactic polyalanine and sequences 1–3.

Two other sequences, lllddd (sequence 1) and dddldd (sequence 2), show intermediate properties between the two extremes. Sequence 1 contained one reversal in chirality and behaves the most like an isotactic chain. Sequence 2 contained two reversals and shows an even lower propensity for forming maximally compact chains. The syndiotactic chain contains five reversals—suggesting that the ability to form a compact conformation roughly scales inversely with the number of changes in chirality through the sequence. We note that for all heterochiral sequences, the number of structures at higher energies eventually exceeds that of isotactic chains (Fig. 4A). This effect also becomes more pronounced as the number of reversals increases.

Although no explicit hydrogen-bonding term is used, the maximally compact isotactic chains form an α-helix (Fig. 4B), with ϕ, ψ angles falling well within allowed regions of Ramachandran space. Sequence 1 forms two α-turns, an αR followed by an αL three-residue turn. The syndiotactic chain forms an open circle of repeating βL and βR, with the N and C termini within 3 Å to 4 Å of each other, suggestive of the ability to form a cyclic peptide.

Using the characteristic ratio as a measure of the average compactness, we compute Cn for conformations within the ensemble where Evdw ≤ 0 kcal/mol. This cutoff is the analog of the excluded volume constraint used in our lattice models. Plotting Cn for various lengths of polyalanine shows a gradual increase in the characteristic ratio as a function of length (Fig. 5). The relative difference between isotactic and syndiotactic chains is smaller, but consistent with the trends for two- and three-dimensional lattice chains. If we look at all structures in the ensemble from low to high energy, the syndiotactic chains still have larger Cn values than isotactic chains at a given length, but the difference is more pronounced (data not shown).

Figure 5.

Figure 5.

Open in a new tab

The characteristic ratio as a function of chain length for the ensemble of isotactic and syndiotactic structures where Evdw ≤ 0 kcal/mol. The monomer length, l, in Equation 1 is 3.8 Å as measured from Cα to Cα.

Discussion

Backbone stereochemistry and the folding landscape

An often used phrasing of the Levinthal paradox presents an abstract protein chain with 100 amino acids, and each residue has 10 possible backbone conformations (approximately three values each of ϕ and ψ). If these rotations are independent of each other in an unfolded state, the protein would have to search through 10100 conformations to find the native state—a hopeless proposition. Criticisms of these assumptions have shown that local excluded volume constraints significantly reduce the number of accessible states for short peptides, effectively “winnowing” the size of fold space for the protein down to a manageable size (Pappu et al. 2000; Fitzkee and Rose 2005). In this context, we have asked whether backbone stereochemistry can modulate the effectiveness of this winnowing process.

When comparing two randomly generated ensembles, one of isotactic, the other syndiotactic polyalanine chains, we find that many more syndiotactic chains are in sterically unhindered states. Since the choice of l or d alanine does not change the flexibility at the monomer level, this effect is due to through-space interactions between residues that are not adjacent in sequence. Differences in the characteristic ratio between isotactic and syndiotactic chains are only observed for lengths greater than three (Fig. 5). Chains of four amino acids can form one turn of an α-helix, and the largest conformational winnowing effects were found in the α-helical region (Pappu et al. 2000). Therefore, the low likelihood of syndiotactic sequences to form an α-helix increases the total number of accessible conformations for short peptides.

The α-helix also allows for backbone interatomic contacts between i, i+3, and i, i+4 positions in sequence. In the ensemble of isotactic polyalanine 6-mers, the lowest energy conformations are α-helices. In lllddd and its sequence stereoisomer, lowest energy conformations contained a pair of three-residue α-turns (Fig. 4). The lowest energy syndiotactic conformation consists of alternating βL and βR conformations, where through-space interactions are between i and i+5 positions in sequence. Extending this repeat would result in a gramicidin-like β-helix. However, when sampling longer syndiotactic sequences, we do not find longer repeats of βLβR. Instead, the lowest energy structures are β-ribbons (repeats of αLβR or αRβL) (Heitz et al. 1981). In the β-ribbon, the primary backbone interaction is a hydrogen bond between the i and i+3 positions. Both the β-helix and β-ribbon have fewer inter-residue contacts than the α-helix, which explains why isotactic sequences are enriched in low-energy structures relative to the various heterochiral sequences.

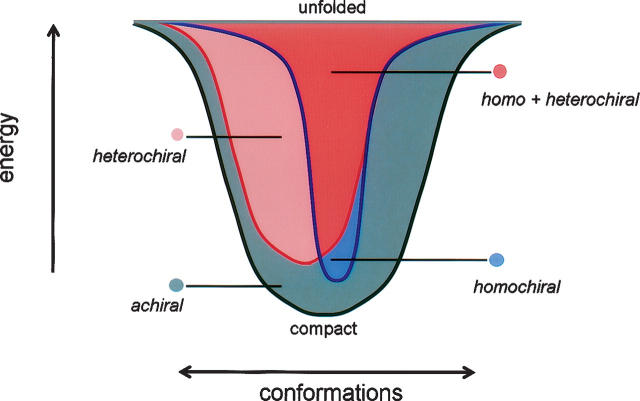
Thus, we find two advantages to protein homochirality. First, an isotactic polypeptide facilitates the formation of α-helices that significantly restrict local fold space. This lowers the number of accessible states to the folding protein, reducing the entropic cost of folding. Second, the ability to form α-helices provides more local inter-residue contacts, increasing the energetic stability of the folded state. A funnel representation of the energy landscape illustrates how stereochemistry influences protein folding (Fig. 6). Homochiral proteins have fewer competing states and access to lower energy native states—hence, the folding funnel is narrower and deeper than the equivalent landscape for a heterochiral protein. An achiral chain would have access to all conformations available to homochiral and heterochiral chains and possibly others.

Figure 6.

Figure 6.

Open in a new tab

Folding funnel representation of hypothetical energy landscapes for homochiral, heterochiral, and achiral chains. Depth along the y-axis corresponds to structural stability (energy), and width of the funnel along the x-axis relates to the number of conformations at a given energy (entropy).

In the late 50s, work in the lab of Linderstrøm-Lang suggested that syndiotactic polyalanine formed an α-helix (Berger and Linderstrøm-Lang 1957). Many other studies, both computational and experimental, have variously supported or contradicted this claim (Takahashi et al. 1969; Hesselink and Scheraga 1972; Colonna-Cesari et al. 1977; Heitz et al. 1981). It is now known that D-alanine in the αR conformation is destabilizing by ∼1 kcal/mol (Fairman et al. 1992; Hermans et al. 1992). However, another helical conformation, the 310 helix, characterized by i,i+3 hydrogen bonding, can accommodate both stereoisomers. This was shown in experiments by Karle and Balaram, where amino-isobutyric acid, which is disubstituted at the Cα position, was introduced into helical peptides, inducing formation of the 310-helix (Karle and Balaram 1990). An analysis of short left-handed helices in the protein database shows a propensity for natural amino acids to favor 310-L instead, of αL geometry (S. Annavarapu and V. Nanda, in prep.). Although short 310-helices are found in proteins, α-helices are more frequent and lower in energy by ∼1.6 kcal/mol per residue (Zhang and Hermans 1994). Thus, a syndiotactic chain would presumably be destabilized in either the 310 or α conformation.

The thermodynamic drive to form stable α-helices that fold quickly could explain why our protein alphabet is predominantly homochiral as was first suggested by Wald (1957). The inclusion of glycine as the only achiral member allows for some use of the right-hand side of Ramachandran space. However, if d-amino acids were part of our genetic complement, the ability to break helices through mutation might have been too costly. Therefore, the synthesis of heterochiral polypeptides is under tight biochemical control. Some, such as the microbial toxin tolaasin, make use of extended helical domains of opposite sense, which could fold independently (Jourdan et al. 2003). Gramicidin, which might be unlikely to form a β-helix due to the entropic costs of folding, is facilitated by the lipid environment. In the nonpolar region of the membrane, the strength of polar interactions are amplified, which conceivably would favor the β-helix over the β-ribbon, because the β-helix satisfies a larger percentage of backbone hydrogen bonds. Natural helical transmembrane proteins can tolerate several glycines in the middle of the α-helix, which would otherwise destabilize folding of a water-soluble protein for much the same reason (Chakrabartty et al. 1991; Lemmon et al. 1992).

This study only considers the effects of excluded volume, but others have suggested that forces such as electrostatics and solvation may also play key roles in stereochemical determinants of structure. Durani and colleagues have recently shown that electrostatic forces, particularly interactions between adjacent peptide dipoles, may play a key role in specifying different solvent sensitivity of isotactic and syndiotactic peptides (Ramakrishnan et al. 2006; Ranbhor et al. 2006). It was originally noted by Flory that poly-L-amino acids were stiffer than expected due to excluded volume effects, to the extent that the characteristic ratio was greater for isotactic than that for syndiotactic sequences (Flory 1969). This is the opposite of our simulation results, although measurements were not conducted on alanine, but on charged amino acids (Brant and Flory 1965; Miller et al. 1967). By not including electrostatics and hydrogen bonding, we are assuming conditions of a “good solvent.” It would be worthwhile to extend our analysis to include these and other intermolecular forces to see how ensemble properties are affected.

The crux of our argument relating chirality to folding rests on the observation that for small chains, backbone homochirality promotes formation of structures with lower contact order. Contact order is used to estimate the rate of folding by normalizing the average sequence separation between contacting residues to the chain length (Plaxco et al. 1998). In a hierarchical folding scenario, secondary structures with more local contacts will fold rapidly, facilitating tertiary assembly (Myers and Oas 2001; Gong et al. 2003). Our study does not address the contribution of chirality to nonlocal interactions that could also facilitate rapid, cooperative folding. A narrow folding landscape, such as the homochiral one we postulated, would require facilitation of both local and nonlocal interactions (Kaya and Chan 2003). This would be an interesting problem for further investigation. Another interesting question is one of sequence specificity and designability. Both our lattice and polyalanine models assume equivalent contact potentials between all residues. It would be interesting to determine whether structures faciliated by homochiral or heterochiral backbones can accomodate many sequences (i.e., have high designability), and additionally, whether the ability for a sequence to specify a unique fold is affected by backbone chirality.

Implications for heterochiral protein and foldamer design

One of the goals in studying the role of backbone stereochemistry in protein folding is to understand how heterochirality can be used in the de novo design of proteins. Our group is exploring computational methods for designing heterochiral proteins (Nanda and DeGrado 2004, 2006). A key design lesson that emerges from this study is the importance of negative design, i.e., the design of specificity as well as stability (DeGrado et al. 1999). Due to the increased local flexibility of the backbone, the existence of competing states nearby in energy becomes a more likely possibility. Ideal designs will not only maximize the stability of the target structure, but will optimize the energy gap between it and competing structures. For example, in the design of a gramicidin-like β-helix, we would want to pick sequences that fold stability into this conformation, but are not compatible with a β-ribbon. Our observations also indicate that reversals in chirality should be introduced judiciously. Where possible, domains of the same chirality should be at least three to four amino acids.

The similar behavior of rectangular lattice and polyalanine chains suggests that there may be general rules governing stereochemical determinants of folding. A study on both square and tetrahedral lattice chain models of side-chain flexibility show that chiral side chains reduce folding entropy over achiral side chains (Zhang et al. 2004). It should be noted that the behavior of our lattice simulations is dependent on the rules chosen. The interaction between adjacent monomers in sequence is governed by the chirality product, ρ. If instead, ρ ≡ –Xi · Xi+1, then observed behavior of isotactic and syndiotactic lattices would be reversed. As another example, a novel foldamer might only be described by rules two and three, meaning adjacent bond vectors are always orthogonal. In such a scenario, isotactic chains longer than eight by definition cannot satisfy the excluded volume constraint. The rules have been chosen based on chemical intuition from proteins, but testing of atomic models and real molecular designs in the laboratory are needed to determine whether these rules can be applied to other foldamers and biomolecules such as β-peptides and polynucleotides.

Materials and Methods

Modeling chirality in a rectangular lattice

In order to incorporate the property of chirality into a rectangular lattice, we define three vectors associated with each monomer in the chain: a bond vector A of length L, which points to the position of the next monomer, and two orthogonal unit vectors a and b, which specify the chirality of the monomer (Fig. 7A). The directions of these vectors for monomer i+1: A′,a′,b′, are determined by the existing values for monomer i and the product, ρ, of the chirality, X, of positions i and i+1. X is either +1 or −1, depending on the chirality of the position. The three rules for positioning the i+1 monomer are (Fig. 7B):

Figure 7.

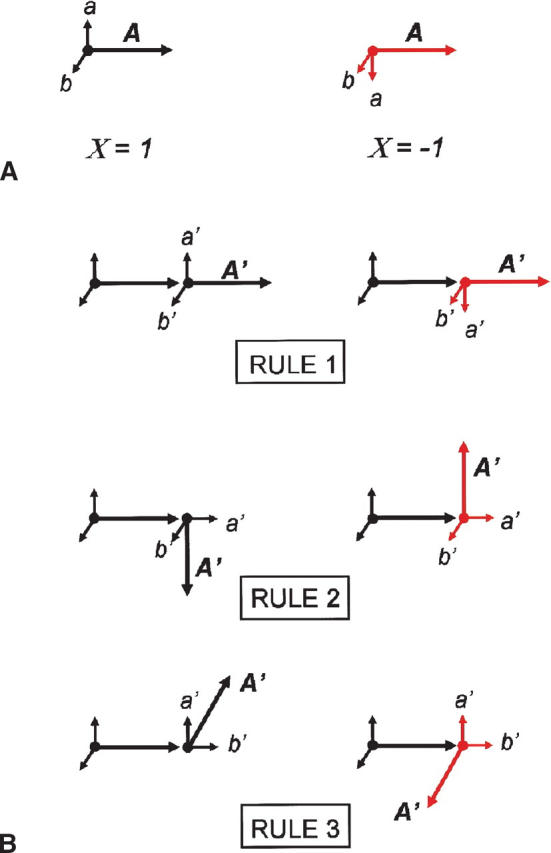
Figure 7.

Open in a new tab

(A) The chirality of a monomer is specified by the bond vector, A and two orthogonal components, a and b. A monomer of X = +1 is related to X = −1 by a mirror transformation. (B) Three rules for adding a monomer with bond vector A′ of either the same or inverse chirality (see Materials and Methods).

Rule 1: A′ = A; a′ = ρa; b′ = b

Rule 2: A′ = ρLa; a′ = L−1A; b′ = b

Rule 3: A′ = ρLb; a′ = a; b′ = L−1A

ρ = Xi · Xi+1; X = ±1.

Rule one corresponds to chain extension and an inversion in the Ab plane if ρ = −1. Rule two corresponds to a rotation in the Aa plane and Rule 3 to a rotation in the Ab plane. Rules two and three also result in an inversion in the ab plane if ρ = −1.

When confining a chain to a two-dimensional lattice, only rules one and two are used. Equivalently, one could also use rules one and three. For an achiral monomer, all directions are possible. Chains are unimolecular and obey the excluded volume constraint, such that two monomers cannot occupy the same lattice point simultaneously. Contacts are counted if two monomers are separated by exactly one lattice spacing and are not adjacent in sequence.

Modeling chirality in a polyalanine chain

Coordinates for all atoms in a fully extended (ϕ = 180°, ψ = 180°) polyalanine chain are generated using ideal bond lengths and angles from the AMBER 94 force field (Cornell et al. 1995). Side-chain methyl group hydrogens are fixed in the staggered conformation. A Monte Carlo conformational search is performed by randomly changing the backbone ϕ and ψ angles for each position in the chain. Allowed conformations for amino acids are chosen based on experimentally observed backbone angles and their relative frequencies in the PDB (Srinivasan and Rose 2002). Allowed angles for d-alanine are the inverse of those for l-alanine. Angles are allowed to vary by ±30.0° around the experimentally specified minima, with biased sampling of deviations closer to zero (θ = θmin ± 30 · a2, where a is a random number between 0 and 1). Energies for the entire chain are computed using a 12–6 Lennard-Jones potential and atom parameters from AMBER 94. Pairwise 1–2, 1–3, and 1–4 atomic interactions and those >8.0 Å apart are excluded from the energy computation. All-atom modeling and energetics calculations were carried out using the program protCAD, which has been previously applied to the modeling of heterochiral peptides (Nanda and Degrado 2004, 2006).

Footnotes

1

For the purposes of this article, isotactic and homochiral are used interchangeably and refer to a polymer where all monomers are the same stereoisomer. Syndiotactic specifically refers to sequential monomers of alternating chirality. Heterochiral designates any sequence containing more than one stereoisomer of the component monomer. Achiral refers to polymers where the monomer has no intrinsic chirality.

Reprint requests to: Vikas Nanda, Center for Advanced Biotechnology and Medicine, Department of Biochemistry, Robert Wood Johnson Medical School, UMDNJ, 679 Hoes Lane West, Piscataway, NJ 08854, USA; e-mail: nanda@cabm.rutgers.edu; fax: (732) 235-4850.

Article published online ahead of print. Article and publication date are at http://www.proteinscience.org/cgi/doi/10.1110/ps.072867007.

References

  1. Anil B., Song, B., Tang, Y., and Raleigh, D.P. 2004. Exploiting the right side of the Ramachandran plot: Substitution of glycines by D-alanine can significantly increase protein stability. J. Am. Chem. Soc. 126: 13194–13195. [DOI] [PubMed] [Google Scholar]
  2. Aravinda S., Shamala, N., Roy, R.S., and Balaram, P. 2003. Non-protein amino acids in peptide design. Proc. Indian Acad. Sci. Chem Sci. 115: 373–400. [Google Scholar]
  3. Bang D., Gribenko, A.V., Tereshko, V., Kossiakoff, A.A., Kent, S.B., and Makhatadze, G.I. 2006. Dissecting the energetics of protein α-helix C-cap termination through chemical protein synthesis. Nat. Chem. Biol. 2: 139–143. [DOI] [PubMed] [Google Scholar]
  4. Berger A. and Linderstrøm-Lang, K. 1957. Deuterium exchange of poly-DL-alanine in aqueous solution. Arch. Biochem. Biophys. 69: 106–118. [DOI] [PubMed] [Google Scholar]
  5. Brant D.A. and Flory, P.J. 1965. The configuration of random polypeptide chains. J. Am. Chem. Soc. 87: 2788–2791. [Google Scholar]
  6. Chakrabartty A., Schellman, J.A., and Baldwin, R.L. 1991. Large differences in the helix propensities of alanine and glycine. Nature 351: 586–588. [DOI] [PubMed] [Google Scholar]
  7. Chan H.S. and Dill, K.A. 1991. Polymer principles in protein structure and stability. Annu. Rev. Biophys. Biophys. Chem. 20: 447–490. [DOI] [PubMed] [Google Scholar]
  8. Cheng R.P., Gellman, S.H., and DeGrado, W.F. 2001. β-Peptides: From structure to function. Chem. Rev. 101: 3219–3232. [DOI] [PubMed] [Google Scholar]
  9. Colonna-Cesari F., Premilat, S., Heitz, F., Spach, G., and Lotz, B. 1977. Helical structures of poly(D-L-peptides). A conformational energy analysis. Macromolecules 10: 1284–1288. [DOI] [PubMed] [Google Scholar]
  10. Cornell W.D., Cieplak, P., Bayly, C.I., Gould, I.R., Merz, K.M., Ferguson, D.M., Spellmeyer, D.C., Fox, T., Caldwell, J.W., and Kollman, P.A. 1995. A 2nd generation force-field for the simulation of proteins, nucleic-acids, and organic-molecules. J. Am. Chem. Soc. 117: 5179–5197. [Google Scholar]
  11. DeGrado W.F., Summa, C.M., Pavone, V., Nastri, F., and Lombardi, A. 1999. De novo design and structural characterization of proteins and metalloproteins. Annu. Rev. Biochem. 68: 779–819. [DOI] [PubMed] [Google Scholar]
  12. Fairman R., Anthony-Cahill, S.J., and DeGrado, W.F. 1992. The helix-forming propensity of D-alanine in a right-handed α-helix. J. Am. Chem. Soc. 114: 5458–5459. [Google Scholar]
  13. Fitzkee N.C. and Rose, G.D. 2005. Sterics and solvation winnow accessible conformational space for unfolded proteins. J. Mol. Biol. 353: 873–887. [DOI] [PubMed] [Google Scholar]
  14. Flory P.J. 1969. Statistical mechanics of chain molecules. Interscience, Stanford, CA.
  15. Ghadiri M.R., Granja, J.R., Milligan, R.A., McRee, D.E., and Khazanovich, N. 1993. Self-assembling organic nanotubes based on a cyclic peptide architecture. Nature 366: 324–327. [DOI] [PubMed] [Google Scholar]
  16. Gong H., Isom, D.G., Srinivasan, R., and Rose, G.D. 2003. Local secondary structure content predicts folding rates for simple, two-state proteins. J. Mol. Biol. 327: 1149–1154. [DOI] [PubMed] [Google Scholar]
  17. Guichard G., Benkirane, N., Zeder-Lutz, G., van Regenmortel, M.H., Briand, J.P., and Muller, S. 1994. Antigenic mimicry of natural L-peptides with retro-inverso-peptidomimetics. Proc. Natl. Acad. Sci. 91: 9765–9769. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Heitz F., Detriche, G., Vovelle, F., and Spach, G. 1981. Sheet structures in alternating poly(D,L-peptides). Macromolecules 14: 47–50. [Google Scholar]
  19. Hermans J., Anderson, A.G., and Yun, R.H. 1992. Differential helix propensity of small apolar side chains studied by molecular dynamics simulations. Biochemistry 31: 5646–5653. [DOI] [PubMed] [Google Scholar]
  20. Hesselink F.T. and Scheraga, H.A. 1972. On the possible existence of α-helical structures of regular-sequence D,L copolymers of amino acids. Conformational energy calculations. Macromolecules 5: 455–463. [Google Scholar]
  21. Hiley B.J. and Sykes, M.F. 1961. Probability of initial ring closure in the restricted random-walk model of a macromolecule. J. Chem. Phys. 34: 1531–1537. [Google Scholar]
  22. Honig B. and Cohen, F.E. 1996. Adding backbone to protein folding: Why proteins are polypeptides. Fold. Des. 1: R17–R20. [DOI] [PubMed] [Google Scholar]
  23. Hunt N.G., Gregoret, L.M., and Cohen, F.E. 1994. The origins of protein secondary structure. Effects of packing density and hydrogen bonding studied by a fast conformational search. J. Mol. Biol. 241: 214–225. [DOI] [PubMed] [Google Scholar]
  24. Irback A. and Troein, C. 2002. Enumerating designing sequences in the HP model. J. Biol. Phys. 28: 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Jourdan F., Lazzaroni, S., Mendez, B.L., Cantore, P.L., Julio, M., Amodeo, P., Iacobellis, N.S., Evidente, A., and Motta, A. 2003. A left-handed α-helix containing both L- and D-amino acids: The solution structure of the antimicrobial lipodepsipeptide tolaasin. Protein Struct. Funct. Genet. 52: 534–543. [DOI] [PubMed] [Google Scholar]
  26. Joyce G.F. 2002. The antiquity of RNA-based evolution. Nature 418: 214–221. [DOI] [PubMed] [Google Scholar]
  27. Joyce G.F., Visser, G.M., van Boeckel, C.A.A., van Boom, J.H., Orgel, L.E., and van Westrenen, J. 1984. Chiral selection in poly(C)-directed synthesis of oligo(G). Nature 310: 602–604. [DOI] [PubMed] [Google Scholar]
  28. Joyce G.F., Schwartz, A.W., Miller, S.L., and Orgel, L.E. 1987. The case for an ancestral genetic system involving simple analogues of the nucleotides. Proc. Natl. Acad. Sci. 84: 4398–4402. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Karle I.L. and Balaram, P. 1990. Structural characteristics of α-helical peptide molecules containing aib residues. Biochemistry 29: 6747–6756. [DOI] [PubMed] [Google Scholar]
  30. Kaya H. and Chan, H.S. 2003. Contact order dependent protein folding rates: Kinetic consequences of a cooperative interplay between favorable nonlocal interactions and local conformational preferences. Proteins 52: 524–533. [DOI] [PubMed] [Google Scholar]
  31. Lemmon M.A., Flanagan, J.M., Treutlein, H.R., Zhang, J., and Engelman, D.M. 1992. Sequence specificity in the dimerization of transmembrane α-helices. Biochemistry 31: 12719–12725. [DOI] [PubMed] [Google Scholar]
  32. Maity H., Lim, W.K., Rumbley, J.N., and Englander, S.W. 2003. Protein hydrogen exchange mechanism: Local fluctuations. Protein Sci. 12: 153–160. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Martinek T.A., Mandity, I.M., Fulop, L., Toth, G.K., Vass, E., Hollosi, M., Forro, E., and Fulop, F. 2006. Effects of the alternating backbone configuration on the secondary structure and self-assembly of β-peptides. J. Am. Chem. Soc. 128: 13539–13544. [DOI] [PubMed] [Google Scholar]
  34. Miller W.G., Brant, D.A., and Flory, P.J. 1967. Random-coil configurations of polypeptide copolymers. J. Mol. Biol. 23: 67–80. [Google Scholar]
  35. Milton R.C., Milton, S.C., and Kent, S.B. 1992. Total chemical synthesis of a D-enzyme: The enantiomers of HIV-1 protease show reciprocal chiral substrate specificity [corrected]. Science 256: 1445–1448. [DOI] [PubMed] [Google Scholar]
  36. Myers J.K. and Oas, T.G. 2001. Preorganized secondary structure as an important determinant of fast protein folding. Nat. Struct. Biol. 8: 552–558. [DOI] [PubMed] [Google Scholar]
  37. Nanda V. and DeGrado, W.F. 2004. Simulated evolution of emergent chiral structures in polyalanine. J. Am. Chem. Soc. 126: 14459–14467. [DOI] [PubMed] [Google Scholar]
  38. Nanda V. and DeGrado, W.F. 2006. Computational design of heterochiral peptides against a helical target. J. Am. Chem. Soc. 128: 809–816. [DOI] [PubMed] [Google Scholar]
  39. O'Neil K.T. and DeGrado, W.F. 1990. A thermodynamic scale for the helix-forming tendencies of the commonly occurring amino acids. Science 250: 646–651. [DOI] [PubMed] [Google Scholar]
  40. Pappu R.V., Srinivasan, R., and Rose, G.D. 2000. The Flory isolated-pair hypothesis is not valid for polypeptide chains: Implications for protein folding. Proc. Natl. Acad. Sci. 97: 12565–12570. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Plaxco K.W., Simons, K.T., and Baker, D. 1998. Contact order, transition state placement and the refolding rates of single-domain proteins. J. Mol. Biol. 277: 985–994. [DOI] [PubMed] [Google Scholar]
  42. Ramakrishnan V., Ranbhor, R., Kumar, A., and Durani, S. 2006. The link between sequence and conformation in protein structures appears to be stereochemically established. J. Phys. Chem. B 110: 9314–9323. [DOI] [PubMed] [Google Scholar]
  43. Ranbhor R., Ramakrishnan, V., Kumar, A., and Durani, S. 2006. The interplay of sequence and stereochemistry in defining conformation in proteins and polypeptides. Biopolymers 83: 537–545. [DOI] [PubMed] [Google Scholar]
  44. Schneider J.P. and DeGrado, W.F. 1998. The design of efficient α-helical C-capping auxiliaries. J. Am. Chem. Soc. 120: 2764–2767. [Google Scholar]
  45. Srinivasan R. and Rose, G.D. 2002. Ab initio prediction of protein structure using LINUS. Proteins 47: 489–495. [DOI] [PubMed] [Google Scholar]
  46. Takahashi A., Mandelkern, L., and Glick, R.E. 1969. Solution, phase coexistence, and related proton nuclear magnetic resonance studies on poly-L- and poly-DL-alanine in helix–random-coil interconverting media. Biochemistry 8: 1673–1684. [DOI] [PubMed] [Google Scholar]
  47. Urry D.W., Goodall, M.C., Glickson, J.D., and Mayers, D.F. 1971. The gramicidin A transmembrane channel: Characteristics of head-to-head dimerized Pi(L,D) helices. Proc. Natl. Acad. Sci. 68: 1907–1911. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Veatch W.R., Fossel, E.T., and Blout, E.R. 1974. The conformation of gramicidin-A. Biochemistry 13: 5249–5256. [DOI] [PubMed] [Google Scholar]
  49. Wald G. 1957. Origin of optical activity. Ann. N. Y. Acad. Sci. 69: 352–368. [DOI] [PubMed] [Google Scholar]
  50. Yee D.P., Chan, H.S., Havel, T.F., and Dill, K.A. 1994. Does compactness induce secondary structure in proteins? A study of poly-alanine chains computed by distance geometry. J. Mol. Biol. 241: 557–573. [DOI] [PubMed] [Google Scholar]
  51. Zhang L. and Hermans, J. 1994. 3(10)-Helix versus α-helix - a molecular-dynamics study of conformational preferences of aib and alanine. J. Am. Chem. Soc. 116: 11915–11921. [Google Scholar]
  52. Zhang J.F., Chen, Y., Chen, R., and Liang, J. 2004. Importance of chirality and reduced flexibility of protein side chains: A study with square and tetrahedral lattice models. J. Chem. Phys. 121: 592–603. [DOI] [PubMed] [Google Scholar]

Articles from Protein Science : A Publication of the Protein Society are provided here courtesy of The Protein Society

RESOURCES