Skip to main content
PMC home page
Genome Research logoLink to Genome Research
letter
. 2008 Feb;18(2):206–213. doi: 10.1101/gr.6888208

Quantitative systems-level determinants of human genes targeted by successful drugs

Lixia Yao 1, Andrey Rzhetsky 1,2,3
PMCID: PMC2203618  PMID: 18083776

Abstract

What makes a successful drug target? A target molecule with an appropriate (druggable) tertiary structure is a necessary but not the sufficient condition for success. Here we analyzed specific properties of human genes and proteins targeted by 919 FDA-approved drugs and identified several quantitative measures that distinguish them from other genes and proteins at a highly significant level. Compared to an average gene and its encoded protein(s), successful drug targets are more highly connected (but far from being the most highly connected), have higher betweenness values, lower entropies of tissue expression, and lower ratios of nonsynonymous to synonymous single-nucleotide polymorphisms. Furthermore, we have identified human tissues that are significantly over- or undertargeted relative to the full spectrum of genes that are active in each tissue. Our study provides quantitative guidelines that could aid in the computational screening of new drug targets in human cells.

Every successful drug, such as Gleevec (counteracting chronic myeloid leukemia), Prozac (an antidepressant), or Viagra (an antidote to erectile dysfunction), affects the well-being of numerous people and brings substantial financial rewards to its inventors and manufacturers. Unfortunately, every highly visible success resides on an iceberg of (invisible) failures. The majority of experimental drugs remain obscure because they never reach consumers and fail to attract the attention of the news media. Some drugs, such as Merck’s Vioxx (a treatment for acute pain in arthritis), do reach consumers, only to be withdrawn later after unanticipated side effects are revealed (Vioxx appears to occasionally trigger a heart attack or stroke).

The development of a new drug is a fusion of art and science: typically it involves finding both a drug target (such as a protein) and a molecule that binds the target as selectively as possible while triggering a desirable physiological change. This search is typically guided by (often scarce) evidence for the disease mechanism, analysis of the chemical structures of drug candidates and their targets, and animal and human trials of promising molecules (Drews 2000, 2003, 2006; Egner et al. 2005). This procedure is staggeringly expensive. Although precise numbers are not available, estimates of the cost of developing a new drug range between 800 and 1200 million dollars (Adams and Brantner 2006). Any technological breakthrough that would reduce the probability of new drug failure and/or the development cycle length would be a major economic and healthcare boon.

To even be considered by a pharmaceutical company, a drug must produce a desirable change in a human physiological state (Zheng et al. 2006). However, we can (presumably) attain comparable physiological changes by modulating different molecules within a complex pathway. What makes some genes better targets than others? Here we suggest, in addition to the traditional drug target analysis focusing on putative links between disease and specific genes, looking at the common sequence-, tissue-, and pathway-level properties of the targets of successful drugs (narrowly defined here as those approved by the U.S. Food and Drug Administration, FDA).

We analyze the intended targets of 919 FDA-approved drugs that interact with human genes and proteins (Wishart et al. 2006). Specifically, we focus on the targets’ topological niches within the molecular network, the properties of their single-nucleotide variation, the tissue-specificity of their expression, and their overlap with essential and disease-predisposing genes.

Results

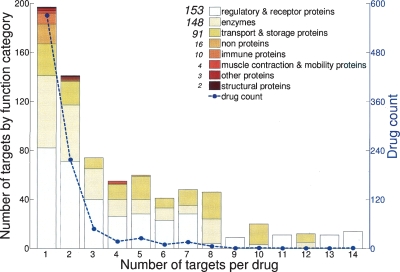
We first looked at the relationships between drugs and their targets, and the functional properties of the successful drug targets (Fig. 1). As would be expected, successful drugs are very specific to their targets: most of them (62%) have only one specific target, although many have two or more (Fig. 1, blue curve). Curiously, most of these multitarget drugs are designed to modulate the central nervous system. The majority (36%) of successful drug targets are regulatory and receptor proteins, such as G-protein-coupled receptors, or GPCRs (Fig. 1, bar plot). Slightly less frequently, successful drug targets are enzymes (35%) or transport and storage proteins (21%). A minority of drug targets are non-proteins (4%, including individual amino acids, DNA, and oligosaccharides), immune proteins (2%), and motility proteins (1%). The remaining 1% comprises other classes of the commonly used chemical taxonomy (e.g., see Chapter 4.3 in Boyer 2006), such as structural proteins.

Figure 1.

Figure 1.

Open in a new tab

Distribution of the number of human gene targets per successful drug. The plot is superimposed on a family classification of drug targets.

We treated the drug targets as nodes within a large undirected graph (molecular-interaction network) (see Methods; Table 1) and considered their topological properties. Specifically, for all drug target nodes, we examined connectivity, betweenness, and the connectedness of their immediate neighbors within the network (clustering). We will discuss these properties one by one, defining each property first. To validate the robustness of our conclusions, we performed exactly the same analysis using five independently produced data sets (see Methods; Table 1).

Table 1.

Comparison of different human molecular interaction data sets

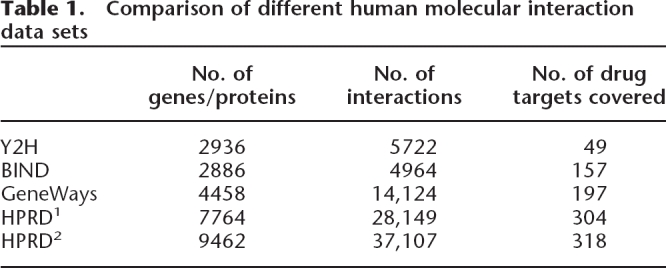
graphic file with name 206tbl1.jpg

Open in a new tab

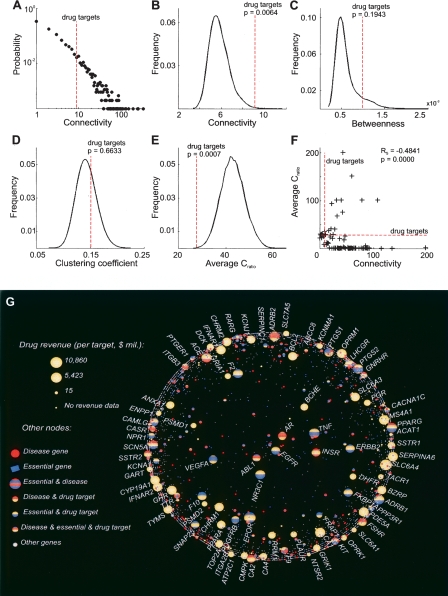
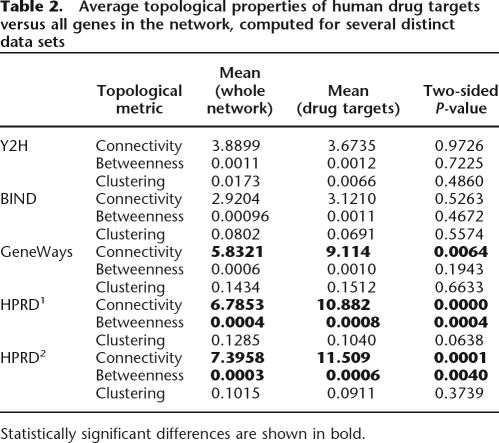
The connectivity of a node within a graph is simply the total number of incoming and outgoing arcs (direct molecular interactions, in our case). As has been previously established, the connectivity distributions for real molecular networks are so-called heavy-tail distributions resembling Zipf’s (Pareto’s or power-law) distribution (Fig. 2A; Barabasi and Bonabeau 2003). The successful drug targets occupy a rather narrow niche within this distribution: their connectivity is significantly higher than that of an average node within the network (in GeneWays it is ∼9.1, P-value = 0.0064 [Fig. 2A,B,F]; in HPRD1 and HPRD2, it is 10.9 and 11.5, P-values = 0 and 0.0001, respectively; the same comparison performed using the smaller Y2H and BIND networks revealed no significant difference [see Table 2]). However, the average connectivity of drug targets is relatively small compared to the maximum connectivity observed in the network (9.1 vs. a maximum of 346 in GeneWays). The most highly connected high-revenue drug targets in the GeneWays network (ABL1, androgen receptor [AR], BCHE, EGFR, INSR, NR3C1, TNF, and VEGFA; see Fig. 2G) are targeted by drugs intended to provide relief for the most life-threatening phenotypes, such as cancer and autoimmune disorders. The successful drugs targeting these highly connected genes and proteins are associated with terrible side effects (think of chemotherapy patients) that are tolerable only in life-or-death situations.

Figure 2.

Figure 2.

Open in a new tab

Molecular network and population-variability properties of targets of FDA-approved drugs. (A) Connectivity distribution for the entire molecular network. (B) Targets of the successful drugs are significantly more connected than an average gene in the network, but are not the most highly connected genes in the network. (C) Drug targets tend to have higher than average betweenness values. (D) The successful drug targets are not statistically different from the rest of the genes in terms of their clustering coefficients. (E,F) Analysis of the ratio (Cratio) of the number of nonsynonymous to synonymous single-nucleotide polymorphisms (SNPs). (E) Successful drug targets have significantly smaller Cratio than human genes on average. (F) The value of Cratio tends to correlate negatively with the gene’s connectivity in the network. (G) Connectivities of genes are superimposed with drug revenue data: the high-revenue drugs tend to target genes and proteins of low connectivity. The position of a gene is determined by its network connectivity. The closer a gene is to the center, the higher its connectivity within the GeneWays molecular network. The size of a gene node is determined by the revenue of the corresponding drug. The color of a gene node is determined by its membership in the three sets of genes: (yellow) drug targets, (blue) essential genes, and (red) disease genes. These three sets of genes overlap significantly.

Table 2.

Average topological properties of human drug targets versus all genes in the network, computed for several distinct data sets

graphic file with name 206tbl2.jpg

Open in a new tab

Statistically significant differences are shown in bold.

The betweenness of a network node is defined as the number of times this node appears in the shortest path between two other network nodes, summed over all node pairs in the network and divided by the total number of node pairs (e.g., Noh 2003). The clustering coefficient of a network node is the ratio of the actual number of direct connections between the immediate neighbors of the node to the maximum possible number of such direct arcs between its neighbors (e.g., Holme and Kim 2002). The clustering coefficient is zero if a node’s neighbors do not interact directly (e.g., a professor who interacts with many graduate students, but whose students avoid talking to one another). The highest clustering coefficient is attained in a complete graph where every node is connected to every other node. The betweenness values of the drug targets in the GeneWays, BIND, and Y2H networks are not significantly different from those of the rest of genes within the network, although the drug targets in the GeneWays network tend to have slightly higher betweenness values than average (P-value = 0.1943; Fig. 2C). The increased average betweenness of drug targets is most obvious in the HPRD1 and HPRD2 networks (P-values = 0.0004 and 0.004, respectively), suggesting that successful drug targets tend to bridge two or more clusters of relatively closely interacting molecules. The clustering coefficients of drug targets are similar to those of the rest of the network nodes in all five data sets (see Table 2; Fig. 2D).

We next asked if proteins that are successful drug targets are less polymorphic (considering only human, intraspecies variation) than human genes on average. To answer this question, we used a large set (16,462 genes) of known human single-nucleotide polymorphisms (SNPs) available at dbSNP (Sherry et al. 2001). To reduce any effects of SNP sampling bias (some genes enjoy more attention on the part of the scientific community than others), instead of studying the absolute number of reported SNPs for each gene, we used the ratio (Cratio) of nonsynonymous to synonymous SNPs (with an expected value of 1 for a perfectly neutral mode of SNP accumulation). The assumption underlying this analysis is that sampling bias for a gene affects synonymous and nonsynonymous SNPs equally.

Our analysis indicates (Fig. 2E,F) that Cratio for successful drug targets is significantly smaller than that for an average human gene (P-value = 0.0007). This result suggests that successful drug targets tend to be less nonsynonymously polymorphic at the human population level than are human genes on average. Furthermore, Cratio is significantly negatively correlated with gene connectivity (Spearman rank correlation coefficient −0.4841, P-value = 0.0000), consistent with the observation that more highly conserved proteins tend to have higher connectivities (Fraser et al. 2002). Another line of evidence shows that highly expressed genes tend to evolve more slowly than those whose expression is low (Drummond et al. 2005). Furthermore, some experimental techniques, such as yeast two-hybrid protein–protein interaction screening, may detect interactions of highly expressed proteins more readily (Bloom and Adami 2003). Hence, relationships between gene expression level, sequence conservation, and connectivity may involve data biases and should be interpreted with caution.

We interpret the results of our SNP analysis as follows: a drug designed to target a protein that is polymorphic among humans may fail for a significant percentage of individuals, because of the lack of a specific interaction between the drug and the protein. Even though pharmaceutical companies are not typically taking into account the SNP properties of prospective drug targets (Johnson and Lima 2003), the successful drugs appear to be those that target proteins that vary less at the population level.

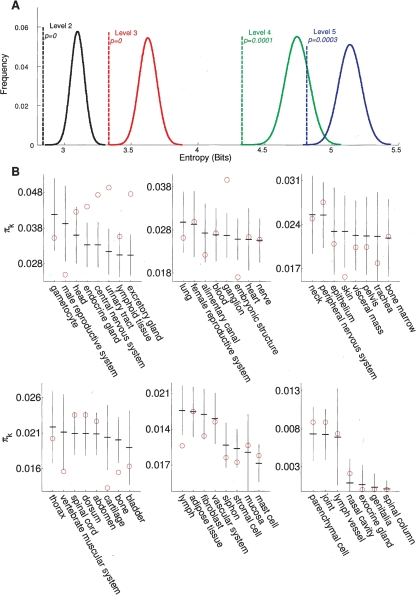
Yet another aspect of the biology of successful drug targets concerns the tissue-specificity of their expression. Chemists involved in drug development know that good drug targets are tissue-specific. But what is the right level of specificity? Typically, this question is answered through trial and error. Herein, we propose a method to quantify this specificity: given a distribution that describes the expression of a target gene over a set of tissues (where the overall expression of the gene is divided over all tissues in proportion to the observed expression levels, so that the total mass of probability over all tissues sums to 1), we use Claude E. Shannon’s method of entropy measurement (Shannon and Weaver 1949) to gauge the tissue-specificity of expression of each drug target. The lowest entropy (highest specificity) would be observed for a hypothetical gene that is expressed in only one tissue, while the highest entropy (lowest specificity) would be observed for a ubiquitously expressed gene. Using the Brenda Tissue Ontology (Schomburg et al. 2004; see Methods), we computed the expression entropy of various drug targets. As a reference, we computed an analogous distribution for randomly sampled human genes (to simulate the null model of expression-independent sampling of genes). Our results show (Fig. 3A) that the expression entropy of successful drug targets is significantly smaller than that of randomly sampled genes, and that the drug target-expression entropy is smaller for the higher (coarser) levels of the ontology.

Figure 3.

Figure 3.

Open in a new tab

Expression patterns of genes targeted by successful drugs. (A) Distribution of Shannon entropy of gene expression for randomly sampled genes and for drug targets; the successful drug targets have significantly lower entropies of expression (higher tissue-specificity) at all four levels. See Methods for details on the tissue ontology levels. (B) Comparison of the expected proportion of drug targets per tissue under unbiased target selection conditions—(vertical solid lines) 95% confidence intervals; (dashes on the vertical lines) means—with (open circles) the actual proportion of successful drug targets per tissue. The plot indicates that there are tissues that are significantly over- and undertargeted.

We next considered another tissue-specificity metric: the nonrandomness of tissue coverage by drug targets (with respect to tissue-specific gene expression levels). For each tissue, we compute a statistic that represents the probability of randomly picking a drug target that is expressed in that tissue (the probability sums to 1 over all tissues; see Methods for details). We then compute a background distribution for this statistic under the assumption that the same number of drug targets is selected randomly out of the pool of all genes. This exercise can direct us to tissues that are significantly “overtargeted” or “undertargeted” (assuming a uniform distribution of efforts and resources among tissues and related maladies). This analysis can be useful in highlighting research opportunities (for undertargeted tissues) and footprints of fads in the pharmaceutical industry (for overtargeted tissues, see Fig. 3B).

Our analysis indicates that among 47 tissues (Level 3 of the Brenda Tissue Ontology), five are significantly overtargeted (endocrine glands, central nervous system, urinary tract, excretory glands, and ganglia), while six are significantly undertargeted (male reproductive system, embryonic structures, skin, cartilage, bone, and lymph; see Fig. 3B). It is likely that some of the tissues (e.g., embryonic) have been deliberately undertargeted because of the potential for dangerous side effects.

Furthermore, we investigated whether a phenotypic classification of genes, such as disease-predisposition status and essentiality, can help us to predict the odds of a gene being successful as a drug target. The term disease gene is commonly used to indicate genes that occasionally harbor germline genetic variation causing a disease phenotype. In this study, we used a list of genes predominantly linked to phenotypes with Mendelian inheritance (Jimenez-Sanchez et al. 2001; see Methods). The essential genes are usually defined through gene knockout experiments in model organisms: if the organism fails to develop and survive after deletion of a gene, the gene is called essential. We approximate the set of human essential genes by the set of human orthologs of essential genes experimentally identified in the mouse (see Methods).

We observed that the targets of successful drugs are significantly over-represented within the sets of disease and essential genes in the GeneWays network (P-values = 3.07 × 10−9 and 0.0025, respectively). Moreover, the three sets (drug targets and disease and essential genes) share a significant three-way overlap (P-value is effectively 0; Fig. 2G).

We conjectured that the status of overlap of a drug target with disease and/or essential genes might be a powerful indicator of side effects of the new drug. When a drug target is also an essential gene, the corresponding drug is likely to threaten the fetus. For example, TNF (tumor necrosis factor α) is targeted by thalidomide, a drug that became infamous for the side effects of its use in the 1950s and 1960s. It was originally prescribed as a sedative and hypnotic treatment for pregnant women. However, even a single tablet ingested by a pregnant woman between the 20th and 36th day after conception almost certainly caused severe deformities in the fetus, with an estimated 10,000 infants affected worldwide. Nevertheless, thalidomide is still the leading treatment for leprosy and multiple myeloma in adults.

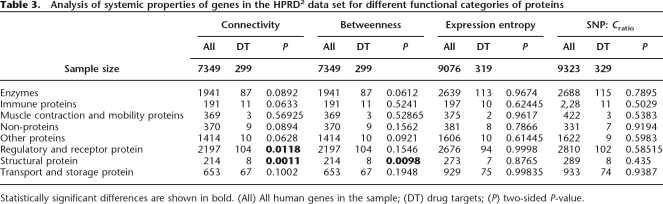
An interesting question is whether the properties of the drug target genes are still distinguishable from the rest of the network when they are compared with genes from similar functional categories. To address this question, we repeated our analyses, dividing the network nodes into eight functional groups (see Table 3). This division into smaller parts inevitably reduced the discriminative power of our test. Nevertheless, for a subset of large-scale properties, such as connectivity and betweenness (see Table 3), drug target genes are still significantly different from the rest of the genes, especially those encoding structural, regulatory, and receptor proteins. We note that, to produce Figure 1A, we manually annotated drug targets by their functional categories. Since we could not easily scale such manual analysis to annotate the entire human network, we used an existing classification of human genes (Thomas et al. 2003), slightly adapted for our purposes (see Supplemental material for details on the mapping of PANTHER categories to our eight functional groups).

Table 3.

Analysis of systemic properties of genes in the HPRD2 data set for different functional categories of proteins

graphic file with name 206tbl3.jpg

Open in a new tab

Statistically significant differences are shown in bold. (All) All human genes in the sample; (DT) drug targets; (P) two-sided P-value.

To make our analysis more relevant to the practice of drug discovery, we experimented with building predictive models that take advantage of drug targets’ systemic properties. Since a method for building the best possible predictor of successful drug targets deserves a study of its own, here we applied only four standard machine-learning approaches: naive Bayesian classifier, logistic regression, and radial basis function (RBF) network and Bayesian networks (see Methods; Fig. 4; Table 4). Our goal was to prove that our classification features (systemic properties of genes and proteins) are informative and practically useful. However, we have little doubt that one could find additional features and more sophisticated algorithms that would make the prediction even better.

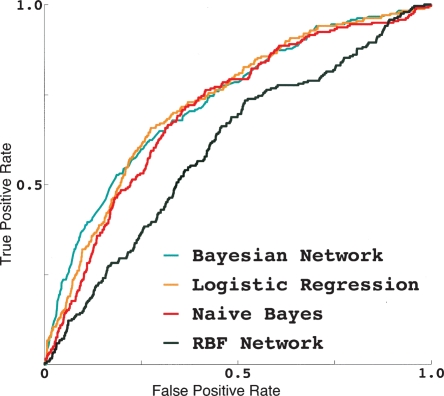
Figure 4.

Figure 4.

Open in a new tab

Receiver operating characteristic (ROC) curves for the four classification algorithms that we used in this study. The shape of each curve indicates the quality of the corresponding method. The closer an ROC curve is to the diagonal of the plot, the worse is the corresponding method. A hypothetical perfect method would have an ROC curve that is a constant function with true positive value 1 and false positive value 0. All four methods that we tested performed significantly better than baseline (ROC score of 0.5, corresponding to a random-guess method) (see Table 4). The logistic regression performed best.

Table 4.

ROC scores (mean ± standard deviation) for the four algorithms used in this study

graphic file with name 206tbl4.jpg

Open in a new tab

The comparison of the performance of the four classifiers in distinguishing successful drug targets from the rest of the human genome is summarized in Table 4. Virtually any real-life classifier makes false-positive and false-negative errors. Given just two disjoint classes of objects, such as successful drug targets (which we label “1”) versus other human genes (which we label “0”), a false-positive error consists of classifying an object that should be labeled 0 into class 1, while a false-negative error consists of labeling with 0 an object that would be correctly labeled 1. True positives and true negatives are correctly classified 1- and 0-objects, respectively. Every classifier can be adjusted in numerous ways to favor false positives over false negatives (or the other way around). Therefore, to compare different classifiers in a meaningful way, it is customary to use a so-called receiver operating characteristic (ROC) score (also known as the area under the ROC curve). The ROC score measures the overall performance of a classifier integrated over the whole range of false-positive and false-negative error rates (Hanley and McNeil 1982). A completely useless (random) classifier has an ROC score of 0.5, while a perfect classifier has a score of 1. (It is possible to build a classifier that has an ROC score of <0.5—it can be immediately improved by flipping the prediction labels.)

All of our four classifiers have ROC scores significantly higher than 0.5 (see Figure 4 and Table 4). (We measured the standard errors of ROC scores using 10-fold cross-validation experiments, where 90% of the data were used for training and 10% for testing.) Therefore, the systemic properties of genes and proteins are, indeed, practically useful for narrowing the list of prospective drug targets.

Discussion

The selection of a prospective drug target is a complicated balance of many considerations. We found that genes associated with successful FDA-approved drugs have several properties at the network, sequence, and tissue-expression levels that significantly distinguish them from other human genes. Specifically, successful drug targets tend to be noticeably better connected (within a molecular network) than the average gene, yet not extremely highly connected. They tend to have higher-than-average betweenness values, and significantly lower-than-average tissue-expression entropies and instances of nonsynonymous SNPs. Finally, the successful human-specific drug targets significantly overlap with essential and disease genes.

Although the drug-target-selection guidelines that we suggest here cannot replace expensive experiments, they can help pharmaceutical researchers narrow the prospective set of drug targets at the earliest stage of a drug development project. Specifically, when the pharmaceutical company must decide which target to pursue among pathologic pathways that are not fully understood, connectivity, betweenness, Cratio, and entropy might be useful quantitative estimates of each prospective target’s expected success rate.

Methods

Data

Our GeneWays molecular-interaction network includes 14,124 direct molecular interactions among 4458 unique human genes (Rzhetsky et al. 2004; I. Iossifov, unpubl.), of which 427 genes are each targeted by at least one of 919 drugs. Our Y2H data set was derived from two yeast two-hybrid studies, one by Stelzl et al. (2005) (1693 genes, 3120 interactions), and one by Rual et al. (2005) (1549 genes, 2611 interactions). To improve the statistical power of our analysis, we combined these sets into a joint Y2H network. Our Bind data set is a subset of the BIND database (Alfarano et al. 2005) that is restricted to low-throughput protein–protein and protein–DNA interactions (January 2006 version). The HPRD1 and HPRD2 data are from the Human Protein Reference Database (Peri et al. 2004) (Release_7_09012007, in binary protein–protein interaction format). In HPRD1, only data from two types of experiments (in vivo and in vitro) are used, while in HPRD2, data from all types of experiments (in vivo, in vitro, and yeast two hybrid) are used.

To analyze the tissue distribution of the drug targets’ expression, we use multitissue gene-expression signatures of about 12,700 human genes obtained from the TissueDistributionDBs (S. Jonnakuty, A. Hotz-Wogenblatt, K. Glatting, and S. Suhai; TissueDistributionDBs: A repository of organism-specific tissue distribution profiles. http://genome.dkfz-heidelberg.de/menu/tissue_db/).

Our disease gene set is derived from a large compendium of genes harboring known germline disease mutations (Jimenez-Sanchez et al. 2001). The original set contains 908 disease genes, of which 445 can be mapped to the GeneWays network. Our essential gene set contains human orthologs of mouse genes that were experimentally shown to result in lethal phenotypes when knocked out (Blake et al. 2003), of which 798 have been mapped to the GeneWays human gene network. The drug revenue data are borrowed from a study by Zambrowicz and Sands (2003). We converted the revenue per drug to revenue per drug target by distributing revenue values for a drug uniformly among corresponding drug targets.

Tissue ontology

The Brenda Tissue Ontology (Schomburg et al. 2004) provides hierarchical controlled vocabularies to describe organism-organ-tissue hierarchies for multiple organisms. The ontology has a directed-acyclic-graph structure, where Level 1 represents species names, Level 2 is the whole body, Level 3 is a body-system classification, Level 4 is an organ-system hierarchy, and Level 5 is a tissue-system tree. We measure the nonrandomness of drug-target tissue coverage using the statistic

graphic file with name 206equ1.jpg

where M is the total number of genes, and πik is the relative expression of the ith gene (potential drug target) in the kth tissue. Tissue-specific gene expression levels, πik’s, are normalized in such a way that

graphic file with name 206equ2.jpg

where T is the total number of tissues assayed for expression of the ith gene. (To qualify as a potential drug target, a gene must be expressed in the target tissue; tissues in which a larger number of genes are expressed therefore have a larger number of potential drug targets. Instead of introducing an artificial expression level cutoff to distinguish an active gene from an inactive one, we introduce a statistic that incorporates the entire continuum of expression values for each gene. The statistic represents the probability of randomly picking a gene as a drug target for a specific tissue, where the likelihood of picking the gene is proportional to its level of expression in the tissue.)

Claude E. Shannon’s entropy (with respect to expression of the ith gene in T tissues) is defined in the following way (Shannon and Weaver 1949):

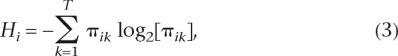graphic file with name 206equ3.jpg

SNPs

We used only validated coding-region nonsynonymous and synonymous SNPs obtained from dbSNP (Sherry et al. 2001), leaving us with a sample of 16,462 human genes, of which 344 are targets for FDA-approved drugs. Cratio is defined in the following way:

graphic file with name 206equ4.jpg

where Nns and Ns stand for the numbers of nonsynonymous and synonymous SNPs reported for a given gene, respectively, and ε is a small pseudo-count intended to eliminate statistical aberrations caused by relatively small sample sizes. In our analysis, we set ε equal to 0.01.

Significance of overlap of gene sets

To assess the significance of the observed overlap between sets of genes, we used a hypergeometric distribution (Johnson and Kotz 1969):

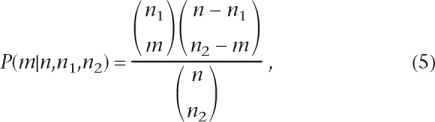graphic file with name 206equ5.jpg

where m is the observed number of genes overlapping between two sets, n is the total number of genes in our model of the molecular network, and n1 and n2 are the numbers of genes in the two sets of genes (such as disease genes and drug targets). Equation 5 gives us the probability of observing exactly m genes overlapping between two independently sampled sets (of size n1 and n2, respectively) without replacement from a gene population of size n. We used the following equation to compute a P-value associated with each quadruplet of numbers (m, n, n1, n2):

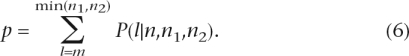graphic file with name 206equ6.jpg

Statistical testing

We used the following bootstrap-based (Efron 1982) testing of significance for connectivity, betweenness, clustering coefficient, Cratio, and tissue-expression entropy analyses. Let n be the total number of human genes in our analysis, of which m are listed as successful drug targets. To test whether the drug targets are significantly different from the rest of genes, for the statistic of focus, we obtain a background distribution for the statistic’s mean for m genes randomly sampled with replacement out of the total collection of n genes, using 20,000 bootstrap samples. We then calculate an empirical two-sided P-value by computing the proportion of bootstrap samples for which the statistic for the randomly sampled genes is more extreme than the statistic’s value for the successful drug targets.

Predictive modeling

The four classifiers that we applied in this study were implemented by the developers of a specialized software package, Weka (Witten and Frank 2005). We used Weka version 3.5.6 for Windows with the default values of parameters. In this application, we had only five features (properties that are used to classify objects) for each node. Four of the features are numerical: connectivity and betweenness (both computed using HPRD2 data), tissue expression entropy, and SNP-based Cratio; one feature, functional family assignment, is categorical. We were able to use 5274 genes (237 of them drug targets) with all five features defined for every node.

Acknowledgments

We thank Murat Çokol, Ivan Iossifov, Raul Rodriguez-Esteban, Tzu-Lin Hsiao, Richard Friedman, Rita Rzhetsky, and Kenneth Smith for comments on the earlier version of the manuscript, and Igor Feldman for providing us with a mapping of disease and essential genes to the GeneWays network. This work was supported by the National Institutes of Health (GM61372) and the Cure Autism Now Foundation.

Footnotes

[Supplemental material is available online at www.genome.org.]

Article published online before print. Article and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.6888208

References

  1. Adams C.P., Brantner V.V., Brantner V.V. Estimating the cost of new drug development: Is it really 802 million dollars? Health Aff. (Millwood) 2006;25:420–428. doi: 10.1377/hlthaff.25.2.420. [DOI] [PubMed] [Google Scholar]
  2. Alfarano C., Andrade C.E., Anthony K., Bahroos N., Bajec M., Bantoft K., Betel D., Bobechko B., Boutilier K., Burgess E., Andrade C.E., Anthony K., Bahroos N., Bajec M., Bantoft K., Betel D., Bobechko B., Boutilier K., Burgess E., Anthony K., Bahroos N., Bajec M., Bantoft K., Betel D., Bobechko B., Boutilier K., Burgess E., Bahroos N., Bajec M., Bantoft K., Betel D., Bobechko B., Boutilier K., Burgess E., Bajec M., Bantoft K., Betel D., Bobechko B., Boutilier K., Burgess E., Bantoft K., Betel D., Bobechko B., Boutilier K., Burgess E., Betel D., Bobechko B., Boutilier K., Burgess E., Bobechko B., Boutilier K., Burgess E., Boutilier K., Burgess E., Burgess E., et al. The Biomolecular Interaction Network Database and related tools 2005 update. Nucleic Acids Res. 2005;33:D418–D424. doi: 10.1093/nar/gki051. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Barabasi A.L., Bonabeau E., Bonabeau E. Scale-free networks. Sci. Am. 2003;288:60–69. doi: 10.1038/scientificamerican0503-60. [DOI] [PubMed] [Google Scholar]
  4. Blake J.A., Richardson J.E., Bult C.J., Kadin J.A., Eppig J.T., Richardson J.E., Bult C.J., Kadin J.A., Eppig J.T., Bult C.J., Kadin J.A., Eppig J.T., Kadin J.A., Eppig J.T., Eppig J.T. MGD: The Mouse Genome Database. Nucleic Acids Res. 2003;31:193–195. doi: 10.1093/nar/gkg047. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Bloom J.D., Adami C., Adami C. Apparent dependence of protein evolutionary rate on number of interactions is linked to biases in protein–protein interactions data sets. BMC Evol. Biol. 2003;3:21. doi: 10.1186/1471-2148-3-21. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Boyer R.F. Concepts in biochemistry. Wiley; New York: 2006. [Google Scholar]
  7. Drews J. Drug discovery: A historical perspective. Science. 2000;287:1960–1964. doi: 10.1126/science.287.5460.1960. [DOI] [PubMed] [Google Scholar]
  8. Drews J. Strategic trends in the drug industry. Drug Discov. Today. 2003;8:411–420. doi: 10.1016/s1359-6446(03)02690-4. [DOI] [PubMed] [Google Scholar]
  9. Drews J. Case histories, magic bullets and the state of drug discovery. Nat. Rev. Drug Discov. 2006;5:635–640. doi: 10.1038/nrd2084. [DOI] [PubMed] [Google Scholar]
  10. Drummond D.A., Bloom J.D., Adami C., Wilke C.O., Arnold F.H., Bloom J.D., Adami C., Wilke C.O., Arnold F.H., Adami C., Wilke C.O., Arnold F.H., Wilke C.O., Arnold F.H., Arnold F.H. Why highly expressed proteins evolve slowly. Proc. Natl. Acad. Sci. 2005;102:14338–14343. doi: 10.1073/pnas.0504070102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Efron B. The Jackknife, the Bootstrap and other resampling plans. Society for Industrial and Applied Mathematics; Philadelphia, PA: 1982. [Google Scholar]
  12. Egner U., Kratzschmar J., Kreft B., Pohlenz H.D., Schneider M., Kratzschmar J., Kreft B., Pohlenz H.D., Schneider M., Kreft B., Pohlenz H.D., Schneider M., Pohlenz H.D., Schneider M., Schneider M. The target discovery process. ChemBioChem. 2005;6:468–479. doi: 10.1002/cbic.200400158. [DOI] [PubMed] [Google Scholar]
  13. Fraser H.B., Hirsh A.E., Steinmetz L.M., Scharfe C., Feldman M.W., Hirsh A.E., Steinmetz L.M., Scharfe C., Feldman M.W., Steinmetz L.M., Scharfe C., Feldman M.W., Scharfe C., Feldman M.W., Feldman M.W. Evolutionary rate in the protein interaction network. Science. 2002;296:750–752. doi: 10.1126/science.1068696. [DOI] [PubMed] [Google Scholar]
  14. Hanley J.A., McNeil B.J., McNeil B.J. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology. 1982;143:29–36. doi: 10.1148/radiology.143.1.7063747. [DOI] [PubMed] [Google Scholar]
  15. Holme P., Kim B.J., Kim B.J. Growing scale-free networks with tunable clustering. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2002;65:026107. doi: 10.1103/PhysRevE.65.026107. [DOI] [PubMed] [Google Scholar]
  16. Jimenez-Sanchez G., Childs B., Valle D., Childs B., Valle D., Valle D. Human disease genes. Nature. 2001;409:853–855. doi: 10.1038/35057050. [DOI] [PubMed] [Google Scholar]
  17. Johnson N.L., Kotz S., Kotz S. Discrete distributions. Wiley; New York: 1969. [Google Scholar]
  18. Johnson J.A., Lima J.J., Lima J.J. Drug receptor/effector polymorphisms and pharmacogenetics: Current status and challenges. Pharmacogenetics. 2003;13:525–534. doi: 10.1097/00008571-200309000-00001. [DOI] [PubMed] [Google Scholar]
  19. Noh J.D.2003Exact scaling properties of a hierarchical network model Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 67045103 . 10.1103/PhysRevE.67.045103 [DOI] [PubMed] [Google Scholar]
  20. Peri S., Navarro J.D., Kristiansen T.Z., Amanchy R., Surendranath V., Muthusamy B., Gandhi T.K., Chandrika K.N., Deshpande N., Suresh S., Navarro J.D., Kristiansen T.Z., Amanchy R., Surendranath V., Muthusamy B., Gandhi T.K., Chandrika K.N., Deshpande N., Suresh S., Kristiansen T.Z., Amanchy R., Surendranath V., Muthusamy B., Gandhi T.K., Chandrika K.N., Deshpande N., Suresh S., Amanchy R., Surendranath V., Muthusamy B., Gandhi T.K., Chandrika K.N., Deshpande N., Suresh S., Surendranath V., Muthusamy B., Gandhi T.K., Chandrika K.N., Deshpande N., Suresh S., Muthusamy B., Gandhi T.K., Chandrika K.N., Deshpande N., Suresh S., Gandhi T.K., Chandrika K.N., Deshpande N., Suresh S., Chandrika K.N., Deshpande N., Suresh S., Deshpande N., Suresh S., Suresh S., et al. Human protein reference database as a discovery resource for proteomics. Nucleic Acids Res. 2004;32:D497– D501. doi: 10.1093/nar/gkh070. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Rual J.F., Venkatesan K., Hao T., Hirozane-Kishikawa T., Dricot A., Li N., Berriz G.F., Gibbons F.D., Dreze M., Ayivi-Guedehoussou N., Venkatesan K., Hao T., Hirozane-Kishikawa T., Dricot A., Li N., Berriz G.F., Gibbons F.D., Dreze M., Ayivi-Guedehoussou N., Hao T., Hirozane-Kishikawa T., Dricot A., Li N., Berriz G.F., Gibbons F.D., Dreze M., Ayivi-Guedehoussou N., Hirozane-Kishikawa T., Dricot A., Li N., Berriz G.F., Gibbons F.D., Dreze M., Ayivi-Guedehoussou N., Dricot A., Li N., Berriz G.F., Gibbons F.D., Dreze M., Ayivi-Guedehoussou N., Li N., Berriz G.F., Gibbons F.D., Dreze M., Ayivi-Guedehoussou N., Berriz G.F., Gibbons F.D., Dreze M., Ayivi-Guedehoussou N., Gibbons F.D., Dreze M., Ayivi-Guedehoussou N., Dreze M., Ayivi-Guedehoussou N., Ayivi-Guedehoussou N., et al. Towards a proteome-scale map of the human protein–protein interaction network. Nature. 2005;437:1173–1178. doi: 10.1038/nature04209. [DOI] [PubMed] [Google Scholar]
  22. Rzhetsky A., Iossifov I., Koike T., Krauthammer M., Kra P., Morris M., Yu H., Duboue P.A., Weng W., Wilbur W.J., Iossifov I., Koike T., Krauthammer M., Kra P., Morris M., Yu H., Duboue P.A., Weng W., Wilbur W.J., Koike T., Krauthammer M., Kra P., Morris M., Yu H., Duboue P.A., Weng W., Wilbur W.J., Krauthammer M., Kra P., Morris M., Yu H., Duboue P.A., Weng W., Wilbur W.J., Kra P., Morris M., Yu H., Duboue P.A., Weng W., Wilbur W.J., Morris M., Yu H., Duboue P.A., Weng W., Wilbur W.J., Yu H., Duboue P.A., Weng W., Wilbur W.J., Duboue P.A., Weng W., Wilbur W.J., Weng W., Wilbur W.J., Wilbur W.J., et al. GeneWays: A system for extracting, analyzing, visualizing, and integrating molecular pathway data. J. Biomed. Inform. 2004;37:43–53. doi: 10.1016/j.jbi.2003.10.001. [DOI] [PubMed] [Google Scholar]
  23. Schomburg I., Chang A., Ebeling C., Gremse M., Heldt C., Huhn G., Schomburg D., Chang A., Ebeling C., Gremse M., Heldt C., Huhn G., Schomburg D., Ebeling C., Gremse M., Heldt C., Huhn G., Schomburg D., Gremse M., Heldt C., Huhn G., Schomburg D., Heldt C., Huhn G., Schomburg D., Huhn G., Schomburg D., Schomburg D. BRENDA, the enzyme database: Updates and major new developments. Nucleic Acids Res. 2004;32:D431–D433. doi: 10.1093/nar/gkh081. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Shannon C.E., Weaver W., Weaver W. The mathematical theory of communication. University of Illinois Press; Urbana: 1949. [Google Scholar]
  25. Sherry S.T., Ward M.H., Kholodov M., Baker J., Phan L., Smigielski E.M., Sirotkin K., Ward M.H., Kholodov M., Baker J., Phan L., Smigielski E.M., Sirotkin K., Kholodov M., Baker J., Phan L., Smigielski E.M., Sirotkin K., Baker J., Phan L., Smigielski E.M., Sirotkin K., Phan L., Smigielski E.M., Sirotkin K., Smigielski E.M., Sirotkin K., Sirotkin K. dbSNP: The NCBI database of genetic variation. Nucleic Acids Res. 2001;29:308–311. doi: 10.1093/nar/29.1.308. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Stelzl U., Worm U., Lalowski M., Haenig C., Brembeck F.H., Goehler H., Stroedicke M., Zenkner M., Schoenherr A., Koeppen S., Worm U., Lalowski M., Haenig C., Brembeck F.H., Goehler H., Stroedicke M., Zenkner M., Schoenherr A., Koeppen S., Lalowski M., Haenig C., Brembeck F.H., Goehler H., Stroedicke M., Zenkner M., Schoenherr A., Koeppen S., Haenig C., Brembeck F.H., Goehler H., Stroedicke M., Zenkner M., Schoenherr A., Koeppen S., Brembeck F.H., Goehler H., Stroedicke M., Zenkner M., Schoenherr A., Koeppen S., Goehler H., Stroedicke M., Zenkner M., Schoenherr A., Koeppen S., Stroedicke M., Zenkner M., Schoenherr A., Koeppen S., Zenkner M., Schoenherr A., Koeppen S., Schoenherr A., Koeppen S., Koeppen S., et al. A human protein–protein interaction network: A resource for annotating the proteome. Cell. 2005;122:957–968. doi: 10.1016/j.cell.2005.08.029. [DOI] [PubMed] [Google Scholar]
  27. Thomas P.D., Campbell M.J., Kejariwal A., Mi H., Karlak B., Daverman R., Diemer K., Muruganujan A., Narechania A., Campbell M.J., Kejariwal A., Mi H., Karlak B., Daverman R., Diemer K., Muruganujan A., Narechania A., Kejariwal A., Mi H., Karlak B., Daverman R., Diemer K., Muruganujan A., Narechania A., Mi H., Karlak B., Daverman R., Diemer K., Muruganujan A., Narechania A., Karlak B., Daverman R., Diemer K., Muruganujan A., Narechania A., Daverman R., Diemer K., Muruganujan A., Narechania A., Diemer K., Muruganujan A., Narechania A., Muruganujan A., Narechania A., Narechania A. PANTHER: A library of protein families and subfamilies indexed by function. Genome Res. 2003;13:2129–2141. doi: 10.1101/gr.772403. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Wishart D.S., Knox C., Guo A.C., Shrivastava S., Hassanali M., Stothard P., Chang Z., Woolsey J., Knox C., Guo A.C., Shrivastava S., Hassanali M., Stothard P., Chang Z., Woolsey J., Guo A.C., Shrivastava S., Hassanali M., Stothard P., Chang Z., Woolsey J., Shrivastava S., Hassanali M., Stothard P., Chang Z., Woolsey J., Hassanali M., Stothard P., Chang Z., Woolsey J., Stothard P., Chang Z., Woolsey J., Chang Z., Woolsey J., Woolsey J. DrugBank: A comprehensive resource for in silico drug discovery and exploration. Nucleic Acids Res. 2006;34:D668–D672. doi: 10.1093/nar/gkj067. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Witten I.H., Frank E., Frank E. Data mining: Practical machine learning tools and techniques. Morgan Kaufman; Amsterdam: 2005. [Google Scholar]
  30. Zambrowicz B.P., Sands A.T., Sands A.T. Knockouts model the 100 best-selling drugs—Will they model the next 100? Nat. Rev. Drug Discov. 2003;2:38–51. doi: 10.1038/nrd987. [DOI] [PubMed] [Google Scholar]
  31. Zheng C., Han L., Yap C.W., Xie B., Chen Y., Han L., Yap C.W., Xie B., Chen Y., Yap C.W., Xie B., Chen Y., Xie B., Chen Y., Chen Y. Progress and problems in the exploration of therapeutic targets. Drug Discov. Today. 2006;11:412–420. doi: 10.1016/j.drudis.2006.03.012. [DOI] [PubMed] [Google Scholar]

Articles from Genome Research are provided here courtesy of Cold Spring Harbor Laboratory Press

RESOURCES