Skip to main content
NCBI home page
Protein Science : A Publication of the Protein Society logoLink to Protein Science : A Publication of the Protein Society
. 2007 Oct;16(10):2233–2239. doi: 10.1110/ps.073004907

The role of the turn in β-hairpin formation during WW domain folding

Tim Sharpe 1,3, Amanda L Jonsson 2,3, Trevor J Rutherford 1, Valerie Daggett 2, Alan R Fersht 1
PMCID: PMC2204123  PMID: 17766370

Abstract

The folding of WW domains is rate limited by formation of a β-hairpin comprising residues from strands 1 and 2. Residues in the turn of this hairpin have reported Φ-values for folding close to 1 and have been proposed to nucleate folding. High Φ-values do not necessarily imply that the energetics of formation are a driving force for initiating folding. We demonstrate by NMR studies and molecular dynamics simulations that the first turn of the hYAP, FBP28, and PIN1 WW domains is structurally dynamic and solvent exposed in the native and folding transition states. It is, therefore, unlikely that the formation of the β-turn per se provides the energetic driving force for hairpin folding. It is more likely that the turn acts as an easily formed hinge that facilitates the formation of the hairpin; it is a nucleus as defined by the nucleation–condensation mechanism whereby a diffuse nucleus is stabilized by associated interactions.

Keywords: protein structure/folding, NMR spectroscopy, computational analysis of protein structure

The transition states for folding of several β-sheet proteins have been characterized by Φ-value analysis (Grantcharova et al. 1998; Martinez and Serrano 1999; Cota et al. 2001; Fowler and Clarke 2001; Garcia-Mira et al. 2004). Recently, attention has focused on small, fast-folding β-sheet peptides that are amenable to simulation, in particular the WW domains. WW domains are small three-stranded β-sheets with a high aromatic content including conserved tryptophan residues (Macias et al. 2000). WW domains have some structural idiosyncrasies: They lack a conventional solvent-inaccessible hydrophobic core, they have abundant, largely solvent-exposed aromatic residues, and they have relatively short β-strands. Accordingly, WW domains may serve as a model for β-hairpin formation (Petrovich et al. 2006).

The folding of several natural WW domain homologs has been studied (Crane et al. 2000; Ferguson et al. 2001a; Jager et al. 2001; Nguyen et al. 2003; Petrovich et al. 2006) as well as a rationally designed WW domain prototype (Macias et al. 2000; Ferguson et al. 2001a). Φ-values are metrics for scoring experimentally the degree of formation of noncovalent interactions relative to the denatured and native states on a scale of 0–1 (Matouschek et al. 1989; Fersht and Sato 2004). There are high Φ-values for mutation of side chains in the first turn of the PIN1 WW domain (Jager et al. 2001) and the FBP28 WW domain (Petrovich et al. 2006). Synthetic peptides with disrupted backbone hydrogen bonding from substitution of specific amide bonds by flexible thio-ether bonds in hYAP (Ferguson et al. 2001b) or ester bonds in PIN1 (Deechongkit et al. 2004) have similar patterns of Φ-values.

For PIN1, the high Φ-values in turn 1 were interpreted as evidence of folding via a hydrophobic zipper mechanism (Jager et al. 2001; Nguyen et al. 2003), propagating away from the structured turn, analogous to a single-sequence nucleation model of the GB1 hairpin (Munoz et al. 1998). All-atom molecular dynamics (MD) unfolding simulations, used in conjunction with Φ-value analysis to study the folding pathway of the FBP28 WW domain, show that the first turn is present as a kink in the backbone of the transition state, but the precise structure of the turn and its associated hydrogen bonds are not formed (Petrovich et al. 2006). Instead, the high Φ-values result from side-chain interactions in the absence of precise native backbone structure. Here, we show that the first turn of WW domains is dynamic even in the native state and discuss what this implies in terms of mechanism of folding.

Results and Discussion

Mobility in the first turn

15N-1H backbone relaxation data were acquired for FBP28 and hYAPtm at 285 K and 288 K, respectively. We have also determined the structure of shortened hYAPtm (A20R, L30Y, D34T) (Jiang et al. 2001; T.J. Rutherford and R. Canales, unpubl.) and there is good agreement with the previous structures of hYAP (Pires et al. 2001). S2 order parameter values derived from model-free analysis had a very similar distribution in hYAPtm and FBP28 (Fig. 1). The first turn and the first residue of the second β-strand of both the hYAP and FBP28 WW domains have lower S2 values (0.68–0.74 for FBP28, 0.73–0.77 for hYAPtm) compared with the second β-strand and the second turn, which form an “island” of higher S2 values in the center of the β-sheet (∼0.81 for FBP28, ∼0.84 for hYAPtm). The lower S2 values reflect the greater mobility of the NH bond vectors of the first turn on the picosecond–nanosecond timescale, compared with the second strand and second turn. We also observed reduced S2 values in the region of T37 (YAP)/S28 (FBP28) in the third β-strand. This region, and T22 (YAP)/T13 (FBP28) in the first turn, make contacts with phosphopeptide ligands in various WW domain ligand complexes (Macias et al. 2002). These residues have been identified as potential sites for regulatory phosphorylation of some WW domains (Shaw et al. 2005). It has been suggested that regions with greater than average motion may trigger conformational changes necessary for ligand binding (Clore and Schwieters 2006).

Figure 1.

Figure 1.

Open in a new tab

(Top left and top middle panels) S2 values derived from NMR 1H-15N backbone relaxation data for FBP28 (285 K) and hYAPtm (288 K). (Top right panel) Crystallographic B factors (temperature factors) were extracted from the structures of PIN1 in bound (1F8A, filled circles) and unbound (1PIN, open circles) states. (Middle and bottom panels) S2 values for FBP28, hYAPtm, and PIN1 were calculated from the autocorrelation function of HN bond vectors with a 250-ps or 2-ns window in two 5-ns molecular dynamics simulations at both 285 K and 298 K.

Crystal structure B-factors (shown in Fig. 1), qualitative analysis of NMR structural restraints (Kowalski et al. 2002), and NMR backbone dynamics studies (Jacobs et al. 2003; Peng et al. 2007) show that the first loop in unbound PIN1 is dynamic on nanosecond–picosecond and millisecond–microsecond timescales. Significant changes in the conformation of turn 1 can be seen in crystal structures of PIN1 in ligand-bound (1F8A) and ligand-free (1PIN) forms (Ranganathan et al. 1997; Verdecia et al. 2000). A recent comprehensive study of PIN1 WW domain backbone dynamics (Peng et al. 2007) showed that the first loop rigidified upon binding to the Cdc25 ligand (S2 values were increased by ∼0.1 for R17, S18, and G20 and by 0.7 for S19). Truncation of the loop (by deletion of S19) reduced both loop mobility and binding affinity. Further recent loop modification experiments showed that shortening the loop, replacing it with the loop from FBP28, and repositioning or deleting R17 abrogates ligand binding (Jager et al. 2006). It appears that mobility in the first loop, observed for FBP28 and hYAPtm by NMR backbone dynamics and for PIN1 by a variety of techniques, is a conserved feature of WW domains and that it has important effects upon ligand binding.

S2 values calculated from low and room temperature (285 K and 298 K) MD simulations of the native state for FBP28, hYAPtm, and PIN1 show that the first turn is highly mobile. Although the S2 values in the first turn are lower than those calculated from NMR measurements, the trends are in good agreement with the NMR data from FBP28 and hYAP and the crystallographic and NMR data for PIN1 (Ranganathan et al. 1997; Peng et al. 2007). The simulations also display a dip in S2 values in the third β-strand, as observed by NMR for FBP28 and hYAPtm.

The flexibility of the backbone of the first turn was also reflected in the increased fluctuations of the α-carbon atoms about the average structure in the first turn compared with the rest of the protein (Fig. 2). In addition, when (ϕ,ψ) space is divided into 5° × 5° bins, the residues of the first turn of FBP28, hYAPtm, and PIN1 populated 72%, 60%, and 39% of all bins, respectively (Table 1). In each case, this represents the highest percentage of (ϕ,ψ) space sampled for the structured region of each protein (i.e., excluding terminal tails if present).

Figure 2.

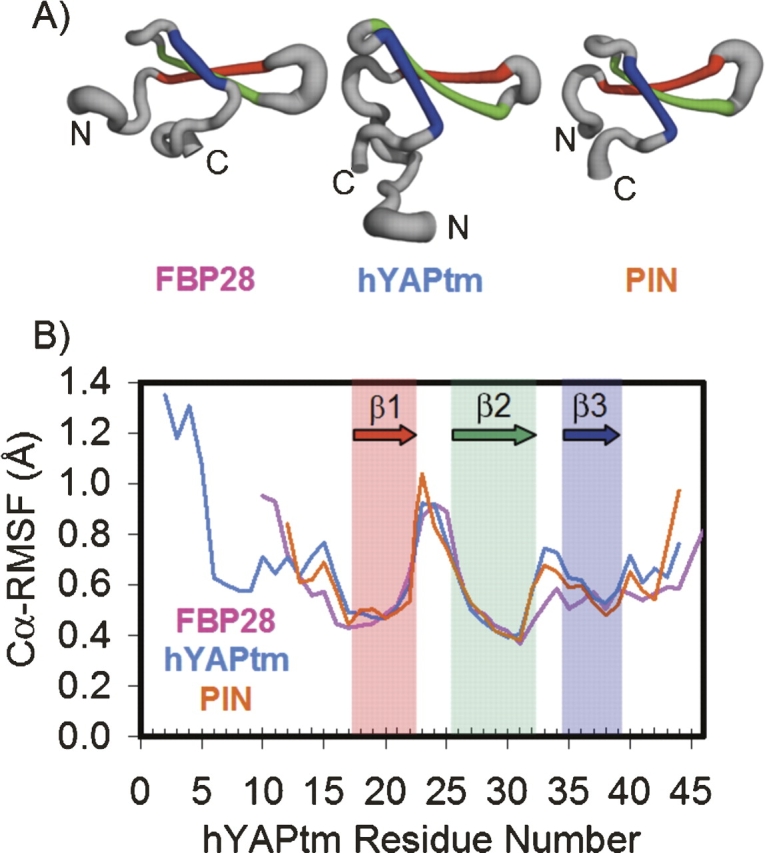
Figure 2.

Open in a new tab

(A) The structure of FBP28, hYAPtm, and PIN colored by secondary structure: Strand 1 is red, strand 2 is green, and strand 3 is blue. The thickness of the ribbon corresponds to the average root-mean-square fluctuation of the α-carbon from the average structure (Cα-RMSF) from the native state simulations at both 285 K and 298 K. This image was generated using PyMOL. (B) Average Cα-RMSF of the native state simulations at both 285 K and 298 K for FBP28, hYAPtm, and PIN1 in pink, light blue, and orange, respectively. An offset was added to the residue numbers of FBP28 and PIN1 so that the residue numbers in the first turn overlapped with the residue numbers of hYAPtm.

Table 1.

Percentage of 5 × 5° Ramachandran bins sampled in the 285 K and 298 K native state simulations

graphic file with name 2233tbl1.jpg

Open in a new tab

Hydrogen bonding in the first turn

Two backbone hydrogen bonds can form in turn 1 of PIN1, FBP28, and hYAPtm. One of these hydrogen bonds involves the NH of the last residue in strand 1 (residue 13 in FBP28 and residue 22 in hYAPtm, for example) and the i + 4 carbonyl group that corresponds to the first residue in strand 2 (residue 17 in FBP28 and residue 26 in hYAPtm). The second hydrogen bond is between the carbonyl group of the last residue in strand 1 with the i + 3 NH group (residue 16 in FBP28 and 25 in hYAPtm). We observed limited amide protection for T22HN of hYAPtm and no protection for G25HN by NMR hydrogen exchange experiments (T.J. Rutherford, unpubl. data). Similar results were obtained for a stabilized circularized FBP28 (T. Sharpe, unpubl. data). No protection from exchange was observed in the turn for wild-type FBP28 and YQJ8 (Macias et al. 2000). Ninety-one percent of the time the i → i + 4 hydrogen bond was intact in hYAPtm in the MD simulations, while the value for the i → i + 3 hydrogen bond was 19%. The corresponding values were 39% and 10% for FBP28. These data show that the hydrogen bonds in turn 1 are dynamic and undergo local exchange with solvent in the native state.

Interpretation of high Φ-values

Φ-value analysis was designed to study the removal of defined interactions in a native structure (“nondisruptive deletions”) and to infer the relative contributions of those interactions in stabilizing transition and ground states (Fersht et al. 1987; Matouschek et al. 1989). A Φ-value of 1 means that the energies of the native and transition states are perturbed equally by the mutation, and a Φ-value of 0 means that the transition and denatured states are perturbed isoenergetically (Matouschek et al. 1989; Fersht et al. 1992; Fersht and Sato 2004). The most suitable Φ-mutations, such as the paradigmatic mutation of a buried hydrophobic residue to a smaller hydrophobic residue and also Ala → Gly scanning (Scott et al. 2007), delete specific interactions observed in the native state. For such mutations, one assumes that a residue with a Φ-value of 1 makes the same set of stabilizing interactions in both the transition and native states, and also fractional values of Φ are a good indication of the extent of bond formation. The equivalence of energetic and structural perturbations results from the deletion of an equivalent set of interactions by mutation. But, Φ-analysis may also be applied for extreme values of 0 and 1 for more drastic mutations and for mutations that do not change well-defined interactions (Matouschek et al. 1989; Fersht and Sato 2004). In those examples, the Φ-values indicate energetic equivalence with denatured and native states, respectively.

The mutations in the first turn of FBP28 are not generally the classical deletion of specific interactions (Petrovich et al. 2006). But, as they give Φ-values of close to 1, the turn is isoenergetic in the transition and native states. Transition state structures identified from unfolding simulations of FBP28 maintain a large fraction of contacts in the native state (average of 1.46 for residues 13–17) in the first turn while the native backbone conformation of the turn was not preserved. The average fraction of contacts in the first turn correlates well with experimental Φ-values in this region (Petrovich et al. 2006). Thus, there are tertiary interactions in the absence of fixed backbone structure in the transition state. We have shown by NMR and MD that the backbone structure is quite malleable in the native state, and MD shows that it is also dynamic in the transition state.

Nucleation and the role of the first turn in folding

The nucleus in the nucleation–condensation mechanism is an unstable species that has to be stabilized by long-range and other interactions as the rest of the protein condenses around it, and the nucleus is loosely defined as the region of the protein that is best formed in the transition state (Itzhaki et al. 1995; Fersht 1997). The first turn in the FBP28 WW domain is a nucleus for folding by that definition, as it is nearly fully formed even though it is energetically weak and dynamic. The fractional Φ-values observed in PIN1 and FBP28 in the first and second strands are what are expected for a nucleation–condensation folding mechanism: The stabilizing interactions are in the process of being formed as the structure condenses around the nucleus (Itzhaki et al. 1995). But, it differs from other nuclei in that it is solvent exposed and it is not stabilized by other residues condensing around it. Even though the turn is not rigid, it still responds to mutations that affect its energy: Any mutation that destabilizes the turn (entropically or enthalpically) will raise the free energy of formation of the transition state for folding and vice versa.

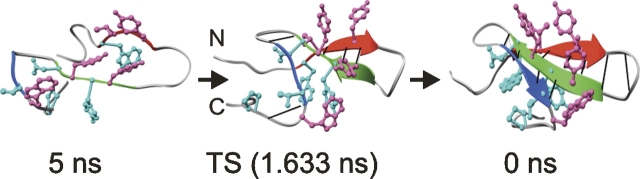
The all-atom MD unfolding simulations of FBP28 show that the backbone structure of the first turn is relatively fluid in the transition state (Petrovich et al. 2006). Consequently, mutations that allow the turn to explore too great an area of Ramachandran space (for example an X → Gly mutation) or those that penalize exploration of the necessary regions of Ramachandran space (for example, a Gly → Ala mutation or Gly deletion) (Jager et al. 2006), could frustrate protein folding and destabilize the native state. Further insights can be gained in silico. As the hairpin has a dynamic turn with rapid fluctuations in native state Ramachandran space, rather than use a model based on the attainment of native (ϕ,ψ) angles as the indicator of nativeness (Munoz et al. 1997, 1998, 2006), we used unfolding simulations that can reproduce the dynamic behavior of the native state with reasonable accuracy. For FBP28 such simulations reveal that hydrogen bonds generally formed between strands 1 and 2 before the backbone hydrogen bonds of the first turn, considering the unfolding simulation in reverse (Fig. 3; Petrovich et al. 2006). The increase in hydrophobic contacts between the residues of the first two strands was preceded by, or concurrent with, the decrease in the distance between the Cα atoms of residues 13 and 17 that define turn 1 and the formation of the backbone hydrogen bond between residues 13 and 17 of turn 1 (Fig. 4). The detailed time course comparing acquisition of interstrand hydrophobic contacts and turn structure indicates that folding proceeds through a loosely structured first turn and cross-strand hydrophobic contacts. However, this is where such labels become somewhat arbitrary—the turn is critical to the process. Indeed, how can a β-hairpin form without a turn? The distinction we make is whether or not the precise structure of the turn is acquired before interactions across the sheet, such as with a zipper. Instead, the simulations show a dynamic, loosely structured turn that serves both to bring the chain around and to adapt as necessary for interstrand interactions to develop.

Figure 3.

Figure 3.

Open in a new tab

First 5 ns of a 373 K, low pH unfolding simulation of FBP28 (Petrovich et al. 2006) shown in reverse. Backbone hydrogen bonds are shown as gray bars. Side chains of the two hydrophobic clusters are shown and colored pink and light blue for cluster 1 and 2, respectively.

Figure 4.

Figure 4.

Open in a new tab

(A) A schematic of the first hairpin with side chains shown in magenta, distance between the α-carbons that define the first turn represented in green, and the hydrogen bond distance in cyan. (B) Number of hydrophobic contacts between the residues of the first two β-strands from a representative 373 K unfolding simulation of FBP28, with time shown in reverse to represent the folding pathway. (C) Distance between the α-carbons of residues 13 and 17 that define the first turn of WW domain. (D) Hydrogen bond distance between residues 13 and 17 of the first turn.

It is an intriguing possibility that the first turn of the WW domains may play an important role in misfolding in addition to the roles in folding and binding outlined above and elsewhere. FBP28 forms amyloid fibers rapidly under physiological conditions (Ferguson et al. 2003). The amyloid fibers are formed from stacked nonnative β-hairpins. The turn between regions of β-space in the hairpin comprises the same residues that form the first turn in the native state, but those residues have a nonnative conformation in the fiber (Ferguson et al. 2006). It may be that the flexibility of the backbone in the first turn, as observed in the native state, also facilitates the adoption of an alternative nonnative structure in the amyloid fiber. Thus, rather than being an optimized β-turn capable of driving folding, the first turn might be passive in folding and well suited for the adoption of multiple conformations, including those involved in ligand binding.

Materials and Methods

NMR backbone dynamics

15N-labeled FBP28 was expressed and purified as previously described (Ferguson et al. 2006). 15N-labeled hYAPtm was provided by Roberto Canales. All NMR data were acquired on a Bruker DRX500 using standard conditions for each protein: 285 K, 20 mM sodium phosphate (pH 6.5), and 30 mM NaCl for FBP28 and 288 K, 50 mM sodium phosphate (pH 6), and 150 mM NaCl for hYAPtm. All data were processed with nmrPipe (Delaglio et al. 1995) and analyzed using Sparky (Goddard and Kneller, 2004). Resonance assignments for FBP28 were made using an 1H-1H-15N TOCSY spectrum and the published assignments for FBP28 under identical conditions (Biomagresbank 4714). For hYAPtm, the assignments were made using standard triple resonance experiments.

NMR 1H-15N backbone relaxation data (R1, R2, and heteronuclear NOE) were acquired for FBP28 and hYAPtm using standard pulse sequences (Kay et al. 1992; Mandel et al. 1995). For R1 and R2 data, peak heights as a function of relaxation delay time (16–1600 ms for R1 and 14–350 ms for R2) were fitted to a single exponential function using Sparky. Heteronuclear NOE values (I/I0) were obtained by taking the ratio of peak heights in spectra obtained in the presence or absence of presaturation of amide proton resonances.

Model-free analysis

S2 values were calculated for FBP28 and hYAPtm using Lipari–Szabo model-free analysis (Lipari and Szabo 1982) performed in Tensor2 (Dosset et al. 2000). The errors for relaxation rates and I/I0 (heteronuclear NOE) were conservatively estimated as 5% of the average value for the structured region of the protein. The rotational correlation times of 4.1 ns for FBP28 and 4.4 ns for hYAPtm were estimated using R2/R1 values from residues with I/I0 > 0.55 and R2/R1 within 1.5 standard deviations of the mean for the structured part of the molecule; the calculation assumed isotropic tumbling. Although FBP28 has been shown to form amyloid fibrils (Ferguson et al. 2003), these correlation times are inconsistent with oligomerization or self-aggregation and are consistent with data for a circularized FBP28 that does not form amyloid fibrils (T. Sharpe, unpubl. data). The data were mostly fitted to the simplest models of internal motion (model 1 or 2), the S2 values reflecting trends clearly visible in the raw R1 and I/I0 data. For FBP28 residues N22, L26, and E27 had small chemical exchange contributions, with Rex between 0.9 and 1.2 s−1.

Molecular dynamics simulations

Two 20-ns simulations were performed at both 285 K and 298 K in ilmm (Beck and Daggett 2004; Beck et al. 2006) using the Levitt et al. force field (Levitt et al. 1995; Armen et al. 2005) with a 10 Å spherical cutoff for nonbonded terms. Each simulation included explicit F3C water molecules (Levitt et al. 1997) at the appropriate density (0.9995 and 0.997 g/mL for 285 K and 298 K, respectively) (Kell 1967). S2 values from molecular dynamics simulations of FBP28, hYAPtm, and PIN1 were calculated from the autocorrelation function of HN bond vectors (Wong and Daggett 1998) with a 250-ps or 5-ns window at 285 K and 298 K.

Acknowledgments

We thank Dr. Neil Ferguson for suggesting these experiments and for many helpful discussions and Dr. Mark Allen for assistance with NMR assignment.

Footnotes

Reprint requests to: Valerie Daggett, Biomolecular Structure and Design Program, University of Washington, Seattle, WA 98195-7610, USA; e-mail: daggett@u.washington.edu; or Alan R. Fersht, e-mail: MRC Centre for Protein Engineering and Cambridge University Chemical Laboratory, MRC Centre, Hills Road, Cambridge CB2 0QH, UK; e-mail: arf25@cam.ac.uk; fax: 44-1223-336445.

Article published online ahead of print. Article and publication date are at http://www.proteinscience.org/cgi/doi/10.1110/ps.073004907.

References

  1. Armen R.S., Bernard, B.M., Day, R., Alonso, D.O., and Daggett, V. 2005. Characterization of a possible amyloidogenic precursor in glutamine-repeat neurodegenerative diseases. Proc. Natl. Acad. Sci. 102: 13433–13438. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Beck D.A. and Daggett, V. 2004. Methods for molecular dynamics simulations of protein folding/unfolding in solution. Methods 34: 112–120. [DOI] [PubMed] [Google Scholar]
  3. Beck D.A.C., Alonso, D.O.V., and Daggett, V. 2006. In lucem molecular mechanics computer program. University of Washington, Seattle, WA.
  4. Clore G.M. and Schwieters, C.D. 2006. Concordance of residual dipolar couplings, backbone order parameters and crystallographic B-factors for a small α/β protein: A unified picture of high probability, fast atomic motions in proteins. J. Mol. Biol. 355: 879–886. [DOI] [PubMed] [Google Scholar]
  5. Cota E., Steward, A., Fowler, S.B., and Clarke, J. 2001. The folding nucleus of a fibronectin type III domain is composed of core residues of the immunoglobulin-like fold. J. Mol. Biol. 305: 1185–1194. [DOI] [PubMed] [Google Scholar]
  6. Crane J.C., Koepf, E.K., Kelly, J.W., and Gruebele, M. 2000. Mapping the transition state of the WW domain β-sheet. J. Mol. Biol. 298: 283–292. [DOI] [PubMed] [Google Scholar]
  7. Deechongkit S., Nguyen, H., Powers, E.T., Dawson, P.E., Gruebele, M., and Kelly, J.W. 2004. Context-dependent contributions of backbone hydrogen bonding to β-sheet folding energetics. Nature 430: 101–105. [DOI] [PubMed] [Google Scholar]
  8. Delaglio F., Grzesiek, S., Vuister, G.W., Zhu, G., Pfeifer, J., and Bax, A. 1995. NMRPipe: A multidimensional spectral processing system based on UNIX pipes. J. Biomol. NMR 6: 277–293. [DOI] [PubMed] [Google Scholar]
  9. Dosset P., Hus, J.C., Blackledge, M., and Marion, D. 2000. Efficient analysis of macromolecular rotational diffusion from heteronuclear relaxation data. J. Biomol. NMR 16: 23–28. [DOI] [PubMed] [Google Scholar]
  10. Ferguson N., Johnson, C.M., Macias, M., Oschkinat, H., and Fersht, A. 2001a. Ultrafast-folding of WW domains without structured aromatic clusters in the denatured state. Proc. Natl. Acad. Sci. 98: 13002–13007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Ferguson N., Pires, J.R., Toepert, F., Johnson, C.M., Pan, Y.P., Volkmer-Engert, R., Schneider-Mergener, J., Daggett, V., Oschkinat, H., and Fersht, A. 2001b. Using flexible loop mimetics to extend ϕ-value analysis to secondary structure interactions. Proc. Natl. Acad. Sci. 98: 13008–13013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Ferguson N., Berriman, J., Petrovich, M., Sharpe, T.D., Finch, J.T., and Fersht, A.R. 2003. Rapid amyloid fiber formation from the fast-folding WW domain FBP28. Proc. Natl. Acad. Sci. 100: 9814–9819. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Ferguson N., Becker, J., Tidow, H., Tremmel, S., Sharpe, T.D., Krause, G., Flinders, J., Petrovich, M., Berriman, J., Oschkinat, H., et al. 2006. General structural motifs of amyloid protofilaments. Proc. Natl. Acad. Sci. 103: 16248–16253. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Fersht A.R. 1997. Nucleation mechanisms in protein folding. Curr. Opin. Struct. Biol. 7: 3–9. [DOI] [PubMed] [Google Scholar]
  15. Fersht A.R. and Sato, S. 2004. ϕ-Value analysis and the nature of protein-folding transition states. Proc. Natl. Acad. Sci. 101: 7976–7981. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Fersht A.R., Leatherbarrow, R.J., and Wells, T.N.C. 1987. Structure–activity relationships in engineered proteins. Analysis of use of binding-energy by linear free-energy relationships. Biochemistry 26: 6030–6038. [DOI] [PubMed] [Google Scholar]
  17. Fersht A.R., Matouschek, A., and Serrano, L. 1992. The folding of an enzyme. I. Theory of protein engineering analysis of stability and pathway of protein folding. J. Mol. Biol. 224: 771–782. [DOI] [PubMed] [Google Scholar]
  18. Fowler S.B. and Clarke, J. 2001. Mapping the folding pathway of an immunoglobulin domain: Structural detail from Φ-value analysis and movement of the transition state. Structure 9: 355–366. [DOI] [PubMed] [Google Scholar]
  19. Garcia-Mira M.M., Boehringer, D., and Schmid, F.X. 2004. The folding transition state of the cold shock protein is strongly polarized. J. Mol. Biol. 339: 555–569. [DOI] [PubMed] [Google Scholar]
  20. Goddard T.D. and Kneller, D.G. 2004. SPARKY 3. University of California, San Fransisco, CA.
  21. Grantcharova V.P., Riddle, D.S., Santiago, J.V., and Baker, D. 1998. Important role of hydrogen bonds in the structurally polarized transition state for folding of the src SH3 domain. Nat. Struct. Biol. 5: 714–720. [DOI] [PubMed] [Google Scholar]
  22. Itzhaki L.S., Otzen, D.E., and Fersht, A.R. 1995. The structure of the transition state for folding of chymotrypsin inhibitor 2 analysed by protein engineering methods: Evidence for a nucleation-condensation mechanism for protein folding. J. Mol. Biol. 254: 260–288. [DOI] [PubMed] [Google Scholar]
  23. Jacobs D.M., Saxena, K., Vogtherr, M., Bernado, P., Pons, M., and Fiebig, K.M. 2003. Peptide binding induces large scale changes in inter-domain mobility in human Pin1. J. Biol. Chem. 278: 26174–26182. [DOI] [PubMed] [Google Scholar]
  24. Jager M., Nguyen, H., Crane, J.C., Kelly, J.W., and Gruebele, M. 2001. The folding mechanism of a β-sheet: The WW domain. J. Mol. Biol. 311: 373–393. [DOI] [PubMed] [Google Scholar]
  25. Jager M., Zhang, Y., Bieschke, J., Nguyen, H., Dendle, M., Bowman, M.E., Noel, J.P., Gruebele, M., and Kelly, J.W. 2006. Structure-function-folding relationship in a WW domain. Proc. Natl. Acad. Sci. 103: 10648–10653. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Jiang X., Kowalski, J., and Kelly, J.W. 2001. Increasing protein stability using a rational approach combining sequence homology and structural alignment: Stabilizing the WW domain. Protein Sci. 10: 1454–1465. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Kay L.E., Nicholson, L.K., Delaglio, F., Bax, A., and Torchia, D.A. 1992. Pulse sequences for removal of the effects of cross correlation between dipolar and chemical-shift anisotropy relaxation mechanisms on the measurement of heteronuclear T1 and T2 values in proteins. J. Magn. Reson. 97: 359–375. [Google Scholar]
  28. Kell G.S. 1967. Precise representation of volume properties of water at one atmosphere. J. Chem. Eng. Data 12: 66–68. [Google Scholar]
  29. Kowalski J.A., Liu, K., and Kelly, J.W. 2002. NMR solution structure of the isolated Apo Pin1 WW domain: Comparison to the X-ray crystal structures of Pin1. Biopolymers 63: 111–121. [DOI] [PubMed] [Google Scholar]
  30. Levitt M., Hirshberg, M., Sharon, R., and Daggett, V. 1995. Potential-energy function and parameters for simulations of the molecular-dynamics of proteins and nucleic-acids in solution. Comput. Phys. Commun. 91: 215–231. [Google Scholar]
  31. Levitt M., Hirshberg, M., Sharon, R., Laidig, K.E., and Daggett, V. 1997. Calibration and testing of a water model for simulation of the molecular dynamics of proteins and nucleic acids in solution. J. Phys. Chem. B 101: 5051–5061. [Google Scholar]
  32. Lipari G. and Szabo, A.J. 1982. Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. 1. Theory and range of validity. J. Am. Chem. Soc. 104: 4546–4558. [Google Scholar]
  33. Macias M.J., Gervais, V., Civera, C., and Oschkinat, H. 2000. Structural analysis of WW domains and design of a WW prototype. Nat. Struct. Biol. 7: 375–379. [DOI] [PubMed] [Google Scholar]
  34. Macias M.J., Wiesner, S., and Sudol, M. 2002. WW and SH3 domains, two different scaffolds to recognize proline-rich ligands. FEBS Lett. 513: 30–37. [DOI] [PubMed] [Google Scholar]
  35. Mandel A.M., Akke, M., and Palmer III, A.G. 1995. Backbone dynamics of Escherichia coli ribonuclease HI: Correlations with structure and function in an active enzyme. J. Mol. Biol. 246: 144–163. [DOI] [PubMed] [Google Scholar]
  36. Martinez J.C. and Serrano, L. 1999. The folding transition state between SH3 domains is conformationally restricted and evolutionarily conserved. Nat. Struct. Biol. 6: 1010–1016. [DOI] [PubMed] [Google Scholar]
  37. Matouschek A., Kellis Jr, J.T., Serrano, L., and Fersht, A.R. 1989. Mapping the transition state and pathway of protein folding by protein engineering. Nature 340: 122–126. [DOI] [PubMed] [Google Scholar]
  38. Munoz V., Thompson, P.A., Hofrichter, J., and Eaton, W.A. 1997. Folding dynamics and mechanism of β-hairpin formation. Nature 390: 196–199. [DOI] [PubMed] [Google Scholar]
  39. Munoz V., Henry, E.R., Hofrichter, J., and Eaton, W.A. 1998. A statistical mechanical model for β-hairpin kinetics. Proc. Natl. Acad. Sci. 95: 5872–5879. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Munoz V., Ghirlando, R., Blanco, F.J., Jas, G.S., Hofrichter, J., and Eaton, W.A. 2006. Folding and aggregation kinetics of a β-hairpin. Biochemistry 45: 7023–7035. [DOI] [PubMed] [Google Scholar]
  41. Nguyen H., Jager, M., Moretto, A., Gruebele, M., and Kelly, J.W. 2003. Tuning the free-energy landscape of a WW domain by temperature, mutation, and truncation. Proc. Natl. Acad. Sci. 100: 3948–3953. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Peng T., Zintsmaster, J.S., Namanja, A.T., and Peng, J.W. 2007. Sequence-specific dynamics modulate recognition specificity in WW domains. Nat. Struct. Mol. Biol. 14: 325–331. [DOI] [PubMed] [Google Scholar]
  43. Petrovich M., Jonsson, A.L., Ferguson, N., Daggett, V., and Fersht, A.R. 2006. Φ-analysis at the experimental limits: Mechanism of β-hairpin formation. J. Mol. Biol. 360: 865–881. [DOI] [PubMed] [Google Scholar]
  44. Pires J.R., Taha-Nejad, F., Toepert, F., Ast, T., Hoffmuller, U., Schneider-Mergener, J., Kuhne, R., Macias, M.J., and Oschkinat, H. 2001. Solution structures of the YAP65 WW domain and the variant L30 K in complex with the peptides GTPPPPYTVG, N-(n-octyl)-GPPPY and PLPPY and the application of peptide libraries reveal a minimal binding epitope. J. Mol. Biol. 314: 1147–1156. [DOI] [PubMed] [Google Scholar]
  45. Ranganathan R., Lu, K.P., Hunter, T., and Noel, J.P. 1997. Structural and functional analysis of the mitotic rotamase Pin1 suggests substrate recognition is phosphorylation dependent. Cell 89: 875–886. [DOI] [PubMed] [Google Scholar]
  46. Scott K.A., Alonso, D.O., Sato, S., Fersht, A.R., and Daggett, V. 2007. Conformational entropy of alanine versus glycine in protein denatured states. Proc. Natl. Acad. Sci. 104: 2661–2666. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Shaw A.Z., Martin-Malpartida, P., Morales, B., Yraola, F., Royo, M., and Macias, M.J. 2005. Phosphorylation of either Ser16 or Thr30 does not disrupt the structure of the Itch E3 ubiquitin ligase third WW domain. Proteins 60: 558–560. [DOI] [PubMed] [Google Scholar]
  48. Verdecia M.A., Bowman, M.E., Lu, K.P., Hunter, T., and Noel, J.P. 2000. Structural basis for phosphoserine-proline recognition by group IV WW domains. Nat. Struct. Biol. 7: 639–643. [DOI] [PubMed] [Google Scholar]
  49. Wong K.B. and Daggett, V. 1998. Barstar has a highly dynamic hydrophobic core: Evidence from molecular dynamics simulations and nuclear magnetic resonance relaxation data. Biochemistry 37: 11182–11192. [DOI] [PubMed] [Google Scholar]

Articles from Protein Science : A Publication of the Protein Society are provided here courtesy of The Protein Society

RESOURCES