Models of S/π interactions in protein structures: Comparison of the H₂S–benzene complex with PDB data

Abstract

S/π interactions are prevalent in biochemistry and play an important role in protein folding and stabilization. Geometries of cysteine/aromatic interactions found in crystal structures from the Brookhaven Protein Data Bank (PDB) are analyzed and compared with the equilibrium configurations predicted by high-level quantum mechanical results for the H₂S–benzene complex. A correlation is observed between the energetically favorable configurations on the quantum mechanical potential energy surface of the H₂S–benzene model and the cysteine/aromatic configurations most frequently found in crystal structures of the PDB. In contrast to some previous PDB analyses, configurations with the sulfur over the aromatic ring are found to be the most important. Our results suggest that accurate quantum computations on models of noncovalent interactions may be helpful in understanding the structures of proteins and other complex systems.

The tertiary structure of proteins is determined by a variety of intermolecular interactions. Traditional hydrogen bonding is one critical noncovalent interaction that can play a large role in determining structure, but many other, weaker, noncovalent interactions can also contribute. Understanding the underlying nature, strength, and directionality of these interactions is important for the prediction of the optimal structure of proteins and the dynamics of their folding. Unfortunately, isolating an individual interaction in a complex protein structure, and separating the effect of this interaction from that of other weak interactions and solvent effects, would be nearly impossible. Computational techniques offer a way to systematically and rigorously characterize the strength of various types of interactions by providing highly accurate potential energy curves for small model systems. For example, converged ab initio computations have deepened our understanding of π–π interactions through studies of the simplest possible prototype system, the benzene dimer (Hobza et al. 1994, 1996; Tsuzuki et al. 1994, 2000, 2002; Jaffe and Smith 1996; Tsuzuki and Lüthi 2001; Sinnokrot et al. 2002; Sinnokrot and Sherrill 2006).

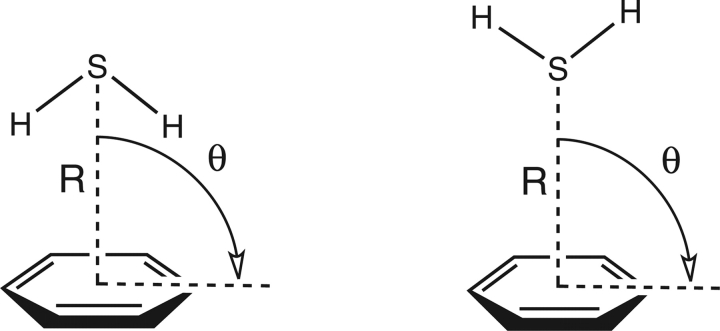
Such an approach assumes that the model system accurately captures the essential physics of the nonbonded interaction as it would occur in larger systems. This study aims to address the validity of this assumption by providing highly accurate potential curves for several model configurations of the H₂S–benzene complex (see Fig. 1) and comparing these results with the preferred geometries of cysteine/aromatic contacts observed in the Brookhaven Protein Data Bank (PDB).

Figure 1.

Variation of R and θ for C_2ν configurations of the H₂S–benzene complex.

Favorable interactions between sulfur and π aromatic systems were first suggested by Morgan et al. (1978) when a series of alternating S and π bonded atoms were identified in several protein structures. Subsequent studies (Reid et al. 1985; Zauhar et al. 2000) examining crystal structures from both the Protein Data Bank and the Cambridge Crystallographic Database have revealed that sulfur–π interactions occur more commonly in protein crystal structures than would be expected from a random association of the structure. A few theoretical studies have also examined these interactions. Cheney et al. (1989) investigated the methanethiol–benzene complex as a model of cysteine–aromatic interactions using Hartree-Fock (HF) and second-order Møller-Plesset perturbation theory (MP2) with several basis sets. After optimizing several initial configurations, they report that the optimum configuration has an inter-fragment separation (distance from sulfur to center of the benzene ring) of 4.4 Å and an angle between the sulfur and the plane of the benzene of 56°. More recent work by Duan et al. (2001) also examined methanethiol–benzene using MP2 in conjunction with larger basis sets and found an optimum configuration in which the sulfur was directly above the benzene ring at an inter-fragment separation of 3.73 Å. For more information about S/π interactions, see the excellent review article by Meyer et al. (2003).

Our previous work with weak interactions (Sinnokrot et al. 2002) suggests that higher-order correlation techniques are required to converge the interaction energy of noncovalent complexes. Tauer et al. (2005) were the first to apply a highly correlated computational technique such as coupled-cluster theory through perturbative triples (CCSD[T]) with sufficiently large basis sets to achieve converged subchemical accuracy results for the H₂S–benzene complex as a prototype for sulfur–π interactions. Although we speak generally of sulfur–π interactions, we are interested both in the interactions of sulfur lone-pairs with the π-systems, as well as the interactions of sulfur-bonded hydrogens pointed at π-systems, which could perhaps be referred to as S–H/π interactions (E. Arunan, pers. comm.). The study by Tauer et al. (2005) found that the inter-fragment separation for the equilibrium geometry of the hydrogens-down C_2ν structure of H₂S–benzene was 3.8 Å, and the interaction energy of the complex at this geometry was −2.74 kcal mol⁻¹ (CCSD[T]/aug-cc-pVQZ results). In this work, we use this hydrogens-down C_2ν structure (and also a hydrogens-up C_2ν structure) as starting configurations and systematically vary both the inter-fragment distance (measured between the sulfur of H₂S and the geometric center of the benzene) and the angle between the sulfur and the perpendicular to the aromatic plane of benzene (see Fig. 1). Based on the potential energy surfaces (in the R/θ space defined), interesting configurations are selected and analyzed using highly correlated techniques similar to those used by Tauer et al. (2005) to determine potential curves for the selected configurations.

Seemingly at odds with the quantum mechanical results of Tauer et al. (2005) for the H₂S–benzene model, Reid et al. (1985) examined 36 proteins from the Protein Data Bank and reported that sulfur atoms prefer to interact with the edge of aromatic rings and avoid the area in the center of the ring around the π-electrons. Zauhar et al. (2000) compared probability distributions for the geometries of divalent sulfurs interacting with six-membered aromatic carbon rings with analogous probability distributions of X–CH₂–X groups interacting with aromatic rings for structures from the Crystallographic Database. From these results, they defined a preferred geometry of interaction in which the divalent sulfur is in plane with the aromatic ring and at a separation of ∼5 Å.

In this work, we directly compare optimum configurations predicted by high-level quantum mechanics with configurations that occur frequently in the PDB by performing an analysis of crystal structures from the Brookhaven Protein Data Bank, in which the same parameters are determined for each sulfur–π interaction in the crystal structure as were varied in the potential energy surfaces. This comparison should help us understand whether quantum mechanical calculations of small model systems can provide reliable predictions of geometric configurations for interactions found in crystal structures.

Computational details

Ab initio calculations

Monomer geometries for hydrogen sulfide and benzene were taken as the best values from the literature: r_e (C–C) = 1.3915 Å and r_e (C–H) = 1.0800 Å for benzene (Gauss and Stanton 2000) and r_e (S–H) = 1.3356 Å and θ_e (H–S–H) = 92.12° for hydrogen sulfide (Edwards et al. 1967). From these monomer geometries, two initial configurations were constructed in which the sulfur of H₂S was placed directly over the center of the benzene ring: one structure with the hydrogens directed toward the ring, and one away from the ring (Fig. 1). From these starting geometries the distance between the sulfur and the ring center (denoted R) was systematically varied in 0.5 Å increments from 3.5 to 7.5 Å. The angle between the sulfur and the normal to the benzene plane (denoted θ) was varied in 15° increments at every R value in the range described. At each R/θ point, the total interaction energy of the complex was determined using MP2 in conjunction with the aug-cc-pVDZ basis set. Though this method is not sufficient to determine accurate total interaction energies, the relative energetics of the configurations, and therefore the qualitative appearance of the surface, can be determined reliably. To verify this assumption, a portion of the surface for configuration B was determined using CCSD(T) in conjunction with the aug-cc-pVTZ basis, and qualitative agreement was found across the region considered. From the R/θ surfaces, interesting configurations were selected for higher-level analysis. For these configurations, potential energy curves were obtained using CCSD(T) in conjunction with the aug-cc-pVTZ basis. Previous work (Tauer et al. 2005) has demonstrated that reliable interaction energies can be produced for the H₂S–benzene complex using this methodology. All energy computations were performed using MOLPRO (Wener et al. 2002).

Protein Data Bank analysis

The data set of PDB structures was determined by selecting protein structures that contained a cysteine residue and at least one phenylalanine, tyrosine, or tryptophan residue with better than 4.2 Å resolution. Histidine residues were excluded because they are frequently charged, and we wanted to avoid entangling a sulfur–π interaction with a cation–π interaction. A custom Perl script was developed that defined the center of each aromatic ring (for tryptophan it defined a center for both the five-membered and the six-membered ring) and determined the distance (denoted R) between that point and the sulfur of the cysteine residue. Any R <12 Å was considered a sulfur–π contact in our analysis. For each of these contacts, the angle (denoted θ) between the vector connecting the ring centroid and the sulfur and the normal to the aromatic ring was determined. If more than one protein structure gave duplicate contacts, only the highest resolution structure was retained in the data set. The final data set contained 753 protein structures, 642 of which had better than 2.5 Å resolution.

The resulting data were binned in 0.5 Å increments for R and 5° increments for θ. However, for each R/θ bin, the corresponding volume of the search area differs. Without correcting for this volume difference, many more contacts appear in bins with larger values for R and θ, even though these contacts are simply the result of the larger search area and not a preference for a particular geometry. To correct this effect, the number of contacts for each R/θ region is divided by the volume element:

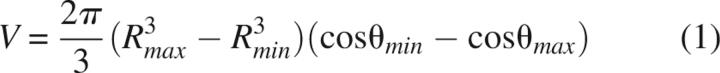where R_max, R_min, θ_max, and θ_min represent the maximum and minimum values defining each bin. Using this normalization factor, a large number of normalized contacts would indicate that more contacts were found in a particular region than would be expected from a random distribution.

Results and Discussion

Configuration selection and ab initio results

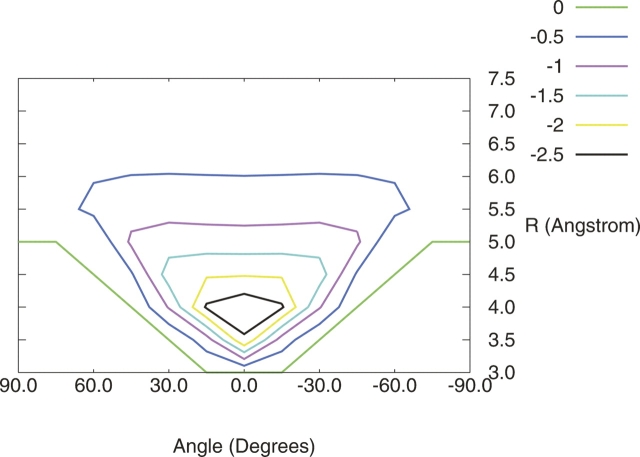
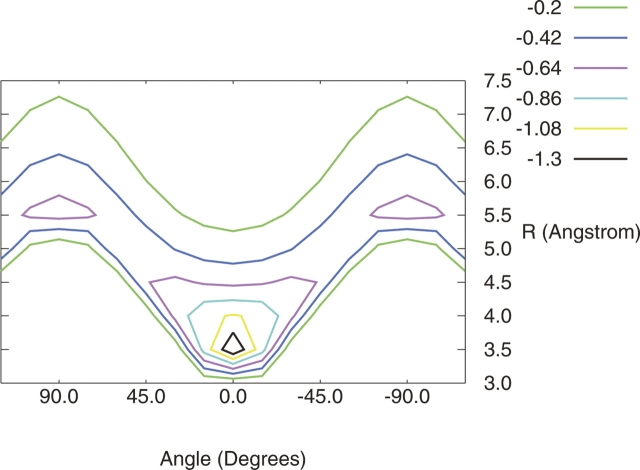
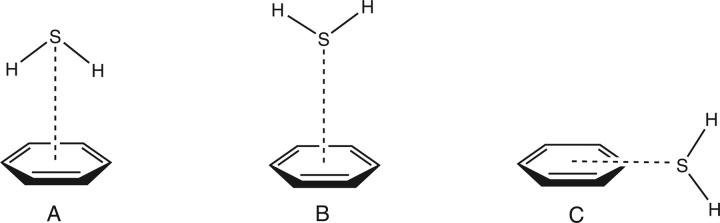
The MP2/aug-cc-pVDZ R/θ surfaces generated for each model configuration depicted in Figure 1 are shown in Figures 2 and 3. Based on these surfaces, three local minima are identified in this R/θ space, which are depicted in Figure 4. For the hydrogens-down configuration (Fig. 2), only one local minimum is found, at very short R (<4 Å) and θ = 0° (configuration A of Fig. 4). This corresponds to the configuration studied in great computational detail by Tauer et al. (2005), who found the equilibrium configuration at R = 3.8 Å with a total CCSD(T)/aug-cc-pVTZ interaction energy of −2.64 kcal mol⁻¹. For the hydrogens-up configuration (Fig. 3), two local minima in R/θ space can be identified. One has a similar configuration to the hydrogen-down minimum, with R ∼3.5 Å and θ = 0°; the other is found at around R = 5.5 Å and θ = 90°.

Figure 2.

Contour plot of the potential energy surface for hydrogens-down configuration of H₂S–benzene; energy (kcal mol⁻¹) as a function of the distance between monomers measured from the H₂S sulfur to center of benzene and the angle between the sulfur and the normal to the benzene ring.

Figure 3.

Contour plot of the potential energy surface for hydrogens-up configuration of H₂S–benzene; energy (kcal mol⁻¹) as a function of the distance between monomers measured from the H₂S sulfur to center of benzene and the angle between the sulfur and the normal to the benzene ring.

Figure 4.

Configurations selected for higher-level analysis.

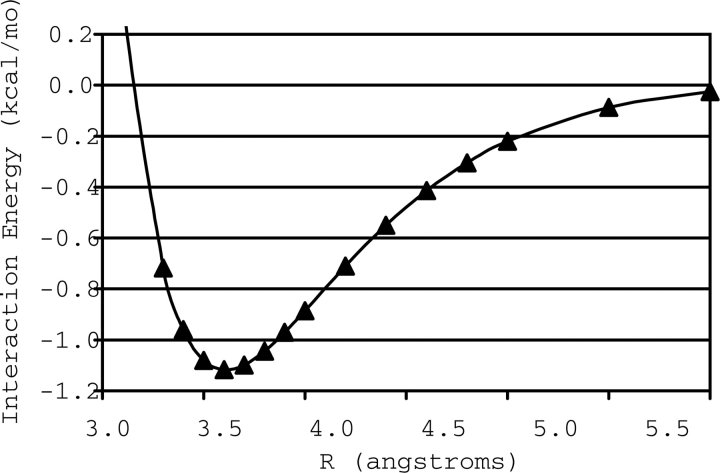
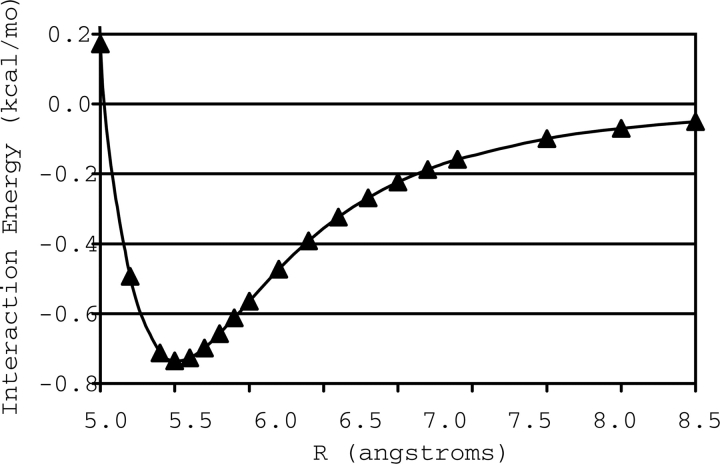
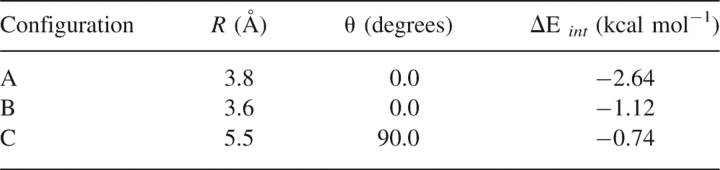
For each of the two local minima in this R/θ space resulting from the hydrogens-up starting configuration (configurations B and C of Fig. 4) that were not included in the study of Tauer et al. (2005), we determined a complete potential energy curve using CCSD(T) with the aug-cc-pVTZ basis, by fixing θ and varying R. The curves are depicted in Figures 5 and 6. The equilibrium configuration for B (θ = 0°) is found at R = 3.6 Å and has a total interaction energy of −1.12 kcal mol⁻¹. For C, where θ = 90°, the equilibrium inter-fragment separation is R = 5.5 Å, and this configuration has a total interaction energy of −0.74 kcal mol⁻¹. The equilibrium geometries and interaction energies of all three model systems are summarized in Table 1.

Figure 5.

Potential energy curve of configuration B of the H₂S–benzene complex.

Figure 6.

Potential energy curve of configuration C of the H₂S–benzene complex.

Table 1.

Equilibrium geometries and CCSD(T)/aug-cc-pVTZ interaction energies for the configurations of the H₂S–benzene complex

The model systems only encompass two possible orientations the hydrogen atoms could adopt relative to the aromatic ring. For this reason, although our configurations A–C are local minima in the R/θ space considered, this does not mean that they are actually local minima in the full 3N-6 dimensional space of all their internal coordinates, or even local minima in the space of all intermolecular degrees of freedom with rigid monomers. Because our goal is not to characterize the spectroscopic properties of the H₂S–benzene complex itself, but to understand the basic energetic properties of the sulfur–π interactions as they may occur within the constraints of protein structures, this is not problematic: The symmetric configurations considered have very similar energies to nearby configurations in which the H₂S is rotated along symmetry-lowering coordinates. Starting from the optimal inter-fragment distances for model configurations A–C, we performed unconstrained geometry optimizations at the MP2/aug-cc-pVDZ level of theory within the appropriate point-group symmetries. Configurations A and C each had two imaginary frequencies and are therefore second-order saddle points, while configuration B is a transition state with only one imaginary frequency. For configuration A, we followed one of the imaginary frequencies to a minimum configuration, which looked like configuration A but with one hydrogen directed toward the center of the ring, as though the H₂S of configuration A had been tipped to the side. This configuration, previously identified by Tauer et al. (2005), was confirmed to be a minimum of the full potential surface by frequency analysis and is in agreement with a minimum configuration identified by E. Arunan (pers. comm.). The minimum configuration differed from configuration A by only 0.02 kcal mol⁻¹, and the optimum inter-fragment separation was very similar, 3.7 Å. Attempts were made to follow the other imaginary frequencies to their corresponding local minima, but the potential surface is so flat in these regions that the optimizations could not converge in a reasonable amount of computational time. Therefore, to further verify that the model configurations considered appropriately describe the preferred geometries of S/π interactions generally, seven alternate configurations, which were selected to mimic the geometries observed in a random sampling of PDB entries, were examined that were similar to our model configurations except for the orientation of the hydrogen atoms. The energy for these configurations was determined at the MP2/aug-cc-pVDZ computational level, and the R and θ values for the configurations were measured and compared with corresponding model configurations. For instance, one alternate configuration examined placed the sulfur directly above the ring (θ = 0) with the H–S–H plane parallel to the aromatic plane. We found that this configuration is similar in energy (within 0.1 kcal mol⁻¹) to the corresponding hydrogens-up configuration (B) despite the differing orientations of the hydrogens. Overall, for all the PDB-like alternative configurations considered, good agreement was found for the interaction energy of the configuration and the symmetric model that would represent it.

If one considers a slightly larger small model system such as methanethiol–benzene, more consideration must be given to the positions of the hydrogen and methyl group than was required for the hydrogens of the simple H₂S model. For a methanethiol–benzene complex, a configuration analogous to configuration A directs a methyl group toward the aromatic ring. This configuration has destabilizing interaction energies for R values <4.0 Å and is not an appropriate representation of a cysteine/aromatic interaction in a protein structure because the aliphatic side chain would likely be in contact with the aromatic ring if the sulfur were to be that close to the ring in that orientation. A more physically motivated methanethiol–benzene model would direct the single hydrogen of methanethiol toward the center of the aromatic ring, as in the minimum energy configuration of H₂S–benzene. We examined this configuration at the MP2/aug-cc-pVDZ computational level for inter-fragment separations from 3.0 to 6.0 Å. The potential energy curves for the methanethiol model and the symmetric H₂S–benzene are nearly parallel and separated by ∼0.5 kcal mol⁻¹.

For methanethiol–benzene complexes in which the hydrogen and the methyl group are directed away from the aromatic ring, configurations analogous to B and C are appropriate models for cysteine/aromatic interactions, and direct comparisons can be made between the methanethiol model and the H₂S model. For the B configurations, partial potential energy curves were compared for R values from 3.0 to 5.5 Å, and the curves were not only almost parallel, but nearly coincident, with differences in the MP2/aug-cc-pVDZ interaction energy always <0.1 kcal mol⁻¹. The difference between the two curves is slightly greater for configurations like C, ∼0.25 kcal mol⁻¹, but the curves are still largely parallel. Overall, H₂S is qualitatively comparable to methanethiol in terms of the preferred interaction geometries it predicts for cysteine/aromatic interactions in protein structures, and, in fact, H₂S is a preferable model in the flexibility it allows in the placement of hydrogen atoms in the model system.

The difference between the methanethiol model and the H₂S model in different configurations suggests how the nature of the interaction changes with changing configuration. For the configurations where θ = 0 and the hydrogens (or methyl group, in the case of methanethiol) are directed toward the aromatic ring (A), the methanethiol–benzene complex is more stabilizing than the corresponding H₂S–benzene complex, suggesting that the increased dispersion interaction of the methyl group increases the interaction energy of the complex. However, if this model is flipped (to configurations like B), the methanethiol complex is less stabilized than the corresponding H₂S model. In this case, the electron donating methyl group has likely increased the electron density on the sulfur atom, and the electrostatic electron repulsion is more destabilizing (though, overall, the dispersion interaction does lead to a stabilizing interaction energy for both complexes). When this model is rotated to the in-plane configuration (C), the trend is reversed and methanethiol–benzene again becomes more stabilized than H₂S–benzene. In this case, the increased electron density on the sulfur atom creates a more favorable interaction with the partially positive hydrogen of the benzene ring, further stabilizing the interaction.

Comparison with data mining results from the Protein Data Bank (PDB)

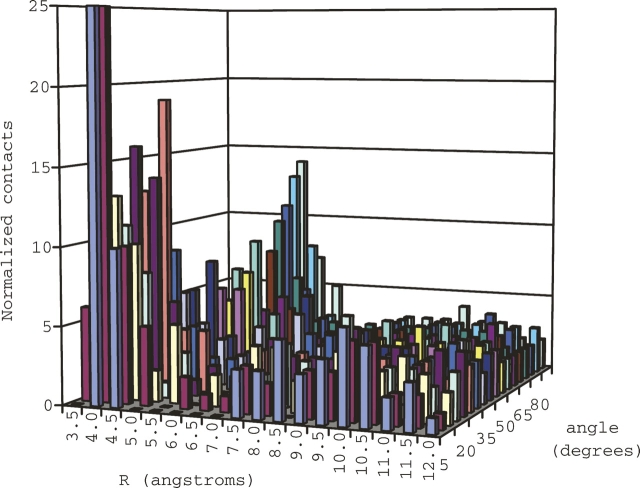
Each contact located by the data-mining script was sorted into bins according to its R/θ value. Each bin has a width of 0.5 Å in R-space and 5° in θ-space. The results were normalized using the volume element described in the computational details. A 2D histogram was constructed to display the R versus θ data (Fig. 7). The histogram shows two significant clusters of peaks. The largest is found for short distances (<4 Å) and small angles (<10°). The tallest peaks in this group are found for R = 3.5–4.0 Å, θ = 0°–10°, which corresponds to the equilibrium geometries of model configurations A and B. A second, shorter cluster of peaks is found for large angles (θ = 75°–90°) around R = 5.5 Å. The largest peaks in this group are found for R = 5.0–5.5 Å, θ = 85°–90°, which corresponds to the equilibrium geometry of model configuration C. Overall, the results indicate that the three configurations suggested by the local minima of the R/θ-surfaces for the simple H₂S–benzene complex are, in fact, the configurations that are found in protein structures in the PDB for cysteine S/π contacts.

Figure 7.

Histogram depicting number of normalized sulfur/π contacts from PDB data mining.

Interestingly, the region of the histogram between R = 5.0–7.0 Å for small angles (< ∼20°) has noticeably few contacts. This is again reflected by quantum mechanical results. Considering the energetics of the transition from configuration B to configuration C (shown in the contour plot of Fig. 3) as one moves to larger inter-fragment separations, the interaction energy of directly above configurations becomes less favorable. The more favorable configurations at these distances are not small angles directly above the center of the ring, but offset configurations with larger values for θ. Indeed, the histogram shows an increase in the number of contacts as one moves to larger angles at these values of R, culminating with the cluster of peaks around θ = 75°–90°. This preference for offset configurations levels off at ∼7.0 Å, when the interaction energy of the complex is very small and all geometries become approximately equally preferred.

Comparison with other database results

Previous database studies, which identified preferred configurations for S/π interactions using only database mining results without any insight from ab initio computations, often came to differing conclusions about the preferred configuration of the interaction. In the study of Reid et al. (1985), 36 high-resolution (better than 2.5 Å resolution) crystal structures were obtained from the Protein Data Bank and analyzed for contacts between sulfur atoms (from cysteine or methionine) and aromatic rings (from phenylalanine, tyrosine, or tryptophan). Several geometric parameters were analyzed including the distance between the sulfur and the aromatic center (analogous to our parameter R) and an angle describing the rise of the sulfur relative to the plane of the aromatic molecule. For each parameter, the number of occurrences was reported over the range of the parameter and compared with the number of occurrences that might be expected randomly, based on volume considerations. However, no two-dimensional correlation is presented to ascertain if particular distances appear more commonly at particular angles.

In the work of Zauhar et al. (2000), the investigators made two-dimensional comparisons to correlate the relationship between the optimum separation distance and the preferred angle relative to the aromatic ring. However, their study examined divalent sulfur groups of the form X–S–X, so they do not consider the possibility of hydrogens interacting with the aromatic ring. This makes their analysis more comparable to our results for configurations B and C, in which the hydrogens are directed away from the ring and the lone pairs of the sulfur atom are interacting with the aromatic system. Their 2D histograms show a maximum at 90° angles (sulfur in-plane with the aromatic ring) for large separations, and 0° or 180° (sulfur directly above or below the aromatic ring) for short separations, in general agreement with our quantum mechanical results. Additionally, they report a local maximum from 5.0–5.5 Å, extending over the 60°–115° angle range. Therefore, they report that the “ideal” sulfur–aromatic interaction geometry (as opposed to an S–H/π interaction geometry) is an in-plane configuration at a separation of ∼5 Å (similar to our configuration C), while our results would suggest it is a configuration in which the sulfur is directly above the aromatic ring at a shorter separation of 3.6 Å, as in the equilibrium geometry for configuration B.

This discrepancy in conclusions may lie in the normalization technique used by Zauhar et al. (2000) in which they compared their probability distributions to analogous probability distributions for C–CH₂–C group interacting with aromatic rings and looked for statistically significant differences between the two distributions. This necessarily assumes that there is no significant interaction between the CH₂ group and the aromatic system, and that it, therefore, can be used for a control. However, we have previously shown (Ringer et al. 2006) that there is a significant interaction between alkyl C–H groups and aromatic rings and that this interaction has distinct geometric preferences which happen to be very similar (R = 3.7 Å and θ = 0°) to the preferred configuration reported in this work for configuration B of the H₂S–benzene complex. The optimum configuration identified by Zauhar et al. (2000) is not necessarily the ideal sulfur–aromatic interaction configuration; rather, it is simply the preferred interaction configuration that is dissimilar to the preferred interaction configuration for alkyl C–H–aromatic interactions.

Conclusions

In this study, three local minima for the H₂S–benzene complex were identified on constrained MP2 potential energy surfaces that varied both the distance between the sulfur and the center of the benzene ring and the angle between the sulfur and the normal to the plane of the aromatic ring. For each configuration identified, CCSD(T) potential energy curves were generated with the aug-cc-pVTZ basis set, which should provide accurate binding energies to within a few tenths of a kcal mol⁻¹. One of these configurations centered the H₂S molecule directly above the center of the benzene ring with the hydrogens directed toward the aromatic ring; this configuration has previously been examined, and the optimum complex configuration has an inter-fragment separation of 3.8 Å and a total interaction energy of −2.64 kcal mol⁻¹. In the other two local minima identified in this study, the hydrogen atoms are directed away from the aromatic ring. For the hydrogens-away configuration centered directly above the benzene ring, the best estimate of the total interaction energy is −1.12 kcal mol⁻¹ with an optimum inter-fragment separation of 3.6 Å. For the hydrogens-away in-plane configuration, the best estimate of the total interaction energy is −0.74 kcal mol⁻¹ with an optimum inter-fragment separation of 5.5 Å.

Taking the H₂S–benzene complex as the simplest prototype for S/π interactions, the optimum geometries predicted by these potential energy curves were compared with the sulfur–π contacts that appear in protein structures from the Brookhaven Protein Data Bank. The number of occurrences for each search area was normalized to account for the different volumes of each area. Two regions of the resulting histogram showed a large number of normalized contacts, indicating that significantly more contacts appear than one would expect from a random distribution of atoms. These regions corresponded to the geometries of the minimum configurations predicted by the ab initio calculations for the H₂S–benzene complex. We believe these results validate the use of quantum mechanics calculations on small model systems to predict the geometries of interactions in protein structures.