The Fixation of Locally Beneficial Alleles in a Metapopulation

Abstract

Extinction, recolonization, and local adaption are common in natural spatially structured populations. Understanding their effect upon genetic variation is important for systems such as genetically modified organism management or avoidance of drug resistance. Theoretical studies on the effect of extinction and recolonization upon genetic variance started appearing in the 1970s, but the role of local adaption still has no good theoretical basis. Here we develop a model of a haploid species in a metapopulation in which a locally adapted beneficial allele is introduced. We study the effect of different spatial patterns of local adaption, and different metapopulation dynamics, upon the fixation probability of the beneficial allele. Controlling for the average selection pressure, we find that a small area of positive selection can significantly increase the global probability of fixation. However, local adaption becomes less important as extinction rate increases. Deme extinction and recolonization have a spatial smoothing effect that effectively reduces spatial variation in fitness.

THE fixation of novel alleles is a longstanding research topic, with work on panmictic populations dating back to the beginning of population genetics (Fisher 1922; Wright 1931). Fixation quantifies the dynamics of a rare allele by describing the probability and the expected time for it to increase to a significant frequency within a population (through selective forces or genetic drift). Fixation is therefore an important factor in determining genetic diversity and the rate of evolution. A low fixation probability and a short fixation time will produce a low genetic diversity where single alleles successively sweep through a population. A high fixation probability, or a long fixation time, will tend to increase the number of alleles segregating in a population, thus increasing genetic diversity. These issues can be of direct practical concern. For example, conservation genetics often aims to maximize the genetic diversity of endangered populations (Robert et al. 2003; Gao and Zhang 2005; Jamieson et al. 2006; Bohme et al. 2007), and health or agricultural programs aim to minimize the fixation probability of alleles for insecticide, drug, or vaccine resistance (McLean 1995; Heinemann 1999; Scott et al. 2000).

Few populations can truly be described as panmictic. Populations are often spatially fragmented and form a metapopulation system (Hanski and Gaggiotti 2004), with individual fragments going extinct and later being recolonized by migrants from surrounding populations. In a metapopulation many factors can vary from deme to deme, such as the selective advantage of an allele, s, the frequency of an allele, or the force of genetic drift. Under certain circumstances the spatial structure of a metapopulation has no effect, and fixation probability will be the same as that for a panmictic population (Maruyama 1970; Nagylaki 1982). In an ideal, panmictic population where individual reproductive success follows a Poisson distribution with mean μ, a favored rare allele that confers a μ = 1 + s has a fixation probability of ∼2s [for small s and where all other alleles confer a μ = 1 (Fisher 1930)]. In general, spatial structure has an important influence on fixation probability (Barton 1993; Whitlock 2003). Some of the effects of spatial structure upon fixation probability were succinctly described by Whitlock (2003), who extended the diffusion approximation of Kimura (1962). This gives an approximation for the fixation probability of an allele in a metapopulation that has a weak, additive benefit in all demes,

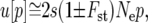(1)

where p is the initial (small) frequency of the allele in the metapopulation, s is its selection coefficient, N_e is the variance effective size of the metapopulation, F_st is a variation on Wright's F-statistic (see Whitlock 2003 for a detailed definition), and the plus/minus sign corresponds to hard/soft selection, respectively. This simple result shows that many mechanisms within a metapopulation (e.g., migration and extinction) largely act on fixation probability indirectly through their effect on the genetic structure and the effective size.

In many cases metapopulations are expected to be spatially heterogeneous and alleles to be locally adapted (i.e., an allele's selection coefficient varies between demes). The inclusion of environmental heterogeneity considerably complicates the theoretical description of fixation and has received little attention. Whitlock and Gomulkiewicz (2005) reviewed the main results to date and developed their own separation-of-timescale approach. In the strong-migration limit, spatial heterogeneity has little effect because the probability of fixation is given by substituting the average selection coefficient (averaged with respect to the stationary distribution of the backward migration matrix) into Kimura's panmictic formula (Nagylaki 1980). At the other extreme, the weak migration limit shows that, compared to the mean field expectation, fixation probability can be enhanced by spatial heterogeneities (Tachida and Iizuka 1991). Singular perturbation techniques have been used in a two-deme system (Gavrilets and Gibson 2002) but the quality of the approximation for the fixation probability can be poor (Whitlock and Gomulkiewicz 2005). In all these approaches extinction of local demes is not considered, despite it being a common metapopulation process (Hanski and Gaggiotti 2004). General results that include extinction into a stepping-stone model have shown that extinction does not qualitatively change the spatial clustering of alleles in a homogeneous environment, but causes drastic changes in an inhomogeneous environment (Kang et al. 1995). Metapopulation processes and local adaption have also been shown to have practical consequences for population management and restoration. In the context of population restoration, Robert et al. (2003) found that the spatial distribution of release sites affects the efficiency of local adaption and consequently the metapopulation's viability.

In this article we analyze the fixation probability and time of a locally adapted allele in a finite, heterogeneous stepping-stone model containing haploid individuals. We investigate the effects of local deme extinction rate, the spatial pattern of selective heterogeneity, the strength of dispersal, and the size of the metapopulation upon the fixation of locally beneficial alleles. The results are compared to theoretical results under the strong-migration limit.

METHODS

We use a spatially explicit simulation of a finite, two-dimensional stepping-stone model with n² demes arranged on a square grid. Neighboring demes are separated by 1 unit of distance. Each deme is assigned to one of two possible habitat types (habitat 1 and 2) and contains N haploid individuals who reproduce at random within the deme. Each haploid individual can be one of two possible genotypes, X and Y: genotype X has a fitness w_X = 1 in all demes, and genotype Y has fitness w_Y = 1 + s₁ in habitat 1, w_Y = 1 + s₂ in habitat 2. Genotype Y will be locally favored over genotype X in habitat i if s_i > 0. All individuals have the following life cycle: (i) birth, (ii) local selection, (iii) migration, (iv) reproduction (random genetic drift), and (v) death. Directly after birth the frequencies of genotypes X and Y in deme k are 1 − p_k and p_k, respectively. After selection the frequency of genotype Y becomes

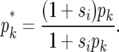(2)

Selection is therefore assumed to be soft. Migration replaces a fraction, m, of the individuals in each deme with individuals that come from within a radius d. The value of d determines the connectivity of the metapopulation, while m determines the strength of the connectance. When d = 1 our migration scheme is identical to a stepping-stone model, while when 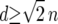the model becomes an island model. Following migration the frequency of genotype Y becomes

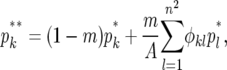(3)

where φ_kl = 1 if 0 < d_k,l ≤ d; otherwise φ_kl = 0, d_k,l is the distance between demes k and l, and 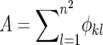. The boundaries of the metapopulation are nonreflecting. Finally, reproduction takes place as a binomial sample of the two genotypes, so that the frequency of genotype Y offspring in the next generation, p′_k, is given by

(4)

Until the end of migration it is assumed that the number of individuals in each deme is large, so that the dynamics are deterministic. The population size of a deme becomes finite, each with N individuals, at some point after migration (i.e., random genetic drift) so that reproduction of genotype Y is a binomial sample of postmigration individuals. Generations are nonoverlapping, so that after reproduction all adult individuals die.

Metapopulation dynamics also affect the genotype frequencies in the system. After individuals have migrated and before reproduction we assume that environmental perturbations can cause each deme to go extinct with probability e (the densities of genotypes X and Y are zero in extinct demes). A deme that has gone extinct will remain empty until recolonization occurs by new immigrants (all individuals will be immigrants, so that m = 1 in Equation 3). The probability that migrants successfully recolonize the deme is given by a recovery probability, r. Like in all patch-occupancy models (Hanski and Gaggiotti 2004), we assume that the number of immigrants is sufficient for the recolonized deme to be immediately close to its carrying capacity, N. The distribution of times from extinction to recolonization will have a geometric distribution with a mean time of 1/r. When d approaches the size of the metapopulation the process of colonization in our model approaches the migrant pool model (Slatkin 1977), while reducing d brings our model closer to the propagule-pool model and the stepping-stone model (Kimura 1953).

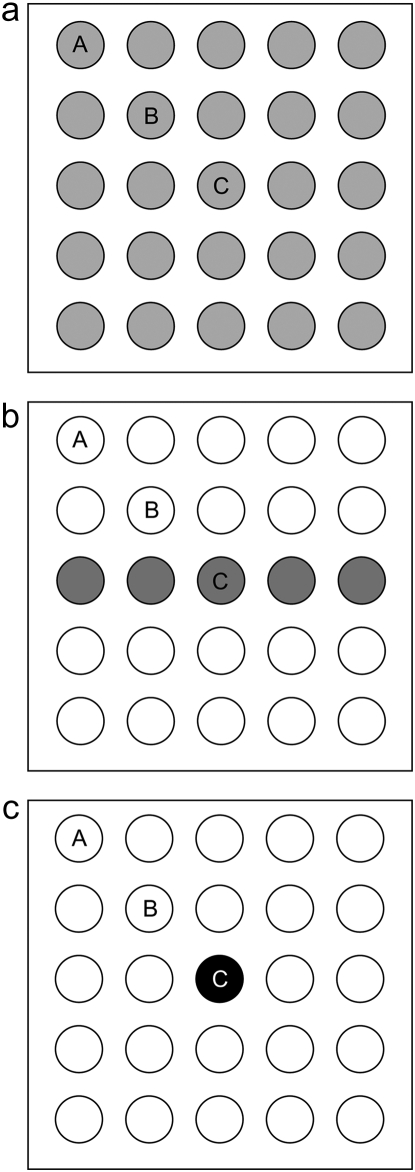
We consider the fixation probability and the fixation time of the beneficial genotype Y under two initial conditions: when one individual of genotype Y enters a single deme ( deme A, B, or C, Figure 1) and when one individual of genotype Y enters each deme of the metapopulation. These two situations could correspond to the random mutation of a genotype X individual and the influx of new migrants across the entire metapopulation, respectively. We compare three different selection landscapes (uniform, linear, and point, Figure 1). In all landscapes, genotype Y is neutral in habitat 1 (s₁ = 0) and has a fitness advantage in habitat 2 (s₂ > 0). We compare different selection landscapes in two ways: one with a constant “average selection coefficient” (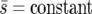) and one with a constant “average selection pressure” (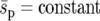), where the fixation probability for weakly selected alleles in the strong-migration limit is constant (Nagylaki 1980). We include these two comparisons because 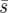is most relevant in applied studies where complete information about dispersal across the landscape is unlikely, whereas 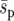correctly accounts for the long-term equilibrium of the dispersal process. For the average selection coefficient, we add up the selection coefficients from all demes and divide by the number of demes. For the average selection pressure, the long-term probability that an individual occupies a patch is calculated from the dominant eigenvector of the migration matrix, and the average selection pressure is then the sum across all demes of the selection coefficients multiplied by their corresponding individual probability of occupancy. For all cases, we analyze the system with (e = 0.4) and without (e = 0) local extinction. We also consider three different sizes of landscape (n² = 25, 49, and 81), a range of recovery probabilities (r = 0.2–1), and a range of dispersal distances (d = 1–8). The model was written in Delphi and is available from the authors upon request.

Figure 1.—

The three selective landscapes for a 5 × 5 metapopulation: (a) uniform, (b) linear, and (c) point. Habitats 1 and 2 are shown by open and shaded demes, respectively. One genotype Y individual was introduced either in every deme or in one of deme A, B, or C.

The model was tested against known analytical results for structured populations with homogeneous selection and no extinction (Maruyama 1970) and also with local extinction of demes (Barton 1993; Whitlock 2003). Known analytical results for homogeneous environments were also compared with the results from our heterogeneous simulations. First, we include deme extinction in the strong-migration limit (Nagylaki 1980) by calculating the expected equilibrium metapopulation size and using this as the effective population size. Second, the result of Whitlock for soft selection (Equations 11 and 17 in Whitlock 2003) is calculated with a homogeneous selection coefficient given by the strong-migration limit (Nagylaki 1980).

RESULTS

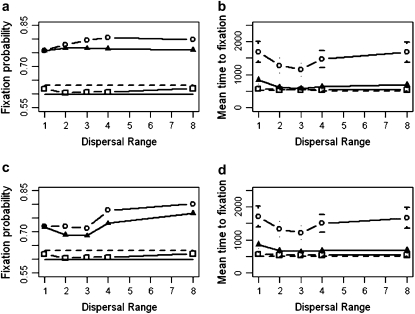
We start by looking at the system with no extinction and an initial condition where one beneficial allele occurs in every deme (Figure 2). Figure 2, a and b, presents fixation probabilities for a constant average selection coefficient, while Figure 2, c and d, presents those for a constant selection pressure. For a uniform landscape, we conclude that our system is close to the strong-migration limit because the fixation probabilities are in good agreement with theory for all dispersal distances (Figure 2, a and c). As the selective landscape becomes less uniform the fixation probability of the beneficial genotype Y increases, irrespective of whether the average selection coefficient (Figure 2a) or the selective pressure (Figure 2c) is held constant. For the “point” landscape under strong dispersal (d = 8), the fixation probability is 0.79, compared to 0.62 for the uniform landscape. We found a similar relative increase for the fixation probability in the point environment when the average selection coefficient 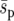was an order of magnitude smaller. The increase in fixation probability with dispersal range, d, was found to be an effect of the finite size of the system. Although local adaption increases the ultimate probability of fixation, it also increases the average time until fixation and the variation about this average (Figure 2, b and d). In the most extreme case, the average time to fixation in the point landscape was over three times that of the uniform landscape.

Figure 2.—

Fixation probability and mean fixation time estimates for genotype Y (from 10,000 simulations) as a function of the dispersal range, d, and the uniform (squares), linear (triangles), and point (circles) selective landscapes shown in Figure 1. (a and b) Constant average selection coefficient 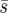=0.02; (c and d) constant selection pressure 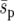= 0.02. The strong-migration limit (fixation probability and time) and the soft-selection prediction of Whitlock (2003) (fixation probability only) are shown as solid and dashed horizontal lines, respectively. The metapopulation is 5 × 5, N = 100, m = 0.05, e = 0, r = 1, and initially one genotype Y individual starts in every deme. Standard deviations are shown by error bars (some error bars are hidden by the symbols).

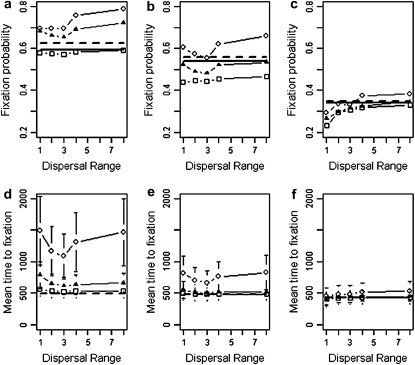
We now introduce local deme extinction into the system. With an extinction rate e = 0.4 and a dispersal range d = 1 the expected proportion of occupied patches at equilibrium is 0.7. The theory of Whitlock (2003) and the strong migration limit predict that increasing the rate of extinction from e = 0 to e = 0.4 will reduce the probability of fixation of a homogeneously selected allele from ∼0.6 to ∼0.35 (Figure 3). Our simulation results show that the effect of environmental extinction on the fixation probability of a locally adapted allele is in broad agreement with the theory for homogeneous selection. Moreover, as the rate of extinction increases, the distinction between a uniformly selected and a locally selected allele weakens, and the results of the homogeneous system become more applicable to the heterogeneous case. Contrary to the situation without extinction, fixation in a metapopulation with strong extinction is largely independent of the selective landscape (Figure 3c). For strong-extinction rates (e = 0.4), reducing the dispersal distance decreases the probability of fixation below the strong-migration predictions for all selective landscapes (Figure 3c), and this effect remains when cyclic boundaries are used. The fixation times follow a similar pattern to the fixation probabilities. As extinction rate increases fixation times decrease (along with their variance) and the effect of different selective landscapes is reduced. Unlike fixation probabilities, the fixation time for the high-extinction rate (e = 0.4) is insensitive to the dispersal range.

Figure 3.—

Estimates of fixation probability and average time to fixation for genotype Y (from 10,000 simulations) when (a and d) e = 0.01, (b and e) e = 0.1, and (c and f) e = 0.4 as a function of the dispersal range, d, and the uniform (squares), linear (triangles), and point (circles) selective landscapes shown in Figure 1. The strong-migration limit (fixation probability and time) and the soft-selection prediction of Whitlock (2003) (fixation probability only) are shown as solid and dashed horizontal lines, respectively. The metapopulation is 5 × 5, 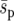= 0.02, N = 100, m = 0.05, r = 1, and initially one genotype Y individual starts in every deme. Standard deviations are shown by error bars (some error bars are hidden by the symbols).

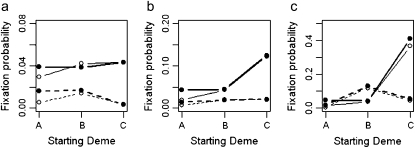
To look at the effect of spatial heterogeneity in more detail we investigated the initial condition of a single, genotype Y individual starting in deme A, B, or C (Figure 1). From the results in Figures 2 and 3 we would predict that the initial location of an allele affects fixation probability only when extinction is low. With no extinction (Figure 4, solid line) the local heterogeneity in selection is clearly visible. For example, in the point environment (Figure 4c) a genotype Y individual starting in deme A has a fixation probability of 0.013 compared to 0.37 for an individual starting in deme C. In agreement with our prediction, increasing extinction rate decreases the importance of spatial heterogeneity in the selective landscape (Figure 4). When e = 0.4 the fixation probability of genotype Y is generally less than that for e = 0, with little distinction between the uniform, linear, and point selective landscapes. Increasing the dispersal range to d = 8 (maintaining the frequency of emigration at m = 0.05) has surprisingly little effect upon the fixation probabilities, suggesting that the heterogeneities in selection have their most important effect early on in the fixation process. However, larger dispersal tends to slightly increase the fixation probability. This effect is most notable for individuals who start out on the edges of the environment. We studied the effect of dispersal upon the time taken for a single copy of genotype Y in deme A to establish in deme C for the point environment (Figure 1c) with no extinction (m = 0.05, 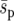= 0.02, N = 100). With long-range dispersal (d = 8) the median time to establish in deme C was 18 generations, and this occurred with a probability of 0.063. In comparison, short-range dispersal (d = 1) had a median time for establishment in deme C of 62 generations, and the probability of this occurring at all was 0.014. The median times taken for genotype Y to reach a frequency of 0.1 in deme C were 36 generations (probability = 0.039) and 82 generations (probability = 0.012) for d = 8 and 1, respectively. The relative difference between d = 1 and d = 8 fixation probabilities is very close to the probabilities for a frequency of 0.1. Therefore the main difference between long and short dispersal in our model occurs in the first 50 generations before genotype Y has been able to establish in the beneficial deme.

Figure 4.—

Fixation probability estimates from uniform (a), linear (b), and point (c) environments for genotype Y (from 30,000 simulations) for one initial individual present in population A, B, or C (Figure 1). Solid and dashed lines are for e = 0 and e = 0.4, while open and solid symbols correspond to dispersal ranges of d = 1 and d = 8, respectively. The metapopulation is 5 × 5, the average selection coefficient is constant 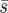= 0.02, N = 100, m = 0.05, and r = 1. Standard deviations are smaller than the symbols.

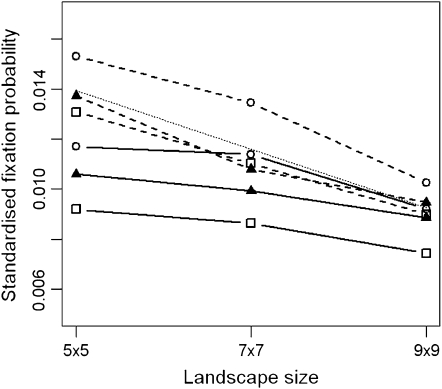
The size of the metapopulation also has an effect upon the fixation probabilities (Figure 5). For a constant selection pressure the effect of increasing the size of the metapopulation is to decrease the standardized fixation probability (fixation probability for genotype Y divided by the initial number of genotype Y individuals). The strength of this effect is greater for the larger dispersal range and is well estimated by the theoretical predictions (Figure 5, shaded dashed line). The larger metapopulations have a larger effective size that increases the efficiency of selection and hence the absolute probability of fixation. However, this increase is less than the increase in the initial number of genotype Y individuals, leading to a decrease in the standardized fixation probability with increasing metapopulation size. The selective landscape has little interaction with the system size because the decrease in standardized fixation probability is approximately the same for the uniform, linear, and point environments.

Figure 5.—

Estimates of the standardized fixation probability (fixation probability per initial number of genotype Y individuals) as a function of the number of demes in the metapopulation (from 10,000 simulations). Squares, triangles, and circles are for uniform, linear, and point selective environments, and solid and dashed lines are for d = 1 and d = 8, respectively. The selection pressure is constant 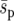= 0.02, N = 100, m = 0.05, e = 0.4, r = 1, and initially one genotype Y individual starts in every deme. The soft-selection prediction of Whitlock (2003) is shown by a shaded dashed line. Standard deviations are smaller than the symbols.

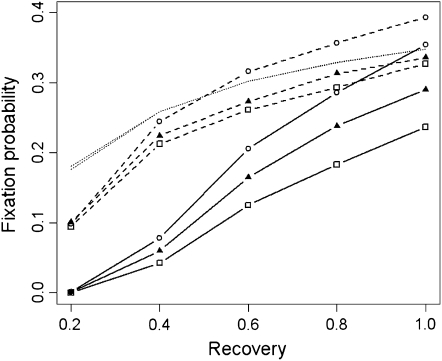
Finally we consider the possibility that extinct demes may stay extinct for more than one generation by changing the recovery rate, r (Figure 6). For e = 0.4, lowering the recovery rate from r = 1 to r = 0.2 reduces the equilibrium proportion of occupied demes from 0.7 to 0.3 for both d = 1 and 8. Reduction in recovery rate led to a further reduction in the difference between selective landscapes. When r = 0.2 the fixation probabilities from point, linear, and uniform environments were indistinguishable. Reduction in recovery rate also led to a reduction in the fixation probability irrespective of the strength of dispersal and the selective landscape. This reduction is in part expected from the theory for homogeneous systems, but the reduction in fixation probability for our heterogeneous system exceeds this expectation. The reduction in fixation probability is less severe and in better agreement with the theoretical estimations when d = 8 because the wider dispersal distance reduces the size of heterogeneities introduced by deme extinctions.

Figure 6.—

Estimates of the fixation probability of genotype Y as a function of the recovery rate, r (from 20,000 simulations). Solid and dashed lines are for d = 1 and d = 8, respectively. Squares, triangles, and circles are for uniform, linear, and point selective environments (Figure 1). The average selection coefficient is constant 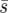= 0.02, N = 100, m = 0.05, e = 0.4, and initially one genotype Y individual starts in every deme. The strong-migration limit and the soft-selection prediction of Whitlock (2003) are shown as the shaded dashed line. Standard deviations are smaller than the symbols.

DISCUSSION

Natural environments are heterogeneous, and selection pressures are partly expected to mirror this heterogeneity. Furthermore, stochastic extinction (either demographic or environmental) and habitat destruction events generate additional variation in the demographic and genetic structure of the metapopulation. Describing the evolution of allele frequencies in such systems is complex and little theoretical work considers the population genetics of a heterogeneous metapopulation (see Gavrilets and Gibson 2002; Whitlock and Gomulkiewicz 2005). Our study has used simulations to look at the effect of heterogeneous selective landscapes and local patch extinction upon the fixation of a novel beneficial allele.

Our study has two main findings: first, when extinction is weak heterogeneous environments increase the fixation probability (and time) for an equivalent average selection coefficient. For the same average selection coefficient, the larger the range in local selection coefficients is, the larger the fixation probability. Therefore, local areas of strong selection have a disproportionate effect upon the ultimate fixation probability. One implication of this result is that the use of a spatial average selection pressure in a heterogeneous habitat will underestimate both the probability of fixation and the time to fixation. Second, as extinction risk increases, the distinction between different selective landscapes is reduced, and fixation probability and time are reduced. Landscape heterogeneities are therefore expected to be least important for systems whose local populations are highly transient.

Some of the behavior of our system can be understood in terms of existing theory. In a finite metapopulation extinction has two effects: a demographic effect by reducing the total metapopulation size (which increases the strength of drift), and a founder effect due to recolonization events. Both of these effects are expected to reduce the efficiency of selection, which will decrease the fixation probability of a beneficial allele. The effect of a reduced metapopulation size can be estimated by substituting the expected metapopulation size into existing theoretical expressions for fixation probability (Nagylaki 1980; Whitlock 2003). These theoretical estimates capture some of the change in fixation probability, but do not include the founder effect of recolonization, and tend to underestimate the reduction in fixation probability (Figures 3, a–c, 5, and 6). The effect of recolonization upon neutral genetic diversity in an infinite-island model has commonly been studied using the migrant- and propagule-pool models (Slatkin 1977). For our system, the migrant-pool model is closest to large dispersal-range cases (d = 8), while the dispersal-range d = 1 case is approaching the propagule-pool model. Previous studies found that local deme extinction and recolonization always reduce the neutral allelic diversity within a deme, and this effect is strongest for the propagule model (Pannell and Charlesworth 1999). From this we would expect selection to become less efficient as extinction rate increases and this inefficiency to be most pronounced in a propagule-pool model. This is consistent with our results, where fixation probability is reduced by deme extinction, and this reduction is strongest for low-dispersal ranges. Although the selective advantage of the beneficial allele is being weakened by extinction, the system is far from being effectively neutral. When the extinction probability is 40%, the probability of fixation is still an order of magnitude above the neutral expectation of 0.01.

Other results from our simulations are harder to explain on the basis of the current theory for uniform selective landscapes. We find that heterogeneous landscapes (Figure 1, b and c) increase the fixation probability compared to a uniform landscape (Figure 1a) with an “equivalent” selection pressure, 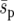(a spatially averaged selection coefficient). Similar results have been noted by Whitlock and Gomulkiewicz (2005). The diffusion approximation agrees relatively well with our results for the uniform landscape, indicating that the average selection is sufficiently weak and migration sufficiently strong for 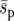to be a valid description of selection in the uniform system. In the heterogeneous landscapes two factors may contribute to an increase in fixation probability. First, since 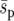is held constant, local selection coefficients become stronger as the landscape becomes more heterogeneous. So selective forces in a heterogeneous landscape may be locally strong even if the global selection pressure is weak (although we continued to see a highly significant effect of heterogeneity when 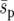was reduced by an order of magnitude). Second, for the spatial average, 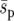, to be relevant to global allele fixation, within-deme allele-frequency changes must spread through the environment and approach a long-term spatial distribution, before significant further change of within-deme allele frequencies. If this is not the case, the selective pressure around beneficial demes will be stronger than 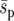, which ultimately affects the balance between drift and selection. Spatial heterogeneity is important in this respect. The long-term spatial distribution is often reached more quickly for a uniform landscape than for a heterogeneous landscape, because in a uniform landscape allele-frequency changes are less spatially variable. In cases of extreme heterogeneity (e.g., Figure 1c) local selective pressures may have to be exceedingly weak before a spatial average selection pressure is meaningful, because it can easily take tens of generations to approach the long-term spatial distribution.

The positive correlation between fixation time and fixation probability, even in the absence of deme extinction, is also not expected from current theory. The diffusion approximations for fixation time (Kimura and Ohta 1969) and fixation probability (Kimura 1962 Whitlock 2003) in a uniform environment predict that an increasing selection coefficient will increase the probability of fixation and decrease the time to fixation (increasing extinction risk will decrease both probability and time until fixation). We observe that locally increasing the selection coefficient (keeping the global selection pressure constant) increases both fixation probability and time. This positive correlation may be expected if the locally adapted allele quickly becomes abundant in its favored deme. Once abundant, the global fixation is determined by a balance between the neutral spread of the allele across the remaining environment (with the favored deme acting as a source) and its loss in the favored deme. Since neutral spread, even in the presence of a source, can take longer than the spread of a homogeneously selected allele, fixation time can increase in our heterogeneous environment even if ultimate fixation is more probable.

When one beneficial allele was introduced into the metapopulation the fixation probability depended upon the deme of introduction and very weakly upon the dispersal range (Figure 4). This suggests that the main determinant of fixation occurs before immigrants have a chance to establish in a population. For our system, an immigrant genotype may take several tens of generations before becoming established in a deme at a nonnegligible frequency. This means that the differential growth rates of genotypes X and Y in habitat 2 have time to play an important role in determining the final fixation probability. This was confirmed by further simulation, where the main distinction between short- and long-range dispersal was the time and the probability of a beneficial allele to become initially established in the habitat for which it was locally adapted (i.e., habitat 2). A beneficial genotype that is already present in its preferred habitat will fix across the whole metapopulation relatively quickly, compared to a genotype starting far away from its preferred habitat. Extinction will make the spatial distribution of genotypes less important, because extinction forces establishment from neighboring demes, effectively smoothing out spatial differences. As extinction risk increases, colonists are more likely to originate from distant demes and the spatial smoothing is increased. This effect is exaggerated in our model by the fact that a deme quickly reaches carrying capacity once colonized. A limited local population growth, for which carrying capacity is achieved only after many generations, will increase the probability that colonists come from nearby demes. Thus, limited local population growth is expected to reduce the homogenizing effect of extinction.

Previous studies found that spatial structure can shape evolutionary and coevolutionary trajectories (Gandon et al. 1996; Thrall and Burdon 1997; Gomulkiewicz et al. 2000; Nuismer et al. 2000). Our results show that increasing the spatial heterogeneity of local selection will promote the fixation probability of a novel beneficial allele. As discussed by Eldredge et al. (2005), the combined effect of landscape structure and dispersal range could play a role in explaining the rate of evolutionary change observed in the fossil record. Our results show that spatial variation in selection pressure can be an important consideration for the fixation of a beneficial allele within a metapopulation. This has practical implications, for example, with pesticide use in modern agricultural systems (Delaney et al. 2006) where the evolution of resistance to a pesticide would reduce the effectiveness of the pest control strategy (Scott et al. 2000). The latest transgenic crops (Christou et al. 2006) will tend to produce a spatially uniform selection intensity for resistance, whereas the spatial distribution of conventional pesticide application depends upon the local farm strategy. Our results indicate that for a fixed average selection pressure (i.e., a fixed average intensity of pesticide application) a uniform pesticide treatment, rather than a treatment that heavily targets certain areas, would minimize the fixation probability of pesticide-resistance alleles. However, a uniform treatment would also minimize the time taken to reach fixation, suggesting that heavily targeting specific areas would be beneficial to slow the spread of resistance once established. Similar issues are raised with concerns of drug and vaccine resistance for human health, where the spatial variation in drug or vaccine use could influence the evolution of the pathogens being controlled (McLean 1995; Heinemann 1999; Gandon et al. 2001). The importance of spatial variation in selective pressures for conservation genetic programs is somewhat different (Robert et al. 2003; Gao and Zhang 2005; Jamieson et al. 2006; Bohme et al. 2007). Here, the goal is to maintain or increase genetic diversity within a population. In this case, a spatially uniform selection pressure would reduce genetic diversity, since it favors selective sweeps (by reducing fixation probability and fixation time), which reduces the number of segregating alleles at a locus. Wild populations can also suffer local extinctions, which will reduce the importance of spatial variation, but also further reduce the fixation probability. This will be enhanced if local population recovery is delayed.

Our results are also relevant at the paleontological scale, where the fossil record commonly shows that a species' long-term rate of evolutionary change is surprisingly low (Eldredge et al. 2005). Understanding this stasis in the fossil record amounts to understanding the process of genotype fixation, because change in the fossil record is seen only after a novel genotype appears in a local population, becomes established, and then spreads over a wide geographical area. Our simple system already shows that spatial variation can have a significant impact on fixation. We see that heterogeneity can increase fixation probability, but at the expense of increasing fixation time. In our system, the process of local establishment in beneficial habitats is relatively rapid, while the spread of locally established genotypes is comparatively slow, suggesting that the final stage of genotype spread is important to understand in relation to stasis.

Our model has density-dependent effects immediately following recolonization, so that once recolonization has occurred a population immediately reaches carrying capacity. Local competitive effects and spatial structure have been shown to be important factors determining the rate of invasion in asexual populations (Gerrish and Lenski 1998; Gordo and Campos 2006; Habets et al. 2007) and are likely to have effects upon the fixation of novel alleles in heterogeneous environments. Including realistic demographic effects following recolonization is expected to change local effective population sizes, the probability of recolonization of neighboring demes, and consequently the overall probability of fixation. Broadening the scope of our simulations to include temporally variable selective landscapes is another topic for further research, with direct relevance to coevolutionary dynamics (Gandon et al. 1996; Thrall and Burdon 1997; Morgan et al. 2005) and adaption to novel environments (Turner and Elena 2000).

Past research has shown that spatial structure can affect the fixation probability of an allele whose selective coefficient is independent of spatial position. Here we show that the spatial pattern of local adaption can also affect the fixation probability of an allele. Strong local adaption increases the probability of fixation across the entire metapopulation, and this effect is strongest when demes are not prone to extinction. Local extinction reduces the probability that a beneficial allele will become fixed and weakens the impact of spatial variation in allele fitness. Developing these results for practical applications will provide valuable management guidance when both genetic and demographic dynamics are important components of a system.