A Bayesian Method for Simultaneously Detecting Mendelian and Imprinted Quantitative Trait Loci in Experimental Crosses of Outbred Species

Abstract

Genomic imprinting is interpreted as a phenomenon, in which some genes inherited from one parent are not completely expressed due to modification of the genome caused during gametogenesis. Subsequently, the expression level of an allele at the imprinted gene is changed dependent on the parental origin, which is referred to as the parent-of-origin effect. In livestock, some QTL for reproductive performance and meat productivity have been reported to be imprinted. So far, methods detecting imprinted QTL have been proposed on the basis of interval mapping, where only a single QTL was tested at a time. In this study, we developed a Bayesian method for simultaneously mapping multiple QTL, allowing the inference about expression modes of QTL in an outbred F₂ family. The inference about whether a QTL is Mendelian or imprinted was made using Markov chain Monte Carlo estimation by comparing the goodness-of-fits between models, assuming the presence and the absence of parent-of-origin effect at a QTL. We showed by the analyses of simulated data sets that the Bayesian method can effectively detect both Mendelian QTL and imprinted QTL.

GENOMIC imprinting is interpreted as a phenomenon, in which some genes inherited from one parent are not completely expressed due to modification of the genome caused during gametogenesis. Subsequently, expression levels of alleles at imprinted genes are dependent on the parent from which they are inherited and the identical allele shows different effects corresponding to the parental origins, which are called the parent-of-origin effects. When one of the paternal allele and the maternal allele at a gene is exclusively expressed and the other is completely silenced, this feature of imprinting is referred to as complete imprinting and the gene can be said to be completely imprinted. On the other hand, when both the paternal allele and the maternal allele at a gene are expressed at different levels depending on the parental origin, this feature of imprinting is referred to as partial imprinting and the gene can be said to be partially imprinted.

It has been shown that some genes and traits were influenced by genomic imprinting in several organisms. Especially in livestock such as pigs, some QTL affecting traits of economical importance, including reproduction and meat productivity, have been reported to be imprinted with allelic effect changed by the parental origin in several researches (Knott et al. 1998; Jeon et al. 1999; Nezer et al. 1999; De Koning et al. 2000; Tuiskula-Haavisto et al. 2004), where interval mapping methods were used in genome scans for imprinted QTL in F₂ families derived from crossing two outbred lines. These interval-mapping methods for imprinted QTL were based on a regression model, where phenotypic values of a trait in F₂ individuals are regressed on the line origin of alleles as well as on the parental origin of alleles that can be traced back from the F₂ individuals to their F₁ parents at a putative QTL in outbred F₂ populations. Recently, interval mapping for exploring imprinted QTL in inbred F₂ populations, derived from crosses between two inbred lines, was also devised by Cui et al. (2006) on the basis of the maximum-likelihood method, where two heterozygous QTL genotypes, say, Q₁Q₂ and Q₂Q₁, with Q₁ and Q₂ being two alleles at a QTL and the first and second alleles indicating paternal and maternal ones, respectively, can be discriminated with the EM algorithm using phenotypic values even in inbred F₂ populations.

In the report by De Koning et al. (2002), the statistical models of interval mapping for imprinted QTL in outbred F₂ families were reviewed and the efficiencies of the models in QTL detection were investigated using simulation experiments. They proposed a two-step statistical procedure to identify the expression mode for a detected QTL as follows: (A) test of H₀: Mendelian QTL model vs. H₁: full imprinted QTL model that assumes the parent-of-origin effects of QTL and thus includes both cases of partial imprinting and complete imprinting and (B) test of H₀: completely imprinted QTL model vs. H₁: Mendelian QTL model. Tuiskula-Haavisto et al. (2004) applied a similar statistical procedure to detection of parent-of-origin effects at QTL in a chicken F₂ population.

Since the model for QTL expression is fixed as a Mendelian QTL model or an imprinted QTL model in the analyses with interval mapping, multiple steps are required to identify the expression mode of QTL, as seen in De Koning et al. (2002) and Tuiskula-Haavisto et al. (2004), which might cause a problem in determining thresholds due to multiple testing. Therefore, methods to simultaneously map multiple QTL are more suitable for detecting imprinted QTL and discriminating between Mendelian and imprinting expressions of QTL.

In this article, we developed a Bayesian method using a Markov chain Monte Carlo (MCMC) algorithm that enabled us to map multiple QTL simultaneously and to infer the expression mode for each detected QTL in F₂ families derived from crossing two outbred lines. We utilized a reversible-jump MCMC (RJ–MCMC) procedure in moving across competing models corresponding to several expression modes of QTL, including Mendelian expression and imprinting expressions that were furthermore classified into partial imprinting and complete imprinting with exclusive paternal or maternal expression. Although several Bayesian methods have been devised for QTL mapping in experimental populations such as F₂ families (Satagopan et al. 1996; Sillanpää and Arjas 1998; Hayashi and Awata 2005) and actual populations of more complicated structure (Heath 1997; Uimari and Hoeschele 1997; Bink and Van Arendonk 1999; Uimari and Sillanpää 2001; Yi and Xu 2001), there have been no Bayesian methods incorporating the procedure of inference for the expression mode of QTL. The power to detect both Mendelian QTL and imprinted QTL and the accuracy in the inference for the expression mode of QTL were evaluated using simulation experiments for the developed Bayesian method.

PREMISE FOR ANALYSES OF IMPRINTED QTL

Outbred F₂ family:

In this study, we consider detection of QTL in a three-generation family derived from a cross between two outbred lines, denoted by P₁ and P₂, in the F₀ generation. The family consists of the two grandparental lines, F₁ parents, and F₂ individuals. We assume that P₁ and P₂ may segregate at the marker loci, but are fixed for alternative alleles at QTL that are indicated by Q₁ and Q₂ for P₁ and P₂, respectively. Moreover, we assumed that the marker information was sufficient to trace the parental origins of QTL alleles back from each F₂ individual to its parents in the F₁ generation and consequently two heterozygote Q₁Q₂ and Q₂Q₁ are discriminated in F₂ individuals, where the first allele and the second allele indicate the paternally inherited allele and the maternally inherited allele, respectively.

Expression modes of QTL:

Expression modes of QTL are here classified into Mendelian expression (E₁), partial imprinting (E₂), where both the paternal allele and the maternal allele are expressed, but at different levels depending on their parental origin, and complete imprinting, which is furthermore divided into exclusive paternal expression (E₃) and exclusive maternal expression (E₄). Under these four modes, E₁, E₂, E₃, and E₄, the genetic contribution of QTL, g, was differently modeled as follows. In the expression mode of E₁, we write g = 2a, d, and −2a for QTL genotypes Q₁Q₁, Q₁Q₂ (Q₂Q₁), and Q₂Q₂, respectively, where 2a and d are regarded as the additive effect and the dominance effect of QTL and there is no difference in genetic contributions between two heterozygotes, Q₁Q₂ and Q₂Q₁. In the expression mode of E₂, denoting the paternally inherited QTL effect by a_pat and the maternally inherited QTL effect by a_mat, we can express the genetic contribution of QTL as g = a_pat + a_mat, a_pat − a_mat + d, −a_pat + a_mat + d, and −a_pat − a_mat, corresponding to QTL genotypes Q₁Q₁, Q₁Q₂, Q₂Q₁, and Q₂Q₂, respectively (De Koning et al. 2000, 2002). In the case of complete imprinting, we obtain g = a_pat for Q₁Q₁ and Q₁Q₂ and g = −a_pat for Q₂Q₁ and Q₂Q₂ under the mode E₃ by taking a_mat = d = 0 in E₂ and g = a_mat for Q₁Q₁ and Q₂Q₁ and g = −a_mat for Q₁Q₂ and Q₂Q₂ under the mode E₄ (De Koning et al. 2000, 2002). Different notations were used in Cui et al. (2006) for the genetic contribution of imprinted QTL.

ESTIMATION PROCEDURE IN BAYESIAN QTL MAPPING

Statistical model for Mendelian and imprinted QTL:

We assume that observations of the phenotype of a trait, y, are available for F₂ individuals of size n as well as marker information, M, including genotypic data at markers for F₀, F₁, and F₂ individuals and the linkage map of markers. We can apply a linear model for y,

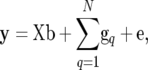(1)

where X is a known design matrix for a vector of nongenetic effect b (including the overall mean), N is the number of QTL affecting a trait, g_q (q = 1, 2, … , N) is an n × 1 vector for the genetic contribution of the qth QTL in F₂ individuals, and e is the vector of residual (environmental) effect following an n-variate normal distribution with mean vector 0 and covariance matrix σ_e²I_n (I_n is the n × n identity matrix). The ith element of g_q, denoted as g_qi, indicates the genetic contribution of the qth QTL for the ith F₂ individual. As described in the previous section, g_qi is expressed in different forms corresponding to the QTL genotype of the individual and the expression mode of the QTL. 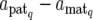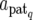For example, when the QTL genotype of the individual is Q₁Q₂, we write the genetic effects at the QTL as g_qi = d_q, + d_q, , or 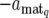, corresponding to the expression mode E₁, E₂, E₃, or E₄, respectively, with subscript q indicating the qth QTL.

Prior and posterior distributions for QTL parameters:

We denote the expression mode of N QTL by S = (S₁, S₂,…, S_N), where S_q is the expression mode of the qth QTL taking E₁, E₂, E₃, or E₄, and genetic effects of the qth QTL by a_q, the components of which are differently specified as a_q = (a_q, d_q), (, d_q), (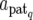), and () depending on S_q = E₁, E₂, E₃, and E₄, respectively. Genetic effects for all QTL are collectively written by a = (a₁, a₂,…, a_q). Let λ_q denote the location of the qth QTL and λ = (λ₁, λ₂,…, λ_N) denote the locations of all QTL. The genotypes at all QTL are written as G_i = (G_1i, G_2i,…, G_Ni) for the ith F₂ individual and the QTL genotypes of all F₂ individuals are given as G = (G₁, G₂,…, G_n), which are sampled on the basis of the marker information M.

The model parameters and QTL genotypes to be inferred via the MCMC algorithm are written as θ = (N, a, λ, S, G, b, σ_e²). The joint prior density function for θ can be calculated as the product of the prior density for each of components:

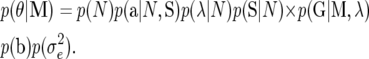(2)

The prior distribution of the number of QTL, p(N), is assumed to be a truncated Poisson distribution with mean μ and a predetermined maximum number (Jannink and Fernando 2004; Sillanpää et al. 2004). The probability distribution of QTL genotypes of F₂ individuals, p(G | M, λ), is given as a product of the probabilities for genotypes at each QTL in each F₂ individual, p(G_qi | M, λ) (q = 1, 2,…, N; I = 1, 2,…, n), which is obtained following the method proposed by Haley et al. (1994). In brief, the probabilities of G_qi being Q₁Q₁, Q₁Q₂, Q₂Q₁, and Q₂Q₂, which are denoted as p_11qi, p_12qi, p_21qi, and p_22qi, respectively, can be calculated on the basis of marker genotypes of the individual and using the recombination frequencies between QTL and markers. Prior distributions of other parameters might be given as uniform distributions or some other distributions according to the prior information available.

Given the number of QTL, N, QTL expression modes, S, and QTL genotypes, G, the distribution of y, p(y | N, S, G, a, b, σ_e²), is written as a normal distribution from (1) as follows:

(3)

Bayesian estimation of θ is carried out on the basis of the posterior distribution p(θ | y, M), which is expressed as

(4)

MCMC sampling is used for Bayesian inference about each of the components of θ. The details of MCMC sampling adopted in this study are described in the appendix.

SIMULATION EXPERIMENTS

We evaluated the efficiency in detecting QTL and the accuracy of the inference about the expression mode of QTL using the proposed Bayesian method by analyzing simulated data sets in F₂ populations derived from a cross between two founder outbred lines, P₁ and P₂. Two scenarios, referred to as case I and case II hereafter, were considered in simulation experiments. In case I, we evaluated the efficiency of the Bayesian method in detecting a single QTL under different expression modes. In case II, we investigated the capability of the Bayesian method to resolve multiple QTL with different expression modes. In both case I and case II, the performances of the Bayesian method were assessed in comparison with the interval-mapping procedure for detecting imprinted QTL.

Evaluation of efficiencies in detecting a single QTL:

In case I, we evaluated the performance of the developed Bayesian method in detecting a single QTL, with Mendelian expression mode (E₁) and completely imprinting modes (E₃ and E₄), on a chromosome when P₁ and P₂ were either fixed for alternative QTL alleles or segregating at frequencies of 0.80 and 0.20 for the positive allele at biallelic QTL in P₁ and P₂, respectively. The structures of a simulated F₂ family and a simulated genome were almost the same as those of De Koning et al. (2002), which are summarized as follows. We generated F₁ individuals by random mating of 20 males in P₁ and 80 females in P₂ (4 females per male), where 20 F₁ males and 80 F₁ females were obtained. They were randomly mated to produce 400 F₂ offspring (5 offspring per female) with equal sex ratio. A biallelic QTL with expression mode E₁, E₃, or E₄ was simulated at 46 cM on a chromosome of 100 cM length, on which 11 markers were located every 10 cM. We simulated eight alleles for every marker, with four line-specific alleles segregating at equal frequencies in P₁ and P₂. The phenotype of each F₂ individual was determined by the sum of an effect of QTL located on a chromosome, 10 unlinked QTL effects, each with an additive effect of 0.25 and segregating at a frequency of 0.5 in both P₁ and P₂, and an environmental effect sampled from a normal distribution with mean of 0 and a variance of 0.47. QTL effects were given as 0.25 and 0.5. The proportion of total variance explained by the simulated QTL, denoted by , ranged from 0.04 (2a = 0.25, d = 0.0) to 0.25 (a_pat = 0.5 or a_mat = 0.5).

We simulated 200 replicates of data, each of which included marker genotypes for all individuals and sex records and phenotypes for F₂ individuals, for each case of variable QTL effects under different expression modes when founder lines were fixed with alternative alleles or segregating at QTL. We first generated 200 replicates of data including the information for genotypes of markers and a simulated QTL, sex records, genetic effects at 10 unlinked loci, and environmental effects for individuals prior to the generation of phenotypic values. Then we obtained the data sets of phenotypic values for F₂ individuals by assigning different expression modes and corresponding genetic effects to the simulated QTL on the basis of the information generated beforehand. Therefore, the same 200 replicates of data sets including marker and QTL genotypes, sex records, genetic effects at 10 unlinked loci, and environmental effects were commonly used for generating phenotypic values for variable genetic effects of QTL under different expression modes. The data of marker genotypes, sex records, and phenotypes were only subject to the analysis, where the model including sex effect was applied although no sex effect was simulated.

Each of 200 replicates was analyzed by the Bayesian method to evaluate the power to detect a simulated QTL and the accuracy of inference about the QTL expression mode. For the prior distribution of the QTL number, p(N), a Poisson distribution with mean 2 was assumed. We assumed that prior probabilities of expression modes for a QTL were p(S = E₁) = 0.6, p(S = E₂) = 0.2, p(S = E₃) = 0.1, and p(S = E₄) = 0.1. The priors of the other parameters, p(a | N, S), p(λ | N), p(b), and p(σ_e²), were assumed to be uniform distributions over ranges of possible values of parameters, where fixed effects b included a general mean and sex effect. For the proposal probabilities of QTL expression modes, which are transition probabilities between QTL expression modes used in the update of S, we assigned the values of δ = 0.2, κ = 0.6, ω = 0.1, η = 0.1, ζ = 0.1 (for δ, κ, ω, η, ζ, see Table 1).

TABLE 1.

Proposal probabilities q(S* | S) for new QTL expression mode S* given current expression mode S

	S*
S	E1	E2	E3	E4
E1	1 − δ	δ	0	0
E2	κ	1 − κ − 2ω	ω	ω
E3	0	η	1 − η	0
E4	0	ζ	0	1 − ζ

E₁, E₂, E₃, and E₄ are Mendelian, partial imprinting, exclusive paternal, and exclusive maternal expressions, respectively.

In case I, we performed 50,000 MCMC cycles with the last 40,000 cycles used for sampling the values of parameters every 10 cycles in the Bayesian analysis. Therefore total number of samples kept was 4000. We made some posterior inference on the basis of the posterior QTL intensity (QI) (Sillanpää and Arjas 1998), which was defined as the relative frequency of the cycles in which a QTL was detected in each bin with length of 1 cM along a chromosome. For the judgment of whether or not QTL detection is successful in each analysis, the total QI summed over all bins of a chromosome was used as the criterion. This summed QI (SQI) can be regarded as the strength of evidence for linkage of QTL to the chromosome. The threshold values for SQI were determined with the analyses of another 200 replicates of data sets generated under the same condition as described above except that there were no QTL segregating between P₁ and P₂ on the chromosome. We evaluated the variation of SQI calculated on a whole chromosomal region (100 bins) through analyses of the 200 null data sets, which included phenotypes determined by effects of 10 unlinked loci and an environmental effect in the absence of QTL on the chromosome, but provided the same data for marker genotypes and sex records of all individuals as the original data sets generated under the presence of a QTL on the chromosome. As a result, we obtained threshold values of SQI of 0.66, corresponding to a type I error of 0.05. This means that the times of SQI exceeding a value of 0.66 by chance are expected to be ≤10 in the analyses of 200 null data sets.

Accordingly, we regarded the detection of QTL as successful when SQI exceeded the specified threshold value. Although there was the possibility that more than one QTL were simultaneously fitted in the model with the Bayesian method, we treated such multiple QTL fitted as an identical QTL. When a QTL was detected, the location of each QTL was estimated as a posterior mean of the positions of fitted QTL. We considered the posterior probabilities for expression modes of QTL to infer the QTL expression modes. The expression mode having the highest posterior probability was regarded as the most probable expression mode for a detected QTL in the analysis of each data set. The posterior distributions for genetic effects of detected QTL were obtained, corresponding to each of the expression modes. Therefore, the QTL effects were estimated under different expression modes.

To compare the efficiencies of detecting QTL and the accuracies of inference about the expression mode of QTL between the Bayesian method and conventional methods, we also analyzed the same data sets with the interval mapping method for imprinted QTL (De Koning et al. 2002). In the analyses with interval mapping, the detection of QTL was attempted on the basis of an F-test of a model assuming no QTL (H₀: null model) vs. a model assuming the presence of QTL with expression mode E₂ (H₁: model E₂) that was regarded as a full model. This test was denoted by T1. Moreover, expression modes of the detected QTL were inferred by carrying out an additional two hypothesis tests, T2 and T3, where T2 is an F-test of the model E₁ (H₀) vs. the model E₂ (H₁) and T3 is another F-test of either the model E₃ or the model E₄ (H₀) vs. the model E₂ (H₁). Accordingly, the interval-mapping (IM) procedure for identifying imprinted QTL consisted of three tests, T1, T2, and T3. The threshold of F-ratios in T1 with a chromosomewise significance level of P = 0.05 was obtained as 4.12 by the analyses of the 200 null data sets generated assuming no QTL. Two statistical tests to infer QTL expression modes, T2 and T3, were carried out on the position of detected QTL with the highest F-ratios in T1; thus, nominal threshold values with a pointwise significance level of P = 0.05 were adopted in T2 and T3. The threshold values of T2 and T3 were obtained as 3.87 and 3.02, respectively, which were the 0.95th quantiles of the corresponding F distributions. The interval-mapping procedure for discriminating QTL expression modes described here was similar to that adopted by Tuiskla-Haavisto et al. (2004), where the F-test of either the model E₃ or the model E₄ vs. the null model was first performed to detect QTL indicating the imprinting expression and then T2 and T3 were considered at the position of the QTL to confirm the expression mode.

The detection of simulated QTL was regarded as successful in IM when T1 was significant at any position on a chromosome. The expression mode of QTL detected in T1 was inferred by additional tests T2 and T3 as follows: QTL expression was inferred as E₁ when T2 was nonsignificant, as E₂ when both T2 and T3 were significant, and as E₃ or E₄ when T2 was significant but T3 was nonsignificant. The estimates for genetic effects of QTL were obtained for each of the QTL expression modes at the position of detected QTL with the highest F-ratio in T1, which were least-squares estimates of models corresponding to QTL expression modes.

Evaluation of efficiencies in resolving multiple QTL:

In case II of the simulation experiments, our objective was to evaluate the efficiencies of the Bayesian method in resolving multiple QTL of different expression modes. We considered a genome consisting of two chromosomes, denoted by LG1 and LG2, each of length 100 cM, on which 11 markers were located every 10 cM for each. We located three biallelic QTL, denoted by QTL1, QTL2, and QTL3, on LG1 and LG2, where QTL1 and QTL2 were linked and located at 25 and 75 cM, respectively, on LG1 and QTL3 was at 65 cM on LG2. We assumed that QTL1, QTL2, and QTL3 were exclusively maternal (E₄) with a genetic effect of , Mendelian (E₁) with 2a₂ = 0.5 and d₂ = 0.0, and exclusively paternal (E₃) with , respectively. We assumed that P₁ and P₂ were fixed with alternative alleles at all three QTL. For the structure of the F₂ family, the generation of marker genotypes, and the effects of unlinked QTL and environmental effect, the same settings as in case I were used. The proportions of total variance explained by QTL1, QTL2, and QTL3 were calculated as , 0.131, and 0.042, respectively, taking the covariance between the effects of QTL1 and QTL2 into consideration.

We generated 100 replicates of data sets in case II. Each data set was analyzed by the Bayesian method to evaluate the power to detect each QTL and the accuracy of inference about QTL expression modes. We performed 100,000 MCMC cycles with the last 80,000 cycles used for sampling the values of parameters every 20 cycles (4000 cycles available for sampling) for the Bayesian estimation. We used SQI obtained on the QTL region as the criterion for successful QTL detection as in case I. The threshold values for the SQIs were determined with the analyses of another 100 data sets generated under the condition that there are no QTL on LG1 and LG2 segregating between P₁ and P₂. Since two chromosomes were considered in case II, the distribution of the maximum value of two SQIs, each obtained in each chromosome, was investigated with 100 null data sets to determine the threshold value corresponding to the prespecified genomewide significance level. We obtained threshold values of SQIs of 0.69, corresponding to genomewide type I error of 0.05. The successful detection of QTL3 was determined on the basis of SQI on LG2, which is QIs summed over all bins of 1 cM length on LG2. The detection of QTL1 and QTL2 located on LG1 was regarded as successful when the SQI calculated in the two respective QTL regions, i.e., [0 cM, 50 cM] and (50 cM, 100 cM] on LG1, exceeded the threshold value of 0.69. Moreover, the capability of simultaneously detecting both QTL1 and QTL2 was evaluated by the fraction of the iterations at which the two QTL were fitted at the same time, in all MCMC iterations. The locations, expression modes, and genetic effects of QTL were estimated as the means of the posterior distributions of the parameters, as described in case I. For discriminating QTL1 and QTL2, the posterior distributions were considered on the two regions, [0 cM, 50 cM] and (50 cM, 100 cM] of LG1, respectively.

We analyzed the same data sets with the IM procedure, consisting of three statistical tests, T1, T2, and T3, in the same way as adopted in case I. The threshold value with genomewide significance level of P = 0.05 in T1 was obtained as 4.75 by the analyses of the 100 null data sets generated in the absence of QTL. For T2 and T3, the threshold values were determined as in case I. The detection of QTL3 was regarded as successful when T1 was significant with a significance level of P = 0.05 at any point on LG2. For QTL1 and QTL2, we decided that the two QTL were simultaneously detected when the F-ratio showed two peaks exceeding the threshold value in the respective regions, [0 cM, 50cM] and (50cM, 100cM] of LG1, and decreased below the threshold value between the two peaks in T1. Only one of QTL1 and QTL2 was judged to be detected, when the F-ratio was significant in either region, [0 cM, 50 cM] or (50 cM, 100 cM] of LG1, or when the F-ratio was significant in both of the regions but the criterion for simultaneous detection of QTL1 and QTL2, as described above, was not fulfilled. In the latter case, either one of QTL1 or QTL2 was determined to be detected according to the position of the maximum F-ratio observed. The estimated location of each detected QTL was obtained as the position showing the peak of the F-ratio. The expression mode of QTL successfully detected in T1 was inferred by T2 and T3 performed at the estimated QTL position. The estimates of QTL effects were obtained under each expression mode as in case I.

RESULTS OF SIMULATIONS

Results of a single-QTL detection:

The power of detecting a single QTL and the estimates of the location, effects, and expression mode of a QTL obtained by analyses of 200 data sets in case I with the Bayesian method and the IM method are shown in Table 2 for some simulated QTL. As the same simulation settings as those in De Koning et al. (2002) were used in case I, the results obtained by the analyses with IM were comparable to the results reported by them. The performance of the Bayesian method in case I, which was similar to that of IM as shown in Table 2, is summarized as follows.

TABLE 2.

Detection and estimation for QTL simulated in case I

				Effectse		Inferred modef
QTL effecta (frequency)	Methodb	Powerc	Positiond	2a or apat	d or amat	E1	E2	E3	E4
A 0.25 (1.0/0.0)	Bayes	0.830	46.1 (9.1)	0.26 (0.06)	0.01 (0.11)	0.785	0.000	0.010	0.035
	IM	0.840	46.4 (12.6)	0.28 (0.06)	0.01 (0.13)	0.775	0.000	0.035	0.030
A 0.5 (1.0/0.0)	Bayes	1.000	45.7 (3.9)	0.48 (0.07)	0.01 (0.10)	0.995	0.005	0.000	0.000
	IM	1.000	45.9 (3.9)	0.50 (0.06)	0.00 (0.11)	0.955	0.045	0.000	0.000
D 0.25 (1.0/0.0)	Bayes	0.955	46.1 (7.1)	0.25 (0.06)	0.24 (0.10)	0.945	0.005	0.005	0.000
	IM	0.965	47.3 (9.5)	0.26 (0.06)	0.26 (0.11)	0.900	0.050	0.005	0.010
E3 0.25 (1.0/0.0)	Bayes	0.995	45.8 (6.6)	0.24 (0.04)	—	0.055	0.050	0.890	0.000
	IM	1.000	46.2 (8.2)	0.26 (0.04)	—	0.045	0.075	0.880	0.000
E4 0.25 (1.0/0.0)	Bayes	0.990	46.0 (5.7)	—	0.25 (0.05)	0.040	0.035	0.000	0.915
	IM	0.995	46.4 (6.4)	—	0.26 (0.04)	0.035	0.040	0.000	0.920
A 0.25 (0.8/0.2)	Bayes	0.435	46.8 (11.4)	0.19 (0.05)	−0.01 (0.11)	0.350	0.000	0.040	0.045
	IM	0.270	45.3 (13.9)	0.23 (0.05)	−0.01 (0.13)	0.205	0.010	0.035	0.020
A 0.5 (0.8/0.2)	Bayes	0.930	45.8 (7.3)	0.30 (0.07)	−0.01 (0.10)	0.840	0.005	0.035	0.050
	IM	0.915	46.4 (9.7)	0.32 (0.07)	−0.01 (0.12)	0.820	0.020	0.040	0.035
D 0.25 (0.8/0.2)	Bayes	0.480	45.8 (11.6)	0.19 (0.05)	0.10 (0.11)	0.395	0.005	0.040	0.040
	IM	0.330	45.0 (13.9)	0.22 (0.05)	0.15 (0.12)	0.275	0.015	0.020	0.020
E3 0.25 (0.8/0.2)	Bayes	0.705	45.7 (9.3)	0.17 (0.05)	—	0.120	0.020	0.565	0.000
	IM	0.605	44.8 (11.5)	0.22 (0.02)	—	0.070	0.055	0.480	0.000
E3 0.5 (0.8/0.2)	Bayes	0.955	45.9 (5.0)	0.31 (0.07)	—	0.050	0.055	0.850	0.000
	IM	0.950	46.3 (6.0)	0.32 (0.07)	—	0.030	0.055	0.865	0.000
E4 0.25 (0.8/0.2)	Bayes	0.660	47.3 (9.5)	—	0.17 (0.04)	0.120	0.010	0.000	0.530
	IM	0.565	49.1 (12.1)	—	0.21 (0.03)	0.130	0.035	0.000	0.400
E4 0.5 (0.8/0.2)	Bayes	0.995	46.5 (5.7)	—	0.29 (0.06)	0.030	0.030	0.000	0.935
	IM	0.995	47.1 (6.5)	—	0.30 (0.06)	0.015	0.080	0.000	0.900

^aA, additive QTL without dominance effect; D, dominant QTL with 2a = d; E₃, QTL with exclusive paternal expression with effect a_pat; E₄, QTL with exclusive maternal expression with effect a_mat (frequency of positive QTL allele in founder lines).

^bBayes, Bayesian method; IM, interval-mapping procedure for imprinted QTL.

^cProportion of replicates with successful detection of QTL based on the threshold of significance level P = 0.05 in a total of 200 replicates.

^dAverage of estimated positions (centimorgans) over the replicates with successful QTL detection. Standard deviations of estimates are given in parentheses.

^eAverage of estimated effects for simulated QTL over the replicates with successful QTL detection, where 2a and d are relevant to Mendelian QTL and a_pat or a_mat is relevant to imprinted QTL. Standard deviations of estimates are given in parentheses.

^fProportion of replicates supporting each QTL expression mode as the most probable state in the replicates with successful QTL detection. Accordingly, the sum of the proportions for E₁, E₂, E₃, and E₄ was equivalent to the power.

When founder lines were fixed for different QTL alleles, the power of the Bayesian method in detecting a QTL was quite high. Even for small additive QTL with effect of 2a = 0.25, detection was successful in 83% of the replicates, where a QTL was correctly inferred as being Mendelian in 94.6% (78.5/83 = 0.946, see Table 2) of the replicates with successful detection. The power was increased to 95.5% for dominant QTL with effects of 2a = d = 0.25 and attained 100% for additive QTL with effect of 2a = 0.5, where a detected QTL was accurately inferred as being a Mendelian QTL in most of the replicates with successful detection (Table 2). When founder lines were fixed with alternative QTL alleles, the Bayesian method also successfully detected an imprinted QTL in most of the replicates, where the powers of detecting QTL were 99.5 and 99% of the replicates under expression modes E₃ (exclusively paternal expression) and E₄ (exclusively maternal expression) with effects of 0.25, respectively. The proportions of accurate inference about QTL expression modes were 89.4 and 92.4% for such QTL under E₃ and E₄, respectively.

When founder lines were segregating for the positive allele of QTL with frequencies of 0.80 and 0.20 in P₁ and P₂, respectively, the powers of the Bayesian method in detecting QTL were decreased for both Mendelian and imprinted QTL. The decrease in powers for Mendelian QTL with the smaller effects (2a = 0.25 or 2a = d = 0.25) was remarkable, where the segregation at QTL in founder lines reduced the powers to 43.5 and 48% for additive and dominant QTL, respectively (Table 2). Spurious imprinting was inferred more frequently. In the additive QTL with 2a = 0.25, the QTL was inferred as being imprinted in 19.6% of the replicates detecting QTL. For the imprinted QTL with smaller effects (a_pat = 0.25 or a_mat = 0.25), the power was also much reduced and the inference about QTL expression mode was less accurate. However, the reduction in the power due to the QTL segregation within founder lines was less for the Bayesian method than IM for small QTL with effects of 0.25 (Table 2).

Results of multiple-QTL resolution:

The power of detecting each of three QTL and the accuracy in estimation of the location and expression mode of each QTL obtained by analyses of 100 data sets using the Bayesian method and IM are shown in Table 3.

TABLE 3.

Detection and estimation for simulated QTL in case II

				Effectd				Inferred modee
Simulated QTL	Methoda	Powerb	Positionc	2a	apat	amat	d	E1	E2	E3	E4
QTL1 (LG1: 25 cM, E4) (amat = −0.25)	Bayes	0.80	25.3 (4.1)	—	—	−0.26 (0.04)	—	0.01 (0.04)	0.01 (0.11)	0.00 (0.00)	0.78 (0.85)
	IM	0.57	28.4 (12.6)	—	—	−0.21 (0.02)	—	0.01	0.21	0.15	0.20
QTL2 (LG1: 75 cM, E1) (2a = 0.5, d = 0.0)	Bayes	0.99	75.4 (3.6)	0.47 (0.08)	—	—	0.03 (0.11)	0.95 (0.83)	0.02 (0.14)	0.02 (0.02)	0.00 (0.01)
	IM	0.98	76.1 (3.9)	0.39 (0.07)	—	—	0.02 (0.14)	0.67	0.14	0.17	0.00
QTL3 (LG2: 65 cM, E3) (apat = 0.2)	Bayes	0.71	61.9 (9.7)	—	0.21 (0.04)	—	—	0.07 (0.13)	0.03 (0.14)	0.61 (0.72)	0.00 (0.01)
	IM	0.64	62.6 (12.5)	—	0.24 (0.03)	—	—	0.12	0.04	0.48	0.00

The proportions of MCMC iterations fitting QTL1 and QTL2 simultaneously in each analysis were averaged as 0.82 ± 0.27.

^aBayes, Bayesian method; IM, interval mapping.

^bProportion of replicates that successfully detected each QTL with genomewide significance level of P = 0.05 in a total of 100 replicates.

^cAverage of estimated QTL positions calculated in the replicates with successful detection of QTL with standard deviations given in parentheses.

^dAverage of estimated QTL effects corresponding to the simulated expression mode over the replicates with successful QTL detection with standard deviations given in parentheses.

^eProportion of replicates supporting each QTL expression mode as the most probable state in the replicates with successful detection of QTL. Averages of posterior probabilities of QTL expression modes are given in parentheses for the Bayesian method. Prior probabilities of expression modes E₁, E₂, E₃, and E₄ were 0.6, 0.2, 0.1, and 0.1, respectively, and transition probabilities among expression modes were set at δ = 0.2, κ = 0.6, ω = 0.1, η = 0.1, and ζ = 0.1.

The Bayesian methods showed higher efficiency in resolving two linked QTL, QTL1 and QTL2, than IM, where the estimates of effects and positions of the two QTL were unbiased and the QTL expression modes were accurately inferred with the Bayesian method although IM often provided biased estimates for effects and the incorrect inference about QTL expression modes for the two linked QTL. For QTL1 with smaller effect (), which was located near QTL2 with greater effects (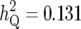), the Bayesian method showed much higher power than IM, where the powers of the Bayesian method and IM were 80 and 57%, respectively. We considered the fractions of the iterations, which accepted the model simultaneously fitting QTL1 and QTL2, in all MCMC iterations for evaluating the capability of the Bayesian method to resolve QTL1 and QTL2. The fractions of the iterations with simultaneous detection of QTL1 and QTL2 were averaged over 100 replicates as 0.82. For QTL3 with the smallest effects (), the Bayesian method showed low power of 71%, but still greater than IM with power of 63%.

Considering the proportions of the replicates correctly inferring the expression mode for each QTL in the replicates with QTL detection, which were regarded as the conditional efficiency of the inference for QTL expression mode given the QTL was detected, the Bayesian method showed such proportions higher than IM. These proportions were 0.98, 0.96, and 0.86 with the Bayesian method for QTL1, QTL2, and QTL3, respectively, while the corresponding proportions with IM were 0.35, 0.68, and 0.75, respectively.

The posterior probabilities for N, the number of QTL fitted in the model with the Bayesian methods, were investigated in the analysis of each data set and averaged over 100 replicates. The averaged posterior probabilities for N are shown in Table 4.

TABLE 4.

Averages of posterior probabilities of QTL number in the analyses of case II with the Bayesian method

Average of posterior probabilities of N						Average of posterior expectations of N
0	1	2	3	4	≥5
0.001 (0.004)	0.036 (0.101)	0.282 (0.234)	0.573 (0.234)	0.099 (0.085)	0.009 (0.011)	2.763 (0.401)

The averages of posterior probabilities and posterior expectations for QTL number over 100 replicates are listed with standard errors given in parentheses.

DISCUSSION

Criterion for QTL detection with the Bayesian method:

The results of a Bayesian QTL analysis are provided as the form of the posterior distributions of parameters including the number of QTL affecting a trait, genetic effects and locations of QTL, and other QTL characteristics such as the QTL expression mode that is of main concern in this study. For the determination of the presence of QTL on the chromosomal region, the posterior probability of QTL linkage to that region, which is an estimate of the posterior distribution for QTL locations, is of greatest interest. The fraction of MCMC iterations in which at least one QTL is located at each bin with some length is defined as the posterior QTL intensity of that bin, denoted by QI, and used as an estimate of the posterior QTL locations (Sillanpää and Arjas 1998, 1999). However, QI is much affected by the length of the bin and will be lower for a bin with smaller length. Thus, QI summed over all bins on a chromosomal region, which is referred to as SQI, was used as a criterion for the determination of the presence of QTL linked to the region in the Bayesian analysis of this study. The threshold of SQI was obtained by the empirical distribution of SQI calculated on each chromosome in the absence of QTL, where null data with no simulated QTL were generated in the simulation experiments. For the threshold of SQI corresponding to the genomewide significance level, the empirical null distribution of maximum SQIs over a whole genome consisting of multiple chromosomes was considered as in the case of the determination of thresholds for a conventional LOD score and F-ratio calculated in the interval mapping. When SQI exceeded a threshold with a genomewide significance level of P = 0.05 on some regions, we determined the presence of QTL on such regions.

We compared the performance between the developed Bayesian method and the IM procedure in the simulation experiments. Although the strict comparison between the Bayesian method and conventional methods is difficult, the comparison based on simulated data is reasonable by controlling the type-I error rate for QTL detection with the Bayesian methods and IM based on the thresholds for SQI and the F-ratio. Therefore, the powers of QTL detection and the proportions of the replicates with accurate inference of QTL expression mode obtained in the simulation study as shown in Tables 2 and 3 could be utilized for suitable evaluation of the performance of the Bayesian method in comparison with IM. The problem of the interpretation for QTL detection with the Bayesian method was reviewed by Wijsman and Yu (2004).

Detection of QTL in the simulation study:

In case I of the simulation experiments, where a single biallelic QTL was located on a chromosome, the power of QTL detection was expected to be similar in the Bayesian method and IM since the advantage of simultaneously fitting multiple QTL in the Bayesian method was not taken for the case of a single QTL. As shown in Table 2, comparable powers of detecting QTL were obtained in case I for the Bayesian method and IM when founder lines were fixed with alternative QTL alleles. The similar powers between the Bayesian method and IM indicated that the comparison of the two methods under the control of type-I error rate was suitable.

In case II where we assumed that three QTL were located on two chromosomes, the Bayesian method showed much higher efficiencies in detecting each QTL and in estimation of QTL effects and expression modes than IM. For the detection of QTL1 and QTL2 with the Bayesian method, SQIs obtained on the partial region of 50 cM length were compared with a threshold corresponding to genomewide type I error of 0.05, which was obtained by considering the empirical variation of maximum values of SQIs calculated on whole-chromosomal regions in the absence of QTL. Accordingly the criterion for the detection of QTL1 and QTL2 might be too strict for the Bayesian method. The averaged posterior probabilities of N shown in Table 4 could be used for evaluation of the efficiency in successfully detecting all simulated QTL with the Bayesian method. The probability of N ≥ 3, which was considered to indicate such power of detecting all QTL, was 0.681.

Prior of QTL expression mode:

In this study, the prior probabilities of QTL expression modes were given as 0.6, 0.2, 0.1, and 0.1 for E₁, E₂, E₃, and E₄, since it is considered that the number of genes with Mendelian expression is generally larger than the number of genes imprinted in a whole genome of organisms. For the probabilities of transition between models of expression modes, we assigned the fixed values of δ = 0.2, κ = 0.6, ω = 0.1, η = 0.1, and ζ = 0.1 in the analysis of this study, following the same prior information for the possible expression mode of genes. In these settings of the prior and transition probabilities for QTL expression modes, the Mendelian expression model was more frequently considered for model fitting in MCMC iterations than other expression models; accordingly, the power and the accuracy of inferring expression modes for imprinted QTL might be reduced. Therefore, we performed additional simulation experiments, where data sets in case II were reanalyzed by the Bayesian method with the prior and transition probabilities for expression modes modified as uniform by assigning the prior probability of 0.25 to each expression mode and giving the values as δ = 0.5, κ = 0.25, ω = 0.25, η = 0.5, and ζ = 0.5 for the transition probabilities among expression modes. The result of this additional analysis is shown in Table 5. In a comparison of Table 5 with Table 3, the power of detecting imprinted QTL (QTL1 and QTL3) was enhanced, while the power for Mendelian QTL (QTL2) was unchanged but it was more frequently misidentified as partially imprinted QTL (E₂), by modifying the prior and transition probabilities of expression modes as uniform. Since the model of E₂ is a full model including E₁, E₃, and E₄ as submodels, the frequency of misidentification for QTL with E₁, E₃, or E₄ as QTL with E₂ depends on the prior and transition probabilities for expression modes.

TABLE 5.

Bayesian analysis for simulated QTL in case II using uniform prior and transition probabilities for expression modes

			Effectc				Inferred moded
Simulated QTL	Powera	Positionb	2a	apat	amat	d	E1	E2	E3	E4
QTL1 (LG1: 25 cM, E4; amat = −0.25)	0.85	25.4 (4.1)	—	—	−0.25 (0.04)	—	0.00 (0.02)	0.02 (0.19)	0.00 (0.01)	0.83 (0.79)
QTL2 (LG1: 75 cM, E1; 2a = 0.5, d = 0.0)	0.98	75.4 (3.5)	0.48 (0.07)	—	—	0.03 (0.11)	0.85 (0.60)	0.11 (0.35)	0.02 (0.03)	0.00 (0.02)
QTL3 (LG2: 65 cM, E3; apat = 0.2)	0.79	61.7 (9.0)	—	0.20 (0.04)	—	—	0.02 (0.05)	0.04 (0.16)	0.73 (0.77)	0.00 (0.03)

Simulated data sets in case II were analyzed by a Bayesian method with the prior and transition probabilities for QTL expression modes modified as uniform, where prior probabilities for E₁, E₂, E₃, and E₄ were 0.25 and transition probabilities among expression modes were set at δ = 0.5, κ = 0.25, ω = 0.25, η = 0.5, and ζ = 0.5. The proportions of MCMC iterations fitting QTL1 and QTL2 simultaneously in each analysis were averaged as 0.87 ± 0.22.

^aProportion of replicates that successfully detected each QTL with a genomewide significance level of P = 0.05 in a total of 100 replicates.

^bAverage of estimated QTL positions calculated in the replicates with successful detection of QTL with standard deviations given in parentheses.

^cAverage of estimated QTL effects corresponding to the simulated expression mode over the replicates with successful QTL detection with standard deviations given in parentheses.

^dProportion of replicates supporting each QTL expression mode as the most probable state in the replicates with successful detection of QTL. Averages of posterior probabilities of QTL expression modes are given in parentheses for the Bayesian method.

From the result of this additional analysis, it was shown that we can enhance the power of detecting the QTL and the accuracy of inference for expression mode of the QTL by arranging the values of these parameters so as to increase the chance that the model of correct expression mode for a QTL is tested for model fitting. However, true expression modes of QTL are usually unknown prior to the analysis and multiple QTL with different expression modes might be involved in the actual analysis. More suitable settings for the values of these parameters would require further investigation. In the actual analysis, it would be either suitable to adopt the prior and transition probabilities for expression modes with larger probability for E₁ than for other expression modes such that the Mendelian expression model is tested more frequently than imprinting expression models on the basis of the general information of a smaller number of genes with imprinting expression or suitable to apply the uniform prior and transition probabilities for expression modes.

Conclusion:

It has been known in mammals that the imprinted genes are not distributed uniformly through the genome, but cluster together (Reik and Walter 2001). Therefore, there is the possibility that multiple linked QTL with different expression modes affect a trait. The development of useful statistical tools for resolving such linked QTL would be desired. The Bayesian statistical framework is more suitable than interval-mapping methods for addressing the problem of separately detecting each of multiple QTL with different expression modes. Bayesian inferences can provide a flexible and useful platform for investigation of genetic structure underlying a phenotype of a trait, which could be more clearly elucidated with the methods for simultaneously detecting multiple QTL affecting the trait. The Bayesian method incorporating variable models for QTL expression, as proposed in this study, could contribute to the exploration of cryptic imprinted QTL that have remained undetected so far with conventional methods.

APPENDIX: MCMC SAMPLING TO ESTIMATE QTL PARAMETERS

The MCMC cycle to estimate parameters θ in the model consists of the following steps: (a) updating the effects at each QTL a = (a₁, a₂,…, a_N), (b) updating the fixed effects b and residual variance σ_e², (c) updating QTL locations λ = (λ₁, λ₂,…, λ_N), (d) updating QTL genotypes G for each F₂ individual, (e) updating the QTL expression mode S = (S₁, S₂,…, S_N), and (f) adding one new QTL to the model or removing one existing QTL from the model.

The QTL effects a are updated locus by locus and component by component via Gibbs sampling. The full conditional distribution of a_q (q = 1, 2,…, N) given other parameters and y is easily constructed by (3) assuming suitable prior distributions. For instance, in the case of S_q = E₃ (exclusive paternal expression) and assuming a uniform prior distribution, a_q = (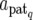) is normally distributed with mean z_q′(y − Xb − )/n and variance σ_e²/n, where z_q′ = (z_q1, z_q2,…, z_qn) are indicator variables for genotypes at the qth QTL of F₂ individuals taking values z_qi = 1 for the genotypes Q₁Q₁ and Q₁Q₂ and −1 for Q₂Q₁ and Q₂Q₂.

An update of the fixed effects b and residual variance σ_e² is also performed with Gibbs sampling. The full conditional distribution of b is normal and that of σ_e² is inverted chi square, when conjugate prior distributions are adopted for the parameters.

Moreover, Gibbs sampling is applicable to an update of QTL genotypes G of F₂ individuals. The full conditional probability for the genotype at the qth QTL for the ith F₂ individual, G_qi, given other parameters and variables is easily obtained. For example, in the case of S_q = E₄ (exclusive maternal expression), the mean of y_i is written as μ₁ = for G_qi = Q₁Q₁ and Q₂Q₁ or μ₂ = for G_qi = Q₁Q₂ and Q₂Q₂, where x_ij is the i, jth component of design matrix X and b_j is the jth component of fixed effects b. Therefore, in the case of S_q = E₄, the full conditional probability that G_qi = Q_kQ_l (k, l = 1, 2) can be written as

where φ(y | μ, σ²) denotes the normal density function with mean μ and variance σ². The QTL genotype G_qi is updated by sampling a new genotype from this probability distribution.

The update of other parameters (steps c, e, and f) is carried out by a Metropolis–Hastings algorithm (Metropolis et al. 1953; Hastings 1970) as described below.

Updating QTL locations and genotypes:

The locations of QTL, λ, are updated for one QTL at a time. For the qth QTL, new proposal values of λ_q, denoted by λ_q*, are sampled from a symmetric uniform distribution centered at the previous values of λ_q. Accordingly, a new genotype at the qth QTL, G_q*, is proposed for each F₂ individual corresponding to the proposed QTL position. We accept λ_q* with probability

where λ* and G* are proposal values of λ and G with the components corresponding to the qth QTL replaced by new values.

Updating QTL expression mode:

The QTL expression modes S are updated QTL by QTL via a RJ–MCMC algorithm (Green 1995). In the update of S, for the present mode of the qth QTL, S_q, the new mode S_q* is proposed with probability distribution q(S_q* | S_q). We chose q(S_q* | S_q) as shown in Table 1, considering inclusion relation between models corresponding to E₁, E₂, E₃, and E₄, where δ, κ, ω, η, and ζ are fixed values between 0 and 1, which are prespecified according to prior information available. The model with E₂ is regarded as a saturated model and the models with E₁, E₃, and E₄ are as submodels of E₂. There is no inclusion relation between models with E₁, E₃, and E₄. Accordingly, we assumed that the probabilities of direct transition between models with E₁, E₃, and E₄ are zero (Table 1); i.e., q(S_q* = E₃ | S_q = E₁) = q(S_q* = E₄ | S_q = E₁) = q(S_q* = E₁ | S_q = E₃) = q(S_q* = E₄ | S_q = E₃) = q(S_q* = E₁ | S_q = E₄) = q(S_q* = E₃ | S_q = E₄) = 0. The dimensionality of a_q is changed along with the update of S_q. Denoting the proposed new values of a_q by a_q*, the components of a_q* are obtained by a transformation of the components of a_q as follows. For S_q = E₁ and S_q* = E₂, a_q and a_q* are written as a_q = (a_q, d_q) and a_q* = (, where we obtain a_q* from a_q using a transformation

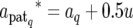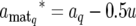with u being a random variable used for dimension matching and sampled from a suitable probability distribution such as a uniform distribution. In the transformation, we can easily show that the Jacobian is |∂a_q*/∂(a_q, u)| = 1. Other forms of transformation with Jacobian = 1 might be possible. For other combinations of S_q and S_q*, a suitable transformation between a_q and a_q* would be found without difficulty. Using a transformation with the Jacobian = 1, the probability of accepting the proposed value S_q* is expressed as

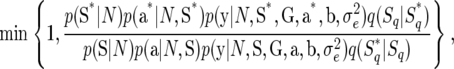where S* and a* are S and a with the qth components replaced by S_q* and a_q*, respectively.

Updating QTL number:

In the update of QTL number, the RJ–MCMC algorithm is also used. The number of QTL, N, is updated by adding one new QTL to a model with probability p_a or deleting one existing QTL from a model with probability p_d in the way described in Jannink and Fernando (2004) and Sillanpää et al. (2004). For a proposed QTL number N*, there are three possible values: N* = N + 1, N* = N − 1, and N* = N with probabilities p_a, p_d, and 1 − p_a − p_d.

When attempting to add one new QTL, first the location of the QTL λ_N* is sampled from a uniform distribution over a whole-genome region and one of the expression modes, E₁, E₂, E₃, and E₄, is randomly assigned to the new QTL following the prior probabilities of the expression modes. Next, the QTL effects are determined from uniform distributions and the genotypes of the new QTL for F₂ individuals are obtained by sampling values from p(G | M, λ). One new QTL is accepted with probability

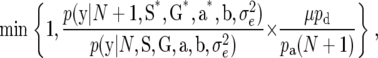where S*, G*, and a* indicate S, G, and a with the N + 1 elements added corresponding to the new QTL.

For deleting one existing QTL, a random choice is made among the existing QTL. The chosen QTL is then proposed to delete from the model. If the qth QTL is proposed to delete, the probability for the deletion is

where S*, G*, and a* correspond to S, G, and a except that the items corresponding to the qth QTL are deleted.