Genetic Design and Statistical Power of Nested Association Mapping in Maize

Abstract

We investigated the genetic and statistical properties of the nested association mapping (NAM) design currently being implemented in maize (26 diverse founders and 5000 distinct immortal genotypes) to dissect the genetic basis of complex quantitative traits. The NAM design simultaneously exploits the advantages of both linkage analysis and association mapping. We demonstrated the power of NAM for high-power cost-effective genome scans through computer simulations based on empirical marker data and simulated traits with different complexities. With common-parent-specific (CPS) markers genotyped for the founders and the progenies, the inheritance of chromosome segments nested within two adjacent CPS markers was inferred through linkage. Genotyping the founders with additional high-density markers enabled the projection of genetic information, capturing linkage disequilibrium information, from founders to progenies. With 5000 genotypes, 30–79% of the simulated quantitative trait loci (QTL) were precisely identified. By integrating genetic design, natural diversity, and genomics technologies, this new complex trait dissection strategy should greatly facilitate endeavors to link molecular variation with phenotypic variation for various complex traits.

LINKAGE analysis and association mapping are two commonly used approaches to dissect the genetic architecture of complex traits (Lander and Schork 1994; Risch and Merikangas 1996; Mackay 2001; Doerge 2002; Darvasi and Shifman 2005). As complementary approaches, linkage analysis often identifies broad chromosome regions of interest with relatively low marker coverage, while association mapping offers high resolution with either prior information on candidate genes or a genome scan with very high marker coverage (Thornsberry et al. 2001; Hirschhorn and Daly 2005). An integrated mapping strategy would combine the advantages of the two approaches to improve mapping resolution without requiring excessively dense marker maps. The possibility of developing such an integrated mapping strategy exists for the model species maize (Zea mays L.), because of the availability of a highly diverse collection of germplasm and the feasibility of creating segregating progenies and immortal genotypes through self-fertilization (Sprague and Dudley 1988; Liu et al. 2003; Flint-Garcia et al. 2005).

The Maize Diversity Group (http://www.panzea.org) has recently developed the largest set of public mapping populations to systematically dissect complex traits in maize. Here, we first introduce nested association mapping (NAM) as a genomewide complex trait dissection strategy that integrates the advantages of linkage analysis and association mapping in a single, unified mapping population. We then discuss population and quantitative genetics aspects of the design. Finally, we examine the statistical power of NAM to dissect complex traits with different genetic architectures through computer simulations.

THEORY AND PRACTICE OF NAM IN MAIZE

Nested association mapping:

The NAM strategy addresses complex trait dissection at a fundamental level through generating a common mapping resource that enables researchers to efficiently exploit genetic, genomic, and systems biology tools. The proposed procedure in NAM involves the following steps: (1) selecting diverse founders and developing a large set of related mapping progenies [preferably recombinant inbred lines (RILs) for robust phenotypic trait collection], (2) either sequencing completely or densely genotyping the founders, (3) genotyping a smaller number of tagging markers on both the founders and the progenies to define the inheritance of chromosome segments and to project the high-density marker information from the founders to the progenies, (4) phenotyping progenies for various complex traits, and (5) conducting genomewide association analysis relating phenotypic traits with projected high-density markers of the progenies.

Building on the genetic principles in previous genomic mapping strategies and methods (Meuwissen et al. 2002; Mott and Flint 2002; Darvasi and Shifman 2005), NAM has the advantages of lower sensitivity to genetic heterogeneity and higher power as well as higher efficiency in using the genome sequence or dense markers while still maintaining high allele richness due to diverse founders (Table 1). While previous joint linkage and linkage disequilibrium (LD) studies focused on mining existing mapping population in pedigrees or heterogeneous stocks (Meuwissen et al. 2002; Mott and Flint 2002; Blott et al. 2003), NAM aims to create an integrated mapping population specifically designed for a full genome scan with high power for quantitative trait loci (QTL) with effects of different sizes.

TABLE 1.

Schematic comparison of the main characteristics of different mapping strategies (following Darvasi and Shifman 2005)

	Linkage analysis	Admixture mapping	Joint linkage and LD mapping (and inbred-by-outbred cross)	Nested association mapping	Association mapping
Allele richness	Low	Low	Intermediate	High	High
Inference from markers in identity-by-state to quantitative trait nucleotides in IBD	Low	Low to intermediate	Intermediate	High	High
No. of SNPs required for whole-genome scan	Low	Low	Intermediate to high	Low (only high for founders)	High
Efficiency in using sequence information	Low	Low	Intermediate	High	Intermediate
Mapping resolution	Poor	Intermediate	Intermediate	Good	Good
Designed mapping population	Yes or no	Yes or No	Mostly no	Yes	No
Sensitivity to genetic heterogeneity	Low	Moderate	High	Low	High
Repeated phenotyping	Possible	Possible	Possible	Yes	Possible
Statistical power	Low to intermediatea	Highb	Intermediate	High	High

^aWith designed mapping populations such as F₂, BC, or RIL, the power of linkage analysis is generally higher in plants than in humans.

^bPower diminishes to zero with equal allele frequencies in the ancestral population (Darvasi and Shifman 2005).

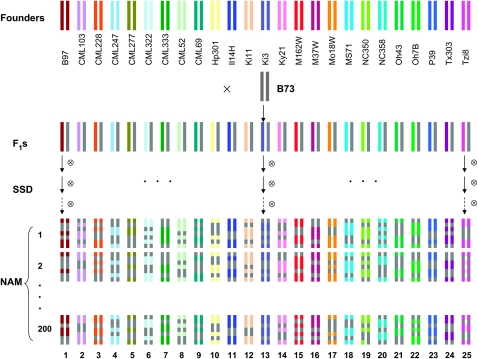
Using maize recombinant inbred lines (RILs) and a reference design as an example (Figure 1), we show that individual progeny represent a mosaic of chromosome segments derived from either one of the diverse founders or the common parent. With common-parent-specific (CPS) markers (i.e., markers for which B73 has a rare allele) scored for both founders and RILs, the marker or sequence information nested between two flanking CPS markers can be predicted for RILs on the basis of marker or genome sequence available for the founders (Figure 2). By choosing diverse founders, linkage disequilibrium within these chromosome segments resulting from historical/evolutionary recombination was mostly preserved in RILs due to the small probability of recombination within the short genetic distances between flanking CPS markers. The potentially confounding effects of genes outside of a specific segment being tested were minimized across the whole RIL populations via the reshuffling of the parental genomes by the recent recombinations during RIL development.

Figure 1.—

Diagram of genome reshuffling between 25 diverse founders and the common parent and the resulting 5000 immortal genotypes. Due to diminishing chances of recombination over short genetic distance and a given number of generations, the genomes of these recombinant inbred lines (RILs) are essentially mosaics of the founder genomes. ×, crossing; ⊗, selfing; SSD, single-seed descent.

Figure 2.—

Diagram of polymorphisms within a pair of CPS markers leading to fine mapping of NAM. (a) Genotyping of both founders and RILs with CPS markers to track the inheritance of chromosome segments that resulted from recent recombination during RIL development; (b) genotyping of founders with high-density SNPs, projecting sequence polymorphism information (biallelic) from founders to RILs, and mapping in high resolution through exploiting both recent and ancient recombination. Black/gray squares, alleles of CPS markers; blue/white squares, same as or different from B73 alleles at random SNPs; color segments, haplotype information from each parent; ×, crossing. Sites enclosed by the vertical bar represent the functional polymorphism.

Maize as a model for dissecting complex traits:

Many attributes of maize makes it an excellent system for studying a wide range of biological phenomena. Maize has more genetic diversity than any other model genetic system; in fact, two maize lines are as different from one another as humans and chimps are from one another (Buckler et al. 2006). It is an outbred species with allelic variation that dates back up to 2 million years, so many of its alleles have experienced climatic variation since the Pleistocene Epoch. This diversity can be used to address issues ranging from crop improvement to the unraveling of the mechanisms in plant development, biochemistry, and physiology to the understanding of the genetic architectures of complex traits. Maize also has tremendous phenotypic diversity and plasticity with varieties that grow only 1 m tall and produce numerous tillers and varieties that tower near 5 m and that range in adaptation from hot desert locations to the high Andes, to the humid tropics, and to the very short growing season of the Gaspe Peninsula, Canada. This range of adaptation also allows a detailed understanding of how a plant's genetic architecture interacts with its environment. Additionally, since maize's genetic architecture evolved in an outbred system, it is an excellent model for the less tractable outbred vertebrates and tree species.

Although there is a sizeable maize research community, there has been little consistent use of common genetic resources. Furthermore, the vast majority of maize genetic trait dissection has been focused on elite maize germplasm from the United States and Europe. Additionally, all the public immortal mapping populations have <400 lines, limiting their mapping power and coverage of allelic diversity. The maize intermated B73-by-Mo17 cross (IBM) population has been the nexus of the community mapping resource (Coe et al. 2002; Lee et al. 2002; Fu et al. 2006), but it captures only a small fraction of the available maize diversity (Flint-Garcia et al. 2005). Because of genetic heterogeneity, QTL mapped in a single two-parent population often have little relevance to QTL segregating in other populations, limiting the scope of inference of QTL studies and the application of marker-based selection in crops (Holland 2007). A maize association panel has also been developed (Flint-Garcia et al. 2005), which has been of use to multiple investigators, but lacks some of the favorable properties of traditional mapping populations (Table 1). Critically, the future of biology will involve systems biology, which requires integration across multiple scales of biology from biochemistry to whole-plant physiology to ecosystems. A large set of maize RILs would allow a wide range of researchers to integrate their research together in community efforts and community databases (e.g., PANZEA, MAIZEGDB, and GRAMENE).

In a large-genome species like maize, where LD decays within 2000 bp in gene regions, it will require several million markers to have a full coverage of all functional polymorphisms. Accordingly, a genomewide association study will require genome sequencing or high-density markers from a large set of diverse germplasm, the cost of which can be prohibitive. Moreover, while maize has low F_st values among subgroups, there is still substantial phenotypic differentiation by geographic subpopulations and breeding programs (Flint-Garcia et al. 2005). This differentiation is probably the product of a relatively modest number of key adaptive genes. Structured association mapping on diverse material will suffer a loss in statistical power in mapping genes whose effects are underlying the structure of the population. Our hypothesis is that these adaptive complexes will be best dissected when diverse inbred lines are crossed to create multiple segregating populations in which the adaptive complexes are broken.

Population design of maize NAM:

The aims of the experimental design in maize NAM were to (1) capture maize genetic diversity, (2) exploit ancestral recombination, (3) efficiently take advantage of next generation sequencing technologies through genetic design, (4) generate mapping materials that can be evaluated for agronomic traits at field locations of temperate regions, (5) develop a mapping population that has sufficient power to detect numerous QTL and resolve them to a level of individual genes, and (6) provide a community resource.

To this end, we have recently developed a large-scale maize mapping population, composed of 5000 RILs derived from the crosses of a common parent (B73) with each of 25 diverse founders (Figure 1). The 26 founder inbreds were B73, B97, CML52, CML69, CML103, CML228, CML247, CML277, CML322, CML333, Hp301, Il14H, Ki3, Ki11, Ky21, M37W, M162W, Mo18W, MS71, NC350, NC358, Oh43, Oh7B, P39, Tx303, and Tzi8 (Maize Molecular and Functional Diversity Project, http://www.panzea.org). The common parent, B73, was crossed to the other 25 founders, followed by selfing, to generate 25 segregating F₂ populations. Out of each F₂ population, 200 RILs were derived through single-seed descent with selfing to the F₆ generation (Figure 1). In theory, these diverse founders should be selected to maximally capture the genetic diversity in maize (Liu et al. 2003; Flint-Garcia et al. 2005). In practice, we applied two restrictions during founder selection: the two most important public U.S. inbred lines (B73 and Oh43) besides Mo17 must be included and the inbred lines must produce seeds in the U.S. summer. Although this last restriction prevented us from sampling genetic diversity from all available germplasm, it reduced overall allelic richness only by 1–2% but made the creation of the material substantially easier. Consequently, the selected founders represented a good balance between theory and practicality.

The choice of a reference design with B73 as a common parent, though not most efficient in terms of generating genetic information, was primarily due to agronomic and physiological considerations. Essentially, crossing the diverse founders to this well-adapted line makes both the development and the trait evaluation of this large population practical to conduct in temperate environments (Hallauer et al. 1988). Moreover, the maize inbred line B73 is one of the most important and widely deployed inbred lines in the history of maize breeding and has also been the subject of extensive genetic, molecular, and genomic studies (Stuber et al. 1992; Morgante et al. 2005). Recently, B73 was chosen as the reference genotype for the maize genome sequencing project. It is also a common practice in plant genetics that diverse materials are crossed to a limited number of elite lines as the first step to introgress useful genes from unimproved germplasm to elite breeding materials. We believe the same principle can be extended to various other genetic designs (Rebai and Goffinet 1993, 2000; Verhoeven et al. 2006). However, caution must be taken because other designs such as the diallel or round robin are likely to result in a series of progenies that have a tremendous variation in flowering time. This masking effect of maturity makes comparison of virtually all other traits difficult.

COMPUTER SIMULATIONS

SNP data:

The SNP haplotype data from the maize founders were used to initiate the computer simulations. The SNP data included 653 random (i.e., not from candidate genes) SNPs scored on the founders and another 678 CPS SNPs simulated to be B73 specific. For the random SNPs, a diverse set of 14 maize inbreds and 16 teosinte (Z. mays ssp. parviglumis) inbreds was used for SNP discovery (Wright et al. 2005). These SNPs were chosen from randomly selected genes of the ∼10,000 maize ESTs in the MMP–DuPont set (Gardiner et al. 2004). The development and scoring of SNP assays were conducted by Genaissance Pharmaceuticals using the Sequenom MassARRAY System (Jurinke et al. 2002). Replicated assays estimated the genotyping error rate to be ∼0.3%. The map locations of these SNPs were based on the corresponding genetic map positions of the unigenes on the integrated genetic and physical map (iMap) (Maize Mapping Project, http://www.maizemap.org), scaled back to the expected map length of an F₂ population. For the simulation study, the genetic map positions were randomly assigned to the CPS SNPs across the genome.

Simulation schemes:

Two general scenarios were investigated. In the first scenario, denoted as complete marker information, we assumed all SNP markers (i.e., both random SNP and CPS SNP sets) were genotyped for all 5000 RILs. In the second scenario, denoted as CPS marker only, we assumed that all the SNPs were genotyped for the 26 founders but only CPS markers were scored in the RILs. Therefore, the genotypes of RILs at random SNPs were not known. For a single RIL population, the genotypes at random SNPs were predicted for each individual RIL on the basis of the flanking CPS markers and the random SNP genotype of the parents. Assuming no double recombination, if two adjacent CPS markers were inherited from the same parent, the random SNPs between these two CPS markers were assigned to the RIL according to that particular parent. If two adjacent CPS markers were inherited from different parents, a recombination event was simulated within the region on the basis of its genetic distance, and allelic assignment was performed accordingly. Preliminary simulation experiments showed that the inaccuracy introduced by this projection process decreased the mapping power only slightly when the genome coverage of CPS markers was >2.5 cM.

A subset (q = 20 or 50) of 653 random SNP markers was assigned as QTL. The additive genetic effect of these QTL followed a geometric series: the effect of the lth QTL was a function of a^l, where a = 0.90 for q = 20 QTL, and a = 0.96 for q = 50 QTL (Lande and Thompson 1990). The genotypic value of each RIL was defined as the sum of genotypic values across all loci (i.e., ). On the basis of previous empirical studies of numerous quantitative traits in maize (Hallauer and Miranda Filho 1988; Flint-Garcia et al. 2005), the heritability on an entry mean basis (h²) was set to either 0.4 or 0.7. The phenotypic value of a RIL was obtained by adding a residual error (ɛ), accounting for 60% (i.e., h² = 0.4) or 30% (i.e., h² = 0.7) of the total variation, to the genotypic value of that RIL (i.e., 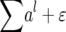). In addition to the sample sizes of 5000 RILs, we also conducted the simulation on the basis of 625, 1250, or 2500 RILs, corresponding to 25, 50, or 100 RILs from each of the 25 crosses. Another corresponding sampling scheme was to sample fewer crosses but each with a constant 200 RILs. To compare these two sampling schemes under an approximately equal total sample size, we chose 3, 6, or 12 crosses, which resulted in 600, 1200, or 2400 RILs, respectively.

A series of experiments were performed to address different scenarios related to the NAM genetic structure. First, we compared two general situations, complete marker information and CPS marker only. For each experiment (i.e., 1 of 32 simulation schemes = 2 marker availability regimes × 2 QTL numbers × 2 heritability levels × 4 sample sizes), 50 runs were conducted with different locations of QTL and different sets of RILs. Second, we confirmed our choice of number of CPS markers based on preliminary experiments by performing extra experiments with 339 CPS markers under the schemes of CPS marker only. Third, we performed experiments for a 678-CPS-markers-only scheme to assess the effect of significance threshold in model selection (α = 10⁻⁵, 10⁻⁷, and 10⁻⁹). Four additional experiments, each with 50 runs, were carried out to examine the consequences of creating the 5000 RILs derived from crossing 8, rather than 25, diverse maize founders, with B73 (i.e., 5000 RILs = 8 populations × 625 RILs/population). These 8 founders were chosen randomly from the 25 maize founders for each run. We assumed CPS marker information only for 5000 RILs for these four experiments (i.e., 2 QTL numbers × 2 heritability levels). Data from each run were analyzed individually and results of the 50 runs were then summarized for each experiment.

Statistical analysis:

The stepwise model selection and effect estimation were based on the equation

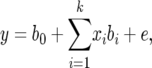(1)

where y is the vector of phenotypic values, b₀ is the intercept, b_i is the effect of the ith detected locus in the final model with a P-value smaller than the threshold value, k is the number of significant loci in the final model, x_i is the incidence vector that relates each b_i to y, and e is the vector of residual variance. The inclusion and retention of a SNP in the model were based on whether it significantly improved model fit by the likelihood-ratio test,

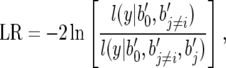(2)

where b′_j is the locus under testing and b′_j≠i are other loci in the model. Given the structure within these NAM populations, we also tested an alternative model that accounts for such structure by including the mean value of each population in the model,

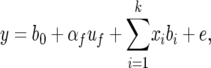(3)

where u_f is the effect of the cross of the founder f with the common parent; α_f is the incidence matrix relating each u_f to y. The corresponding likelihood-ratio test is

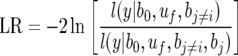(4)

The inclusion or exclusion of a locus in the model was based on these likelihood-ratio tests, which follow a χ²-distribution with 1 d.f. (Lynch and Walsh 1998). Thresholds for a SNP to both enter and remain in the model were set to α = 10⁻⁷ to minimize false positives that can occur when testing many loci (Lander and Kruglyak 1995). To examine the effect of thresholds on model selection, experiments were also performed with alternative thresholds of α = 10⁻⁵ and 10⁻⁹ for the CPS marker-only situation.

The model selection process started by including the single most significant locus in the model and then rescanning the genome to detect the next most significant locus among the remaining loci. Each time a new locus was added to the model, all loci in the new model were retested and any nonsignificant loci were then excluded from the model before the next round of selection. The model selection terminated when no more loci were significant, all loci already in the model were significant, or the locus entering the model was excluded in the immediate previous run. Because of the stringent significance threshold value and the small number of parameters relative to the sample size, other model selection criteria were not studied.

We assumed that the marker or sequence information for the 26 founders was known and that the true QTL were a subset of the random SNPs tested. Therefore, model selection was performed on the QTL and the rest of the SNP markers simultaneously. We chose a stringent criterion for the definition of true positives. A true positive was counted only when a QTL itself was identified as significant in the final model; all other cases were counted as false positives even when a significant marker was immediately adjacent to a QTL. The power to detect a QTL was calculated as the number of runs in which a particular QTL was detected out of the 50 runs. The average power was calculated for each run as the proportion of QTL correctly identified out of the total number of QTL simulated and then averaged over 50 runs for each simulation scheme. The false-discovery rate (FDR) was calculated as the number of false positives divided by the total number of significant loci detected in the final model for each run and averaged over 50 runs for each simulation scheme.

The R² value was calculated as the proportion of the total sum of squares explained by the final model and averaged for each simulation scheme. To examine the relationship between the size of the QTL effect and power to detect QTL, the average power was also calculated for the first and last quartile QTL (i.e., the largest 5 QTL and the smallest 5 QTL when q = 20 and the largest 12 QTL and the smallest 12 QTL when q = 50). The trend lines were plotted for power vs. QTL effect as percentage of phenotypic variance explained.

Linkage analysis without projection:

Additional experiments were conducted to compare the NAM and the traditional approach to analyze the data without projection of founder SNP information between CPS markers (Xu 1998). In this linkage analysis of multiple line crosses, a unique allele was specified for each founder at the locus under investigation. A true positive was counted when any loci located within the intervals that contain a QTL were retained in the final model. This was a very relaxed definition of true positives compared with NAM, for which a more strict definition of true positives was used. Four experiments (2 QTL numbers × 2 heritability levels), each with 20 runs, were studied with 5000 RILs for NAM analysis and traditional linkage analysis.

RESULTS

NAM founders:

The selection of the 26 diverse founders was primarily based on genotype data of 94 microsatellite markers to maximally capture the genetic diversity of maize from a worldwide collection (Liu et al. 2003; Flint-Garcia et al. 2005). The random SNP set was drawn from genotype data on the founders with known map positions. The CPS SNP set was simulated to be randomly located across the genome. The 678 CPS SNPs provided average marker coverage of a SNP each 2.5 cM of the maize genome. Among the 25 populations, the proportions of the random SNPs segregating in 21–25, 16–20, 11–15, 6–10, and 1–5 populations were 10, 11, 18, 26, and 35% on average, respectively. Consistent with previous studies that showed the high diversity of the founders (Liu et al. 2003; Flint-Garcia et al. 2005), genomewide analysis of these 653 random SNPs among 26 founders indicated a low level of LD (average pairwise r² = 0.04 for all markers on a same chromosome).

Model comparison:

We chose the model selection approach with a maximum-likelihood framework for mapping multiple QTL because marker density is high and issues of missing values, residual heterozygosity, and model dimensionality could be conveniently handled in empirical data analyses (Broman and Speed 2002; Sillanpaa and Corander 2002; Yi et al. 2005). Given the genetic structure and experimental design of the NAM population, we tested two models, one accounting for the family structure and one reduced model without accounting for such structure. Because many (20 or 50) QTL were simulated, it was expected that the mean value of a specific cross effect may be a result of the aggregation of effects of minor QTL. Including the family structure of 5000 RILs in the model led to a slightly reduced statistical power as well as a smaller R² explained by the final selected significant markers. The loss of power resulted from the fact that trait differences between the founders and their derived populations were due to multiple QTL differentiating these founders. Presumably, accounting for the natural groupings of RILs in the model absorbed part of the effect of some QTL that collectively differentiate the founders, decreasing the chance to detect these segregating loci. Moreover, ignoring the structure did not increase the risk of false positives due to the diversity of the founders and genome reshuffling during the RIL development. Accordingly, further analyses were conducted on the reduced model without the structure. However, we suggest that all approaches should ultimately be tested with empirical data given that the detection of epistasis (which was ignored in this study) may require proper modeling of the genetic background effects.

Complete marker information:

In this first simulation scheme, we assumed all SNP markers (i.e., both random SNP and CPS SNP sets) were genotyped for all 5000 RILs. This would be the ideal situation in terms of power but may be prohibitively expensive in terms of cost. It approximates the maximum power of this population when millions of SNPs can be scored across this large panel. The genetic architecture of a complex trait was modeled with different trait heritabilities (h² = 0.4 or 0.7), different numbers of causal polymorphisms (q = 20 or 50 QTL), and different additive genetic effects (Lande and Thompson 1990; Mackay 2001). With a stringent significance level (α = 10⁻⁷) (Lander and Kruglyak 1995) to control for the genomewide error rate, the average R² explained by the final multiple-QTL model using complete marker information for 5000 RILs was 0.33 for a trait with a heritability of 0.4 (h² = 0.4) and 0.65 with h² = 0.7. Note that the heritability imposes an approximate upper limit to the R² of a QTL model; thus a QTL model with R² of 0.65 for a trait with h² = 0.7 has explained ∼93% of the genetic variation. The average power to detect QTL (i.e., identify the exact SNP simulated to be the causal polymorphism) was 0.47 with h² = 0.4 and 0.73 with h² = 0.7 (Table 2). The corresponding FDR (Benjamini and Yekutieli 2005) was 0.16 with h² = 0.4 and 0.10 with h² = 0.7, indicating that 84 or 90% of loci declared significant are located exactly at the position where a QTL was simulated.

TABLE 2.

The average power of NAM under different genotyping and trait complexity schemes with 5000 RILs

	Complete marker information for RILs				CPS markers only for RILs
h2 = 0.4		h2 = 0.7		h2 = 0.4		h2 = 0.7
	q = 20	q = 50	q = 20	q = 50	q = 20 (%)	q = 50 (%)	q = 20 (%)	q = 50 (%)
Average power	0.60	0.33	0.85	0.60	0.57 (95)	0.30 (91)	0.79 (93)	0.54 (90)
FDR	0.14	0.17	0.09	0.11	0.17 (125)	0.23 (135)	0.15 (167)	0.17 (155)
R2	0.35	0.31	0.66	0.64	0.31 (89)	0.29 (94)	0.60 (91)	0.58 (91)
First-quartile QTL	0.94	0.76	0.96	0.92	0.90 (96)	0.70 (92)	0.92 (96)	0.89 (97)
Fourth-quartile QTL	0.15	0.02	0.63	0.16	0.09 (60)	0.02 (100)	0.50 (79)	0.12 (75)

Heritability (h²) of the trait was either 0.4 or 0.7, the number of QTL (q) controlling the trait was either 20 or 50, and the effects of QTL followed a geometric series. The values in parentheses correspond to the percentage of parameter values observed using only CPS markers relative to complete marker information.

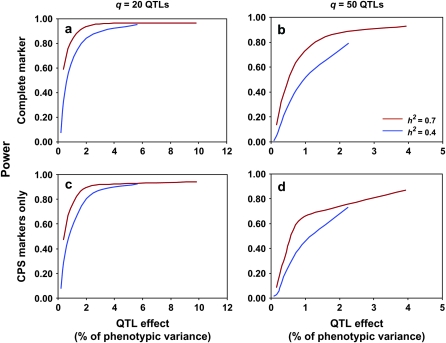
With varying sizes of genetic effects simultaneously underlying a complex trait, we were able to examine the relationship between QTL effect and detection power. As expected, the average power to detect the first-quartile QTL, which explained a combined 64% of the total genetic variance, was much higher (0.76–0.96) than that of the last-quartile QTL (0.02–0.63), which explained only a combined 3% of the total genetic variance (Table 2). With q = 20, the power was ∼0.80 to detect a QTL explaining ≥0.8% of the total phenotypic variance when h² = 0.7, while the same power was achieved for a QTL explaining 1.6% of the phenotypic variance when h² = 0.4 (Figure 3).

Figure 3.—

Statistical power of NAM to detect QTL with different genetic effects with 5000 phenotyped RILs. Complete information available for both CPS markers and random markers: (a) q = 20 QTL and (b) q = 50 QTL. Only CPS markers available: (c) q = 20 QTL and (d) q = 50 QTL.

CPS markers only:

In the second scenario, we assumed that all SNPs were genotyped for the 26 founders but only CPS markers were scored for the RILs. Therefore, the genotypes of RILs at random SNP loci were not known. In each single RIL population, genotypes at the random SNPs were predicted for each individual RIL on the basis of the flanking CPS markers and the random SNP genotype of the parents. Through this projection, we achieved genomewide high-resolution mapping in a cost-effective way. The average R² explained by the final multiple-QTL model was 0.30 with h² = 0.4 and 0.59 with h² = 0.7. The average power to detect QTL was 0.44 with h² = 0.4 and 0.66 with h² = 0.7 (Table 2). The corresponding FDRs were 0.20 with h² = 0.4 and 0.16 with h² = 0.7, indicating that 80–84% of the declared significant loci were located exactly at the position where a QTL was simulated.

We further examined the power of NAM with a smaller number of founders but a greater number of RILs per cross. With the same total number of 5000 maize RILs, choosing a smaller set of eight founders with 625 RILs per cross is less optimal than the current scheme in terms of both power and FDR (supplemental Figure 1 at http://www.genetics.org/supplemental/).

Complete marker vs. CPS markers only:

By carrying out simulations under two different genotyping scenarios, we directly compared the potential power and the power retained by scoring RILs with CPS markers only. For the CPS marker-only scheme, the genetic structure of the NAM population was exploited to greatly reduce the genotyping burden while maintaining sufficient power. With 5000 RILs, the average power achieved by scoring CPS markers only for RILs was 94% of that of the complete marker scheme when q = 20 and 90% when q = 50 (Table 2).

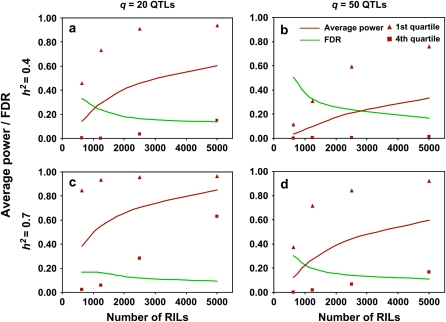
Phenotyping proportions:

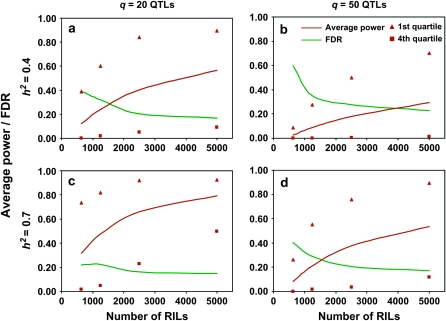
We further examined the power retained if only a portion of the NAM population was evaluated for the trait of interest. When complete markers were scored for 2500 RILs, the average power to detect QTL was 63–83% of that for 5000 RILs (Figure 4). The increase in sample size from 2500 to 5000 RILs had a more prominent effect on the last-quartile QTL than the first quartile with q = 20. The gain in accuracy by increasing sample size, as observed as smaller FDR and increased power to detect the last-quartile QTL, was greatest with h² = 0.7 and q = 20. In general, the patterns of the changes for both the power and the FDR when only CPS markers were scored (Figure 5) were similar to that when complete markers were available for 5000 RILs (Figure 4).

Figure 4.—

Average power and FDR of NAM with different numbers of phenotyped RILs when complete markers are genotyped for RILs. (a) q = 20 QTL and h² = 0.4; (b) q = 50 QTL and h² = 0.4; (c) q = 20 QTL and h² = 0.7; (d) q = 50 QTL and h² = 0.7.

Figure 5.—

Average power and FDR of NAM with different numbers of phenotyped RILs when only CPS markers are genotyped for RILs. (a) q = 20 QTL and h² = 0.4; (b) q = 50 QTL and h² = 0.4; (c) q = 20 QTL and h² = 0.7; (d) q = 50 QTL and h² = 0.7.

With sample sizes of 625, 1250, 2500, and 5000, the relative power achieved by scoring RILs for CPS markers only, compared to both CPS and random markers, was 77, 83, 88, and 91%, respectively. The corresponding ratios of FDR (i.e., CPS marker only vs. complete marker information) were 1.25, 1.32, 1.31, and 1.46. Sampling across all populations resulted in higher power than sampling fewer populations each with a constant number of individuals (supplemental Figure 2 at http://www.genetics.org/supplemental/), which agreed with a previous linkage-mapping study (Xu 1998).

CPS marker density and significance threshold:

Besides experiments conducted on the basis of 678 CPS markers and a significant threshold of α = 10⁻⁷, additional experiments were performed to examine the effects of CPS marker density and significance threshold. With the same significance threshold of α = 10⁻⁷, a less dense CPS marker coverage leads to a lower power and a higher FDR (supplemental Figure 3 at http://www.genetics.org/supplemental/). This reduction in power and an increase in FDR were consistent with different sample sizes. Presumably, a more stringent significance threshold in model selection affects the discovery of true positives as well as false positives. These changes in turn affect the statistical power and FDR. With 678 CPS markers, the threshold of α = 10⁻⁷ gave a better balance for both power and FDR than either a more liberal threshold of α = 10⁻⁵ or a more conservative threshold of α = 10⁻⁹ (supplemental Figure 4 at http://www.genetics.org/supplemental/). Again, the effects of significance level on power and FDR were generally consistent across different sample sizes.

Mapping without projection:

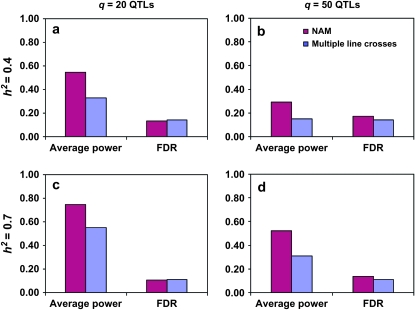
We have also examined the power of a traditional mapping strategy, in which no founder SNP information between two adjacent CPS markers was projected. For all cases examined, even with a more strict definition in true positives, the NAM genotyping and analysis strategy resulted in much higher power and comparable FDR than the traditional linkage analysis without projection of founder information (Figure 6).

Figure 6.—

Comparison of average power and FDR for NAM analysis and traditional linkage analysis of multiple line crosses. Significance threshold was set at α = 10⁻⁷. (a) q = 20 QTL and h² = 0.4; (b) q = 50 QTL and h² = 0.4; (c) q = 20 QTL and h² = 0.7; (d) q = 50 QTL and h² = 0.7. For NAM analysis, SNP information between CPS markers was projected from founders to 5000 RILs and a true positive was counted only if the QTL locus was retained in the final model; for linkage analysis, no projection was done and a unique allele was assumed for each founder and a true positive was counted as long as the locus retained in the final model was located within the region containing a QTL.

DISCUSSION

Complex trait dissection in many species has largely relied on two main approaches, linkage analysis and association mapping (Andersson and Georges 2004; Flint et al. 2005; Hirschhorn and Daly 2005). While methods for linkage analysis using designed mapping populations have long been employed (Doerge 2002), methods for association mapping with population-based samples were more recently developed to overcome the hidden population structure or cryptic relatedness within collected samples (Falush et al. 2003; Yu et al. 2006). Statistical methods for joint linkage and linkage-disequilibrium mapping strategy have been studied for natural populations (Wu and Zeng 2001; Wu et al. 2002) and crossing an inbred to a heterogeneous stock has also been examined (Mott and Flint 2002). For a general complex pedigree, fine mapping via combining linkage and linkage-disequilibrium information at previously mapped QTL regions has identified candidate gene polymorphisms (Meuwissen et al. 2002; Blott et al. 2003). Previous studies of genetic designs with multiple line crosses have shown an improved power and mapping resolution over a single population (Rebai and Goffinet 1993; Xu 1998; Rebai and Goffinet 2000; Yi and Xu 2002; Jansen et al. 2003; Li et al. 2005; Verhoeven et al. 2006). These studies, however, exploited mainly the linkage information of multiple line crosses. Genetic mapping using sequence information of a single chromosome from four mouse inbred strains has been studied recently (Shifman and Darvasi 2005). Various studies have been conducted on using flanking markers to infer the identity-by-descent (IBD) information of QTL (Lander and Green 1987; Jiang and Zeng 1997; Meuwissen and Goddard 2001). In NAM, the nucleotide polymorphisms within tagging SNPs can be tested more directly because high-density SNPs on founders can be obtained and this information can be projected onto the progeny through flanking CPS SNPs. Rather than inferring multiple alleles at each testing locus as in previous methods, NAM reduced the testing to exact biallelic contrasts across the whole population. Nevertheless, these various methods of IBD estimation are useful in cases where the founder information is not available or complicated pedigree or population design makes the projection of information unreliable.

In NAM, the advantages of designed mapping populations from linkage analysis and of high resolution from association mapping were integrated through the development of a large number of RILs from diverse founders. While the CPS markers allowed the prediction of transmission of chromosome segments in RILs, the short range of LD within these segments across the diverse founders enabled improved mapping resolution. The genetic background effect of these parental founders on mapping individual QTL, which can be a hurdle for association mapping, is systematically minimized by reshuffling the genomes of the two parents of each cross during RIL development as well as by the combined analysis of all RILs across all 25 crosses. In general, the strategy of projecting sequence information, nested within informative markers, from the most connected individuals to the remaining individuals is applicable to a wide range of species, including humans, mice, Arabidopsis, and rice. A recent study has verified the strategy of genotype inference for related individuals within human pedigrees (Burdick et al. 2006). However, a balanced design with well-chosen diverse founders in NAM, if possible for a particular species, would provide higher power and finer resolution than exploiting an existing pedigree.

As in general association mapping, the mapping resolution offered by NAM largely depends on the linkage disequilibrium among the founder individuals. Empirical studies with maize candidate genes sequenced across diverse lines have shown a rapid decay of LD over 2000 bp (Wilson et al. 2004). Recent genomewide analysis in diverse accessions of Arabidopsis (Nordborg et al. 2005) and breeds of dog (Canis familiaris) (Lindblad-Toh et al. 2005) agreed with this pattern: LD decays rapidly across genetically diverse germplasm. With the NAM strategy, this advantage in resolution is fully utilized without the coupled drawback—the need for good candidate genes or a large number of markers—by projecting the genomic information from the founders to the RILs. An explicit study in mapping resolution should be carried out once high-density markers are available for founders. To address this issue on the basis of available information, we defined the true positives strictly as identifying the exact functional SNPs rather than surrounding markers in the current study. Accordingly, our result on power analysis is a combination of the traditional power (i.e., detecting the signal) with resolution (i.e., precision of the signal). Nevertheless, given the diversity of these maize founders and the rapid LD decay within 2000 bp, mapping resolution for NAM is expected to be high.

As in previous studies, a higher heritability always gave higher power to detect QTL, particularly for those QTL with moderate to small effect. Even though heritability varies for different physiological, biochemical, and agronomic traits (Hallauer and Miranda Filho 1988; Flint-Garcia et al. 2005), improved experimental design and manageable repetition can often be implemented to increase heritability (Lynch and Walsh 1998; Holland et al. 2003). For a given trait, our results underscore the importance of accurate phenotyping procedures in complex trait dissection (Flint-Garcia et al. 2005; Yu et al. 2005). Although improving the heritability by repeated measurement of the immortal genotypes is not a simple issue given the varying levels of residual variance and genotype-by-environment interaction (Bernardo 2002; Holland et al. 2003), a 3.5-fold increase in the number of testing environments will increase the heritability from 0.4 to 0.7, assuming a constant genotype-by-environment interaction.

The features of the genetic structure of RILs have been recently studied for two-, four-, and eight-way crosses following either selfing or sib mating (Broman 2005). Interestingly, the 95th percentile of the length of the smallest chromosome segments was 2.2 cM for RILs derived from a two-way cross with selfing (Broman 2005). Given the similar genetic map sizes between maize and mouse, Broman's findings would partly explain the feasibility of predicting marker information on the basis of CPS markers and parental genomic information. We speculate that the NAM strategy may also be applicable to the eight-way RILs in the mouse. However, there are several interesting contrasts between the NAM population and the mouse eight-way cross. In maize, which has very low LD and tremendous genetic diversity, the focus of RIL generation was to capture a wide array of alleles by using many founders, rapid production of RILs, and minimized physiological variation by crossing to a reference line. In contrast, the mouse has low diversity (Ferris et al. 1982; Beck et al. 2000) and high LD but the eight-way cross produces more recombinations per line, which helps compensate for the high LD, and the mixing ensures that a fuller range of epistatic interactions are produced (Churchill et al. 2004). The 5000 maize RIL population captures ∼200,000 independent recombination breakpoints, compared to 135,000 breakpoints in the 1000 mouse RILs from an eight-way cross (Churchill et al. 2004).

Given known genome sequences of the founders, the number of polymorphic loci to be tested can be on the order of millions (Lander and Kruglyak 1995). In the current simulation, we used 653 SNP loci that are available on these founders with their identified map positions and additionally simulated a set of 678 CPS SNPs. We acknowledge that it would be more desirable if a much larger set of empirical SNPs with known map positions were used. The same principle underlying NAM, however, should also apply given the features of the genetic structure of RILs (Broman 2005). The frequencies of the causative SNPs affect the power of detection (Pritchard and Cox 2002; W. Y. Wang et al. 2005). Because we have focused on the average power of quantitative traits controlled by many QTL, this issue was not explicitly studied. Nevertheless, we expect these random SNPs to cover the whole spectrum of frequency distribution and to be relatively free of ascertainment bias since the sampling of alleles for SNP discovery included both domesticated maize and its wild relatives (Wright et al. 2005).

In the ongoing Maize Molecular and Functional Diversity Project (http://www.panzea.org), we have selected 1536 B73-rare SNP loci (resulting in an average intermarker interval of ∼1.1 cM) to genotype both the founders and the 5000 RILs. This would yield at least the same information content as the CPS markers simulated in this study, as we set the selection criterion for these B73-rare SNPs to be segregating in >17 populations. A funded sequencing project is now being carried out to discover and genotype over 1 million SNPs on the 26 diverse founders. In this study, we adopted a stringent α-level of 10⁻⁷ (Lander and Kruglyak 1995) to address the issue of multiple testing and balance the power of QTL detection and FDR (Yu et al. 2005). We also demonstrated the effect on power and FDR with additional thresholds of 10⁻⁵ and 10⁻⁹. In practice, procedures of FDR control based on empirical P-values for a specific experiment have been developed (Benjamini and Hochberg 1995; Benjamini and Yekutieli 2005) and compared (Qian and Huang 2005). The ultimate power of NAM may decrease due to the bias introduced by the model selection process with a larger numbers of markers (Bogdan and Doerge 2005). While the forward selection with backward elimination procedure was investigated in the current study, future investigation of other model selection methods (Broman and Speed 2002) should be carried out. This problem, however, can be alleviated with Bayesian methods in which many possible models are summarized with posterior distributions rather than selecting a single “final” model (Xu 2003; Sillanpaa and Bhattacharjee 2005; H. Wang et al. 2005; Yi et al. 2005; Zhang et al. 2005).

In this study, we have focused on detecting QTL with additive effects. Nonadditive effects, undoubtedly, contribute to variation in complex traits but have been very elusive (Carlborg and Haley 2004). Most empirical studies have demonstrated the relative importance of additive effects (Hallauer and Miranda Filho 1988; Yu and Bernardo 2003; Laurie et al. 2004), and theoretical studies with complex gene networks have always identified a significant portion of variation attributable to additive effects (Cooper et al. 2005). Nevertheless, we are currently investigating, through computer simulations, the potential of this large-scale RIL population for identifying epistatic effects and will conduct further analysis with empirical data. As for detecting QTL with small effects, the total genetic variance explained by the last-quartile QTL combined was only 3%, which made them very difficult to detect by default.

In light of recent advances in high-throughput genotyping technology, we examined the potential of genomewide fine mapping of QTL with a large population size. While the ultimate power of NAM awaits the collection, analysis, and verification of the empirical data, we demonstrated in this study the general strategy of NAM and the power it affords through computer simulations. NAM would have the cost-effective benefit of allowing us to conduct genomewide fine mapping by sequencing only the 26 founders of NAM and genotyping the 5000 RILs with finite marker sets with 192-fold less cost compared to sequencing all 5000 RILs or some other association-mapping population with 5000 individuals. The same strategy can be easily extended to other species with partial or complete genome sequence, such as Arabidoposis, rice, sorghum, soybean, or mice, if community efforts are joined to create a similar mapping population (Churchill et al. 2004). Given the rapid advancement in sequencing and genotyping technology (Shendure et al. 2004, 2005) as well as statistical methodology (Sillanpaa and Corander 2002), the NAM strategy and the large complex trait dissection platforms should greatly facilitate gene identification for various complex traits.