Abstract
Failure to account for family structure within populations or in complex mating designs via uninformed applications of permutation testing will lead to inflated type I error rates. Careful consideration of the design factors is essential since some situations allow several valid permutation strategies, and the choice that maximizes statistical power will not always be intuitive.
WHEN any statistical method is applied incorrectly, misleading conclusions are to be expected. With this in mind, we are motivated by both the application of a simple permutation test and the message conveyed by Zou et al. (2006) in which the performance of a permutation test is assessed. Zou et al. address a problem in QTL mapping analysis of recombinant inbred lines (RILs), which has been previously addressed by Belknap (1998), concerning the use of strain means vs. individual level data models. Although the essentially equivalent performance of these two models is well known anecdotally, Zou et al. focus on the performance of a simple permutation application which unfortunately is applied incorrectly in the context of the full data model.
The concept of permutation, as proposed by Fisher (1935) and as applied to QTL mapping by Churchill and Doerge (1994), relies on exchangeability. In simple experimental designs, such as an intercross or a backcross mapping population, the individual units can safely be assumed to be exchangeable. In more complex designs it is often, but not always, possible to identify exchangeable units and thus to construct a permutation test. It is important to realize that several other designs exist in which a simple permutation test has been or could readily be misapplied, for example, the advanced intercross (AI) and heterogeneous stock (HS) breeding designs. In both the AI and HS designs, the animals that are assayed may number in the hundreds or even thousands, but these animals are often the progeny of a penultimate generation consisting of a much smaller number of lineages. Failure to account for the family structure in these populations by naive application of permutation testing will lead to inflated type I error rates.
Permutation tests require relatively few assumptions and can be applied in a wide variety of settings. However, they are not without potential pitfalls. Correlation structure, whether it is known from the design or hidden due to unaccounted factors, can produce misleading results. The optimal choice of permutation strategy requires careful consideration of the experimental design. Design factors may be fixed or random, nested or crossed, and it is these features that determine which strategy should be used. To construct a permutation test, one must decide which units are to be permuted, whether the permutations should be restricted, and whether it is best to permute raw data or residuals. The implications of these choices have been exhaustively characterized in all combinations by Anderson and Ter Braak (2003). Their results sometimes run counter to our intuitions. In general they find that permutation of residuals under a reduced model has the best power while still controlling type I errors. However, this does not apply as a universal recommendation.
Using the notation of Zou et al. (2006) with the explicit addition of the random line effect, Bi, the ANOVA model for the RI line experiment considered by Zou et al. can be written as
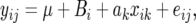 |
where i = 1, … , L and j = 1, … , ni, such that there are a total of L lines used for QTL mapping, and each line has ni individuals measured for the quantitative trait yij. The additive effect, assuming a single-marker analysis, of the putative QTL is denoted as ak. Each individual within a given line i will have the same genotype xik, and thus the random effect Bi is nested within the fixed effect. Typically, one would want to test the higher-order, fixed effect (i.e., the additive effect). For this case, Anderson and Ter Braak (2003) recommend the exact test in which data are permuted as units within levels of the random factor. This is the permutation test recommended by Zou et al. (2006). All other permutation strategies, including restricted permutation of residuals under the reduced model ak = 0 and unrestricted permutation of the data, can produce inflated type I error rates when errors are not normal. Mostly important to this discussion is the fact that the effect is most pronounced when the variance of the nested factor (the polygenic background variance) is large. Furthermore, to maximize the power on a per-measurement basis, investigators are well advised to increase the number of lines and to use minimal within-line replication (also see Belknap 1998).
In summary, there are many ways to construct a permutation test. Careful consideration of the nature of the design factors is essential to making the correct choice. In some cases there are several valid permutation strategies and the choice that maximizes power will not always be intuitively obvious.
References
- Anderson, M. J., and C. J. F. Ter Braak, 2003. Permutation tests for multi-factorial analysis of variance. J. Statist. Comput. Simul. 73(2): 85–113. [Google Scholar]
- Belknap, J. K., 1998. Effect of within-strain sample size on QTL detection and mapping using recombinant inbred mouse strains. Behav. Genet. 28(1): 29–38. [DOI] [PubMed] [Google Scholar]
- Churchill, G. A., and R. W. Doerge, 1994. Empirical threshold values for quantitative trait mapping. Genetics 138: 963–971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher, R. A., 1935. The Design of Experiments, Ed. 3. Oliver & Boyd, London.
- Zou, F., Z. Xu and T. Vision, 2006. Assessing the significance of quantitative trait loci in replicable mapping populations. Genetics 174: 1063–1068. [DOI] [PMC free article] [PubMed] [Google Scholar]


