The α-helix folds on the millisecond time scale

Abstract

It has long been believed that nucleation of the α-helix is a very fast reaction, occurring in around 10⁻⁷ s. We show here that helix nucleation, in fact, takes place on the millisecond time scale. The rate of α-helix nucleation in two polyalanine-based peptides and in lysine and glutamic acid homopolymers was measured directly by stopped-flow deep UV CD with synchrotron radiation as the light source. Synchrotron radiation CD gives far superior signal to noise than a conventional instrument. The 16-aa AK peptide folds with first-order kinetics and a rate constant of 15 s⁻¹ at 0°C. The rate-determining step is presumably the initiation of a new helix, which occurs at least 10⁵ times slower than expected. Helix folding occurs in at least two steps on the millisecond time scale for the longer peptides, with a transient overshoot of helix content significantly greater than at equilibrium, similar to that seen in the folding of several proteins. We suggest that the overshoot is caused by the formation of a single long helix followed by its breakage into the two or more helices present at equilibrium.

If we are to clearly understand protein folding, it is essential to understand the folding of the major substructures, the α-helix and β-sheet. Relaxation times for the helix/coil transition of Glu and Lys homopolymers previously have been measured by electric field jump (1, 2), temperature jump (3–5), and resonant ultrasound methods (6–8). Temperature jump, IR spectroscopy (9), and N-terminal reporter group fluorescence (10) also have been applied to measure the kinetics of unfolding of a 21-residue poly(Ala)-based helical peptide.

There are two microscopic rates in helix folding (11). First, there is the fast propagation of an existing helix by the addition of a single residue to the end of a helix. The rate of initiation of a new helix, presumably by the formation of a single turn, stabilized by one i, i+4 hydrogen bond, will be slow because it requires the entropically unlikely event of the simultaneous restriction of three successive residues. Previous results have been used to derive a rate for extension of helices by a single turn of 1 × 10⁷ to 7 × 10¹⁰⋅s⁻¹ and to infer very fast initiation rates for the coil-to-helix transition.

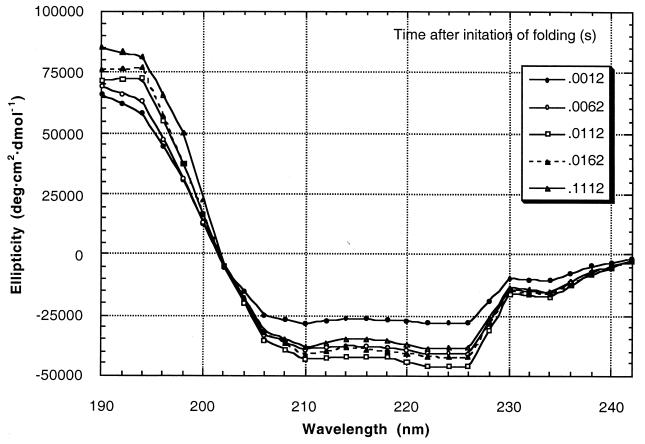
Here we directly measure the rate of nucleation of α-helices from the denatured state. Helix formation in AK16 (sequence Ac-YGAAKAAAAKAAAAKA-NH₂) was initiated by a 10-fold dilution from 5 M GuHCl and in AQ28 (sequence Ac-A(QAAAA)₅QGY-NH₂) by a 20-fold dilution from 6 M GuHCl. We also studied poly(l-lysine) and poly(l-glutamic acid). The 3-kDa poly(Lys) sample consisted of polymers in the molecular mass range of 1.5 to 4.5 kDa; 5-kDa poly(Lys) ranged from 1.6 to 10 kDa; 4.4-kDa poly(Glu) ranged from 3 to 14 kDa; 7-kDa poly(Glu) ranged from 3 to 22 kDa; and 20-kDa poly(Glu) ranged from 6 to 40 kDa. These polypeptides form α-helices when neutral and random coil when charged. Initiation of helix folding therefore was performed by a pH jump, from 8.0 to 11.5 for poly(Lys) and from 8.0 to 3.3 for poly(Glu). Kinetic data was acquired from 0°C to 62°C for AK16 and at 20°C for AQ28, poly(Glu), and poly(Lys). Helix content was monitored by stopped-flow CD spectroscopy using synchrotron radiation. The use of synchrotron radiation instead of a UV lamp improves the signal/noise ratio in excess of 100-fold in the 190-nm range. We therefore were able to acquire CD spectra of 4.4-kDa poly(Glu) from 190 nm to 242 nm every 2.5 ms with a resolution of 2 nm as it folded (Fig. 1). This performance is unheard of with a conventional instrument.

Figure 1.

CD spectra of 4.4-kDa poly(Glu) during folding. Spectra were acquired every 2.5 ms for 110 ms though only five spectra are shown here for clarity.

MATERIALS AND METHODS

Poly(Glu) and poly(Lys) were purchased from Sigma, and their molecular weights were checked by matrix-assisted laser desorption ionization/time of flight mass spectrometry at the Michael Barber Centre for Mass Spectrometry (University of Manchester Institute of Science and Technology) and on a Superose 12 FPLC column.

Peptides were synthesized by the solid-phase method using fluorenylmethoxycarbonyl chemistry. 9-Fluorenylmethoxycarbonyl amino acids were coupled to Rink amide resin by using 2-(1H-Benzotriazole-1-yl)-1,1,3,3-tetramethyluronium tetrafluoroborate, N,N-diisopropyl-ethylamine, and 1-hydroxybenzotriazole. N termini were acetylated with acetic anhydride/pyridine. Peptides were cleaved from the resin by using 95% trifluoroacetic acid/5% anisole. Peptides were purified by diethyl ether precipitation and C₁₈ reverse-phase FPLC, and their molecular weights were checked by fast atom bombardment mass spectrometry. Peptide purity was checked by analytical C₁₈ FPLC.

Stopped-flow CD data were measured by using the high-intensity CD facility on station 13.1b of the Central Laboratory of the Research Councils Daresbury Laboratory Synchrotron Radiation Source. Samples of poly(Glu) and poly(Lys) were dissolved in 10 mM sodium phosphate buffer, pH 8.0, at a concentration of 0.2 mg⋅ml⁻¹. The samples were mixed at 20°C with an equal volume of 10 mM sodium acetate buffer, pH 2.7 [for poly(Glu)] or 15 mM sodium hydroxide, pH 12.3 [for poly(Lys)] in a fast stopped-flow device (dead time 0.6–1.2 ms). AK16 and AQ28 were dissolved in 5 M GuHCl, 10 mM sodium phosphate buffer, pH 7.0, at a concentration of 0.55 mM. Folding was initiated by a 10- or 20-fold dilution by aqueous buffer. Final conditions were peptide concentration 0.1 mg⋅ml⁻¹, pH 3.3 [poly(Glu)], 0.1 mg⋅ml⁻¹, pH 11.5 [poly(Lys)], or 50 μM, pH 7.0 (AK16 and AQ28). CD data were collected after mixing, with a resolution of 1.0–2.5 ms, by using a PC-based data acquisition system (Applied Photophysics, Surrey, U.K.). The dead time was 0.6 ms (see the supplemental data, Figs. 9 and 10, at the PNAS web site, www.pnas.org). The reproducibility of our work was confirmed by studying the folding of 17-kDa poly(Glu) and 25-kDa poly(Lys) under identical conditions by using an Applied Photophysics Pi*-180 CDF spectrometer. There was more noise in the data and a longer dead time on this machine, but the kinetics were identical, thus showing we were not observing a machine artifact. We also reproduced published stopped-flow CD data on protein folding. Typically, each experiment was repeated 10 times and the data were averaged. The system was calibrated by using a 1.0 mg⋅ml⁻¹ solution of (+)-10-camphorsulfonic acid.

RESULTS

Helix Folding and Unfolding Rates.

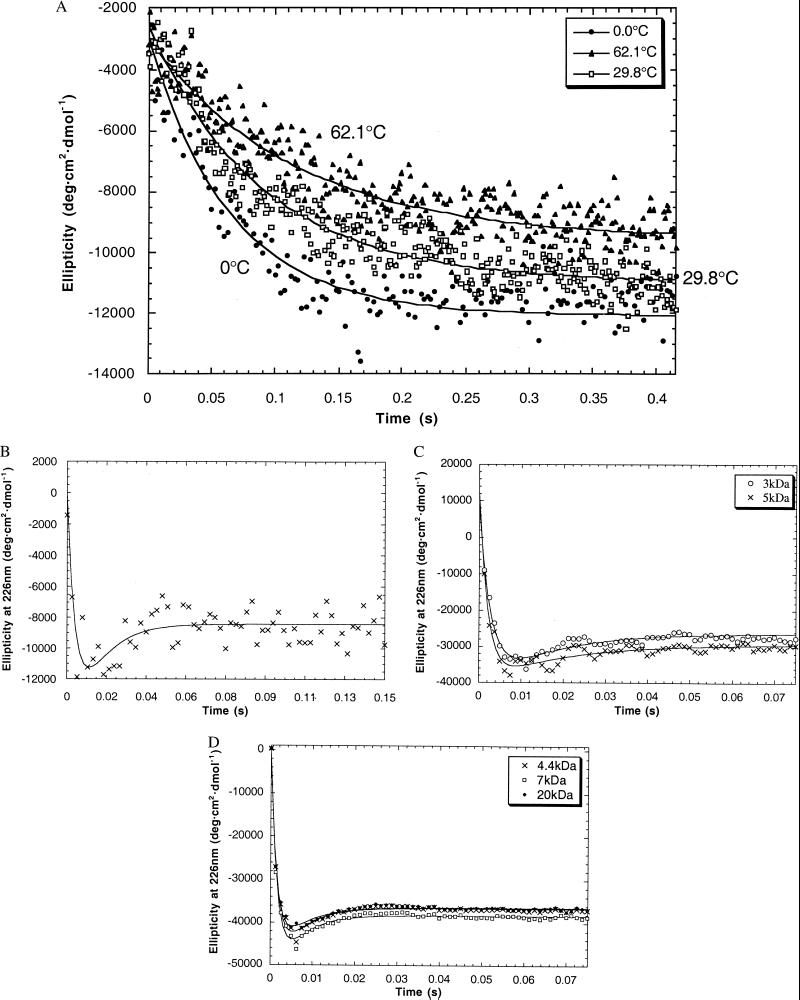
Kinetic data was acquired for all the peptides at 222 nm or 226 nm, where there is a strong negative signal in the α-helix CD spectrum (Fig. 2). The AK16 data fitted to a single exponential with no overshoot (Table 1). The folding rate and final helix content (θ₂₂₂ at equilibrium) both decrease with increasing temperature. We separately measured θ₂₂₂ at equilibrium in the folding buffer at temperatures from 0 to 62°C and duplicated the final helix contents found in the kinetics experiment. The signal/noise for the AK16 and AQ28 is poorer as the data was acquired in the presence of GuHCl, which absorbs strongly in the UV. An Arrhenius plot of the AK16 data yields ΔH^‡ = −1.5 kcal⋅mol⁻¹.

Figure 2.

Refolding kinetics of α-helix formation monitored by stopped-flow CD at 222 nm or 226 nm. Data were fitted to the equations θ = A (1 − e^−kt) + θ(U) or

(27). (A) AK16. (B) AQ28. (C) Poly(Lys). (D) Poly(Glu). Data were fitted to the three-state U → I → F mechanism by using kaleidagraph (Synergy Software, Reading, PA). Parameters fitted: U->I rate constant (k₁), I->F rate constant (k₂), θ₂₂₆ (U), θ₂₂₆ (I), and θ₂₂₆ (F). Errors are SE after kaleidagraph fitting.

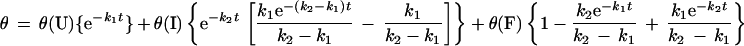Table 1.

Kinetic parameters for α-helix formation in AK16

T, °C	k, s−1	θ222 at equilibrium
0	15.2  ±  0.7	−12,100  ±  500
4.2	16.3  ±  0.4	−12,800  ±  400
8.8	15.2  ±  0.4	−12,900  ±  300
13.2	22.4  ±  1.0	−11,700  ±  400
18.8	19.3  ±  0.8	−11,800  ±  400
29.8	11.1  ±  0.4	−11,000  ±  300
36.6	8.3  ±  0.5	−9,300  ±  300
45.0	8.3  ±  0.6	−9,000  ±  300
52.5	7.0  ±  0.5	−10,000  ±  300
62.1	8.6  ±  0.5	−9,600  ±  300

We studied the rate of unfolding of 4.4-kDa poly(Glu) by a pH jump and of AK16 by jumping from 0.00 M GuHCl to 5.45 M GuHCl (see the supplemental data at www.pnas.org; Fig. 5) and found that the peptide was completely unfolded within the dead time of the stop-flow device, in agreement with the earlier work. In contrast, our helix folding rates are far slower, perhaps, because the rate-determining step in our kinetics is the initiation of a new helix, whereas previous workers studied a shift in the helix/coil equilibrium within highly helical peptides, where the observed rate amplitude largely arises from crossing the propagation barrier. Alternatively, helix initiation rates could be very sequence dependent. Comparison with our rates suggests that helix propagation is at least 10⁵ times faster than initiation. Slow helix initiation therefore could be the rate-limiting step for protein folding. This observation is interesting as a number of proteins have been shown to fold in 1 ms or less (12). Helix nucleation is surprisingly slow; perhaps the rate-limiting step is forming a larger structure than simply one helix turn with one hydrogen bond.

Comparison to Temperature Jump Experiments.

Can our results be reconciled with previous work that concluded that helix folding from the all-coil state occurs on the submicrosecond time scale? We believe that they can and suggest the following explanation. Our work studies folding from a fully unfolded state where the rate-limiting step for folding is crossing the nucleation barrier. After successful nucleation, propagation occurs on the submicrosecond time scale, which is far faster than can be detected in our experiments. Hence we observe simple first-order kinetics for AK16 and a time constant for nucleation of ≈50 ms at room temperature.

A similar peptide, called suc-F_S, with sequence succinyl-AAAAA-(AAARA)₃A-NH₂ was studied by laser-induced temperature jump from 9.3°C to 27.4°C with the mean helix content monitored by IR spectroscopy (9). A time constant of 160 ns for the relaxation was observed. By assuming a two-state equilibrium, the equilibrium constant for folding at 27.4°C was 10, and a folding time constant of 16 ns was inferred.

The difficulty with this analysis is that the helix/coil equilibrium is not two-state; rather, peptides form a complex mixture of fully helix, fully coil, and, most commonly, helices with disordered, frayed termini. When a temperature jump experiment is performed on a very helical peptide, such as suc-F_S, a decrease in helix content is observed. What is the origin of this change? There are two possibilities: an increase in the population of the all-coil conformation and an increase in the amount of fraying. Crucially, increasing the population of the all-coil conformation can occur only by crossing the nucleation barrier while fraying results solely from crossing the propagation barrier. One therefore may expect two kinetic processes in a temperature jump (11). First, there will be a fast rate from increasing the amount of fraying, and second, there will be a slower rate resulting from breaking down all the helical structure and crossing the propagation barrier. Williams et al. (9) observed a single exponential from shifting the helix/coil equilibrium so they observed predominantly only one of these alternatives. We can use helix coil theory (13) to estimate how much of the observed change arises from these sources.

We treat suc-F_S as a homopolymer with a good N-cap at the N terminus. If the observed helix content is 90.9% (as K = 10 at 27.4°C), we can reproduce this with 21 residues, and the plausible helix/coil parameters n(succinyl) = 20, w = 1.81, n = 1, c = 1, and v = 0.048. Helix/coil theory gives the partition function Z = 2841, and so the all-coil population is 1/Z = 0.035%. In all other conformations, the mean number of hydrogen-bonded residues (maximum 17) is the noncoil population (2840/2841) × 17 × observed helix content (0.909) = 15.45. At equilibrium, the nonhydrogen-bonded residues arise from two sources: frayed helices and the all-coil conformation. Their populations are: frayed helices, (17–15.45) × (2840/2841) = 1.54 residues; and all coil, 17 × (1/2841) = 0.006 residues.

Hence in this case, almost all of the nonhelical residues are present at the termini of frayed helices.

The temperature jump experiment starts at 9.3°C. The thermodynamic parameters of Williams et al. (9) give a helix content of 96.3% at this temperature. This stability can arise if n(succinyl) = 30, w = 2.83, n = 1, c = 1, and v = 0.048. The same calculation as above gives the nonhelical residues present as: frayed helices, 0.63 residues; and all coil, 3.2 × 10⁻⁶ residues.

When helix content is jumped from 96.3% to 90.9%, the change in nonhelical population from fraying is therefore 1.54 − 0.63 = 0.91 residues and from increasing the all-coil population as 0.006 − 3.2 × 10⁻⁶ = 0.006 residues. The temperature jump experiment is therefore totally dominated by perturbing the amount of fraying at the helix termini, and the amplitude arising from crossing the nucleation barrier is negligible. We therefore conclude that previous workers were measuring propagation rates, not nucleation rates. Thompson et al. (10) studied helix kinetics in MABA-A₅-(AAARA)₃-A-NH₂ by monitoring the N-terminal MABA fluorescence after temperature jump finding relaxation rates around 10⁸⋅s⁻¹. Their single exponential kinetics are likely to result from rapid N-terminal fraying, crossing only the propagation barrier, as their calculations indicate.

The above calculation makes a number of assumptions, but it is robust and holds for a range of helix/coil parameters. It is for an extreme case, however, with very helical peptides, such as suc-F_S, poly(Lys), or poly(Glu). We therefore repeated the calculation for other helix contents (not shown). In general, as the helix content decreases, the importance of increasing the all-coil population grows, but fraying always contributes more, unless the helix content is very low (about 25%). This conclusion suggests that if a temperature jump experiment was performed on a less helical peptide, two phases may be observed: a fast phase from fraying on the submicrosecond time scale followed by a slow phase from nucleation on the millisecond time scale.

Longer Peptides Fold with a Transient Overshoot in Helix Content.

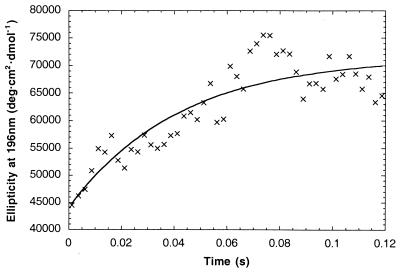
The AQ28, poly(Lys) and poly(Glu) data fit well to a three-state mechanism (coil → intermediate → equilibrium, Fig. 2). Rate constants for the two steps are given in Table 2. Fitting data in the 206-nm to 234-nm range all gave similar results. In contrast, the 4.4-kDa poly(Glu) data from 190 nm to 200 nm fitted to a single exponential, with a rate constant of ≈25 s⁻¹ (Fig. 3).

Table 2.

Kinetic parameters for α-helix formation in poly(Glu) and poly(Lys)

Peptide	k1, s−1	k2, s−1	Overshoot,* %
Poly(Glu) 4.4 kDa	600  ±  50	180  ±  30	15
Poly(Glu) 7 kDa	610  ±  50	180  ±  30	14
Poly(Glu) 20 kDa	690  ±  40	150  ±  20	13
Poly(Lys) 3 kDa	360  ±  30	65  ±  7	26
Poly(Lys) 5 kDa	490  ±  50	53  ±  6	21
AQ28 2.4 kDa	180  ±  140	75  ±  75	25

^*Overshoot (%) was calculated as (most negative ellipticity/equilibrium ellipticity) × 100 − 100. 

Figure 3.

Refolding kinetics of α-helix formation in 4.4-kDa poly(Glu) monitored at 196 nm. Data were fitted to the equation, giving k = 24 ± 6 s⁻¹.

The ellipticity at 226 nm (θ₂₂₆) in poly(Glu), poly(Lys), and AQ28 transiently achieves a minimum considerably greater than that of the native state after 2–10 ms. Peptides with mean molecular masses from 3 to 20 kDa all show overshoots from 13% to 26%. Overshoots at this wavelength have been observed in the folding of several proteins, including hen lysozyme (14), F2-V8 (15), and β-lactoglobulin (16), but their cause is not clear. While θ₂₂₂ is commonly used to quantify secondary structure in proteins the overshoot has been attributed to disulfide bonds (17), “some kind of non-native interactions” (7), and “nonpeptide chromophores” (18). Any of these explanations would impair the validity of CD measurements as a probe of peptide secondary structure.

Kinetics in the 190-nm Region.

The very slow phase shown by the results in the 190-nm region (Figs. 1 and 3) is puzzling. In contrast to 222 nm, the peak in the 190-nm region increases with time without an overshoot. The 190-nm signal could be perturbed by the strong and variable negative random coil peak in the 190-nm region or by amino acid side chains. The intensity and shape of the 190-nm peak varies considerably with φ, ψ angles within the helix (19) and depends on helix length, unlike 222 nm (20), which means that it is difficult to interpret the 190-nm signal quantitatively. Whatever the explanation for the absence of the overshoot at 190 nm, however, it remains true that the kinetics are considerably slower than expected.

Why an Overshoot?

Poly(Glu) and poly(Lys) have no disulfides, aromatics groups, or tertiary structure, so the overshoot at 222 nm cannot be attributed to them. There appears to be a large and rapid generation of high ellipticity at 226 nm followed by relaxation to equilibrium with a smaller ellipticity. But why should the ellipticity go through an overshoot? There are several possibilities.

Aggregation.

The peptide could form monomeric α-helices, which subsequently aggregate to structures with a lower helix content. Poly(Glu) is known to aggregate slowly below pH 4.6, and our data were collected at pH 3.3 (21, 22). Aggregation is unlikely, however, for the following reasons. Equilibrium is reached within 100 ms whereas precipitation caused by aggregation can take several hours (23). The kinetics of folding of 4.4-kDa poly(Glu) were invariant at concentrations from 0.05 mg⋅ml⁻¹ to 5 mg⋅ml⁻¹ (see the supplemental data at www.pnas.org; Fig. 6), indicating that we are observing first-order transitions, not an oligomerization. We repeated the experiment jumping to pH 4.8 where poly(Glu) is always monomeric (14). At pH 4.8 a lower helix content was observed at equilibrium, as expected, but the percentage size of the overshoot was unchanged (see the supplemental data at www.pnas.org; Fig. 7). Whereas poly(Lys) can convert to β-sheet after heating for several minutes at high pH (24, 25), our CD spectra after 100 ms of folding at 20°C show no sign of β-sheet formation. AK-based peptides have been shown to be monomeric up to 4 mM (26), far in excess of the concentration of 50 μM used in our experiments, and AQ-based peptides have been shown to be monomeric under the conditions studied here (27, 28).

3₁₀-helix formation.

It has been proposed that the 3₁₀-helix is an intermediate on the pathway of α-helix formation (29) and that poly(Ala)-based peptides (30) and poly(Lys) (31) form a significant amount of 3₁₀-helix at equilibrium. The CD spectra we acquire (Fig. 1), however, do not show the distinctive features of the 3₁₀-helix (32).

Poly(Pro)II helix formation.

There is evidence that unordered polypeptides form a substantial population of poly(Pro)II helix (33). The slow helix nucleation we observe therefore may result from the peptides needing to fold from a poly(Pro)II helix or some other metastable structure. We do not observe the characteristic spectrum of poly(Pro)II, however, but do observe an isodichroic point at 202 nm, suggesting that only α-helix or coil are present at all times.

Change in φ, ψ angles.

The helical CD spectrum changes significantly if the geometry of the helix is altered by varying the backbone φ, ψ angles (14). It therefore is possible we are observing a slow cooperative transformation from the peak of the overshoot as a result of tilting the planes of the peptide bonds relative to the helix axis. We do not see why the helix should form this metastable structure; however, nor do we expect this tilting to be very slow.

The remaining possibility, which we favor, is that the results show the slow gain and subsequent loss of monomeric α-helical structure. But why should the α-helix content show an overshoot?

We suggest that the overshoot arises from two factors. First, while helix initiation is slow, the conversion of an existing helix into two helices also will be slow because it requires the simultaneous breakage of three backbone hydrogen bonds. Second, the mean helix content of a peptide consisting of a single helix is higher than the mean helix content of the peptide with several helices present at equilibrium, as shown by consideration of the effects of the “one-sequence approximation” within helix-coil theory (34–36).

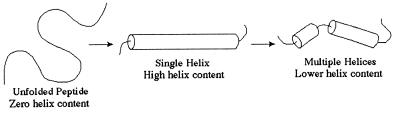
A possible explanation for the overshoot is as follows (Fig. 4). The fully charged peptide is entirely unfolded and extended. After initiation the helix will propagate rapidly, forming a very long helix, including nearly all the residues. This single-helix conformation will have a high helix content, giving the maximum ellipticity observed in the kinetics. At equilibrium the peptide will have many conformations containing two or more helices, perhaps in helix–turn–helix or antiparallel coiled-coil motifs. The transition from the single-helix conformation to multiple helices requires either the nucleation of a new helix in a coil region or the breakage of the long helix. Both of these steps are slow; hence, the rate from the peak of the overshoot to equilibrium is slow and there is a decrease in helix content.

Figure 4.

α-Helix folding model.

There is no overshoot for the short peptide AK16 as conformations with multiple helices are insignificantly populated because of its short length. Hence, these kinetics simply show the relaxation rate for crossing the nucleation barrier. The longer peptide, AQ28, folds faster than AK16 as it has more potential nucleation sites and has an overshoot as it forms multiple helices at equilibrium.

We note one difficulty with the model. It does not explain the 190-nm kinetics. Further data is needed to help understand this phenomenon. Our main conclusion, that the α-helix folds far slower than previously thought, is, however, not affected by this caveat.

Folding from Partly Folded Peptides.

To further test this model, we measured the folding kinetics for 4.4-kDa poly(Glu) jumping from pH 5.5 to 3.5 (see the supplemental data, Fig. 8, at www.pnas.org). The data showed that the majority of the peptides population had reached equilibrium within the dead time, whereas a minor population folded with an overshoot at identical time scales compared with jumping from pH 8.8. At pH 5.5, most peptides contain one or more helices that will very rapidly propagate and hence reach equilibrium within the dead time. A small number of peptides will be 100% coil; these will fold with an overshoot. When 4.4-kDa poly(Glu) is jumped from low to high pH the observed change in helix content is all lost within the dead time (see the supplemental data at www.pnas.org; Fig. 5). This result is consistent with fast fraying from helix ends, crossing the low propagation barrier.

DISCUSSION

We believe that our data and temperature jump experiments can be reconciled if they are measuring different contributions to helix folding kinetics. On the other hand, different peptides were used here from the temperature jump work and their initiation rates may well be significantly different. We suggest that helix nucleation takes place on the millisecond time scale and helix propagation on the submicrosecond time scale. Further experiments are needed to test this hypothesis.

It is remarkable that our peptides fold more slowly than a number of proteins. If our observation of slow helix nucleation is general, then protein folding models that assume that the first step in folding is the initiation of any helices stable in isolation may have to be rethought. It is possible, however, that helices within proteins fold more quickly than in our peptides for several reasons. Side-chain interactions or capping interactions present in protein helices (but not those studied here) may speed up nucleation. Helix initiation in a hydrophobically collapsed state may be faster. Denatured proteins may not be fully unfolded and possess prenucleated helices that only need to propagate. Oas and coworkers (37, 38) have shown that λ repressor folds on the submillisecond time scale, explained by a diffusion-collision between fast initiating helices. It therefore may be the case that slow initiation in the helices studied here is atypical.

In conclusion, we have shown that stopped-flow synchrotron CD can give outstanding information on the kinetics of secondary structure formation, α-helix initiation in our peptides is at least 10⁵ times slower than expected and long α-helices can fold with an overshoot in helix content.