Temperature dependence of the two-dimensional infrared spectrum of liquid H₂O

Abstract

Two-dimensional infrared photon-echo measurements of the OH stretching vibration in liquid H₂O are performed at various temperatures. Spectral diffusion and resonant energy transfer occur on a time scale much shorter than the average hydrogen bond lifetime of ≈1 ps. Room temperature measurements show a loss of frequency and, thus, structural correlations on a 50-fs time scale. Weakly hydrogen-bonded OH stretching oscillators absorbing at high frequencies undergo slower spectral diffusion than strongly bonded oscillators. In the temperature range from 340 to 274 K, the loss in memory slows down with decreasing temperature. At 274 K, frequency correlations in the OH stretch vibration persist beyond ≈200 fs, pointing to a reduction in dephasing by librational excitations. Polarization-resolved pump-probe studies give a resonant intermolecular energy transfer time of 80 fs, which is unaffected by temperature. At low temperature, structural correlations persist longer than the energy transfer time, suggesting a delocalization of OH stretching excitations over several water molecules.

Water displays a variety of anomalies that are closely related to its microscopic structure (1). In the liquid phase, water molecules form an extended disordered network of intermolecular hydrogen bonds. According to the traditional picture of time-averaged water structure, each water molecule forms four hydrogen bonds, two by donating its H atoms and two by accepting H bonds at the more electronegative oxygen atom (2, 3). At a temperature of 300 K, ≈90% of water molecules are hydrogen-bonded. This picture is supported by molecular dynamics simulations (4–8) and a large body of experimental results (1, 3, 9–12).^§

The structure of the hydrogen bond network fluctuates on a multitude of time scales between 10 fs and ≈10 ps, including changes of molecular orientations and distances, the breaking and reformation of hydrogen bonds, and slower rotational motions (4–8). Understanding the nature of such fluctuations and their influence on the macroscopic properties of water requires experimental probes that provide insight into (transient) local structures and are sensitive to microscopic changes in the molecular network. The vibrational spectra of water reflect the dynamical structure of the hydrogen bond network and, thus, are one of the most direct probes of the underlying interactions (13–15). So far, most studies of liquid H₂O have concentrated on the OH stretching band, displaying a maximum at ≈3,400 cm⁻¹ and a broad asymmetric spectral envelope with a width (full width at half maximum) of 270 cm⁻¹. With decreasing temperature, the maximum of the band shifts to lower frequencies, and a reshaping of the envelope occurs. The distribution of hydrogen bond geometries and strengths results in a distribution of OH stretching frequencies with weakly and strongly bonded OH stretching oscillators absorbing at high and low frequencies, respectively. Thus, the red-shift in absorption for lower temperatures points to an overall enhancement of hydrogen bonding and structural correlation. However, the distribution of transition frequencies undergoes rapid fluctuations—i.e., spectral diffusion—because of the fluctuating forces the molecular network exerts on a particular oscillator (16). Spectral diffusion is connected with vibrational dephasing, the loss of the quantum phase between the v₀ and v₁ wavefunctions of the OH stretching oscillator. In addition, the (resonant) transfer of OH quanta between neighboring oscillators causes both spatial and spectral diffusion. Non-Condon effects resulting in a variation of the vibrational transition dipole with frequency originate from the influence of fluctuating forces on the vibrational coordinate (17).

Steady-state linear infrared spectroscopy measures the time-averaged vibrational absorption. Even when combined with high-level theoretical calculations, it does not allow for a clear separation of broadening mechanisms and, thus, analysis of the fluctuations characteristic for the hydrogen bond network. In contrast, nonlinear vibrational spectroscopy in the ultrafast time domain provides highly specific insight into the time evolution of vibrational excitations under the influence of a fluctuating bath (18, 19). Third-order photon-echo and pump-probe spectroscopies use an excited oscillator as a probe of structural dynamics and follow its time evolution. Such a probe is most sensitive within the excited-state lifetime of the oscillator but depending on the repopulation kinetics of its ground state also provides insight into slower processes.

Spectral diffusion and vibrational dephasing in water were first studied using HOD in D₂O or H₂O as a model system in which diluted OH or OD stretching oscillators are embedded in a fluctuating D₂O or H₂O network (20–27). Here, resonant energy transfer between the diluted stretching oscillators occurs on a time scale distinctly slower than spectral diffusion, in contrast to neat H₂O or D₂O (28). The first femtosecond two- and three-pulse photon-echo experiments with homodyne detection of the nonlinear signal from HOD in D₂O have revealed an ultrafast, sub-100-fs decay component of the macroscopic third-order polarization, followed by slower sub-picosecond and picosecond kinetic components (23, 24). Such fast spectral diffusion and dephasing have been attributed to the fluctuating forces that the hydrogen bond network exerts on the hydrogen-bonded OH stretching oscillator. Upon hydrogen bonding, the diagonal anharmonicity of the oscillator is substantially enhanced compared with a free OH group, making the hydrogen-bonded oscillator much more sensitive to the fluctuating force. This picture is in agreement with theoretical simulations reproducing the time scales of spectral diffusion and providing the corresponding frequency fluctuation correlation function of the system (29–31). The fluctuating electric fields interacting with a hydrogen-bonded oscillator represent the major source of spectral diffusion (31–34).

Additional insight originates from measuring vibrational photon echoes with heterodyne detection and deriving 2D spectra from them. Two-dimensional spectra span the real and imaginary part of the third-order polarization along two frequency axes, the excitation frequency v₁ und the detection frequency v₃ (35–37). Measuring 2D spectra as a function of the population time T provides direct insight into the redistribution of vibrational transition frequencies and the different broadening processes of individual components of the spectra. Frequency correlations extracted from 2D spectra of HOD in H₂O or D₂O display a decay with sub-50-fs, 400-fs, and 1.4-ps components (25, 38, 39). Different assignments were made for the fast components, whereas the slowest component was interpreted as a result of hydrogen bond-breaking and -making dynamics. Probing the OD stretch in the HOD/H₂O system (37) offers a somewhat extended time range of these studies because of the longer lifetime of the OD stretch (1.8 ps) relative to the OH stretch (700 fs). The OD/H₂O 2D IR spectrum provides a detailed description of the bath dynamics well out to the diffusive limit.

Recently, we have reported the first 2D IR study of the OH stretching vibration of neat H₂O in which the resonant transfer of OH stretching quanta between adjacent molecules adds another component to the ultrafast dynamics (40). The initial spectrum was found to be clearly inhomogeneously broadened; however, the frequency correlations were effectively washed out within 50–100 fs under ambient conditions. The fast time scales of vibrational dephasing indicated that the frequency modulation is dominated by the high-frequency librations of the intermolecular spectrum. The dynamic range of the pure H₂O studies is, however, limited by energy transfer effects. The loss in frequency correlations was faster than the energy transfer time of ≈80 fs and strong spectral modulation of the ground state bleach was observed, consistent with a process dominated by librations. In this article, we report the temperature dependence of the 2D OH stretching spectra of liquid water over a wide temperature range from 274 to 340 K. Using a nanofluidic cell designed for preparing sub-micrometer-thick water layers and femtosecond pulses spectrally covering the full OH stretching band, we observe pronounced changes of the 2D spectra with temperature. At 300 K, an initial loss of frequency correlations occurs on a 50-fs time scale, and resonant intermolecular energy transfer occurs within 100 fs. The loss in memory is found to be very sensitive to temperature, whereas the intermolecular energy transfer time appears to be unaffected by the temperature change. At 274 K, frequency correlations in the OH stretch vibration persist beyond ≈200 fs, pointing to a reduction in the dephasing rate through librational degrees of freedom. Such correlations persist longer than the energy transfer time, suggesting a delocalization of the OH stretching excitation over several molecules.

Results and Discussion

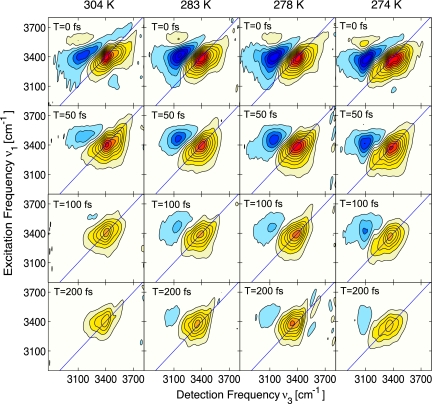
Echo correlation spectra were taken for population times T = 0, 50, 100, and 200 fs at temperatures between 274 and 340 K. The absorptive component of the echo signal (Fig. 1) has two clear peaks corresponding to the v_0–1 and v_1–2 transitions of the OH stretching oscillator. The positive peak along the diagonal originates from the ground state bleach and stimulated emission involving the v_0–1 transition, whereas the off-diagonal negative peak reflects absorption of the v_1–2 transition. Because of vibrational anharmonicity, the latter peak is red-shifted by ≈250 cm⁻¹.

Fig. 1.

Absorptive components of the 2D IR echo spectra of pure liquid H₂O for various population times and temperatures, arranged vertically for population times 0, 50, 100, and 200 fs, and horizontally for temperatures of 304, 283, 278, and 274 K. The plots for each set of temperatures are normalized to the peak amplitude of the v_0–1 transition at T = 0 fs. Contour lines correspond to 10% changes in amplitude.

Spectral overlap of the two transitions distorts the relative and absolute peak positions. With decreasing temperature the peaks become red-shifted along both axes, and the relative intensity of the negative peak increases. At all temperatures, the T = 0 spectra are similarly elongated along the diagonal, showing strong frequency correlations or inhomogeneous broadening due to local structures that have not yet experienced rearrangement. With lower temperatures, the shape of the v_0–1 peak tapers increasingly from blue to red. Nevertheless, the antidiagonal width of the spectra is essentially independent of frequency, as is evident from the cross-sections shown in Fig. 2.

Fig. 2.

Antidiagonal slices of the 2D spectrum at population times, T = 0, for temperatures of 304, 283, 278, and 274 K. Peaks corresponding to the antidiagonal passing through diagonal frequencies of 3,300, 3,400, and 3,500 cm⁻¹ are normalized with respect to the v_0–1 peak. Similar peak widths are observed regardless of the spectral position of the antidiagonal. The apparent increased amplitude in the negative feature at 3,300 cm⁻¹, attributed to excited state absorption, is due to the normalization used to enable comparison of the relative linewidths of the ground state transitions.

As the hydrogen bond network evolves in time, structural rearrangement and relaxation cause spectral diffusion to occur with different time scales across the spectrum. At 304 K, the red side of the v_0–1 transition has lost most of the initial frequency correlations by T = 50 fs, in agreement with our previous studies (40). The diagonal is, however, clearly further elongated or inhomogeneously stretched on the blue side of the 2D spectrum at these times. Because of the larger bandwidth and higher central frequency of these pulses compared with the previous measurements (40), the dynamics on the blue side of the spectrum are observed here for the first time. At T = 100 fs, the differences in line broadening across the v_0–1 peak under ambient conditions are significantly reduced and become effectively indistinguishable by T = 200 fs. Spectra taken beyond T = 200 fs are not shown because the population of excited vibrations is diminished and the thermal signal obscures any remnant of the initial frequency correlations. We note here that spectra were also collected at higher temperatures up to 340 K but were largely indistinguishable from the room temperature results.

Marked changes in the 2D spectra are noted as the temperature is decreased from ambient conditions. Reaching a temperature of 278 K, frequency correlation on both the blue side and the red side of the v_0–1 spectrum becomes longer-lived. A dramatic change occurs in the spectral response on the red side when the sample temperature is reduced to 274 K, now showing strong frequency correlations that persist out beyond T = 200 fs. The slowing down of spectral diffusion with decreasing temperature is also obvious from the behavior of the v_1–2 spectrum. At 304 K, spectral diffusion leads to a disappearance of the v_1–2 peak well within the lifetime of the v₁ state of 200 fs. In contrast, the spectra for a temperature of 274 K exhibit the v_1–2 feature up to population times of 200 fs although the population lifetime of the v₁ state is somewhat shorter (see below).

In addition to the photon-echo experiments, we performed temporally and spectrally resolved pump-probe experiments with parallel and crossed polarizations of the pump and probe pulses. In Fig. 3, results are shown for a temperature of 274 K as a representative example. Polarized pump-probe spectra were taken with parallel and crossed polarizations up to T = 1.5 ps. Both polarization conditions exhibit a fast exponential decay followed by a rise with a 1.3-ps time constant at later times T corresponding to energy delocalization and dissipation in the excited sample, respectively (40, 41). The fast decays in the amplitudes of the different polarization components are caused by both orientational (energy transfer and rotational motions) and population relaxation. In Fig. 4a, the spectrally integrated r(t) is plotted as a function of pump-probe delay for three different temperatures. The initial value of anisotropy decreases from 0.4 at a temperatures T > 295 K to 0.3 at T = 274 K, whereas the decay time of 80 ± 15 fs remains unchanged (Fig. 4b).

Fig. 3.

Spectrally resolved pump-probe measurement of pure water at 274 K for (a) parallel polarization between pump and probe, and (b) perpendicular polarization between pump and probe. (c) Pump probe cross-sections integrated across the v_1–2 transition (3,050–3,150 cm⁻¹) for parallel (green) and perpendicular (blue) polarizations. (d) Pump probe cross-sections integrated across the v_0–1 transition (3,300–3,600 cm⁻¹) for parallel (black) and perpendicular (red) polarizations.

Fig. 4.

Polarization anisotropy decay and population lifetime. (a) Anisotropy decay for 304, 283, and 274 K, respectively. (b) Results of fitting for population lifetime, T1 (circles), and polarization anisotropy decay (squares).

The lineshapes of the OH stretching 2D and linear absorption spectra are determined by both intra- and intermolecular couplings. We first consider intramolecular couplings that influence the microscopic character of OH stretching excitations. The water monomer in the gas phase and in solution displays distinct absorption bands of the symmetric and asymmetric OH stretching modes, both being well separated from the v₂ overtone of the OH bending mode at lower frequency. In liquid H₂O, hydrogen bonding enhances the diagonal anharmonicities of the stretching oscillators and lowers their v_0–1 transition frequencies to an extent that depends on the local hydrogen bond strength.

Symmetry breaking and spectral diffusion, which originate from interactions in the disordered and fluctuating structure of the molecular network in neat H₂O, lead to a strong mixing of the two stretching modes. The anharmonic coupling of the OH stretching and bending oscillators leads to a Fermi resonance of the v₁ OH stretching and the v₂ OH bending states, adding OH bending character to an OH stretching excitation (44, 45).

The population lifetime of OH stretching excitations, shown in Fig. 4 as a function of temperature, varies between 180 fs at 274 K and 300 fs at 340 K. This lifetime is substantially shorter than the time scale of molecular rotations (>700 fs) and the average lifetime of hydrogen bonds (≈1 ps). Thus, the reshaping of the 2D spectra shown in Fig. 1 mainly reflects spectral diffusion due to the fastest structural fluctuations of water and to processes of resonant intermolecular energy transfer. Structural fluctuations on this time scale involve intermolecular modes such as librations and/or hydrogen bond modes. Spectral diffusion and vibrational dephasing in water are dominated by fluctuating electric fields, and because of the long-range character of this interaction, molecular motions over a spatially extended range around the probe contribute to such processes.

The 2D spectra plotted in Fig. 1 cover the full range of the OH stretching absorption. At a population time T = 0, they are elongated along the diagonal, demonstrating the initial inhomogeneous frequency distribution on both the v_0–1 and v_1–2 transitions. This inhomogeneity is due to the distribution of hydrogen bond strengths in the network of water molecules, translating into a distribution of (red-shifted) transition frequencies. As population time evolves, spectral diffusion randomizes the initial frequency distribution, eventually resulting in more or less circular envelopes of the 2D spectra. The time evolution of the 2D spectra displays two major trends:

• (i)Spectral diffusion at frequencies below 3,500 cm⁻¹ is substantially faster than for higher frequencies. In the red part of the 2D spectra, one observes a rapid frequency randomization and concomitant reshaping of the 2D spectra toward a circular envelope within the first 50 fs (see also ref. 40). In contrast, the diagonal extension of the 2D envelopes toward high frequencies, which is most clearly pronounced in the T = 50 fs spectra, persists for a longer period. The high-frequency part of linear OH stretching absorption has been attributed to water molecules with non- or weakly hydrogen-bonded OH groups (17, 32, 46). A similar picture has been developed for the high-frequency part of the 2D spectra of HOD in D₂O (47). Free or weakly hydrogen-bonded O-H stretching oscillators display a diagonal anharmonicity and a v_0–1 transition dipole that are substantially smaller than in a hydrogen-bonded geometry, as is evident from studies of water monomers in nonpolar solution (48). The reduced anharmonicity results in a reduced modulation of vibrational transition frequencies by fluctuating electric fields, and thus spectral diffusion slows down. In addition, the rate of resonant intermolecular energy transfer, a process contributing to vibrational dephasing and spectral diffusion, becomes smaller because of the reduced dipole–dipole coupling. In contrast, free OH groups are a short-lived species because the reformation of broken hydrogen bonds at ambient temperature occurs on a time scale of ≈200 fs (8, 49). Hydrogen bond reformation is connected with a jump of the vibrational transition frequency—i.e., spectral diffusion—and consequently the reformation time sets an upper limit for the time scale of frequency randomization in the high-frequency part of the spectrum.

• (ii)With decreasing temperature, spectral diffusion slows down, as is evident from the slower reshaping of the spectra for temperatures of 274 and 278 K. Previous studies of neat water (40) and HOD in H₂O/D₂O (49) suggest that the fastest decay of spectral and thus structural correlation is due to librational degrees of freedom that are thermally excited in the fluctuating equilibrium geometry of the hydrogen bond network. At 304 K, such decay occurs on a sub-50-fs time scale, roughly corresponding to the period of librational excitations between 650 and 1,000 cm⁻¹—i.e., in the range of the librational L2 band of water (13, 14, 41, 50). The thermal population of excited librational states in this range is reduced by a factor of ≈1.5 when going from 304 to 274 K. Moreover, the L2 band narrows and shifts to somewhat higher frequencies with decreasing temperature, leading to a substantial decrease of spectral density between 200 and 700 cm⁻¹ (50). Here, it is important to note that the number of hydrogen bonds only increases by ≈10% in going from room temperature to the lowest temperature. This increase results in a larger fraction of water molecules forming four hydrogen bonds. The decrease in temperature significantly decreases the thermal population of librations above 200 cm⁻¹ that give rise to the fast dephasing (40). The decrease in thermal occupation of these librations more than compensates for the relatively smaller change in the collective degree of hydrogen bonding that acts to increase the length scale of the frequency correlations. The net effect is slower spectral diffusion at lower temperatures. In addition to slowing down the initial decay component, the subsequent (sub)picosecond loss of spectral correlation may also change but cannot be probed much beyond the 200-fs lifetime of the OH stretch.

We now discuss the pump-probe data and in particular the decay of polarization anisotropy. The initial decay of the enhanced v_1–2 absorption and of the bleaching on the v_0–1 transition is due to the v₁ population decay of the OH stretching oscillator with the time constants as shown in Fig. 4b. At ambient temperature, the v₁ state of the OH stretching mode is in Fermi resonance with the v₂ state of the OH bending mode (45). The population decays from the combined OH stretch/bend states to the v₁ and eventually to the v₀ state of the OH bending oscillator, the energy difference being transferred to intermolecular vibrations. Direct evidence for this stepwise relaxation scenario comes from recent femtosecond studies of librational absorption (41). The increase of the v₁ lifetime with temperature has been attributed to an increasing energy mismatch between the v₁ state of the OH stretching and the v₂ state of the OH bending mode caused by the greater diagonal anharmonicity of the OH stretch (42). The OH stretch undergoes a larger red-shift in its spectrum than the corresponding OH bend with increasing degree of hydrogen bonding, and the shifts are in the opposite direction, which acts to increase the degree of Fermi resonance in the coupling between the OH stretch and OH bend overtone as the temperature is lowered.

Weakening and/or breaking of hydrogen bonds with increasing temperature shifts the v₁ state to higher energies, whereas the v₂ state remains unchanged or in the case of hydrogen bond breaking undergoes a slight shift to lower frequencies. The slow rise in the pump-probe signals occurring at longer time delays (Fig. 3) reflects the dissipation and spatial redistribution of excess energy in the hydrogen bond network, as has been discussed elsewhere (41, 42).

The spectrally integrated anisotropy decay plotted in Fig. 4a decays with a time constant of ≈80 fs, which is independent of temperature (Fig. 4b). The initial value of the anisotropy is between 0.3 and 0.4. At all temperatures, the anisotropy decay is substantially faster than the population lifetime of the v₁ state of the OH stretching mode. We assign the decay in the polarization anisotropy to energy transfer to waters with random orientations relative to the initially excited site. The energy transfer time measured in this way is only an upper limit and may represent more than one transfer step in the loss of anisotropy (28, 40). There are other potential contributions to the loss of anisotropy such as librational and rotational reorientations of molecules and an intramolecular excitation transfer between stretching excitations localized on one of the OH groups. Inertial librational components were specifically modeled using molecular dynamics calculations and found to contribute no more than 20% to the initial decay.^¶ Rotational diffusion occurs on much longer time scales and can be ruled out (51). The concept of an anisotropy loss by intramolecular excitation transfer has recently been invoked to explain the behavior of water monomers with a symmetric and antisymmetric OH stretching vibration (52). Because of the mixed character of OH stretching excitations in bulk water (see above), this mechanism plays a minor role here. In addition, the polarization anisotropy decays to zero, not some intermediate value, indicative of the degree of excitation transfer between the symmetric and antisymmetric modes (28). We thus conclude that resonant intermolecular energy transfer governs the fast anisotropy decay.

It is interesting to compare the time scale on which the anisotropy decays to that of the frequency correlation loss mapped in the 2D spectra (Fig. 5). At ambient temperature, spectral diffusion occurs on a sub-50-fs time scale, somewhat faster than the anisotropy decay. In this limit, energy transfer occurs as a mainly incoherent process. It represents an additional contribution to the loss of spectral correlations that is dominated by high-frequency librations. Under such conditions, the spatial correlation length of OH stretching excitations is very short and may not extend beyond neighboring molecules. At lower temperatures, the frequency correlations clearly persist for longer than 200 fs, the lifetime of the OH stretching excitations, whereas the energy transfer process occurs within this time interval (cf. Fig. 4). This means that the distribution of transition frequencies, and thus acceptor frequencies, shows only moderate changes on the time scale of the transfer. In this limit, the spatial correlation length of the OH stretching excitation extends over a group of molecules—i.e., the initial OH stretching excitation is delocalized and the energy transfer may be of partially coherent character.

Fig. 5.

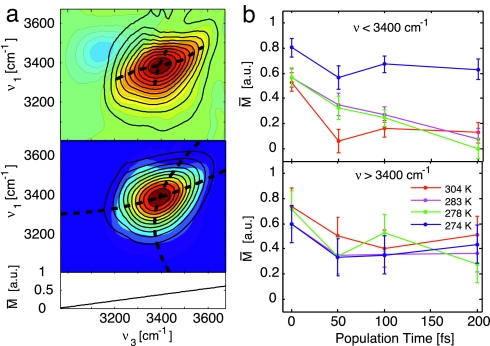
Interpretation of the correlation spectrum. (a) Eccentricity analysis of the 2D IR spectra for T = 50 fs at 283 K. (Upper) The 2D spectrum (colored contours) is fit with a double Gaussian along slices of v₃ to compensate for the interference with the excited state absorption that is opposite in sign. This negative-going peak is subtracted from the data (black contours), and the peaklines are found along v₃ and v₁ (dashed lines). (Lower) Reconstructed 2D spectrum (black contours) using a second-order polynomial fit of the peaklines (dashed lines). From fitting and comparing multiple datasets, the error is estimated to be 11%. (b) Wavelength-dependent eccentricity as a function of population time averaged over the red side of the spectrum, v₃ < 3,400 cm⁻¹, and over the blue side for v₃ > 3,400 cm⁻¹.

So far, a theoretical treatment of the latter scenario in a disordered molecular network, and thus a calculation of the spatial correlation length has not been reported. A minimum correlation length can, however, be estimated by considering incoherent energy transfer within a period in which spectral diffusion is negligible. In this picture, individual incoherent transfer events between neighboring molecules sample a certain part of the molecular network, the dimension of which is taken as a minimum value of the spatial correlation length. Using this approach and an energy transfer time of 80 fs to neighboring waters within a sampling time interval of 200 fs, the OH vibrational stretch lifetime, we derive a minimum correlation length of the order of 4.4 Å (Fig. 6) at the lowest temperature, 274 K, corresponding to ≈15 water molecules.

Fig. 6.

Correlation length scale of the OH stretch at 274 K compared with the average interatomic distance. Assuming diffusive migration of the excitation, the persistence of the frequency correlation in relation to the spatial motion of the excitation gives a lower limit to the ensemble-averaged length scale for the frequency correlations of >15 waters at this temperature.

In this regard, the energy transfer process itself holds a number of interesting questions with respect to the character of the process. First, the energy transfer rate should depend on the spectral position within the OH stretching band because there is a predicted strong decrease of the transition dipole moment toward high frequencies due to non-Condon effects (17). As a result, a substantially slower energy transfer is expected at high frequencies. With the present signal-to-noise ratio, this expectation is not born out. Higher time resolution and probe wavelengths over a wider bandwidth will help resolve this issue. Second, the associated intermolecular coupling strength has not been well characterized theoretically. For nearest-neighbor interactions, the distance between molecules is of the same order as the extension of the vibrational dipoles, making approximations based on point dipoles questionable. Here, much more sophisticated calculations are required to link the measured energy transfer rates to the microscopic couplings.

In conclusion, our results suggest that ultrafast librational fluctuations within the hydrogen-bonded network dominate the initial dephasing of the OH stretching excitations at most temperatures, while increased spatial correlations in the hydrogen bond network preserve the excited frequency correlations at temperatures near freezing. A better understanding of the dynamics of pure water and the microscopic mechanisms that lead to energy redistribution and spectral diffusion within the hydrogen-bonded network requires new theoretical models that include the dynamics of the fluctuating network of hydrogen bonds, energy transfer mechanisms, and anharmonic couplings sensitive to details in the intermolecular potential.

Materials and Methods

Experiments were performed with a temperature controlled nanofluidic cell in which the pathlengh of 400 nm was actively stabilized to within a few nanometers. The diffractive optic-based three-pulse echo setup (40) provided passive phase stabilization for extended data collection periods using heterodyne detection. Details of the cell design and integration into the optical setup are given in supporting information (SI) Methods and SI Figs. 7 and 8. For a more quantitative analysis of the shape of the 2D spectra, we consider the eccentricity M that is defined as M = (a² − b²⁾/(a² + b²) for an elliptic shape of the spectrum (a, b: diagonal and antidiagonal width of the spectrum) (53). (See SI Methods for details on this analysis.) Fig. 5a shows the results of the eccentricity analysis for a particular 2D measurement before and after correction for the excited-state contribution. In Fig. 5b, the obtained values for the eccentricity parameter are plotted as a function of population time T for the different temperatures of the water sample. The eccentricity for frequencies below 3,400 cm⁻¹ shows the slowing down of spectral diffusion with decreasing temperature. The values derived from the 274-K spectra display a slower decrease than the data for higher temperatures. At high frequencies, this effect is less pronounced.

The population relaxation effects are isolated by constructing the magic-angle decays in which the energy dissipation kinetics, or thermal effect, at later times is explicitly taken into account (40). The magic-angle decay is given by I_ma(t) = 1/3(I_‖(t) + 2I_⊥(t)), where I_‖ is the intensity of the parallel component and I_⊥(t) is the perpendicular intensity component of the excitation. The fits were averaged over the v_1–2 spectrum where the thermalization signal is weakest (42). In Fig. 4b, the T₁ values derived in this way are plotted as a function of sample temperature. Both the absolute numbers and the increase of lifetime with temperature agree well with previous measurements (40–42).

The decay of spatial orientation of the excited vibrational dipoles is reflected in the transient polarization anisotropy r(t) given by r(t) = (I_‖(t) − I_⊥(t))/(I_‖(t) + 2I_⊥(t)) (43). To calculate r(t), the pump-probe spectra were integrated in the central spectral region to minimize noise contributions from regions of smaller signal where the v_0–1 and v_1–2 transitions interfere. Independent checks of the red and blue spectral features, with reduced integration bandwidths, gave similar decay profiles.