Electrically driven motor in the outer hair cell: Effect of a mechanical constraint

Abstract

The outer hair cell has a unique voltage-dependent motility associated with charge transfer across the plasma membrane. To examine mechanical changes in the membrane that are coupled with such charge movements, we digested the undercoating of the membrane with trypsin. We inflated the cell into a sphere and constrained the surface area by not allowing volume changes. We found that this constraint on the membrane area sharply reduced motor-associated charge movement across the membrane, demonstrating that charge transfer is directly coupled with membrane area change. This electromechanical coupling in the plasma membrane must be the key element for the motile mechanism of the outer hair cell.

The outer hair cell changes the length of its cylindrical cell body in response to changes in the membrane potential (1–5), reaching a frequency of at least 20 kHz (6, 7). Because of its strategic location in the inner ear connecting the basilar membrane and the reticular lamina, this mechano-receptor cell presumably serves as an actuator in a feedback loop affecting vibrations of these tissues and thereby modulating the sensitivity of the mammalian ear (see refs. 8 and 9 for review). For this reason, the mechanism of this motility and its biological function have been a focus of intense research. For operating at high frequencies, a direct transduction mechanism would be advantageous. Indeed, the cell appears to be driven by a membrane-based motor that directly uses electrical energy available at the plasma membrane. The lateral membrane of the cell has charges that are transferable across the membrane (10–12), analogous to gating charges of voltage-gated ion transporters. These charges enable the cell to obtain electrical energy. If the electrical energy obtained by charge transfer across the membrane is directly converted into mechanical energy in a manner similar to piezoelectricity, the charge transfer must be reciprocally affected by an externally applied tension. That has indeed been experimentally verified (12–14), leading to estimates of the area change of a single motor unit (7, 12, 13).

However, the simple characterization of the motor as described above is somewhat uncertain because of the structural complexity of the lateral membrane of the outer hair cell. The structural complexity obscures the molecular identity of the motor. In addition, the lateral membrane, where the motor resides, has an intricate structure of many elements (see ref. 15 for review) whose role in motility is uncertain. These factors leave uncertainties in the magnitude of tension that affects the motor.

To characterize the elements of the motile mechanism in the plasma membrane, we examine a simplified system, in which the cortical cytoskeleton is digested with trypsin (13, 16, 17). The cells treated internally with trypsin can no longer maintain their ordinary cylindrical shape and become spherical when the internal pressure is elevated. The conspicuous length changes (up to 5%), which are elicited by changes in the membrane potential of untreated cells, are not as obvious in modified rounded cells (13). The spherical geometry of the cell can be exploited to impose an area constraint by controlling the cell volume because the sphere minimizes the surface-to-volume ratio. If charge transfer and membrane area change are coupled, a constraint on the membrane area should reduce charge transfer across the membrane. Such an effect should be observed in the membrane capacitance because transfer of membrane charge contributes to the membrane capacitance. We therefore examined the voltage dependence of the membrane capacitance and the cell radius. We found that an area constraint reduces charge transfer, and thus area change and charge transfer are coupled in enzyme-treated cells. The present result could shed light on the molecular basis of the hair cell motor.

METHODS

Bullas were obtained from guinea pigs (Protocol 193, National Institute of Neurological Disorders and Stroke/National Institute on Deafness and Other Communication Disorders). The organ of Corti was dissociated from opened cochleas by teasing with a fine needle under a dissection microscope. The strips of organ of Corti thus obtained were tritulated three times gently with a plastic pipette and placed in the chamber mounted on an inverted microscope. Isolated outer hair cells with the regular shape were chosen for experiments. The pipette resistance was between 2 and 3 MΩ when filled with an intracellular medium. The internal solution consisted of 140 mM CsCl, 2 mM CaCl₂, 5 mM EGTA, 10 mM Hepes, 0.2 mg/ml trypsin (type I, Sigma). The external solution contained 140 mM NaCl, 5 mM CsCl, 2 mM MgCl₂, 1 mM CaCl₂, 2 mM CoCl₂, 10 mM Hepes, and 5 mM glucose. These channel-blocking media facilitated capacitance measurements (see below). The osmolarity of both media was adjusted to 300 mOsm/kg with glucose. In all media, the pH was adjusted to 7.4. A patch amplifier (EPC-7, List Electronics, Darmstadt, Germany) was used for whole-cell voltage clamp experiments. A train of voltage pulses was generated with an ITC-18 interface (Instrutech, Mineola, NY) by using the igor program (WaveMetrics, Lake Oswego, OR) with a software module created by R. J. Bookman’s laboratory at the University of Miami (http://chroma.med.miami.edu/cap).

The membrane capacitance was determined by capacitive currents elicited by voltage jumps (18). The sampling interval of the data acquisition was 10 μs. The relaxation time τ of the capacitive currents was larger than 140 μs. The access resistance R_a was (8.6 ± 2.7)MΩ. The membrane resistance R_m was somewhat dependent on the membrane potential and was between 0.2 GΩ and 1.5 GΩ. At the extremes of the membrane potential, R_m was (0.4 ± 0.1) GΩ and was (0.9 ± 0.5) GΩ in the middle range. The membrane potential was corrected for the access resistance, although the corrections were negligible in most cases.

Video images of the cell obtained with Hoffman differential contrast optics (Modulation Optics, Greenvale, NY) on a Nikon microscope were recorded during the experiment and digitized off-line with the nih image program (W. Rasband, National Institute of Mental Health). The resolution of the digitized image was 4.04 pixels per μm. With our setup, about half of the entire cell edge was usually associated with continuous maxima or minima of light intensity. The edge of this part of the cell was scanned along either the x or y axis so that light intensity profiles crossing the cell edge were obtained. The individual intensity profile near the maxima or minima was fit with a parabola, by using 9 pixels. With the fit, the positions of these extrema, which have subpixel precision, were regarded as the outline of the cell. These positions were traced automatically with a macro similar to the one previously described (19). The other half of the cell outline was accompanied by continuous maxima of light intensity gradient. The intensity gradient around a pixel was converted into a pixel value by the “find edges” function of the program. This preprocessing allowed us to trace the gradient maxima. By avoiding transition zones between the two kinds of edges, we could fit the traced outline of the cell with a circle. The reproducibility of this method can reach 10 nm, which we regard as the precision of our method in describing small radius changes. The actual cell radius, however, has uncertainties of about 0.5 μm because of the resolution limit imposed by the wavelength (20).

Positive or negative pressure was applied to the pipette through a solenoid valve (General Valve, Fairfield, NJ), which was connected to a reservoir with a diaphragm air pump (Thomas Scientific, Swedesboro, NJ) driven with a variable power supply. The pressure at the reservoir was monitored with a pressure gauge (model 68370, Cole–Parmer, Vernon Hills, IL). The area stiffness K of the cell membrane was determined by the pressure–radius relationship, assuming that membrane tension and pressure are related by Laplace’s law.

RESULTS

Experiments were performed on isolated outer hair cells in the whole-cell recording configuration (see Methods). Pressure up to about 1 kPa could be delivered to the patch pipette while maintaining the configuration. The patch pipette contained trypsin typically at 0.2 mg/ml concentration. The voltage dependence of the capacitance was determined with a pair of ascending and descending staircase voltage waveforms (Fig. 1B). After the whole-cell recording configuration was established, positive pressure up to 0.5 kPa was applied to the pipette. On application of this positive pressure at the pipette, the intracellular medium that contained trypsin was injected into the cell, inflating the cell into a sphere (Fig. 2A Inset). The shape change was irreversible, unlike untreated cells. The cell remained spherical even after removal of positive pressure.

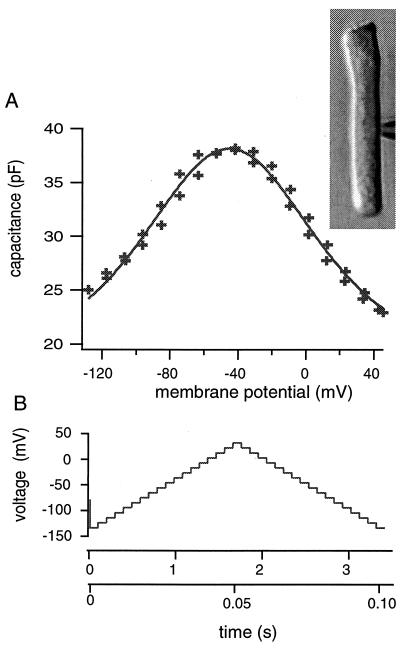
Figure 1.

The membrane capacitance (A) of an outer hair cell (Inset) just before the trypsin-containing pipette medium is injected. The voltage dependence is obtained by using a waveform that consists of an ascending staircase followed by a descending one (B). The short waveform has 3-ms steps and the total duration of 105 ms (lower time scale). The long waveform has 100-ms steps and the total duration of 3.5 s (upper time scale). The membrane capacitance is obtained from capacitive charge transfer elicited at each voltage step. Using either the long or the short waveform does result in a clear difference in the capacitance. The solid line in A represents the best fit with Eq. 1. The solid line represents a best fit, which gives q* = (0.75 ± 0.06) e, C_pk = (19.1 ± 1.2) pF (or N = (2.2 ± 0.3) × 10⁷), V₀ = (−46.0 ± 0.8) mV, and C_lin = (18.2 ± 1.5) pF.

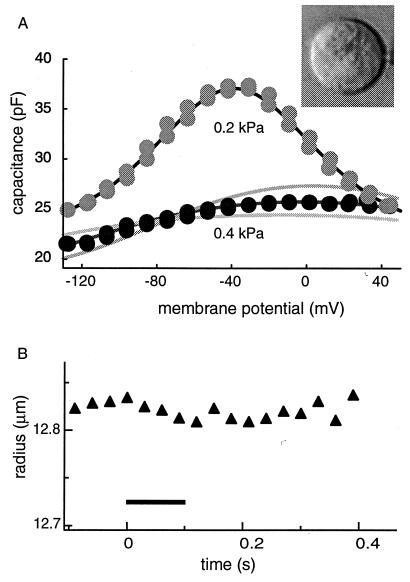
Figure 2.

The membrane capacitance and the cell radius examined with the short waveform (105 ms long with 3-ms steps). By applying pressure of 0.5 kPa to the patch pipette, the trypsin-containing (0.2 mg/ml) pipette medium is injected into the cell. The cell shape turns into a sphere (Inset). The same cell is shown in Fig. 1. (A) The membrane capacitance obtained with the short voltage waveform has a shallow bell-shaped voltage dependence at 0.4 kPa pipette pressure (●). When pipette pressure is reduced to 0.2 kPa (), the membrane potential shows a voltage dependence as large as the one obtained before trypsin digestion (1A). (B) The cell does not show a noticeable radius changes during the waveform, which starts from time 0 and lasts for 105 ms (▴). The duration of the waveform is marked with a bar. Pipette pressure (P₀) is 0.4 kPa. The upper solid line in A represents a fit to Eq. 1 with q* = q, C_pk = 4q²N/k_BT, and q*V_pk = ΔF′₀. The fit gives q = (0.90 ± 0.4) e, N = (2.2 ± 0.2) × 10⁷, V_pk = (−38.7 ± 0.5) mV, and C_lin = (22.3 ± 0.6) pF. The lower dark line is a fit to a two-state model with a constant area constraint, by using the same values for q and N (see text). The parameter values used are: K = 0.13 N/m, q = 0.9 e, n = 2.2 × 10⁷, a = 5 nm², and C_lin = 16 pF. The reason for the difference in the linear capacitance is unclear. The two lighter lines represent 10% increase (Lower) and decrease (Upper), respectively, in the parameter a, which is the area difference in the two motor states. An additional source of error in estimating the area difference a is the uncertainty in parameters K and n (= N/4πR²), because the quantity Kna² works as one parameter in Eq. 2. This factor leads to about 10% error in estimating a for a given value of q.

Observations with the Short Voltage Waveform.

With pipette pressure above 0.3 kPa, the peak height of the bell-shaped voltage dependence of the membrane capacitance was drastically reduced (Fig. 2A Lower) in all 15 cells examined, if the intervals between steps that form the staircase waveforms were short (3 ms). The radius of the cell did not change beyond experimental uncertainties during the waveform (Fig. 2B).

On reducing the pipette pressure lower than about 0.3 kPa, the cell always showed the steeply voltage-dependent membrane capacitance (Fig. 2A Upper) similar to the one before digestion (Fig. 1A). No change in the radius of the cell was observed during the waveform.

To concisely describe the bell-shaped voltage dependence of the capacitance we used the following function,

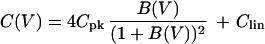1

with B(V) = exp[q*(V − V_pk)/k_BT]. This function has a peak value C_max = C_pk + C_lin at V = V_pk. The constant q* is inversely related to the width of the peak. The quantities k_B and T are respectively Boltzmann’s constant and the temperature. The meaning of Eq. 1 is examined in Discussion. The effect of pressure is shown in Fig. 3, by using the curve fit with Eq. 1.

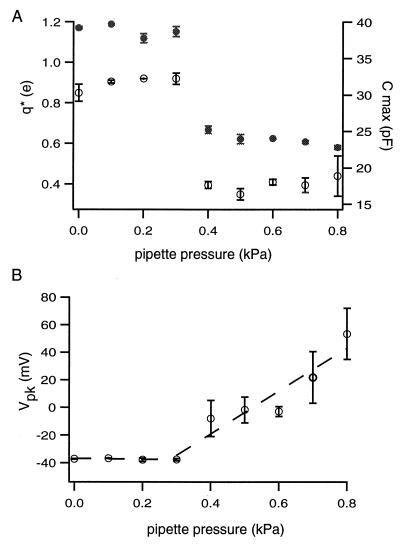
Figure 3.

Pipette pressure dependence of the capacitance peak. The voltage dependence of the membrane capacitance is fit with Eq. 1 to characterize the peak. The quantities plotted are the peak capacitance C_max (= C_pk + C_lin), the peak voltage V_pk, and q*. The quantity q* is inversely related to the broadness of the peak. The quantity q* is the same as the motor charge q for pipette pressure below 0.3 kPa (see text). If pipette pressure is below 0.3 kPa, all three quantities are approximately constant. If pipette pressure increases beyond that range, both C_max (●) and q* (○) sharply decrease at about 0.3 kPa (A). The peak voltage V_pk increases linearly with pipette pressure above 0.3 kPa (B). The slope is (155 ± 27) mV/kPa. Error bars indicate standard deviations.

The peak capacitance C_max was approximately constant below 0.3 kPa. It showed a sharp decrease approximately at 0.3 kPa and remains relatively unchanged at pressure above 0.3 kPa. The quantity q* showed a pressure dependence similar to the peak capacitance. The peak voltage was constant for pipette pressure below 0.3 kPa and rose with pressure above 0.3 kPa.

Observations with the Long Voltage Waveform.

For pipette pressure below 0.3 kPa, the capacitance-voltage plots did not depend on the duration of the waveforms. A long waveform with 100-ms voltage steps and a short waveform with 3-ms steps gave indistinguishable capacitance-voltage plots. The cell radius did not show a detectable change during the long waveform if pipette pressure was below 0.3 kPa.

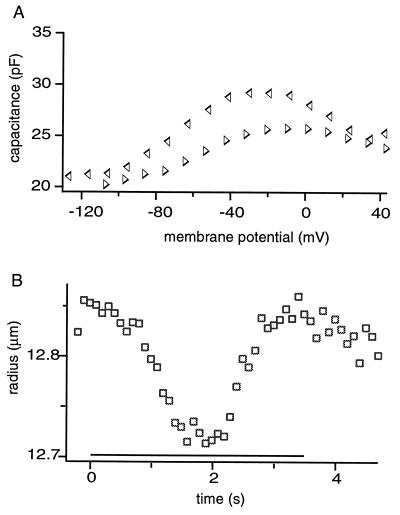
If pipette pressure was above 0.3 kPa, the long waveform with 100-ms steps, the membrane capacitance observed was larger and showed hysteresis (Fig. 4). The difference in the capacitance obtained with an ascending staircase and a descending one was appreciable if the experiment started from an ascending one (Fig. 4A). The cell radius decreased by up to about 1% during the waveforms (Fig. 4B). The magnitude did not increase with a further increase in the pipette pressure.

Figure 4.

The membrane capacitance and the cell radius of a trypsin-treated cell examined with the long staircase waveform (3.5 s long with 100-ms steps) at pipette pressure 0.5 kPa. Data points are from the same cell as shown in Fig. 2. (A) The values for the membrane capacitance obtained with the ascending (▹) part of the waveform are smaller than those obtained with the descending (◃) part, resulting in hysteresis in the voltage dependence. (B) The cell undergoes radius reduction up to 1% during the long waveform (□).

The Area Modulus of the Cell Membrane.

The area modulus K was determined by the experimental relationship between pipette pressure (up to about 1 kPa) and the radius R at the holding potential of −75 mV. The slope of the plot gave (0.13 ± 0.02) N/m.

DISCUSSION

Our most striking observation is the effect of pipette pressure on the membrane capacitance of the cell, which has a bell-shaped voltage dependence. The unusual voltage dependence of the membrane capacitance has been attributed to charges associated with the cell’s motile mechanism, which is voltage dependent (10–12). We call this motile mechanism simply a motor. As we will see in the following, the effect of pressure and the waveform duration on the membrane capacitance is hard to understand if charge transfer is not coupled with area change. We will first discuss the effect of trypsin treatment and then proceed to discuss the effect of the spherical geometry of the cell on the motor.

Effect of Trypsin Treatment.

The effect of trypsin digestion is evident in irreversible loss of the characteristic cell shape. Unlike untreated cells, trypsin-treated cells do not recover their cylindrical shape after the removal of positive pressure to the pipette. This irreversibility confirms breakdown of the cytoskeleton. The elastic property of the membrane in treated cells is characterized by the area modulus. The value 0.13 ± 0.02 for the area modulus K of trypsin-digested cells is larger by at least a factor two than those of undigested cells: 0.07 N/m (21) and 0.054 N/m (22). Standard values for the modulus of lipid bilayers range from 1.5 to 10 N/m (23). These values are consistent with the interpretation that the area modulus of the untreated membrane is primarily determined by the cytoskeletal undercoating (24) (the plasma membrane is somewhat folded) and that its digestion bring the system closer to the lipid bilayer, resulting in an increase of the modulus.

The proteolytic digestion by itself does not reduce the motor charge significantly, because at pipette pressures lower than 0.3 kPa, the bell-shaped voltage dependence of the membrane capacitance of the cell is similar to the one before the treatment. This observation is consistent with an earlier report by Huang and Santos-Sacchi (17). It is consistent with the idea that the motor charge is associated with an intrinsic membrane protein, because membrane proteins tend to be resistive to proteolytic treatments.

Effect of Spherical Geometry.

The marked reduction in the capacitance is observed if the pipette pressure exceeds 0.3 kPa and if the duration of the staircase waveform is short. No clear radius changes are detected under this condition. The membrane capacitance appears larger if longer waveforms are used. With longer waveforms, the cell radius changes. These observations indicate that the reduction of the capacitance is not simply caused by pressure but also by area constraint associated with the spherical geometry of the cell.

The sphere is distinguished from other shapes in that it has the largest volume-to-surface ratio. The surface area of a spherical cell cannot be reduced without decreasing its volume. [In contrast, in a sufficiently long cylindrical cell, the surface area can be reduced by decreasing the length and increasing the radius while keeping the volume constant. The necessary condition for such deformations is that the cell length is greater than twice the diameter. Even the shortest outer hair cells seem to satisfy the condition (25).] In addition, the intracellular fluid, which is primarily made of water, is virtually incompressible. Thus a decrease of surface area of the spherical cell must be accompanied by volume outflow. Therefore if depolarization is associated with reduction in the membrane area, we can constrain the membrane area by applying a depolarizing voltage waveform with a duration shorter than the time scale in which volume flow becomes important. Longer waveforms allow increased volume flow, imposing less constraint. For the actual cell to satisfy this geometrical condition, the cell membrane must be well inflated, requiring pressure above a certain level.

Our observation is thus qualitatively consistent with the interpretation that the reduced capacitance observed above 0.3 kPa with the short voltage waveform is due to area constraint. If the long voltage waveform is imposed on the cell, the membrane motor changes the cell radius as expected. Are the observed radius changes of the cell driven by the membrane motor alone?

What Can Change the Cell Radius?

We can show that these volume changes are not caused by an electrolyte flow accompanied by electric currents elicited by the voltage waveform imposed. Let us examine possible volume changes caused by such electrolyte flow. When a voltage waveform is imposed on a cell in the whole-cell recording configuration, electrolyte gain or loss from the cell occurs because of the different ion selectivities at the cell membrane and at the pipette tip (26). This effect is greatest if the cell membrane is permeable to a single monovalent ion and the pipette tip has no selectivity. Our voltage waveform rises about 150 mV from the holding potential to its peak in 1.5 s. Because the resistance is on the average about 0.5 GΩ, the electricity passed is 2.3 × 10⁻¹⁰ C or 2.3 fmol monovalent ions, which means the maximum gain or loss is 1.2 fmol monovalent salt (26). This electrolyte gain or loss corresponds to a volume change of about 8 μm³, because physiological media are approximately equivalent to 150 mM monovalent salt. Such a volume change results in a change of about 5 nm in the radius, somewhat below our detection limit. Thus the effect of ionic currents is too small to account for the observed radius changes that exceed 100 nm (Fig. 4B). The radius changes observed must be attributed to conformational changes of the membrane motor.

Pressure Below 0.3 kPa.

If the pressure applied is below 0.3 kPa, the peak capacitance is larger (Fig. 2A). These rounded cells show neither noticeable shifts of the peak voltage nor changes in the peak height of the capacitance (Fig. 3). Such insensitivity to pressure, however, is not observed with untreated cells. The membrane capacitance of untreated cells shows a positive shift in its peak voltage and a reduction of peak height in response to increased pressure (13). A reduction in pressure results in the opposite effect. (This effect extends to negative pressure, introducing uncertainties in the comparison of the motor charge before and after the trypsin treatment.) The absence of such pressure effects below 0.3 kPa in trypsin-treated cells must indicate that the motor is not subjected to mechanical forces. If that is true, the radius of the cell under this condition should also be insensitive to the membrane potential. Indeed, we did not detect radius changes elicited by voltage waveforms, long or short, while pipette pressure was lower than 0.3 kPa. For this reason, we believe that the plasma membrane under this condition is slack. That requires that some other structure counters pressure below 0.3 kPa. We speculate that the submembranous cisternae system is the most likely candidate, because it is a continuous structure beneath the plasma membrane and should be insensitive to trypsin. This interpretation is consistent with our observation that the rounded cells did not readily collapse with negative pipette pressure. The pressure independence of the membrane capacitance under this condition, despite its unidentified origin, should enable us to determine the motor charge of trypsin-treated cells because the motor state is determined by the voltage alone (see below).

Quantitative Explanation.

In an attempt to quantitatively explain the effect of a mechanical constraint that is observed with the short waveform in the pressure range above 0.3 kPa (Figs. 2 and 3), we examine a simple model, which has three major assumptions: (i) The total membrane strain, which is held constant because of the constraint, is a sum of motor displacement and elastic displacement. (ii) Motor displacement is caused by conformational transitions of the motor. (iii) A single motor unit has two states, and transitions between these states involve transfer of charge q across the membrane and a change a in the membrane area. These assumptions imply a 100% efficiency in the motor in energy conversion and are similar to those made previously (27). They were used for a cell with cylindrical geometry, whereas these assumptions are now used for a spherical cell. Because of the spherical geometry of the cell, membrane tension T_m is now isotropic, so that a single parameter a can describe the area difference between the two motor states. The free energy ΔF of a motor unit in the state with larger membrane area (extended state) relative to the state with smaller area is then given by ΔF₀ − qV_m −aT_m, where ΔF₀ is a term independent of the membrane potential V_m or on membrane tension T_m. The states of the motor follow the Boltzmann distribution. Namely, the fraction f_ℓ of the motor in the extended state is given by

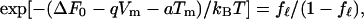where k_B is Boltzmann’s constant and T is the temperature. The membrane potential V_m is controlled by the patch electrode. Here a is positive and q is negative, because an increase of V_m decreases f_ℓ (an increase of T_m increases f_ℓ). For the spherical cell with radius R, we assume that membrane tension T_m satisfies Laplace’s law, T_m = ½ RP. An increase in tension T_m must accompany an increase in pressure P, even though the cell volume does not change. Because the treated cell is elastic and is characterized by the elastic area modulus K, tension T_m of the spherical membrane is also given by Kɛ_e with elastic area strain ɛ_e. The total area strain ɛ_tot of the cell may be given by a sum of the elastic area strain ɛ_e and the strain caused by motor displacement, which is represented by naf_ℓ. Here n is the number of the motor units in a unit membrane area, a is the difference of the motor unit in the two conformations, and f_ℓ is the fraction of the motor in the extended state. Thus T_m = K(ɛ_tot − naf_l) = ½ RP.

Because we constrain the volume of the spherical cell, the total area strain ɛ_tot remains constant. If pressure is P₀ when the membrane potential is extremely negative so that f_ℓ is unity, we obtain K(ɛ_tot − na) = ½ RP₀. This relationship enables us to eliminate ɛ_tot from the expression for T_m, leading to

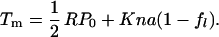The fraction f_ℓ of the motor in the extended state is then related to the membrane potential V_m in the form,

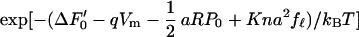2

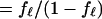with a redefined constant term ΔF′₀ = ΔF₀ − Kna². With increasing stiffness K, the last term in the exponential function in Eq. 2 becomes increasingly sensitive to f_ℓ, requiring decreasing changes in f_ℓ to compensate for a given change in the voltage V_m. That means an increase in the stiffness K reduces the membrane potential dependence of the motor state f_ℓ.

In the following, we describe how Eq. 2 is used to determine the motor parameters, namely the area difference a, the motor charge q, and the number N of motor units. The motor state f_ℓ is related to the voltage-dependent component C_m(V_m) of the membrane capacitance by

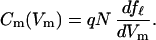If the plasma membrane is not taut, i.e., at pressure below 0.3 kPa, the last two terms in the exponential function in Eq. 2 are absent. The absence of these terms leads to an explicit expression of the capacitance C_m, which is equivalent to the first term of Eq. 1 with q* = q, C_pk = 4q²N/k_BT, and q*V_pk = ΔF′₀. This condition allows us to determine the charge q and the number N of the motor unit from the voltage dependence of the capacitance.

With pipette pressure above 0.3 kPa, the capacitance is calculated by solving Eq. 2 with respect to f_ℓ for small increments of V_m and then evaluating the voltage derivative numerically. The membrane capacitance depends on the area modulus K of the membrane, the area difference a, and static pressure P₀. Thus we need to know static pressure P₀ and the elastic modulus to determine the area difference a. For P₀ we used pipette pressure at the holding potential of −75 mV, at which the motor units are mostly in the extended state. With the experimentally determined value of (0.13 ± 0.02) N/m for the area modulus K, we can estimate the area difference a from the voltage dependence of the membrane capacitance. The curve fit gives about 5 nm² for the area change a of a motor unit with a relative error somewhat larger than 10% (Fig. 2A and its legend).

Alternatively, the area change a is obtained from the pressure dependence of the voltage V_pk that maximizes the capacitance. It is easy to see from the equation that the effect of pressure P₀ is in shifting the voltage dependence by ½ aRP₀/q without significantly changing the peak shape. Experimental shift in the peak capacitance voltage V_pk is approximately linear to applied pressure with the slope (155 ± 27) mV/kPa (Fig. 3B). The area change a of the motor unit is then (3.3 ± 0.5) nm².

These two estimates based on Eq. 2 are further consistent with a value obtained with a more direct estimation. The maximum change in the radius that we observed with a large-tipped patch pipette (≈2 μm diameter) is about 1%, which corresponds to about 2% change in the surface area. This area change is caused by the motor, as we discussed earlier. The number of motor units determined with capacitance measurement is (13 ± 3) million for the cell, which is rounded up into a sphere of (13.3 ± 0.9) μm. Thus the magnitude of the area change per motor unit is (3.4 ± 0.8) nm², close to the previous two estimates. Because this estimate is not of experimental data from the native cylindrical conformation is obtained by assuming a_z = 10 nm² and a_c = −3 nm² (24). The value for a = (a_z + a_c) is therefore 7 nm². The value obtained here is about 4 nm².as dependent on details of the model as Eq. 2, the agreement with the other two estimates indicates that the essential features of our observation are captured by the model.

CONCLUSIONS

The present observations demonstrate that the membrane motor in trypsin-digested outer hair cells can directly convert electrical energy into mechanical energy. The motor gains electrical energy by its charge transferable across the membrane. Because transfer of charges and change in the membrane area are coupled, the conversion of energy by the motor is direct. Not only does the membrane potential change the membrane area, but constraint on the membrane area restricts charge transfers across the membrane as well. We observed the effect of constraint in all 15 cells examined. We can characterize the motor as follows: a motor unit undergoes an area change of about 4 nm² while transferring electric charge of (0.87 ± 0.14) e across the plasma membrane. The density of the motor units is extremely high and is about (6,000 ± 2,000) per μm², which correlates best with the density of 10-nm particles (15, 16). The resistance to trypsin treatment strongly indicates that the motor observed is most likely an integral membrane protein.

These basic properties of the motor unit in trypsin-treated cells show a strong resemblance to those obtained in untreated cells. In particular, it is quite surprising that the magnitude of the unit area change, which could be affected by the presence of the cytoskeleton, is not too different from the value obtained from untreated cells that retain their characteristic cylindrical shape.§ We believe that this agreement gives a clue for elucidating the structure of the membrane motor in the intact hair cells.