Skip to main content
PMC home page
Protein Science : A Publication of the Protein Society logoLink to Protein Science : A Publication of the Protein Society
. 2007 Jun;16(6):1214–1222. doi: 10.1110/ps.062734207

Similarities in the thermodynamics and kinetics of aggregation of disease-related Aβ(1–40) peptides

Jessica Meinhardt 1, Gian Gaetano Tartaglia 2, Amol Pawar 2, Tony Christopeit 1, Peter Hortschansky 3, Volker Schroeckh 3, Christopher M Dobson 2, Michele Vendruscolo 2, Marcus Fändrich 1
PMCID: PMC2206661  PMID: 17525469

Abstract

Increasing evidence indicates that polypeptide aggregation often involves a nucleation and a growth phase, although the relationship between the factors that determine these two phases has not yet been fully clarified. We present here an analysis of several mutations at different sites of the Aβ(1–40) peptide, including those associated with early onset forms of the Alzheimer's disease, which reveals that the effects of specific amino acid substitutions in the sequence of this peptide are strongly modulated by their structural context. Nevertheless, mutations at different positions perturb in a correlated manner the free energies of aggregation as well as the lag times and growth rates. We show that these observations can be rationalized in terms of the intrinsic propensities for aggregation of the Aβ(1–40) sequence, thus suggesting that, in the case of this peptide, the determinants of the thermodynamics and of the nucleation and growth of the aggregates have a similar physicochemical basis.

Keywords: conformational disease, kinetics, neurodegeneration, protein folding, Alzheimer's disease

Amyloid fibrils represent a specific group of polypeptide aggregates characterized by a highly ordered β-sheet structure that gives rise to a fibrillar overall arrangement (cross-β structure) (Dobson 2003; Selkoe 2003). These fibrils have been associated with aging and with several neurodegenerative conditions, such as Alzheimer's and Creutzfeldt-Jakob diseases (Dobson 2003; Selkoe 2003). Increasing evidence shows that, despite the generic nature of amyloid structures (Chiti et al. 1999; Dobson 2001; Fändrich and Dobson 2002; Fändrich et al. 2001; Krebs et al. 2004), the propensity to form aggregates is strongly influenced by the nature of the amino acid side chains along with the properties of the environment in which aggregation occurs (Chiti et al. 2003; DuBay et al. 2004; Fernandez-Escamilla et al. 2004; Tartaglia et al. 2004; Christopeit et al. 2005; Thompson et al. 2006). The physicochemical factors affecting such propensities have been mapped out experimentally through mutational studies for a range of systems where the effects on the rate of aggregation were examined (Chiti et al. 2002; Wurth et al. 2002; Christopeit et al. 2005; O'Nuallain et al. 2005). This property (termed here “growth rate,” kg) reports on the efficiency by which the early oligomeric species of low molecular weight are extended into larger aggregates. This rate was shown to depend, in the case of unstructured polypeptide chains, on intrinsic properties such as β-sheet and α-helical propensity, hydrophobicity, charge, aromaticity, and sequential context, along with properties of the physicochemical environment, such as pH, ionic strength, and temperature (Chiti et al. 2003; DuBay et al. 2004; Tartaglia et al. 2004; Christopeit et al. 2005). These studies have provided the basis for empirical equations for the prediction of absolute or environment-dependent aggregation propensities (Chiti et al. 2003; DuBay et al. 2004; Tartaglia et al. 2004; Pawar et al. 2005). In the case of globular proteins in their native states, additional factors are involved that are associated with the conversion, at least locally, into unstructured species (Chiti et al. 2000; Fändrich et al. 2003).

Aggregation reactions normally consist of two consecutive phases: a lag phase in which a steady-state distribution of oligomeric species is established, and a growth phase in which oligomers larger than a critical nucleus size are extended to form much larger aggregates or fibrils (Harper and Lansbury 1997; Dzwolak et al. 2004). The growth rate measures the efficiency of the growth phase, whereas the duration of the lag phase, i.e., the lag time (tl), describes the time required for the nucleation reaction to take place. Recently, analysis of the aggregation behavior of mutants of the Alzheimer's Aβ(1–40) peptide, in which residue 18 was systematically replaced with other amino acids, revealed that kg and tl are related properties (Christopeit et al. 2005). This observation suggests that, at this position of the sequence, similar specific physicochemical interactions are involved in both steps of the aggregation reaction (Christopeit et al. 2005). Within the set of Aβ(1–40) variants of residue 18, a further correlation was observed between the kinetics and the thermodynamics of aggregation, in that those variants that aggregate very readily, as defined by the rate of aggregation, are also those that are thermodynamically most favorable for aggregation, as defined by critical concentration measurements (Hortschansky et al. 2005b). In this work, we show that similar effects are observable at several positions of the Aβ(1–40) sequence, and not just for residue 18, thus implying that, in the case of this peptide, the physicochemical determinants of the nucleation and growth and of the thermodynamics of aggregation are similar.

Results

In the present work, we study variants of the Aβ(1–40) peptide in which single amino acid replacements are present at different positions of the sequence and, therefore, within very different sequential contexts. We examined the eight known natural variants of Aβ(1–40), most of which are associated with familial Alzheimer's disease, namely H6R, D7N, A21G (termed the “Flemish” mutant), E22G (“Arctic”), E22Q (“Dutch”), E22K (“Italian”), and D23N (“Iowa”). The eighth variant (A2T) is a natural polymorphism with no apparent association with disease (Peacock et al. 1993). We illustrate the location of the mutated residues within a structural model of the Aβ(1–40) peptide in the fibril (Fig. 1A; Petkova et al. 2002) and for the aggregation propensity profile of this peptide, calculated by using the Zyggregator method (Fig. 1B; Pawar et al. 2005).

Figure 1.

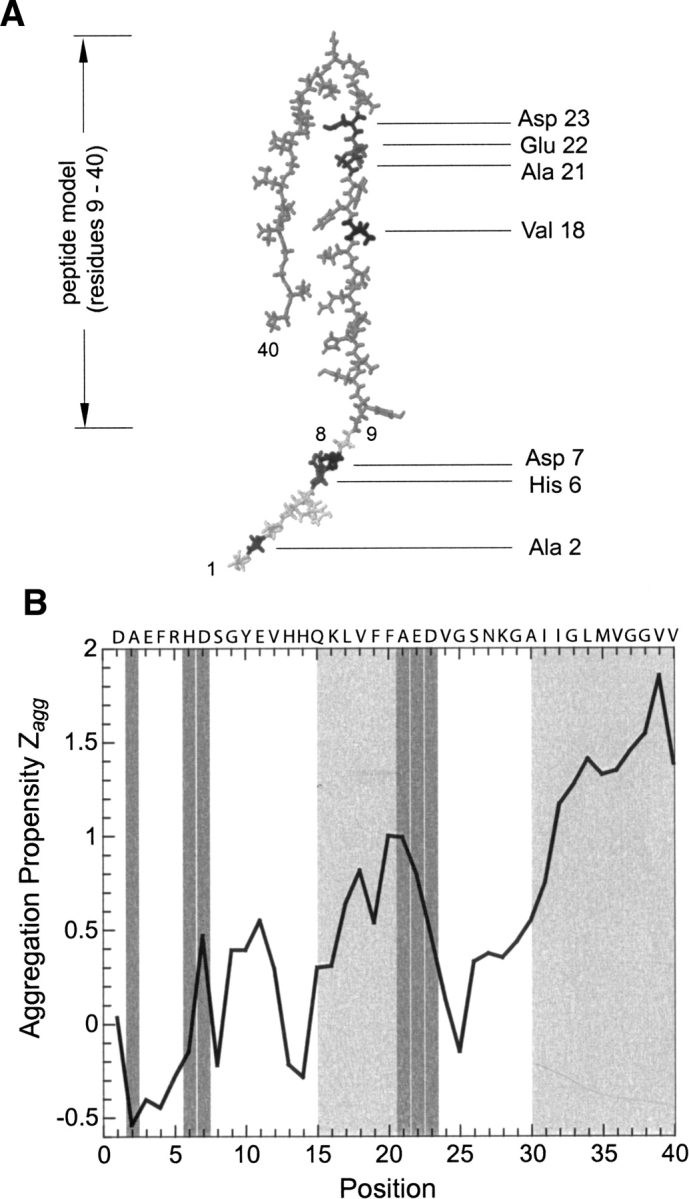
Figure 1.

Open in a new tab

Location of the mutations within the Aβ(1–40) peptide. (A) Location of the mutated residues within the structural model of the Aβ(1–40) peptide (Petkova et al. 2002). Note that residues 1–8 are added here for completion, while they are not part of the structural model. The model was constructed based on literature data (Petkova et al. 2002) using the program Insight and displayed using the program Rasmol. (B) Profile of the aggregation propensity (Zagg) (Pawar et al. 2005). Light-gray areas indicate the aggregation-prone regions, as defined by the height of the aggregation propensity (Zagg) per residue; dark-gray areas show the location of the mutated residues.

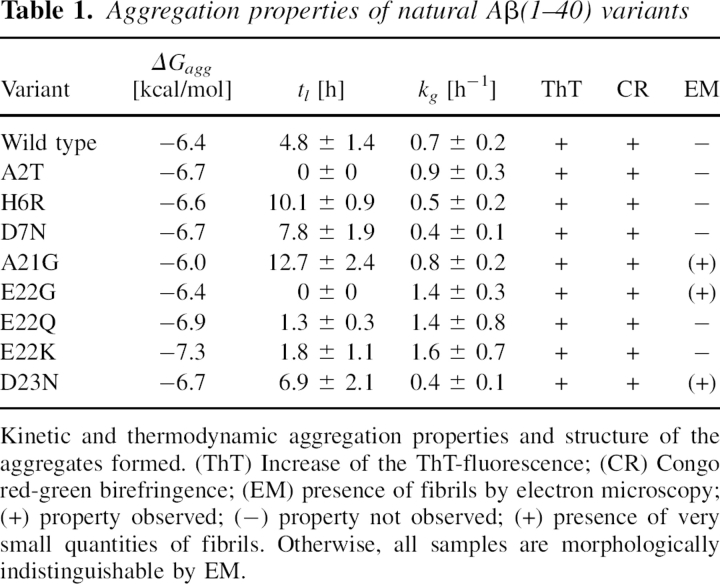
All peptides were generated by using a recombinant Escherichia coli expression system that enables the efficient production of different sequence variants of the Aβ(1–40) peptide (Christopeit et al. 2005; Hortschansky et al. 2005a). Pure peptides were fully oxidized to generate a sulfoxide of methionine 35. Since the reduced peptide is very prone to oxidation (Watson et al. 1998), this treatment minimizes the risk that oxidation occurs and interferes with our measurements. Data from these oxidized peptides are directly comparable to a previous data set that was obtained under the same conditions, but by using Aβ(1–40) variants that vary only in residue 18 (Christopeit et al. 2005; Hortschansky et al. 2005a,b). These peptides were examined both with respect to their thermodynamic and kinetic aggregation behavior. The thermodynamic measurements are based on determination of the critical concentration (cc) of each peptide variant and allow calculation of the free energy of aggregation ΔGagg (Oosawa and Asakura 1975). The kinetic measurements were performed by monitoring, with thioflavin-T fluorescence, the time-dependent formation of aggregates. From the resulting curves we determined the values of tl and kg.

The aggregates that we describe in this work are distinct from the simple protein precipitates that arise from oversaturation, which retain the native structure of their constituent proteins. Thus, aggregates are associated with a specific type of β-sheet structure that may not be present in the native globular protein, and is defined by a regular pattern of intermolecular backbone hydrogen bonds. Such aggregates form under conditions of at least partial denaturation and consist of β-sheets that are defined by specific infrared and X-ray diffraction properties and usually by their affinity for certain dyes (thioflavin-T and Congo red) (Jackson and Mantsch 1991; Fink 1998; Fändrich et al. 2001; Zandomeneghi et al. 2004; Christopeit et al. 2005). Beside occurring as amyloid fibrils, aggregates can also be nonfibrillar. In these cases, the β-sheets and the overall aggregate structures possess no preferential orientations. However, nonfibrillar and fibrillar aggregates are distinguished here from filaments and oligomers formed by native, globular proteins, such as actin or tubulin fibrils. Under the conditions adopted for the present study, aggregates are formed in all samples analyzed here. These aggregates are characterized by their ability to bind ThT, thereby increasing the fluorescence of this dye. Furthermore, ThT-free samples exposed to the same incubation conditions show a high affinity for Congo red dye and they give rise to green birefringence in their Congo-red bound form when viewed in a polarizing microscope (Table 1). These properties are characteristics of polypeptide aggregates and amyloid structures (Westermark et al. 1999). However, none of these properties is exclusively specific to the formation of linear aggregates or fibrils (Christopeit et al. 2005). Consistent with these observations, we find by electron microscopy that only A21G, E22G, and D23N—among the mutational variants that we considered—form detectable amounts of well-ordered fibril structures (Table 1), while all other variants of the Aβ(1–40) peptide produce only nonfibrillar aggregates. Since all peptides were disaggregated and filtered prior to analysis, these data suggest that the A21G, E22G, and D23N mutations have a particular strong tendency to form highly ordered nuclei leading to amyloid-like structures, while the other variants form less well-ordered nuclei and aggregates. However, the fibrils seen in A21G, E22G, and D23N samples are sparse, and most aggregates formed in these reactions are nonfibrillar. Hence, in further discussion we relate the presently determined thermodynamic and kinetic properties to aggregate formation without assuming specifically the formation of an amyloid-like cross-β structure. In the case of mutations carried out at the single position 18 of Aβ(1–40), at least, it was found recently that mutation affects the formation of amyloid fibrils and nonfibrillar aggregates in a similar manner (Peim et al. 2006).

Table 1.

Aggregation properties of natural Aβ(1–40) variants

graphic file with name 1214tbl1.jpg

Open in a new tab

The comparison of the values of ΔGagg, kg, and tl obtained for the wild-type peptide and the various mutants studied here (Table 1) indicates that several of the natural and mostly disease-related mutations promote aggregation. This conclusion is suggested both by the acceleration of the aggregation kinetics and by the higher thermodynamic propensity of aggregation, as expressed by ΔGagg. Examples of such behavior are the A2T and E22G mutants. Both peptide variants aggregate without a discernible lag phase, indicating that the time required for nucleation is shorter than the dead time of the experiment (about 15 min). For both these mutants, we report here a tl value of 0 h. The aggregation behavior of these two variants differs considerably, however, from the properties of other variants, for example, A21G, which appear less favorable for aggregation than the wild-type Aβ(1–40) peptide, based on the measured ΔGagg and tl values.

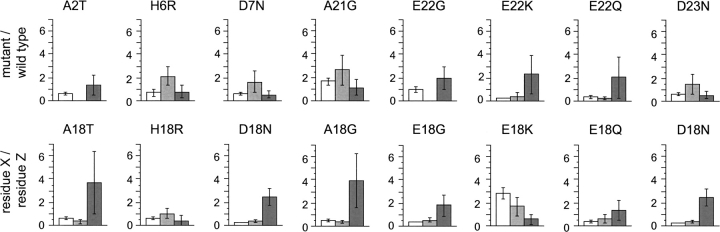
Next, we explored whether the effects of mutations are similar depending on their location within the sequences of the Aβ(1–40) peptide. Comparison with equivalent mutants of position 18 shows a strong context dependence (Fig. 2), which affects not only the absolute values of kg, tl, or cc but also the ratios kg(X)/kg(Z), tl(X)/tl(Z), or cc(X)/cc(Z) of a Z → X replacement (Fig. 2). For example, there is a clear difference in the effect of an alanine to glycine mutation on the values of kg(X)/kg(Z), tl(X)/tl(Z), or cc(X)/cc(Z), depending on whether this replacement occurs at position 18 or at position 21, such as in the “Flemish” mutation (Fig. 2). In contrast, we find that replacement of alanine with threonine has very similar effects on kg(X)/kg(Z), tl(X)/tl(Z), and cc(X)/cc(Z), irrespective of whether it occurs at position 2, such as in the natural variant, or at position 18, which we generated in vitro (Christopeit et al. 2005; Hortschansky et al. 2005b). This context dependence is not obviously correlated with the aggregation propensity profile (Fig. 1B), for the latter indicates that both positions 18 and 21 are in a region that is very prone to aggregation. Although positions 2 and 18 occur in regions of the peptide that differ considerably in their contribution to the aggregation properties (Fig. 1B), the effect of Ala → Thr mutations on kg(X)/kg(Z), tl(X)/tl(Z), or cc(X)/cc(Z) are rather similar at these two positions (Fig. 2).

Figure 2.

Figure 2.

Open in a new tab

Context dependence of the effects of mutations on the aggregation process. Comparison of the effect of a mutation of residue Z into residue X at different positions as indicated (top, natural Aβ[1–40] variants) and at position 18 (bottom). Data are represented here as cc(X)/cc(Z) (white bar), tl(X)/tl(Z) (gray bar), and kg(X)/kg(Z) (dark-gray bar). Error bars show standard deviations. The data for valine 18 variants are taken from Christopeit et al. (2005) and Hortschansky et al. (2005b).

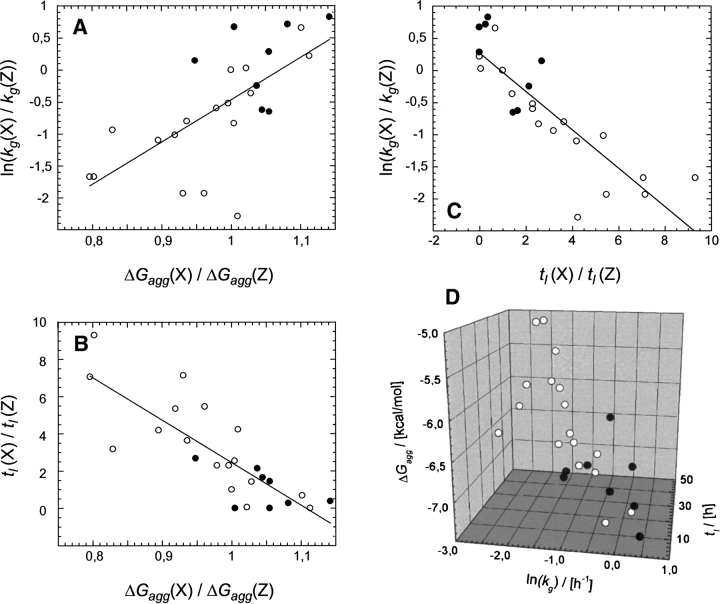
Although these data demonstrate that the effect of mutation depends strongly on the sequential or conformational context, a plot of ln(kg) vs. tl shows a significant correlation (correlation coefficient 0.85) (Fig. 3C). These data are further support to the conclusion that variants that nucleate very readily (short tl values) also extend these nuclei very rapidly (large kg values) (Christopeit et al. 2005). A linear fit such as the one shown in Figure 3C is feasible for a narrow range of kg and tl values, while a recent analysis of a much larger and diverse data set suggest that the equation kg = α/tl provides a better overall description (Fändrich 2007). For the present data set, however, such a fit would be associated with the problem that several tl values were, due to the absence of a discernible lag phase, set to 0 h (Christopeit et al. 2005), and would dominate a kg = α/tl fit severely.

Figure 3.

Figure 3.

Open in a new tab

Correlation between ΔGagg, ln(kg), and tl. (A,B) Plot of ΔGagg(X)/ΔGagg(Z) vs. ln[kg(X)/kg(Z)] (A) or vs. tl(X)/tl(Z) (B), where X is the mutant and Z the wild-type residue. (C) Correlation of ln[kg(X)/kg(Z)] and tl(X)/tl(Z). (D) 3D-correlation plot of the absolute values. Filled symbols: natural Aβ(1–40) variants; open symbols: data from valine 18 variants of Aβ(1–40). Fitting of the data points with a straight line gives coefficients of correlation of 0.67 for ΔGagg and kg, 0.82 for ΔGagg and tl, and 0.85 for tl and kg, irrespective of whether the kg, ΔGagg, and tl values are normalized to the wild-type values or not.

When the two kinetic properties are compared with ΔGagg, it is evident that fast-aggregating sequences generally tend to also have a high thermodynamic propensity to aggregate (Fig. 3A,B). Remarkably, these dependencies apply not only to the relative effects of mutation, in which the mutant is compared with the wild type (Fig. 3A–C), but also when comparing the total values of the three properties ΔGagg, kg, and tl (Fig. 3D). Furthermore, the data points from the presently studied variants of different positions in the sequence are highly consistent with those from variants of residue 18 only. Hence, mutations affect ΔGagg, kg, and tl in a correlated manner, even if they occur within regions that differ in their intrinsic aggregation propensities as defined by the Zagg score (Fig. 1B), where the coefficient of correlation between ΔGagg and kg is 0.67, and between ΔGagg and tl is 0.82.

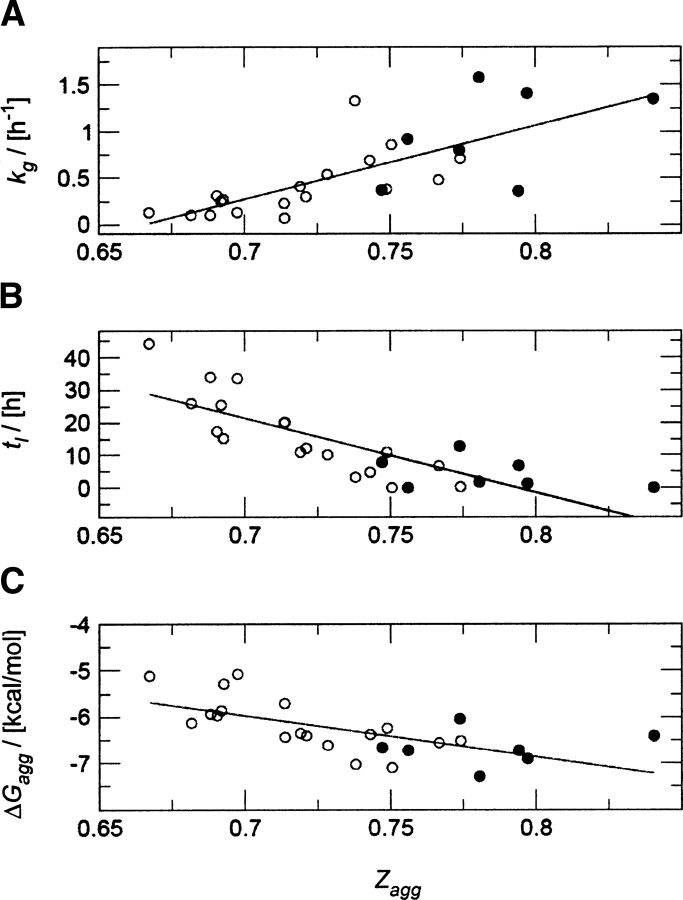
In order to rationalize the dependence of the aggregation behavior on the physicochemical properties of Aβ(1–40) caused by mutations, we compared these results with predictions of the changes in the intrinsic aggregation propensities in each case. These predictions are based on the computation of the Zagg score, which represents the intrinsic aggregation propensity of a polypeptide chain. The Zagg score is calculated by a method that exploits an empirical correlation between experimentally determined values for the growth rate kg and intrinsic properties of the polypeptide chain, such as hydrophobicity, α-helical and β-sheet propensities, charges, or the presence or absence of distinctive bipolar patterns (Pawar et al. 2005). Indeed, when we compare the predicted aggregation propensity (Zagg score) for the valine 18 variants examined previously (Christopeit et al. 2005) and the set of mutants studied here with the experimentally determined values for the growth rate kg, we find a statistically significant correlation (Fig. 4A). Variants predicted to be particularly prone to aggregation also show fast growth kinetics (correlation coefficient 0.76). Next, we examined the relationship between the Zagg score and the nucleation behavior expressed in terms of the lag time. We found a negative proportionality between tl and the calculated Zagg scores (Fig. 4B) with a correlation coefficient of −0.82 (Table 2), i.e., polypeptides with a short lag time are associated with high aggregation propensity values. Finally, Figure 4C shows the correlation between ΔGagg and the aggregation propensity predictions, represented by the Zagg scores, which indicates that a large Zagg score is generally associated with a mutational variant with a low ΔGagg value; the coefficient of correlation between ΔGagg and Zagg is −0.66. This analysis strongly supports the idea that, despite the context dependencies described above, common physicochemical principles may determine both the thermodynamics and kinetics of aggregation, which are defined by the ΔGagg values and the length of the lag phase and the growth rate.

Figure 4.

Figure 4.

Open in a new tab

Correlation between the experimental measurements (kg, tl, and ΔGagg) and the predicted aggregation propensities (Zagg): (A) kg and Zagg (coefficient of correlation 0.76), (B) tl and Zagg (coefficient of correlation −0.82), (C) ΔGagg, and Zagg (coefficient of correlation −0.66). Filled symbols indicate natural Aβ(1–40) variants and open symbols the data from valine 18 variants of Aβ(1–40).

Table 2.

Importance of individual factors in the predictions of the aggregation propensities

graphic file with name 1214tbl2.jpg

Open in a new tab

We analyzed the contributions of individual terms in the predictions (Pawar et al. 2005) to the quality of the fit between the Zagg score and the thermodynamic and kinetic properties studied here. This analysis indicates that the distribution of hydrophobic and hydrophilic residues and the presence or absence of electrostatic charges represent the common physicochemical principles for the lag time and the growth rate. Table 2 reports the coefficients of correlation between lag times, growth rates, and ΔGagg, respectively, with the Zagg scores calculated by using either all of the factors (column 2) or individual factors only (columns 3–6). Comparison of the three values with the Zagg score results in correlation coefficients of −0.66, 0.76, and −0.82. The positive and negative signs of these correlations arise from the definition of the values, i.e., a high propensity of aggregation is associated with a high Zagg score and kg value and with small tl and ΔGagg values. It is clear that tl, kg, and ΔGagg are all very sensitive to hydrophobicity and to the electrostatic charge. We found that hydrophobicity has a negative correlation (correlation coefficient −0.36 ± 0.02) with tl and a positive one with kg (correlation coefficient 0.46 ± 0.03), suggesting that the aggregation process of more hydrophobic sequences is characterized by shorter lag times and faster growth rates. In contrast, the electrostatic charge has a positive correlation (correlation coefficient 0.37 ± 0.05) with tl and a negative one with kg (correlation coefficient −0.40 ± 0.03), suggesting that the aggregation process of more charged sequences is characterized by shorter lag times and faster growth rates. Both the kinetic and thermodynamic properties are relatively insensitive, in the algorithm used for the analysis, to secondary structure propensities. Finally, we mention the effects of patterning of polar and nonpolar residues on the thermodynamics and kinetics of aggregation. The importance of alternating patterns of polar and nonpolar residues in promoting aggregation has been studied in detail by Hecht and coworkers (West and Hecht 1995; West et al. 1999; Broome and Hecht 2000). Although such patterns have been found previously to be highly correlated with kg (DuBay et al. 2004), the sequence of the Aβ(1–40) peptide as well as those of the mutants considered here do not contain these type of patterns, suggesting that the differences in the aggregation behavior arise mainly from other factors.

Discussion

We have presented a kinetic and thermodynamic analysis of the aggregation propensities of all known natural sequence variants of the Alzheimer's Aβ(1–40) peptide and from experiments carried out under identical conditions. The experimental results have been rationalized through theoretical predictions of the aggregation propensities of these mutational variants. We have found that several of such variants (A2T, E22G, E22K) are significantly more aggregation-prone than the wild-type sequence (Table 1). In contrast, the Flemish mutant (A21G) produces somewhat mixed results. While the ΔGagg and tl values of this variant are lower than those of the wild type, kg values seems to be slightly higher. This observation is consistent with the previous notion that kg values are more difficult to define experimentally and perhaps less reliable (Christopeit et al. 2005).

We have analyzed our results in light of literature data available for the natural variants of the Aβ(1–40) peptide. Such comparisons are made difficult, however, by the sometimes extremely different environmental conditions and methods of investigation and by the use of peptides of different lengths or fragments. For example, the “Flemish” mutant (A21G) was reported to delay aggregation in Aβ(1–40) (Walsh et al. 2001; Fernandez-Escamilla et al. 2004), while the “Arctic” mutation (E22G) was found to accelerate its fibrillogenesis (Nilsberth et al. 2001; Lashuel et al. 2003). These observations are consistent with the findings of the present study that used the oxidized forms of Aβ(1–40). Furthermore, the present data confirm the previous observations that the “Dutch” mutation (E22Q) promotes aggregation or aggregate stability (Fraser et al. 1992; Van Nostrand et al. 2001; Bitan et al. 2003). Often, however, only single aggregation traces are reported for each of the mutants, and comparisons of different studies and of peptides of different lengths lead to a mixed outcome. For example, Aβ(1–40) peptides carrying the “Italian” mutation (E22K) were reported to have aggregation propensities almost indistinguishable from the wild type (Miravalle et al. 2000), although this mutation seems to promote aggregation when inserted into Aβ(1–42) (Murakami et al. 2002). In addition, the “Iowa” variant (D23N) was found to accelerate the formation of aggregates of the Aβ(1–40) peptide (Lashuel et al. 2003), while a study of the Aβ(1–42) peptide showed a kinetic behavior close to, or slower than wild type (Murakami et al. 2002). Although these results might be related to the different peptide lengths or different experimental setups, other mutants have similar effects when inserted into Aβ(1–40) or Aβ(1–42) or when using different conditions, for example, the “Flemish” (Walsh et al. 2001; Murakami et al. 2002) or the “Dutch” mutations (Fraser et al. 1992; Van Nostrand et al. 2001; Murakami et al. 2002; Bitan et al. 2003).

These apparently conflicting results could also be explained by the strong influence of stochastic factors that give rise to a discernible heterogeneity of the kinetic traces used to monitor the aggregation process (Hortschansky et al. 2005a; Pellarin and Caflisch 2006). Moreover, there is the general problem of comparing peptides from different sources (Zagorski et al. 1999). For these reasons, the values reported here are averages from 10 separate measurements, and all peptides were generated by using the same production and purification scheme. In our study, four natural variants aggregate faster than wild-type Aβ(1–40), while the other four do not. These results strongly suggest that beside the intrinsic physicochemical factors promoting the aggregation propensity of disease-related polypeptide variants, further cellular factors must be considered to explain the origins of certain disease phenotypes. Consistent with this conclusion, the A2T variant aggregates much more readily than the wild type, although the intrinsically high aggregation propensity of this mutant is not known to give rise to familial Alzheimer's disease (Peacock et al. 1993).

Our previous analysis of 18 single-site mutants of position 18 of the Aβ(1–40) sequence revealed a relationship between the two kinetic parameters kg and tl and also between these two properties and ΔGagg (Christopeit et al. 2005; Hortschansky et al. 2005b). As that study was limited to one position along the sequence of Aβ(1–40), we have extended this analysis to the eight known natural single-site variants of Aβ(1–40) in the present study. These data support the view that for the Aβ(1–40) peptide, the determinants of the nucleation step are similar to those of the growth reaction in the aggregation process. Furthermore, those sequences that aggregate rapidly are also those that have the highest thermodynamic propensities to aggregate (ΔGagg). These relationships seem largely unaffected by the position of the mutation. However, it is also clear that all peptides compared in the present study are very similar and arise from single-site replacements of the same host sequence, the Aβ(1–40) peptide.

Comparison of the valine 18 variants with the present set of natural variants show differences in the extent to which the ratios kg(X)/kg(Z), tl(X)/tl(Z), or cc(X)/cc(Z) are affected by the mutation, suggesting their dependence on the structural context (Fig. 2). Such context dependences can arise either directly from the proximity of certain residues within the sequence or indirectly from different conformations, for example, depending on whether the replaced residue occurs within the center of a β-strand, at its ends, or within a loop. Therefore, it is important to establish whether the correlation between kg, tl, or ΔGagg does still hold when comparing mutants at different positions in the sequence.

We have found that the changes in the thermodynamics of the Aβ(1–40) peptide caused by a mutation, measured through ΔGagg, correlate well with the predicted changes in the intrinsic aggregation propensity, Zagg. In addition, the Zagg scores correlate well with the changes in the lag times and growth rates. This is a surprising result, because the algorithm developed to calculate the Zagg scores was derived from experimental growth rates; it indicates, therefore, that the factors governing the lag time are the same as those determining the growth rate, at least for Aβ(1–40). Since the oligomeric species present in the lag phase appear to be the species responsible for high toxicity (Bucciantini et al. 2002; Silveira et al. 2005; Lesne et al. 2006), it is tempting to speculate that these results could contribute to our understanding of the neurotoxicity of different peptides. Comparison of the two kinetic parameters and also the ΔGagg values with a variety of physicochemical properties suggests that within the precision of the measurement, hydrophobicity has the greatest relative influence on tl and, therefore, on the nucleation reaction (Table 2). This result would imply that hydrophobic interactions are particularly important for the association of peptide molecules onto pre-existing nuclei or for the initial interactions of the soluble species, leading to nucleus formation, resembling perhaps the hydrophobic collapse reaction known from native protein-folding reactions (Miranker and Dobson 1996).

The critical nucleus size is defined as the number of molecules capable of forming an oligomer in which the enthalpy gain in forming intermolecular interactions balances the entropy loss in losing diffusional mobility. In principle, the interactions stabilizing the oligomer need not be specific and they can be different from those responsible for growth, since the latter are likely to involve specific networks of hydrogen bonds in highly organized structures. We have shown that targeted mutations have the same effect on nucleation and growth (Fig. 3), thus strongly suggesting that despite variations, the same key interactions are involved in both processes. Kelly and colleagues recently suggested that the interaction of just two molecules is rate limiting in the aggregation process of the Aβ(1–40) peptide (Bieschke et al. 2005). Although more quantitative estimations are necessary, a critical nucleus of aggregation formed by two or three molecules would suffice, in principle, to provide a molecular mechanism that explains the observed effect. These observations would suggest that the same type of association between peptide pairs during growth also plays an important role in the nucleation process, while the formation of larger critical nuclei would involve more complex processes, resulting in distinct effects of mutations on the nucleation and on the growth steps.

Conclusions

We have shown here that the in vitro aggregation kinetics and thermodynamics of mutational variants of the Aβ(1–40) peptide are highly correlated and that it is possible to rationalize them based on intrinsic properties of the polypeptide chain. In addition, the context dependence that we found for specific amino acid replacements indicates the importance of the structure of the oligomeric species along the aggregation pathway. Therefore, it will be interesting to test whether the relationships that we found here between lag times, growth rates, and the thermodynamics of aggregation would also be found for polypeptide sequences differing in their hydrophobicity and charge distributions from the ones examined here.

Materials and Methods

Mutagenesis and oxidation of Aβ(1–40)

Mutagenesis, expression, and purification of the Aβ(1–40) peptide variants were performed as described previously (Christopeit et al. 2005; Hortschansky et al. 2005a). Based on a Coomassie-stained protein gel, the purity of the peptide was estimated to be better than 95%. Pure peptides were oxidized by incubation of 5 mg/mL of the peptide in 3% H2O2 for 4 h at 20°C (Christopeit et al. 2005). The oxidized peptide was repurified with reversed-phase chromatography and lyophilized. The identity of all peptides was verified by mass spectrometry after oxidation.

Polarization and electron microscopy analysis

Congo-red staining of fibril solutions dried on glass slides was performed according to published methods (Christopeit et al. 2005) and analyzed using a Leica DM/DR x450 polarizing microscope with parallel (bright field) or crossed polarizers (dark field). Electron microscopy was carried out of samples from the kinetic analysis after 4 d of incubation as described previously (Fändrich et al. 2003), using an EM 400 T Philips electron microscope.

Kinetic and thermodynamic aggregation measurements

All kinetic data were recorded at 37°C using a BMG FLUOstar Galaxy reader (BMG) and black-wall 96-well plates (Nunc). A detailed description of these methods can be found elsewhere (Christopeit et al. 2005; Hortschansky et al. 2005a). The samples contained 120 μM Aβ(1–40) peptide, 20 μM ThT, and 10 mM sodium azide solution in 50 mM sodium phosphate buffer (pH 7.4). The aggregation kinetics were recorded experimentally for 10 individual samples of each mutational variant. From each experimental trace, the two kinetic parameters were extracted, and the values then averaged over all traces to give the reported values kg and tl. For analysis of the critical concentration, peptides were dissolved in 50 mM sodium phosphate buffer (pH 7.4) at 1.0–1.5 mg/mL concentration and UV sterilized by irradiation at 254 nm for 1.5 h. Incubation at 37°C was carried out for 28 d in oil-free tubes (MoBiTec) and terminated by spinning down the sample for 30 min at 120,000 rpm (513,000g) and 4°C in a Beckman TLA-100 tabletop centrifuge using a TLA-120.2 fixed angle rotor. After centrifugation, the supernatant was taken off and the soluble peptide fraction was determined using a Micro-BC-Assay (Interchim). The latter was calibrated with a standard of wild-type Aβ peptide that was prepared based on the optical absorption at 280 nm (Pace et al. 1995; Hortschansky et al. 2005b). Measurements were carried out in the standard range, where linear regression produces a correlation of better than 0.95. The critical concentration cc is converted into the Gibb's free energy of aggregation, ΔGagg, as described by the simple formula ΔGagg = −RT ln (1/cc) (Oosawa and Asakura 1975).

Aggregation propensity prediction

We used the Zyggregator algorithm (available for academic use at http://www-vendruscolo.ch.cam.ac.uk/zyggregator.php) to analyze the behavior of the Aβ(1–40) peptide in terms of its physicochemical properties (Pawar et al. 2005). The intrinsic aggregation propensity score, Zagg, was calculated for the wild-type sequence and all experimentally characterized mutants.

Conflict of interest

The authors claim a conflict of interest arising from a commercial partner that precludes free distribution of any DNA constructs described here. Basis vectors are available from commercial vendors.

Acknowledgments

This work was supported by the Deutsche Forschungsgemeinschaft (DFG). M.F. acknowledges a BioFuture grant from the Bundesministerium für Bildung und Forschung (BMBF). The research of M.V. and C.M.D. is supported by the Leverhulme Trust. We thank S. Fricke, U. Knüpfer, and R. Wenderoth for technical assistance as well as M. Nache for molecular modeling.

Footnotes

Reprint requests to: Marcus Fändrich. Leibniz-Institut für Altersforschung, Beutenbergstraße 11, D-07745 Jena, Germany; e-mail: fandrich@fli-leibniz.de; fax: 49 3641 656310; or Michele Vendruscolo, University of Cambridge, Department of Chemistry, Lensfield Road, Cambridge, UK; e-mail: mv245@cam.ac.uk; fax: 44-1223-763418.

Abbreviations: Aβ, amyloid-β peptide; cc, critical concentration; CR, Congo red; ΔGagg, Gibb's free energy of aggregation; EM, electron microscopy; kg, growth rate; ThT, thioflavin-T; tl, lag time; Zagg, calculated propensity of aggregation.

References

  1. Bieschke J., Zhang, Q., Powers, E.T., Lerner, R.A., and Kelly, J.W. 2005. Oxidative metabolites accelerate Alzheimer's amyloidogenesis by a two-step mechanism, eliminating the requirement for nucleation. Biochemistry 44: 4977–4983. [DOI] [PubMed] [Google Scholar]
  2. Bitan G., Vollers, S.S., and Teplow, D.B. 2003. Elucidation of primary structure elements controlling early amyloid β-protein oligomerization. J. Biol. Chem. 278: 34882–34889. [DOI] [PubMed] [Google Scholar]
  3. Broome B.M. and Hecht, M.H. 2000. Nature disfavors sequences of alternating polar and non-polar amino acids: Implications for amyloidogenesis. J. Mol. Biol. 296: 961–968. [DOI] [PubMed] [Google Scholar]
  4. Bucciantini M., Giannoni, E., Chiti, F., Baroni, F., Formigli, L., Zurdo, J., Taddei, N., Ramponi, G., Dobson, C.M., and Stefani, M. 2002. Inherent toxicity of aggregates implies a common mechanism for protein misfolding diseases. Nature 416: 507–511. [DOI] [PubMed] [Google Scholar]
  5. Chiti F., Webster, P., Taddei, N., Clark, A., Stefani, M., Ramponi, G., and Dobson, C.M. 1999. Designing conditions for in vitro formation of amyloid protofilaments and fibrils. Proc. Natl. Acad. Sci. 96: 3590–3594. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Chiti F., Taddei, N., Bucciantini, M., White, P., Ramponi, G., and Dobson, C.M. 2000. Mutational analysis of the propensity for amyloid formation by a globular protein. EMBO J. 19: 1441–1449. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Chiti F., Taddei, N., Baroni, F., Capanni, C., Stefani, M., Ramponi, G., and Dobson, C.M. 2002. Kinetic partitioning of protein folding and aggregation. Nat. Struct. Biol. 9: 137–143. [DOI] [PubMed] [Google Scholar]
  8. Chiti F., Stefani, M., Taddei, N., Ramponi, G., and Dobson, C.M. 2003. Rationalization of the effects of mutations on peptide and protein aggregation rates. Nature 424: 805–808. [DOI] [PubMed] [Google Scholar]
  9. Christopeit T., Hortschansky, P., Schroeckh, V., Gührs, K., Zandomeneghi, G., and Fändrich, M. 2005. Mutagenic analysis of the nucleation propensity of oxidized Alzheimer's β-amyloid peptide. Protein Sci. 14: 2125–2131. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Dobson C.M. 2001. The structural basis of protein folding and its links with human disease. Philos. Trans. R. Soc. Lond. B Biol. Sci. 356: 133–145. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Dobson C.M. 2003. Protein folding and misfolding. Nature 426: 884–890. [DOI] [PubMed] [Google Scholar]
  12. DuBay K.F., Pawar, A.P., Chiti, F., Zurdo, J., Dobson, C.M., and Vendruscolo, M. 2004. Prediction of the absolute aggregation rates of amyloidogenic polypeptide chains. J. Mol. Biol. 341: 1317–1326. [DOI] [PubMed] [Google Scholar]
  13. Dzwolak W., Smirnovas, V., Jansen, R., and Winter, R. 2004. Insulin forms amyloid in a strain-dependent manner: An FT-IR spectroscopic study. Protein Sci. 13: 1927–1932. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Fändrich M. 2007. Absolute correlation between lag time and growth rate in the spontaneous formation of several amyloid-like aggregates and fibrils. J. Mol. Biol. 365: 1266–1270. [DOI] [PubMed] [Google Scholar]
  15. Fändrich M. and Dobson, C.M. 2002. The behaviour of polyamino acids reveals an inverse side chain effect in amyloid structure formation. EMBO J. 21: 5682–5690. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Fändrich M., Fletcher, M.A., and Dobson, C.M. 2001. Amyloid fibrils from muscle myoglobin. Nature 410: 165–166. [DOI] [PubMed] [Google Scholar]
  17. Fändrich M., Forge, V., Buder, K., Kittler, M., Dobson, C.M., and Diekmann, S. 2003. Myoglobin forms amyloid fibrils by association of unfolded polypeptide segments. Proc. Natl. Acad. Sci. 100: 15463–15468. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Fernandez-Escamilla A.M., Rousseau, F., Schymkowitz, J., and Serrano, L. 2004. Prediction of sequence-dependent and mutational effects on the aggregation of peptides and proteins. Nat. Biotechnol. 22: 1302–1306. [DOI] [PubMed] [Google Scholar]
  19. Fink A.L. 1998. Protein aggregation: Folding aggregates, inclusion bodies, and amyloid. Fold. Des. 3: R9–23. [DOI] [PubMed] [Google Scholar]
  20. Fraser P.E., Nguyen, J.T., Inouye, H., Surewicz, W.K., Selkoe, D.J., Podlisny, M.B., and Kirschner, D.A. 1992. Fibril formation by primate, rodent, and Dutch-hemorrhagic analogues of Alzheimer amyloid β-protein. Biochemistry 31: 10716–10723. [DOI] [PubMed] [Google Scholar]
  21. Harper J.D. and Lansbury Jr, P.T. 1997. Models of amyloid seeding in Alzheimer's disease and scrapie: Mechanistic truths and physiological consequences of the time-dependent solubility of amyloid proteins. Annu. Rev. Biochem. 66: 385–407. [DOI] [PubMed] [Google Scholar]
  22. Hortschansky P., Schroeckh, V., Christopeit, T., Zandomeneghi, G., and Fändrich, M. 2005a. The aggregation kinetics of Alzheimer's β-amyloid peptide is controlled by stochastic nucleation. Protein Sci. 14: 1753–1759. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Hortschansky P., Christopeit, T., Schroeckh, V., and Fändrich, M. 2005b. Thermodynamic analysis of the aggreg ation propensity of oxidized Alzheimer's β-amyloid variants. Protein Sci. 14: 2915–2918. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Jackson M. and Mantsch, H.H. 1991. Protein secondary structure from FT-IR spectroscopy: Correlation with dihedral angles from three-dimensional Ramachandran plots. Can. J. Chem. 69: 1639–1642. [Google Scholar]
  25. Krebs M.R.H., MacPhee, C.E., Miller, A.F., Dunlop, I.E., Dobson, C.M., and Donald, A.M. 2004. The formation of spherulites by amyloid fibrils of bovine insulin. Proc. Natl. Acad. Sci. 101: 14420–14424. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Lashuel H.A., Hartley, D.M., Petre, B.M., Wall, J.S., Simon, M.N., Walz, T., and Lansbury Jr, P.T. 2003. Mixtures of wild-type and a pathogenic (E22G) form of Aβ40 in vitro accumulate protofibrils, including amyloid pores. J. Mol. Biol. 332: 795–808. [DOI] [PubMed] [Google Scholar]
  27. Lesne S., Koh, M.T., Kotilinek, L., Kayed, R., Glabe, C.G., Yang, A., Gallagher, M., and Ashe, K.H. 2006. A specific amyloid-β protein assembly in the brain impairs memory. Nature 440: 352–357. [DOI] [PubMed] [Google Scholar]
  28. Miranker A.D. and Dobson, C.M. 1996. Collapse and cooperativity in protein folding. Curr. Opin. Struct. Biol. 6: 31–42. [DOI] [PubMed] [Google Scholar]
  29. Miravalle L., Tokuda, T., Chiarle, R., Giaccone, G., Bugiani, O., Tagliavini, F., Frangione, B., and Ghiso, J. 2000. Substitutions at codon 22 of Alzheimer's Aβ peptide induce diverse conformational changes and apoptotic effects in human cerebral endothelial cells. J. Biol. Chem. 275: 27110–27116. [DOI] [PubMed] [Google Scholar]
  30. Murakami K., Irie, K., Morimoto, A., Ohigashi, H., Shindo, M., Nagao, M., Shimizu, T., and Shirasawa, T. 2002. Synthesis, aggregation, neurotoxicity, and secondary structure of various Aβ1-42 mutants of familial Alzheimer's disease at positions 21-23. Biochem. Biophys. Res. Commun. 294: 5–10. [DOI] [PubMed] [Google Scholar]
  31. Nilsberth C., Westlind-Danielsson, A., Eckman, C.B., Condron, M.M., Axelman, K., Forsell, C., Stenh, C., Luthman, J., Teplow, D.B., Younkin, S.G., et al. 2001. The “Arctic” APP mutation (E693G) causes Alzheimer's disease by enhanced Aβ protofibril formation. Nat. Neurosci. 4: 887–893. [DOI] [PubMed] [Google Scholar]
  32. O'Nuallain B., Shivaprasad, S., Kheterpal, I., and Wetzel, R. 2005. Thermodynamics of Aβ(1-40) amyloid fibril elongation. Biochemistry 44: 12709–12718. [DOI] [PubMed] [Google Scholar]
  33. Oosawa F. and Asakura, S. 1975. Thermodynamics of the polymerisation of protein. Academic Press, London, UK.
  34. Pace C.N., Vajdos, F., Fee, L., Grimsley, G., and Gray, T. 1995. How to measure and predict the molar absorption coefficient of a protein. Protein Sci. 4: 2411–2423. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Pawar A.P., DuBay, K.F., Zurdo, J., Chiti, F., Vendruscolo, M., and Dobson, C.M. 2005. Prediction of “aggregation-prone” and “aggregation-susceptible” regions in proteins associated with neurodegenerative diseases. J. Mol. Biol. 350: 379–392. [DOI] [PubMed] [Google Scholar]
  36. Peacock M.L., Warren Jr, J.T., Roses, A.D., and Fink, J.K. 1993. Novel polymorphism in the A4 region of the amyloid precursor protein gene in a patient without Alzheimer's disease. Neurology 43: 1254–1256. [DOI] [PubMed] [Google Scholar]
  37. Peim A., Hortschansky, P., Christopeit, T., Schroeckh, V., Richter, W., and Fändrich, M. 2006. Mutagenic exploration of the cross-seeding and fibrillation propensity of Alzheimer's β-amyloid peptide variants. Protein Sci. 15: 1801–1805. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Pellarin R. and Caflisch, A. 2006. Interpreting the aggregation kinetics of amyloid peptides. J. Mol. Biol. 360: 882–892. [DOI] [PubMed] [Google Scholar]
  39. Petkova A.T., Ishii, Y., Balbach, J.J., Antzutkin, O.N., Leapman, R.D., Delaglio, F., and Tycko, R. 2002. A structural model for Alzheimer's β-amyloid fibrils based on experimental constraints from solid state NMR. Proc. Natl. Acad. Sci. 99: 16742–16747. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Selkoe D.J. 2003. Folding proteins in fatal ways. Nature 426: 900–904. [DOI] [PubMed] [Google Scholar]
  41. Silveira J.R., Raymond, G.J., Hughson, A.G., Race, R.E., Sim, V.L., Hayes, S.F., and Caughey, B. 2005. The most infectious prion protein particles. Nature 437: 257–261. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Tartaglia G.G., Cavalli, A., Pellarin, R., and Caflisch, A. 2004. The role of aromaticity, exposed surface, and dipole moment in determining protein aggregation rates. Protein Sci. 13: 1939–1941. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Thompson M.J., Sievers, S.A., Karanicolas, J., Ivanova, M.I., Baker, D., and Eisenberg, D. 2006. The 3D profile method for identifying fibril-forming segments of proteins. Proc. Natl. Acad. Sci. 103: 4074–4078. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Van Nostrand W.E., Melchor, J.P., Cho, H.S., Greenberg, S.M., and Rebeck, G.W. 2001. Pathogenic effects of D23N Iowa mutant amyloid β-protein. J. Biol. Chem. 276: 32860–32866. [DOI] [PubMed] [Google Scholar]
  45. Walsh D.M., Hartley, D.M., Condron, M.M., Selkoe, D.J., and Teplow, D.B. 2001. In vitro studies of amyloid β-protein fibril assembly and toxicity provide clues to the aetiology of Flemish variant (Ala692 → Gly) Alzheimer's disease. Biochem. J. 35: 869–877. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Watson A.A., Fairlie, D.P., and Craik, D.J. 1998. Solution structure of methionine-oxidized amyloid β-peptide (1-40). Does oxidation affect conformational switching? Biochemistry 37: 12700–12706. [DOI] [PubMed] [Google Scholar]
  47. West M.W. and Hecht, M.H. 1995. Binary patterning of polar and nonpolar amino acids in the sequences and structures of native proteins. Protein Sci. 4: 2032–2039. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. West M.W., Wang, W., Patterson, J., Mancias, J.D., Beasley, J.R., and Hecht, M.H. 1999. De novo amyloid proteins from designed combinatorial libraries. Proc. Natl. Acad. Sci. 96: 11211–11216. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Westermark G.T., Johnson, K.H., and Westermark, P. 1999. Staining methods for identification of amyloid in tissue. Methods Enzymol. 309: 3–25. [DOI] [PubMed] [Google Scholar]
  50. Wurth C., Guimard, N.K., and Hecht, M.H. 2002. Mutations that reduce aggregation of the Alzheimer's Aβ42 peptide: An unbiased search for the sequence determinants of Aβ amyloidogesis. J. Mol. Biol. 319: 1279–1290. [DOI] [PubMed] [Google Scholar]
  51. Zagorski M.G., Yang, J., Shao, H., Ma, K., Zeng, H., and Hong, A. 1999. Methodological and chemical factors affecting amyloid β peptide amyloidogenicity. Methods Enzymol. 309: 189–204. [DOI] [PubMed] [Google Scholar]
  52. Zandomeneghi G., Krebs, M.R., McCammon, M.G., and Fändrich, M. 2004. FTIR reveals structural differences between native β-sheet proteins and amyloid fibrils. Protein Sci. 13: 3314–3321. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Protein Science : A Publication of the Protein Society are provided here courtesy of The Protein Society

RESOURCES