Using surface envelopes to constrain molecular modeling

Abstract

Molecular density information (as measured by electron microscopic reconstructions or crystallographic density maps) can be a powerful source of information for molecular modeling. Molecular density constrains models by specifying where atoms should and should not be. Low-resolution density information can often be obtained relatively quickly, and there is a need for methods that use it effectively. We have previously described a method for scoring molecular models with surface envelopes to discriminate between plausible and implausible fits. We showed that we could successfully filter out models with the wrong shape based on this discrimination power. Ideally, however, surface information should be used during the modeling process to constrain the conformations that are sampled. In this paper, we describe an extension of our method for using shape information during computational modeling. We use the envelope scoring metric as part of an objective function in a global optimization that also optimizes distances and angles while avoiding collisions. We systematically tested surface representations of proteins (using all nonhydrogen heavy atoms) with different abundance of distance information and showed that the root mean square deviation (RMSD) of models built with envelope information is consistently improved, particularly in data sets with relatively small sets of short-range distances.

Despite the increasing success of large-scale structure determination efforts (including recent efforts in structural genomics [Todd et al. 2005]), there is still a need for robust structure modeling methodologies. First, structural genomics efforts are likely to yield members of a fold family, and other members may have to be modeled from these examples. Second, some structures may not be determined for technical reasons. Finally, even when component structures are determined, it will often be necessary to assemble the components into larger complexes, sometimes with modeling.

Modeling makes use of many data sources, including those that produce distances (such as NMR [Tzakos et al. 2006], fluorescence resonance energy transfer [FRET {dos Remedios and Moens 1995}], and cross-linking [Kunkel et al. 1981]); those that produce surface accessibility (such as chemical footprinting [Nguyenle et al. 2006]); those that produce overall dimensions (such as hydrodynamic sedimentation measurements [Lebowitz et al. 2002] and small-angle X-ray scattering [Svergun and Koch 2002]); and overall shape information (such as from electron microscopy [EM] or low-resolution crystallography [Rossmann et al. 2005]). Recent advances in the ability to determine overall shapes based on electron microscopy have visualized molecular structures of significant size, but usually with a limited resolution of 6–9 Å (Chiu et al. 2005). The challenge in using EM data, however, is that the overall surface may be well-defined, but the location of individual atoms is not specified. Although some reference markings may be defined using antibody or heavy-atom “tags,” these can involve significant additional labor (Buchel et al. 2001). Nonetheless, the information content of a medium-high resolution surface envelope should markedly reduce the space of molecular structures that are compatible with the envelope. While generally not sufficient to uniquely define a structure, the envelope is useful in the context of other structural measurements, such as distance information taken from the sources mentioned. Our work is focused on developing methods to use envelope information to assist in building models of molecular assemblages.

In previous work, we reported a data structure called the “surface envelope” (SE) that could be used to represent the shape of a molecule (Dugan and Altman 2004). An SE is a cubic grid-based structure (with grid-variable dimensions) that represents the overall shape of a molecule at any resolution. We developed a fitness metric that scores the degree of match between a molecular model and a target SE. The fitness metric searches for the best rotation/translation of the model so that it matches the SE. We showed that the fitness function tracks well with the RMSD, with high fitness scores corresponding to low RMSD matches between the model and the target structure from which the SE was generated.

In this paper, we present results showing that an SE can be used prospectively in computational modeling to constrain the molecular structure produced from a set of distance constraints. The goal is to produce a molecular model with a shape similar to the shape encoded with the SE data structure while also satisfying the distance constraints. Our method works best with high-resolution shape data in the 3–4 Å resolution range, but it can be applied to any data set. We use “prospective” to distinguish a method that uses the SE actively in the search for conformations from methods that use the SE simply as a postmodeling filter to throw away incompatible models. Our previous work showing the correlation between molecular shape and RMSD demonstrates the filtering capability of SE, but here we show the value of directly integrating the SE data into the optimization routines for building molecular models. Ideally, the modeling process will use SE data to more quickly converge to a global minimum of our objective function, reducing the measured residuals between the constraints (interatomic distances and SE shape) and the corresponding measurements from atom positions in the model.

The details of our method are provided in the Materials and Methods section, but the key features can be summarized here. First, we use the grid-based SE, aligned to the “model-under-construction,” to evaluate which atoms are occupying the molecular shape and which are not. Second, we compute the derivative of the fitness function to estimate where atoms that are not currently within the target SE shape should move in order to occupy the shape. Third, we employ increasingly “fuzzy” versions of the SE to ensure that the derivative of the fitness function with respect to the atom position is never zero, to ensure that atoms are always moving toward positions that are contained within the SE.

We have validated our method in the context of a distance-geometry algorithm called GNOMAD (Williams et al. 2001). GNOMAD uses nonlinear optimization techniques to estimate molecular structure based on an objective function that is optimal when all constraints (in this case, distance and surface) are satisfied. GNOMAD uses the derivative of the objective function to guide its search. GNOMAD has been shown in previous work to be fast and accurate (Williams et al. 2001). In our validation experiments, we show that the addition of surface information, through our SE data structure, can provide information equivalent to 10%–40% of short-range distances. That is, in some cases a low-RMSD structure can be computed with 60% of short-range distances alone, or 20% of those distances along with an SE. Thus, we are able to provide a first-order quantification of the relative value of surface information in molecular modeling, in “units” of percent-of-short-range-distances.

Results

We validated our method on synthetic distance and SE data computed from eight different crystallized proteins. The first two are fragments of the N-terminal region from complete structures, the third is a complete structure, and the fourth is a CATH domain from the Hodor set (Hodor et al. 1999). The molecular sizes range from 56 atoms through 717 atoms. In each of the four experiments, the same experimental design was used: 48 different distance input sets were created by taking six random samples of short-range distances <6 or 10 Å, in order to simulate distances derived experimentally from cross-linking or NMR. Four different fractions of these short-range distances were used: 20%, 30%, 40%, and 60%. We have found in previous work that 60% of short-range distances is typically sufficient to reconstruct a structure with high precision (Chen et al. 1996, 1998, 1999; Schmidt et al. 1998). Four fractions, two distance cutoffs, and six samples of each, leads to 4 × 2 × 6 = 48 different distance sets. We graph each of these as shown in Figure 1A,H, with the Y-axis indicating the RMSD (to the known structure) of the computed model with SE data added to the distance data set and the X-axis indicating the RMSD of the model computed without the SE data. The short-range distances provided were all exact with low variance. We have previously documented the loss in precision in GNOMAD when using noisier distance data. The SE for each known structure was computed with a grid size of 3.7 Å, as detailed in Materials and Methods.

Figure 1.

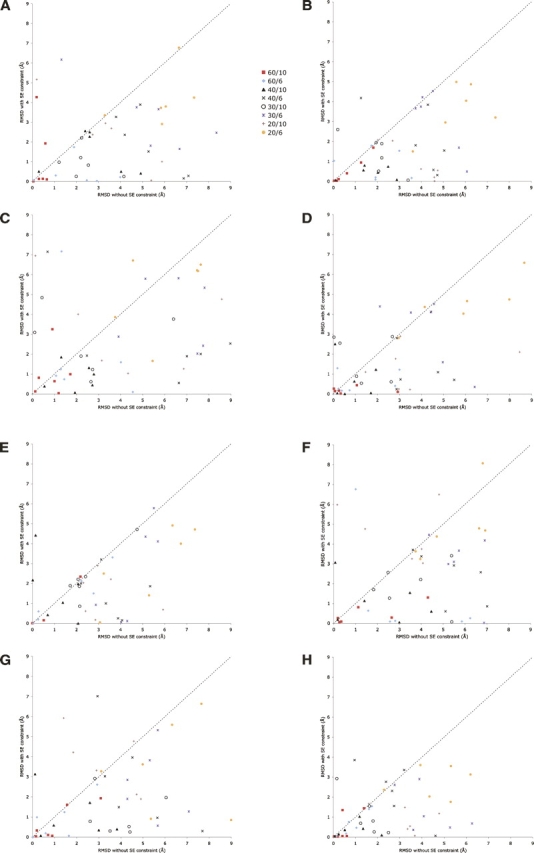
(A) Modeling results for ribosomal structure (1ctf). This graph compares the RMSD of resulting models of 1ctf, derived both with and without SE data. In all modeling runs, sets of interatomic distances were included spanning 20%–60% of short-range distances, as described in the text. The distance range was taken as either 6 or 10 Å. The key indicates the percentage and distance range applied. (B) Modeling results for protein 1myt; (C) modeling results for plant seed protein Crambin, 1crn; (D) modeling results for virus coat protein, 2bbv; (E) modeling results for chain B of the HPP precursor protein, 1ivy; (F) modeling results for chain O of the RNA binding attenuation protein, 1wap; (G) modeling results for actin binding protein, 1svr; and (H) modeling results from chain E from the virus coat protein, 2bbv.

Figure 1A presents results from the full-atom modeling of the first 171 atoms (24 residues) of protein 1ctf (PDB entry codes). This graph shows 48 different points representing 96 different modeling runs for this structure. The first 48 runs used distinct distance data sets, and the second 48 runs used the same distance sets, with the addition of a 3.7 Å SE generated from the crystal structure of 1ctf. Figure 1B presents results from the full-atom modeling of the first 283 atoms (36 residues) of protein 1myt. Figure 1C presents results from the full-atom modeling of plant seed protein Crambin (1crn, 327 atoms). Figure 1D presents results from the full-atom modeling of chain E from the virus coat protein with 2bbv, 125 atoms. Figure 1E presents results from the full-atom modeling of chain B of the HPP precursor protein with 1ivy, 399 atoms. Figure 1F presents results from the full-atom modeling of chain O of the RNA binding attenuation protein with 1wap, 519 atoms. Figure 1G presents results from the full-atom modeling of the actin binding protein with 1svr, 717 atoms. Figure 1H presents results from the full-atom modeling of a fragment of chain E from the virus coat protein with 2bbv, 56 atoms.

The changes that we introduced into the GNOMAD code for determining structure from distances slowed the code considerably. In general, GNOMAD produces structures in a few minutes, and these modifications increased running time by 10-fold. We attribute the increase to the unoptimized computation of surface to model match, the blurring procedure, and (most of all) the finite-difference estimate of derivatives of the augmented objective function.

Discussion

Several existing tools assist in applying shape information in the determination of 3D biomolecular structures. Current techniques include manual and semi-automated procedures (Volkmann and Hanein 2003), secondary structure mapping and fold detection (Dror et al. 2007), reduced-detail representations and conformational flexibility fitting (Wriggers et al. 2004), and mapping density onto a 3D grid (Topf et al. 2005). Our method is fully automated and does not include secondary structures or a reduced complexity density representation. We apply a 3D cubic grid for the electron density values with the SE.

Examination of Figure 1A,H, shows the clear benefit of using shape information in the modeling process. In almost all cases, addition of the SE data type caused the resulting model RMSD to improve relative to the crystal. In some cases, these improvements were dramatic, causing models in the 6–7 Å range with distance information alone to move close to 0 Å RMSD after adding the SE. It should be noted that the results presented have a stochastic nature to them because the procedure for aligning the current best molecular model to the surface envelope includes random perturbations to improve the fit (Dugan and Altman 2004). Therefore, no single data point would appear in the same place given the same starting conditions. It is still informative to examine overall trends in the data. Not surprisingly, the envelope data helps low-abundance data sets the most; the 20% and 30% of short-range distance data sets often show the greatest improvements with the SE data. When using extremely low percentages of distances, such as only one or two distance constraints, models converge quickly to minima that conformed to both the shape and the distance constraints but had very high RMSD when compared to the solved structure.

Conversely, a few of the modeling runs actually produced worse structures after adding SE data. These are easy to identify because they generally come from runs that never converge to low error and thus do not converge. If at the end of the modeling run, the model does not satisfy the input data, then the structure with the lowest observed error during the modeling run provides the run RMSD value. In practice, the high constraint error makes it clear that the run had not converged.

Our distance sets were generated by measuring the distance in a solved structure between two random residues without regard for their 3D position. The particular residues for which there are distance constraints can affect the precision greatly. Particularly when coupled with shape information, certain “strategic” distances could greatly increase the accuracy of resulting models for a given amount of distances. Unfortunately, most experimental methodologies do not allow distances to be selectively probed (FRET being an exception), so we simulated the most likely scenario: randomly measured distances.

We were concerned that the addition of SE data might make the optimization landscape rougher and result in poor convergence. However, there were surprisingly few examples to support local-minima issues with the SE data. However, local minima were most likely when the addition of SE made structural models worse; adding the shape information sometimes made convergence of the nonlinear minimization more difficult than using distance sets alone. We did not find any particular distance set to stand out as difficult in terms of convergence; the distance sets were randomly generated and were internally self-consistent with the solved structure. For the cases with poor structural models using SE data and sparse distance sets, we sometimes find low-error solutions that do not produce models with low RMSD. For denser distance sets, high-RMSD solutions are typically local minima that are easy to recognize: They have high error in the resulting distances, and our system is unable to find the correct solution.

Another factor affecting the outcome of our method is the intrinsic shape of the protein. The more spherical the protein (the closer to 1 for the ratio of min to max principal component of 3D density), the lower the contribution of shape information to modeling.

Data quality is a major factor in modeling protein structures. The effect on model quality from errors depends on many factors, including the kinds of errors and the degree or severity of the error. For example, mislabeling residues for distance constraints could greatly increase the chance of nonconvergence, resulting in model with extremely high error (fortunately, often easily detected). Individual errors in the distances for some distance constraints would produce internally inconsistent data sets, and our modeling system may not converge depending on the magnitude of the errors. Our method is fairly robust with respect to errors in the SE, as we use the envelope data for deriving gradient information. As long as gradients are similar, errors in actual values in the SE would create minimal changes in resulting protein models.

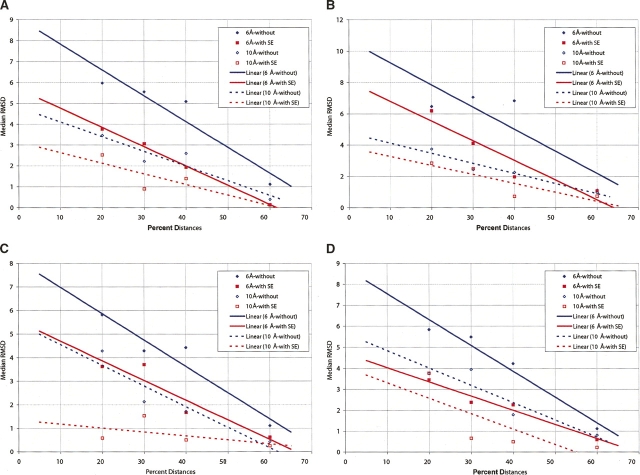
Given the models created both with and without shape information, it is interesting to estimate the value of the SE in terms of percentage of distances saved. In other words, “What percentage of available distances is equivalent to adding shape information for producing models with similar RMSD?” Figure 2, A and B, shows two graphs derived from the 1ctf and 1crn runs above. For each group of six random-distance sets, the median RMSD is plotted against the percentage of distances used. The four cases represent two different distance cutoffs (6 and 10 Å) both with and without SE data. Linear approximations to the median RMSD are shown with straight lines. Examination of the horizontal distance between the solid lines provides the estimate of the improvement due to assigning SE with 6 Å distances (as measured in percent distances). Similarly, the dotted lines pertain to 10 Å data. With 6 Å data, the SE is “worth” ∼10% additional distances when 60% of distances are provided and ∼15% when a lower fraction of distances is provided. The 10 Å data show that the SE has less value. For these data, the value of the SE is about the same as providing an additional 10% of the short-range distances. These are, to our knowledge, the first direct-assessment methods of the relative value that shape information provides in modeling. As we discussed previously (Dugan and Altman 2004), surface information is most useful for modeling when the shape is highly eccentric.

Figure 2.

(A) Estimation of the value SE contributes to modeling in 1ctf. This graph presents the median RMSD over the six random-distance sets in each of four cases for the 1ctf structure. Data at 6 and 10 Å, both with and without SE data, are included. Lines are linear approximations to the median RMSD values. By looking at the horizontal distance between the lines, we can estimate the value of adding SE data during modeling (1ctf). (B) Estimates of the value that SE contributes to modeling in 1crn, (C) 1myt, and (D) 1svr.

Figure 2C presents a similar analysis of 1myt. For the 10 Å data and large fractions of the short-range distances, the SE adds almost nothing, but for 10 Å runs and <40% of short-range distances, the SE contributes significantly. Figure 2D presents similar data for 1svr.

Materials and Methods

The overall features of the SE data structure are described elsewhere (Dugan and Altman 2004). Briefly, each molecular density data set is mapped to a cubic 3D grid, and the grid boxes are filled with atomic density linearly proportional to the contents of the initial data set. During modeling, the molecule is aligned with the SE by first aligning the principal inertial components of the grid and the molecule and then by refining the registration and checking for symmetry. Once the SE and the molecule are aligned, we define a score based on the match between SE grid boxes that have density and whether atoms in the model fill those grid boxes (at any level of abstraction).

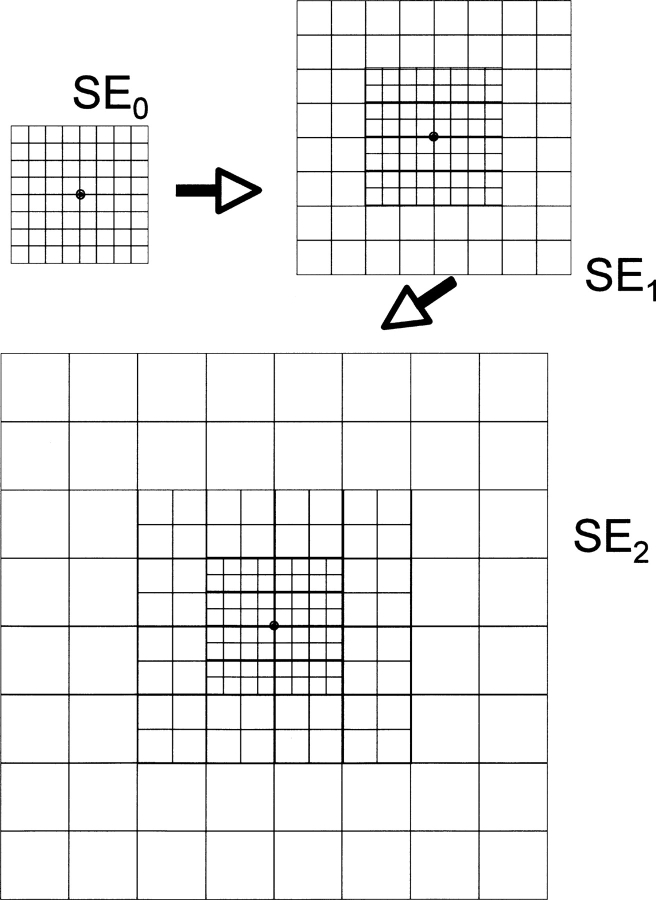
The general method for using an SE match as part of a molecular structural modeling optimization involves ensuring that the score function for the SE is both differentiable and always defined. This ensures that atoms can be “pulled” into density by the optimizer no matter where they land on previous iterations. As discussed below, we created a hierarchical data structure with multiple SE to support modeling. This hierarchical structure allows expanding and blurring, as described in the next two subsections. Expanding and blurring allow us to create a lower-resolution set of envelopes, each one successively larger than the previous, with respect to the box size and the total three-dimensional extent. These larger envelopes guarantee that the fitness function for any individual atom (and therefore its gradient) is always computable. The initial SE has the label layer 0, which is blurred and then expanded to create layer 1. The process is iterated through blurring and then expanding on layer n to create layer n + 1. The current implementation creates five layers (layers 0–4), but that number is adjustable to accommodate larger models.

Several methods for different starting structures were tested as part of the research. For the results presented here, atoms were placed in random position in a box ±10 Å from the origin. Other methods tested included iterative buildup along the backbone chain, iterative addition of atoms by traversal of distance constraints, depth first and breadth first. In all of these test cases, minimal additional value was added to the resulting models, so random initial placement of all atoms was used in final runs.

We used the GNOMAD optimization code for estimating molecular structure from distances. Details of GNOMAD have been published previously (Williams et al. 2001), but they can be summarized here. GNOMAD creates a nonlinear objective function that is minimized when all distance and angle constraints are satisfied. It uses a line-search method that can guarantee that all structures have no atomic collisions, because each atom is placed in an unoccupied location at each step of the optimization.

GNOMAD updates the coordinated locations of one atom at a time instead of simultaneously updating the positions of all the atoms in the molecule or some group of atoms. This atom-based approach reduces the dimensionality of the system and makes constraint enforcement more tractable. The GNOMAD objective function is based on the sum-of-squares of the weighted residuals. Residuals are the difference between input data (an interatomic distance) and the corresponding calculated value from the current model which requires that all elements of the objective function be differentiable. GNOMAD is fast and has been shown to produce low residual structures from distance information.

Fitness function

During atom-based modeling, we need a measure of how accurately any particular atom meets the shape of the SE after the model is aligned to the SE. We use an atom-based score function for this measure:

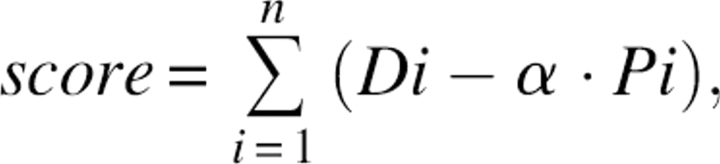where i = counts over all atoms in the model, D_i = density value from SE at atom position i, α = an adjustable scaling factor, and P_i = penalty function for regions of SE near atom i not filled with atoms in the model. P_i is calculated for each atom and is equal to zero for each box i in the SE that contains an atom and is equal to the density value in the box (a value from 0 to 1) if no nearby atom can account for the atom density expected in box j.

During modeling, the movement of each atom requires the gradient and an estimation of the Hessian (second partial derivatives) of the fitness function. For the SE, we can understand these quantities as the direction an atom must move to make its position better with respect to the shape. This numerical requirement from the optimization method means we calculate and maintain gradient information in each box of the SE and use these gradients during modeling to move atoms. The actual calculation of the gradient is a finite-difference estimation based on values within the SE.

The modeling process moves atoms one by one, and often these atoms move far outside the initial constraining SE data. This means the SE constraint must provide some information both about atom fitness (objective-function values) and about the gradient outside the initial ranges of the shape data. To address this issue, the shape information in the SE is encoded in a multilevel, hierarchical set of SE data structures to expand the initial data into a format that spans a larger 3D space. Each level of the hierarchy is a separate, self-consistent SE, maintaining its own data and reporting its own objective function, gradient, and Hessian data.

Gradients

Each box in each SE in the constraint has a gradient vector associated with it. For the initial SE data (in SE₀), representing the lowest layer on the hierarchy, the gradients are all set to zero if the density number in the box is >0.125. This value represents the minimum density that can explain an atom resting within this box (it occurs if the atom is exactly resting in one corner of the box). All the other boxes in the SE each have a gradient vector calculated using

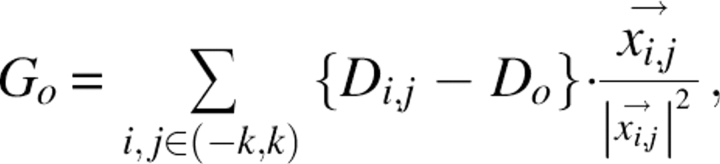where k is the gradient extent, typically set to one, representing the number of neighboring boxes in each direction to include in the gradient calculation. D _o is the density number in the current box, D_i,j is the density of the box offset (i,j) from the current box, and 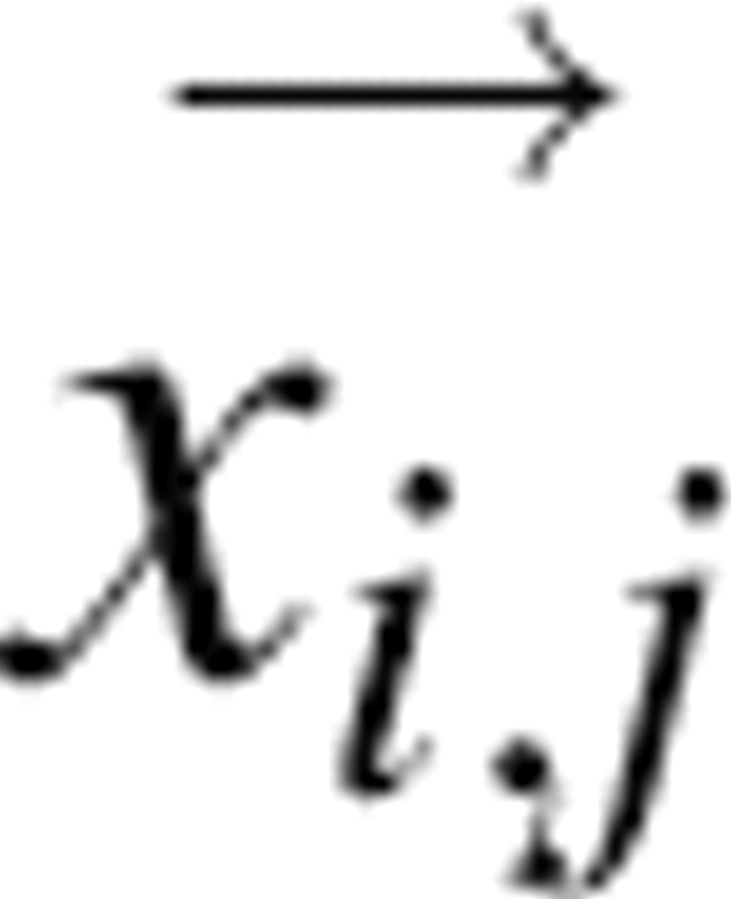is the vector from the center of the current box to the box offset by (i,j).

Multiple envelopes

Using a hierarchical set of SEs for the molecular shape has several advantages. Primarily, this provides a solution to having objective-function values and gradient information span the whole 3D range of atom positions. There are multiple different SE layers, each with a different box width. During the modeling process, shape information for any one particular atom position comes from a single SE layer. The smallest SE layer, SE₀, is 3.7 Å on each side of the cube. Successive SE_n are factors of two larger in each dimension, so SE₁ has boxes that are 7.4 Å on each side and SE₂ has boxes that are 14.8 Å on each side.

The algorithm selects the SE layer to apply on the basis of density numbers: The lowest SE in the hierarchy with a nonzero density value is used for any particular location. This means that if an atom is within the input shape data, then SE₀ is used. If SE₀ has 0 density at that position, then SE₁ is checked, and so on, until the lowest layer SE is found to have density greater than zero. In this way, each SE is maintained as a separate data structure that does not interact with any of the others. Figure 3 shows SE₁ and SE₂ for 1svr. The two SEs are presented with a similar size scale to emphasize the differences created by the expansion and blurring steps. The blue arrows represent gradient direction.

Figure 3.

(A) SE₁ for 1svr showing arrows for the gradient vectors. (B) SE₂ for 1svr on the same size scale as A, also showing gradient vectors with blue arrows.

For each step of the hierarchical SE data structure generation, one envelope (SE_n) is used to create the next higher layer envelope (SE_{n + 1}). Figure 4 shows a schematic of the process. Expansion means increasing the box width of the SE _{n + 1} to be larger than the box width of SE_n. To accomplish this, boxes in SE_n are grouped into contiguous sets of eight boxes meeting at a single corner. These eight boxes are merged to create a single box in SE _{n + 1}, and the maximum density value is applied to the new box. The result of this operation doubles the width of each box, and does not change the overall extent of the SE in space.

Figure 4.

Schematic diagram showing the expansion operation on a 2D grid. Expansion of SE₀ yields SE₁, and expansion of SE₁ yields SE₂. The widths of the boxes are twice as long in each dimension after expansion. The grids are shown to relative scale, so SE₁ contains the volume covered by SE₀ but extends it. Likewise, SE₂ extends the area covered by SE₁. This is all done to ensure that any atom in space has a nonzero derivative with respect to the objective function (which is blurred onto this expandable grid as illustrated in Fig. 5).

The blurring operation acts on SE _{n + 1} and changes the density numbers in each box. Figure 5 shows a schematic of the process. A 3D convolution kernel of magnitude three is marched over every box and contributes 1/27th of its density value to each of its 26 neighbors and to itself. Only these contributions are counted in the SE after blurring; the initial density values are discarded. The blurring operation does not change the width of the boxes, but it increases the extent of the SE _{n + 1} by two box widths in each direction. This increase comes from the neighbor contributions from boxes on the current edge into previously empty (zero-density number) boxes.

Figure 5.

Schematic diagram showing two successive blurring operations on a 2D grid. Density numbers in each grid point are “spread” to adjacent boxes in the SE during blurring.