Abstract
Protein aggregation is a commonly occurring problem in biology. Cells have evolved stress-response mechanisms to cope with problems posed by protein aggregation. Yet, these quality control mechanisms are overwhelmed by chronic aggregation-related stress and the resultant consequences of aggregation become toxic to cells. As a result, a variety of systemic and neurodegenerative diseases are associated with various aspects of protein aggregation and rational approaches to either inhibit aggregation or manipulate the pathways to aggregation might lead to an alleviation of disease phenotypes. To develop such approaches, one needs a rigorous and quantitative understanding of protein aggregation. Much work has been done in this area. However, several unanswered questions linger, and these pertain primarily to the actual mechanism of aggregation as well as to the types of intermolecular associations and intramolecular fluctuations realized at low protein concentrations. It has been suggested that the concepts underlying protein aggregation are similar to those used to describe the aggregation of synthetic polymers. Following this suggestion, the relevant concepts of polymer aggregation are introduced. The focus is on explaining the driving forces for polymer aggregation and how these driving forces vary with chain length and solution conditions. It is widely accepted that protein aggregation is a nucleation-dependent process. This view is based mainly on the presence of long times for the accumulation of aggregates and the elimination of these lag times with “seeds”. In this sense, protein aggregation is viewed as being analogous to the aggregation of colloidal particles. The theories for polymer aggregation reviewed in this work suggest an alternative mechanism for the origin of long lag times in protein aggregation. The proposed mechanism derives from the recognition that polymers have unique dynamics that distinguish them from other aggregation-prone systems such as colloidal particles.
Keywords: Polyglutamine, Protein aggregation, Solvent quality
Introduction
Protein aggregation is a process by which homogeneous protein solutions phase-separate into a dilute supernatant of soluble, isolated proteins and a protein-rich phase characterized by significant intermolecular interactions. A range of neurodegenerative and systemic diseases are associated with protein aggregation [1]. Proteins prone to aggregation and associated with disease tend to be intrinsically disordered and this disorder promotes non-specific self-association between these proteins [2, 3]. The overall rate of aggregation and final morphologies of aggregates depend on thermodynamic parameters, solution conditions, and protein concentration [4-6]. Additionally, aggregates tend to be rich in β-sheets and this is true irrespective of amino acid sequences of proteins that form aggregates [1].
Dobson has suggested that aggregation is a generic property of polypeptides [7]. Given this, how do typical proteins avoid this problem at finite concentrations in vivo? Rapid and efficient folding is one way to avoid aggregation [7-14]. Additionally, there are quality control mechanisms to process and / or clear unfolded, misfolded, and aggregated proteins [15-17]. Yet, these mechanisms can become overwhelmed when confronted with chronic aggregation-related stress [16, 18, 19]. Therefore, inhibition of protein aggregation is an important goal and to do so via rational means requires quantitative understanding of why and how different proteins form aggregates.
In this review, we focus on a description of the concepts borrowed directly from polymer physics [20-28] that provide the necessary framework for understanding the driving forces and mechanisms for protein aggregation. In our parlance, protein aggregation refers is all-encompassing because we do not distinguish between ordered versus amorphous aggregates. We highlight concepts that are likely to be helpful in developing new experimental and computational methods to probe relevant species along aggregation pathways. Proteins that are prone to aggregation are more like synthetic polymers because they tend to be intrinsically disordered [2]. Hence, as Dobson has noted, there must be unifying themes that underlie the self-assembly and aggregation of both intrinsically disordered proteins (IDPs) and synthetic polymers [7]. This logic provides the motivation for the discussion that follows.
The driving forces for homopolymer or heteropolymer aggregation are the balance between chain-chain and chain-solvent interactions and the magnitude and nature of spontaneous conformational fluctuations that promote intermolecular associations. The theories discussed below apply most directly to low-complexity IDP sequences that tend to be lacking in pronounced preferences for specific secondary and tertiary structures under physiological conditions. These sequences include homopolymers such as polyglutamine and block-copolymeric sequences such as exon 1 of huntingtin, the N-domain of the yeast prion protein Sup35, and α-synuclein. Inasmuch as sequences differ from each other mainly in the degree of disorder (quantified in terms of conformational fluctuations), the theories we describe are generalizable, albeit in nuanced forms, to describe the aggregation of generic, partially unfolded proteins. However, such generalizations are realizable if we incorporate consequences of the heteropolymeric nature of protein sequences into the proposed theoretical framework.
Solvent quality and conformational equilibria of polymers
Conformational and phase equilibria of both synthetic polymers and IDPs are governed by the balance of chain-solvent, chain-chain, and solvent-solvent interactions [20]. In dilute solutions, a single, linear, flexible polymer can be in one of two stable macrostates, viz., the swollen coil, favored in a good solvent, and the compact globular state, favored in a poor solvent. The preferred macrostate can be discerned from the scaling of quantities such as the average radius of gyration (Rg) with chain length N, which follows a power law of the form Rg = RoNν [29]. For chains in a good solvent Rg ~ N0.59 [20, 29]. The second virial coefficient B2 is a measure of the effective pairwise inter-residue interactions. In a good solvent, B2 > 0, i.e., the effective pairwise inter-residue interactions are repulsive because the chain-solvent contacts are preferred to chain-chain contacts. Conversely, intra-chain interactions are preferred to chain-solvent interactions in a poor solvent and Rg ~ N1/3. In this case, the B2 is negative because pairwise inter-residue interactions are net attractive. Consequently, compact, roughly spherical conformations dominate the ensemble [20, 29].
As solvent quality changes from good to poor or vice versa, polymers go through the theta point, (see Figure 1). At this point, the chain is an ideal Flory random-coil characterized by maximal conformational entropy [20, 29]. Consequently, Rg ~ N1/2 and B2 is zero because of exact cancellation between intra-chain steric repulsions and solvent-mediated attraction between chain residues. Coil-to-globule and globule-to-coil transitions are reversible and the sharpness of the transition depends on both chain flexibility and the magnitude of the third virial coefficient (C3) [30, 31]. The latter measures the magnitude of the effective three-body interactions within the chain [20]. As the value of C3 becomes small, the transition between the coil and globule states becomes sharper. The sharpness of this transition also increases as a function of increasing chain length, (see Figure 1).
Figure 1.
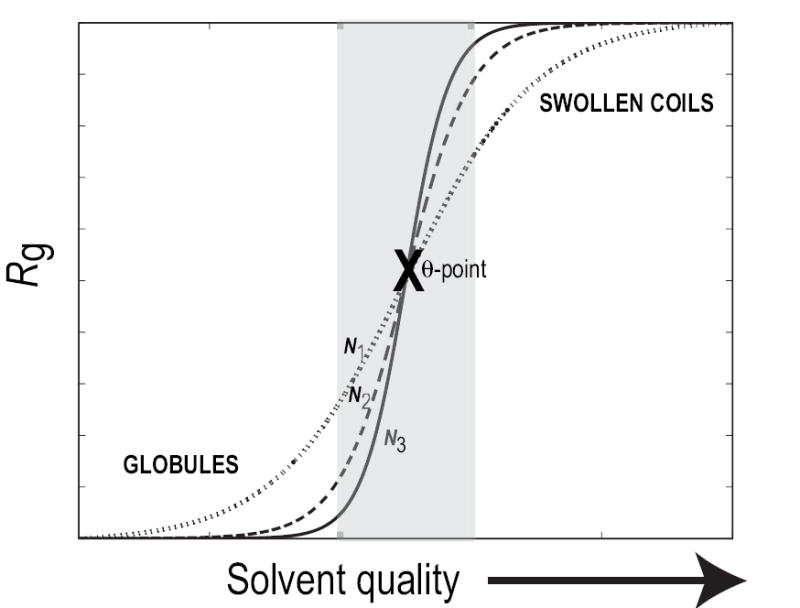
Sketch of the coil-to-globule transition for generic, flexible polymers as a function of solvent quality. The abscissa shows improving solvent quality, i.e., it goes from being poor to good. In a poor solvent, the chain prefers compact species, with small Rg, and in a good solvent the chain is swollen, with large Rg, to promote favorable contacts with the surrounding solvent. The transition between these two stable states is sharp, and the sharpness increases with chain length, N. In the schematic, N1 > N2 > N3 and the shaded region delineates the transition region. The midpoint of the transition, which is reliably identified for longer chains, is the theta point.
Distinction between aggregation of short peptides and full-length proteins
It is important to note that there are crucial differences between short peptides and full-length IDPs / proteins. Separation between length scales is an important hallmark of polymers [20, 32] and this leads to the idea of “blobs” as illustrated in Figure 2. A blob is the length scale beyond which the balance of chain-chain, chain-solvent, and solvent-solvent interactions is at least of order kBT. Here, T is temperature, and kB is Boltzmann’s constant. In a good solvent, the balance of interactions between blobs is net repulsive and the chain swells to accommodate favorable contacts with the surrounding solvent (Figure 2A). In a poor solvent, the balance of interactions between blobs is net-attractive, the chain compacts, and an ensemble of dense, roughly spherical conformations is preferred (Figure 2B).
Figure 2.
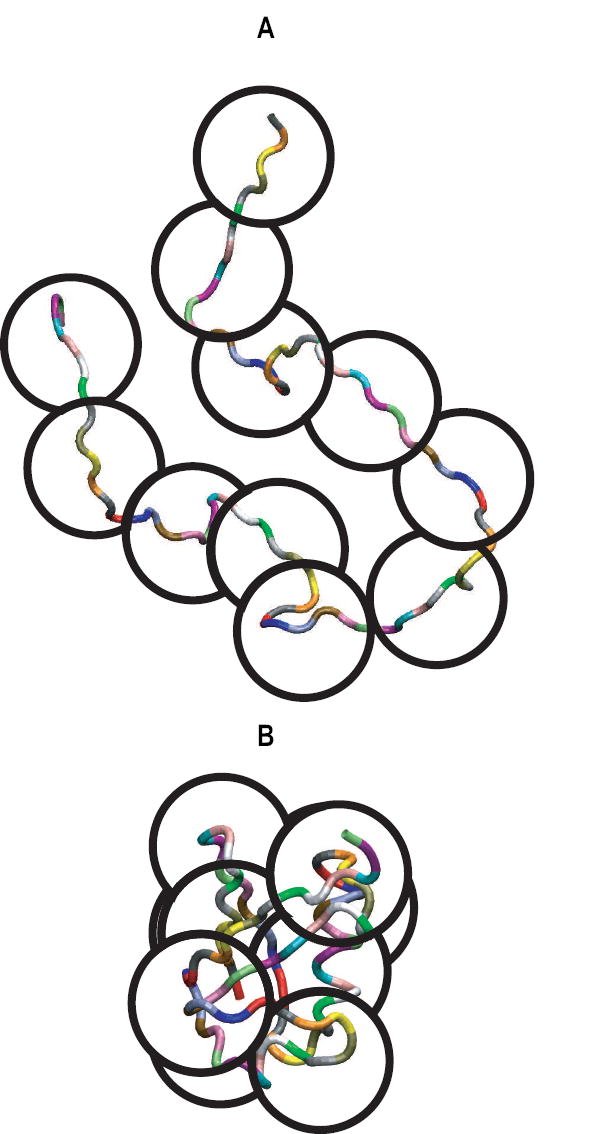
Illustration of the parsing of a full-length protein sequence into blob-sized segments. The figure also shows the mutual repulsion of these blobs in a good solvent (top) and the mutual attraction of blobs in a poor solvent (bottom). Here, the number of residues in a blob is taken to be 7 and this is based on previous analysis of correlation lengths within protein sequences [33].
In direct contrast, within a blob, the balance of interactions is smaller than kB T. If there are gT residues in a blob, then the radius of gyration of the blob scales as and this scaling holds irrespective of solvent quality [20]. Recently we estimated gT to be ca. 7 residues for a range of protein sequences [33]. Proteins that possess multiple segments of length gT can undergo dramatic changes in size and shape as a function of solvent quality and these conformational equilibria contribute to their phase behavior as a function of protein concentration. Conversely, conformational equilibria make minor contributions to phase behavior of peptides that are ca. gT residues in length. The driving forces and the mechanistic details of aggregation of blob-sized peptides are similar to those of small molecules. This distinction is important in light of several experimental and computational studies, which focus on the aggregation of short peptides [34-39]. Here, we discuss the physical principles of polymer aggregation that are relevant to proteins with multiple segments of length gT.
Thermodynamic phase diagram for polymer solutions
Figure 3 shows the sketch of a typical phase diagram for a polymer solution with an upper solution critical temperature [20]. Here, temperature is used to depict solvent quality. As T increases, solvent quality improves, and as T decreases, solvent quality becomes poor. An alternative way to label the ordinate is with the symbol χ, which refers to the Flory interaction parameter. χ quantifies the balance of chain-solvent, chain-chain, and solvent-solvent interactions. It is a multi-valued function of thermodynamic parameters and solution conditions and reflects the diverse ways in which solvent quality may be varied. For example, solvent quality for a protein solution varies by changing temperature, the hydrostatic pressure, concentrations of cosolutes such as osmolytes and denaturants, salt concentration, and pH, either individually or collectively [40, 41]. In the following discussion, we restrict our attention to a binary mixture and changes in solvent quality realized via changes in T alone. The abscissa, labeled ϕ in Figure 3, denotes the fraction of the volume in the mixture that is occupied by the polymer. ϕ, is bounded, 0 ≤ ϕ ≤ 1, and is used here as a short-hand notation for polymer concentration where ϕ → 0 denotes dilute polymer solutions and ϕ → 1 denotes a polymer melt.
Figure 3.
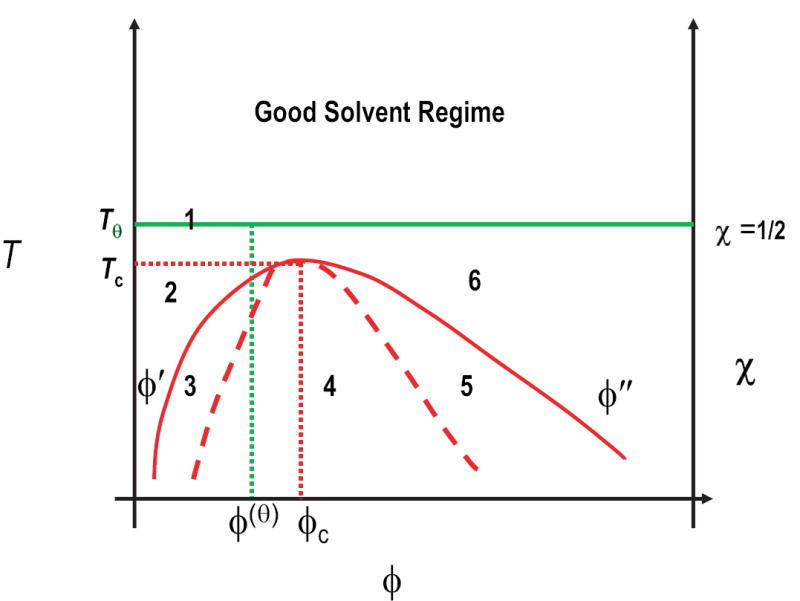
Typical thermodynamic phase diagram for polymer solutions. The ordinate denotes improving solvent quality expressed either as temperature or as Flory’s χ-parameter. At the theta-temperature, Tθ, and beyond (good solvent regime) no phase separation is observed. The overlap concentration at the theta point is marked by the green dotted line. For T < Tθ, a homogeneous mixed phase of polymer in solvent is formed in region 2, and of solvent in polymer in region 6. Conversely, phase separation is realized in regions 3, 4, and 5. The solid red curve denotes the binodal, while the dashed red curve denotes the spinodal. The dotted red lines denote the critical point (ϕc, Tc), while ϕ′ and ϕ″ indicate the polymer volume fractions on the coexistence curve (binodal) for a specific temperature, and hence define the miscibility gap.
In Figure 3, Tθ is the theta temperature. At T=Tθ, polymers seldom contact each other when ϕ is small because they are in a very dilute solution. Chains entangle with each other for polymer concentrations that are greater than the internal concentration within an individual polymer coil. This is known as the overlap concentration ϕ(θ), which decreases with increasing chain length. For T > Tθ, solvent quality becomes increasingly good, and the miscibility of polymers increases. Phase separation and aggregation are not realizable in good and theta solvents. Therefore, we do not discuss these regimes of the phase diagram.
As temperature decreases, solvent quality gets poorer, and for T < Tθ the polymer collapses to minimize the interface with the surrounding solvent. As polymer concentration increases in a poor solvent, the system can separate into distinct solvent-rich and polymer-rich phases. The solid red curve in Figure 3, known as the binodal, is the phase boundary or coexistence curve in a binary mixture. For T < Tθ, Figure 3 shows five distinct regimes. Region 2 is the dilute solution limit where polymers collapse to form isolated globules. For any combination of T and ϕ that places the system in one of regions 3, 4, or 5, the system separates into two distinct phases with concentrations ϕ′ and ϕ″, respectively. Here, ϕ′ is the overall composition for the dilute solution phase of isolated polymer globules and ϕ″ is the composition of the polymer aggregate.
Within the three regions encompassed by the binodal, the free energy of the phase-separated state G12(ϕ) is lower than the free energy of the homogeneous, mixed state, Gmix(ϕ). Hence, the system reaches a more stable state by forming two separate phases. Regions 3, 4, and 5 are distinguished based on the sign of . In regions 3 and 5, and in region 4, . This means that in region 3, even though the phase-separated state is thermodynamically favored, the mixed state is locally stable. Therefore, within region 3, phase separation requires the formation of a nucleus of the globally stable, phase-separated state, which has to form in the old phase. Phase separation progresses only if a large enough fluctuation causes the nucleus to grow past a critical size.
Region 4, bound by the dashed red curve known as the spinodal, is different because the mixed state is unstable, and the smallest perturbation in ϕ causes spontaneous phase separation via so-called spinodal decomposition, i.e., for combinations of T and ϕ that place the system in region 4, phase separation is a downhill process. Region 5 in Figure 3 lies between the high concentration arms of the spinodal and the binodal. In this region, there is a barrier for growing the soluble phase within the polymer-rich aggregate.
Of particular interest is the critical point marked as (ϕc, Tc) in Figure 3, which is the point where the spinodal and binodal meet. Theory and experiment show that critical concentration decreases with increasing chain length because ϕc ~ N−1/3[42]. Conversely, the critical temperature increases with chain length because , i.e., longer chains phase-separate at higher temperatures. The miscibility gap, which is measured as (ϕ″−ϕ′) varies as (Tc−T)1/3 [20] with the result that as chain length increases, Tc increases, and the concentration range over which phase separation (aggregation) is thermodynamically favored also increases.
Summary of the foregoing discussion
Phase separation / aggregation require that proteins be in poor solvents. In such a milieu, polymers form homogeneously mixed solutions of isolated globules under dilute solution conditions. As ϕ increases, we enter the two-phase regime where there is a clear driving force for phase separation.
In a poor solvent, the drive for phase separation increases with increasing chain length. This is borne out by the fact that, while the critical concentration ϕc decreases with increasing N, the critical temperature Tc increases. Similarly, the miscibility gap, (ϕ″−ϕ′) increases with N and this is a measure of the concentration range over which the phase-separated state is thermodynamically favored.
Protein solutions are prepared by specifying the initial value of ϕ and T. If the system finds itself in region 3, between the binodal and the spinodal, then the quench-depth is the “distance” of (ϕ, T) from the point (ϕb, T), located on the binodal. Smaller the quench-depth, the farther the system is from the spinodal, and vice versa. Pan et al. [43] have used neutron scattering and Monte Carlo simulations to study the initial stages of phase separation in a polymer blend. They find that the critical nucleus size decreases monotonically with increasing quench depth.
The magnitude of fluctuations in conformation and concentration dictates the overall rate of phase separation / aggregation. Fluctuations are largest at the critical point, (ϕc,Tc). Away from the critical point, between the binodal and spinodal, solvent quality decreases and fluctuations in conformation and concentration become smaller vis-à-vis the critical point.
Points 3 and 4 emphasize that the magnitudes of spontaneous fluctuations (in conformation and concentration) and nucleus size will vary with quench depth. This is important because standard analyses of kinetic data for protein aggregation [44-47] do not account for quench-depth dependent rates of conformational fluctuations and nucleus size. These effects are lumped into pre-equilibrium constants, and if these constants are set to be small, the implicit assumption is that rates of conformational fluctuations are considerably larger that bimolecular rate constants. However, as will be discussed later, this assumption ignores all of the nuances of polymer dynamics in poor solvents.
Within the envelope of the spinodal, region 4 of Figure 3, the homogeneously mixed state is unstable; there are no free energy barriers to overcome, and even the smallest fluctuations in ϕ or T will lead to downhill phase separation / aggregation. Within this region, the overall rate of aggregation is limited by two factors, namely intra- and inter-molecular chain diffusion. [48].
Characteristics of the dilute, solvent-rich, and concentrated, polymer-rich phases
We conclude our discussion of phase diagrams with a description of characteristics and energetics of the solvent-rich (region 2) and polymer-rich (regions 5 and 6) phases depicted in Figure 3. Typically, the soluble phase comprises of roughly spherical globules. Residues within a globule make favorable contacts with each other and residues on the surface of the globule make contacts with the surrounding solvent. Within a globule, pairs of spatially adjacent blob-sized segments realize attractive contacts. Conversely, a blob-sized segment that is exposed to solvent is deprived of the favorable intra-polymer interactions and the free energy penalty for exposing the blob to solvent leads to surface tension effect. The unfavorable surface free energy for a globule may be written as kBT(2χ-1)4/3N2/3 [20]. It therefore increases with increasing N and with increasing poorness of the solvent. As a result, globules stick to each other to minimize unfavorable interfaces with the surrounding solvent. For homopolymers, a single χ value characterizes the balance of chain-chain and chain-solvent interactions and χ varies with T. For a heteropolymer, there will be a distribution of χ values. Therefore, the strengths of attractive interactions between blobs and the energy penalty associated with the unfavorable interface between a blob and the solvent will depend on the sequence characteristics of blobs. This suggests that some regions within the sequence should be more prone to facilitating aggregation and this appears to be consistent with published findings.[49, 50]
Conformational heterogeneity provides an additional driving force for the association of globules. For IDPs and partially unfolded proteins, the conformational ensemble in a poor solvent will be heterogeneous because there is no unique way to partition residues in the chain between the interior and the surface of a globule and conformations of equivalent compactness have equivalent stability. This situation is especially true for homopolymeric sequences. Conformational heterogeneity of IDPs and partially unfolded proteins leads to increased exposure of solvophobic blobs. This in turn increases the likelihood of making either specific or non-specific intermolecular contacts as a way to reduce the exposure of solvophobic blobs. In direct contrast, for sequences that fold into well-defined three-dimensional structures a single family of self-similar globular conformations is preferred over all other globular conformations. Furthermore, the surface tension is nearly zero in folded globules [51] because the surface exposed residues are typically charged or polar.
Association of globules leads to the formation of large clusters [20]. With increasing cluster size, pairs of blobs between chains have access to attractive intermolecular, inter-blob interactions. Therefore, the driving force for confining the chain in globular geometries is counterbalanced and in the polymer-rich phase, each chain unravels to sample diverse conformations. As a direct consequence, theory and experiment have shown that in the polymer-rich phase, i.e., in the aggregate, the scaling of single chain radii of gyration with chain length takes the form Rg ~ N1/2 in contrast to the N1/3 scaling seen for individual chains in the soluble phase. [20, 48] The result is local ordering of chains to promote favorable inter-molecular interactions. However, unraveled chains can sample a larger ensemble of conformations and there should be significant long-range disorder in aggregates. The striking prediction is that individual polymers within an aggregate behave like classical Flory random coils [29] and therefore the aggregate is congruent with a polymer melt [20, 29].
The prediction that conformational entropy is maximized for individual chains in the context of aggregates is at odds with models in which aggregates are essentially linear assemblies, with individual proteins in β-sheet rich structures as repeating units. An aggregate is a mimic of a polymer melt if polypeptides that aggregate are very long homopolymers. For short, heteropolymeric sequences, some amount of water is trapped within the aggregate, and the aggregate deviates from a polymer melt. The degree of conformational disorder for individual chains within the aggregate should vary with the extent of solvent retention within the aggregate. If significant amount of solvent is entrapped, then the drive to minimize the interface with the solvent will also promote specific ordered associations between and within individual polypeptides. Conversely, as the solvent content within aggregates decreases, the ability of chains to diffuse freely around each other should increase, and in aggregates that are entirely devoid of solvent, conformational entropy is maximized and the aggregate is akin to a polymer melt. We are unaware of measurements of water content within protein aggregates, although Perutz et al. [52] suggested that polyglutamine aggregates are akin to water-filled nanotubes, a proposal that has been questioned by reanalysis of their data [53]. have been ewhich in turn should result in significant polymorphism in aggregate structures. The prediction of melt-like behavior for aggregates is strictly true for homopolymers or for heteropolymers that are orders of magnitude larger than typical proteins. Conversely, for shorter, amphipathic sequences such as proteins or homopolymers capped by charged residues, fibrilliar aggregates may be the dominant species. The predicted intrinsic conformational disorder of individual chains within an aggregate will still be manifest as heterogeneity in fibril morphology and structural parameters within fibrils. This polymorphism will vary with the way aggregates are prepared [54-56]. Kodali and Wetzel [57] have recently reviewed growing evidence for such polymorphism in fibrillar aggregates and these observations are consistent with the underlying polymer theory.
Applicability of polymer physics concepts to study of aggregation-prone IDPs
We have summarized several concepts from polymer theory that focus on characteristics of polymers in poor solvents. How well do the characteristics discussed above apply to IDPs that phase-separate and form intermolecular aggregates? The concepts discussed above are of particular relevance to polyglutamine aggregation. There are nine neurodegenerative diseases, including Huntington’s disease, which are associated with expanded polyglutamine domains in different proteins and the deposition of neuronal intranuclear inclusions (NIIs) rich in polyglutamine aggregates [58]. In polyglutamine disorders, ages-of-onset of disease show nonlinear, inverse correlation with the length of polyglutamine expansions. Products of proteolysis are rich in polyglutamine and their aggregation appears to be essential for toxicity because inhibiting polyglutamine aggregation reduces neurodegeneration [59].
To be competent for aggregation, it must be true that aqueous milieus are poor solvents for polyglutamine or any other aggregation-prone system. The poorness of solvent can be established through quantitative studies of chain size in dilute solutions. Recent work of Lee et al. on α-synuclein [60] and Mukhopadhyay et al. [61] on the N-domain of Sup35 show that these molecules prefer an ensemble of collapsed states in aqueous milieus and this explains their propensity to phase-separate as concentration increases. We measured the scaling of hydrodynamic sizes for monomeric polyglutamine in aqueous solution at ca. 25°C and showed that size scales as N1/3 with chain length [62]. Interestingly, while the free energy of hydration for primary and secondary amides is highly favorable [63], we found that even short polyglutamine chains (ca. N=15) prefer collapsed structures that minimize interactions with aqueous solvents. Vitalis et al.[64] analyzed results from molecular simulations on a 20-mer of polyglutamine and concluded that the drive of the chain to solvate itself through favorable backbone-backbone, backbone-sidechain, and sidechain-sidechain associations leads to the preference for collapsed structures in dilute solutions. Experiments have also shown that the tendency to form intermolecular aggregates increases with polyglutamine length. Wetzel and coworkers have carried out a series of experiments based on a variety of spectroscopic and other probes to quantify the overall rate of aggregation as a function of chain length and concentration [45, 54, 65-67]. Their conclusions are consistent, at least qualitatively, with the expectations from polymer theory as discussed above and demonstrated in Figure 3.
Unresolved issues in the study of aggregation-prone IDPs
Despite the impressive progress made by Wetzel [45, 54, 65-67] and others [68-72] in the area of polyglutamine aggregation, there are significant gaps in our knowledge because not much is known about intermolecular associations and intramolecular conformational fluctuations that occur at very low protein concentrations (nM - μM). This knowledge is of utmost importance to understand the phenomenon of polyglutamine aggregation in vivo. In other words, we do not have the requisite information needed to construct a detailed phase diagram for polyglutamine or any other aggregation-prone IDP sequence. The challenges are multi-fold: Details of polymer phase diagrams are typically uncovered through a combination of probes based on osmometry, X-ray / neutron scattering, as well static and dynamic laser light scattering [20]. Of particular importance is the low concentration arm of the binodal. With synthetic polymers, one can study polymers that are very long (N is ca. 105 or longer), and this allows one to monitor reversible and irreversible associations that occur at very low concentrations [73-77]. These probes become difficult to use at low concentrations for studying polypeptides of biologically relevant lengths. Consequently, we have very little information regarding the dilute solution arm of the binodal for polyglutamine and other aggregation-prone IDPs. An alternative approach would be to use molecular and mesoscopic simulations to predict the desired phase diagram [78]. This requires simulations of multiple chains to capture the balance between intra- and intermolecular associations and such calculations are challenging because of the computational expense involved. Coarse-graining schemes are useful [79], but here one has to be careful to keep from smearing out the essential details that distinguish one aggregation prone sequence from another.
Through methodological advances on both the computational and experimental fronts, we are in the process of advancing both molecular simulations and fluorescence correlation spectroscopy (FCS) based methods to interrogate the essential details of the phase diagrams for polyglutamine as a function of chain length and other aggregation-prone proteins. This is work in progress and details will be forthcoming in the near future. The remainder of this review will highlight predictions from a quantitative theory for polymer aggregation developed by Raos and Allegra and this will set the stage for future work.
Theoretical predictions for mechanism of polymer aggregation in poor solvents
Raos and Allegra [21-23, 80-82] have developed a “Gaussian cluster” model to make quantitative predictions regarding the association and aggregation of homopolymers in poor solvents. The main predictions of their theory are as follows:
Isolated polymeric globules can associate to form macromolecular clusters. The favorable free energy of intermolecular association and the temperature at which stable clusters form should increase with increasing chain length.
Within a cluster, each chain expands slightly beyond the sizes of isolated globules to promote favorable intermolecular association. The degree of expansion depends on chain length, the quench-depth, and cluster size, and increases with all three parameters.
For clusters of ca. 60 molecules, Rg for individual molecules scales as N1/3 and for clusters larger than 60 Rg ~ N1/2, although the transition between the two regimes is not necessarily sharp.
Most strikingly, Raos and Allegra predict that the binodal and spinodal for a long polymer should essentially coincide with each other. Therefore, they suggest that the nucleus is “either a single chain or a portion of a single chain” [22]. The more accurate interpretation is that there is no pronounced barrier for intermolecular associations in homopolymeric systems. Instead, clusters of macromolecules should form readily, and as the cluster become large enough, the interfacial tension per molecule in the cluster decreases, thus facilitating the transition into the polymer-rich phase.
Implications of theoretical predictions for kinetics of aggregation-prone IDPs
The major implications from the theory of Raos and Allegra [22] merit further discussion in the context of protein aggregation. Their model predicts that macromolecular clusters should form as either thermodynamic or kinetic intermediates. Several authors have presented evidence for such clusters or oligomers for a variety of aggregation-prone IDPs [83-92]. Sizes of oligomers vary from one system to another and depend on the method of detection and the solution conditions. Additionally, the model of Raos and Allegra predicts that there is no specific conformational pre-requisite for cluster formation, i.e., clusters are likely to be realized via non-specific associations. For proteins, the implication is that clusters can form without regard to β-sheet content within each chain.
The second prediction of Raos and Allegra appears to be at odds with findings in the amyloid literature, which suggest that the mechanism of aggregation proceeds through the formation of a structured nucleus, which presents a single, well-defined barrier [45]. It is noteworthy that Krishnan and Lindquist [93] have challenged this view in their recent work on the aggregation of a yeast prion. The conclusion that aggregation is limited by homogeneous nucleation is made mainly on the presence of a discernible and long lag time for the growth of the large, insoluble, β-sheet-rich aggregates and the elimination of these lag times with seeding. Both features can be reconciled by the alternative theory of Raos and Allegra.
Long lag times could also be due to slow chain dynamics in poor solvents [48]. In an intrinsically disordered system, there is a thermodynamic driving force for conversion between conformationally distinct globules of equivalent compactness. In recent work, we analyzed these dynamics in monomeric polyglutamine [64]. We found that the dynamics of converting between distinct conformations can be fit to a stretched exponential, which is the hallmark of glassy systems with a broad distribution of heterogeneous barriers that primarily hinder chain diffusion irrespective of chain conformation and oligomer structure. These types of barriers are different from structured nuclei that are the hallmarks of theories used to describe protein aggregation [44, 46, 47].
Once substantial phase separation occurs, the slow chain dynamics do not contribute significantly to the kinetic behavior of the system. This is the regime most readily monitored in experiments, where one follows the growth of the aggregate. During this kinetic phase, chains readily sequester into the rapidly growing aggregate; Chain dynamics will only control rearrangement within the insoluble phase, and most time-resolved experiments are blind to the details of dynamics in entangled polymer melts. The combination of slow polymer dynamics during cluster formation, rapid sequestration of chains into an aggregate past the point of substantial phase separation and the inability of most experiments to monitor chain dynamics in the polymer melt provide a composite, albeit alternative explanation for observation of long lag times and the elimination of these lag times via “seeding”.
Tests of the predictions made by Raos and Allegra
Wu and coworkers [73]have used a combination of static and dynamic laser light scattering as well as ultra-sensitive differential scanning calorimetry to study both coil-to-globule transitions and intermolecular associations in two types of systems. These are poly(N-isopropylacrylamide), which is a homopolymer that is analogous to polyglutamine, and poly(N-isopropylacrylamide-co-potassium acrylate) as well poly(N-isopropylacrylamide-co-sodium acrylate), which are copolymers with ionic groups. Zhang and Wu [73] have recently reviewed their main findings, which appear to be in general agreement with the predictions of Raos and Allegra. In the homopolymeric systems, clusters, which they refer to as mesoglobules, are kinetic intermediates. Conversely, in the copolymer studies, the mesoglobules appear to be thermodynamically stable, equilibrium intermediates characterized by micellar architectures, with charged groups situated on the surface of clusters. Figure 4 depicts a scheme that summarizes the predictions of Raos and Allegra and the experimental findings of Wu and coworkers.
Figure 4.
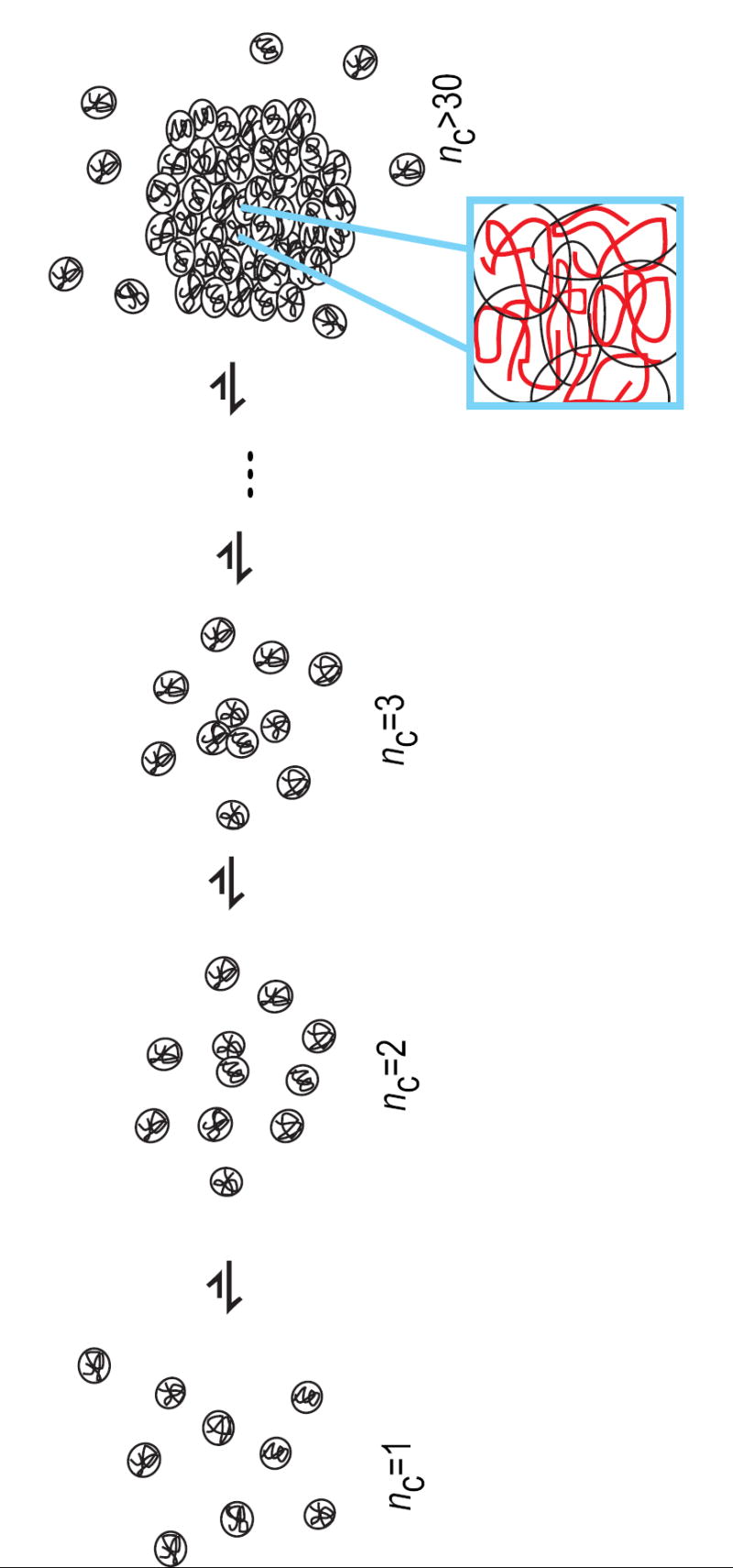
Sketch of the process by which clusters of globules are predicted to form during the lag phase in protein aggregation. Each species in the schematic is labeled by the size of the largest cluster within the species, nc. The conformational ensemble for the monomer is heterogeneous as is the ensemble of oligomer species that forms via intermolecular associations. Additionally, there will be multiple routes to cluster formation and the clusters could either be kinetic or equilibrium intermediates. For isolated globules and for small clusters, individual chains experience finite surface tension due to unfavorable interfaces with the surrounding solvent. Consequently, conformational conversion in smaller clusters will be slow. The stabilities of clusters, the rates for conformational conversion, and the surface tension per chain will vary with chain length, protein sequence, protein concentration, and solution conditions. When the cluster size grows, individual chains become sequestered from unfavorable interfaces with solvent and average surface tension per molecule becomes negligible. This in turn promotes the unraveling and entanglement of individual chains. Ordered aggregation follows rapidly because of chain entanglement. The key point is that, there are no prerequisites for specific conformations of individual chains or cluster sizes for formation and growth of clusters of chains in poor solvents.
The work of Wu and coworkers points the way to several ingenious analyses of laser light scattering data that reveal important dynamical and equilibrium properties of the coil-to-globule transition and of intermolecular associations. Some of these analyses can be adapted to FCS studies of aggregation-prone IDPs. Additionally, as Wu and coworkers have demonstrated, the use of scattering-based techniques [73], including X-ray / neutron scattering and light scattering, combined with theory and simulation should be very useful in the study of aggregation-prone IDPs. Several groups in the amyloid field are already pursuing these types of multi-faceted approaches [5, 84, 94-107]. However, we remain blind to interactions and conformational fluctuations that occur at low concentrations. This is the most serious challenge to overcome because it provides a direct way to connect in vitro aggregation studies to the situation in vivo, where protein concentrations are seldom in the micromolar ranges, although macromolecular crowding might modulate effective concentrations of proteins.
Conclusions
We have reviewed a set of polymer physics concepts that are relevant for obtaining detailed, quantitative understanding of the driving forces for and the mechanism of protein aggregation. The main messages are three-fold: First, it is important to pursue methods of investigation that will yield complete phase diagrams for aggregation-prone proteins. Of particular importance is the low concentration arm of the binodal. Secondly, polymer theories suggest alternative explanations for the source of long lag times that are associated with protein aggregation. Specifically, the proposed coincidence of the binodal and spinodal suggest that the process of phase separation / aggregation is limited by slow chain dynamics as opposed to a well-defined barrier with a structured nucleus. Investigating intermolecular associations in the low concentration regime using novel experiments and simulations provides one way to assess the validity of theoretical predictions. Finally, the fact that Rg of individual polymers in an aggregate should scale as N1/2 with chain length is interesting because it suggests that conformational entropy is maximized in this state. While this might seem counterintuitive at first glance, it provides a rationalization for the observed polymorphisms in the structures of aggregates. Additionally, this theoretical result provides a strategy for modeling the conformations that individual polypeptides adopt in the context of aggregates.
Acknowledgments
We are grateful to Carl Frieden for helpful discussions. This work was supported by the National Institutes of Health Grant RO1 NS056114 to RVP. SLC is supported by a pre-doctoral fellowship from the National Science Foundation.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Chiti F, Dobson CM. Annual Review Of Biochemistry. 2006;75:333–366. doi: 10.1146/annurev.biochem.75.101304.123901. [DOI] [PubMed] [Google Scholar]
- 2.Uversky VN, Fink AL. Biochimica Et Biophysica Acta-Proteins And Proteomics. 2004;1698:131–153. doi: 10.1016/j.bbapap.2003.12.008. [DOI] [PubMed] [Google Scholar]
- 3.Linding R, Schymkowitz J, Rousseau F, Diella F, Serrano L. Journal Of Molecular Biology. 2004;342:345–353. doi: 10.1016/j.jmb.2004.06.088. [DOI] [PubMed] [Google Scholar]
- 4.Kim YS, Randolph TW, Seefeldt MB, Carpenter JF. Amyloid, Prions, And Other Protein Aggregates, Pt C. 2006:237–253. doi: 10.1016/S0076-6879(06)13013-X. [DOI] [PubMed] [Google Scholar]
- 5.Wetzel R. Accounts Of Chemical Research. 2006;39:671–679. doi: 10.1021/ar050069h. [DOI] [PubMed] [Google Scholar]
- 6.Edwin NJ, Bantchev GB, Russo PS, Hammer RP, McCarley RL. New Polymeric Materials. 2005;916:106–118. [Google Scholar]
- 7.Dobson CM. Seminars In Cell And Developmental Biology. 2004;15:3–16. doi: 10.1016/j.semcdb.2003.12.008. [DOI] [PubMed] [Google Scholar]
- 8.Thirumalai D, Klimov DK, Dima RI. Current Opinion In Structural Biology. 2003;13:146–159. doi: 10.1016/s0959-440x(03)00032-0. [DOI] [PubMed] [Google Scholar]
- 9.Onuchic JN, Nymeyer H, Garcia AE, Chahine J, Socci ND. Advances In Protein Chemistry. 2000;53:87–152. doi: 10.1016/s0065-3233(00)53003-4. [DOI] [PubMed] [Google Scholar]
- 10.Onuchic JN, Luthey-Schulten Z, Wolynes PG. Annual Review Of Physical Chemistry. 1997;48:545–600. doi: 10.1146/annurev.physchem.48.1.545. [DOI] [PubMed] [Google Scholar]
- 11.Jager M, Zhang Y, Bieschke J, Nguyen H, Dendle M, Bowman ME, Noel JP, Gruebele M, Kelly JW. Proceedings Of The National Academy Of Sciences Of The United States Of America. 2006;103:10648–10653. doi: 10.1073/pnas.0600511103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Fersht AR, Daggett V. Cell. 2002;108:573–582. doi: 10.1016/s0092-8674(02)00620-7. [DOI] [PubMed] [Google Scholar]
- 13.Haacke A, Broadley SA, Boteva R, Tzvetkov N, Hartl FU, Breuer P. Human Molecular Genetics. 2006;15:555–568. doi: 10.1093/hmg/ddi472. [DOI] [PubMed] [Google Scholar]
- 14.Sakahira H, Breuer P, Hayer-Hartl MK, Hartl FU. Proceedings Of The National Academy Of Sciences Of The United States Of America. 2002;99:16412–16418. doi: 10.1073/pnas.182426899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Huff ME, Balch WE, Kelly JW. Current Opinion In Structural Biology. 2003;13:674–682. doi: 10.1016/j.sbi.2003.10.010. [DOI] [PubMed] [Google Scholar]
- 16.Westerheide SD, Morimoto RI. Journal Of Biological Chemistry. 2005;280:33097–33100. doi: 10.1074/jbc.R500010200. [DOI] [PubMed] [Google Scholar]
- 17.McClellan AJ, Tam S, Kaganovich D, Frydman J. Nature Cell Biology. 2005;7:736–741. doi: 10.1038/ncb0805-736. [DOI] [PubMed] [Google Scholar]
- 18.Riley BE, Iwata A, Kopito RR. Autophagy. 2006;2:362–362. [Google Scholar]
- 19.Kerner MJ, Naylor DJ, Ishihama Y, Maier T, Chang HC, Stines AP, Georgopoulos C, Frishman D, Hayer-Hartl M, Mann M, Hartl FU. Cell. 2005;122:209–220. doi: 10.1016/j.cell.2005.05.028. [DOI] [PubMed] [Google Scholar]
- 20.Rubinstein M, Colby RH. Polymer Physics. Oxford University Press; Oxford: 2003. [Google Scholar]
- 21.Ganazzoli F, Raos G, Allegra G. Macromolecular Theory and Simulations. 1999;8:65–84. [Google Scholar]
- 22.Raos G, Allegra G. Journal of Chemical Physics. 1997;107:6479–6490. [Google Scholar]
- 23.Raos G, Allegra G. Journal of Chemical Physics. 1996;104:1626–1645. [Google Scholar]
- 24.Grosberg AY, Kuznetsov DV. Macromolecules. 1993;26:4249–4251. [Google Scholar]
- 25.Grosberg AY, Kuznetsov DV. Macromolecules. 1992;25:1970–1979. [Google Scholar]
- 26.Grosberg AY, Kuznetsov DV. Macromolecules. 1992;25:1991–1995. [Google Scholar]
- 27.Grosberg AY, Kuznetsov DV. Macromolecules. 1992;25:1996–2003. [Google Scholar]
- 28.Grosberg AY, Kuznetsov DV. Macromolecules. 1992;25:1980–1990. [Google Scholar]
- 29.Flory PJ. Principles of Polymer Chemistry. Cornell University Press; Ithaca, NY: 1953. [Google Scholar]
- 30.Steinhauser MO. Journal Of Chemical Physics. 2005;122(Art No 094901) doi: 10.1063/1.1846651. [DOI] [PubMed] [Google Scholar]
- 31.Imbert JB, Lesne A, Victor JM. Physical Review E. 1997;56:5630–5647. [Google Scholar]
- 32.Grosberg AY, Khokhlov AR. Statistical Physics of Macromolecules. AIP Press; New York: 1994. [Google Scholar]
- 33.Tran HT, Pappu RV. Biophysical Journal. 2006;91:1868–1886. doi: 10.1529/biophysj.106.086264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Nelson R, Sawaya MR, Balbirnie M, Madsen AO, Riekel C, Grothe R, Eisenberg D. Nature. 2005;435:773–778. doi: 10.1038/nature03680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Sawaya MR, Sambashivan S, Nelson R, Ivanova MI, Sievers SA, Apostol MI, Thompson MJ, Balbirnie M, Wiltzius JJW, McFarlane HT, Madsen AO, Riekel C, Eisenberg D. Nature. 2007;447:453–457. doi: 10.1038/nature05695. [DOI] [PubMed] [Google Scholar]
- 36.Sambashivan S, Liu YS, Sawaya MR, Gingery M, Eisenberg D. Nature. 2005;437:266–269. doi: 10.1038/nature03916. [DOI] [PubMed] [Google Scholar]
- 37.Pellarin R, Caflisch A. Journal Of Molecular Biology. 2006;360:882–892. doi: 10.1016/j.jmb.2006.05.033. [DOI] [PubMed] [Google Scholar]
- 38.Cecchini M, Curcio R, Pappalardo M, Melki R, Caflisch A. Journal Of Molecular Biology. 2006;357:1306–1321. doi: 10.1016/j.jmb.2006.01.009. [DOI] [PubMed] [Google Scholar]
- 39.Nguyen PH, Li MS, Stock G, Straub JE, Thirumalai D. Proceedings Of The National Academy Of Sciences Of The United States Of America. 2007;104:111–116. doi: 10.1073/pnas.0607440104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Bondos SE. Current Analytical Chemistry. 2006;2:157–170. [Google Scholar]
- 41.Vernaglia BA, Huang J, Clark ED. Biomacromolecules. 2004;5:1362–1370. doi: 10.1021/bm0498979. [DOI] [PubMed] [Google Scholar]
- 42.Muthukumar M. Journal of Chemical Physics. 1986;85:4722–4728. [Google Scholar]
- 43.Pan AC, Rappl TJ, Chandler D, Balsara NP. Journal Of Physical Chemistry B. 2006;110:3692–3696. doi: 10.1021/jp055239m. [DOI] [PubMed] [Google Scholar]
- 44.Ferrone F. Amyloid, Prions, And Other Protein Aggregates. 1999:256–274. [Google Scholar]
- 45.Chen SM, Ferrone FA, Wetzel R. Proceedings of the National Academy of Sciences of the United States of America. 2002;99:11884–11889. doi: 10.1073/pnas.182276099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Ferrone FA. Amyloid, Prions, And Other Protein Aggregates, Pt B. 2006:285–299. [Google Scholar]
- 47.Powers ET, Powers DL. Biophysical Journal. 2006;91:122–132. doi: 10.1529/biophysj.105.073767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Chuang J, Grosberg AY, Tanaka T. Journal of Chemical Physics. 2000;112:6434–6442. [Google Scholar]
- 49.Tartaglia GG, Cavalli A, Pellarin R, Caflisch A. Protein Science. 2005;14:2723–2734. doi: 10.1110/ps.051471205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Pawar AP, DuBay KF, Zurdo J, Chiti F, Vendruscolo M, Dobson CM. Journal Of Molecular Biology. 2005;350:379–392. doi: 10.1016/j.jmb.2005.04.016. [DOI] [PubMed] [Google Scholar]
- 51.Wagoner JA, Baker NA. Proceedings Of The National Academy Of Sciences Of The United States Of America. 2006;103:8331–8336. doi: 10.1073/pnas.0600118103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Perutz MF, Finch JT, Berriman J, Lesk A. Proceedings of the National Academy of Sciences of the United States of America. 2002;99:5591–5595. doi: 10.1073/pnas.042681399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Sikorski P, Atkins E. Biomacromolecules. 2005;6:425–432. doi: 10.1021/bm0494388. [DOI] [PubMed] [Google Scholar]
- 54.Chen SM, Berthelier V, Hamilton JB, O’Nuallain B, Wetzel R. Biochemistry. 2002;41:7391–7399. doi: 10.1021/bi011772q. [DOI] [PubMed] [Google Scholar]
- 55.Tycko R. Quarterly Reviews Of Biophysics. 2006;39:1–55. doi: 10.1017/S0033583506004173. [DOI] [PubMed] [Google Scholar]
- 56.Paravastu AK, Petkova AT, Tycko R. Biophysical Journal. 2006;90:4618–4629. doi: 10.1529/biophysj.105.076927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Kodali R, Wetzel R. Current Opinion In Structural Biology. 2007;17:48–57. doi: 10.1016/j.sbi.2007.01.007. [DOI] [PubMed] [Google Scholar]
- 58.Bates GP. Nature Reviews Genetics. 2005;6:766–773. doi: 10.1038/nrg1686. [DOI] [PubMed] [Google Scholar]
- 59.Walsh R, Storey E, Stefani D, Kelly L, Turnbull V. Neurotoxicity Research. 2005;7:43–57. doi: 10.1007/BF03033775. [DOI] [PubMed] [Google Scholar]
- 60.Lee JC, Lai BT, Kozak JJ, Gray HB, Winkler JR. Journal Of Physical Chemistry B. 2007;111:2107–2112. doi: 10.1021/jp068604y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Mukhopadhyay S, Krishnan R, Lemke EA, Lindquist S, Deniz AA. Proceedings Of The National Academy Of Sciences Of The United States Of America. 2007;104:2649–2654. doi: 10.1073/pnas.0611503104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Crick SL, Jayaraman M, Frieden C, Wetzel R, Pappu RV. Proceedings Of The National Academy Of Sciences Of The United States Of America. 2006;103:16764–16769. doi: 10.1073/pnas.0608175103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Wolfenden R. Biochemistry. 1978;17:201–204. doi: 10.1021/bi00594a030. [DOI] [PubMed] [Google Scholar]
- 64.Vitalis A, Wang X, Pappu RV. Biophys J. 2007 doi: 10.1529/biophysj.107.110080. biophysj.107.110080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Bhattacharyya AM, Thakur AK, Wetzel R. Proceedings of the National Academy of Sciences of the United States of America. 2005;102:15400–15405. doi: 10.1073/pnas.0501651102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Thakur AK, Wetzel R. Proceedings of the National Academy of Sciences of the United States of America. 2002;99:17014–17019. doi: 10.1073/pnas.252523899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Chen S, Berthelier V, Yang W, Wetzel R. Journal of Molecular Biology. 2001;311:173–182. doi: 10.1006/jmbi.2001.4850. [DOI] [PubMed] [Google Scholar]
- 68.Muchowski PJ, Schaffar G, Sittler A, Wanker EE, Hayer-Hartl MK, Hartl FU. Proceedings Of The National Academy Of Sciences Of The United States Of America. 2000;97:7841–7846. doi: 10.1073/pnas.140202897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Zhang XQ, Smith DL, Merlin AB, Engemann S, Russel DE, Roark M, Washington SL, Maxwell MM, Marsh JL, Thompson LM, Wanker EE, Young AB, Housman DE, Bates GP, Sherman MY, Kazantsev AG. Proceedings of the National Academy of Sciences of the United States of America. 2005;102:892–897. doi: 10.1073/pnas.0408936102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Scherzinger E, Lurz R, Turmaine M, Mangiarini L, Hollenbach B, Hasenbank R, Bates GP, Davies SW, Lehrach H, Wanker EE. Cell. 1997;90:549–558. doi: 10.1016/s0092-8674(00)80514-0. [DOI] [PubMed] [Google Scholar]
- 71.Ross CA, Poirier MA, Wanker EE, Amzel M. Proceedings of the National Academy of Sciences of the United States of America. 2003;100:1–3. doi: 10.1073/pnas.0237018100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Scherzinger E, Sittler A, Schweiger K, Heiser V, Lurz R, Hasenbank R, Bates GP, Lehrach H, Wanker EE. Proceedings of the National Academy of Sciences of the United States of America. 1999;96:4604–4609. doi: 10.1073/pnas.96.8.4604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Zhang G, Wu C. In: Advances in Polymer Science: Conformation-Dependent Design of Sequences in Copolymers I. Khokhlov AR, editor. Springer; Berlin/Heidelberg: 2006. pp. 101–179. [Google Scholar]
- 74.Yuan G, Wang X, Han CC, Wu C. Macromolecules. 2006;39:3642–3647. [Google Scholar]
- 75.Luo S, Xu J, Zhu Z, Wu C, Liu S. Journal of Physical Chemistry B. 2006;110:9132–9139. doi: 10.1021/jp061055b. [DOI] [PubMed] [Google Scholar]
- 76.Xu J, Zhu Z, Luo S, Wu C, Liu S. Physical Review Letters. 2006;96(Art No 027802) doi: 10.1103/PhysRevLett.96.027802. [DOI] [PubMed] [Google Scholar]
- 77.Chen H, Zhang Q, Li J, Ding Y, Zhang G, Wu C. Macromolecules. 2005;38:8045–8050. [Google Scholar]
- 78.Dima RI, Thirumalai D. Protein Science. 2002;11:1036–1049. doi: 10.1110/ps.4220102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Nguyen HD, Hall CK. Journal of the American Chemical Society. 2006;128:1890–1901. doi: 10.1021/ja0539140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Raos G, Allegra G. Macromolecules. 1996;29:8565–8657. [Google Scholar]
- 81.Raos G, Allegra G. Macromolecules. 1996;29:6663–6670. [Google Scholar]
- 82.Allegra G, Ganazzoli F, Raos G. Trends In Polymer Science. 1996;4:293–298. [Google Scholar]
- 83.Meier JJ, Meier Rx, Lin CY, Gurlo T, Haataja L, Jayasinghe S, Langen R, Glabe CG, Butler PC. American Journal Of Physiology-Endocrinology and Metabolism. 2006;291:E1317–E1324. doi: 10.1152/ajpendo.00082.2006. [DOI] [PubMed] [Google Scholar]
- 84.Smith AM, Jahn TR, Ashcroft AE, Radford SE. Journal Of Molecular Biology. 2006;364:9–19. doi: 10.1016/j.jmb.2006.08.081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Kayed R, Glabe CG. Amyloid, Prions, And Other Protein Aggregates, Pt C. 2006:326–344. [Google Scholar]
- 86.Glabe CG, Kayed R. Neurology. 2006;66:S74–S78. doi: 10.1212/01.wnl.0000192103.24796.42. [DOI] [PubMed] [Google Scholar]
- 87.Yang FS, Lim GP, Begum AN, Ubeda OJ, Simmons MR, Ambegaokar SS, Chen PP, Kayed R, Glabe CG, Frautschy SA, Cole GM. Journal Of Biological Chemistry. 2005;280:5892–5901. doi: 10.1074/jbc.M404751200. [DOI] [PubMed] [Google Scholar]
- 88.Glabe C, Kayed R, Sokolov Y, Hall J. Neurobiology Of Aging. 2004;25:S75–S76. [Google Scholar]
- 89.Wacker JL, Zareie MH, Fong H, Sarikaya M, Muchowski PJ. Nature Structural & Molecular Biology. 2004;11:1215–1222. doi: 10.1038/nsmb860. [DOI] [PubMed] [Google Scholar]
- 90.Kayed R, Head E, Thompson JL, McIntire TM, Milton SC, Cotman CW, Glabe CG. Science. 2003;300:486–489. doi: 10.1126/science.1079469. [DOI] [PubMed] [Google Scholar]
- 91.Walsh DM, Klyubin I, Fadeeva JV, Cullen WK, Anwyl R, Wolfe MS, Rowan MJ, Selkoe DJ. Nature. 2002;416:535–539. doi: 10.1038/416535a. [DOI] [PubMed] [Google Scholar]
- 92.Nettleton EJ, Tito P, Sunde M, Bouchard M, Dobson CM, Robinson CV. Biophysical Journal. 2000;79:1053–1065. doi: 10.1016/S0006-3495(00)76359-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Krishnan R, Lindquist SL. Nature. 2005;435:765–772. doi: 10.1038/nature03679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Dumoulin M, Kumita JR, Dobson CM. Accounts Of Chemical Research. 2006;39:603–610. doi: 10.1021/ar050070g. [DOI] [PubMed] [Google Scholar]
- 95.Fink AL. Accounts Of Chemical Research. 2006;39:628–634. doi: 10.1021/ar050073t. [DOI] [PubMed] [Google Scholar]
- 96.Bieschke J, Zhang QH, Bosco DA, Lerner RA, Powers ET, Wentworth P, Kelly JW. Accounts Of Chemical Research. 2006;39:611–619. doi: 10.1021/ar0500766. [DOI] [PubMed] [Google Scholar]
- 97.Johnson SM, Wiseman RL, Sekijima Y, Green NS, Adamski-Werner SL, Kelly JW. Accounts Of Chemical Research. 2005;38:911–921. doi: 10.1021/ar020073i. [DOI] [PubMed] [Google Scholar]
- 98.Cruz L, Urbanc B, Borreguero JM, Lazo ND, Teplow DB, Stanley HE. Proceedings Of The National Academy Of Sciences Of The United States Of America. 2005;102:18258–18263. doi: 10.1073/pnas.0509276102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Lazo ND, Grant MA, Condron MC, Rigby AC, Teplow DB. Protein Science. 2005;14:1581–1596. doi: 10.1110/ps.041292205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Lazo N, Condron MM, Grant MA, Rigby AC, Teplow DB. Neurobiology Of Aging. 2004;25:S149–S149. [Google Scholar]
- 101.Kad NM, Myers SL, Smith DP, Smith DA, Radford SE, Thomson NH. Journal Of Molecular Biology. 2003;330:785–797. doi: 10.1016/s0022-2836(03)00583-7. [DOI] [PubMed] [Google Scholar]
- 102.Smith JF, Knowles TPJ, Dobson CM, MacPhee CE, Welland ME. Proceedings Of The National Academy Of Sciences Of The United States Of America. 2006;103:15806–15811. doi: 10.1073/pnas.0604035103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Fandrich M, Zandomeneghi G, Krebs MRH, Kittler M, Buder K, Rossner A, Heinemann SH, Dobson CM, Diekmann S. Acta Histochemica. 2006;108:215–219. doi: 10.1016/j.acthis.2006.03.012. [DOI] [PubMed] [Google Scholar]
- 104.Frankenfield KN, Powers ET, Kelly JW. Protein Science. 2005;14:2154–2166. doi: 10.1110/ps.051434005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Ignatova Z, Gierasch LM. Biochemistry. 2005;44:7266–7274. doi: 10.1021/bi047404e. [DOI] [PubMed] [Google Scholar]
- 106.Hurshman AR, White JT, Powers ET, Kelly JW. Biochemistry. 2004;43:7365–7381. doi: 10.1021/bi049621l. [DOI] [PubMed] [Google Scholar]
- 107.Padrick SB, Miranker AD. Biochemistry. 2002;41:4694–4703. doi: 10.1021/bi0160462. [DOI] [PubMed] [Google Scholar]


