Skip to main content
PMC home page
Protein Science : A Publication of the Protein Society logoLink to Protein Science : A Publication of the Protein Society
. 2007 Nov;16(11):2412–2426. doi: 10.1110/ps.072895107

Fold assessment for comparative protein structure modeling

Francisco Melo 1, Andrej Sali 2,3,4
PMCID: PMC2211691  PMID: 17905832

Abstract

Accurate and automated assessment of both geometrical errors and incompleteness of comparative protein structure models is necessary for an adequate use of the models. Here, we describe a composite score for discriminating between models with the correct and incorrect fold. To find an accurate composite score, we designed and applied a genetic algorithm method that searched for a most informative subset of 21 input model features as well as their optimized nonlinear transformation into the composite score. The 21 input features included various statistical potential scores, stereochemistry quality descriptors, sequence alignment scores, geometrical descriptors, and measures of protein packing. The optimized composite score was found to depend on (1) a statistical potential z-score for residue accessibilities and distances, (2) model compactness, and (3) percentage sequence identity of the alignment used to build the model. The accuracy of the composite score was compared with the accuracy of assessment by single and combined features as well as by other commonly used assessment methods. The testing set was representative of models produced by automated comparative modeling on a genomic scale. The composite score performed better than any other tested score in terms of the maximum correct classification rate (i.e., 3.3% false positives and 2.5% false negatives) as well as the sensitivity and specificity across the whole range of thresholds. The composite score was implemented in our program MODELLER-8 and was used to assess models in the MODBASE database that contains comparative models for domains in approximately 1.3 million protein sequences.

Keywords: fold assessment, model assessment, statistical potentials, protein structure modeling, protein structure prediction

The number of known protein sequences has increased rapidly in the last two decades, as a consequence of many genome sequencing projects (Liolios et al. 2006). The number of known protein structures is also growing, partly due to the ongoing efforts in structural genomics (Montelione and Anderson 1999), albeit at a much slower rate than the number of known sequences. To help reduce this gap, several large-scale protein structure modeling efforts are generating millions of protein structure models of varying accuracy (Sanchez and Sali 1998; Guex et al. 1999; Jones 1999; Bonneau et al. 2002b; Kihara et al. 2002; Eswar et al. 2003; Kim et al. 2003, 2004; Lu et al. 2003; McGuffin and Jones 2003; Schwede et al. 2003; Shah et al. 2003; Zhang et al. 2003). The most accurate of these servers apply comparative protein structure modeling that involves finding a template structure similar to the target sequence, aligning the target to the template, building the model for the target, and assessing the model (Marti-Renom et al. 2000; Fiser et al. 2001; Contreras-Moreira 2002; Krieger 2003; Kopp and Schwede 2004; Moult 2005; Petrey 2005; Dunbrack Jr. 2006; Ginalski 2006; Xiang 2006).

The prediction of the accuracy of a model is necessary for determining the information that can be extracted from it (Marti-Renom et al. 2000; Baker and Sali 2001). Comparative models generally reflect errors in (1) fold assignment, (2) alignment between the target sequence and the template structure, (3) position and conformation of regions without a template (e.g., inserted loops), (4) smaller backbone changes between the target and the template in the correctly aligned regions, and (5) side-chain packing (Marti-Renom et al. 2000).

In comparative modeling, sequence identity above 40% is a relatively good predictor of the overall accuracy of the model (Sanchez and Sali 1998). However, if the target–template sequence identity falls below 30%–40%, the sequence identity becomes unreliable as a measure of the model accuracy; models that deviate significantly from the average accuracy are frequent. In this modeling regime, factors such as template selection and alignment accuracy usually have a large impact on the model accuracy. The alignment errors increase rapidly below 30%–40% sequence identity and become the most frequent cause of the largest errors in comparative models when the fold assignment is correct. Moreover, when a model is based on a target–template alignment with a statistically insignificant score, the model may have an entirely incorrect fold. Unfortunately, the building of comparative models based on <30%–40% sequence identity is common (Pieper et al. 2006). It is in such cases that the best possible model evaluation is especially needed.

Many tools for assessing protein structure models have been described (Marti-Renom et al. 2000). Some use statistical potentials or molecular mechanics force fields to assess the accuracy of the model. They include contact potentials (Miyazawa and Jernigan 1985; DeBolt and Skolnick 1996; Park and Levitt 1996; Park et al. 1997; Melo et al. 2002), residue–residue distance-dependent potentials (Sippl 1993; Jones 1999; Xia et al. 2000; Melo et al. 2002), residue-based solvent accessibility potentials (Jones et al. 1992; Sippl 1993; Melo et al. 2002), atomic solvent accessibility, and pairwise interaction potentials (Melo and Feytmans 1997, 1998; Lazaridis and Karplus 1998; Samudrala and Moult 1998; Lu and Skolnick 2001; Zhou and Zhou 2002; Wang et al. 2004; Eramian et al. 2006). In addition to these statistical potential or energy-based methods, other methods assess a model by measuring how common its geometrical features are compared with those in well-refined, high-resolution structures. For example, the stereochemical quality is measured by z-scores for bond lengths, angles, distances, torsion angles, and planarity (Laskowski et al. 1993), deviations from known atomic radii or volumes (Pontius et al. 1996), atomic packing and excluded volume (Gregoret and Cohen 1991), occluded surface of residues (Pattabiraman et al. 1995), and residue–residue contact area difference (Abagyan and Totrov 1997).

In addition, multivariate model assessment methods have been described, including the GenThreader program (Jones 1999), MODPIPE model assessment modules (Sanchez and Sali 1998), and the SVMod program (Eswar et al. 2003; Eramian et al. 2006). GenThreader was developed to assess the folds of models generated by threading, and it is based on a neural network that combines several protein model features, such as the alignment score, model length, alignment length, and statistical potentials, into a single composite score. Later, an improved version of GenThreader has been reported (McGuffin and Jones 2003), using the same approach, but with a modified alignment score that now takes into account PSI-BLAST (Altschul et al. 1997) searches against structural alignment profiles from FSSP (Holm and Sander 1994a) and PSIPRED predicted secondary structure (McGuffin et al. 2000). Early versions of our fold assessment for large-scale comparative modeling by MODPIPE used the pG score that depends on the PROSAII combined statistical potential z-score (Sippl 1993) and protein model length. Another composite score, the SVMod function (Eswar et al. 2003; Eramian et al. 2006), aims to identify the most accurate model among alternatives based on a linear combination of the DOPE atomic distance-dependent statistical potential (Eramian et al. 2006), residue-level surface, pairwise, and combined statistical potentials (Melo et al. 2002), and two PSIPRED/DSSP scores (Kabsch 1983; Jones 1999).

There are various assessment problems in protein structure modeling: evaluating whether or not a given model has the correct fold, picking the most accurate model out of many alternative models (such as those generated based on different templates and/or alignments), estimating the overall geometrical accuracy of a model, and estimating the geometrical accuracy of the individual regions of the model. In general, different types of an assessment problem benefit from specialized scores and classifiers: It has been demonstrated that distinct scoring functions perform differently depending on the problem they are used to solve (Park et al. 1997). For this reason, we focus here specifically on the fold assessment problem, which is to assess whether or not a given model has the correct fold. In comparative modeling, a model will have the correct fold if the correct template is picked and if the template is aligned at least approximately correctly with the target sequence (Marti-Renom et al. 2000). The fold of a model is typically assessed by a measure of target–template sequence similarity (Chothia and Lesk 1986), a statistical potential z-score (Sippl 1993), or conservation of the key functional or structural residues in the model (Jin et al. 2000). However, these measures are imperfect, resulting in relatively large nonzero false-positive and false-negative rates.

We build on our previously reported statistical potential that was optimized and tested for fold assessment (Melo et al. 2002). We already highlighted several limitations of fold assessment based on a single statistical potential score (Melo et al. 2002). Most importantly, the prediction of model accuracy varies significantly depending on the size and completeness of the assessed model. Assessment of small and/or incomplete models (<100 residues), corresponding to ∼20% of all models calculated in automated and large-scale modeling of whole genomes (Sanchez and Sali 1998; Melo et al. 2002), is especially difficult. We suggested that additional attributes of a model should be considered to improve the accuracy of fold assessment. Here, we found informative model features as well as used them with an optimized multivariate classifier. In particular, we developed a genetic algorithm protocol for finding an optimized nonlinear transformation of model features that minimizes the classification error. A total of 21 model features were calculated and tested using a large benchmark of comparative models with correct and incorrect folds, resulting in an optimized assessment of whether or not a given comparative model has the correct fold.

We start by reporting what features were found to be most informative for optimal classification (Results and Discussion). We also test our optimal composite score and compare its accuracy with that of other fold assessment schemes. Next, we summarize the major conclusions of this work (Conclusions). We end by describing our genetic algorithm approach for selecting and combining the model features that are optimal for fold assessment (Materials and Methods). We also describe the sets of comparative models for training the classification method and assessing its accuracy.

Results and Discussion

Our objective was to develop an optimal classifier for assessing whether or not a given comparative model has the correct fold. To achieve this aim, we first calculated a large set of correct and incorrect comparative models. These models were subdivided to obtain training and testing sets of models. The training set was used to produce an optimal classifier. The testing set was used to assess the accuracy of the optimal classifier and a number of its suboptimal variants. To develop the classifiers, 21 model attributes or features that could possibly be informative for a native or misfolded state were calculated for each model. The features were then combined linearly and nonlinearly to produce composite scores, which in turn were evaluated for their ability to assess whether or not a model has the correct fold. Composite scores consisting of linear combinations of features were built and optimized using a simple neural network. Nonlinear combinations of features were produced by our genetic algorithm as well as a Bayesian classification. For details about the procedures, see Materials and Methods.

Single feature classification

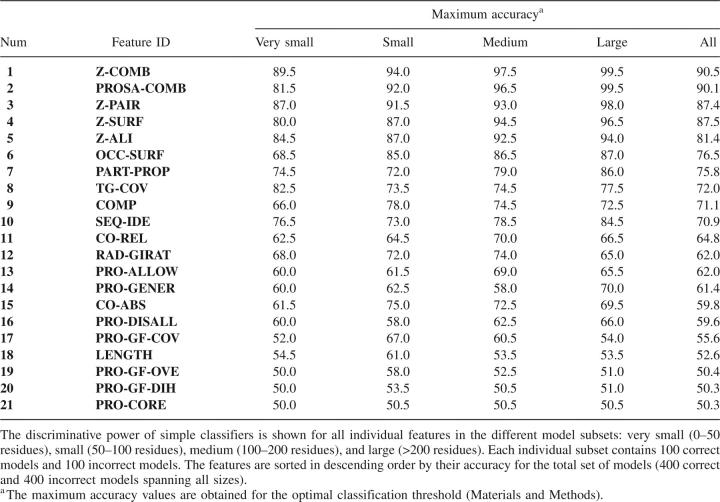
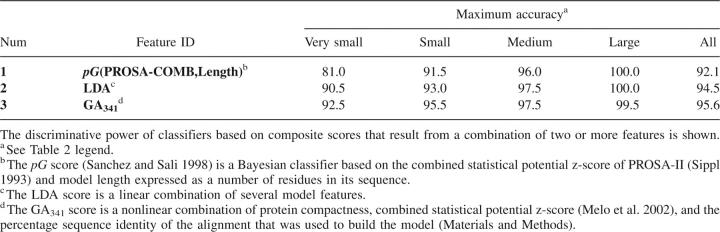
We start by assessing the classification performance of each single feature (Table 1) with the aid of the testing set of models, which included a representative subset of models spanning all protein sizes (Materials and Methods). The maximal accuracy for each feature is shown in Table 2. The highest accuracy is achieved by the statistical potential z-scores, followed by alignment scores, protein packing, and the fraction of hydrophobic burial. At the end of the list is a group of features that are not much more useful than a random classification, including geometrical descriptors and stereochemical quality. Several conclusions are reached, as follows.

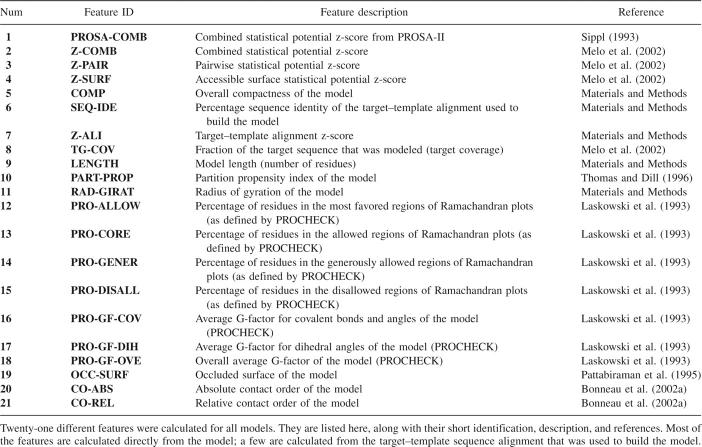
Table 1.

List of protein model features

graphic file with name 2412tbl1.jpg

Open in a new tab

Table 2.

Discriminative power of classifiers based on a single model feature

graphic file with name 2412tbl2.jpg

Open in a new tab

First, the statistical potentials derived from known protein structures capture many relevant aspects that differentiate between the correct and incorrect folds. The z-score for a combined distance-dependent and accessible surface statistical potential is more accurate than the z-scores for the individual statistical potentials, in agreement with previous studies (Sippl 1993; Melo et al. 2002).

Second, a global measure of local compatibility between the sequence and its modeled structure, such as the alignment score used here, captures several aspects of model accuracy. Although the distributions of the percentage sequence identity for the alignments used to build the correct and incorrect models are strongly overlapping (Melo et al. 2002), the target–template alignment z-score is able to separate the two distributions to a useful degree.

Third, because the native structures are generally densely packed and have most hydrophobic residues buried, atomic packing density and fraction of buried hydrophobic residues are capable of discriminating between the correct and incorrect models in ∼75% of the cases.

Fourth, the target coverage (fraction of the target sequence that was possible to model) exhibits a relatively high accuracy in the classification of very small models compared with that for the larger models. This finding reflects a stronger bias against incomplete models in the testing set of correct small models compared with the larger models, and is in agreement with previous results (Melo et al. 2002).

Finally, the poor accuracy of stereochemical quality measures reflects good stereochemistry of most MODELLER models, irrespective of the final model accuracy. Thus, a model with good stereochemistry does not guarantee a correct protein structure prediction. Stereochemical quality is a minimal requirement for a model, and any protein structure modeling software should be able to generate models with at least correct stereochemistry, thus invalidating the use of this feature for model assessment.

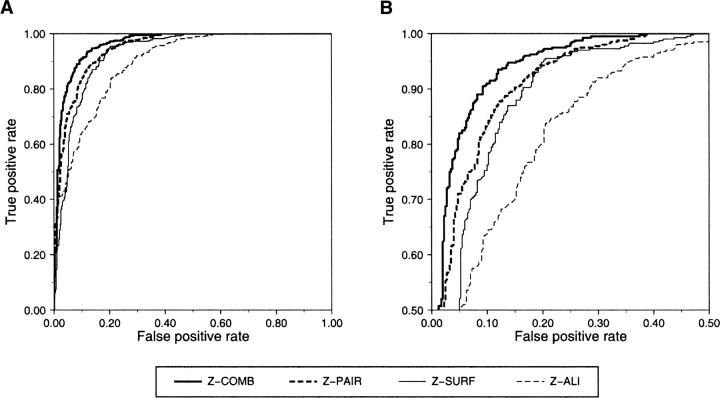
The most accurate single feature classifiers (as measured by maximal accuracy; Table 2) were also assessed by more robust and threshold-independent receiver operating characteristic (ROC) curves (Fig. 1). These curves represent the trade-off between the rates of false positives and true positives as the feature threshold for class separation is varied from a minimum to a maximum value. The combined statistical potential z-score exhibits the highest accuracy, followed by the distance-dependent statistical potential, then the surface-accessible statistical potential, and finally the sequence alignment z-score. A statistically significant improvement is achieved when the distance-dependent and accessible surface terms are combined (Table 4, see below).

Figure 1.

Figure 1.

Open in a new tab

ROC curves of the most accurate classifiers based on single features. ROC curves are shown for the single features (Table 1) that are most accurate for fold assessment (Table 2). (A) The combined statistical potential z-score (Melo et al. 2002) of the model (thick continuous line), pairwise statistical potential z-score (Melo et al. 2002) of the model, (thick dashed line), accessible surface statistical potential z-score (Melo et al. 2002) of the model (thin continuous line), and z-score of the target–template alignment (thin dashed line). (B) Same as A, but magnified.

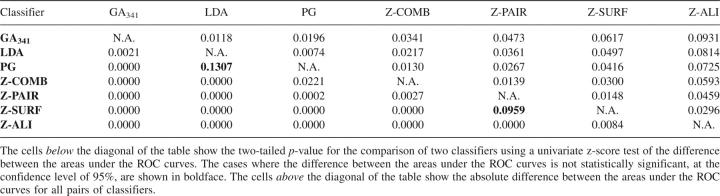
Table 4.

Statistical significance of the difference between the areas under two ROC curves

graphic file with name 2412tbl4.jpg

Open in a new tab

Multiple feature classification

There are several methods for finding combinations of two or more features that result in an optimized classifier. Among the most popular techniques are principal component analysis (Jolliffe 2002), neural networks (Haykin and Haykin 1998), support vector machines (Christianini and Shaw-Taylor 2000), and genetic algorithms (Goldberg 1989). In this work, we used a simple neural network based on the perceptron algorithm to generate linear combinations of features (linear discriminant analysis or LDA). In addition, we designed our own GA-based method to evolve a set of mathematical functions, resulting in either linear or nonlinear combinations of two or more features (Materials and Methods). We calculated an optimized classifier, based on exploring all 21 features and the training model set, with each of the three methods. The optimized discriminant function produced by the perceptron algorithm is a linear combination of five model features:

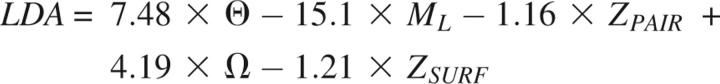graphic file with name 2412equ1.jpg

where Θ is model compactness, Ω is the percentage sequence identity of the alignment used to build the model, ML is model length, and ZPAIR and ZSURF are the model z-scores for the residue distance and accessibility statistical potentials (Melo et al. 2002), respectively. On the other hand, the optimized discriminant function evolved by the genetic algorithm is a nonlinear combination of three model features:

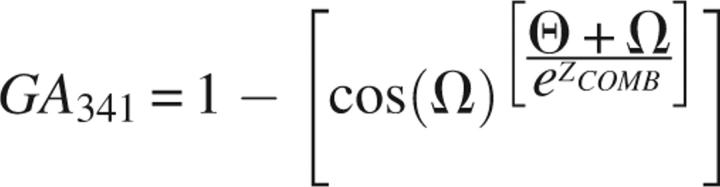graphic file with name 2412equ2.jpg

where ZCOMB is the model's z-score for the combined (distance and accessibility) residue-level statistical potential (Melo et al. 2002).

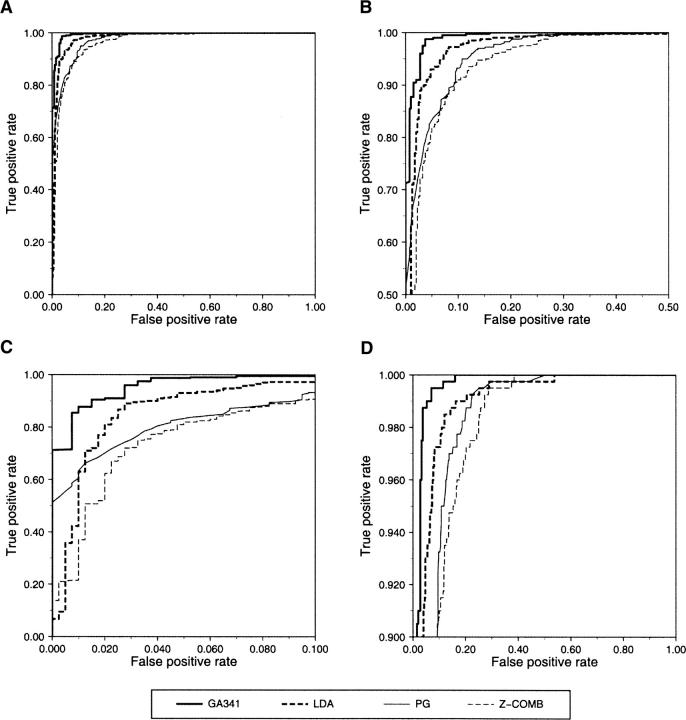
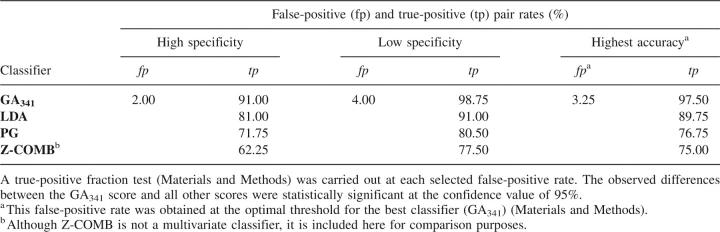
We compared the accuracy of these discriminant functions with the accuracies of (1) the combined statistical potential z-score (Melo et al. 2002) and (2) the pG score from our previous study (Fig. 2; Sanchez and Sali 1998). The pG score is a Bayesian classifier that gives the probability of the model having the correct fold. It is based on two features: the combined statistical potential z-score of the model calculated using PROSAII (Sippl 1993), and model length. pG outperforms the combined statistical potential z-score (Tables 2, 3); the differences of the areas under the corresponding ROC curves are statistically significant (Table 4). Although the maximal accuracy of LDA is better than that of pG (Table 3), the two ROC curves cross each other at a low rate of false positives (Fig. 2C). While LDA performs better at medium and high sensitivities, the pG score is a more specific classifier of model accuracy. The difference between the areas under the ROC curves of LDA and pG is not statistically significant at the confidence level of 95% (Table 4). The maximal accuracy results and ROC analysis clearly show that the GA341 score has the highest accuracy, for the testing set of models (Table 3; Fig. 2). The difference in accuracy between GA341 and all other methods is statistically significant (Table 4). The GA341 score is also better than any other method at high specificity and sensitivity values (Fig. 2; Table 5). The observed differences are statistically significant at the confidence level of 95%.

Figure 2.

Figure 2.

Open in a new tab

ROC curves of the most accurate classifiers based on a combination of multiple features. The ROC curves are shown for several of the most accurate combined scores (Tables 2, 3). (A) The ROC curves for the GA341 discriminant function (thick continuous line), LDA discriminant function (thick dashed line), pG score (thin continuous line), and the combined statistical potential z-score of the model (thin dashed line). (B) Same as A, but magnified. (C) Magnified X-axis allows a better comparison of the classifier specificities. (D) Magnified Y-axis allows a better comparison of the classifier sensitivities.

Table 3.

Discriminative power of classifiers based on a combination of model features

graphic file with name 2412tbl3.jpg

Open in a new tab

Table 5.

True-positive rates of multivariate classifiers obtained at some fixed false-positive rates

graphic file with name 2412tbl5.jpg

Open in a new tab

The GA341 discriminant function

The GA341 discriminant function exhibits several interesting properties. First, its domain is restricted to the range between 0 and 1, irrespective of the input variable values (whose ranges are also well defined). Thus, it is a numerically robust function.

Second, the shape of the GA341 surface is primarily determined by the balance between the percentage sequence identity and the combined statistical potential z-score, with the compactness acting only to fine-tune the final score (Fig. 3). The sequence identity feature captures the fact that similar sequences generally have similar structures (Chothia and Lesk 1986, 1987). The combined statistical potential z-score attempts to capture the fact that proteins with undetectable sequence similarity can also have similar structures (Holm and Sander 1993a,b, 1994b, 1995). The fold assessment is most difficult when the two main individual scores oppose each other. For example, a model that was built based on a low sequence identity with the template will only be classified by the GA341 discriminant function as correct if the statistical potential z-score is sufficiently negative (Fig. 3). Alternatively, a model that shares a high sequence similarity with the template used to build it will only be classified as incorrect if it has a sufficiently positive statistical potential z-score. The balance between the sequence identity and the statistical potential z-score in the GA341 discriminant function is clearly defined by a hyperbolic shape in the imaginary projection of the decision hypersurface (i.e., GA341 = 0.7) onto the X–Y plane for fixed values of compactness (Fig. 3, right column).

Figure 3.

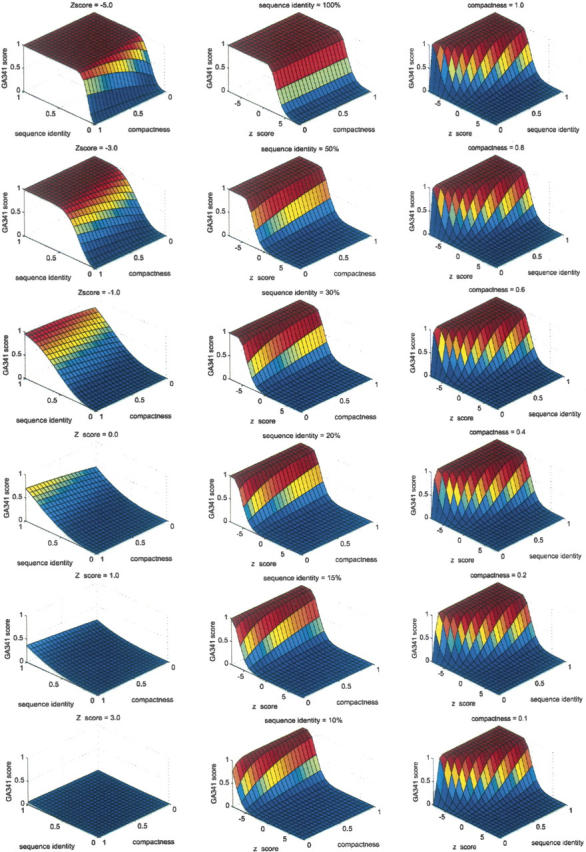
Figure 3.

Open in a new tab

The GA341 discriminant function. The discriminant function values range from 0 to 1, with higher values corresponding to correct models. Because the function depends on three variables, each column represents the three-dimensional surface of the discriminant function when one variable is fixed at a single value. (Left column) Combined statistical potential z-score (Melo et al. 2002) of the model is fixed (values increase from top to bottom). (Middle column) Percentage sequence identity of the alignment used to build the model is fixed (values decrease from top to bottom). (Right column) Model compactness is fixed (values decrease from top to bottom).

Third, when both the sequence identity and the statistical potential z-score are independently favoring an incorrect or correct model, the GA341 function will also converge to its extreme value of either 0 or 1, respectively (Fig. 3).

Finally, the GA341 surface is smooth, a desirable feature of any scoring function used in classification. The smoothness also indicates that GA341 is not a result of overfitting to the training set of models. GA341 has the following properties: (1) Given a very negative statistical potential z-score, a very low percentage sequence identity is needed to classify the model as incorrect; in such cases, the compactness is a modulator of the decision hypersurface. (2) Given a high percentage of sequence identity, the model will be classified as correct, irrespective of the compactness or the statistical potential z-score; when the percentage sequence identity is <50%, the compactness acts to fine-tune the discriminant function decision hypersurface. (3) At the boundaries where the statistical potential z-score and percentage sequence identity are balanced in their opposing assessments (i.e., the accuracy of a model is most uncertain), different compactness values will determine the final classification outcome; compact models are more likely to be assessed as correct than noncompact models.

Bayesian fold assessment with the GA341 discriminant function

We also tested fold assessment with a naive Bayesian classifier (Duda et al. 2001), p(GA341,length), that combines the GA341 score and the model length (i.e., the number of residues in the modeled sequence) (Fig. 4). Although the accuracy of this Bayesian classifier is not better than that of GA341 on its own (data not shown), we use it anyway because the 0–1 scale of probability is more meaningful than the arbitrary scale of the GA341 score. The conditional probability that the model is correct, pC(GA341,length), was calculated by applying the Bayes rule based on the training data (Materials and Methods). Finally, the model is typically predicted to have the correct fold when the conditional probability pC is larger than the optimal classification threshold of 0.7. This threshold gives the false-positive rate of 3.25% and the false-negative rate of 2.5%, for our testing set of models (Table 5).

Figure 4.

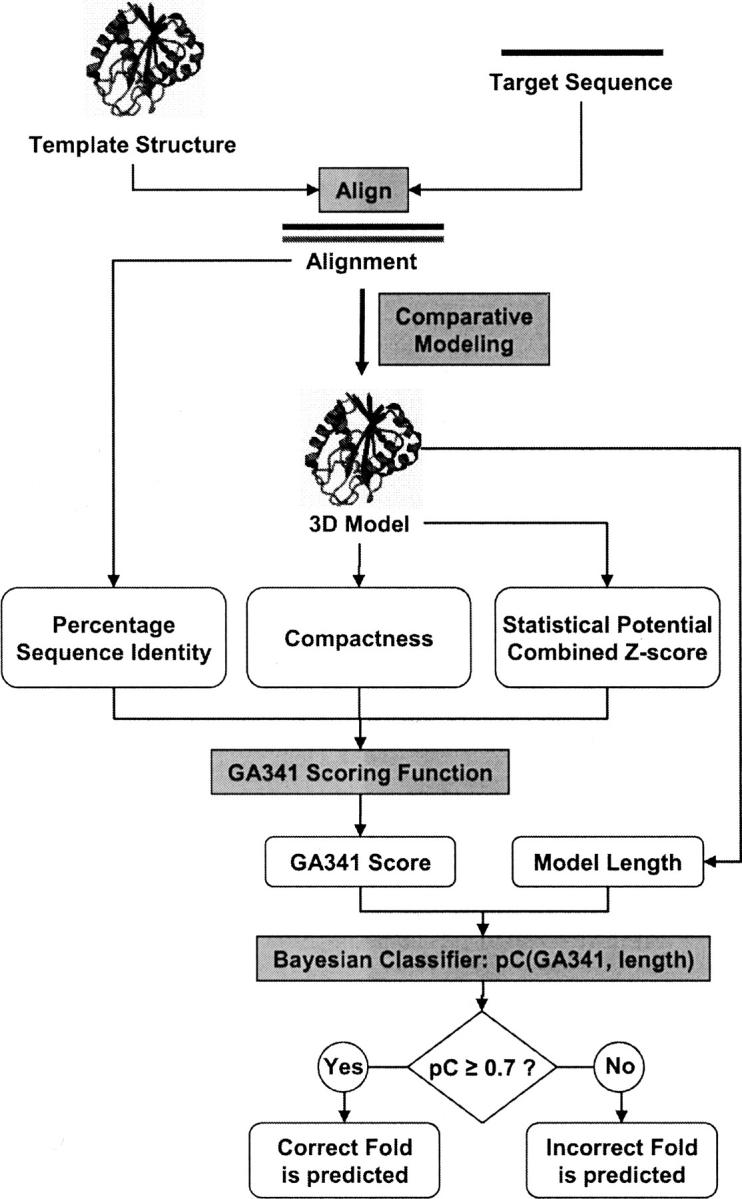
Figure 4.

Open in a new tab

Fold assessment scheme. The GA341 score depends on three variables: The percentage sequence identity is calculated from the alignment that was used to build the model, while the compactness (Materials and Methods) and the combined statistical potential z-score (Melo et al. 2002) are calculated from the 3D model itself. Next, the length of the model and the GA341 score are plugged into a naive Bayesian classifier to obtain the conditional probability that the model is correct, pC(GA341,length). Typically, pC ≥ 0.7 predicts that the model is correct; otherwise, it is classified as incorrect.

The accuracy of the pC composite score compares favorably to that of the pG score initially used in MODPIPE (Sanchez and Sali 1998; Fig. 2; Tables 3, 5). The improvement in the accuracy of fold assessment by the new composite discriminant function (Table 5) is significant for large-scale comparative modeling. For example, a 1% improvement in the accuracy of fold assessment for the ∼4.2 million models in the MODBASE database (Pieper et al. 2006) translates into ∼42,000 additional models being correctly classified.

Fold assessment with other programs for prediction of model accuracy

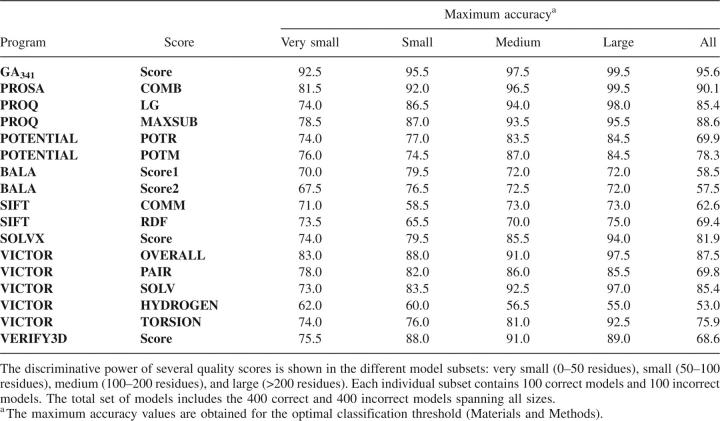
Whether or not the fold of a given model is correct can also be assessed with methods that predict the degree of the overall geometrical accuracy of a given model. Therefore, to provide another baseline for evaluating the GA341 scoring function, we also applied our fold assessment benchmark to all available assessment programs tested at CASP and CAFASP meetings (Moult et al. 2005): PROQ, PROSA, POTENTIAL, BALA, SIFT, SOLVX, VICTOR, MODCHECK, and VERIFY3D. For each method, an optimal cutoff on the corresponding quality criterion was found by maximizing the discrimination between the correct and incorrect models.

All tested methods perform worse than our composite score (Table 6). The COMB and MAXSUB scores of PROSA and PROQ, respectively, exhibited the best overall performance among the tested “CASP” methods, achieving a maximum accuracy of 90.1% and 88.6% for the complete set of models (in comparison, GA341 accuracy was 95.6%). Most of the scores have difficulty assessing very small models, with the OVERALL score from VICTOR achieving the best results among the tested “CASP” methods; its maximum accuracy is 83% compared with 92.5% for GA341.

Table 6.

Discriminative power of the quality scores from commonly used assessment programs

graphic file with name 2412tbl6.jpg

Open in a new tab

These results support the distinction between a binary fold assessment and prediction of the degree of the overall model accuracy. When assessing a model, the fold should be assessed first by the best available fold assessment method; if the fold is assessed as correct, the model accuracy can then be predicted by the best method for predicting model accuracy.

The development of accurate fold assessment methods as the one described here is useful for large-scale comparative modeling, where many models are built based on low sequence similarity between the target protein and the template structure. It is also useful and relevant for fold recognition and ab initio protein structure prediction.

Conclusions

First, a robust and accurate genetic algorithm-based approach to finding nonlinear classifiers was developed; it is in principle applicable to any classification problem, not only to fold assessment as described here.

Second, statistical potential z-scores and the z-score of the target–template alignment are the most important features for assessing the fold of a comparative model (Fig. 1; Table 2).

Third, integrating additional model features of mediocre utility as single classifiers nevertheless substantially increases the accuracy of fold assessment by an optimized composite score (Tables 2, 3; Figs. 1, 2).

Fourth, the fold of small and very small models (often models with a low target coverage) is the most difficult to assess (Tables 2, 3).

Fifth, existing programs for the prediction of model accuracy do not perform well in fold assessment, suggesting that each specific model assessment software should be used for the particular task that it was developed (Table 6).

Finally, all automated methods for large-scale protein structure modeling should use a model assessment tool validated on a large and representative benchmark set; even a small improvement in the classification error rate can correspond to the elimination of thousands of incorrect models.

Materials and Methods

Benchmark set of comparative models

As previously described (Sanchez and Sali 1998; Melo et al. 2002), a set of 9645 comparative models for proteins of known structure was calculated by MODPIPE (Sanchez and Sali 1998), relying on MODELLER (Sali and Blundell 1993). This set of models is representative of large-scale comparative modeling because models were built for all nonredundant chains in the Protein Data Bank (PDB) (Berman et al. 2002). The models were classified as correct or incorrect depending on their structural similarity to the actual structure of the target protein; the fold is correct when >30% of its Cα atoms are within 3.5 Å of their native positions upon least-squares superposition of the two structures with the SUPERPOSE command of MODELLER. The choice of this necessarily arbitrary cutoff is justified by the fact that even models with only 30% native overlap can be helpful for useful hypothesizing about the modeled protein (Marti-Renom et al. 2000; Baker and Sali 2001). The fold of a model is incorrect when <15% of its Cα atoms are within 3.5 Å of their native positions. A total of 3375 correct models and 6270 incorrect models were obtained. The correct models were built on the basis of the correct templates and mostly correct alignments between the target sequences and the template structures. The incorrect models were built on the basis of a template with an incorrect fold, a template structure with large rigid body shifts relative to the target structure, or an incorrect alignment with the correct template. From these models, 400 correct and 400 incorrect models were randomly selected, subject to the uniform sampling of protein sizes, as follows (Melo et al. 2002). Each set of 400 models included: 100 very small models (<50 residues), 100 small models (50–100 residues), 100 medium models (100–200 residues), and 100 large models (>200 residues). This 400/400 set was used to test the classifiers. The remaining 2975 correct and 5870 incorrect models were used as a training set to generate the classifiers. These sets of comparative models are available at http://protein.bio.puc.cl/models.html and http://salilab.org/models.html.

Protein model features

A total of 21 features potentially informative about the accuracy of a model were calculated for both the correct and incorrect models (Table 1). The discriminant power of each model feature was evaluated not only individually but also in linear and nonlinear combinations of two or more features. Most of the features involved statistical potential scores, stereochemistry quality descriptors, geometrical descriptors, and measures of protein packing. In addition, several attributes that are specific to comparative modeling, such as target coverage and a score of the target–template alignment that was used to build the model, were also considered. Next, we define each one of these 21 features.

The model length corresponds to the number of modeled residues in the target sequence. The percentage sequence identity is the total number of identical residues in the target–template alignment divided by the length of the shortest sequence in the alignment, multiplied by 100. The z-score of the target–template alignment is (μ − S)/σ where S is the sum of the substitution scores (obtained from the MODELLER as1.mat residue similarity matrix) (Sali and Blundell 1993) for the aligned residue pairs, μ is the average of the distribution of 200 scores obtained by swapping the residue pairs within each of the target and template sequences, and σ is the standard deviation of this distribution. The partition propensity of a model is a measure of the burial of nonpolar groups (Thomas and Dill 1996). The total occluded surface of residues in the model was calculated with the program OS (Pattabiraman et al. 1995). The absolute contact order and relative contact order of a model describe the average sequence separation of residues that are found at a distance ≤8 Å within the structure (Bonneau et al. 2002a). The statistical potential z-scores of a model were obtained for pairwise distance-dependent (Melo et al. 2002), accessible surface (Melo et al. 2002), and combined potentials (Sippl 1993; Melo et al. 2002). The compactness Θ of a model is ∑i=1 n V i AA/V, where n is the number of residues in the protein, V i AA is the volume of residue i (Bondi 1964), and V is the volume of the sphere spanned by the maximal observed Euclidean distance between any pair of non-hydrogen atoms in the protein. Some selected stereochemical quality features of a model, such as the percentage of residues in the most favorable, allowed, generously allowed, and disallowed regions of the Ramachandran plot as well as the dihedral angles, covalent bonds, and overall G factors, were calculated with the PROCHECK program (Laskowski et al. 1993). The pG score of a model (Sanchez and Sali 1998) is the probability of the correct fold that depends on model length and the PROSAII combined statistical potential z-score (Sippl 1993). The target coverage is the fraction of the target protein chain sequence that was modeled. Finally, the radius of gyration was calculated as the square root of the average atomic distance between the residue side-chain centroids and the center of mass of the protein.

Classification methods

Three different classification methods were used and assessed in this work, including our own genetic algorithm for nonlinear discriminant analysis, a linear discriminant analysis, and a Bayesian classification. The major goal was to minimize the misclassification rate of the correct and incorrect models. We also aimed to learn which of the 21 tested criteria were the most informative about the accuracy of a model. The 21 features were first evaluated independently and then in combination with each other.

Nonlinear discriminant analysis

Genetic algorithms are frequently used to solve problems that require exploration of a huge space of states (Goldberg 1989). In our application, a genetic algorithm generated nonlinear transforms of combinations of up to seven of the 21 model features (Table 1) to produce a single composite score whose distributions for the correct and incorrect training models were minimally overlapping (Fig. 5). More specifically, the genetic algorithm evolved chromosomes that encoded mathematical expressions performing linear and/or nonlinear transformations of two or more model features (Fig. 5A): First, a large population of chromosomes is initialized with random values (initialization step). Second, each chromosome is decoded and its fitness calculated (evaluation step). Third, based on the fitness of each chromosome, a biased selection process is carried out, favoring chromosomes with better fitness values. And finally, the selected chromosomes are randomly mated in pairs by mimicking recombination and mutation in sexual reproduction. After several cycles of evaluation, selection, and reproduction, an optimal solution of the problem evolves (Fig. 5A). Any genetic algorithm needs an encoder and a decoder for coding an instance of a solution as a linear string of numbers. The coding scheme of the genetic algorithm developed here faced the challenge of representing many mathematical functions in a linear string of numbers. This challenge was met by defining two components for each gene within a chromosome (Fig. 5B). The first component of a gene holds a “type,” and the second gene component holds a “value” for the type. Four possible types were defined: a coded variable, a coded unary operator, a coded binary operator, and a stop code. In the case of variables, values from 0 to N − 1 are possible, where N is the total number of variables or model features. For unary operators, 11 values were defined, including the unary mathematical functions log, ln, sin, cos, abs, inv, exp, and sqrt. For binary operators, addition, subtraction, multiplication, division, and exponentiation were included (Fig. 5B). Given a particular chromosome, the decoding proceeds from left to right using the prefix or Polish notation (Fig. 5C). The chromosomes are decoded until a stop type is found or the last gene is reached. Finally, each chromosome is evaluated by testing its ability to discriminate between the training sets of the correct and incorrect models (Fig. 5D). The fitness of a chromosome was defined as the maximal accuracy of the corresponding ROC curve (Fig. 5D; below).

Figure 5.

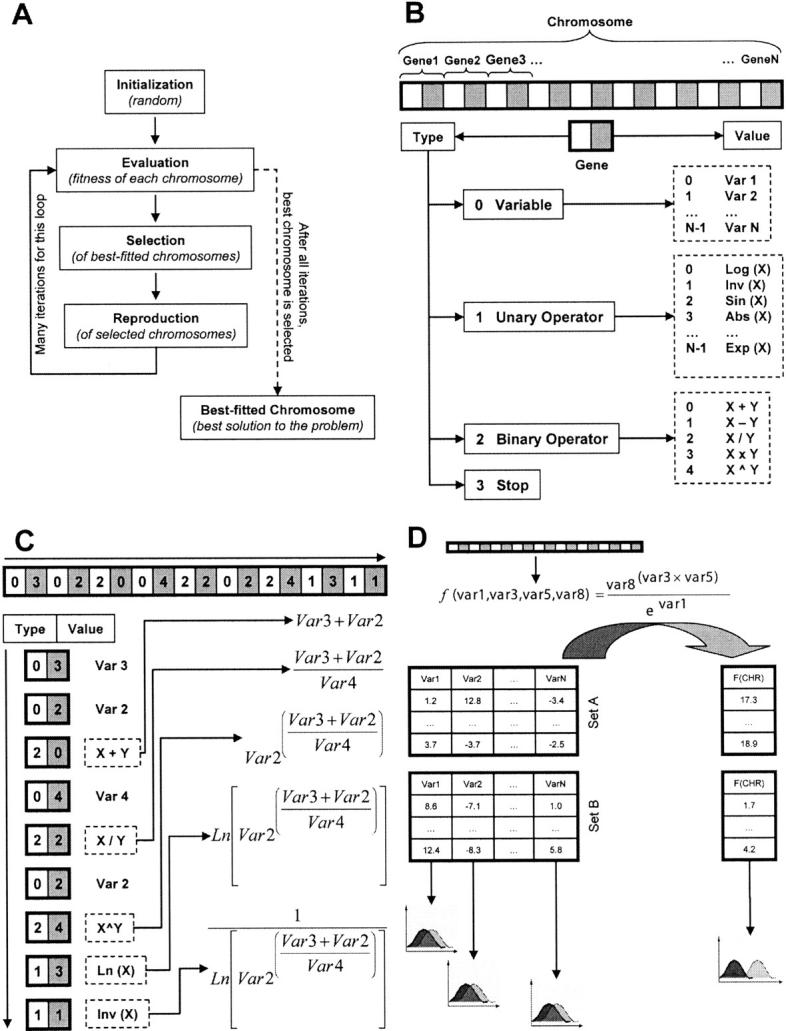
Figure 5.

Open in a new tab

Genetic algorithm for finding optimal feature subsets and multivariate classifiers. (A) Typical flowchart of a genetic algorithm. (B) Coding of a mathematical expression into a linear string of numbers. (C) Decoding a chromosome by following the prefix or Polish notation from left to right. The dashed line represents the action of an operator. (D) Calculation of the fitness value for a chromosome. For details see Materials and Methods.

Linear discriminant analysis (LDA)

Discriminant analysis also combines feature variables by maximizing the difference between the correct and incorrect models in the training set. In contrast to the genetic algorithm above, the discriminant score is a weighted sum of the individual feature values. Because all variables are normalized by the standard deviation of their corresponding distributions, absolute weights rank the variables in terms of their discriminating power, the largest absolute weight being associated with the most discriminating feature. We used a perceptron algorithm (Watkin et al. 1993) implemented in a PERL script. Optimal classifiers involving up to seven features were calculated.

Bayesian classification

A naive Bayes classifier is a simple probabilistic classifier based on the Bayes' theorem and the assumption of statistical independence between the combined features (Duda et al. 2001). As a result, only the variances of the variables for each class need to be determined and not the entire covariance matrix. The same relative importance was assigned to all classification errors. Thus, the Bayes classification rule minimizes the probability of the classification error. All possible pairwise combinations of 21 features were evaluated.

Assessment of classifiers

ROC curves were calculated for each classifier (Fawcett 2004) and used to assess its performance. A ROC curve plots the true-positive rate (tp) on the Y-axis against the false-positive rate (fp) on the X-axis (Swets 1988; Swets et al. 2000; Fawcett 2004). A ROC graph depicts relative trade-offs between benefits (true positives) and costs (false positives) for all possible decision thresholds.

If the model is correct and it is classified as correct, the prediction is a true positive (TP). If the model is correct and it is classified as incorrect, the prediction is a false negative (FN). If the model is incorrect and it is classified as incorrect, the prediction is a true negative (TN). If the model is incorrect and it is classified as correct, the prediction is a false positive (FP). The true-positive and false-positive rates are:

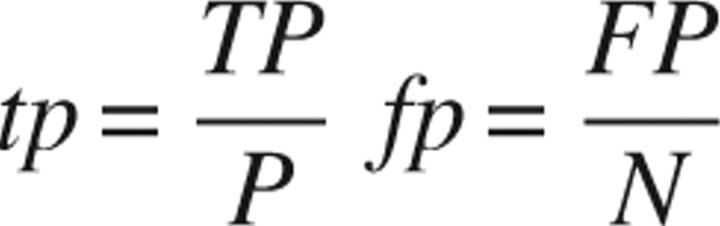graphic file with name 2412equ3.jpg

where TP is the count of true positives, P is the sum of true positives and false negatives, FP is the count of false positives, and N is the sum of true negatives and false positives.

In addition to the ROC curves, which constitute the best way to compare two classifiers (Swets 1988), we also calculated the overall accuracy of each classifier:

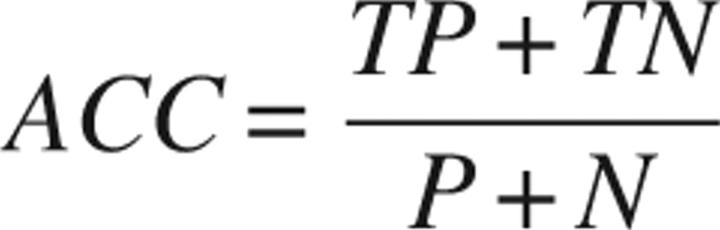graphic file with name 2412equ4.jpg

where TN is the count of true negatives. Because the accuracy depends on the particular decision threshold that is used to classify the instances, we only calculated the accuracy at the optimal threshold. The optimal threshold is uniquely defined by the point in the ROC curve that has the minimal distance from the point at fp = 0.0 and tp = 1.0, corresponding to the upper-left corner of the ROC graph. The accuracy obtained at the optimal threshold defines the maximal accuracy of a classifier.

Two statistical tests were used to assess the statistical significance of the observed differences between two classifiers based on their calculated ROC curves (Metz et al. 1984, 1998; Metz 1986). First, a univariate z-score test of the difference between the areas under the two ROC curves (the area test); the null hypothesis is that the data sets arose from binormal ROC curves with equal areas beneath them. Second, a univariate z-score test of the difference between the tp's on the two ROC curves at a selected fp (a true-positive fraction test); the null hypothesis is that the data sets arose from binormal ROC curves having the same tp at the selected fp. These statistical tests were performed with ROCKIT software, release 1.1B2, which was kindly provided to us by Charles E. Metz from the Department of Radiology at the University of Chicago.

Model assessment programs

Several computer programs for assessing the accuracy of a given protein structure model were downloaded from the CAFASP (Critical Assessment of Fully Automated Structure Prediction) Web site and tested for fold assessment. These programs included PROQ (http://www.sbc.su.se/∼bjornw/ProQ), POTENTIAL (http://cafasp4.cse.buffalo.edu/progs/mqaps/), BALA (http://cafasp4.cse.buffalo.edu/progs/mqaps/), SIFT (http://sift.cchmc.org/sift_doc.html), SOLVX (http://ekhidna.biocenter.helsinki.fi/solvx/start), VICTOR (http://protein.cribi.unipd.it/frst/), and Verify3D (Luthy et al. 1992; http://nihserver.mbi.ucla.edu/Verify_3D/). Programs MODCHECK (http://www.biocentre.rdg.ac.uk/bioinformatics/ModFOLD/) and PHYRE (http://www.sbg.bio.ic.ac.uk/∼phyre/), also listed on the CAFASP Web site, were not assessed because they were not easily available as stand-alone software.

Software availability

The software for calculating both the GA341 and the pC(GA341, length) scores is distributed as a PC LINUX executable file and is freely available at http://protein.bio.puc.cl/fold-assess.html and http://salilab.org/fold-assess.html. A module to assess protein structure models with the pC(GA341,length) classifier has also been incorporated into our comparative modeling software, MODELLER (Sali and Blundell 1993), release 8v0 and onward (http://salilab.org/modeller).

Acknowledgments

We thank our group members, especially Marc A. Marti-Renom, Narayanan Eswar, M.S. Madhusudhan, Min-Yi Shen, David Eramian, Damien Devos, Ismael Vergara, Evandro Ferrada, and Tomás Norambuena, for many discussions about the model assessment problem. We also thank Ben Webb for implementing the module of fold assessment described in this work in our MODELLER software. This work has been supported in part by FONDECYT (grant 1051112) to F.M. as well as the Sandler Family Supporting Foundation, NIH R01 GM54762, and NIH U54 GM62529 grants to A.S. We also thank IBM, Hewlett-Packard, NetApp, and Intel for computer hardware gifts.

Footnotes

Reprint requests to: Francisco Melo, Pontificia Universidad Catolica de Chile, Alameda 340, Facultad de Ciencias Biologicas, Laboratorio de Bioquimica, Santiago, Chile; e-mail: fmelo@bio.puc.cl; fax: 56-2-222-5515.

Article published online ahead of print. Article and publication date are at http://www.proteinscience.org/cgi/doi/10.1110/ps.072895107.

References

  1. Abagyan R.A. and Totrov, M.M. 1997. Contact area difference: A robust measure to evaluate accuracy of protein models. J. Mol. Biol. 268: 678–685. [DOI] [PubMed] [Google Scholar]
  2. Altschul S.F., Madden, T.L., Schaffer, A.A., Zhang, J., Zhang, Z., Miller, W., and Lipman, D.J. 1997. Gapped BLAST and PSI-BLAST: A new generation of protein database search programs. Nucleic Acids Res. 25: 3389–3402. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Baker D. and Sali, A. 2001. Protein structure prediction and structural genomics. Science 294: 93–96. [DOI] [PubMed] [Google Scholar]
  4. Berman H.M., Battistuz, T., Bhat, T.N., Bluhm, W.F., Bourne, P.E., Burkhardt, K., Feng, Z., Gilliland, G.L., Iype, L., Jain, S., et al. 2002. The Protein Data Bank. Acta Crystallogr. D Biol. Crystallogr. 58: 899–907. [DOI] [PubMed] [Google Scholar]
  5. Bondi A. 1964. Van der Waals volumes and radii. J. Phys. Chem. 68: 441–451. [Google Scholar]
  6. Bonneau R., Ruczinski, I., Tsai, J., and Baker, D. 2002a. Contact order and ab initio protein structure prediction. Protein Sci. 11: 1937–1944. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Bonneau R., Strauss, C.E., Rohl, C.A., Chivian, D., Bradley, P., Malmstrom, L., Robertson, T., and Baker, D. 2002b. De novo prediction of three-dimensional structures for major protein families. J. Mol. Biol. 322: 65–78. [DOI] [PubMed] [Google Scholar]
  8. Chothia C. and Lesk, A.M. 1986. The relation between the divergence of sequence and structure in proteins. EMBO J. 5: 823–826. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Chothia C. and Lesk, A.M. 1987. The evolution of protein structures. Cold Spring Harb. Symp. Quant. Biol. LII: 399–405. [DOI] [PubMed] [Google Scholar]
  10. Christianini N. and Shaw-Taylor, J. 2000. An introduction to support vector machines and other kernel-based learning methods, 1st ed. Cambridge University Press, Cambridge, UK.
  11. Contreras-Moreira B., Fitzjohn, P.W., and Bates, P.A. 2002. Comparative modelling: An essential methodology for protein structure prediction in the post-genomic era. Appl. Bioinformatics 1: 177–190. [PubMed] [Google Scholar]
  12. DeBolt S.E. and Skolnick, J. 1996. Evaluation of atomic level mean force potentials via inverse folding and inverse refinement of protein structures: Atomic burial position and pairwise non-bonded interactions. Protein Eng. 9: 637–655. [DOI] [PubMed] [Google Scholar]
  13. Duda R., Hart, P.E., and Stork, D.G. 2001. Pattern classification, 2d ed. John Wiley and Sons, New York.
  14. Dunbrack R.L. 2006. Sequence comparison and protein structure prediction. Curr. Opin. Struct. Biol. 16: 374–384. [DOI] [PubMed] [Google Scholar]
  15. Eramian D., Shen, M.Y., Devos, D., Melo, F., Sali, A., and Marti-Renom, M.A. 2006. A composite score for predicting errors in protein structure models. Protein Sci. 15: 1653–1666. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Eswar N., John, B., Mirkovic, N., Fiser, A., Ilyin, V.A., Pieper, U., Stuart, A.C., Marti-Renom, M.A., Madhusudhan, M.S., Yerkovich, B., et al. 2003. Tools for comparative protein structure modeling and analysis. Nucleic Acids Res. 31: 3375–3380. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Fawcett T. 2004. ROC graphs: Notes and practical considerations for researchers. Kluwer Academic Publishers, The Netherlands.
  18. Fiser A., Sanchez, R., Melo, F., and Sali, A. 2001. Comparative protein structure modeling. In Computational biochemistry and biophysics (eds. M. Watanabe et al.), pp. 275–312. Marcel Dekker, New York.
  19. Ginalski K. 2006. Comparative modeling for protein structure prediction. Curr. Opin. Struct. Biol. 16: 172–177. [DOI] [PubMed] [Google Scholar]
  20. Goldberg D.E. 1989. Genetic algorithms in search, optimization, and machine learning. Addison-Wesley, Boston, MA.
  21. Gregoret L.M. and Cohen, F.E. 1991. Protein folding. Effect of packing density on chain conformation. J. Mol. Biol. 219: 109–122. [DOI] [PubMed] [Google Scholar]
  22. Guex N., Diemand, A., and Peitsch, M.C. 1999. Protein modelling for all. Trends Biochem. Sci. 24: 364–367. [DOI] [PubMed] [Google Scholar]
  23. Haykin S.S. and Haykin, S. 1998. Neural networks: A comprehensive foundation, 2d ed. Prentice Hall, Lebanon, IN.
  24. Holm L. and Sander, C. 1993a. Globin fold in a bacterial toxin. Nature 361: 309. doi: 10.1038/361309a0. [DOI] [PubMed] [Google Scholar]
  25. Holm L. and Sander, C. 1993b. Protein structure comparison by alignment of distance matrices. J. Mol. Biol. 233: 123–138. [DOI] [PubMed] [Google Scholar]
  26. Holm L. and Sander, C. 1994a. The FSSP database of structurally aligned protein fold families. Nucleic Acids Res. 22: 3600–3609. [PMC free article] [PubMed] [Google Scholar]
  27. Holm L. and Sander, C. 1994b. Structural similarity between plant endochitinase and lysozymes from animals and phage: An evolutionary connection. FEBS Lett. 340: 129–132. [DOI] [PubMed] [Google Scholar]
  28. Holm L. and Sander, C. 1995. Evolutionary link between glycogen phosphorylase and a DNA modifying enzyme. EMBO J. 14: 1287–1293. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Jin S., Martinek, S., Joo, W.S., Wortman, J.R., Mirkovic, N., Sali, A., Yandell, M.D., Pavletich, N.P., Young, M.W., and Levine, A.J. 2000. Identification and characterization of a p53 homologue in Drosophila melanogaster . Proc. Natl. Acad. Sci. 97: 7301–7306. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Jolliffe I.T. 2002. Principal component analysis, 2d ed. Springer-Verlag, New York.
  31. Jones D.T. 1999. GenTHREADER: An efficient and reliable protein fold recognition method for genomic sequences. J. Mol. Biol. 287: 797–815. [DOI] [PubMed] [Google Scholar]
  32. Jones D.T., Taylor, W.R., and Thornton, J.M. 1992. A new approach to protein fold recognition. Nature 358: 86–89. [DOI] [PubMed] [Google Scholar]
  33. Kabsch W.a.S.C. 1983. Dictionary of protein secondary structure: Pattern recognition of hydrogen-bonded and geometrical features. Biopolymers 22: 2577–2637. [DOI] [PubMed] [Google Scholar]
  34. Kihara D., Zhang, Y., Lu, H., Kolinski, A., and Skolnick, J. 2002. Ab initio protein structure prediction on a genomic scale: Application to the Mycoplasma genitalium genome. Proc. Natl. Acad. Sci. 99: 5993–5998. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Kim D., Xu, D., Guo, J.T., Ellrott, K., and Xu, Y. 2003. PROSPECT II: Protein structure prediction program for genome-scale applications. Protein Eng. 16: 641–650. [DOI] [PubMed] [Google Scholar]
  36. Kim D.E., Chivian, D., and Baker, D. 2004. Protein structure prediction and analysis using the Robetta server. Nucleic Acids Res. 32: W526–W531. doi: 10.1093/nar/gkh468. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Kopp J. and Schwede, T. 2004. The SWISS-MODEL repository of annotated three-dimensional protein structure homology models. Nucleic Acids Res. 32: D230–D234. doi: 10.1093/nar/gkj056. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Krieger E., Nabuurs, S.B., and Vriend, G. 2003. Homology modeling. Methods Biochem. Anal. 44: 509–523. [DOI] [PubMed] [Google Scholar]
  39. Laskowski R.A., MacArthur, M.W., Moss, D.S., and Thornton, J.M. 1993. PROCHECK: A program to check the stereochemical quality of protein structures. J. Appl. Crystallogr. 26: 283–291. [Google Scholar]
  40. Lazaridis T. and Karplus, M. 1998. Discrimination of the native from misfolded protein models with an energy function including implicit solvation. J. Mol. Biol. 288: 477–487. [DOI] [PubMed] [Google Scholar]
  41. Liolios K., Tavernarakis, N., Hugenholtz, P., and Kyrpides, N.C. 2006. The Genomes On Line Database (GOLD) v.2: A monitor of genome projects worldwide. Nucleic Acids Res. 34: 332–334. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Lu H. and Skolnick, J. 2001. A distance-dependent atomic knowledge-based potential for improved protein structure selection. Proteins 44: 223–232. [DOI] [PubMed] [Google Scholar]
  43. Lu L., Arakaki, A.K., Lu, H., and Skolnick, J. 2003. Multimeric threading-based prediction of protein-protein interactions on a genomic scale: Application to the Saccharomyces cerevisiae proteome. Genome Res. 13: 1146–1154. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Luthy R., Bowie, J.U., and Eisenberg, D. 1992. Assessment of protein models with three-dimensional profiles. Nature 356: 83–85. [DOI] [PubMed] [Google Scholar]
  45. Marti-Renom M.A., Stuart, A., Fiser, A., Sanchez, R., Melo, F., and Sali, A. 2000. Comparative protein structure modeling of genes and genomes. Annu. Rev. Biophys. Biomol. Struct. 29: 291–325. [DOI] [PubMed] [Google Scholar]
  46. McGuffin L.J. and Jones, D.T. 2003. Improvement of the GenTHREADER method for genomic fold recognition. Bioinformatics 19: 874–881. [DOI] [PubMed] [Google Scholar]
  47. McGuffin L.J., Bryson, K., and Jones, D.T. 2000. The PSIPRED protein structure prediction server. Bioinformatics 16: 404–405. [DOI] [PubMed] [Google Scholar]
  48. Melo F. and Feytmans, E. 1997. Novel knowledge-based mean force potential at atomic level. J. Mol. Biol. 267: 207–222. [DOI] [PubMed] [Google Scholar]
  49. Melo F. and Feytmans, E. 1998. Assessing protein structures with a nonlocal atomic interaction energy. J. Mol. Biol. 277: 1141–1152. [DOI] [PubMed] [Google Scholar]
  50. Melo F., Sanchez, R., and Sali, A. 2002. Statistical potentials for fold assessment. Protein Sci. 11: 430–448. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Metz C.E. 1986. ROC methodology in radiological imaging. Invest. Radiol. 21: 720–733. [DOI] [PubMed] [Google Scholar]
  52. Metz C.E., Wang, P.L., and Kronman, H.B. 1984. A new approach for testing the significance of differences between ROC curves measured from correlated data. In Information processing in medical imaging (ed. F. Deconinck), pp. 432–445. Nijhoff, The Hague.
  53. Metz C.E., Herman, B.A., and Roe, C.A. 1998. Statistical comparison of two ROC curve estimates obtained from partially paired data sets. Med. Decis. Making 18: 110–121. [DOI] [PubMed] [Google Scholar]
  54. Miyazawa S. and Jernigan, R.L. 1985. Estimation of effective interresidue contact energies from protein crystal structures: Quasi-chemical approximation. Macromolecules 18: 534–552. [Google Scholar]
  55. Montelione G.T. and Anderson, S. 1999. Structural genomics: Keystone for a human proteome project. Nat. Struct. Biol. 6: 11–12. [DOI] [PubMed] [Google Scholar]
  56. Moult J. 2005. A decade of CASP: Progress, bottlenecks and prognosis in protein structure prediction. Curr. Opin. Struct. Biol. 15: 285–289. [DOI] [PubMed] [Google Scholar]
  57. Moult J., Fidelis, K., Rost, B., Hubbard, T., and Tramontano, A. 2005. Critical assessment of methods of protein structure prediction (CASP)-Round 6. Proteins S7: 3–7. [DOI] [PubMed] [Google Scholar]
  58. Park B.H. and Levitt, M. 1996. Energy functions that discriminate X-ray and near-native folds from well-constructed decoys. J. Mol. Biol. 258: 367–392. [DOI] [PubMed] [Google Scholar]
  59. Park B.H., Huang, E.S., and Levitt, M. 1997. Factors affecting the ability of energy functions to discriminate correct from incorrect folds. J. Mol. Biol. 266: 831–846. [DOI] [PubMed] [Google Scholar]
  60. Pattabiraman N., Ward, K.B., and Fleming, P.J. 1995. Occluded molecular surface: Analysis of protein packing. J. Mol. Recognit. 8: 334–344. [DOI] [PubMed] [Google Scholar]
  61. Petrey D.a.H.B. 2005. Protein structure prediction: Inroads to biology. Mol. Cell 20: 811–819. [DOI] [PubMed] [Google Scholar]
  62. Pieper U., Eswar, N., Braberg, H., Madhusudhan, M.S., Davis, F., Rossi, A., Marti-Renom, M.A., Karchin, R., Webb, B., Melo, F., et al. 2006. MODBASE, a database of annotated comparative protein structure models, and associated resources. Nucleic Acids Res. 33: 291–295. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Pontius J., Richelle, J., and Wodak, S.J. 1996. Deviations from standard atomic volumes as a quality measure for protein crystal structures. J. Mol. Biol. 264: 121–136. [DOI] [PubMed] [Google Scholar]
  64. Sali A. and Blundell, T.L. 1993. Comparative protein modelling by satisfaction of spatial restraints. J. Mol. Biol. 234: 779–815. [DOI] [PubMed] [Google Scholar]
  65. Samudrala R. and Moult, J. 1998. An all-atom distance-dependent conditional probability discriminatory function for protein structure prediction. J. Mol. Biol. 275: 895–916. [DOI] [PubMed] [Google Scholar]
  66. Sanchez R. and Sali, A. 1998. Large-scale protein structure modeling of the Saccharomyces cerevisiae genome. Proc. Natl. Acad. Sci. 95: 13597–13602. [DOI] [PMC free article] [PubMed] [Google Scholar]
  67. Schwede T., Kopp, J., Guex, N., and Peitsch, M.C. 2003. SWISS-MODEL: An automated protein homology-modeling server. Nucleic Acids Res. 31: 3381–3385. [DOI] [PMC free article] [PubMed] [Google Scholar]
  68. Shah M., Passovets, S., Kim, D., Ellrott, K., Wang, L., Vokler, I., LoCascio, P., Xu, D., and Xu, Y. 2003. A computational pipeline for protein structure prediction and analysis at genome scale. Bioinformatics 19: 1985–1996. [DOI] [PubMed] [Google Scholar]
  69. Sippl M.J. 1993. Recognition of errors in three-dimensional structures of proteins. Proteins 17: 355–362. [DOI] [PubMed] [Google Scholar]
  70. Swets J.A. 1988. Measuring the accuracy of diagnostic systems. Science 240: 1285–1293. [DOI] [PubMed] [Google Scholar]
  71. Swets J.A., Dawes, R.M., and Monahan, J. 2000. Better decisions through science. Sci. Am. 283: 82–87. [DOI] [PubMed] [Google Scholar]
  72. Thomas P.D. and Dill, K.A. 1996. Statistical potentials extracted from protein structures: How accurate are they? J. Mol. Biol. 257: 457–469. [DOI] [PubMed] [Google Scholar]
  73. Wang K., Fan, B., Levitt, M., and Samudrala, R. 2004. Improved protein structure selection using decoy-dependent discriminatory functions. BMC Struct. Biol. 4: 8. doi: 10.1186/1472-6807-4-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  74. Watkin T.L.H., Rau, A., and Biehl, M. 1993. The statistical mechanics of learning a rule. Rev. Mod. Phys. 65: 499–556. [Google Scholar]
  75. Xia Y., Huang, E.S., Levitt, M., and Samudrala, R. 2000. Ab initio construction of protein tertiary structures using a hierarchical approach. J. Mol. Biol. 300: 171–185. [DOI] [PubMed] [Google Scholar]
  76. Xiang Z. 2006. Advances in homology protein structure modeling. Curr. Protein Pept. Sci. 7: 217–227. [DOI] [PMC free article] [PubMed] [Google Scholar]
  77. Zhang Y., Kolinski, A., and Skolnick, J. 2003. TOUCHSTONE II: A new approach to ab initio protein structure prediction. Biophys. J. 85: 1145–1164. [DOI] [PMC free article] [PubMed] [Google Scholar]
  78. Zhou H. and Zhou, Y. 2002. Distance-scaled, finite ideal-gas reference state improves structure-derived potentials of mean force for structure selection and stability prediction. Protein Sci. 11: 2714–2726. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Protein Science : A Publication of the Protein Society are provided here courtesy of The Protein Society

RESOURCES