Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2008 Jan 23.
Published in final edited form as: J Biomech. 2007 Jun 29;40(15):3438–3447. doi: 10.1016/j.jbiomech.2007.05.023

A Finite Element Exploration of Cartilage Stress Near an Articular Incongruity During Unstable Motion

Curtis M Goreham-Voss †, Todd O McKinley *, Thomas D Brown *,†,§
PMCID: PMC2212609  NIHMSID: NIHMS34228  PMID: 17604036

Abstract

Both instability and residual articular incongruity are implicated in the development of post-traumatic osteoarthritis following intra-articular fracture, but currently no information exists regarding cartilage stresses for unstable residual incongruities. In this study, a transversely isotropic poroelastic cartilage finite element model was implemented and validated within physiologically relevant loading ranges. This material model was then used to simulate the loading of cartilage during stable and unstable motion accompanying a step-off incongruity residual from intra-articular fracture, using load data from previous cadaver tests of ankle instability. Peak solid-phase stresses and fluid pressure were found to increase markedly in the presence of instability. Solid phase transients of normal stress increased from 2.00 to 13.8 MPa/s for stable compared to unstable motion, and tangential stress transients increased from 17.1 to 118.1 MPa/s. Corresponding fluid pressure transients increased from 15.1 to 117.9 MPa/s for unstable motion. In the most rapidly loaded sections of cartilage, the fluid was found to carry nearly all of the normal load, with the pressurization of the fluid resulting in high solid matrix tangential stresses.

Keywords: Articular Cartilage, Finite Element Analysis, Poroelastic, Incongruity, Instability

Introduction

Post-traumatic osteoarthritis (OA) is a form of degenerative joint disease secondary to significant injury such as intra-articular fracture or ligament tears. It has been estimated that over 5 million people in the U.S. suffer or have suffered from significantly symptomatic post-traumatic OA, resulting in over $3 billion of direct healthcare expenditure and nearly $12 billion of total costs per year (Brown et al., 2006). Current treatment options for OA (Buckwalter and Brown, 2004) are far from ideal for the younger, more active patients most likely to present with post-traumatic OA. The lack of effective, long-term treatment underscores the importance of forestalling or preventing the onset of post-traumatic OA.

The exact mechano-pathology of post-traumatic OA is not well understood, although many studies have demonstrated that cartilage responds unfavorably to abnormal mechanical stimuli. Various researchers have shown that cartilage undergoes significant microscopic damage and chondrocyte death after a single impact of the type that could cause intra-articular fracture (Borrelli et al., 1997; Ewers et al., 2001; Jeffrey et al., 1995; Milentijevic and Torzilli, 2005; Thompson et al., 1991). Other studies have shown that cartilage subjected repeatedly to chronically elevated loads, typical of residual post-traumatic articular surface incongruity or instability, will sustain matrix damage, altered biosynthesis, and chondrocyte death (Chen et al., 1999; Kurz et al., 2001; Milentijevic and Torzilli, 2005; Quinn et al., 2001). Post-traumatic residual incongruities, such as articular surface defects and step-offs, have been studied with respect to their influence on contact surface area and corresponding increases in peak contact pressures (Brown et al., 1988; Brown et al., 1991). However, clinical experience shows that the presence versus absence of instability is a stronger predictor of osteoarthritis than incongruous but otherwise stable joints (Kannus and Jarvinen, 1988; Lovasz et al., 2001; Lansinger et al., 1986; Rasmussen, 1973). Furthermore, most incongruity studies have used static methods which are incapable of detecting instability-associated contact abnormalities. In recent dynamic joint testing, it has been shown that injury-associated incongruity likely causes unstable motion under certain conditions (McKinley et al., 2006a; McKinley et al., 2006b). These cadaveric ankle studies demonstrated that joint instability can cause abnormal contact stresses and high contact stress gradients (McKinley et al., 2004; McKinley et al., 2006a). This suggests that the sudden loads experienced by articular cartilage in an incongruous, unstable joint may lead to the development of post-traumatic OA, for reasons that are still not well understood. However, previous mechanical contact studies of incongruities have been limited to loading abnormalities that occur on the joint surface. They provide no direct information on injury-associated changes in interstitial loads that occur immediately adjacent to or on the chondrocytes. Lack of information about how injury affects loads within the cartilage interstitium is a major impediment to understanding the pathomechanical etiology of post-traumatic OA.

One of the difficulties arising in quantifying the effect of such mechanical stimuli on cartilage is the complex nature of the articular cartilage tissue (Mow et al., 2005). Many mathematical models of cartilage have been created to provide insight into the behavior of the solid and fluid components of cartilage during to loading. Most continuum models currently in use have their conceptual basis in mixture theory, arising either from the biphasic theory of Mow et al. (Mow et al., 1980) or from poroelasticity formulations, which are equivalent when the fluid phase is inviscid (Simon, 1992). The initial mixture theory cartilage models have since been expanded to include additional phases (Myers et al., 1984), anisotropy (Federico et al., 2005; Fortin et al., 2000; Wilson et al., 2004), intrinsic viscoelasticity (DiSilvestro et al., 2001; Huang et al., 2003; Li and Herzog, 2004; Wilson et al., 2004; Yang and Smolinski, 2006), and nonlinearities of permeability and of elastic moduli (Federico et al., 2005; Huang et al., 2003; Li et al., 2002; Li et al., 1999; Soltz and Ateshian, 2000; Wilson et al., 2004).

To date, few attempts have been made to simulate multiphasic cartilage behavior in anatomic settings, with physiological loading magnitudes and rates. Federico et al. studied the effect of fluid flow boundary conditions on cartilage response using biphasic spherical surface cartilage contact (Federico et al., 2004). Ferguson et al. used an axisymmetric poroelastic cartilage model to study the ability of the acetabular labrum to seal fluid between cartilage layers in contact under quasi-physiologic loading (Ferguson et al., 2000). A recent study by Han et al. is perhaps the only poroelastic cartilage study to date investigating the effects of abnormal loading for fully anatomic cartilage geometry (Han et al., 2005). There, a static compressive load was applied to a model of a cat patellofemoral joint, with the patella being held shifted relative to the femur to investigate the effect of joint misalignment. The dynamic response of cartilage to abnormal, highly transient shifts of appositional loading suspected of leading to post-traumatic OA has yet to be explored.

In the present study, a plane-strain finite element model of distal tibial cartilage was developed to quantify the effect of transient, unstable motion on cartilage stresses in the vicinity of a step-off incongruity. The clinical scenario modeled in this investigation was a residual, coronally-directed step-off incongruity of the distal tibia, typical of a malunited pilon fracture. Previous work with this model has shown that such a step-off results in an ankle that will shift from being stable to unstable with minimal changes in extrinsic loading. In order to properly model the cartilage response to transient, elevated loading, a transversely isotropic poroelastic material model was first developed and validated. Articular surface loads from dynamic tests of motion of a cadaver ankle with a step-off incongruity (McKinley et al., 2004; McKinley et al., 2006a) were applied to an anatomically-based mesh incorporating this material model, to investigate the effects of joint instability on cartilage stresses and stress gradients. The goals of the study were to determine the extent to which unstable motion affects the stresses and stress gradients in cartilage at or near an incongruity, and to investigate the interaction of the fluid and solid phases of cartilage, particularly under highly transient loading characteristic of instability. The model geometry and loading were designed to simulate an ankle a short time after reconstructive surgery, before remodeling begins, but with more vigorous activity than the immediate rehabilitation phase.

Methods

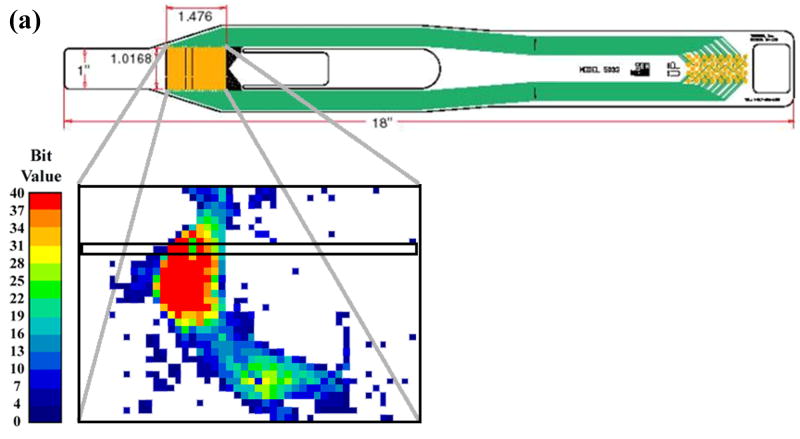
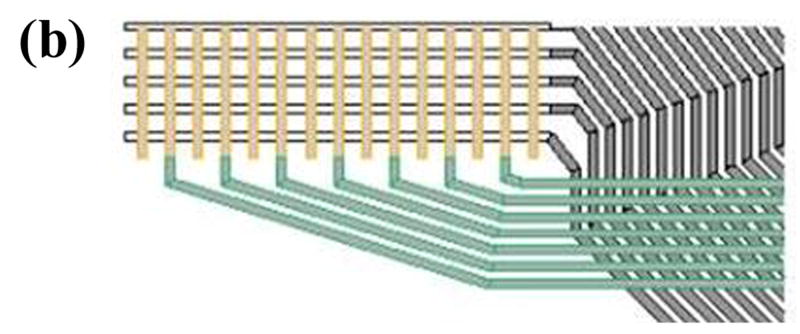
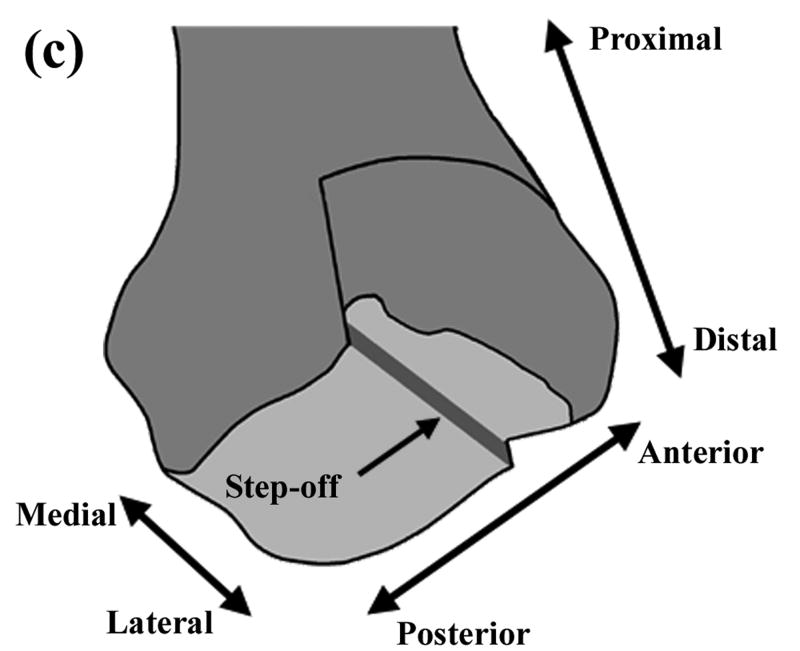
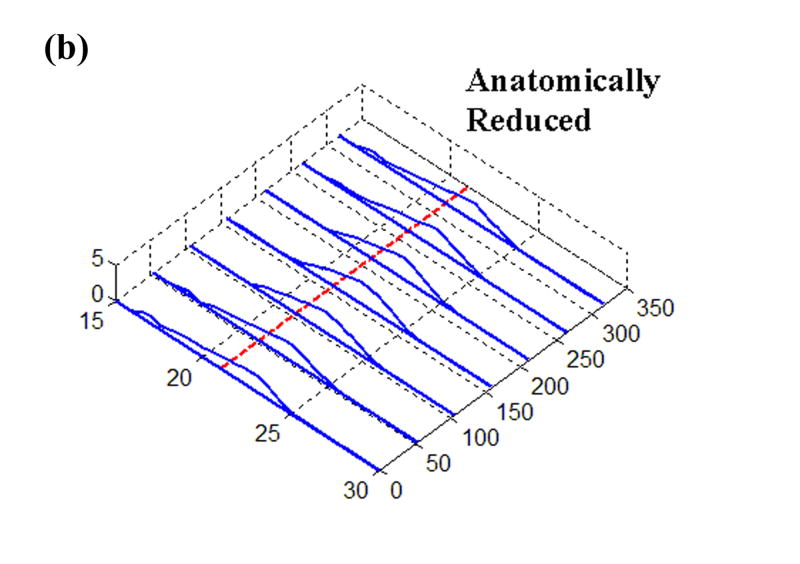
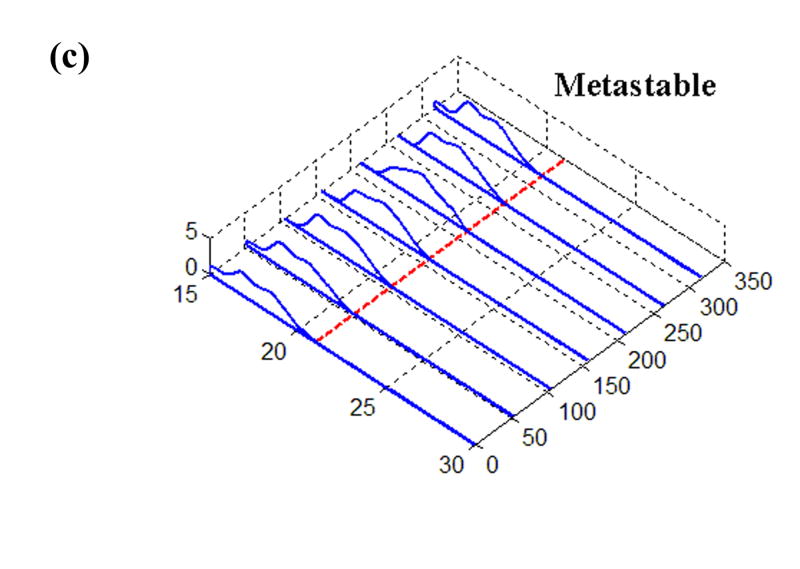
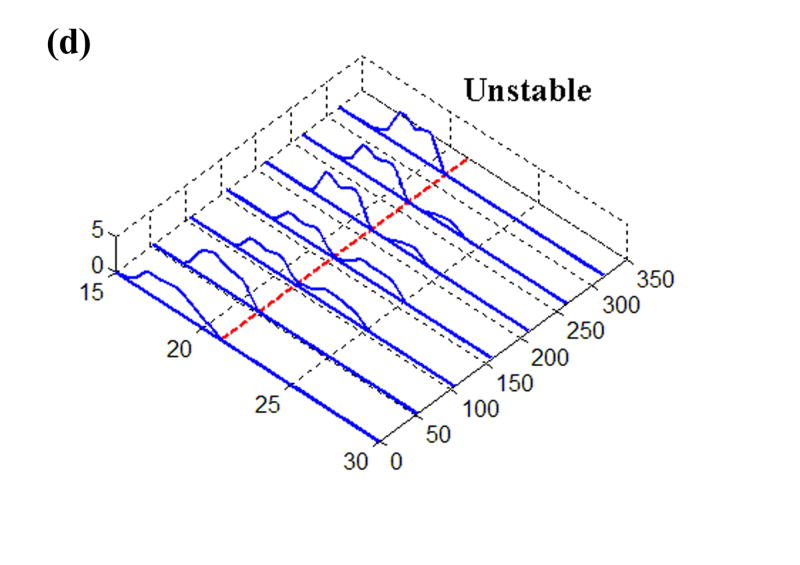
The earlier experimental work used for loading inputs involved cadaveric joints mounted in a custom-built apparatus that applied loads and plantar/dorsiflexion rotations representative of the stance phase of the gait cycle. From those studies, transient contact stress distributions measured with a Tekscan sensor were available for various situations of stable and unstable movement. The sensor used in that work returned contact stresses at 1,472 sites, arranged in a grid of 46 columns and 32 rows, encompassing approximately 970 mm2 (Fig. 1). For the present study, the time history of a representative single row of sensel measurements was extracted and normalized to a constant resultant force, before being applied as a distributed surface pressure to the articular surface of a plane-strain finite element model. (The experimental model of a step-off incongruity involved a “prismatic” saw-cut osteotomy spanning the entire width of the articular surface, and thus lent itself well to plane strain idealization.) Four loading cases were considered (Fig. 2): (a) Stable: cartilage fully intact, motion normal; (b) Anatomically Reduced: bone fragment separated, but placed back in correct location, representing a perfect anatomical reduction; (c) Metastable: a 2 mm step-off incongruity is created and the contact load moves up to the incongruity, but never crosses it, so that the displaced fragment is never loaded; (d) Unstable: a 2 mm step-off incongruity is created and an unstable motion occurs, such that the fragment is loaded suddenly as the contact patch shifts abruptly across the incongruity.

Figure 1.

Figure 1

Figure 1

Figure 1

Open in a new tab

(a) Schematic of Tekscan sensor and sample instantaneous Tekscan output for contact stress in an intact ankle. The outlined box indicates the sensel row used for load data for the present finite element study. (b) Close-up schematic of grid array of conductors. (c) Representation of the modeled distal tibia articular surface step-off incongruity.

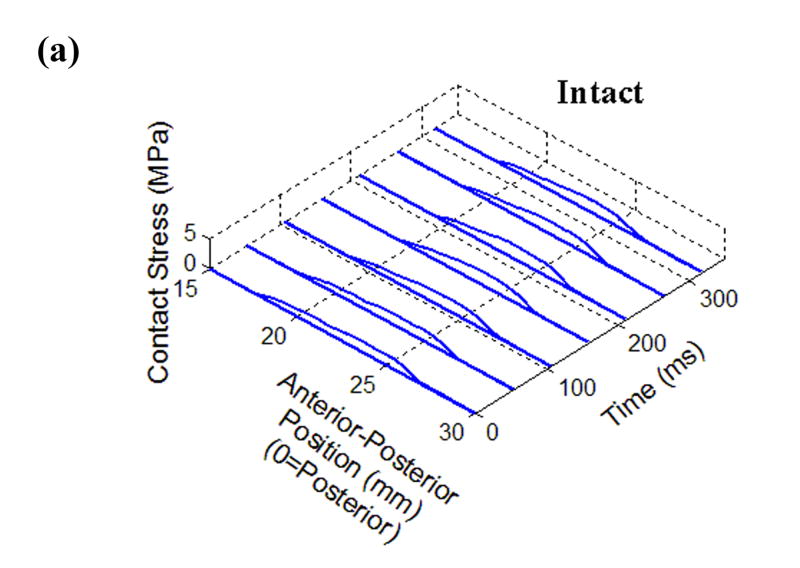
Figure 2.

Figure 2

Figure 2

Figure 2

Figure 2

Open in a new tab

Time histories of Tekscan contact stresses from (a) Intact, (b) Anatomically Reduced, (c) Metastable, and (d) Unstable load cases. The dashed line at 21 mm denotes the fracture location, where applicable.

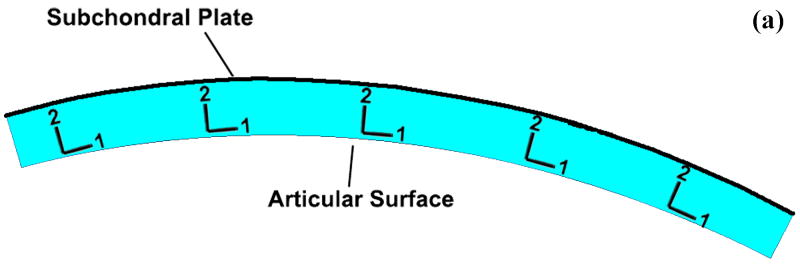
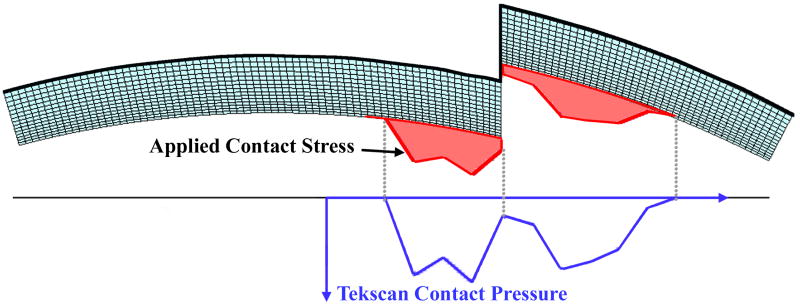
To generate the mesh, a mid-sagittal section profile of the distal articular surface was replicated from a Sawbones surrogate tibia model. This profile was extruded to define a uniformly thick 1.5 mm cartilage layer. The cartilage layer was meshed with 1310 4-node plane strain elements (ABAQUS type CPE4P), that support a degree of freedom for fluid pressure. For the step-off and anatomically reduced models, the anterior 1/3 of the cartilage was detached from the posterior 2/3, and for the step-off models this fragment was displaced 2 mm proximally (Fig. 3). The cartilage was considered rigidly fixed at its interface with the subchondral plate. The above-described four load profiles were applied to the articular surface, in the form of time-varying distributed surface pressures (Fig. 4). It is important to note that the analyses performed are not contact problems. Rather, contact pressures obtained via cadaveric tests are applied to the tibial articular surface as external loads. Since the Tekscan sensor used to record the contact pressures records the total load passing through the joint, these pressures were applied to the articular surface as total pressures as opposed to pressures on only the fluid or solid phase.

Figure 3.

Figure 3

Figure 3

Figure 3

Open in a new tab

Cartilage geometry for (a) intact, (b) anatomically reduced, and (c) step-off models. Local material directions are as indicated in Figure 3a.

Figure 4.

Figure 4

Open in a new tab

Load profile application. Tekscan contact pressures are registered up to the articular surface of the FE model. The contact pressures are then applied as normal distributed pressures as shown by the shaded profile. The contact pressure profile shown here is for one instant in time; it varies both in magnitude and distribution throughout the analysis.

On the models including a step-off, the fluid was allowed to drain freely from the fractured surface (that is, the surfaces normal to the articular surface that have been exposed by the fracture) by setting the pore fluid pressure to zero. On the articular surface, Hou et al. have shown for poroelastic contact models that regions in contact should satisfy the biphasic jump condition, that is, the fluid velocity should be continuous across the contact interface (Hou et al., 1989), while non-contacting regions should be free-draining. Since the current formulation is not formally a contact model, the biphasic jump condition cannot be precisely implemented, although a close approximation was implemented by assuming that any fluid flow between contacting cartilage would be negligible compared to the fluid flow from the free-draining regions. This seemed particularly appropriate for the current study since the Tekscan sensor from which the contact pressures were taken would effectively seal the surface to fluid flow. The fluid boundary conditions were implemented by using the FLOW subroutine in ABAQUS to set the outward normal fluid velocity to be dependent on the applied articular surface traction such that:

Vn=ks∗Pandks= ≫k/L where unloaded (free-draining)ks=0 where loaded (sealed) (1)

Here, Vn is the outward normal fluid velocity, ks is the surface permeability, k is the permeability of the underlying elements, L is a characteristic length of the underlying elements, and P is the pore fluid pressure at the articular surface. By setting ks ≈ 103*k/L in the unloaded regions, free-draining (pore fluid pressure = 0) conditions were enforced, while ks = 0 in the loaded region prevented fluid flow in the implied region of contact. The initial void ratio was set to 4, meaning that 80% of the cartilage volume was fluid (Mow et al., 2005).

A transversely-isotropic, poroelastic cartilage material model was used in this study. A local material orientation was used (Figure 3), with the ‘1’ direction being parallel to the articular surface and the ‘2’ direction normal to the surface. The ‘1-3’ plane is therefore the plane of isotropy. The permeability used was 1.14×10-15 m4/(N-s) (Athanasiou et al., 1991). The fluid was assumed to be water, with a density of 1 g/cm3. The normal (E2) and tangential (E1=E3) moduli of elasticity were 0.55 MPa and 33 MPa, respectively (Boschetti et al., 2004; Charlebois et al., 2004). Two distinct Poisson ratios are required for transverse isotropy: ν13 characterizes the response within the plane of isotropy to stress within that plane, while ν23 characterizes the response within the plane of isotropy to stress normal to that plane. For this study, ν13 was taken as equal to 0.146 (Federico et al., 2005), and ν23 as 0.074 (Athanasiou et al., 1991). Reported values for the shear modulus in the ‘1-2’ plane vary widely, from 0.1 to 4 MPa (Appleyard et al., 2001; Oakley et al., 2004). Most available measurements of shear moduli are taken in the superficial or middle zones; however, very recently researchers have begun to show that shear stiffness increases in the deeper layers, similar to compressive stiffness (Buckley et al., 2007; Wong et al., 2007). Since the dominant shearing action in the present study occurs at the cartilage-subchondral plate interface, a shear modulus of 2.5 MPa was used for this analysis, in order to fall within the stiffer end of the reported range of shear moduli. An overview of studies of the shear modulus of articular cartilage can be found in the supplemental material published electronically with this paper.

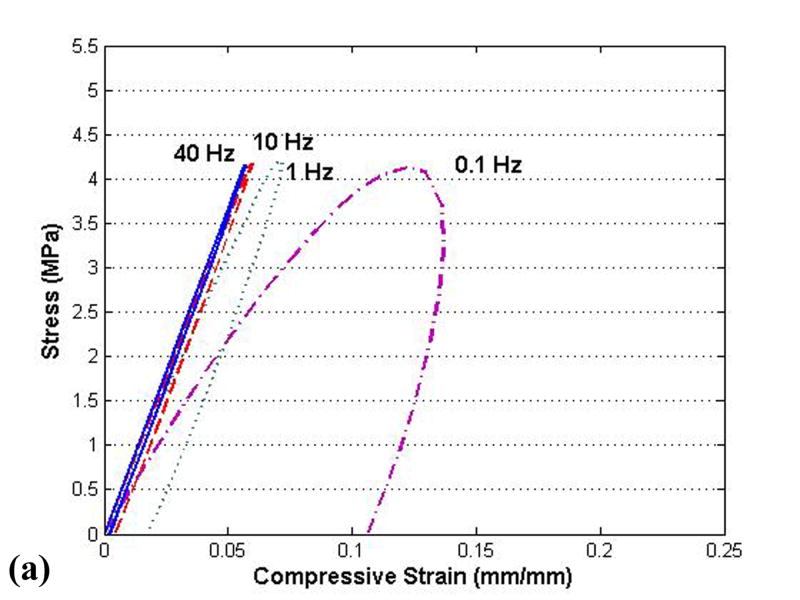
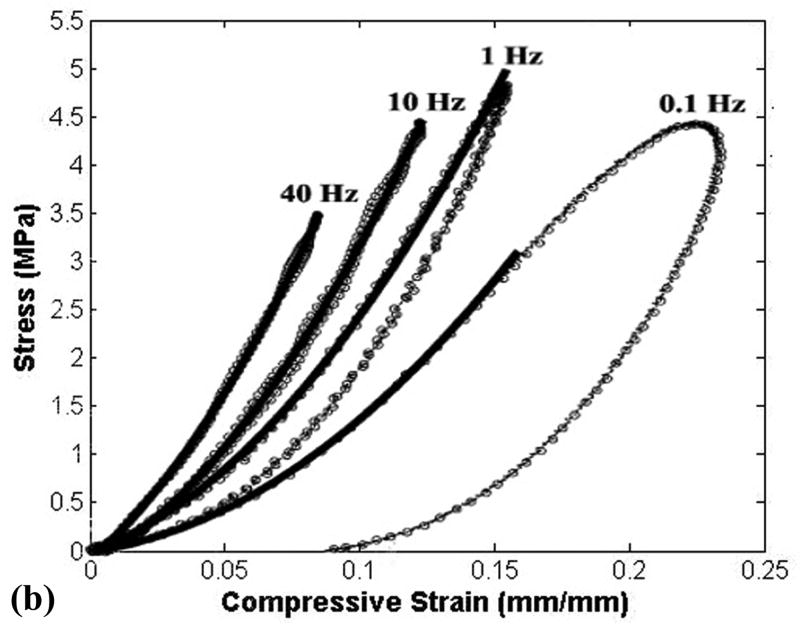
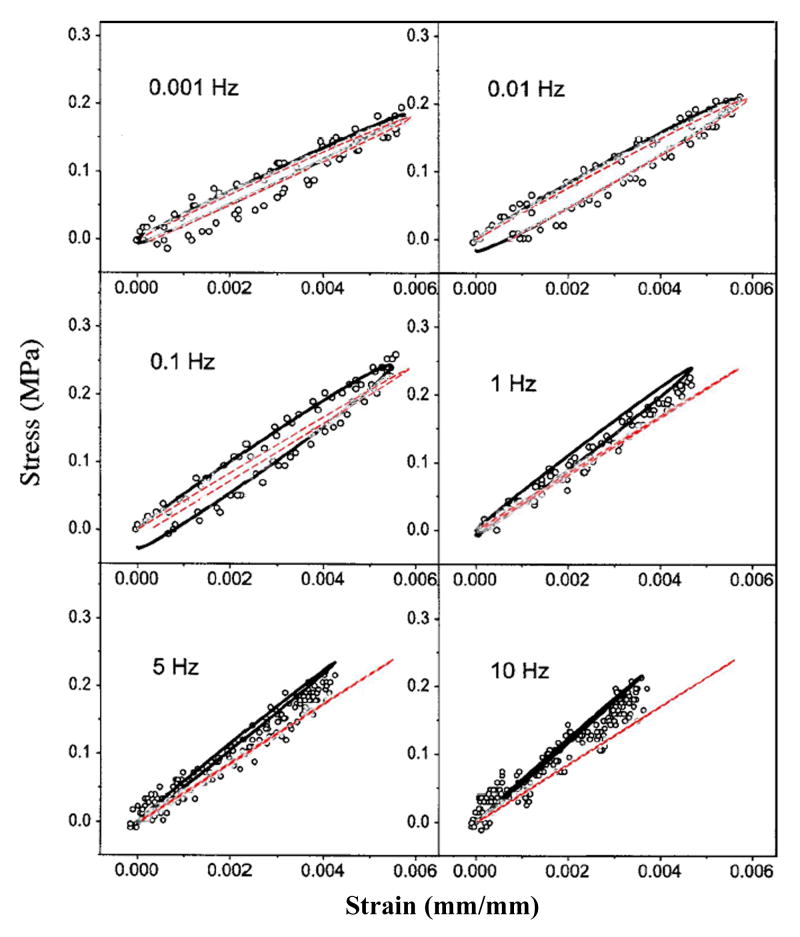
Simulations were first run for geometrically simplified specimens, to evaluate the behavior of the above material model, with geometry, loading, and boundary conditions chosen to match those documented by Park et al. in their dynamic physical tests of cylinders in compression (Park et al., 2004) and of strips in tension (Park and Ateshian, 2006). Simulation of unconfined compression (Fig. 5) showed reasonable nominal agreement for apparent stiffness, for levels of hysteresis, and for rate-dependence, implying appropriate values of normal stiffness and permeability in the numerical model. Similarly reasonable rate-dependence of stiffness and hysteresis were apparent in the tensile results (Fig. 6). This latter correspondence with experimentally measured tensile stiffness lent credence to the transverse stiffness of the model.

Figure 5.

Figure 5

Figure 5

Open in a new tab

(a) Results from present finite element tests of material behavior of cylindrical plugs loaded in unconfined compression, compared to corresponding published results (b) from Park et al. (Park et al., 2004, by permission1). The stress-strain curves from Park et al. are for one typical specimen, which was utilized to demonstrate the rate-dependence and hysteresis of the cartilage. However, this particular specimen is approximately 1.8 times softer than their reported average material behavior, suggesting an even closer correspondence of the present FE results.

1Reprinted from Osteoarthritis and Cartilage, Volume 12, Park S, Hung CT, Ateshian GA, “Mechanical response of bovine articular cartilage under dynamic unconfined compression loading at physiological stress levels.” pp. 65-73, Copyright 2004, with permission from Osteoarthritis Research Society International.

Figure 6.

Figure 6

Open in a new tab

Results from tests of material behavior in tension. Results for the present material model (dashed lines) are overlaid on published results from Park et al. (solid lines) (Park and Ateshian, 2006, by permission2).

2Reprinted from Journal of Biomechanical Engineering, Volume 128, Park S, Ateshian GA, “Dynamic response of immature bovine articular cartilage in tension and compression, and nonlinear viscoelastic modeling of the tensile response.” pp. 623-630, Copyright 2006, with permission from the American Society of Mechanical Engineers.

The simulations were performed using the poroelastic analysis in ABAQUS v. 6.5.1. Solid matrix stress components and invariants were output, along with fluid pressure, relative fluid velocity, and void ratio. Temporal gradients were calculated via Python script, using 3-point Lagrangian differencing.

Results

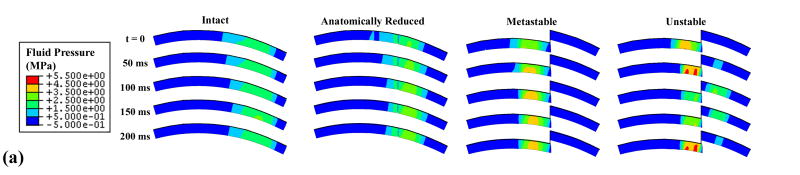
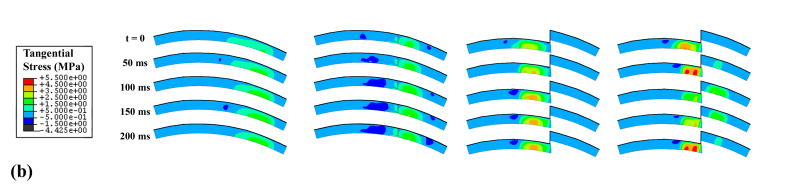
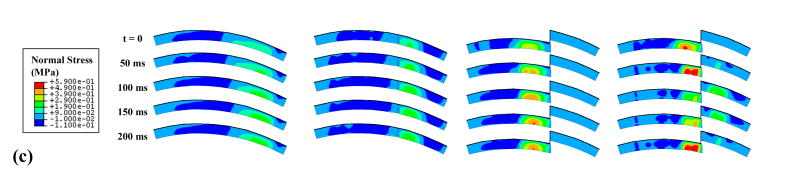
Unstable motion resulted in higher and more concentrated solid matrix stresses and fluid pressures than did the intact model (Fig. 7). The rapid loading and unloading of the displaced fragment in the unstable model involved fragment full engagement and then disengagement within approximately one-quarter of a second. The stress magnitudes and distributions for the intact model showed little change throughout the simulation. As expected, the anatomically reduced model produced results very similar to the intact model. Peak stresses in the metastable step-off case approached the edge of the incongruity, but the displaced fragment was never loaded.

Figure 7.

Figure 7

Figure 7

Figure 7

Open in a new tab

Comparison of four load case results for (a) fluid pressure, (b) tangential stress in solid matrix, and (c) normal stress in solid matrix.

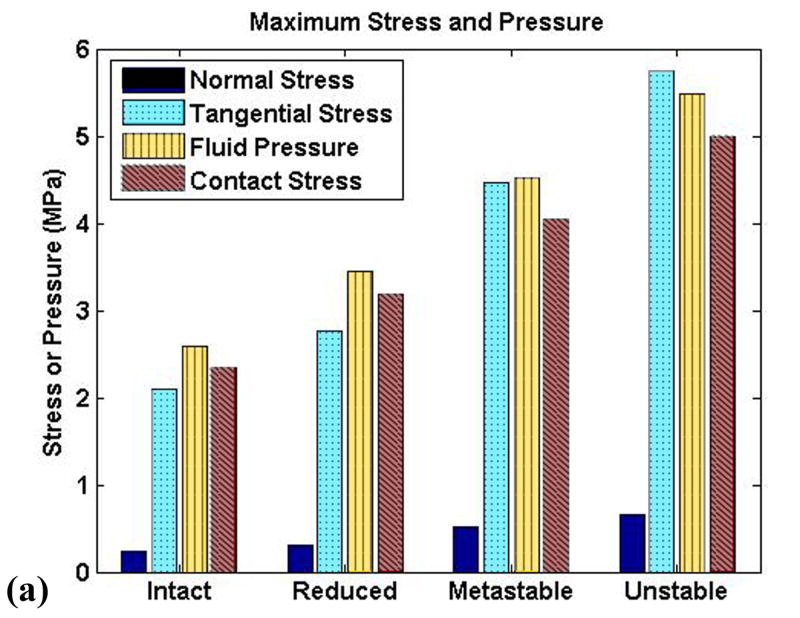
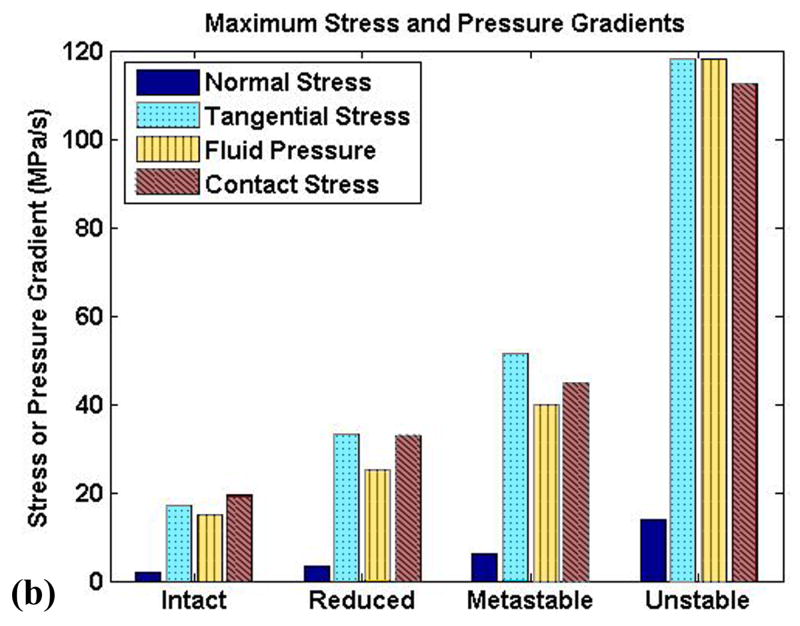
The (spatially and temporally) maximum solid matrix stress components increased monotonically from the intact model to the unstable model (Fig. 8a), reflecting the increase in contact pressure. The fluid pressure also increased correspondingly, with the unstable model having peak pressures more than two times higher than the intact model, and with instantaneous peak temporal gradients of stress and pressure increasing seven-fold (Fig. 8b). The rate of load application increased monotonically from intact to unstable, but with a dramatic jump between the metastable and unstable models. The temporal gradients of fluid pressure and of the tangential component of the solid matrix stress closely mirrored that of the applied load. The normal stress component temporal gradient showed similar trends, but of lesser magnitude.

Figure 8.

Figure 8

Figure 8

Open in a new tab

Peak (a) stresses and (b) temporal stress gradients for the four study cases.

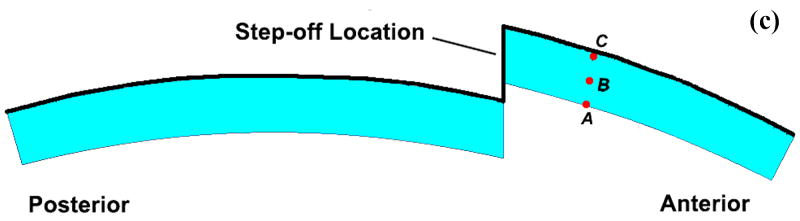
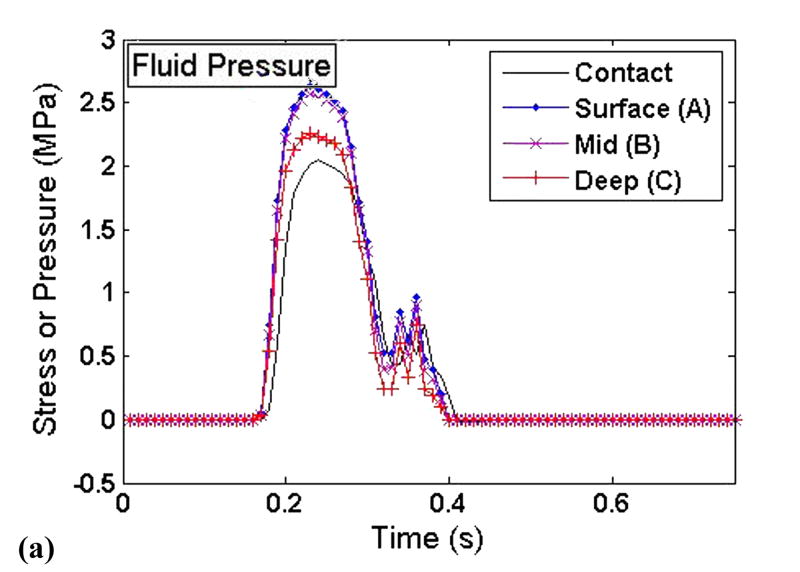
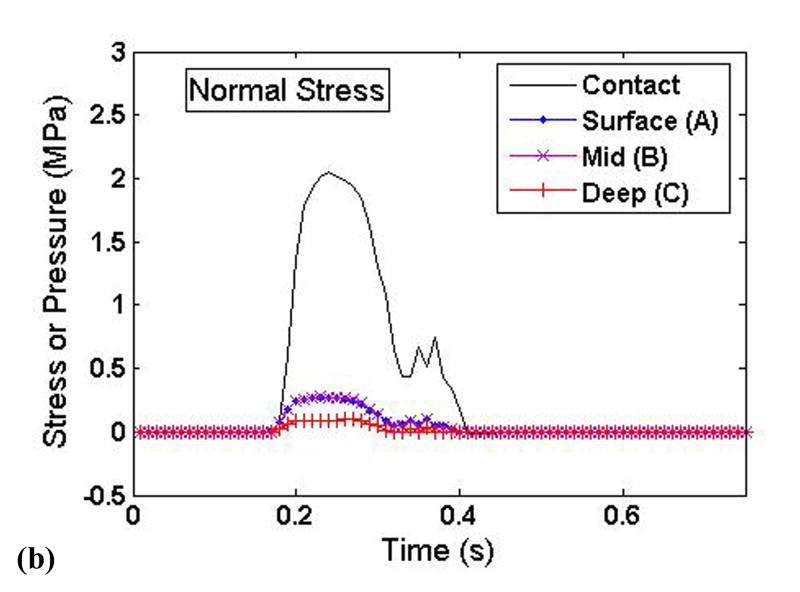
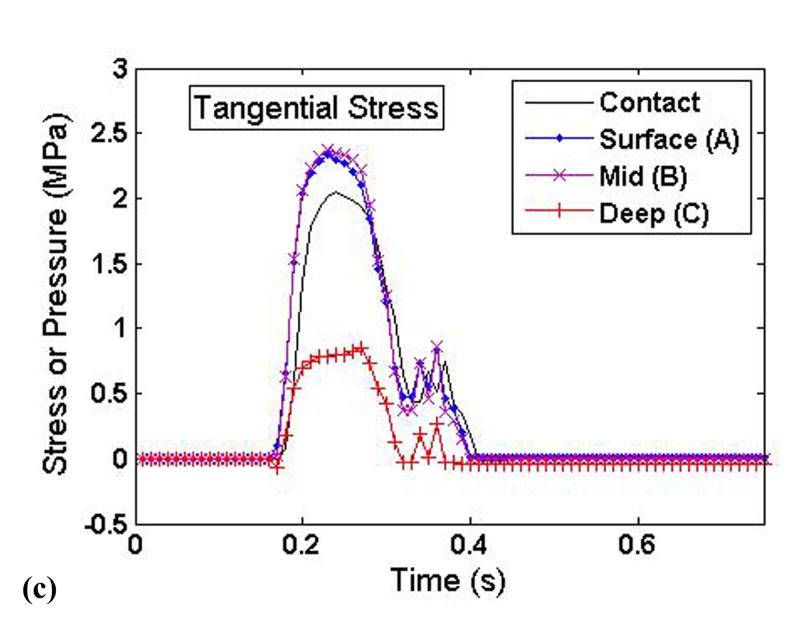
To elucidate the interplay of the solid and fluid phases of cartilage under severe loading transients, time histories of the stress components and the fluid pressure were taken from three points at varying cartilage depths on the displaced fragment of the unstable model (points A, B, and C in Figure 3). These histories are plotted such that the relative fluid and solid phase load carriage could be evaluated throughout the cartilage depth (Fig. 9).

Figure 9.

Figure 9

Figure 9

Figure 9

Open in a new tab

Time histories of the (a) fluid pressure, (b) solid matrix normal stress, and (c) solid matrix tangential stress at varying cartilage depths on the displaced fragment of the unstable model.

The fluid pressure (Fig. 9a) closely mimicked, and indeed slightly exceeded, the applied contact pressure. There was little depth-wise variation of fluid pressure, with only a slight drop-off occurring in the deepest region of cartilage. By contrast, the tangential solid phase stresses showed a pronounced depth-wise reduction in magnitude (Fig. 9c). The normal component of solid matrix stress was approximately one order of magnitude less than the fluid pressure, and also displayed a significant depth-wise drop (Fig. 9b). The tangential component of solid matrix stress was less than the fluid pressure, although generally within the same order of magnitude.

Discussion

The goal of this study was to quantitatively explore how abrupt appositional shifts in the presence of an unstable step-off articular incongruity affect cartilage stresses, toward appreciating whether such effects might be deleterious to cartilage well-being. In particular, the finite element study presented here allows for the quantification of stresses throughout the depth of the cartilage thickness, as compared to cadaver tests which only offer a picture of stresses on the cartilage surface. Since chondrocytes live throughout the depth of the cartilage, rather than directly on the surface, it is important to include full-thickness cartilage stresses when investigating the relationship between mechanical stress environments and cartilage degeneration. The results from the simulations showed that unstable motion led to appreciable changes in cartilage stress throughout the thickness (Fig. 7), involving more concentration, and more migration anterior-posteriorly over the cartilage. In contrast, the intact model had lower stresses, that were distributed over a larger portion of the cartilage, and that did not change position substantially. The motion of the unstable model, especially across the incongruity, resulted in high peak stresses near the step-off, and in dramatic peak stress transients.

Stress transients have been shown to be an important consideration for cartilage health and osteoarthritis. Milentijevic and Torzilli found cell death in cartilage loaded at 25 MPa/s (Milentijevic and Torzilli, 2005), a loading rate exceeded by all cases in the present study except the fully intact model. This suggests that even very small amounts of instability may compromise chondrocyte viability, especially with chronic repetition. In another study, Chen et al. subjected canine cartilage explants to loads between 2.5 and 20 MPa. In this experiment, cartilage matrix damage occurred once the loading rate exceeded 30 MPa/s, regardless of the loading magnitude (Chen et al., 1999). Furthermore, Quinn et al. found that at sub-impact (but still abnormal) loading rates, cell death was localized primarily within the superficial region, a finding also reflected in the work of Milentijevic and Torzilli (Milentijevic and Torzilli, 2005; Quinn et al., 2001). This correlates well with results from the present study, regarding maximum solid matrix stress transients and maximum fluid pressure transients occuring near the articular surface.

The finding regarding the majority of load being carried by the fluid phase (Fig. 9) corroborates similar findings by others (Krishnan et al., 2003; Park et al., 2003). This result is not surprising, considering the low compressive stiffness of the solid matrix. The high stresses in the tangential direction are a result of the fluid pressure. During compression, the fluid phase attempts to flow laterally out from under the load, but the extremely low permeability prevents the fluid from doing so without deforming the solid phase in the direction of flow. Due to the high tangential stiffness of the solid matrix, the flow of the fluid phase is severely restricted. The fluid under the applied load pressurizes, thus carrying the normal load and increasing the tangential stress. Borrelli et al. hypothesized that cartilage fracture under sudden loads is a result of collagen fibril rupture (Borrelli et al., 1997), a contention supported by the high tangential stresses exhibited in this study.

As expected, the fluid phase was found to pressurize very quickly in the unstable load case, in response to the sudden engagement of the displaced fragment. The results shown in Figure 7a show that this fluid pressurization was nearly uniform throughout the cartilage depth, effectively resulting in a hydrostatically pressurized contact region in the most rapidly loaded section. In contrast, the solid matrix stress components decreased in magnitude throughout the cartilage depth. This indicates that the fluid phase not only carried the predominant portion of the load, but that it redistributed some of that load over a larger area, resulting in depth-wise decrease of solid matrix stresses. In other regions of the unstable model, including near the step-off on the non-displaced portion of the cartilage, the fluid pressurization is much less uniform, displaying considerable spatial variation. The abnormalities of fluid pressure seen in this study would of course also affect the loading and deformation of individual chondrocytes (Wu and Herzog, 2006).

The present study has limitations inherent in the simplifications invoked for the cartilage constitutive model. Human cartilage is not homogeneous throughout its depth, as modeled here. On intuitive grounds it might be argued that the tangential stiffness of cartilage would be lowest in the deeper layers, where the orientation of collagen fibrils is primarily normal to the subchondral plate. However, Verteramo and Seedhom have shown that at higher strain rates the tensile stiffness of cartilage in the deep layers is not significantly different from that in the superficial zone (Verteramo and Seedhom, 2004). Furthermore, in the present formulation the cartilage properties for the solid matrix were assumed to be linear elastic. These cartilage properties were chosen - and validated - for physiological loading magnitudes and rates, similar to those expected for this study, to clarify that the effects of this simplification were minimal. Finally, cartilage was modeled using a plane strain formulation, a simplification that appears very reasonable for a step-off, given the geometry under study and the contact stress distributions from the Tekscan measurements. Obviously, many of these simplifications can be redressed in further refinements of this exploratory model.

In summary, this study has demonstrated that unstable motion of an ankle joint with a step-off incongruity caused significant changes in the loading of articular cartilage. Abnormal loading associated with instability resulted in increased stress magnitudes and loading rates. The fluid phase reacted quickly to uptake load, serving to protect the solid matrix from an excessive level of normal stress, but at the expense of elevated solid stresses in the tangential direction. There is of course a potential for chondrocyte damage from such fluid pressurization itself. The changes in the mechanical stress environment documented in this study may be related to the poor clinical outcome of unstable joints described in the Introduction. Continued investigation into the mechano-pathology of post-traumatic OA should help clarify the relative importance of solid matrix stresses, fluid pressure, and their transients in causing OA, to hopefully provide surgeons with more objective information regarding the necessary precision to reduce the propensity for arthritis following intra-articular fracture.

Supplementary Material

01

Acknowledgments

This research was supported by funding from the National Institute of Health (AR48939), the Centers for Disease Control (R49 CCR721745), and a National Science Foundation Graduate Research Fellowship (CMGV). The authors are grateful for technical assistance provided by Drs. Donald D. Anderson, Douglas R. Pedersen, M. James Rudert, and Y. Tochigi.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Appleyard RC, Swain MV, Khanna S, Murrell GA. The accuracy and reliability of a novel handheld dynamic indentation probe for analysing articular cartilage. Physics in Medicine and Biology. 2001;46:541–550. doi: 10.1088/0031-9155/46/2/319. [DOI] [PubMed] [Google Scholar]
  2. Athanasiou KA, Rosenwasser MP, Buckwalter JA, Malinin TI, Mow VC. Interspecies comparisons of in situ intrinsic mechanical properties of distal femoral cartilage. Journal of Orthopaedic Research. 1991;9:330–340. doi: 10.1002/jor.1100090304. [DOI] [PubMed] [Google Scholar]
  3. Borrelli J, Jr, Torzilli PA, Grigiene R, Helfet DL. Effect of impact load on articular cartilage: Development of an intra-articular fracture model. Journal of Orthopaedic Trauma. 1997;11:319–326. doi: 10.1097/00005131-199707000-00003. [DOI] [PubMed] [Google Scholar]
  4. Boschetti F, Pennati G, Gervaso F, Peretti GM, Dubini G. Biomechanical properties of human articular cartilage under compressive loads. Biorheology. 2004;41:159–166. [PubMed] [Google Scholar]
  5. Brown TD, Anderson DD, Nepola JV, Singerman RJ, Pedersen DR, Brand RA. Contact stress aberrations following imprecise reduction of simple tibial plateau fractures. Journal of Orthopaedic Research. 1988;6:851–862. doi: 10.1002/jor.1100060609. [DOI] [PubMed] [Google Scholar]
  6. Brown TD, Johnston RC, Saltzman CL, Marsh JL, Buckwalter JA. Post-traumatic osteoarthritis: A first estimate of incidence, prevalence, and burden of disease. Journal of Orthopaedic Trauma. 2006;20:739–744. doi: 10.1097/01.bot.0000246468.80635.ef. [DOI] [PubMed] [Google Scholar]
  7. Brown TD, Pope DF, Hale JE, Buckwalter JA, Brand RA. Effects of osteochondral defect size on cartilage contact stress. Journal of Orthopaedic Research. 1991;9:559–567. doi: 10.1002/jor.1100090412. [DOI] [PubMed] [Google Scholar]
  8. Buckley MR, Gleghorn JP, Cohen I, Bonassar LJ. Depth dependence of shear properties in articular cartilage. Transactions of the 53rd Annual Meeting of the Orthopaedic Research Society; San Diego, CA. 2007. [Google Scholar]
  9. Buckwalter JA, Brown TD. Joint injury, repair, and remodeling: Roles in post-traumatic osteoarthritis. Clinical Orthopaedics and Related Research. 2004:7–16. [PubMed] [Google Scholar]
  10. Charlebois M, McKee MD, Buschmann MD. Nonlinear tensile properties of bovine articular cartilage and their variation with age and depth. Journal of Biomechanical Engineering. 2004;126:129–137. doi: 10.1115/1.1688771. [DOI] [PubMed] [Google Scholar]
  11. Chen CT, Burton-Wurster N, Lust G, Bank RA, Tekoppele JM. Compositional and metabolic changes in damaged cartilage are peak-stress, stress-rate, and loading-duration dependent. Journal of Orthopaedic Research. 1999;17:870–879. doi: 10.1002/jor.1100170612. [DOI] [PubMed] [Google Scholar]
  12. DiSilvestro MR, Zhu Q, Wong M, Jurvelin JS, Suh JK. Biphasic poroviscoelastic simulation of the unconfined compression of articular cartilage: I--simultaneous prediction of reaction force and lateral displacement. Journal of Biomechanical Engineering. 2001;123:191–197. doi: 10.1115/1.1351890. [DOI] [PubMed] [Google Scholar]
  13. Ewers BJ, Dvoracek-Driksna D, Orth MW, Haut RC. The extent of matrix damage and chondrocyte death in mechanically traumatized articular cartilage explants depends on rate of loading. Journal of Orthopaedic Research. 2001;19:779–784. doi: 10.1016/S0736-0266(01)00006-7. [DOI] [PubMed] [Google Scholar]
  14. Federico S, Grillo A, La Rosa G, Giaquinta G, Herzog W. A transversely isotropic, transversely homogeneous microstructural-statistical model of articular cartilage. Journal of Biomechanics. 2005;38:2008–2018. doi: 10.1016/j.jbiomech.2004.09.020. [DOI] [PubMed] [Google Scholar]
  15. Federico S, La Rosa G, Herzog W, Wu JZ. Effect of fluid boundary conditions on joint contact mechanics and applications to the modeling of osteoarthritic joints. Journal of Biomechanical Engineering. 2004;126:220–225. doi: 10.1115/1.1691445. [DOI] [PubMed] [Google Scholar]
  16. Ferguson SJ, Bryant JT, Ganz R, Ito K. The acetabular labrum seal: A poroelastic finite element model. Clinical Biomechanics (Bristol, Avon) 2000;15:463–468. doi: 10.1016/s0268-0033(99)00099-6. [DOI] [PubMed] [Google Scholar]
  17. Fortin M, Soulhat J, Shirazi-Adl A, Hunziker EB, Buschmann MD. Unconfined compression of articular cartilage: Nonlinear behavior and comparison with a fibril-reinforced biphasic model. Journal of Biomechanical Engineering. 2000;122:189–195. doi: 10.1115/1.429641. [DOI] [PubMed] [Google Scholar]
  18. Han SK, Federico S, Epstein M, Herzog W. An articular cartilage contact model based on real surface geometry. Journal of Biomechanics. 2005;38:179–184. doi: 10.1016/j.jbiomech.2004.03.010. [DOI] [PubMed] [Google Scholar]
  19. Hou JS, Holmes MH, Lai WM, Mow VC. Boundary conditions at the cartilage-synovial fluid interface for joint lubrication and theoretical verifications. Journal of Biomechanical Engineering. 1989;111:78–87. doi: 10.1115/1.3168343. [DOI] [PubMed] [Google Scholar]
  20. Huang CY, Soltz MA, Kopacz M, Mow VC, Ateshian GA. Experimental verification of the roles of intrinsic matrix viscoelasticity and tension-compression nonlinearity in the biphasic response of cartilage. Journal of Biomechanical Engineering. 2003;125:84–93. doi: 10.1115/1.1531656. [DOI] [PubMed] [Google Scholar]
  21. Jeffrey JE, Gregory DW, Aspden RM. Matrix damage and chondrocyte viability following a single impact load on articular cartilage. Archives of Biochemistry and Biophysics. 1995;322:87–96. doi: 10.1006/abbi.1995.1439. [DOI] [PubMed] [Google Scholar]
  22. Kannus P, Jarvinen M. Osteoarthrosis in a knee joint due to chronic posttraumatic insufficiency of the medial collateral ligament. Nine-year follow-up. Clinical Rheumatology. 1988;7:200–207. doi: 10.1007/BF02204455. [DOI] [PubMed] [Google Scholar]
  23. Krishnan R, Park S, Eckstein F, Ateshian GA. Inhomogeneous cartilage properties enhance superficial interstitial fluid support and frictional properties, but do not provide a homogeneous state of stress. Journal of Biomechanical Engineering. 2003;125:569–577. doi: 10.1115/1.1610018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Kurz B, Jin M, Patwari P, Cheng DM, Lark MW, Grodzinsky AJ. Biosynthetic response and mechanical properties of articular cartilage after injurious compression. Journal of Orthopaedic Research. 2001;19:1140–1146. doi: 10.1016/S0736-0266(01)00033-X. [DOI] [PubMed] [Google Scholar]
  25. Lansinger O, Bergman B, Korner L, Andersson GBJ. Tibial condylar fractures. A twenty-year follow-up. Journal of Bone and Joint Surgery. 1986;68:13–19. American. [PubMed] [Google Scholar]
  26. Li LP, Herzog W. The role of viscoelasticity of collagen fibers in articular cartilage: Theory and numerical formulation. Biorheology. 2004;41:181–194. [PubMed] [Google Scholar]
  27. Li LP, Shirazi-Adl A, Buschmann MD. Alterations in mechanical behaviour of articular cartilage due to changes in depth varying material properties--a nonhomogeneous poroelastic model study. Computer Methods in Biomechanics and Biomedical Engineering. 2002;5:45–52. doi: 10.1080/10255840290008088. [DOI] [PubMed] [Google Scholar]
  28. Li LP, Soulhat J, Buschmann MD, Shirazi-Adl A. Nonlinear analysis of cartilage in unconfined ramp compression using a fibril reinforced poroelastic model. Clinical Biomechanics (Bristol, Avon) 1999;14:673–682. doi: 10.1016/s0268-0033(99)00013-3. [DOI] [PubMed] [Google Scholar]
  29. Lovasz G, Park SH, Ebramzadeh E, Benya PD, Llinas A, Bellyei A, Luck JV, Jr, Sarmiento A. Characteristics of degeneration in an unstable knee with a coronal surface step-off. Journal of Bone and Joint Surgery. 2001;83:428–436. doi: 10.1302/0301-620x.83b3.9674. British. [DOI] [PubMed] [Google Scholar]
  30. McKinley TO, Rudert MJ, Koos DC, Brown TD. Incongruity versus instability in the etiology of posttraumatic arthritis. Clinical Orthopaedics and Related Research. 2004:44–51. doi: 10.1097/01.blo.0000131639.89143.26. [DOI] [PubMed] [Google Scholar]
  31. McKinley TO, Rudert MJ, Koos DC, Pedersen DR, Baer TE, Tochigi Y, Brown TD. Contact stress transients during functional loading of ankle stepoff incongruities. Journal of Biomechanics. 2006;39:617–626. doi: 10.1016/j.jbiomech.2005.01.036. [DOI] [PubMed] [Google Scholar]
  32. McKinley TO, Rudert MJ, Tochigi Y, Pedersen DR, Koos DC, Baer TE, Brown TD. Incongruity-dependent changes of contact stress rates in human cadaveric ankles. Journal of Orthopaedic Trauma. 2006;20:732–738. doi: 10.1097/01.bot.0000211150.00919.0e. [DOI] [PubMed] [Google Scholar]
  33. Milentijevic D, Torzilli PA. Influence of stress rate on water loss, matrix deformation and chondrocyte viability in impacted articular cartilage. Journal of Biomechanics. 2005;38:493–502. doi: 10.1016/j.jbiomech.2004.04.016. [DOI] [PubMed] [Google Scholar]
  34. Mow VC, Gu WY, Chen FH. Structure and function of articular cartilage and meniscus. In: Mow VC, Huiskes R, editors. Basic orthopaedic biomechanics and mechanobiology. Lippincott Williams & Wilkins; Philadelphia, PA: 2005. pp. 181–258. [Google Scholar]
  35. Mow VC, Kuei SC, Lai WM, Armstrong CG. Biphasic creep and stress relaxation of articular cartilage in compression? Theory and experiments. Journal of Biomechanical Engineering. 1980;102:73–84. doi: 10.1115/1.3138202. [DOI] [PubMed] [Google Scholar]
  36. Myers ER, Lai WM, Mow VC. A continuum theory and an experiment for the ion-induced swelling behavior of articular cartilage. Journal of Biomechanical Engineering. 1984;106:151–158. doi: 10.1115/1.3138473. [DOI] [PubMed] [Google Scholar]
  37. Oakley SP, Lassere MN, Portek I, Szomor Z, Ghosh P, Kirkham BW, Murrell GA, Wulf S, Appleyard RC. Biomechanical, histologic and macroscopic assessment of articular cartilage in a sheep model of osteoarthritis. Osteoarthritis and Cartilage. 2004;12:667–679. doi: 10.1016/j.joca.2004.05.006. [DOI] [PubMed] [Google Scholar]
  38. Park S, Ateshian GA. Dynamic response of immature bovine articular cartilage in tension and compression, and nonlinear viscoelastic modeling of the tensile response. Journal of Biomechanical Engineering. 2006;128:623–630. doi: 10.1115/1.2206201. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Park S, Hung CT, Ateshian GA. Mechanical response of bovine articular cartilage under dynamic unconfined compression loading at physiological stress levels. Osteoarthritis and Cartilage. 2004;12:65–73. doi: 10.1016/j.joca.2003.08.005. [DOI] [PubMed] [Google Scholar]
  40. Park S, Krishnan R, Nicoll SB, Ateshian GA. Cartilage interstitial fluid load support in unconfined compression. Journal of Biomechanics. 2003;36:1785–1796. doi: 10.1016/s0021-9290(03)00231-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Quinn TM, Allen RG, Schalet BJ, Perumbuli P, Hunziker EB. Matrix and cell injury due to sub-impact loading of adult bovine articular cartilage explants: Effects of strain rate and peak stress. Journal of Orthopaedic Research. 2001;19:242–249. doi: 10.1016/S0736-0266(00)00025-5. [DOI] [PubMed] [Google Scholar]
  42. Rasmussen PS. Tibial condylar fractures. Impairment of knee joint stability as an indication for surgical treatment. Journal of Bone and Joint Surgery. 1973;55:1331–1350. American. [PubMed] [Google Scholar]
  43. Simon BR. Multiphasic poroelastic finite element models for soft tissue structures. Applied Mechanics Reviews. 1992;45:191–218. [Google Scholar]
  44. Soltz MA, Ateshian GA. A conewise linear elasticity mixture model for the analysis of tension-compression nonlinearity in articular cartilage. Journal of Biomechanical Engineering. 2000;122:576–586. doi: 10.1115/1.1324669. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Thompson RC, Jr, Oegema TR, Jr, Lewis JL, Wallace L. Osteoarthrotic changes after acute transarticular load. An animal model. Journal of Bone and Joint Surgery. 1991;73:990–1001. American. [PubMed] [Google Scholar]
  46. Verteramo A, Seedhom BB. Zonal and directional variations in tensile properties of bovine articular cartilage with special reference to strain rate variation. Biorheology. 2004;41:203–213. [PubMed] [Google Scholar]
  47. Wilson W, van Donkelaar CC, van Rietbergen B, Ito K, Huiskes R. Stresses in the local collagen network of articular cartilage: A poroviscoelastic fibril-reinforced finite element study. Journal of Biomechanics. 2004;37:357–366. doi: 10.1016/s0021-9290(03)00267-7. [DOI] [PubMed] [Google Scholar]
  48. Wong BL, Bae WC, Chun J, Gratz KR, Sah RL. Micro-mechanics of cartilage articulation: Effect of degeneration on shear deformation. Transactions of the 53rd Annual Meeting of the Orthopaedic Research Society; San Diego, CA. 2007. [Google Scholar]
  49. Wu JZ, Herzog W. Analysis of the mechanical behavior of chondrocytes in unconfined compression tests for cyclic loading. Journal of Biomechanics. 2006;39:603–616. doi: 10.1016/j.jbiomech.2005.01.007. [DOI] [PubMed] [Google Scholar]
  50. Yang Z, Smolinski P. Dynamic finite element modeling of poroviscoelastic soft tissue. Computer Methods in Biomechanics and Biomedical Engineering. 2006;9:7–16. doi: 10.1080/10255840500529540. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

01
NIHMS34228-supplement-01.tif (714KB, tif)

RESOURCES