Theoretical Calculations of the Catalytic Triad in Short-Chain Alcohol Dehydrogenases/Reductases

Abstract

Three highly conserved active site residues (Ser, Tyr, and Lys) of the family of short-chain alcohol dehydrogenases/reductases (SDRs) were demonstrated to be essential for catalytic activity and have been denoted the catalytic triad of SDRs. In this study computational methods were adopted to study the ionization properties of these amino acids in SDRs from Drosophila melanogaster and Drosophila lebanonensis. Three enzyme models, with different ionization scenarios of the catalytic triad that might be possible when inhibitors bind to the enzyme cofactor complex, were constructed. The binding of the two alcohol competitive inhibitors were studied using automatic docking by the Internal Coordinate Mechanics program, molecular dynamic (MD) simulations with the AMBER program package, calculation of the free energy of ligand binding by the linear interaction energy method, and the hydropathic interactions force field. The calculations indicated that deprotonated Tyr acts as a strong base in the binary enzyme-NAD⁺ complex. Molecular dynamic simulations for 5 ns confirmed that deprotonated Tyr is essential for anchoring and orientating the inhibitors at the active site, which might be a general trend for the family of SDRs. The findings here have implications for the development of therapeutically important SDR inhibitors.

INTRODUCTION

The enzymes involved in catalyzing oxidation of alcohols and reduction of aldehydes/ketones by using nicotinamide adenine dinucleotide phosphate (NAD(P)(H)) as a coenzyme are termed alcohol dehydrogenase (ADH; Enzyme Commission number (EC) 1.1.1.1). These enzymes are found in almost all organisms; and despite their similar functions, they differ in primary as well as three-dimensional (3D) structures. Hence, they are classified into different enzyme families such as the short-chain dehydrogenase/reductase (SDR) and medium-chain dehydrogenase/reductase superfamilies (1–3). The SDR family constitutes a functionally heterogeneous group of enzymes with >3000 primary sequences spanning several EC classes (1,4–6). The pairwise sequence identities within the SDR family is quite low (10%–30%), whereas their 3D structures show a highly similar α/β folding pattern (1,6). As SDRs are expected to be involved in a variety of human diseases, they are potential therapeutic targets (6).

The ADHs in Drosophila (DADH) belong to the SDR family, whose physiological functions involve metabolism and detoxification of alcohols, with ethanol as an energy source (7,8). Nearly 60 DADHs from different Drosophila species are known and biochemically characterized (9). Some DADHs have been studied structurally (10–12) (Fig. 1) and by enzyme kinetics to elucidate their structure-function relationships (13–15). DADHs consist of two identical subunits of ∼27,000 Da each (∼255 amino acids) (16,17), where each subunit folds into a central seven- or eight-stranded β-sheet, flanked on each side by three α-helices and a loop region that forms the active site (10,11). DADHs convert short- and medium-chain primary and secondary alcohols to their corresponding aldehydes/ketones (15), using NAD⁺ as coenzyme (Eq. 1). In addition, the DADHs oxidize aldehydes to their corresponding carboxylic acids (Eq. 2) (18–20):

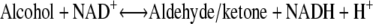(1)

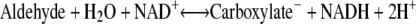(2)

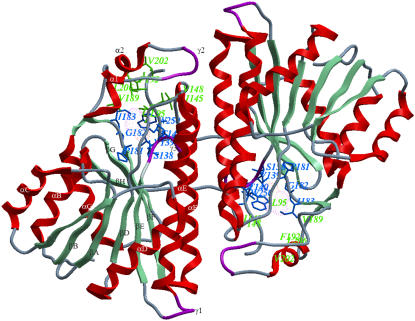
FIGURE 1.

Ribbon representation of the dimer association of DlADH (PDB ID: 1SBY). Secondary structure nomenclature is as suggested in the publication of the x-ray structure (10) and is shown for one of the subunits. Amino acids lining the R1 and R2 pockets of the active site are shown by the green and blue stick models, respectively. The color coding of secondary structures is red for α-helices, aquamarine for β-strands, magenta for 3–10 helices (γ), and blue for loops. The designation of the active site pockets was followed from the description of crystallographic studies by Benach (11).

Secondary alcohols were found to be better substrates than primary alcohols; and R(−) secondary alcohols are better substrates than S(+) secondary alcohols (15). Enzyme kinetic studies indicate a compulsory ordered pathway (Scheme 1) where the coenzyme binds before the substrate (15,21). Site-directed mutagenesis and structural studies suggest that one amino acid between β-strand E and α-helix F (Ser-138) and two amino acids in α-helix F (Tyr-151 and Lys-155) (Drosophila lebanonensis numbering) at the active site are involved in the catalytic reaction (1,22,23) (Fig. 1). These amino acids are denoted the catalytic triad of SDRs (10,11,22–24) and represent the most characteristic feature of the entire family (1,25,26). Tyr-151 is strictly conserved, whereas Ser-138 and Lys-155 are conserved in most of the SDRs (1).

SCHEME 1.

Compulsory ordered ternary complex mechanism describing the kinetics of DADH catalysis. O is NAD⁺, R is NADH, S is alcohol, and P is aldehyde/ketone. The constants (k and k′) are individual kinetic constants.

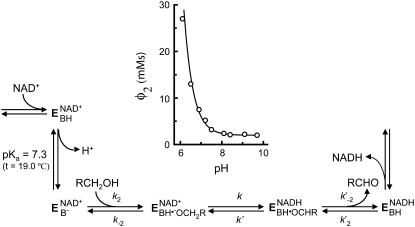
Experimental studies of DADHs showed that a proton at the active site is released upon formation of the binary E·NAD⁺ complex (Fig. 2), whereas protons are not released upon formation of the ternary complexes or the binary E·NADH complex (27–30). The release of proton from the binary E·NAD⁺ complex is essential for alcohol binding and catalysis as well as for binding alcohol competitive inhibitors. The amino acid responsible for the proton release is not known. pH dependence of ligand binding indicated that Tyr-151 or Lys-155 could be responsible for the proton release (30). However, comparison of the reaction mechanism of DADHs with that of horse liver ADH indicated that the proton release produced a negative charge at the active site. This negative charge acts as a strong base or nucleophile for extracting a proton from the bound alcohol. The most plausible candidate for the proton release was Tyr-151 (28). Later, x-ray crystallographic studies showed that the OH group of the substrates in the ternary complexes is located between Tyr-151 and Ser-138 (11,12,22,24). In these structures, the Tyr-OH group is positioned in a hydrogen-bonding distance to the O2′ atom of the NAD-ribosyl moiety, and Lys-155 is positioned close to both the O2′ and O3′ atoms of NAD-ribosyl moiety. Site-directed mutagenesis studies of Tyr-151, Lys-155, and Ser-138 in DADH and other SDRs indicated that all three residues were important for enzyme activity (31,32). A kinetic study of DADH showed that the pK_a ionization enthalpy of the proton-releasing residue was unusually high, suggesting that Ser-138 rather than Tyr-151 is the catalytic residue (29). In such a scenario, the pK_a value of Tyr-151 is already down perturbated (<6) in the binary E·NAD⁺ complex, and hence not detected during the enzyme kinetic studies. Kinetic studies of two other SDR enzymes suggest that the conserved Tyr acts as the strong base (33,34). A recent study on SDR enzymes reveals a possible water channel in the interior of the enzyme that connects the protein surface with the active site through Lys-155, and hence this channel could be involved in a proton relay system (35). Theoretical calculations of possible ionizable groups in the DADH binary complex result in a pH curve that is almost identical to the experimental curve. In the theoretical curve, the ionization of Tyr-151 and Lys-155 is shown to be coupled (36). The pH dependence of the proton abstraction correlates with the reorganization of the hydrogen-bonding network at the active site, where the O2′ group of the NAD⁺-ribose plays a central role by coupling the Tyr-OH group with the side-chain nitrogen in Lys-155 and the water channel.

FIGURE 2.

Mechanism proposed for DADH catalysis. E represents the enzyme, and BH represents an ionizing group with a pK_a value of 7.1 and 7.3 in DlADH at 23.5°C and 19.0°C, respectively (27,71), and 7.6 in DmADH^S (slow alleloenzyme) at 23.5°C (28,30). The insert shows the variation of Φ₂ with varying pH for DlADH at 19.0°C, where Φ₂ = (1/k₂)(1 + (k₋₂/k)(1 + (k′/k′₋₂))) and the kinetic constants are those in Scheme 1. It was shown that only k₂, i.e., the k_on velocity for the alcohol, varied with pH, and hence Φ₂ = Φ*₂ (1 + ([H⁺]/K_a)). The theoretical curve is based on a pK_a of 7.3 and a Φ*₂ of 2.0 mMs.

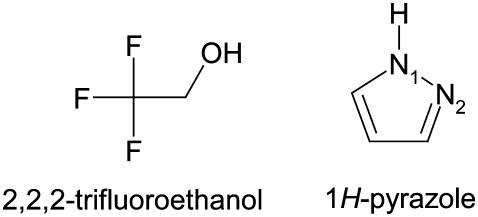
We used molecular modeling of two SDR enzymes to increase the understanding of the role of the triad in the catalytic process. The enzyme models of D. lebanonensis ADH (DlADH) and Drosophila melanogaster ADH (DmADH) were created with different ionization scenarios of the triad that might be possible upon inhibitor binding. As the catalytic triad is highly conserved among the SDRs, knowledge about the ionization of this triad of DlADH and DmADH may help to develop inhibitors of human SDRs. Based on their experimental dissociation constants (Kd) with DlADH (27) and DmADH (30) (Table 1), two alcohol competitive inhibitors, pyrazole (PYR) and 2,2,2-trifluoroethanol (TFE) (Fig. 3), were automatically docked by the Internal Coordinate Mechanics (ICM) program, version 3.0.28 (37), to the active site of DlADH (Protein Data Bank (PDB) ID: 1SBY) and DmADH (PDB ID: 1MG5). The complexes were studied by molecular dynamic (MD) simulations by the AMBER 7.0 (38) suite of programs, and the free energies of inhibitor binding were calculated with linear interaction energy (LIE) (39–41) and Hydropathic INTeractions (HINT) (42) methods.

TABLE 1.

Experimental inhibition constants (K_EO,_I) obtained from kinetic studies

	DmADH (30)			DlADH (27,66)
	PYR	TFE		PYR	TFE
pH	KEO,I (μM)	KEO,I (mM)	pH	KEO,I (μM)	KEO,I (mM)
10	4.5 (−7.26)	1.1 (−4.01)	10	12 (−6.69)
9.5	4.3 (−7.29)	1.1 (−4.01)	9.5	14 (−6.58)	2.5 (−3.53)
8.5	4.5 (−7.26)	1.1 (−4.01)	9	12 (−6.69)
7.5	8.8 (−6.86)	2.1 (−3.63)	8	15 (−6.55)
6.6	26 (−6.23)	7.3 (−2.9)	7	22 (−6.32)
5.9	37 (−6.02)	9.3 (−2.7)	6	63 (−5.71)

E = enzyme, O = NAD⁺, and I = inhibitor. The values in parentheses are the corresponding free energy of binding (kcal/mol) calculated by ΔG = −RTlnK_i.

FIGURE 3.

2, 2, 2-trifluoroethanol (TFE) and 1H-PYR.

MATERIALS AND METHODS

The structures of DlADH and DmADH consist of two identical subunits. The docking by ICM was performed in both subunits, whereas 750 ps MD and subsequent LIE calculations were performed for one subunit only. However, for one of the putative ionization scenarios, 5 ns MD followed by LIE analyses were performed for both the subunits of the DADHs.

ICM docking and binding energy calculations

Preparation of enzyme and ligand models

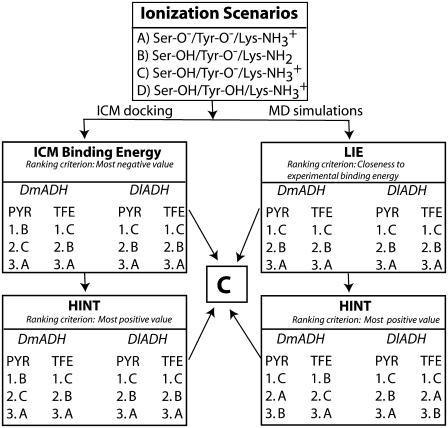
The x-ray crystallographic structure of the ternary complexes—DlADH·NAD⁺·TFE (PDB ID: 1SBY) and DmADH·NADH·acetate (PDB ID: 1MG5)—were loaded into the ICM program, with subsequent deletion of the cofactors and ligand molecules. NAD⁺ was inserted into the DmADH model by superimposing the PDB files 1SBY and 1MG5. The default macro of ICM was used for adding and optimizing the hydrogen atoms, assigning ECEPP/3 (43) partial charges, and subsequent local minimizations for relieving bad contacts. The minimization was carried out in the presence of restraints so that the enzyme conformations remained close to the x-ray crystallographic coordinates. Upon release of a proton, a negative charge at the active site is formed to facilitate ligand binding to the E·NAD⁺ complex. So, enzyme models with three different charge scenarios of the catalytic triad that may explain the experimental observations were constructed for the DADHs. A fourth scenario was also constructed with the entire catalytic triad protonated. Such a scenario should not allow ligand binding to the E·NAD⁺ complex but was included as a test of the docking procedure. Enzyme models with the following charge scenarios were constructed (DlADH numbering):

1. Ser-138 and Tyr-151 deprotonated and Lys-155 protonated ()

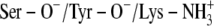2. Ser-138 protonated and Tyr-151 and Lys-155 deprotonated (Ser-OH/Tyr-O⁻/Lys-NH₂)

3. Ser-138 and Lys-155 protonated and Tyr-151 deprotonated ()

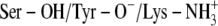4. Ser-138, Tyr-151, and Lys-155 protonated ()

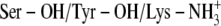The possibility of a coupled ionization between Tyr-151 and Lys-155 as previously suggested by theoretical calculations (36) corresponds to scenario (C). The coordinates of TFE were extracted from PDB ID 1SBY, whereas the structure of PYR was constructed by ICM, as an experimental structure for PYR is not available. The ICM program was used to assign atomic point charges to the inhibitors and to optimize the potential energy using the MMFF94 force field (44).

Docking and scoring protocol

Flexible ligand docking was performed with the default script in ICM for rigid targets with grid potentials into both DmADH and DlADH. Grid maps with grid spacing of 0.5 Å were created manually. The grid maps included the amino acids suggested by the x-ray crystallography complexes as part of the binding site. During the docking process, the ligand position and the conformations were changed randomly with pseudo-Brownian movements of the entire ligand or by rotation of torsion angles followed by a double-energy Monte Carlo (MC) minimization scheme as previously described (37). This procedure included an analytical gradient minimization in the ECEPP/3 force field (43) and an optimization in the MMFF94 force field (44). The metropolis (45) rule was applied to accept or reject the new conformations. Both the length of the docking run and the local minimization were determined automatically, depending on the size and number of the torsion angles of the ligand. A stack of 20 geometrically different target-ligand complexes were accumulated based on their ICM pose scoring. The energy terms used in the process were as follows:

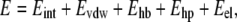(3)

where E_int is the internal energy of the ligand calculated by the ECEPP/3 force field; and E_vdw, E_hb, E_hp, and E_el are the van der Waals forces (vdW), hydrogen bonding, hydrophobic, and electrostatic interactions, respectively, between the target and the ligand. Grid points were assigned on the rigid conformation of the enzyme. On every grid point, the interaction energies were precalculated for efficiency.

Out of the stack of 20 complexes, only “true” poses were considered for further analyses. A pose was defined “true” if TFE was oriented in a binding mode similar to that observed in the 1SBY complex. For PYR, a pose was defined as “true” when 1), the carbon atom with a double bond to the nitrogen atom was oriented into the R1 binding pocket; 2), the N1-H bond was positioned in the region of the catalytic amino acids Ser-138 and Tyr-151; and 3), the N2 was positioned close to the C4 position of nicotine amide ring. Thus, the accepted complexes were further evaluated by calculating the binding energies by ICM.

Calculation of binding energies by ICM

Free energies of binding were calculated using the rapid exact boundary element solution (46–48) of the Poisson equation to evaluate the electrostatic contribution to the interactions. This method globally optimizes the surface side-chain orientations to derive the binding energies from a realistic model of the solvated states of the molecules (49). The energy scheme for partitioning was as follows:

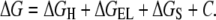(4)

ΔG_H accounts for the variations of the water/nonwater interface area, calculated as the product of the solvent-accessible surface area (calculated by rolling a sphere with a radius of 1.4 Å along the surface of the molecule) by surface tensions (30 cal/mol/Ų). ΔG_EL is the sum of the ΔG_DESOLV (resulting from desolvation of partial charges transferred from aqueous medium to the receptor-binding cavity) and ΔG_COUL (coulombic interactions between ligand and protein). ΔG_S is composed of two terms—ΔG_SSC and ΔG_SL. ΔG_SSC represents the decrease in conformational freedom of the functional groups buried upon complexation. This term is calculated for each side chain from its solvent-accessible surface. ΔG_SL represents the loss of degree of freedom of torsion angles in the ligand upon complexation (0.5 × number of frozen variables) (37). The term C is a constant term that reflects the changes of the entropy of the system due to a decrease in the concentration of free molecules (cratic factor) and loss of rotational/translational degrees of freedom. The following protocol was used for binding energy calculations (49):

1. The energy of the system was optimized by the ICM local minimization procedure.

2. ICM double-energy minimization was performed for relaxing the solvent-accessible side chains.

3. The target and ligand were separated.

4. The ligand torsion angles were unfixed according to the stereochemical considerations followed by MC simulation.

5. For the target, the solvent accessible side chains within 4 Å of the interaction interface were relaxed.

MD simulations and LIE analysis

MDs were performed both for TFE and PYR in complex with the three possible enzyme models of DlADH and DmADH bound to the coenzyme. For LIE analysis, it is necessary to perform separate MDs of target-ligand complexes and the ligands. The SANDER module of the AMBER suite of programs was used for MD. The Cornell et al. (50) force field was used for amino acids, whereas the generalized force field (51) was used for the inhibitors.

The active forms of DlADH and DmADH are dimers of two identical subunits (254 and 255 amino acids, respectively). In both enzymes, the active site of one subunit is closed by the C-terminal end (amino acids 250–254, DlADH nomenclature) of the other subunit (11,52). To reduce computational time, MDs were performed for 750 ps with one subunit. However, to test if such a simplification could affect the LIE calculations, MD simulations for 5 ns with subsequent LIE analyses were also performed for dimeric ternary complexes of TFE and PYR with both DlADH and DmADH (ionization scenario C; ).

Target and ligand preparation for MD

The x-ray crystallographic structure of DlADH·NAD⁺·TFE (PDB ID: 1SBY) was used as the input structure for the simulations of TFE with the different charge scenario models of DlADH. The starting structures of TFE for the MDs with DmADH were created by superimposing the DlADH·NAD⁺·TFE x-ray structure with the slow allelo form DmADH·NADH·acetate (PDB ID: 1MG5) x-ray structure. The starting models with PYR were created by superimposing PYR on top of the TFE structure in the complexes with DlADH and DmADH. The LEAP module of AMBER was used to add hydrogen atoms to enzyme models and to build the PYR structure.

The AMBER force fields lack atomic charges and parameters for NAD⁺, TFE, PYR, and the deprotonated amino acids Tyr and Ser. Models of these chemical entities were initially minimized by the SANDER module of AMBER, followed by optimization with AM1-BCC (53). Electrostatic potentials were calculated quantum mechanically with the Gaussian98 program (54), using the HF/6-31G* basis set. The ANTECHAMER module of AMBER was then used to obtain restrained electrostatic potential-based charges (55).

MD protocol

Most of the calculations were performed using four processors on an HP Superdome (Hewlett Packard, Palo Alto, CA) with 550 MHz, but some were performed with Xeon 2 processors (Intel, Santa Clara, CA). All-atom models of the two inhibitors and the target-ligand complexes were solvated by a rectangular box of TIP3P water molecules (56) and neutralized by adding counterions. The water molecules were ∼10 Å from the solute atoms in all directions (∼10,000 waters for monomeric complexes, ∼16,000 for the dimeric complexes, and ∼500 for the inhibitors). An identical solvation protocol was used for all molecular systems. The particle mesh Ewald method (57) and periodic boundary condition were applied for calculating long-range electrostatic interactions. The SHAKE option (58) with a tolerance of 10⁻⁶ and Berendsen temperature coupling (59) were applied to fix all the bonds involving hydrogen atoms. The time step was 1 fs. A nonbonding cutoff radius of 9 Å was also applied during the MDs. The nonbonded pair list was updated every 15 steps. Trajectory and structure analyses were performed by the CARNAL and ANAL modules of AMBER, and visualization was performed by ICM and visual molecular dynamics (60).

The molecular systems were energy minimized for 2500 cycles, initially by the steepest decent method then by the conjugate gradient method, to remove steric contacts. The obtained complexes were equilibrated for 50 ps by constant volume dynamics followed by 600 ps constant pressure solute equilibration at 1 atm. The temperature fluctuations and the potential energies were monitored during the equilibration period. After equilibration, 100 ps production MD was performed, giving a total MD time of 750 ps. The coordinate sets were collected every 0.2 ps during the production MDs, which were used to calculate the free energies of binding by the LIE method.

Using scenario C (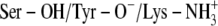), the ternary E·NAD⁺·inhibitor complexes were simulated for 200 ps constant volume dynamics, followed by 4.8 ns constant pressure dynamics to study the atomic fluctuations in both the ligand and the enzyme during dynamics. The trajectories between 840 ps and 5 ns were used for LIE analyses.

Calculation of binding energies with the LIE method

The value of the LIE method is in the linear response approximation of the electrostatic contribution to the free energy of binding. The nonpolar contribution is estimated by using an empirically derived parameter that scales intermolecular vdW interactions from MDs. Two MDs are required: one for the free ligand in solution and another for the target-ligand complex in solution. The LIE equation is as follows:

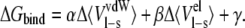(5)

〈〉 Denotes MD or MC averages of the nonbonded vdW and electrostatic (el) interactions of the ligand and its surrounding environment (l-s). Δ indicates the change of average energies between the target-bound and -free states of the ligand. The ANAL module of AMBER was used to decompose the total energy of interactions between the ligand and its surroundings into the vdW and electrostatic contributions. The α- and β-values are coefficients for the nonpolar and polar contributions, respectively, and γ is a constant term. The coefficients of the LIE equation were adopted from Hansson et al. (61) (α = 0.181 for both inhibitors, β = 0.37 and 0.43 for TFE and PYR, respectively, and γ = 0).

HINT scoring

The HINT force field was used for binding energy prediction based on experimentally determined LogP_{octanol/water} values. Therefore, HINT estimates not only the enthalpic but also the entropic contributions to the free energy of binding. All noncovalent interactions (hydrogen bonds, acid-base, hydrophobic-hydrophobic, acid-acid, base-base, hydrophobic-polar) are analyzed and scored using the same mathematical protocol. The partition method for protein is dictionary (62) by which HINT calculates the LogP_{octanol/water} based on residue type and solvent condition. Ligands are usually analyzed by an approach adopted from Hansch and Leo's CLOG-P method (63). The total HINT score is the sum of all atom-atom interactions (42). As different ionization patterns were analyzed, the inferred option was used as the solvent condition to automatically choose the state of each amino acid in the protein. The HINT option that corrects the S_i terms for backbone amide nitrogens (64) by adding 20 Ų was used in this study to improve the relative energetics of inter- and intramolecular hydrogen bonds involving nitrogens. HINT scores were calculated using the “all” options, which treat all hydrogens explicitly.

The HINT calculation was performed on the monomeric complexes from MDs and on the dimeric complexes generated by ICM docking. The optimum pH level of inhibitor binding to the enzymes may not correspond to the pH at which crystallographic structures were solved or binding analyses were experimentally performed. HINT scores suggest a significant correlation between the experimental and computational titration curves, leading to the identification of the best HINT score model as the most probable protonation state (65). Unlike the binding energies calculated by ICM and LIE, a more positive HINT score indicates stronger interaction.

RESULTS AND DISCUSSION

The DADHs have been extensively studied by enzyme kinetics, structural, mutagenesis, and computational studies, and a lot of experimental data have been generated. The structural and mechanistic similarities within the SDR family indicate that the DADHs are valuable model systems for studying the structure-function relationships of SDRs. In this study, theoretical calculations were used to gain insight into the ionization scenario upon inhibitor recognition and binding. Theoretical calculations of target-ligand binding affinities contribute molecular insight into the binding process and complement the macroscopic properties measured by experimental studies. The basic mechanisms behind the effects of biologically active molecules involve a process of molecular recognition and complexation. The electrostatic contribution to the process is very important.

The structural and functional similarities within the SDR family indicate that the ionization of highly conserved catalytic residues at the active site is similar for most of the enzymes within the family. The calculations of DlADH and DmADH with PYR and TFE (both inhibitors form dead-end complexes with the two enzymes (21,27,30,66,67)) should give identical conclusions. The ionization scenario giving the highest HINT score (highest positive value), strongest ICM binding energy (most negative value), and a LIE free energy of binding closest to the experimental binding energy (Table 1) is considered the most probable scenario when inhibitors bind to the binary E·NAD⁺ complex of SDRs.

Ranking the ligand binding affinities by molecular modeling is challenging and important for guiding drug design. Most of the scoring functions developed for ranking protein-ligand poses are based on known 3D structures of both proteins and ligands. The number of known 3D structures is still small, which limits the generation of empirical parameters for the scoring functions. Therefore, a scoring function works best for a set of ligands which are structurally related to the training set of the program.

ICM docking, binding energy calculations, and HINT scoring before MD

ICM has previously been found to identify active ligands in virtual screening studies and to reproduce x-ray crystallographic protein-ligand binding poses (68), indicating that ICM is a valuable tool for docking small molecular enzyme inhibitors. Therefore, the ICM program was used for automatic docking and scoring.

The topology of the alcohol binding cavity in the DADH·NAD⁺ complex was first predicted from kinetic studies with well-defined alcohols (15,66,69,70). The prediction was confirmed and further refined by x-ray crystallographic data from studies of DlADH (11). Briefly, the binding cavity of the DADH is hydrophobic and bifurcated dived into the R1 and R2 pockets based on the interactions with the alkyl chains of secondary alcohols. The R1 pocket is longer than the R2 pocket (10 Å at its longest) and further subdivided into R1(a) and R1(b), whereas R2 is wider than R1.

In this study, the criterion for discriminating the docking poses was similarity with the ligand-binding mode observed in the x-ray crystallographic complex of DlADH (1SBY). In three of the four different ionization scenarios of DlADH, ∼15 of the 20 poses suggested by the docking program were in agreement with the crystallographic pose, as indicated by the root mean-square deviation (RMSD) values in Table 2. However, for ionization scenario D, where the catalytic triad was fully protonated (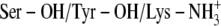), no acceptable binding poses were observed. This is in agreement with the kinetic studies indicating that alcohols and alcohol competitive inhibitors bind only to a binary DADH·NAD⁺ complex that has lost a proton at the active site (Fig. 2) and not to a complex where all three amino acids of the catalytic triad are protonated (27,28,30,71). Thus, the ICM docking results here must be regarded as reliable for DlADH and DmADH and hence gave a plausible picture of the ionization state of the catalytic triad. The binding poses where the ligands showed strongest interactions with the surrounding amino acids are shown in Table 2. Both subunits of the enzymes were included during the docking process and in the subsequent calculations of binding energies.

TABLE 2.

ICM binding energy (kcal/mol) and the corresponding HINT score for binding PYR and TFE to the enzyme models with different ionization scenarios at the active site

	DmADH				DlADH
	PYR		TFE		PYR		TFE
Ionization scenario	ICM	HINT	ICM	HINT	ICM	HINT	ICM	HINT
A:	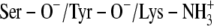−4.34	−113	−6.93	390	−4.13	−23	−7.13 (0.66)	−1148
B: Ser-OH/Tyr-O−/Lys-NH2	−6.21	575	−7.82	649	−5.07	229	−8.25 (0.00)	605
C:	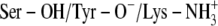−4.98	−79	−8.24	653	−6.11	609	−8.32 (0.03)	654
D:	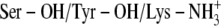NB		NB		NB		NB

Values in parenthesis are the RMSD values in Å of the heavy atoms of TFE from the x-ray crystallographic structure (PDB ID: 1SBY) for that particular pose. NB denotes “not bound”.

The ICM and HINT scoring indicated that TFE binds more strongly to the DADH·NAD⁺ complex than to PYR (Table 2). This is contrary to what the experimentally derived data show (Table 1). PYR and TFE differ in structure, size, and polarity, indicating that their intrinsic errors during the docking process also should differ (Fig. 3). Therefore, it could not be expected that the ranking between PYR and TFE would be in agreement with the experimental observations. The main goal in this study was to determine the ionization scenario that binds the two dead-end inhibitors. Based on the experimental observations, the scenario should be similar in both enzymes for both inhibitors. Therefore, the ICM and HINT scorings were used to obtain a ranking of the PYR-enzyme complexes relative to each other and of the TFE-enzyme complexes relative to each other. The best-scored scenario among four different sets of target-inhibitor complexes (DmADH·NAD⁺·PYR, DlADH·NAD⁺·PYR, DmADH·NAD⁺·TFE, and DlADH·NAD⁺·TFE) was considered the most probable when an inhibitor binds to the binary E·NAD⁺ complex.

Comparison between the experimentally determined and ICM calculated binding energies of TFE for DADHs showed that the ICM calculations strongly overestimated the binding energies with ∼−3.5 to −5 kcal/mol (Tables 1 and 2). Despite this overestimation, the poses characterized by the strongest TFE interaction to the binary DlADH·NAD⁺ complex (Table 2) were very similar to the binding pose of TFE in the x-ray crystallographic structure. Scenario A, with both Ser-138 and Tyr-151 deprotonated, did not reproduce the crystallographic binding pose of TFE to the binary DlADH·NAD⁺ complex as well as scenario C (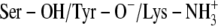) and scenario B (Ser-OH/Tyr-O⁻/Lys-NH₂) did. The TFE docking poses with scenarios B and C were nearly 100% similar to the x-ray crystallographic binding pose of TFE to the binary DlADH·NAD⁺ complex. Both the ICM and HINT scoring ranked scenario C as the best (Table 2 and Scheme 2). The 3D structure of the ternary complex of TFE with DmADH·NAD⁺ has not been experimentally determined. However, the ICM and HINT calculations here led to similar conclusions as those for the DlADH complex, with C as the best-ranked scenario (Table 2 and Scheme 2).

SCHEME 2.

Summary of theoretical calculations. Scenario D is not included in the ranking.

So far, no experimental 3D structures of a DADH·NAD⁺·PYR complex have been reported. Hence we could not compare the docked complex with an experimentally derived structure. In this work, both ICM and HINT scoring ranked scenario B as the best for DmADH and scenario C as the best for DlADH (Table 2 and Scheme 2). Comparison between the experimentally determined (Table 1) and ICM calculated binding energies (Table 2) of PYR for DADHs showed that the ICM calculations reproduced the experimentally determined energies which were in the range from −5.7 to −7.3 kcal/mol.

To summarize the ICM and HINT scoring of the complexes before MDs, scenario C was shown as the best in six out of eight rankings, whereas two of the rankings showed scenario B as the best (Table 2 and Scheme 2). Thus, based on the ICM binding energy and the HINT scoring before MD simulations, scenario C is regarded as the most probable ionization of the catalytic amino acids in the binary DADH·NAD⁺ complex to which the inhibitors, and hence alcohols, bind.

MD simulations

Completeness of equilibration

To obtain reliable and thermally averaged energies for the LIE analysis, the MDs must be sufficiently long. In this study, the vdW and electrostatic contributions to ligand binding between 650 and 750 ps of MDs were used for the LIE analysis of the monomeric complexes, and the corresponding interactions between 840 ps and 5 ns were used for dimeric complexes. During the MD equilibration period, the fluctuations of potential, kinetic, and total energy, temperature, pressure, and volume of the molecular systems were monitored to ensure that the systems were fully equilibrated before the production phase. Table 3 shows the nonbonded interactions between 650 and 750 ps of the MDs with the monomeric enzyme with scenario C. These values indicated that the nonbonded energy converged within the MD period, giving a stable average of the binding energy.

TABLE 3.

Average vdW and electrostatic interaction energies (kcal/mol) between the ligand and the surroundings (DADH and solvent molecules) in the ternary complexes at different time intervals during the 750 ps MDs with the 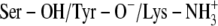scenario using one subunit

			Time (ps)
Ligand	Interaction	DADH	650–700	700–750	650–750
PYR	vdW	DlADH	−11.55 (1.76)	−11.27 (1.57)	−11.41 (1.67)
		DmADH	−10.82 (2.07)	−11.48 (2.91)	−11.15 (2.02)
	electrostatic	DlADH	−13.35 (2.23)	−14.03 (2.21)	−13.69 (2.25)
		DmADH	−15.17 (4.01)	−17.26 (3.85)	−16.21 (4.06)
TFE	vdW	DlADH	−9.53 (2.25)	−9.51 (2.16)	−9.52 (2.20)
		DmADH	−9.64 (2.36)	−9.91 (2.09)	−9.78 (2.23)
	electrostatic	DlADH	−19.61 (2.64)	−19.65 (2.72)	−19.56 (2.56)
		DmADH	−18.45 (2.48)	−18.40 (2.34)	−18.42 (2.41)

Values in parentheses show standard deviations (SD) from the mean value. The MD simulations with the other scenarios followed a similar trend.

van der Waals and electrostatic interactions

A fundamental assumption for the LIE approach is that the nonpolar contributions to the free energy of binding can be estimated by using empirically derived parameters, whereas the electrostatic contribution to the free energy of binding is linearly approximated. Three statistical normality tests (Ryan-Joner, Anderson-Darling, and Kolmogorov-Smirnov) were performed for the vdW interactions between a ligand and its surroundings in all scenarios (72). The p-value was <0.01 for vdW interactions, which indicates that the interaction energies departed significantly from normality. This observation supports the assumption that the parameter α in Eq. 4 should be derived empirically. Similar tests for the electrostatic interactions did not indicate significant departure from normality, supporting the LIE approach that the electrostatic interaction parameter is linearly related.

As the vdW interactions of the ligand with the surrounding amino acids were not normally distributed, a nonparametric analysis of variance (ANOVA) (Kruskal-Wallis) test was performed using MINITAB 14 (73) to study the possible differences in medians of target-ligand vdW interactions in different ionization scenarios. This indicated a highly significant difference in medians (p = 0.000) between the different ionization scenarios for both ligands, denoting that the ligands showed significantly different vdW interactions with the surrounding environments in these scenarios. The parametric tests, one-way ANOVA and the Dunnett test, for electrostatic interactions indicated significant difference (p = 0.000) among the ionization scenarios. These tests support the scope of the LIE method and the use of the LIE method for the molecular systems in this study.

LIE analysis

LIE calculations have previously been found to satisfactorily reproduce experimental binding energies of several molecular systems (39–41). Therefore, it could be expected that a theoretical ionization scenario corresponding to the actual ionization of the residues at the active site would result in a calculated binding energy that correlates with the experimental obtained value. However, when a modeled ionization scenario deviates from the real ionization scenario, the calculated binding energy will also deviate from the experimentally obtained value. The theoretical binding energy will be either larger or smaller than the experimental value, depending on the charge distribution of both the unnatural modeled scenario and the ligand. The calculations of the LIE values are based on MD trajectories, and during MD even an unnatural scenario may adopt favorable interactions with the inhibitor structure and obtain favorable LIE values. Using the LIE approach for calculating protein-ligand complex with charged groups (binding site and ligand) at the binding interface is challenging (74). The absolute binding energy is the difference between the desolvation energy and the protein-ligand complex energy. The LIE approach uses an explicit solvation model, such that the desolvation free energy should be quite reasonably handled. However, charged ligands and charged binding sites correspond to large desolvation and protein-ligand complex energies; and therefore, the calculation of the absolute binding energy may adopt large numerical errors.

In this study we compared binding site architectures with different charge distribution and ligands with different polarity. The differences in the number and distribution of charged groups between the scenarios and the differences in polarity and the size between PYR and TFE may result in different intrinsic errors between the scenarios and between PYR and TFE in the calculation of LIE values (Table 4). The LIE approach is therefore not straightforward for our molecular systems. Our approach was therefore to evaluate the ionization scenarios for each inhibitor separately, and the scenario with the LIE value closest to the experimental binding energies in Table 1 (pH range 6–10) was considered the most probable.

TABLE 4.

Binding free energies (kcal/mol) calculated by the LIE method

	DmADH		DlADH
Ionization scenario	PYR	TFE	PYR	TFE
A: 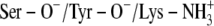*	−12.09	−9.0	−8.52	−8.85
B: Ser-OH/Tyr-O−/Lys-NH2*	−8.06	−7.99	−7.02	−8.39
C: 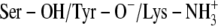*	−6.78	−7.79	−6.47	−7.58
C: 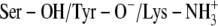†	−7.03‡/−6.50§	−7.99‡/−8.35§	−7.85‡/−7.89§	−8.40‡/−7.60§

^*Energy after MD of the monomer (subunit A).

^†energy after MD of the dimer.

^‡subunit A.

^§subunit B.

As shown in Table 4, LIE values for PYR binding to scenario C were in the range of the experimentally obtained binding energies for both DADHs. The LIE values of −6.78 kcal/mol for DmADH and −6.47 kcal/mol for DlADH are well within the range of the experimentally obtained energies of −6.0 to −7.3 kcal/mol and −5.7 to −6.7 kcal/mol, respectively. The differences in experimentally derived binding energy between the two enzymes are also reflected in the LIE values. The LIE values for scenarios A and B were outside the experimentally derived values for both the enzymes, although scenario B is much closer than scenario A.

As for ICM, the LIE values for TFE binding deviated largely from the experimentally determined binding energies. Contrary to the experimental data, the LIE values also indicated that TFE binds more strongly than PYR to both DADHs. Table 3 indicates that the main reason for that were stronger electrostatic interactions. On average, PYR exhibited ∼−2 kcal/mol stronger vdW interactions than TFE did with the enzymes during 650–750 ps of MDs. This difference is comparable to the experimental observations (Table 1) that indicated ∼−3 kcal/mol stronger binding of PYR than TFE (Table 1). However, for the electrostatic interactions, this was completely reversed (Table 3). The polar TFE corresponds to larger desolvation energy than the stable ring system of PYR, and the calculated LIE values may give larger numerical errors. This suggests that different LIE parameters should be used for TFE and PYR. Scenario C gave the LIE values that were the least overestimated for both enzymes.

Except for the monomeric PYR-DmADH complex, the calculated binding energies of scenario C were stronger after 5 ns of MD with both subunits than after MD with the monomeric enzyme forms. The inhibitors also bound with similar strength to both subunits (Table 4). The reason, most probably, is that the C-terminal of subunit A participates in binding the ligand to subunit B and vice versa, as seen in the x-ray crystallographic structures (10,11). This indicates that different γ-values might be used for monomeric and dimeric LIE calculations of DmADH and DlADH.

In summary, the LIE analysis indicated that scenario C gave LIE values closest to the experimental observation and hence scenario C is regarded as the most probable ionization of the catalytic triad in the binary DADH-NAD⁺ complex that binds inhibitors and alcohols.

HINT scoring after 750 ps MD

The complexes showing the highest HINT scores represent the ionization state and the protonation level most favorable for the protein-ligand binding process (75). The HINT scores indicated that there was a consistent rise-up of the predicted binding energies for the two first added protons and a sharp drop-off for the third proton positioned on Tyr-151 (Table 5). This behavior is similar to that of a kinetic titration curve and suggests that the optimum binding coincides with the number of added protons at the maximum HINT score. The HINT scores indicated that scenario C showed optimum binding in all cases, except for TFE binding to DmADH. However, the values for scenarios C and B were very close (544 vs. 548). Based on the HINT scores after MDs, scenario C should be considered the most probable when the inhibitors interact with their target and thereby confirm the ICM and HINT scoring on the complexes before MDs.

TABLE 5.

HINT scoring of PYR and TFE in the ternary complexes after 750 ps MD simulations

	DmADH		DlADH
Ionization scenario	PYR	TFE	PYR	TFE
A:	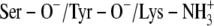532	536	360	442
B: Ser-OH/Tyr-O−/Lys-NH2	468	548	458	391
C:	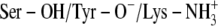717	544	559	572

Hydrogen-bonding pattern during MD simulations

The local pH and thereby the ionization states of the catalytic triad strongly influence the free energy of ligand binding and the target-ligand hydrogen bonds. Computational drug design and virtual screening of databases against protein targets are most often carried out without considering local pH or ionization states of amino acids or ligands. Very often, the pH for crystal growing and the optimum pH for ligand binding do not correspond to each other and thus give different binding patterns. Proton migration across hydrogen bonds is also identified as a probable mechanism for biological activity (76). Understanding the molecular features caused by the local pH and the hydrogen-bond patterns is therefore important for understanding the molecular mechanism of target-ligand interactions.

A clear pattern of hydrogen bonds was observed during the MDs. Hydrogen bonds between the ligand and the enzyme models were monitored during the final 100 ps of the 750 ps MDs of the monomeric complexes. The percentage occupancy of the hydrogen bonds was calculated as the percentage of the sampled coordinate sets during the period with the particular hydrogen bond present (atomic distance <3.1 Å). The hydrogen bonds in Tables 6 and 7 suggest the following:

1. In ionization scenarios A and B, the ligands formed stable hydrogen bonds mainly with one of the surrounding amino acids (mostly Tyr, or either Ser or Thr). In these two scenarios, only one nitrogen atom (N1-H) of PYR was involved in hydrogen bonding. Only scenario C exhibited dynamic hydrogen bonding, where Tyr-O⁻ remained hydrogen bonded to the proton-donating atom of the inhibitor during the final 100 ps of MD. However, this particular hydrogen bond was also observed for the other enzyme models with Tyr-O⁻. The MDs of TFE with scenario C indicated that a stabilizing hydrogen bond could be formed between TFE-OH and ribose-O2′ atom, whereas PYR was stabilized by the OH group of Ser-138.

2. At the active site of DlADH, both PYR and TFE exhibited more favorable hydrogen bonds than that observed with DmADH. With DlADH, dynamic hydrogen bonds were formed between the inhibitors and Tyr, Ser, and possibly ribose-O2′. Of the two inhibitors, TFE seemed to exhibit the most favorable (in terms of occupancy) hydrogen bonds.

3. During the MDs with the dimer, the active site of the two subunits showed some differences in hydrogen bonds with the ligands. In DmADH, subunit A exhibited a higher hydrogen-bond occupancy than subunit B, whereas in DlADH the differences between the subunits were less pronounced.

4. During the MDs with scenario C and an inhibitor, a lower hydrogen-bond occupancy was observed with one subunit than with both subunits. The reason for this was that the C-terminal end of one subunit also contributes to the active site (R2 pocket) of the second subunit.

5. The hydrogen-bonding pattern at the active site indicated that Tyr-151 is the base for proton extraction. Furthermore, Ser-138 (in both DmADH and DlADH) and possibly NAD⁺ ribose-O2′ (with TFE) and Thr-140 (with PYR) were involved in dynamic hydrogen bonds that stabilized the ligand at the binding site.

TABLE 6.

Observed hydrogen bonds (atomic distance <3.1 Å) between the ligand and the amino acids of DlADH during 650–750 ps of MD simulations

	TFE		PYR
Ionization scenario	Donor/acceptor	Occupancy (%)	Donor/acceptor	Occupancy (%)
A:	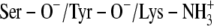TFE/Tyr-151	100	PYR-N1/Ser-138	90.4
			PYR-N1/Thr-140	64.6
B: Ser-OH/Tyr-O−/Lys-NH2	Ser-138/TFE	19.8	PYR-N1/Ser-138	52
	NAD-O2′/TFE	25	PYR-N1/Tyr-151	99.8
	TFE/Tyr-151	100
	TFE /NAD-O2′	20.2
C: 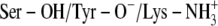†	NAD-O2′/TFE	32.4	Thr-140/PYR-N1	29.2
	Ser-138/TFE	26.4	Ser-138/PYR-N1	85.6
	TFE/Tyr-151	100	PYR-N1/Tyr-151	68
	TFE/NAD-O2′	26.8
C: 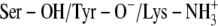‡	NAD-O2′/TFE	32	Ser-394/PYR-N1	52.4
	Ser-394/TFE	20.8	PYR-N1/Ser-394	24.8
	TFE/Tyr-407	100	PYR-N1/Tyr-407	94
	TFE/NAD-O2′	28.8

Hydrogen bonds observed in >20% of the sampled coordinate sets are included. Occupancy indicates the percentage of sampled coordinate sets with that particular hydrogen bond shorter than 3.1 Å.

^†subunit A of the dimer.

^‡subunit B of the dimer.

TABLE 7.

Observed hydrogen bonds (atomic distance <3.1 Å) between the ligand and the amino acids of DmADH during 650–750 ps of MD simulations

	TFE		PYR
Ionization scenario	Donor/acceptor	Occupancy (%)	Donor/acceptor	Occupancy (%)
A:	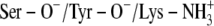TFE/Tyr-152	100	PYR-N1/Ser-139	100
			PYR-N1/Thr-141	28.4
B: Ser-OH/Tyr-O−/Lys-NH2	TFE/Tyr-152	100	PYR-N1/Tyr-151	99.6
C: 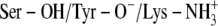†	NAD-O2′/TFE	51.4	Ser-139/PYR-N1	71.6
	TFE/NAD-O2′	34.7	PYR-N1/Tyr-151	99.6
	TFE/Tyr-152	100
C: 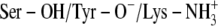‡	TFE/Tyr-411	100	Ser-396/PYR-N1	31.6
			PYR-N1/Ser-3946	19.6
			PYR-N1/Tyr-409	100

Hydrogen bonds observed in >20% of the sampled coordinate sets are included. Occupancy indicates the percentage of sampled coordinate sets with that particular hydrogen bond shorter than 3.1 Å.

^†subunit A of the dimer.

^‡subunit B of the dimer.

Determinants of ligand-receptor interactions

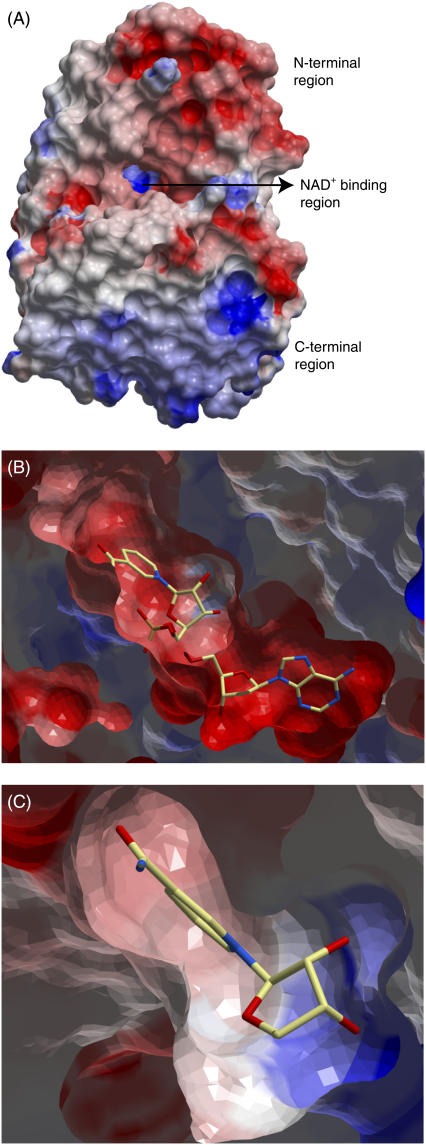
The volume of the binding pockets of DmADH and DlADH are similar (∼461 ų and ∼458 ų, respectively) and is mainly occupied by a NAD⁺ molecule in the binary complexes. The R1 pocket is mainly hydrophobic and formed by hydrophobic amino acids in the helices α1 (Phe-192, Val-189), α2 (Val-202, Leu-206), the N-terminal end of αF (Val-148), β1-strand (Ile-183), two amino acids (Leu-95 and Ile-145) in the loop regions, and NAD⁺ (atom C7N) (Fig. 1). The shorter but wider R2 subpocket is formed by the following amino acids: Val-139 and Thr-140 in 3₁₀-helix between βE and αF, Pro-181 (backbone O) in βF, Gly-182 (backbone O and Cα) and Ile-183 (backbone N) between βF and β1, and Trp-250 from the other subunit. Although the amino acids lining the active site of DmADH and DlADH are 100% conserved, the active site of DlADH is more electropositive than that of DmADH (12,77). We observed that the N-terminal part that contains the active site is more electronegative, whereas the C-terminal part is more electropositive (Fig. 4 A); so the subunit association regions are electrostatically complementary to each other (Fig. 1). In the binary DlADH·NAD⁺ complex (PDB ID: 1A4U), the entire region, except for the region near Lys-155, has a negatively charged electrostatic surface (Fig. 4 B). But in the ternary complexes of both DmADH and DlADH, only the adenine binding part was electronegative (Fig. 4 C). In these complexes, the nicotinamide binding site is slightly electronegative, whereas the ribose binding region is strongly electropositive, indicating a positively charged surface in the region of Lys-155. This positively charged surface indicates that scenario B is less likely.

FIGURE 4.

Electrostatic surface of the x-ray structure of DlADH. The most electronegative surfaces are in red, whereas the most electropositive areas are in blue. (A) Electrostatic surface of the entire monomeric DlADH. (B) Closer view of the NAD⁺ binding region in the apo form of DlADH active site, viewed as in A. NAD⁺ is shown in a position that corresponds to the position in the binary x-ray crystal structure complex. The NAD⁺ molecule is shown as a stick model and colored according to atom type (carbon-yellow, nitrogen-blue, oxygen-red). A cutting plane has been inserted in the region of the NAD⁺ molecule, and the NAD⁺ bond that is missing in the figure is due to the cutting plane. (C) A closer view of the electrostatic surface of the nicotinamide and ribose binding regions of the active site cavity of the ternary x-ray crystallographic complex DlADH·NAD⁺·TFE (PDB ID: 1SBY). The nicotinamide-binding site is slightly electronegative, whereas the ribose-binding region is strongly electropositive.

The ICM docking and HINT scores indicated that the most probable ionization scenario of the catalytic triad after the proton release from the binary complex is scenario C. To check if the simplification of using one subunit for MDs and LIE analyses biased the calculations, 5 ns MDs were performed for the ternary dimeric complexes of both enzymes using scenario C. Important atomic distances between the target and the inhibitors were studied during the MDs.

MD of DlADH·NAD⁺·PYR:

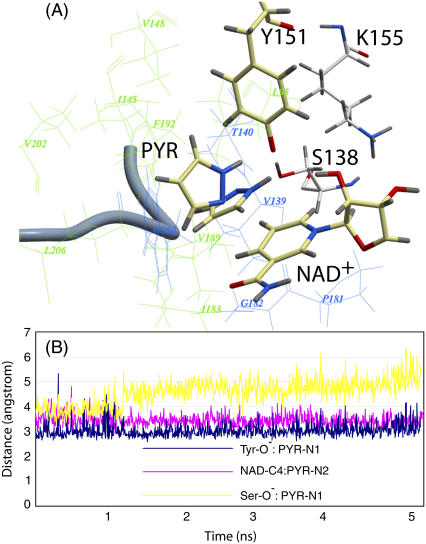
The overall RMSD of backbone atoms between the starting and final structures from 5 ns of MD was 0.97 Å and 1.28 Å for subunits A and B, respectively (Fig. 5, A and B). The largest differences were seen in the 3–10 helix situated between αE and αE and in the C-terminal part of each subunit lining the binding site region of the neighboring subunit. The RMSDs of the backbone atoms of the 3–10 helix between the initial and final structures were between 1 and 1.5 Å, whereas the corresponding RMSDs for C-terminal amino acids were ∼1.5 Å. The 3–10 helix is rather distal to the active site and should not affect the ligand binding. But the C-terminus lines the binding pocket of the other subunit; therefore fluctuations in this region can affect the ligand position at the active site. In subunit B, the ligand binding induced an RMSD of >1 Å between the initial and the final structures of the amino acids in the α1 helix (Leu-207 and Ser-208) and in the α2 helix (Pro-187, Leu-188, Val-189, and His-190). These amino acids are located at the active site. In the starting complex, the PYR ring was coplanar to the nicotinamide moiety of NAD⁺. During MD, the plane of the PYR ring was changed to a perpendicular position (Fig. 5 A), which also is observed in the x-ray crystallographic structure of the horse liver ADH·NAD⁺·PYR ternary complex (78,79). The planarity of the PYR ring was changed around 1275 ps of MD and fluctuated around a perpendicular position relative to NAD⁺ for the remaining simulation period (Fig. 5 B). The atomic distance between PYR-N2 and NAD-C4 and between PYR-N1 and Tyr-O⁻ remained almost stable during the MD period. But the distance between PYR-N1 and Ser-OH changed abruptly at ∼1275 ps. Similar movements were observed in both subunits of DlADH. In both subunits, the N1-H group of PYR was directed toward the Tyr-O⁻, which indicated that the partly positive charge at the C4 atom of the nicotinamide moiety is the main factor for binding PYR-N2 and for the orientation of PYR inside the binding cavity.

FIGURE 5.

Ternary DlADH·NAD⁺·PYR complex with the 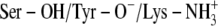ionization scenario of the catalytic triad after 5 ns of MD. (A) Amino acids lining the R1 (wire model in green) and R2 (wire model in blue) subpockets of the active site. The nicotinamide and ribose ring of NAD⁺, the catalytic triad (Ser-138, Tyr-151, and Lys-155), and PYR are shown as stick models with coloring according to the atom type (carbon-yellow, nitrogen-blue, oxygen-red, and hydrogen-gray). The ribbon represents the C-terminal loop of the other subunit acting as a lid of the active site cavity. PYR is shown both before and after the 5 ns of MD. The ring was parallel to the nicontinamide ring of the NAD⁺ ring at the start of the MD but tilted to perpendicular during the MD. (B) Fluctuation of atomic distances between PYR and atoms of the active site during the MD.

MD of DmADH·NAD⁺·PYR:

The RMSD of backbone atoms between the starting and final structures of 5 ns of MD was 0.88 Å and 1.06 Å for subunit A and subunit B, respectively. None of the active site residues had an RMSD from the initial structure of more than 1 Å after MD. As in the MD of DlADH, the PYR ring was changed from a coplanar to a perpendicular orientation relative to the nicotinamide moiety of NAD⁺. This change was seen at ∼580 ps for subunit A and slightly later for subunit B. In contrast to the MD with DlADH, the PYR ring did not stay in a stable perpendicular position relative to NAD⁺ for the rest of the MD period but changed between coplanar and perpendicular orientations. However in most of the sampled coordinate sets, the ring was observed in a perpendicular orientation. The atomic distances between PYR-N2 and NAD-C4 in the DmADH complex (Fig. 5 B) were less stable than the corresponding distance in DlADH during the MD, which reflects the continuous changes between a coplanar and a perpendicular orientation of the PYR ring.

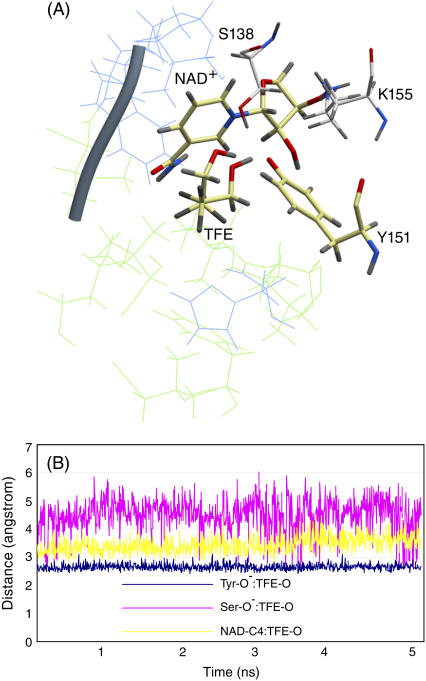
MD of DADH·NAD⁺·TFE:

The overall RMSD of backbone atoms between the starting and final structure of 5 ns of MD was 0.92 Å and 2.61 Å for subunit A and subunit B, respectively (Fig. 6, A and B). The distances from TFE-O to Tyr-O⁻, Ser-OH, and NAD⁺-C4 were consistently fluctuating around ∼2.5 Å, ∼4.5 Å, and ∼3.5 Å, respectively, in both subunits (Fig. 6 B). Similar fluctuations were also observed during the MD with DmADH. The most significant movement observed in both subunits of the enzymes was the movement of the C1-atom of TFE. In the starting position for MD, H_S and H_R of C1 of TFE were 4.3 Å and 7.4 Å from the NAD⁺-C4, which closely resembles the x-ray crystallographic mode. After 5 ns MD, C1 was changed from its starting position by a rotation of the axis C1-C2 of almost 180°, so that the distances of H_S and H_R from NAD⁺-C4 were 4.8 Å and 5.6 Å, respectively. The C2-atom remained almost in the same position in the R1 pocket, although the direction of the C1-C2 axis moved from R1(b) to R1(a). This suggests that the dipole induced by the three fluoroatoms at the C1 position of TFE is stabilized by the C7-amide of NAD⁺, which makes up the floor of the R1(b) part of the alcohol binding site. Such a stabilization of the polar group of the substrate by the C7-amide of NAD⁺ is also observed in the x-ray structure of the ternary E·NADH·acetate complex, where one of the oxygen atoms in acetate was localized in this part of the R1 pocket and the methyl group was localized in the R2 pocket (12).

FIGURE 6.

Ternary DlADH·NAD⁺·TFE complex with the 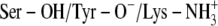ionization scenario at the active site. (A) Amino acids lining the R1 (wire model in green) and R2 (wire model in blue) subpockets of the active site. Only selected active site residues are included. The nicotinamide and ribose ring of NAD⁺, catalytic triad (Ser-138, Tyr-151, and Lys-155), and TFE are shown as stick models colored according to the atom type (carbon-yellow, nitrogen-blue, oxygen-red, and hydrogen-gray). (B) Fluctuation of atomic distances between TFE and atoms of the active site during the MD.

The vdW and electrostatic energies of the ligand with the active site amino acids were calculated for the coordinate set after 5 ns MDs. As expected, the amino acids in the R1 pocket gave more favorable vdW interactions than did those in the R2 pocket. In DmADH, PYR exhibited more favorable (−10.76 vs. −3.02 kcal/mol) interactions than TFE, partly due to the unfavorable hydrophobic contacts of Tyr-152 with TFE. In contrast, active site amino acids in DlADH showed similar magnitude (−8.79 vs. −9.61 kcal/mol) of hydrophobic interactions to PYR and TFE.

The deprotonated Tyr-151 showed strong electrostatic interaction with TFE, which overcame the unfavorable interactions of Ser-138 and Lys-155. This strong interaction may have contributed to the overestimation of the LIE values of TFE. PYR interacted with Tyr-155 with electrostatic energies of −14.1 and −7.9 kcal/mol in DmADH and DlADH, respectively. For TFE, the corresponding electrostatic energies were −26.45 and −21.88 kcal/mol, respectively.

CONCLUSIONS

The overall 3D folding and the catalytic triad amino acids are highly conserved within the family of SDRs. Therefore, knowledge about the ionization of the catalytic triad of the DADHs is helpful in the design of inhibitors for human SDRs. The results of the calculations are summarized in Scheme 2. The scenario giving the strongest ICM binding energy, highest HINT score value (largest positive value), and a free energy of binding (LIE values) closest to the experimental results (Table 1) was considered the most probable scenario when an inhibitor binds to the binary E·NAD⁺ complexes of SDRs. Scheme 2 indicates that scenario C (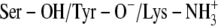) is the most probable of the catalytic triad of SDRs.

HINT scores showed clearly that Lys-155 should be in the charged condition, which is supported by the electrostatic surface analysis of the active site of binary and ternary complexes of DADHs and MD-based binding energies. As shown in Scheme 2, some of the calculations were in favor of scenario B (Ser-OH/Tyr-O⁻/Lys-NH₂). However, deprotonation of both Lys-155 and Tyr-151 at the catalytic site should be considered highly unfavorable for the following reasons: 1), The positively charged Nζ of Lys-155 can be appreciably bonded (distance is ∼3 Å) to both the O2′ and the O3′ atoms of NAD⁺-ribose, which is important for binding and orienting the NAD⁺ molecule at the active site (12). 2), The positively charged Lys-155 also contributes to lowering the pK_a of Tyr-151 and Ser-138 in contrast to a neutral Lys. Hydrogen bonding and trajectory analyses suggested that Ser-138 stabilized the ligand by dynamic hydrogen bonding with the ligand. Based on the familiar conservation and structural similarities, this network of interactions might be a general trend among the SDRs.

During the MDs, the inhibitors changed their positions within the active site. This was not surprising when we consider the structure of the active site and the substrate specificity of DADHs. These enzymes are most active with secondary alcohols, where the active site cleft close to the C1 atom of an alcohol is quite wide. The movement of TFE during the MDs suggested that the two polar parts of the inhibitor are partly fixed. The CF3 group of TFE is locked by the partly polar floor of the R1(b) site (the C7-amide of NAD⁺), and the OH group is locked by the side chain oxygen of Tyr-151. However, the methylene group of TFE was moved significantly, so that the pro-R hydrogen moved closer to the C4 position of NAD⁺ from the starting structure. Despite the movement of the methylene group of TFE, the pro-S hydrogen was closest to the C4 position of NAD⁺. Therefore TFE must be regarded as an appropriate model for the binding of ethanol in the ternary complex and reflects the stereochemistry of the reaction where the pro-S hydrogen is transferred from ethanol to NAD⁺ (80,81). The MDs of the alcohol competitive inhibitor PYR with DlADH and DmADH suggested that the plane of the ring favored the perpendicular position relative to the si-face of the nicotinamide ring. Hence, orientation of PYR inside the binding cavity is influenced by the positively charged C4 atom of NAD⁺, the OH group of the Tyr-151 side chain, and, partly, the OH group of the Ser-138 side chain. This is similar to the binding of PYR to horse liver ADH, where the two nitrogen atoms in PYR are oriented against the active site zinc atom and the C4 atom of NAD⁺, whereas its perpendicular position against the nicotinamide ring is stabilized by stacking against Phe-93 (78,79). The MD simulations and affinity calculations emphasize the importance of the charge of the catalytic residues as well as the size and nature of the active site topology close to the catalytic residues in the development of inhibitors against SDR enzymes, where small inhibitors might be more mobile in the active site than larger inhibitors.

The overestimation of TFE affinities compared with experimental observations is explainable, and the affinity predictions for PYR and the MD simulations were in agreement with experimental observations. Our calculations therefore indicate that the DlADH and DmADH are valuable model systems for studying the ionization conditions and inhibitor binding of the SDR superfamily of enzymes using theoretical calculations. This study also confirms the fact that the use of theoretical calculations for predicting and comparing binding affinities of structurally different ligands is challenging.