Packaging of a Polymer by a Viral Capsid: The Interplay between Polymer Length and Capsid Size

Abstract

We report a study of the in vitro self-assembly of virus-like particles formed by the capsid protein of cowpea chlorotic mottle virus and the anionic polymer poly(styrene sulfonate) (PSS) for five molecular masses ranging from 400 kDa to 3.4 MDa. The goal is to explore the effect on capsid size of the competition between the preferred curvature of the protein and the molecular mass of the packaged cargo. The capsid size distribution for each polymer was unimodal, but two distinct sizes were observed: 22 nm for the lower molecular masses, jumping to 27 nm at a molecular mass of 2 MDa. A model is provided for the formation of the virus-like particles that accounts for both the PSS and capsid protein self-interactions and the interactions between the protein and PSS. Our study suggests that the size of the encapsidated polymer cargo is the deciding factor for the selection of one distinct capsid size from several possible sizes with the same inherent symmetry.

INTRODUCTION

Viral capsids are often monodisperse and highly symmetric nanocontainers with diameters ranging from ∼20 to 120 nm (1). They possess an evolved economy of design (2) and in many instances are made up of multiple copies of only a single protein. The mechanisms by which viral genomes are packaged into capsids can be classified into two categories—those that require energy input and those that do not. The genomes of many double-stranded DNA (dsDNA) viruses, such as bacteriophages, are actively packaged into capsids by motor proteins (3). The work required to package the DNA gives rise to an internal pressure that depends on both the genome length and the capsid volume and may be as high as 60 atm (4,5). In contrast, many single-stranded RNA (ssRNA) plant viruses are capable of self-assembling spontaneously in vitro to form infectious virus particles (6–8). In recent years these protein shells have been employed for the encapsidation of particles and molecules with novel electronic and optical properties (9–11). Here the packageability necessarily depends both on the cargo and the capsid size.

These facts naturally raise the following question: what determines the size of a virus or virus-like particle (VLP)? It is clear that the size of the genome (packaged cargo) plays a role. The capsid sizes of both icosahedral ssRNA plant viruses and icosahedral dsDNA bacteriophages increase with increasing genome size, albeit with different scaling relations. In the latter case the dsDNA is essentially hexagonally close-packed, with the capsid volume and genome length bearing an approximately linear relation to one another. This is particularly evident in the case of bacteriophage T4 mutants, where the length of the packaged DNA is found to scale linearly with the capsid volume (12). For ssRNA icosahedral viruses, there are no systematic experimental studies that address the dependence of capsid size on genome size. It is evident, however, that genome length alone does not determine capsid size or even capsid shape. For example, the RNAs of tobacco mosaic virus (TMV) and turnip yellow mosaic virus (TYMV) are both about 6000 nucleotides in length. But when TMV RNA is mixed with TMV capsid protein (CP), it assembles into rod-like virions 300 nm long and 20 nm in diameter, whereas when TYMV RNA and TYMV CP assemble in vivo, icosahedral virions 30 nm in diameter are formed (13). Finally, and most germane to our study, when TMV RNA is mixed with the CP of cowpea chlorotic mottle virus (CCMV) (whose RNAs are only half as long), icosahedral capsids are formed that are larger than those of wild-type (wt) CCMV (14).

We hypothesize that the shapes and sizes of viral capsids are determined by a balance between the size of the ssRNA genome and the spontaneous curvature of the CP. This article reports results from experiments designed to explore this relation. We focus our attention on CCMV, which has long been regarded as a model system for the study of self-assembly and replication of icosahedral viruses (7,15–19). CCMV has a multipartite genome consisting of four genes spread out over three different RNA molecules, which are about 3200, 2800, and 2100 nucleotides long. The RNAs are packaged in identical T = 3 capsids, the first two alone and the third with a subgenomic RNA 900 nucleotides in length; note that 3000 (±200) nucleotides are present in each capsid. Of the myriad of known animal and plant viruses, CCMV belongs to the subset that have the ability to form spontaneously in vitro: its self-assembly process is determined largely by free energy minimization and requires no external energy input (20). Formation of viral particles is driven by interactions between the anionic viral RNA and cationic CP residues (21,22). The pioneering work of Bancroft and co-workers (14,23) demonstrated the ability of CCMV CP to also encapsidate a wide range of ssRNAs of other viruses and nonviral anionic polymers.These VLPs have capsids that are invariably icosahedral but differ in size (7,14,15,23,24).

In the above cases it is difficult to deduce the influence of genome size on the size of the assembled VLP because the different RNA molecules employed differ widely in their secondary and tertiary structures (25). Little information is currently available to predict the three-dimensional solution structure of long RNA molecules comparable in length to the ssRNA molecules of the CCMV genome (25,26). In this study, the CCMV viral RNAs have been replaced by poly(styrene sulfonate) (PSS), with the aim of learning how the size of the resulting VLPs can be controlled by changing the cargo size. Unlike the situation for large ssRNA molecules, the size and shape of PSS are well documented and can simply be correlated with molecular mass and linear charge density (27). The polymer is commercially available in a wide range of molecular masses, and the persistence length (∼1 nm) and charge density (≈1 e⁻/3 Å) of fully sulfonated PSS are comparable to those of ssRNA. This allows us to apply the basic physics of linear polymers to interpret the experimental results we obtain for capsid size distributions as functions of polymer length.

The formation of VLPs containing gold nanocrystals of different sizes has recently been reported. In particular, Dragnea and co-workers (28) have utilized CPs from brome mosaic virus and shown that increasing sizes of polymer-grafted nanoparticle cores can lead to larger capsids. Loo et al. (29) have worked with a single size of gold nanocrystal, demonstrating that they can be efficiently packaged by first attaching DNA oligonucleotides to the gold cores, followed by incubation with complementary ssRNAs and CPs (from red clover necrotic mosaic virus). These studies are closely related to ours, even though they do not address the interaction between CP and a highly flexible and compressible polyelectrolyte. Packaging of low-molecular-mass (10 kDa) PSS by CCMV CP has been reported (30), but the flexible polymers involved are significantly smaller than the sizes of the capsids. Ren et al. (31) have investigated the packaging by hibiscus chlorotic ringspot virus (HCRSV) CP of poly(styrene sulfonic acid) (PSA) molecules of varying molecular masses, but no capsid sizes were measured.

In this work, we determine the size distributions of VLPs formed from reactions of CCMV CP with PSS samples of increasing sizes (all comparable to or larger than the capsid sizes), separately determining the sizes of the free PSS molecules and of the resulting VLP capsids. Even though the size and charge of the polymer cargo increases monotonically over a broad range (e.g., a factor of 3 in radius of gyration and 10 in total charge), only two discrete sizes of VLP are observed, corresponding to two icosahedral-symmetry structures (T = 2 and T = 3) involving 120 and 180 copies of CP, respectively. Furthermore, the size distribution is unimodal, with the size jumping discontinuously from 22 (T = 2) to 27 nm (T = 3) at a PSS molecular mass of 2 MDa. The fact that a broad range of polymer charge (molecular mass, size) can be packaged in a single size of capsid is not inconsistent with the recent theoretical suggestion (32,33) that the packaged charge correlates with the total charge associated with the CPs. Rather, it indicates that although there might be an optimum charge ratio, it is not strongly preferred.

EXPERIMENTAL METHODS

All procedures outlined in the Experimental Methods section were performed at 4°C unless otherwise specified.

CCMV purification

CCMV was purified from infected California Blackeye Cowpea (Vigna ungiculata) leaves 14 days postinfection. The virus purification protocol was modified from that used by Rao and co-worker (34). Briefly, the infected leaves were homogenized in a blender in virus extraction buffer (0.5 M sodium acetate, 0.08 M magnesium acetate, pH 4.5) and subsequently filtered through cheesecloth to remove the leaf tissue. The filtrate was emulsified with chloroform and centrifuged at 12,000× g for 15 min. The aqueous upper phase was extracted and centrifuged again at 204,000× g for 55 min to pellet the virions. The pellet was hydrated overnight in virus suspension buffer (50 mM sodium acetate, 8 mM magnesium acetate, pH 4.5), and the suspension was loaded onto a 10–40% sucrose gradient and centrifuged at 210,000× g for 50 min. The band corresponding to CCMV virions was extracted and centrifuged again at 204,000× g for 100 min to pellet the purified virions. The pellet was resuspended in the virus suspension buffer and stored at −80°C until use. The purity of the sample was checked by measuring the ratio of absorbances at 260 and 280 nm. All samples used in our study had A_260nm/A_280nm > 1.65. The CCMV concentration was estimated from the O.D. at 260 nm (35).

CCMV CP purification

Purified CCMV CP was obtained by initially dissociating CCMV virions in high-salt buffer (0.5 M calcium chloride, 1 mM EDTA, 1 mM PMSF, 1 mM DTT, 50 mM Tris-hydrochloride, pH 7.5). The solution was centrifuged at 14,000 rpm for 30 min to remove partially dissociated virions and precipitated nucleotides. The supernatant from this low-speed centrifugation step was dialyzed in viral assembly buffer (50 mM sodium chloride, 10 mM potassium chloride, 5 mM magnesium chloride, 1 mM DTT, 50 mM Tris-hydrochloride, pH 7.2) for 24 h and centrifuged at 353,000× g for 90 min to remove nucleoprotein aggregates. Finally, the supernatant from the high-speed centrifugation was dialyzed against storage buffer (1 M sodium chloride, 1 mM EDTA, 1 mM DTT, 1 mM PMSF, 20 mM Tris-hydrochloride, pH 7.5) and stored at 4°C until use. The CP was typically used within 48 h of purification. To check the protein purity, its UV absorbance was measured, and only samples yielding A_280nm/A_260nm > 1.70 were used in the experiments. The CP concentration was estimated using a calibration curve obtained from a Bradford assay.

In vitro assembly of VLPs and empty capsids

All PSS samples were purchased from Scientific Polymer Products (Ontario, NY) and were used without further purification. Table 1 lists the molecular masses, polydispersity indices, and measured hydrodynamic radii for the PSS samples used in our experiments. Five PSS samples with molecular masses ranging from 400 kDa to 3.4 MDa were used. Each experiment consisted of five independent self-assembly reactions carried out simultaneously, one for each molecular mass of PSS listed in Table 1. CP purified from the same batch was used in all five reactions. The CP concentration in each reaction was held constant at 0.15 μg/μl, and the molar ratio of CP to PSS was 360:1. The reaction mixtures were dialyzed against the assembly buffer for 24 h. A sixth reaction mixture, which did not contain PSS, was also included for each experiment as a negative control, serving as a secondary check for protein purity. Formation of capsids in the absence of PSS is far less efficient; there is a much lower yield, and the capsids display a distinctly different morphology than those formed in the presence of PSS (24,36). Assembly of empty CCMV capsids was carried out by overnight dialysis of CP against the empty-capsid assembly buffer (1 M sodium chloride, 1 mM EDTA, 1 mM DTT, 50 mM sodium acetate, pH 4.8).

TABLE 1.

Properties of PSS used in packaging experiments

Reaction	Mol. mass (kDa)	Polydispersity index*	Hydrodynamic radius† (nm)
1	408	1.24	18.3
2	691	1.16	25.0
3	1010	1.18	32.6
4	2040	1.07	36.6
5	3441	1.01	42.8

^*Polydispersity index data were supplied by Scientific Polymer Products.

^†Hydrodynamic radii of PSS were measured by dynamic light scattering in the viral assembly buffer.

Transmission electron microscopy

Carbon-coated transmission electronic microscopy (TEM) grids were prepared by vacuum evaporation of carbon onto parlodion-covered commercial 400-mesh copper grids (Ted Pella, Redding, CA). All grids were glow-discharged immediately before use. Samples were spread onto TEM grids immediately after the packaging reactions. All samples from the same experiment were prepared, imaged, and photographed in one session. Sample grids were stained with 2% uranyl acetate and imaged with a JEOL 100CX electron microscope at 100-keV acceleration voltage.

TEM image analysis

TEM negatives were scanned with a Minolta Dimage Scan MultiPro scanner (Minolta, Osaka, Japan) for image analysis. To perform quantitative analysis of the particles, scanned images were imported into Adobe Photoshop 7.0 (Adobe Systems, San Jose, CA) and enlarged digitally to 200% of their original sizes. The intensity and contrast of the images were adjusted to optimize the image quality.

The diameter of each particle was obtained by taking the geometric mean of two orthogonal measurements. To construct the particle size distribution histograms, a minimum of 100 particles per sample was measured. A binning interval of 1 nm was used to construct the VLP size distribution histogram; fractional frequency was calculated by dividing the particle count within a size interval by the total particle count from the sample.

Dynamic light scattering

Hydrodynamic radii of the PSS samples listed in Table 1 were measured using a DynaPro-MS laser light scattering instrument (Wyatt Technology, Santa Barbara, CA). All PSS samples were prepared in the assembly buffer and passed through a 0.22-μm syringe filter (Millipore Corp., Billerica, MA) before measurement.

RESULTS

VLP formation and packaging of PSS by the CCMV protein

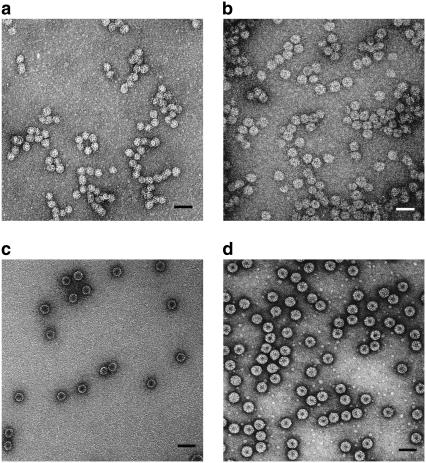
Fig. 1, a and b, shows representative TEM images from two of the five packaging reactions listed in Table 1. For comparison, images of the empty CCMV capsid (c) and wt CCMV (d) are also shown. VLPs with spherical morphology formed readily in Reactions 1–5. The different preparations are clearly distinguishable. Prominent dark centers in all the empty capsids arise from penetration of the stain into the largely vacant interior. Similarly, the smaller dark centers in the images of wt CCMV capsids are consistent with the small central void that is known to exist in the packaged RNA in Bromoviruses (37). In contrast, there is markedly less stain penetration into the cores of the VLPs or, at most, a small apparently void region, which suggests that the PSS occupies the interior.

FIGURE 1.

TEM images of capsids formed in self-assembly reactions. Samples were stained with 2% uranyl acetate. (a) VLPs formed with 700-kDa PSS. The mean capsid size for VLPs is 22 nm. (b) VLPs formed with 3.4-MDa PSS. The mean capsid size is 27 nm. (c) Empty CCMV capsids formed by dialysis of CP in buffer with high salt and low pH. The dark core in the center indicates the penetration of stain into “void” (aqueous solution) space, which is notably absent in the interiors of VLPs filled with PSS. (d) wt CCMV capsids in virus suspension buffer. Scale bars are 50 nm.

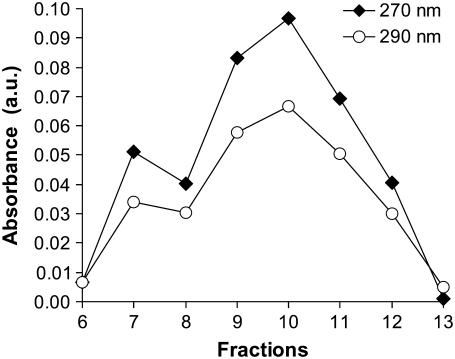
Additional evidence of PSS encapsidation by CP was provided by UV absorbance measurements of VLP 2M that was fractionated on a sucrose gradient, as shown in Fig. 2. Comigration of the absorbances at 270 nm, where the PSS absorbs strongly, and at 290 nm, where only the CP has significant absorption, demonstrates that the protein and polymer (CP and PSS) are found in the same fractions. Further, the strongest absorbances are located mainly in fractions 7–13. In contrast, on the same gradient, the wt CCMV formed a band between fractions 11 and 16 and peaked at fraction 13 (data not shown). The width of the VLP 2M band was comparable to that of the wt CCMV, suggesting that the VLP population was relatively homogeneous, which is confirmed by direct measurements of the size distributions with EM, as discussed below. The encapsidation of PSS by CCMV CPs has also been reported by Sikkema et al. (30) for a much lower-molecular-mass (9.9 kDa) polymer that was labeled with dansyl chloride. They employed fast performance liquid chromatography to separate the products and showed that the CP and labeled PSS comigrated, consistent with the PSS being packaged inside the VLPs.

FIGURE 2.

Separation of the products of the 2-MDa PSS plus CP assembly reaction on a 10–40% sucrose gradient. Comigration of species absorbing strongly at both 270 and 290 nm was found for fractions 7–13. The absorbances peaked at fraction 10.

As a further test that PSS was packaged inside the VLPs and not adsorbed on the capsid, we have begun a study of the packaging of fluorescent (rhodamine-labeled) PSS under the same assembly conditions (Y. Hu, A. Anavitarte, B. Ng, A. Zelikin, F. Caruso, C. M. Knobler, and W. M. Gelbart, unpublished). Preliminary data show that when the assembly products are fractionated on a sucrose gradient, the fluorescent PSS and CP comigrate, as in the case of the unlabeled PSS shown in Fig. 2. Moreover, the rhodamine fluorescence is not markedly diminished in the presence of the quencher methyl viologen, demonstrating that the labeled PSS was protected from the quencher by the capsid. In contrast, the fluorescence of a control sample containing only free fluorescent PSS was significantly diminished at the same quencher concentration. Similarly, fluorescence is quenched when free labeled PSS is added to a solution of wt CCMV, indicating that it is not sufficient for the PSS to adsorb on the outside of capsids but rather that it must be packaged inside to be protected against quenching. These results suggest that the PSS in the assembly reactions reported in this work is indeed packaged inside the capsids and not adsorbed outside.

VLP size distributions

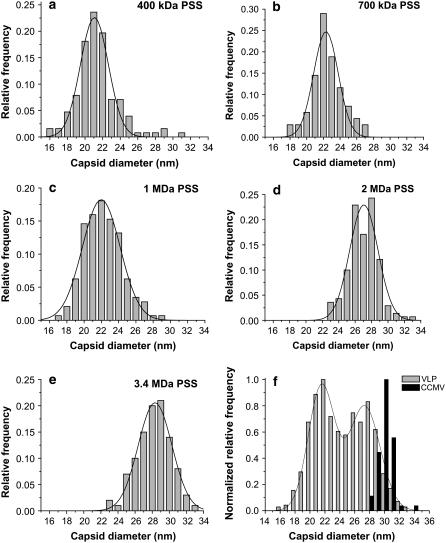
The normalized VLP capsid size distributions for Reactions 1–5 are shown in Fig. 3; they are each based on measurements of more than 100 particles. The size distributions for each reaction are unimodal; they have been fitted to Gaussians, and the parameters that have been derived are given in Table 2. Fig. 3 f shows the bimodal distribution obtained by combining the data from Reactions 1–5. A fit of two Gaussians gives peaks at 21.5 ± 0.9 and 27.3 ± 1.0 nm. Nearly all capsid sizes measured fall into the range of 16–34 nm. The widths of the VLP size distributions, as measured by the standard deviations of the Gaussian fits, are essentially identical for all five packaging reactions, and they are comparable to the width we measure for wt CCMV, 1.70 nm. Although some of the dispersion in capsid sizes is related to variations in experimental conditions such as drying, we expect that there should be a dispersion in size even in the absence of such artifacts because capsids in solution are dynamic objects that have breathing modes.

FIGURE 3.

Normalized VLP capsid size distribution histograms for Reactions 1–5. For each reaction, one dominant capsid size was found: (a) VLP 400 kDa, (b) VLP 700 kDa, (c) VLP 1 MDa, (d) VLP 2 MDa, (e) VLP 3.4 MDa; and (f) a combined histogram of capsids from all five reactions. A fit of the histogram to two Gaussians indicates that the capsid sizes converge to two values: 22 nm and 27 nm. These values agree well with the sizes of T = 2 and T = 3 capsids formed by CCMV CPs.

TABLE 2.

Summary of the Gaussian fit of the VLP size distributions from Reactions 1–5.

		Peak
Reaction	PSS mol. mass (kDa)	Position* (nm)	Width† (nm)
1	408	21.1	3.2
2	691	22.3	3.2
3	1,010	22.0	4.4
4	2,040	27.1	3.6
5	3,441	28.3	4.0

^*Peak positions and peak widths were determined by fitting the normalized size distribution data with Gaussian functions.

^†Full width at half-maximum of the Gaussian fit.

The fact that the sizes of hundreds of VLP capsids from five independent packaging reactions converge to the two discrete values of 22 and 27 nm strongly implies that they are determined by the inherent icosahedral symmetry of the protein shells. Indeed, it has been established that the CCMV CP forms icosahedral structures with Caspar-Klug triangulation numbers T = 1, 3, 4, and 7 (14–16,24). “T = 2,” a “pseudo-”/non-Casper-Klug structure involving 120 CPs that form a dodecahedron arising from pentamers of dimers, has also been reported for CCMV CP self-assembly reactions (19). Without an image reconstruction analysis based on cryo-EM or x-ray diffraction, the assignment of a T number to a particular species is difficult. Absolute measurements of capsid diameters by TEM have sometimes been employed but are questionable because it is well established that the drying of the sample results in shrinkage that cannot easily be quantified.

If we assume, however, that the staining and sample drying on the TEM grid affects all the VLPs to the same degree, we can deduce the T numbers from the ratios of the capsid diameters associated with the peaks in Fig. 3. The number of CPs in a capsid is 60T. If the unit area per CP is constant, the total capsid surface area, which is proportional to the square of the capsid diameter, scales linearly with T:

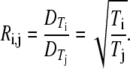(1)

Here 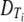is the diameter of capsid with T = i.

Experimental support for the validity of Eq. 1 can be found in the literature. For example, the hepatitis B virus (8,39) can assemble into particles of two sizes, known from cryo-EM to be T = 3 and T = 4 structures; the ratio R_4,3 of their diameters is 300 Å:260 Å = 1.15, which is in excellent agreement with 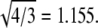Similarly, the assembly of empty capsids of CCMV can produce T = 2 and T = 3 particles (19), with diameters of 280 and 230 Å; these give R_3,2 = 1.22, in good agreement with 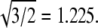Furthermore, T = 4 and T = 7 capsids have been identified in cryo-EM studies of P22 procapsids (40); the ratio R_7,4 of their average diameters, 1.33, can be compared with 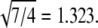Finally, CCMV capsids of three sizes, established by cryo-EM to be T = 1, 2, and 3, were shown to be assembled in vitro from a CP that lacked most of the N-terminal domain (16); their diameters of 290, 250, and 180 Å give R_3,2 = 1.2, R_3,1 = 1.6, and R_2,1 = 1.4, in good agreement with values of 1.2, 1.7 and 1.4, calculated from Eq. 1.

These data lend confidence to the use of Eq. 1 to identify the T numbers of the two capsid types for the VLPs that we have studied. The values of 21.5 and 27.3 nm for the two diameters give R = 1.27, corresponding to the expected ratio for T = 2 and 3, i.e., R = 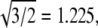and differing significantly from the ratios that would be obtained for other reasonable choices of T numbers.

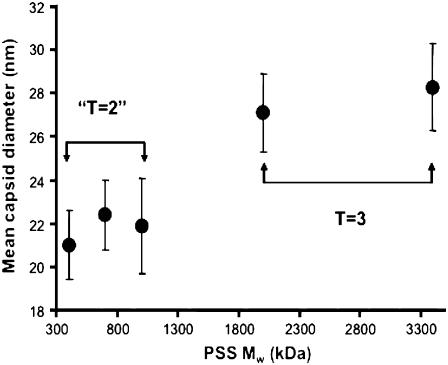
Fig. 4 shows the mean capsid diameter as a function of PSS molecular mass. A jump in T number from T = 2 to T = 3 occurs between molecular masses of 1 MDa and 2 MDa. This switch of the capsid size to a larger T number strongly suggests that for each type of capsid there exists a maximum capacity for efficient packaging. As the packaged cargo size increases, the size of the capsid increases correspondingly. The discreteness of this capsid-size transition results from the inherent icosahedral symmetry property of the CPs. This preference of the CP for discrete sizes is mirrored in the widths of the size distributions. It is significant (see Table 2) that the VLPs have essentially identical widths despite the variations in the polydispersities of the different PSS polymers. It is notable, as well, that the widths are quite similar to that of wt CCMV (Fig. 3 f). The compressible PSS is able to accommodate to the capsid diameters preferred by the protein, but only to a limited degree, which is why larger VLPs are found for higher molecular masses of polymer.

FIGURE 4.

Mean capsid size as a function of packaged PSS molecular mass. A jump in the capsid size was observed when the molecular mass increased from 1 to 2 MDa.

DISCUSSION

The measurements presented above naturally raise the question of the maximum cargo size that can be packaged by CCMV capsids. When CCMV CP assembles with viral RNA to make wt T = 3 virions, there are clearly limits to how many nucleotides can be efficiently packaged within each capsid. As noted earlier, the RNA content is either RNA1, consisting of 3200 nt, or RNA2, consisting of 2800 nt, or a combination of RNA3 (2100 nt) and the subgenomic RNA4 (900 nt) involving a total of 3000 nt. This is consistent with small-angle x-ray scattering measurements (A. Gopal, A. Yoffe, L.-T. Fang, B. Ng, D. Egecioglu, M. Niebuhr, C. M. Knobler, and W. M. Gelbart, unpublished.) showing that the radius of gyration, R_g, of RNA1 or of RNA2 is only slightly larger than that of the T = 3 capsid. In contrast, the hydrodynamic radii of the large PSS molecules that have been encapsidated in the work presented here are as much as four times larger than the capsid radii, and their R_gs are still 80% larger (41). The difference is that base-pairing interactions resulting from self-complementarity give the ssRNA a complex, compact branched structure, whereas the linear PSS is a relatively compressible random coil whose compaction is driven by electrostatic interactions with the positively charged tails of the CP.

The packaging of cargo other than viral RNA requires a different balance between the size of the polymer and the preferred radius of curvature of the CP. Note that if the preference of the CPs to aggregate with a particular radius of curvature were sufficiently strong, there would only be a single VLP size regardless of the PSS molecular mass and of the overall and relative concentrations of CP and PSS. The switch to larger VLP size on increasing the PSS molecular mass can be understood by a simple model incorporating the physics of capsid self-assembly and polymer confinement. This model reflects two basic criteria for the formation of a stable capsid. First, for a given PSS size, the capsid should be sufficiently large that the changes in polymer energy and entropy related to confinement are not too costly. Second, the capsid should be small enough that the PSS is able to neutralize the positively charged amino acid residues on the inner capsid surface without strong absorption onto that surface and attendant loss of configurational entropy.

The free energy of the VLP includes: 1), the self-energy of the aggregated CP capsomers, i.e., protein pentamers and hexamers, E_capsid; 2), the self-energy of the PSS chain, E_{PSS energy}; 3), the configurational entropy of the PSS chain, E_{PSS entropy}; and 4), the attraction between PSS and the inside of the shell, E_int:

(2)

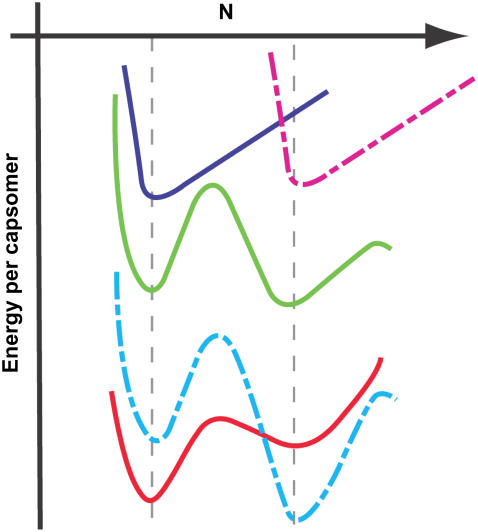
Because the screening length under our assembly buffer condition is comparable to the PSS monomer size, both on the order of 1 nm, E_int in Eq. 2 can be described by a “contact” energy per monomer, 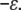E_{PSS energy} can be treated via the usual monomer excluded-volume interaction and is related to the second virial coefficient. The fact that the PSS chain is flexible with a persistence length comparable to its monomer size allows the chain entropy contribution E_{PSS entropy} to be described by the familiar gradient-squared term with a coefficient varying inversely with monomer size and volume fraction (42). Note that the distribution of RNA within the capsid does not need to be specified beforehand but follows from the free energy minimization. Finally, the self-energy of the capsid can be treated by a simple Hamiltonian developed in our earlier work to explain the origin of icosahedral symmetry in viruses (43). The green curve in Fig. 5 illustrates schematically the self-energy E_capsid per capsomer as a function of the total number of capsomers in a capsid, N, for a range of N values bracketing two neighboring T structures, e.g., T = 2 and T = 3. This is the type of energy dependence that is calculated in a model treating CP hexamers and pentamers as attracting disks whose centers are restricted to lie on the surface of a sphere of radius R. Monte Carlo simulation provides the equilibrium spatial distributions of capsomers for each N and R with subsequent minimization with respect to R giving the energy per capsomer for each N (43). As N approaches infinity, the energy per capsomer levels off asymptotically to a value corresponding to that of a planar hexagonal array of CPs. Note that the two minima shown in the figure are separated by only a small energy difference, Δɛ. Because this difference is often not large compared with the thermal energy kT, one expects to observe both structures with their relative populations given by the corresponding Boltzmann factor [].

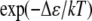FIGURE 5.

Schematic illustration of the VLP size selection mechanism by the PSS molecular mass. The green line represents the self-energy per capsomer in an empty capsid as a function of the number of capsomers per capsid. For convenience it is shown as a continuous curve, but in reality it has meaning only for integral values of N. The energy minima correspond to structures with specific T-number icosahedral symmetry whose formation is energetically favorable. The upper blue and dashed red curves represent the interaction energy per capsomer of a given molecular mass PSS as a function of capsid size for each of two chain lengths; for a given PSS molecule, the interaction energy goes through a minimum as the capsid size varies. The optimal size for the VLP is determined by superimpositions (see lower red and dashed blue curves) of the capsomer-capsomer and the chain-capsomer interaction energy curves.

The above calculations (43) take into account only the protein-protein interactions, but empty CCMV capsids do not arise under physiological conditions in the absence of PSS or ssRNA because the energy minima corresponding to T = 2 and T = 3 empty capsids (as shown in Fig. 5) are not sufficiently low compared with the chemical potential of unaggregated CP subunits in solution. To drive the capsomer aggregation and the spontaneous assembly of capsids, it is necessary to reduce the pH and raise the ionic strength or to add an anionic polymer (such as PSS or ssRNA) or an anionic colloidal particle (such as functionalized gold nanoparticles and quantum dots) (11,28). The energies associated with confining the PSS chain inside the viral capsid are given by the remaining contributions E_{PSS energy}, E_{PSS entropy}, and E_int in Eq. 2. The treatment of these terms is analogous to the case of a semidilute polymer solution confined inside a spherical cavity on which the polymer adsorbs, as given by Ji and Hone (42) and van der Schoot and Bruinsma (44) for flexible linear polymers of a fixed length. For particular values of the PSS monomer-capsid contact energy −ɛ, monomer-monomer energy, and chain length, a minimum in interaction energy per unit capsid surface area exists as a function of the capsid radius. This is shown schematically by the top two (blue and dashed red) curves in Fig. 5, which give the PSS-capsid interaction energy per unit area of the interior surface as a function of the total capsomer number N (capsid area), for chains of two different lengths, smaller on the left, larger on the right. The position and depth of the minima depend quantitatively on the values of the monomer-capsid contact energy, the monomer excluded volume, and PSS length, but the existence of a preferred capsid size as found in our experiments can be qualitatively explained as the balance between the PSS chain self-repulsion and its attraction to the interior surface of the confining capsid.

Combining the above two curves by adding the capsid self-energy (green curve) to the contributions from the confined PSS chain (upper curves) results in the lower curves in the figure. Note that, for the case shown here, the chain contribution “selects” the smaller or larger capsid size, according to the chain length. This is consistent with our finding that VLP size is shifted to larger T numbers by increasing the PSS molecular mass. It is in accord, as well, with Monte Carlo simulations of the packaging of small polyelectrolytes in spheres with a charged inner surface (45). These show that for a given capsid size and charge on the interior there is a range of polymer lengths for which encapsidation can be spontaneous. Further, according to this model, the minimum in the free energy occurs where the polymer and capsid charges are equal in magnitude. It is evident from our theory that there is no fixed maximum T number because there can be several minima that are accessible for larger cargo size. In the case of CCMV, for example, Verduin and Bancroft (14) found T = 7 capsids when TMV RNA (twice as long as each CCMV RNA) was packaged.

Belyi and Muthukumar (32) have recently demonstrated for a number of ssRNA viruses that there is a simple linear relation between the RNA charge per capsid, Λ, and Q, the total charge on the basic peptide residues that protrude into the capsid interior:

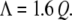(3)

For example, in the case of wt CCMV, there are 3000 nt in each capsid, which compares well with the value 2900 (= 1.6 × 10 × 180) calculated for the 10 basic residues at the N-termini of its 180 CPs. Although Eq. 3 was derived by modeling viral ssRNA as a linear homopolyelectrolyte, it cannot account for our present results on the packaging of PSS by viral protein. In all of the packaging reactions we have studied, the total number of negative charges on the PSS far exceeds the number of charges on the protein tails, e.g., by a factor of 9 in the case of the 3.4-MDa polymer. In essence, the genome lengths calculated by Belyi and Muthukumar are “optimal” values, which does not preclude the packaging of longer linear polyelectrolytes as shown in this work, or of a range of ssRNAs (7,8,46,47), albeit at lower efficiency. To further elucidate the physical basis of virion and VLP sizes, it will be important to perform systematic measurements of the relative packaging efficiencies for a series of viral-like ssRNAs and linear polyelectrolytes with different chain lengths and charge densities.

Finally, we note that Schneemann (48) has recently reviewed a wide range of examples of the self-assembly of ssRNA with CP (both in vitro and in vivo) in which the packaged RNA is shown to develop a significant degree of icosahedral symmetry. This effect arises from the (predominantly electrostatic) interactions between the cationic residues of the CPs and the anionic backbone of the ssRNA, both for wt and heterologous RNA molecules. Although the main thrust of the article is to elucidate the nature and extent of the icosahedral order, it raises many of the same physical questions that we have featured here, in particular the “structural plasticity” (48) of ssRNA and the need for consistency between its intrinsic size and that of the capsid preferred by the aggregating protein. Clearly, it is still an open question whether the RNA directs the assembly of a capsid of a given geometry or whether this is determined by the spontaneous radius of the protein shell, with the flexible, compressible, RNA simply “going along for the ride,” or—as is more likely—some combination of the two in which the balance varies from one self-assembling virus to the next.