A Method to Determine Dielectric Constants in Nonhomogeneous Systems: Application to Biological Membranes

Abstract

Continuum electrostatic models have had quantitative success in describing electrostatic-mediated phenomena on atomistic scales; however, there continues to be significant disagreement about how to assign dielectric constants in mixed, nonhomogeneous systems. We introduce a method for determining a position-dependent dielectric profile from molecular dynamics simulations. In this method, the free energy of introducing a test charge is computed two ways: from a free energy perturbation calculation and from a numerical solution to Poisson's Equation. The dielectric profile of the system is then determined by minimizing the discrepancy between these two calculations simultaneously for multiple positions of the test charge. We apply this method to determine the dielectric profile of a lipid bilayer surrounded by water. We find good agreement with dielectric models for lipid bilayers obtained by other approaches. The free energy of transferring an ion from bulk water to the lipid bilayer computed from the atomistic simulations indicates that large errors are introduced when the bilayer is represented as a single slab of low dielectric embedded in the higher-dielectric solvent. Significant improvement results from introducing an additional layer of intermediate dielectric (∼3) on each side of the low dielectric core extending from ∼12 Å to 18 Å. A small dip in transfer free energy just outside the lipid headgroups indicates the presence of a very high dielectric. These results have implications for the design of implicit membrane models and our understanding of protein-membrane interactions.

INTRODUCTION

Our present understanding of biomolecular function would not have been possible without reference to a hierarchy of simplified theoretical and computational models. Continuum electrostatic theories and models occupy a prominent place in this hierarchy. These theories deal with the response of a complex material such as water and solvated ions to an external electric field usually through the Poisson or Poisson-Boltzmann equation. These theories are useful by virtue of being relatively simple and intuitive. They are analytically solvable for simple geometries, and rapid methods exist for their numerical solution in problems containing complex geometries. From their solution, the free energy of solvation can be directly determined, which is difficult in more detailed models. Although fundamentally macroscopic theories, they have had widespread quantitative success for describing electrostatic-mediated phenomena on atomistic scales such as predicting free energies of solvation of ions and small ligands, computational docking and drug design, predicting pKa shifts of chemical groups, predicting the effects of added salt, and predicting changes in protein folding and binding stability by charge mutations. Continuum electrostatics has also been combined with molecular dynamics simulations to study the folding of peptides and small proteins, usually through the application of the generalized Born approximation. The literature describing these theories and applications is vast; however, a number of recent reviews exist on the application of continuum electrostatics theory to biomolecules (1–5) and methods based on the generalized Born equation (6).

A crucial parameter in continuum electrostatics is the relative dielectric susceptibility or dielectric constant. The dielectric constant describes the local polarizability of the medium in response to an external electric field. It is assumed frequently that the polarization response is linear, local in space, in the direction of the applied field and isotropic. The dielectric constant also has a frequency dependence, although the relevant quantity is usually its zero frequency value. In all instances the dielectric constant is a function of position, although many systems are sharply divided into solvent and solute regions and each region has a nearly constant value of dielectric. In this situation, one must choose the two dielectric constants for solute and solvent and the location of the dielectric boundary, a choice that is known to strongly affect the results of continuum calculations (7). It is often useful to represent a portion of the system explicitly but treat the remainder of the system implicitly with continuum electrostatics. In this context, the dielectric constant is not a universal parameter, but rather a function of what aspects of the system response are treated implicitly and what aspects of the system response are treated explicitly (8). There is wide choice in the explicit/implicit division. In some instances one might choose to treat only the high-frequency electronic polarizability implicitly and to treat the lower frequency vibrational and orientational polarizability explicitly. More commonly, one might choose to treat the response of the surrounding solvent bath, usually water and ions, implicitly and any solute molecules explicitly. For systems with lipid bilayers, one can even treat the lipid molecules implicitly as a continuum dielectric (9,10). In such a system, the dielectric constant must vary continuously from its large value in the surrounding water to a low value in the bilayer interior.

If continuum electrostatics is to be reliable as a predictive theory, then the choice of dielectric constant should be nearly consistent for different types of problems. For example, the choice of dielectric constant that properly models pKa calculations in a protein should be similar to the choice of dielectric constant that works for studying electrostatic stabilization of protein complexes and similar to the macroscopic dielectric constant of bulk protein—provided that all the explicitly represented charge rearrangements are properly accounted for. That being said, adjusting the dielectric constant for the particular problem of interest, i.e., fitting, will clearly result in better agreement for that problem.

For an inhomogeneous system, a difficult problem is how to compute the position-dependent dielectric constant, which will be referred to as the dielectric profile. Examples of such systems include a protein in aqueous solvent or small molecules in a lipid bilayer surrounded by aqueous solvent. For bulk materials, the dielectric constant is typically determined using the Fröhlich-Kirkwood theory (11–13). This method uses the fact that spontaneous polarization fluctuations of a material induce a dielectric response or reaction field from the surrounding medium, which then acts to further polarize the material. The bulk dielectric constant of a material can then be assessed from the correlation of spontaneous polarization with its own reaction field. In inhomogeneous systems, the response of a system to its own reaction field is complex and a direct application of the Fröhlich-Kirkwood theory is not possible; but, for systems with enough spatial symmetry, variants of the theory have been applied with some success. For example, two calculations have been made of the dielectric profile of an implicit lipid bilayer surrounded by solvent. In the first calculation, it was assumed that dipole fluctuations in different layers of the bilayer are not directly coupled but only indirectly through interactions with the reaction field of the surrounding medium (14). A later study found an analytic solution for the polarization response of this system to an external electric field that did include direct electrostatic interactions between different parts of the bilayer/water system. This analytic result was used to compute a dielectric profile from simulations (15). In this manuscript, we present a new approach to determining the dielectric constant of inhomogeneous systems. As a proof of concept, we apply this method to determining the dielectric profile of a lipid bilayer surrounded by water. In our approach, test particles are used to determine the local average electrostatic field and its fluctuations. The dielectric profile of the system is then determined by matching the field fluctuations to the response expected by a numerical solution of Poisson's equation. This method has a number of advantages:

1. There is no need for an analytic solution of the polarization response of the system to an applied electric field. The polarization response is determined rapidly using numerical methods. Because numerical methods are used to determine the dielectric profile, this method can be easily applied to systems with complex, nonsymmetric geometries.

2. Although the optimal choice of dielectric constant for different problems should be roughly consistent with each other, some differences will arise from inherent limitations of the continuum electrostatics model. In this case, the best choice of dielectric constant is the one that best fits the problem being modeled. In most microscopic calculations, the primary interest is the free energy of solvation of small molecules, ligands or peptides. By fitting our dielectric constant to reproduce the local solvation free energy, we are more likely to accurately model these types of problems. The determination of dielectric constants based on large-scale dipole fluctuations is a very different type of problem, less likely to produce quantitatively precise estimates of free energies of solvation.

In the following sections, we describe our approach and apply it to determine the dielectric profile of a lipid bilayer surrounded by water.

METHODS

The atomistic simulations are carried out with the GROMACS suite of programs (16). Our system is composed of 128 POPC (1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine) molecules, 64 lipids per leaflet, oriented with the bilayer normal in the z direction. This is surrounded on both sides by 4204 water molecules. Two uncharged Leonard-Jones (LJ) particles are added to the system. The initial bilayer structure was generated by starting from a previously equilibrated POPC bilayer with 32 lipids (17) and doubling the system along each direction in the plane of the bilayer to a total size of 128 lipids. Additional waters were added away from the bilayer. The box dimensions are ∼60 Å × 60 Å × 78 Å. The G45A3 force field was used for the POPC lipids (18) with the partial charges of Chiu et al. (19). We used the SPC water model (20). The system was simulated in the NpγT ensemble at 300 K with 1 bar of external pressure and zero surface tension. Particle-Mesh-Ewald was used for the electrostatics calculations (21,22) with a 14 Å cutoff, a 64 Å × 64 Å × 96 Å grid, fourth order Lagrange interpolation, a Gaussian screening function with a width of 4.48 Å, and tinfoil boundaries at infinity. Leonard Jones interactions are switched off smoothly between 12 and 14 Å. A 16 Å pair-list was updated every 10 integration steps. A 4 fs integration time step was used. All bonds involving hydrogen were held rigid with the LINCS algorithm (23). Water molecules were held rigid with the SETTLE algorithm (24). Temperature and pressure were maintained with a Nose-Hoover thermostat (25,26) and the method of Andersen, Parrinello and Rahman (27,28) with uniform box scaling in the plane of the bilayer and independent box scaling in the z direction. Center of mass motion was removed every 10 integration steps.

The LJ particle in each simulation was restrained by a potential of the form 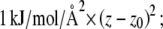the average z coordinate of all the nitrogen atoms in the POPC molecules was defined as the zero value of z. The second LJ particle is restrained by the same type of potential, but with z₀ replaced by z₀ − 30 Å. The LJ particles are free to move in the plane of the bilayer. Separate simulations were carried out for both the small and the large LJ particles at each value of z₀ from 0 to 30 Å in steps of 2 Å.

The simulations for the large LJ particles were begun by placing the particles approximately at their target depths. This was followed by a short minimization, equilibration of 4.2 ns, and a production run of 10 ns (14.2 ns total). The small LJ particle simulations were begun by replacing the large particles with small ones in the final state found after 14.2 ns of simulation. This was followed by an additional equilibration of 2.3 ns and a production run of 4.0 ns (6.3 ns total).

The free energy of charging was determined by computing the energy change for the system created by adding a test charge to each LJ particle individually of −0.01|e|, −0.001|e|, 0.001|e|, or 0.01|e|. In addition, 0.0|e| was added as a reference. The free energy change, determined from Eq. 1 was fit to a quadratic form to determine the quadratic dependence of free energy on the charge. The average free energy change at −30 Å and +30 Å was subtracted to determine the free energy for transferring a charged particle from water to any given depth in the bilayer (ignoring the linear free energy component due to the static electrostatic potential created by the bilayer).

The Poisson equation was solved with APBS (29–31) using a uniform grid of dimension 161 Å × 161 Å × 161 Å with a grid spacing of 0.3 Å. A multi-grid cycle was used for minimization with four levels. The potential at the grid boundaries was fit to the result from a single Debye-Huckel calculation with an exterior dielectric of 61 (to match SPC water). Tests indicate that replacing the anisotropic membrane/water environment with a single bulk continuum beyond 24 Å (as done here) results in an error of <1 kJ/mol of total free energy. For comparing to the atomistic simulations, the energy change was computed for transferring the LJ particles from bulk water to the desired depth in the bilayer, which required two calculations, a reference calculation without a bilayer, and a calculation with the dielectric modified outside the LJ particle to represent the bilayer. The variable dielectric of the bilayer was introduced by modifying the dielectric grids produced by APBS. No dielectric smoothing was used. Particle charges were smoothed over several grid points using a 4th order spline fit. The dielectric inside the LJ particles was set at a value of 1. The radius of the particles was set at the appropriate Born radius needed to match the average charging free energy at −30 Å and +30 Å: 2.5 Å for the large particle and 1.27 Å for the small particle. It should be noted that these radii match closely the radii necessary to reproduce the transfer free energies from water to the bilayer center.

For fitting of the dielectric constant, Fletcher-Reeves conjugate gradient minimization (32) was used as implemented in the Gnu Scientific Library (http://www.gnu.org/software/gsl/). The actual quantity that was minimized was

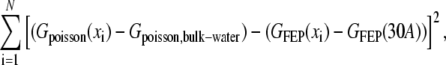where G_poisson(x) is a calculation of the free energy of charging a test particle at a position x relative to the bilayer center; G_{poisson,bulk-water} is the free energy of charging that test particle in an infinite bath of water; and G_FEP(x) is the free energy of charging a test particle from free energy perturbation. The sum is over all test charges: both large and small test particles at distances ranging from 0 Å to 30 Å from the bilayer center.

THEORETICAL BACKGROUND

In a system, the introduction of a small test charge δq is going to change the energy in proportion to the local electrostatic potential 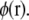The local electrostatic potential is a function of the instantaneous conformation of the bath. In our example problem, the bath is lipid bilayer plus surrounding water. Over a long period of time, the instantaneous potential takes on a distribution 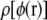of values at each position r. Because the energy change due to the test charge is proportional to the potential, this also determines the distribution of energy changes that would result when a test charge is introduced.

The change in free energy of the system created by adding a small test charge can also be determined from standard free energy perturbation formulas: (33)

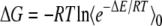(1)

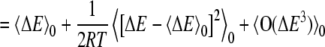(2)

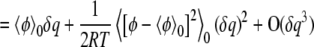(3)

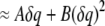(4)

ΔG is the change in the Gibbs free energy for adding charge, R is the ideal gas constant, T is the temperature, ΔE is the change in energy due to adding the test charge, and square brackets indicate an average over the unperturbed system (i.e., without the test charge). For small charges, we can truncate this expression after the second term. For systems without mobile charges, the response of the bath in continuum electrostatic models is assumed to be linear in the applied charge. For systems that satisfy linear response this quadratic expression holds regardless of the magnitude of the test charge.

The use of periodic boundary conditions does add one complication: the total energy change is no longer a strictly a linear function of the test charge because, 1), the reaction field at infinity introduces a potential energy change that is quadratic in the introduced charge, and 2), the total system charge is no longer zero. These effects change the energy quadratically in the introduced charge when Ewald summation is used (34–36). This introduces additional quadratic terms in the free energy, so, strictly speaking, Eqs. 2 and 3 are no longer equivalent, but differ by terms quadratic in δq. We will show numerically that these correction terms are negligible for our particular problem.

We use molecular dynamics simulations to determine the quadratic dependence of the free energy at the location of an introduced test charge, viz. coefficients A and B. This can be done by introducing a small test charge, determining the change in free energy using Eq. 1 and fitting this to a quadratic dependence. Alternatively, one can determine the coefficients by determining the distribution of electrostatic potential values directly from Eq. 3.

We can determine the dielectric constant from the B coefficient, which is a function of the position r. We treat the static potential (i.e., the A coefficient) separately from the potential fluctuations. One could attempt to replace the static potential with a static charge distribution that would also polarize the dielectric medium. We do not do that here because we are interested primarily in the dielectric profile.

For a system in which the medium is described by Poisson's equation, that is a medium with a local, linear polarization response and no mobile charges, the free energy of charging varies quadratically with the charge. This quadratic dependence occurs, 1), because Poisson's equation is linear, so the electrostatic potential at each point in space is a linear function of the introduced charge δq, and 2), because the total free energy change is given by 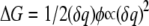(37). Thus there is a natural correspondence between the quadratic dependence of free energy on the test charge as determined by Poisson's equation and the quadratic dependence from free energy perturbation and linear response theory. The dielectric constant as a function of position can then be determined by requiring the coefficients of the quadratic terms determined from a simulation and from the solution of Poisson's equation to match.

To summarize our method:

1. We simulate our system to determine the quadratic dependence of the free energy on the magnitude of a test charge introduced at multiple, pre-defined positions. This determines the B(r) coefficient at these positions. Alternatively, electrostatic potential fluctuations may be used to determine the coefficient B(r).

2. With trial values for the dielectric profile ɛ(r), the Poisson equation is numerically solved to determine the quadratic free energy dependence at each test charge position. The best result for ɛ(r) is obtained by minimizing the discrepancy in free energy between the simulations and the Poisson equation for all test charge positions simultaneously.

Simulations can be done with explicit test particles; alternatively, the atoms of the solute and solvent molecules can be used directly as test-charge points. The latter method may potentially introduce artifacts because the intramolecular solvent response may be quite different from the solvent response around an external particle. For that reason we believe it is usually more appropriate to simulate the system with an external test particle. This test particle is simulated with zero charge, and a test charge is subsequently added to its center. Multiple test charges may be included simultaneously in many instances as long as they are explicitly modeled in the solution of Poisson's Equation. Details of implementation of our approach are given in Methods.

APPLICATION TO MEMBRANE DIELECTRIC

We apply our method to determine the dielectric profile of a model lipid bilayer surrounded on both sides by water. Although lipid bilayers are frequently modeled as simple low-dielectric slabs, their actual dielectric profile is more complex. Previous membrane simulations have revealed the basic features of the dielectric profile (14,15). The most important difference between these computed profiles and a single-slab model is that a region of intermediate dielectric constant extends deep into the bilayer core. This region of intermediate dielectric creates the possibility for binding of molecules to the lipid-water interface. This type of interfacial binding has been studied intensely for a number of years and reviewed in White and Whimley (38). Recent all-atom simulations (17) have suggested that interfacial binding can occur because the region of low dielectric in the bilayer center is much thinner than the region of low surface tension. (Surface tension here is not the bilayer surface tension but the free energy for introducing an uncharged nonpolar molecule into the bilayer/water system divided by the surface area of that molecule.) This discrepancy creates an interfacial region with a large dielectric constant but a low surface tension that accommodates large molecules that are too polar to enter the bilayer core. The different dependence of dielectric constant and surface tension necessary to capture this effect has also been incorporated into a generalized Born model of the bilayer (39).

Our system is composed of 128 POPC (1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine) molecules, 64 lipids per leaflet. This is surrounded on both sides by 4204 water molecules. Two uncharged Leonard-Jones (LJ) particles are added to the system. These particles are free to move in the plane of the bilayer, but their motion in the z direction, i.e., perpendicular to the plane of the bilayer, is harmonically restrained, allowing motion of at most a few Angstroms. One particle is harmonically restrained about a position z₀ relative to the bilayer center, defined as the average position of the lipid choline nitrogen atoms on both leaflets. The other particle is harmonically restrained about a position z₀ − 30 Å, so that as one particle moves through one bilayer leaflet away from the center, the other particle moves through the other bilayer leaflet toward the center. Two sets of simulations were carried out, with the radii of the test particles set to different values. In each set of simulations, z₀ varied from 0 to 30 Å in 2 Å increments. The system is periodic in three dimensions and simulated in an NpγT ensemble. An illustration of the system is shown in Fig. 1. Further details of the simulation are provided in Methods.

FIGURE 1.

Illustration of the simulated system used to determine the dielectric constant. The system contains 128 POPC lipids, 4204 SPC waters, and two uncharged LJ cavities. One cavity is harmonically restrained in its z motion relative to the bilayer about a position z₀. The other cavity is harmonically restrained in its z motion relative to the bilayer about a point at z₀ − 30 Å. This allows both bilayer leaflets to be studied simultaneously from a single simulation. A separate simulation was carried out for each value of z₀ from 0 to 30 Å in 2 Å increments. The system is periodic in three dimensions.

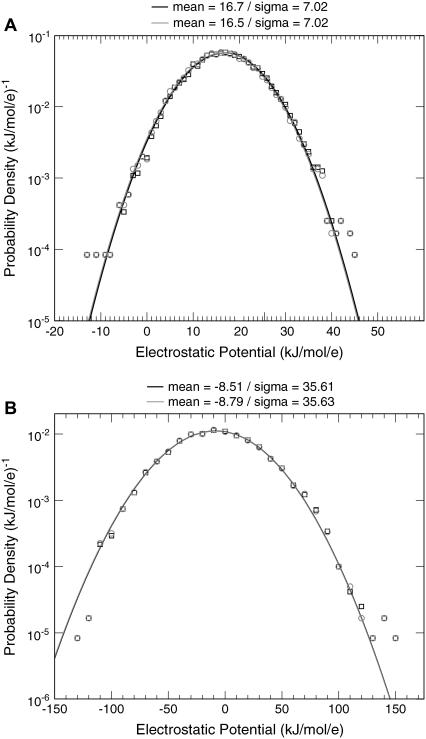
After the simulations are finished, a small test charge is added to each test particle, and the free energy change is determined by free energy perturbation. (Because each simulation contains two test particles, charge was added to only one test particle at a time.) This free energy is fitted to Eq. 4 to determine the A and B coefficients. The test charge is either +0.001|e| or −0.001|e|. The distribution of electrostatic potential values, 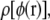determined from these test charges is shown in Fig. 2. (We show only the results for a particle at the bilayer center and a particle at 30 Å from the bilayer center.)

FIGURE 2.

Distribution of instantaneous values of the electrostatic potential for the simulation of large LJ particles at the center of the lipid bilayer (A) and 30 Å from the center (B). The electrostatic potential is estimated for convenience to be 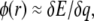where δE is the change in potential energy of the system created by placing a charge δq on the Leonard-Jones test particle. This expression is exact for a nonperiodic system but in error by a term quadratic in δq for periodic systems. To show that these quadratic terms are negligible, we show that the calculations are essentially identical for two test charges of different magnitude: 0.001|e| in squares and 0.01|e| in circles. Solid curves are two-parameter Gaussian fits to the distribution with adjustable mean and standard deviation (σ). The distribution of electrostatic potential values is very close to a Gaussian distribution as predicted by linear response theory and in agreement with the postulates underlying the description of continuum electrostatics as described by Poisson's equation.

Analytic results show that the energy change due to the introduction of a test charge δq into a neutral unit cell results in a small quadratic deviation from Coulomb's law (34–36). We need to show that this does not materially alter our results. Test charges of +0.01|e| and −0.01|e| were used to compute 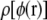in addition to charges of +0.001|e| and −0.001|e| as shown in Fig. 2. From this figure, we can see that the relative differences in the distribution 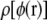determined from different-sized test charges are small, meaning that the errors introduced by using a nonneutral cell have an inconsequential effect on our estimated distribution 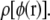Furthermore, Fig. 2 shows that the total energy change from adding +0.01|e| to a test particle is a small enough perturbation for the approximations in moving from Eqs. 1 to 2 to be valid.

The distribution 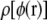can be fitted to high accuracy with a Gaussian distribution, which is consistent with our assumption of linear response and the assumption of a fixed, charge-independent dielectric constant. Because of the large dielectric constant in the solvent, we can only be confident that this result holds to ∼0.1|e| for test particles with |z| > 18 Å. Obviously dielectric saturation will eventually occur for some large charges.

To compute the effect of charging our test particles using a continuum description we need to assign a radius to our test particles, which is not necessarily identical to the van der Waals radius. We choose the radius of our test particles to be equivalent to the Born radius of an ion (40) with the same charging free energy as our test particle has when 30Å from the bilayer center. The dielectric constant is chosen to be that of bulk SPC water, 61 ± 1 (41). In other words, the radii for the continuum calculations are chosen to provide exact agreement between the continuum electrostatic calculations of an ion in an infinite bath of water and our free energy perturbation calculations at 30 Å.

After choosing the appropriate test-particle radii, the free energy for charging each of the test particles is computed by numerically solving Poisson's equation. The dielectric profile is systematically adjusted to maximize agreement between these continuum calculations and our atomistic simulations.

The bilayer/water dielectric profile is modeled as a series of slabs of constant dielectric. Each slab is 2 Å in thickness. Slabs extend from the bilayer center to 30 Å, and beyond 30 Å, the dielectric constant is assumed to take its bulk value of 61. Breaking the dielectric into slabs is a convenient discretization and parameterization procedure. The dielectric constants within the individual slabs are varied so that the free energy of charging all large and small cavities as determined from Poisson's equation matches the free energy of charging as determined from our atomistic simulations (discarding the linear free energy term corresponding to the static membrane electrostatic potential). The dielectric constants are initially adjusted manually. This is followed by a round of conjugate gradient minimization. Poisson's equation is solved using the APBS program (29–31). Details are provided in Methods.

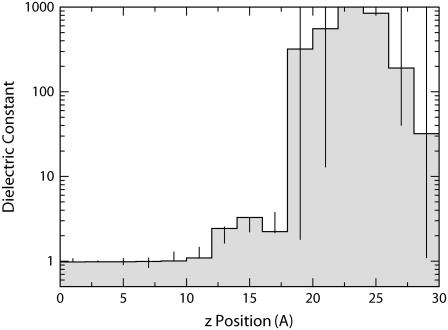
The dielectric profile resulting from this fitting is shown in Fig. 3. The corresponding agreement between the Poisson and molecular dynamics calculations of ΔΔG are shown in Fig. 4. There are a number of notable features in the dielectric profile shown in Fig. 3. First, a region of high dielectric constant extends deep into the bilayer. The lowest dielectric core extends only out to ∼12 Å from the center. Second, this core region is bounded by a deep-interfacial layer of intermediate dielectric, with a dielectric constant ∼3, extending to ∼18 Å. Third, a region of very high dielectric extends from this region to ∼28 Å from the center. Our simulations cannot definitively set the value of the dielectric constant in this region, although it is several times larger than the value of bulk water and is consistent with a peak value of infinity in this region. The large dielectric is physically reasonable, because the lipid headgroups contain a very large permanent dipole between the positively charge choline groups and the negatively charged phosphate groups. Beyond this high dielectric region, the dielectric constant is similar to bulk water. The existence of an intermediate dielectric layer flanking the core has been observed in previous simulations (14,15) of lipid bilayers. In addition, one simulation (15) also found a region of higher-than-bulk-water dielectric near the lipid phosphatidyl-choline groups.

FIGURE 3.

Dielectric profile fit to match the free energy of transfer from Poisson calculations with the free energy of transfer from atomistic simulations as closely as possible (Fig. 4). The dielectric profile is represented as 15 layers of constant dielectric of 2 Å in thickness from 0 to 30 Å. Beyond 30 Å, the dielectric is assumed to take the bulk value of SPC water, 61. Bars indicate approximate confidence limits. These are determined by fitting the large and small cavities in each leaflet separately, four sets of independent data points. The maximum value and minimum values from these four independent fits are used as the upper and lower confidence limits. The value of the high dielectric region between 22 and 24 Å cannot be precisely determined; however, its value is larger than all the other surrounding layers. This multi-layer dielectric profile can be approximated closely by a “two-slab model” in which the dielectric constant from 0 to 12 Å takes a value of 1, the dielectric constant from 12 to 18 Å takes a value of ∼3, and the dielectric constant beyond 18 Å takes the value of bulk water. The abrupt onset of the intermediate dielectric at 12 Å corresponds to the water boundary, and the high dielectric peak corresponds approximately to the location of the POPC headgroups (Fig. 5).

FIGURE 4.

Free energy for transferring an ion with a charge of 1|e| from bulk water to a given depth in the bilayer. Points are computed from atomistic simulations. Solid lines connect points computed from Poisson's equation using the dielectric profile of Fig. 3. The z position of each ion is taken to be the mean position of the restrained test particles in their uncharged state.

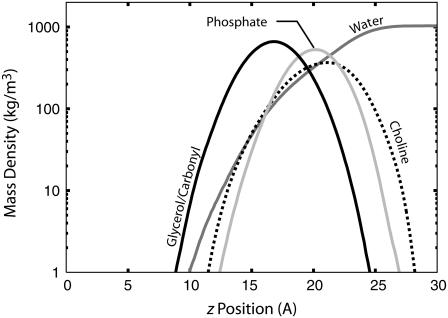
To gain some insight into the dielectric profile shown in Fig. 3, we computed the density profiles of water and the various POPC chemical groups along the z axis. Fig. 5 shows that the density of water becomes significant at ∼12 Å from the bilayer center and reaches bulk value at ∼25 Å. The polar carbonyl/glycerol groups also start ∼10 Å from the bilayer center and peak at ∼16 Å. The presence of water, at a reduced density, and the carbonyl/glycerol groups perhaps explains the intermediate value of the dielectric constant in this region. The choline (net charge +|e|) and phosphate (net charge −|e|) groups, together forming a large dipole, are centered near 20 and 21 Å, respectively. This region approximately coincides with the region of high dielectric (between 18 and 28 Å).

FIGURE 5.

Distribution of water and phosphatidylcholine (PC) headgroups along the z axis. The region of intermediate dielectric (∼3) located between 12 and 18 Å from the bilayer center seems to largely correspond to the location of the carbonyl groups and water buried deep in the membrane. The large dielectric peak that occurs between 18 and 28 Å corresponds roughly to the region near the peaks of the negatively charged phosphate groups and the positively charged choline groups, although it is shifted by a few angstroms away from the bilayer interior.

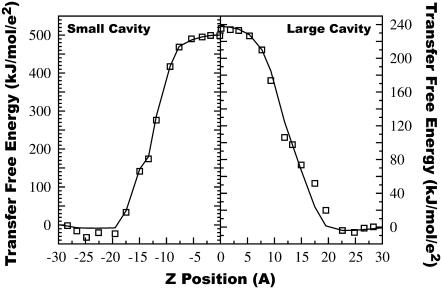
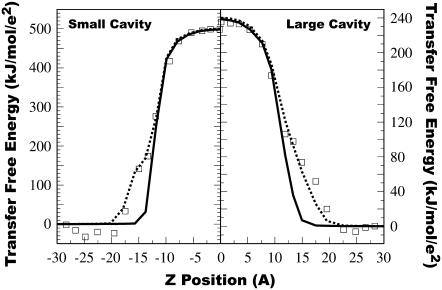
The transfer free energy obtained from the simulations, shown in Fig. 4, allows us to directly address the question: how accurate are models of the lipid bilayer that represent it as a single low-dielectric slab? The results of replacing our complex dielectric profile by a single-slab model of the bilayer are shown in Fig. 6. In this calculation, the core of the bilayer is given a dielectric of 1, and it extends to 13 Å from the center. Beyond this, the dielectric constant is set to that of bulk water. Although a single-slab model can properly model the core, the region between 13 Å and 18 Å from the bilayer center is improperly treated as bulk solvent. Transfer free energies from water to this region are in error by as much as 60 kJ/mol for the large LJ particle. Increasing the thickness of the low dielectric core would not result in significant improvement, because a comparable amount of error would occur in the opposite direction, viz., over-estimation of the free energy of transfer in this intervening region.

FIGURE 6.

Average free energy of transfer from bulk water to a particular position from the bilayer center as determined from simulations using both small and large LJ particles (squares). The curves are numeric solutions to the Poisson equation using a single-slab model (solid) and a two-slab model (dotted). In the single-slab model, the bilayer is modeled as a single slab with a uniform dielectric constant of 1 extending from 0 to 13 Å embedded in the higher-dielectric aqueous region. In the two-slab model, the central bilayer core has a dielectric constant of 1 and extends from 0 to 12 Å, and this is flanked by a region with a dielectric of 3 from 12 to 18 Å. Beyond that, the dielectric takes on the value of bulk water.

Replacing the single-slab model with a two-slab model results in significant improvement (Fig. 6). In the two-slab model, there is a low dielectric core with dielectric 1 extending to 12 Å. (The thickness of the low dielectric core region was reduced from 13 to 12 Å to compensate for small changes in the profile created by the reduction in dielectric constant outside this region from 61 to 3.) This is surrounded by a single interfacial region of dielectric 3 extending from 12 Å to 18 Å. Beyond 18 Å the dielectric constant assumes the value of bulk water. This two-slab model captures nearly all the variation in the transfer free energy. The only thing missing from this model is the negative free energy of transfer for particles moving from bulk water into the outer-most interfacial layer. This negative free energy of transfer is caused by the region of high dielectric interface not included in the two-slab model. An additional high dielectric slab can be added to capture this effect if desired.

DISCUSSION

We have applied a simple, intuitive method for determining the dielectric profile in a complex, nonhomogeneous system, which is to fit the dielectric profile to optimize the match between Poisson's equation and atomistic simulations in charging free energy. The primary advantage of this over existing methods is that no analytic solution for the response of the system to an external electric field is necessary. Thus, it can be applied easily to systems with complex geometries.

The primary limitation of the method is its requirement of multiple simulations to place test particles at different positions. This difficulty can be partially overcome by carrying out the simulation with multiple test particles simultaneously. This should not introduce much error provided the test particles are widely separated. Furthermore, one could if necessary solve Poisson's equation with the other test particles present to correct for their effect. A much larger perturbation might be introduced if one attempted to insert a test particle into a well-packed system such as a protein core.

In instances such as this, it might be more prudent to use the protein atoms themselves as sites for perturbing the charge. Likewise, individual water molecules could be used as sites for introducing excess charge. This approach has the advantage that only a single simulation will provide multiple sites for charge perturbation, one for each atom. We do not know if the dielectric constant introduced in this way would differ significantly from the dielectric constant determined from using test particles due to the fact that the charge introduced is within the same molecule or not. Certainly some dielectric changes will occur with bonded and near-bonded atoms, which might conceivably make the intramolecular polarization different from the polarization experienced by an external test particle.

In all instances, this method is bound by the limitations of atomistic simulations. These simulations may miss long-time relaxations. The long-time relaxations will most likely work to reduce the apparent dielectric constant in the region of a test particle, because shorter simulations will usually underestimate the fluctuations in the local electrostatic potential.

The most serious limitation of the current calculation is that it is based on an atomistic model that does not include electronic polarization. The dielectric constant in the bilayer core has a dielectric constant of 1 in atomistic simulation, when in reality electronic polarization should result in a dielectric constant closer to that of bulk alkanes, which is ∼2 (42). This factor of 2 will result in a factor of 2 difference in the value of the electrostatic component of the transfer free energy from bulk water to the bilayer interior.

Throughout the calculation, we have assumed that the bilayer and water can be treated as an electrostatic continuum with a local, linear, and isotropic dielectric response. These assumptions are frequently made for small molecules in an aqueous environment; however, significantly less confidence can be given to them when the whole membrane is treated implicitly. A number of significant differences exist between pure aqueous solvent and the membrane/water environment. The primary difference is that water molecules are smaller than organic molecules, justifying the treatment of them as a continuum; whereas, lipid molecules are often much larger than the solute of interest. The large size of the lipid molecules opens the possibility that the electrostatic interactions for solutes smaller that the lipid molecules may be quite different than electrostatic interactions for large solutes. In particular, local interactions between the solute and the lipid molecules may be communicated some distance through the bonded structure of the lipid molecules. Some attempts have been made to account for the finite size of water solvent dipoles, e.g., the semi-microscopic Langevin Dipoles model (see Shutze and Warshel for a review of these and related methods) (8). The Langevin Dipoles model has also been used to model a lipid bilayer and its surrounding solvent (43), albeit without detailed information on the appropriate dipole density and dipole magnitude to use in this model. Although in this article we have matched continuum electrostatic calculations and all-atom simulations, a similar procedure could be applied to determine the proper parameters for a Langevin Dipole model. Further comparisons between continuum calculations and atomistic simulation will be needed, however, to determine the effective error in treating the bilayer as a continuum.

A second potential difficulty with our continuum calculations is that lipids in a bilayer are arranged in a strongly anisotropic local environment, which makes an anisotropic polarization response a real possibility. Anisotropy in the polarization fluctuations suggests that the correct local dielectric constant is also anisotropic. Previous simulations of a DPPC (di-palmitoyl-phosphatidylcholine) membrane have found that the polarization fluctuations in the plane of the bilayer are ∼10 times greater than polarization fluctuations in the direction of the bilayer normal (44). Although conversion of these polarization fluctuations normal to the bilayer into a spatially resolved anisotropic dielectric constant was not possible, an average over the whole unit cell suggests a mean value in the normal direction of ∼3, significantly less than the average value of 89 for directions in the bilayer plane (15). Our calculation method can be used to determine an anisotropic local dielectric constant; however, this cannot be done precisely using a single test charge as done here. Multiple pairs of test charges separated in the plane of the bilayer and normal to the bilayer may, however, be able to accurately determine the anisotropic response.

The use of multiple test charges would also allow us to evaluate our choice of test particle radius. It is certainly possible that the large lipid molecular size will necessitate increasing the test particle radius at different positions in the bilayer, or using a larger probe radius for determining a molecular surface. The latter issue may be particularly important, considering that the large size of lipid molecules will sterically exclude them from many cavities accessible to water molecules. Unfortunately, simulations that use a single, spherical test particle do not provide enough information to separate the test particle radius from the local dielectric constant with any degree of precision.

Considering this uncertainty, our calculated dielectric profile is properly understood as a “best-fit” isotropic profile for calculations on smaller solutes. Despite these caveats, our estimated dielectric profile for a POPC bilayer agrees well with the results of Stern and Feller (15) who used a method based on Fröhlich-Kirkwood theory to compute the dielectric profile of a DPPC (dipalmitoylphosphatidylcholine) bilayer using a different force field. Their computed dielectric constant is ∼1 from 0 to 10 Å, 4 from 10 to 15 Å, 180 from 15 to 20 Å, 210 from 20 to 25 Å and like bulk water beyond 25 Å [Table III of Stern and Feller (15)].

Despite their simplicity, continuum electrostatics treatments have been enormously helpful for rapid quantitative assessments and for intuitive explanations of complex phenomena. Our method provides a quantitative approach to assign dielectric profiles in nonhomogeneous systems, which should go far in addressing ongoing debates about the proper dielectric constants to assign to these systems.