Stability and Kinetic Properties of C5-Domain from Myosin Binding Protein C and its Mutants

Abstract

The impact of three mutations of domain C5 from myosin binding protein C, correlated to Familial Hypertrophic Cardiomyopathy, has been assessed through molecular dynamics simulations based on a native centric protein modeling. The severity of the phenotype correlates with the shift in unfolding temperature determined by the mutations. A contact probability analysis reveals a folding process of the C5 domain originating in the region of DE and FG loops and propagating toward the area proximal to CD and EF loops. This suggests that mutation effects gain relevance in the proximity to the area where folding originates. The scenario is also confirmed by the analysis of the kinetics of 27 test mutations evenly distributed throughout the entire C5 domain.

INTRODUCTION

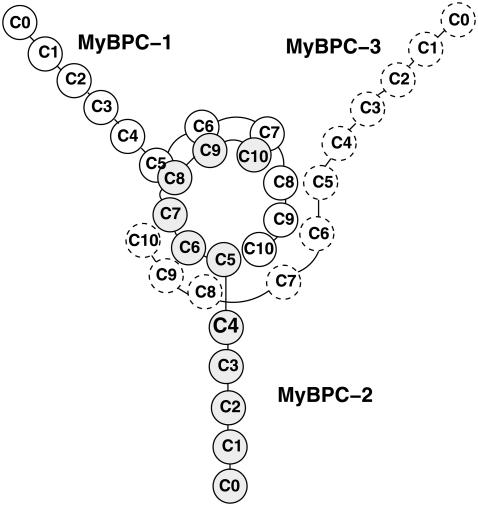
Familial Hypertrophic Cardiomyopathy (FHC) is a cardiac disorder characterized by left ventricular hypertrophy. The prevalence of the disease in the population is 0.2% and represents the most common cause of sudden cardiac death in young competitive athletes (1). FHC is clinically heterogeneous with different forms caused by mutations in 10 genes encoding cardiac sarcomeric proteins, the most important of which are the β-myosin heavy chain, the cardiac troponin T, titin, and cardiac myosin binding protein C (MyBP-C) (2). MyBP-C mutations are found in 20–45% of the FHC patients (3), so that alterations on this protein represent the second-most common cause of the disease. Both nonsense (premature termination of translation) and missense (amino-acid substitution) mutations have been found to correlate with the disease. Whereas nonsense mutations on MyBP-C gene result in a mild phenotype (3), a number of missense mutations lead to a severe phenotype and the precise mechanism through which they cause the pathology is still unknown (4). MyBP-C is a linear sequence of 11 IgI-like and fibronectin-like domains, referred to as C0–C10, working as potential regulators of cardiac contractility (1). A structural arrangement has been proposed by Moolman-Smook (5,6) whereby three MyBP-C molecules form a collar around the thick filament (Fig. 1). In particular, domains C5–C10 in each molecule participate in formation of the collar while domains C0–C4 protrude into the interfilament space and interact with subfragment 2 of myosin acting as a brake for muscular contraction (7). The collar is stabilized by specific interactions between domains C5–C8 of a molecule and domains C7–C10 of the neighboring one. Mutations on MyBP-C might either prevent the C0–C4 region from interacting with the S2 fragment (hypercontractility) or force a carboxy-truncated mutant to permanently interact with S2 (hypocontractility) (5).

FIGURE 1.

Moolman-Smook model of MyBP-C arrangement in the sarcomere: the trimeric collar surrounding the thick filament is stabilized by interactions between domains C5–C8 and C7–C10.

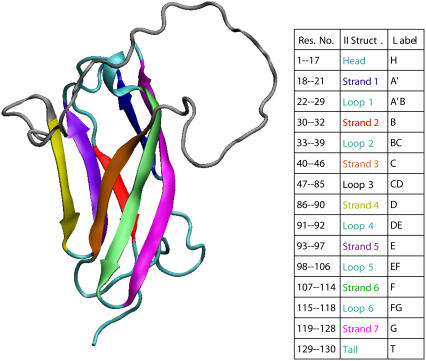
In this work we focus on domain C5, taking advantage of the availability of structural and thermodynamic experimental data collected by Idowu et al. (8). This domain, belonging to the Immunoglobulin superfamily, is characterized by a β-sandwich structure with two twisted β-sheets closely packed against each other. The first β-sheet is formed by strands C, F, G, and A′, while the second β-sheet comprises strands B, D, and E (see Fig. 2). A specific feature of the cardiac MyBP-C isoform is the presence of two long insertions not present in the fast and slow skeletal isoforms. The first insertion is 10-residues-long and is located in the linker between the C4 and C5 domains. Thermodynamic measurements on the Δ1–7 deletion mutant (8), however, showed that this protein segment contributes significantly to the stability of domain C5 so that it cannot be regarded as a simple linking element between two subsequent units of MyBP-C. The second insertion is 28 residues in length and it resides in the CD loop (8) that, owing to its high mobility, destabilizes the protein lowering the folding temperature as compared to other Ig-domains (8). This loop is suspected to form an SH3 domain recognition sequence presumably binding to the CaM-II-like kinase that copurifies with MyBP-C (9).

FIGURE 2.

The secondary structure elements of domain C5 of MyBP-C. The residues have been renumbered 1–130. The β-strands are highlighted in color and labeled according to the table (figure produced by the VMD software (30)).

Three FHC-causing mutations have been identified on C5 domain: Asn⁷⁵⁵Lys, Arg⁶⁵⁴His, and Arg⁶⁶⁸His. The first one lies on the FG-loop and leads to a significant destabilization of the protein yielding a severe phenotype (6,8). Conversely, the Arg⁶⁵⁴His and Arg⁶⁶⁸His mutations, causing a much milder phenotype, are not particularly destabilizing and their pathogenic role is possibly related to the impairment of binding with specific ligands. Residue Arg⁶⁵⁴, in fact, is located on the negatively charged CFGA′ surface, and it may regulate the specificity of the binding of positively charged substrates (4,6,8). A role in ligand binding is also postulated for Arg⁶⁶⁸ (10).

This work explores through MD simulations the role of the above-mentioned FHC-causing mutations within the framework of a coarse-grained native centric model. Native centric models, or simply Gō-models, minimize the frustration of the free energy hypersurface, thus reducing the risk for the protein to get trapped in a metastable minimum. This approach is particularly meaningful when the folding process is strongly driven by the topological properties of the native state (11–17). This is the case of domain C5 of MyBP-C, belonging to the Ig-superfamily where both transition and native states are stabilized by the same contacts dictated by protein topology (18) so that the members of this group share similar folding pathways.

We consider a heavy-map Gō model where native contacts are identified on the basis of the steric hindrance of side chains to complete the topological description with some specific chemical features. Since we address the problem of discriminating the effects of mutations, we also introduced some amount of heterogeneity in the energetic couplings of the Gō force field. This approach is particularly suitable for C5 domain where pathological mutations Arg⁶⁵⁴His and Arg⁶⁶⁸His are modeled through the removal of the same number of native contacts. The relevance of this approach for a reliable mutation analysis was suggested, for example, in Matysiak and Clementi (19), where available experimental data on single mutations of S6 ribosomal protein and its circular permutants, were reproduced with correlation coefficients larger than 0.9.

METHODS

In this article, we consider a variant of Gō-like force field proposed by Clementi et al. (13). The polypeptide chain is represented only through C_α carbon positions. The interaction between residues is defined by the potential energy

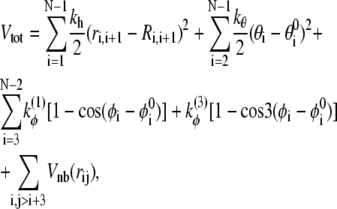(1)

where the nonbonded interaction potential V_nb reads

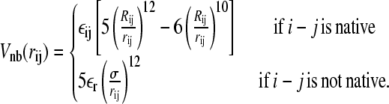(2)

In the above equations, r_ij is the distance between residues i and j; θ_i is the bending angle identified by the three consecutive C_α values i − 1, i, and i + 1; and φ_i is the dihedral angle defined by the two planes formed by four consecutive C_α values i − 2, i − 1, i, and i + 1. The symbols with the superscript 0 and R_ij are the corresponding quantities in the native conformation. The force-field parameters are proportional to the energy scale ε₀ = 0.3 Kcal/mol, such that 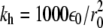(r₀ = 3.8 Å), k_θ = 20ε₀, 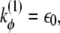and 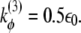The parameters of the repulsive Lennard-Jones terms between nonnative contacts are chosen as follows: σ = 5.0 Å, ε_r = 2/3ε₀. Two residues i and j interact attractively whenever their side chains have at least a pair of heavy atoms closer than a distance cutoff R_c = 5 Å. The condition selects 227 residue-residue contacts on the PDB structure 1GXE. The strength of attractive native interactions ε_ij is weighted according to the number of atomic contacts, ε_ij = ε₀(1 + n_ij/n_max), where n_ij is the number of atomic contacts between residues i and j in the PDB structure normalized to the maximal value of this quantity n_max = 43 found for the couple Lys⁴⁵-Tyr¹⁰⁹. The heterogeneity in residue contact energies was introduced in this work through their rescaling according to the number of atomic overlaps. This strategy is supported by the experimental and theoretical findings. In particular, the experimental mutation analysis on barnase by Serrano et al. (20) showed a nontrivial correlation between the destabilization induced by the mutation and the number of methyl or methylene side groups surrounding the deleted group. Moreover, theoretical arguments in agreement with our simple approach can be found in the literature (21–23) where linear correlation is found between pairwise sum of the buried surface area and contact potential of Miyazawa and Jernigan (24).

We performed Langevin MD simulations within Leap-Frog integration scheme with time step h = 5 × 10⁻³ τ and a friction coefficient γ = 0.05 τ⁻¹, where the time unit 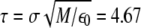ps (M is the average mass of an amino-acid residue estimated to 110 Da). In this work, we considered unfolding rather than folding simulations. Simulations of protein unfolding under denaturing conditions are commonly employed (25,26) to gain insight on the folding mechanism in physiological state. This approach was originally developed within the framework of all-atom MD (see, for example, (26)), because high temperature computations drastically increase the reaction rate, thus significantly reducing the computational time. When coarse-grained models are used, however, as is our case, the key issue is not the computational load but rather the possibility to avoid kinetic traps due to the residual energetic and topological frustration of the force field. It is important to stress that, when using the unfolding strategy, extreme caution must be paid, because an increase in temperature may actually change the reaction mechanism rather than simply accelerating the same process (27). As a result, the folding pathway determined under strong folding conditions may not be the reverse of the unfolding pathway derived in strong denaturing conditions. 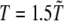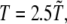To overcome this difficulty, we do not follow the unfolding process at a single high temperature; instead, we gradually heat the system in 50 temperature steps from to where 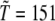K sets the temperature scale. Care is also paid in the temperature-jump simulations, by driving the system to a temperature just slightly above the unfolding point of the wild-type (WT), so that the unfolding mechanism can be safely assumed as being the reverse of folding. Moreover, the experimental evidence (8) that domain C5 of MyBP-C acts as a two-state folder with no intermediates along the folding route, lends further support to the suitability of unfolding simulations for the study of this protein. In fact, in a recent article (28), Karplus showed that when a protein can fold along alternative pathways, some of which involved misfolded intermediates, the unfolding simulation then preferentially follows the path with the lowest free energy barriers neglecting the alternative routes. As a consequence, unfolding studies are better suitable to proteins lacking off-pathway intermediates as is the case of domain C5 of MyBP-C.

The C5 domain of MyBP-C, as many small single-domain proteins, folds and unfolds in an all-or-none process without populating partly structured intermediates (8). The kinetics of the reaction U ↔ F, starting from an initial condition with proteins initially in the native state, can thus be modeled as

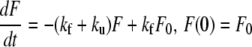where F represents the folded protein concentration, and k_u and k_f are the rates of unfolding and unfolding, respectively. The value F₀ is the total concentration of the protein that remains constant throughout the process. Normalization of F(t) to F₀ yields the probability that the protein be folded at time t:

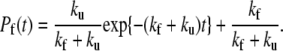(3)

The time course of P_f was computed by averaging in a series of 10³ independent temperature-jump simulations starting from low temperature conformations equilibrated at T = 225 K for a period of 10³τ and then heated at temperature T = 332 K just above the transition point of WT and mutants. Equation 3, when fitted to simulation data, yields estimates of the rates k_f and k_u, enabling a direct comparison between the kinetics of WT and mutants.

During the simulated T-jump experiments, we also computed the probability of any single native contact being intact. As the simulations were performed at a temperature just little higher than the transition point, it is reasonable to assume that the folding pathway is well described by the reverse of the sequence of contact breakdown in the T-jump simulations.

The dynamics of dissolution of interactions between couples of secondary structure elements X, Y was also tracked through the evolution of local native contacts (29) (also referred to as “partial overlaps”). This quantity was computed by averaging over all trajectories ending up in an unfolded conformation according to the equations

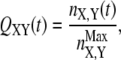(4)

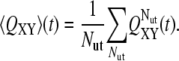(5)

In Eq. 4, n_X,Y and 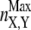indicate the number of contacts between X and Y at time t and in the native structure, respectively, and N_ut is the number of trajectories leading to the denaturation of the protein. X and Y are any of the 15 secondary structure elements shown in Fig. 2. In this protein, 120 unique (X, Y) pairs are possible, but only 13 of them are particularly relevant to monitor the reaction. Pairs CF, FG, and A′G are indicators of the status of β-sheet CFGA′; pairs BE and DE probe the condition of sheet BDE. The interactions among the loops on the same side of the molecule as the long CD loop are studied by analyzing the couples A′-A′B, A′B-EF, and CD-EF. In a similar fashion, the interactions among the loops on the opposite side of the molecule with respect to the CD loop, are monitored through the status of the pairs HG, H-BC; H-FG, HH, and BC-FG (with H being the N-terminal 1–17 segment). Two parameters were also introduced to follow the interactions between the two β-sheets and between any β-strand and any loop.

RESULTS

An unfolding simulation of the wild-type (WT) sequence was performed by gradually heating the protein from temperature T = 225 K to T = 375 K in 50 temperature intervals. For each temperature, 5 × 10⁷ time steps were spent for the equilibration, followed by a production stage of 5 × 10⁸ time steps. A similar schedule was employed to simulate the unfolding of the three missense mutants Asn¹¹⁵Lys, Arg¹⁴His, and Arg²⁸His (notice that protein residues have been renumbered 1–130 as a restriction to the C5 domain only). A residue mutation is implemented in the Gō-model by turning all the native contacts in which the site is involved, into nonnative ones (31). The pathological mutations that we analyze, are strongly nonconservative, causing a significant change of the physical-chemical properties of the residue, justifying their modeling through the removal of all the contacts. We draw the attention on the fact that contacts between residues are weighted with the number of atomic overlaps. This implies that the removal of a single residue-residue contact corresponds to the cut of a different number of atomic interactions. As an example, we consider the mutations on sites 14 and 28. In both cases we delete three residue-residue contacts but in the former case we cut 16 atomic contacts while in the latter 28 are cleaved. In our opinion, this difference is relevant, and it is neglected by all Gō models with homogeneous energy couplings. The role of the amino-terminal region of the protein was also investigated through unfolding simulations of a deletion mutant where the first seven residues of the C5 domain were removed.

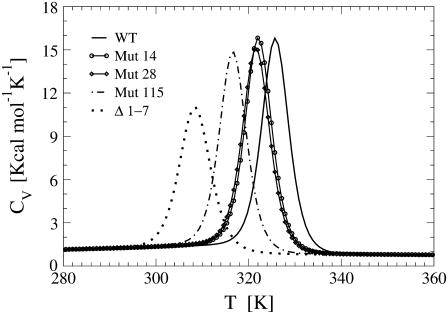
The presence of a single sharp peak in the thermograms of both WT and all the mutants (Fig. 3), suggests for these proteins a cooperative, two-state unfolding mechanism.

FIGURE 3.

Thermal behavior of heat capacity of the WT C5 domain, the missense mutants deprived of the native contacts of Arg¹⁴, Arg²⁸, and Asn¹¹⁵, and the deletion mutant lacking the 1–7 subsequence. Using the weighted histogram method, computations have been performed with the data collected during unfolding simulations.

Mutations on Arg¹⁴ and Arg²⁸ appear to cause just a moderate destabilization of the protein as they determine a little shift of the unfolding temperature to lower values. The mutation of Asn¹¹⁵, on the other hand, results in a more pronounced decrease of the transition temperature, suggesting a more destabilizing effect in agreement with experimental data. The NMR spectra recorded by Idowu et al. (8), in fact, show that the Asn¹¹⁵Lys mutant is unstable and largely unfolded as compared to the wild-type C5 motif. The NMR spectrum of the Δ1–7 deletion mutant also lacks the peak dispersion typical of folded proteins and the molecule appears to be unstructured. This finding is consistent with our result that the amino-truncated protein is characterized by the largest shift in the unfolding temperature T_u, thus resulting in the most destabilized mutant.

The extent of the transition temperature decrease is clearly related to the number of contacts removed to implement the mutations. The removal of only three contacts to simulate the mutations on Arg¹⁴ and Arg²⁸, in fact, results in small and almost identical shifts of the positions of the peaks of the corresponding C_V plots. The mutation of Asn¹¹⁵ produces a more relevant temperature shift because it entails the cleavage of 10 residue contacts. Finally, the removal of the N-terminal 1–7 fragment results in the loss of 41 native contacts determining the largest displacement of the thermogram. Not only the number, but also the position, of the removed contacts plays a relevant role. The C_V plot displacements of the different mutants, in fact, do not reflect the ratio of the lost contacts. As an example, the deletion mutant features a temperature shift twice larger than that of Mut¹¹⁵, in contrast with a 4:1 ratio of removed native contacts. A possible explanation of this mismatch is that the contacts involving Asn¹¹⁵ occupy a central position in the graph of interactions while those involving the first seven N-terminal residues are more peripheral.

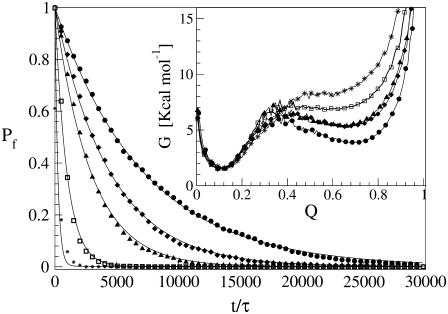
The early unfolding behavior of the WT sequence of domain C5 was compared to that of the three missense and Δ1–7 deletion mutants through T-jump simulations. The proteins were first equilibrated at very low temperature T_low = 225 K for 2 × 10⁵ time steps and then heated to a temperature slightly higher than the unfolding point of the WT T_high = 332 K. We stress that the choice of T_high = 332 K provides a common denaturing temperature for both WT and mutants, representing also a reference point for the comparison of the kinetic rates of all the molecular species under examination. Finally, a temperature slightly higher than the unfolding temperature of mutants and WT, allows the denaturation to occur in reasonably short simulation times. The molecules were kept at T = T_high for 6 × 10⁶ time steps and during this period the nativeness of the proteins was checked every 10³ time steps by monitoring the fraction of contacts still intact. When the overlap fell below a threshold Q_u = 0.25 the protein was regarded as being unfolded. The progress of the denaturation process was measured by tracking the fraction of folded trajectories as a function of time, P_f (t), plotted in Fig. 4 for the WT and mutants together with the free energy profiles at temperature T = T_high (inset). Fig. 4 shows that all the mutations speed up the unfolding process. As an example, Mut¹¹⁵ and the deletion mutant become denatured in all trajectories no later than t = 5000 τ. Mut²⁸ conversely, appears to be more stable and it resists until t = 15,000 τ before unfolding in all runs. The behavior of Mut¹⁴, finally, is similar to that of the WT sequence, and even if the 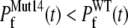for t > 2500 τ, the difference never exceeds 15%. The kinetic behavior is consistent with the free energy profiles (inset, Fig. 4) showing the mutations to reduce the unfolding barrier while simultaneously increasing the folding one. Equation 3 was fitted to the P_f (t) plots so as to estimate the kinetic rates. The excellent fit testified by correlation coefficients, always higher than 0.997, shows that both WT and mutants behave as two-state folders. Due to the high simulation temperature T = T_high = 332 K, the unfolding rates dominate the process being, on average, eight orders-of-magnitude larger than folding ones. Table 1 summarizes the impact of mutations on the unfolding rate by the following ranking: < < < <

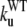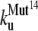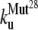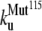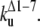
FIGURE 4.

Comparison of unfolding kinetics of WT domain C5 with its deletion and missense mutants through the evolution of the fraction of folded trajectories P_f (t). (Circles refer to WT, diamonds to Mut¹⁴, triangles to Mut²⁸, squares to Mut¹¹⁵, and stars, to the deletion mutant.) The solid lines represent the exponential fits according to Eq. 3. (Inset) Free energy profiles of WT and mutants at the temperature of the T-jump simulations T = T_high = 332 K as a function of the fraction of native contacts Q. Time is in units τ = 4.67 ps.

TABLE 1.

Unfolding rates of WT and mutants determined from the fitting of the P_f(t) plots shown in Fig. 4 using Eq. 3

Species	ku[τ−1]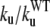
WT	1.41 × 10−4	1
Mut14	2.26 × 10−4	1.61
Mut28	3.46 × 10−4	2.47
Mut115	1.04 × 10−3	7.43
Δ1–7	1.46 × 10−3	15.93

The unfolding rates can be ranked as: < < < < .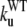

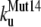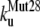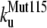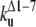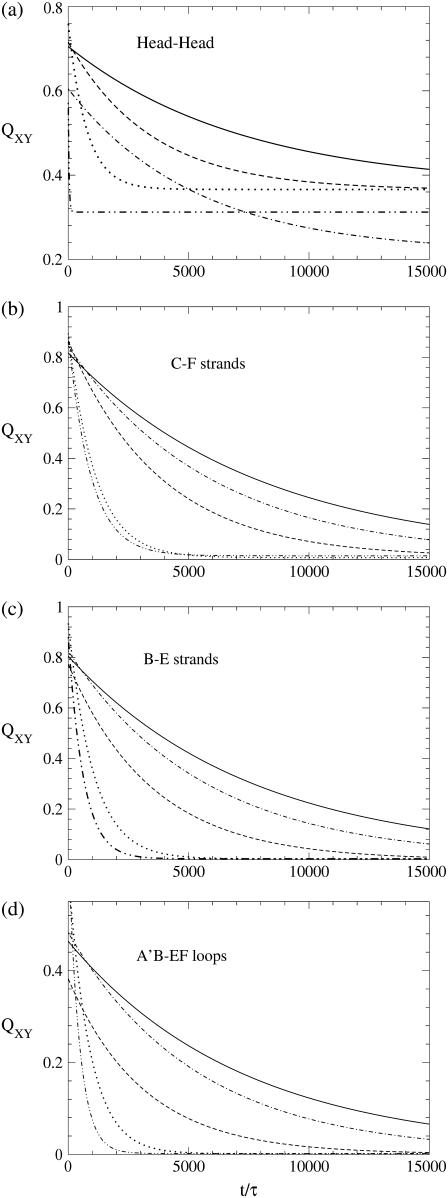
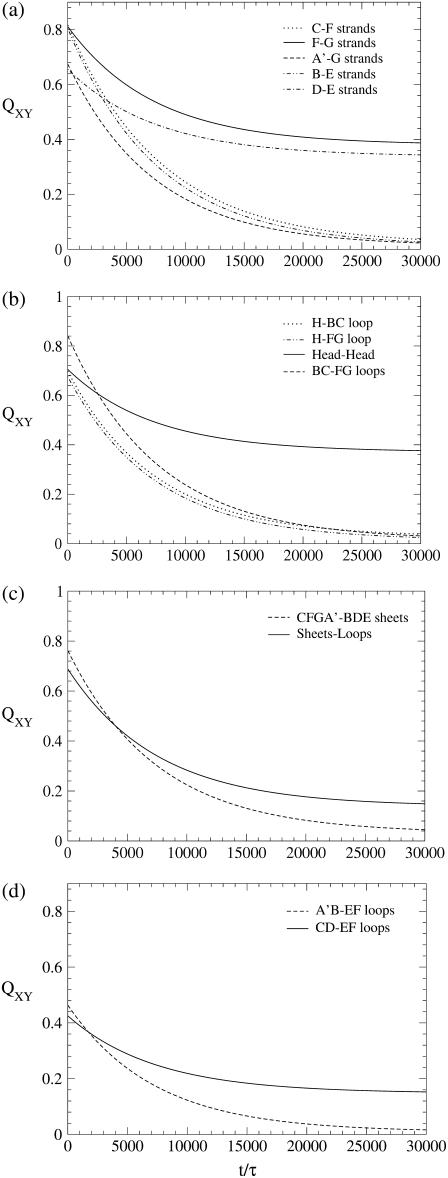
The analysis of the kinetics of local native contacts enables us to explore the local folding/unfolding mechanism occurring in different regions of the protein. Fig. 5 shows the partial overlaps of four different structural elements of domain C5 to assess the impact of the mutations on each of them. Attention is focused on four regions of the protein. First of all, β-sheet CFGA′ is monitored in Fig. 5 b, through the interactions between strands C and F, while β-sheet BDE is analyzed in Fig. 5 c through the breakdown of contacts between strands B and E. The network of interactions among Head, BC loop, and FG loop (referred to as “lower loops”) is followed in Fig. 5 a by monitoring the contacts within the Head region; finally in Fig. 5 d, we consider the evolution of the contacts between A′B and EF loops that, together with the CD loop, we name the “upper loops”. The deletion of the 1–7 fragment and the removal of contacts of residue 115 (located in the FG loop) are chemical transformations taking place in the region of the lower loops, and it is therefore not surprising that they significantly speed up the breakdown of Head-Head contacts as shown in Fig. 5 a. Panels b–d of Fig. 5, however, indicate that Mut¹¹⁵ and Δ1–7 have a nontrivial long-range effect, strongly favoring the dissolution of both β-sheets and destabilizing the interactions of the upper loops. The importance of mutations Mut¹¹⁵ and Δ1–7 can be better appreciated by comparison with Mut¹⁴. Residue 14, in fact, is located in the Head region, and the effect of its mutation is only local. As it increases the velocity of breakdown of Head-Head contacts (Fig. 5 a), its impact on the other protein regions is negligible, as seen by Q_XY(t) plots almost identical to that of the WT (Fig. 5, b–d). The behavior of Mut²⁸ finally appears to be intermediate between the two extremes. The study of partial overlaps also provides useful information about the unfolding and folding mechanisms. Fig. 6 illustrates the time evolution of the Q_XY parameters of the WT, revealing the existence of two families of curves characterized by different slopes. Fig. 6, a and b, in particular, show that short-range contacts such as those linking the consecutive strands F-G and D-E and those connecting residues of the Head region with each other, decay more slowly than long-range contacts and their partial overlap reach a stable value at ∼40%. Since we work in a moderately denaturing condition, the unfolding can be considered reversible, and the features of the Q_XY plots suggest that short-range contacts are the first to appear during folding. Fig. 6 a indicates that the F-G contacts act as a nucleus for the formation of the CFGA′ sheet that is completed much later when the fraction of F-G and A′-G contacts reaches a comparable level. In a similar way, the D-E contacts may represent a nucleus for the formation of the BDE sheet that gains its final conformation when the increase of the fraction of B-E contacts allows strand B to join the structure. A comparison of panels a and c in Fig. 6 shows that the dissolution/formation of the hydrophobic core follows the same dynamics as the destruction/formation of the two β-sheets. It follows that, in domain C5, the two sheets come close to each other during the process of assembling their structures. A final remark refers to the interactions among the higher loops (Fig. 6 d), whose Q_XY parameter does not exceed 50% even at the beginning of the unfolding process, as a consequence of the very high mobility of these poorly structured regions.

FIGURE 5.

Local native contacts computed according to Eqs. 4 and 5. The curves are the fits with an exponential to simulation data. (Curves: solid, WT; dotted-dashed, Mut¹⁴; dashed, Mut²⁸; dotted, Mut¹¹⁵; and double-dotted-dashed, Δ1–7 deletion mutant.) The quantity 〈Q_XY〉(t) represents the fraction of native contacts formed between the structural elements X and Y at time t. Mut¹¹⁵ and Δ1–7 exert long-range influence on the molecule, whereas Mut¹⁴ and Mut²⁸ operate on a shorter length scale. Time is in units τ = 4.67 ps.

FIGURE 6.

Time course of local native contacts (Eqs. 4 and 5) of WT domain C5 in four different regions of the molecule. (a) β-sheets; (b) lower loops; (c) sheet-sheet and loop-sheet interactions; and (d) upper loops. The data have been fitted with an exponential to improve readability. Time is in units τ = 4.67 ps.

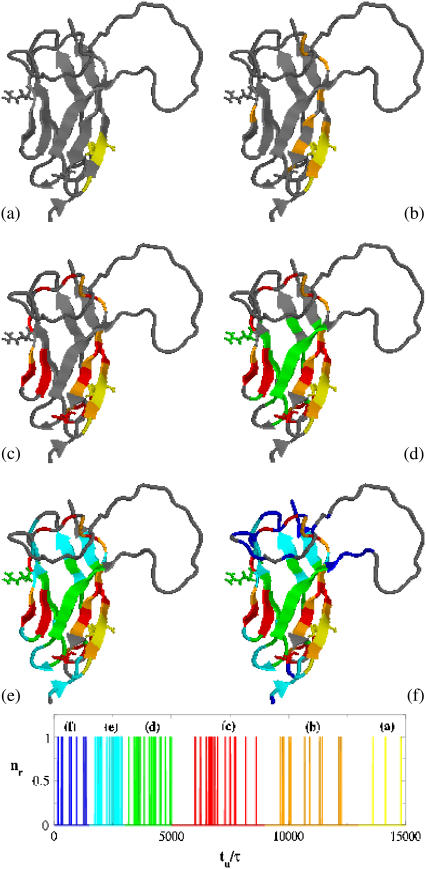
Further understanding of the unfolding/folding mechanism can be attained by the analysis of the time evolution of native contact probabilities that, for a T-jump simulation, show a monotonic decay. We assume a contact to be broken when the probability P_ij reaches a cutoff value π = 0.5. We then compute the average time of threshold crossing for all contacts involving the same bead, as an estimate of the unfolding time of that residue. The folding mechanism, i.e., the order according to which residues assume their native position, can be determined by sorting their average unfolding times in a decreasing order. The discontinuous blocks observable in the histogram of unfolding times identify the key stages of the folding process, when groups of residues take their native conformation in a coordinated manner. The folding process is expected to proceed according to the following stages:

• Stage 1: Formation of FG contacts in proximity of the FG loop (Fig. 7, a and b).

• Stage 2: Appearance of DE hairpin (Fig. 7 c).

• Stage 3: Strand C joins the FG hairpin while strand B moves close to the DE hairpin (Fig. 7 d).

• Stage 4: Stabilization of C-terminal ends of strands G and A′ and A′B and EF loops in their native conformation (Fig. 7, e and f).

FIGURE 7.

Representation of the folding pathway of domain C5 from MyBP-C. (a–f) The regions in color indicate residues in nativelike conformation; gray segments are still coil. (Blue, 0 < t_u < 1.5 × 10³; cyan, 1.5 × 10³ < t_u < 3 × 10³; green, 3 × 10³ < t_u < 5× 10³; red, 5 × 10³ < t_u < 9 × 10³; orange, 9 × 10³ < t_u < 1.3 × 10⁴; and yellow, t_u > 1.3 × 10⁴.) The bars represent the distribution of the unfolding times. Time is in units τ = 4.67 ps.

The folding mechanism of the C5 domain thus appears to be mainly driven by conformational entropy. The short-range contacts of the FG and DE hairpins, in fact, are the first to appear during refolding, as their formation is accompanied with a modest loss in conformational entropy. In particular, the DE and FG loops, comprising two and four residues, respectively, are the shortest loops of the C5 domain and it is therefore not surprising that the refolding of the two hairpins starts in this region. On the contrary, the major length of the A′B, CD, and EF loops determines their late refolding. This pathway suggests a way to rationalize the different impact of the FHC-causing mutations on C5 domain. For example, residue 115, being located in the FG loop, when mutated is likely to hinder the very first events of folding upon mutation. Residue 28, conversely, is located in the BDE sheet, but outside the crucial DE hairpin. Therefore its mutation is expected to influence only the structuring of the protein portion near the long A′B, CD, and EF loops, thus resulting in a mild phenotype.

To test our explanation of the pathogenic role of the mutations on residues 14, 28, and 115, we performed temperature-jump simulations of 27 other mutants obtained by changing residues evenly distributed in all districts of domain C5. The results of our simulations are summarized on Table 2. Tables 1 and 2 show that the most destabilizing mutations, characterized by 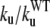≥ 5, are located on strand F (residues 111, 112, 113), on the FG-loop (residue 115), on strand E (residue 93), on the BC-loop (residue 35), and on strand C (residue 43). This distribution confirms the conclusions drawn after analyzing the folding mechanism of the wild-type protein: the strand F and the FG-loop are the most sensitive regions to mutations, explaining the severe phenotype from FHC mutation of residue 115. Our kinetic analysis also underscores the importance of strand E, which is the central element of the BDE sheet and acts as a bridge between strands B and D. Tables 1 and 2 show that residue 28, due to its position, is surrounded by a set of residues such as 20, 21, 22 (strand A), 42, 44, 46 (strand C), 127, and 128 (strand G). A mutation on this set has a moderate impact on the unfolding rates, thus explaining the mild clinical phenotype deriving from the mutation of residue 28.

TABLE 2.

Kinetic parameters of test-mutants determined from temperature-jump simulations: unfolding rates and unfolding rates normalized to the k_u of the WT

Residue	Sec. Struct.	ku[τ−1]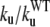
Res 12	Head	1.43 × 10−4	1.01
Res 20	A′	4.18 × 10−4	2.96
Res 21	A′	4.12 × 10−4	2.92
Res 22	A'B	2.10 × 10−4	1.43
Res 31	B	6.65 × 10−4	4.72
Res 35	BC	8.81 × 10−4	6.25
Res 36	BC	3.52 × 10−4	2.50
Res 42	C	3.07 × 10−4	2.18
Res 43	C	1.16 × 10−3	8.23
Res 44	C	3.01 × 10−4	2.13
Res 46	C	1.64 × 10−4	1.16
Res 86	D	2.14 × 10−4	1.52
Res 90	D	1.93 × 10−4	1.37
Res 91	DE	2.75 × 10−4	1.95
Res 93	E	6.80 × 10−4	4.82
Res 96	E	1.64 × 10−3	11.63
Res 97	E	5.60 × 10−4	3.98
Res 109	F	2.66 × 10−4	1.89
Res 111	F	1.40 × 10−3	9.93
Res 112	F	7.70 × 10−4	5.46
Res 113	F	1.46 × 10−3	10.35
Res 118	FG	3.18 × 10−4	2.26
Res 120	G	5.57 × 10−4	3.95
Res 121	G	3.83 × 10−4	2.72
Res 126	G	4.92 × 10−4	3.49
Res 127	G	3.74 × 10−4	2.65
Res 128	G	3.50 × 10−4	2.48

The most destabilizing mutations are marked in bold.

CONCLUSION

The molecular impact of three mutations, Asn⁷⁵⁵Lys, Arg⁶⁵⁴His, and Arg⁶⁶⁸His, on the domain C5 from MyBP-C related to FHC has been studied through MD simulations. As Ig-like proteins tend to fold and unfold along a common pathway dictated by the geometry of the common structural core (18), C5 domain was modeled through a heavy map Gō-like force field with heterogeneous energy couplings. We preferred to run unfolding rather than folding simulations to avoid kinetic traps related to residual energetic and topological frustration. To determine the kinetics of the folding process by inverting to the unfolding pathway, we performed temperature jump simulations at a temperature just little above the transition point of both WT and mutants. The destabilizing effect of mutations can be quantified by the corresponding shift in the unfolding temperature. The simulations show that the mutation of Asn⁷⁵⁵ is particularly destabilizing, causing a large decrease in the transition temperature. This result is consistent with the NMR spectra recorded by Idowu et al. (8), signaling the absence of structure for the mutant even at low temperature. Residues Arg⁶⁵⁴ and Arg⁶⁶⁸, on the other hand, when mutated determine similar and more limited shifts of the peaks of the C_V plots, suggesting a very small influence of these two residues on protein stability.

The role of the N-terminal region was also investigated, studying a deletion mutant where the first seven residues had been removed. The significant decrease in T_u of the truncated protein suggests that the N-terminal region with its 10-residue-long insert, typical of the cardiac isoform, is not just a linker between the C4 and C5 domains, but it gives a nontrivial contribution to the stability. The low “contact betweenness” (32), however, hints at the involvement of the N-terminal residues in contacts forming a subgraph only weakly connected to the main network. It is thus possible that the N-terminal contacts do form only when the C5 domain is dissected from the rest of the protein and that the natural role of this region is more related to the binding with domain C8, complementing the negatively charged CFGA′ surface (8).

The kinetic unfolding simulations show that the mutations determining the largest decrease in the unfolding temperature also induce the highest speedup of the unfolding process. In particular, the mutants retain the two-state unfolding mechanism but they tend to reduce the unfolding barrier while simultaneously increasing the folding one. The analysis of the local native contacts shows that the mutations on Arg⁶⁵⁴ and Arg⁶⁶⁸ only have a local effect, whereas the mutation of Asn⁷⁵⁵ and the Δ1–7 deletion have a strong influence even on regions at the opposite end of the molecule. An even stronger evidence is provided by the contact probabilities P_ij(t), indicating the folding reaction to start from the region of the DE and FG loops and to proceed toward the region of the CD and EF loops. This may explain the importance of Asn⁷⁵⁵, which is located in the zone where the folding originates. By contrast, Arg⁶⁶⁸ lies near the opposite end of the protein where the folding is almost concluded, explaining the modest kinetic and thermodynamic effect of mutating this residue. This conclusion was supported by performing temperature-jump simulations on 27 test mutants, proving the importance of the FG-loop and of the central strands of the two β-sheets (strands E and F). The simulations also showed the existence of a strip of residues (including Arg⁶⁶⁸) on the side of the β-strands close to the CD and EF loops, whose mutation only marginally affects the folding/unfolding kinetics.

Another interesting feature of the cardiac C5 domain is the destabilizing effect of the long CD loop, characterized by a 28-residue-long insert and lowering the folding temperature with respect to other Ig domains, which we investigated in a different work (32). There we found a charge unbalance and a low hydrophobicity of the CD loop, accompanied by a high concentration of Pro, Glu, and Asp. This supports the idea that the C5 domain of MyBP-C can be considered a natively unfolded protein, i.e., a protein lacking a compact, globular structure under physiological conditions (33,34). The high mobility of the unstructured CD loop leads to a reduced number of stabilizing contacts with the EF loop, which is possibly compensated for by a higher relevance of lower loops providing an interpretation for the different pathologic role of the three FHC-related mutations.