Fast Fluorescence Laser Tracking Microrheometry, I: Instrument Development

Abstract

To gain insight into cellular mechanotransduction pathways, we have developed a fluorescence laser tracking microrheometer (FLTM) to measure material rheological features on micrometer length scales using fluorescent microspheres as tracer particles. The statistical analysis of the Brownian motion of a particle quantifies the viscoelastic properties of the probe's environment, parameterized by the frequency-dependent complex shear modulus G*(ω). This FLTM has nanometer spatial resolution over a frequency range extending from 1 Hz to 50 kHz. In this work, we first describe the consecutive stages of instrument design, development, and optimization. We subsequently demonstrate the accuracy of the FLTM by reproducing satisfactorily the known rheological characteristics of purely viscous glycerol solutions and cross-linked polyacrylamide polymer networks. An upcoming companion article will illustrate the use of FLTM in studying the solid-like versus liquid-like rheological properties of fibroblast cytoskeletons in living biological samples.

INTRODUCTION

Mechanotransduction studies seek to elucidate the mechanisms by which cells sense mechanical stimuli and incorporate these cues into integrated biochemical responses. This discipline, along with cell mechanics in general, is conjectured to play preeminent roles in pathologies including atherosclerosis, myopathies, and cartilage damage (1), as well as in cell activities such as cell migration, intracellular transport, and regulation of gene expression (2–5). Probing the rheology of biological systems provides quantitative insight into mechanotransduction by assessing how living cells tune their viscoelasticity in response to their complex environment and to their own specific needs. The flourishing of techniques for measuring cellular viscoelastic parameters attests to the increasing interest in cell rheology.

To determine the cellular mechanical behavior on biologically relevant length scales, different microrheology schemes have been developed. Microrheology methods fall into two broad classes: active techniques (e.g., micropipette aspiration, atomic force microscopy, and magnetic manipulation), where external forces are applied to cells, and passive techniques (e.g., dynamic light scattering, laser tracking microrheology), which examine the motion of particles due to thermal fluctuations (6–15). The main strength of passive microrheology is its broad bandwidth range, which takes advantage of the white spectrum of the thermal energy of the embedded probes. The particles' displacement amplitude is related to the viscoelastic properties of the surrounding medium: the more viscous or stiff its microenvironment, the more confined a probe's Brownian motion (16,17). The sensitivity of passive microrheometers to the local surroundings of the probes can be minimized by employing two-particle microrheology (18,19). By cross correlating the motion of pairs of tracer particles, two-particle microrheology eliminates the influence of local heterogeneities in structure and mechanics, and thereby yields a more accurate assessment of the sample's bulk rheology. The novel instrument presented in this article complements and enhances this landscape of passive rheometers.

We have developed a fluorescence laser tracking microrheometer (FLTM) by incorporating high-sensitivity fluorescence detection electronics to an existing white light LTM design (15). This FLTM belongs to the broad class of fluorescent single-particle tracking (SPT) instruments developed over the past several decades that has provided many important insights into cellular mechanical processes. SPT has played important roles in studies such as the quantification of biomolecules' diffusion coefficients, the discovery of normal and anomalous diffusion processes, or the distinction between active and passive transport mechanisms (20–23). SPT with a single green fluorescence protein molecule is even possible today (24). SPT approaches are of course critical in the understanding of molecular motors and their mechanochemical power transduction mechanisms (25–27). The combination of SPT and optical trapping has further enabled imaging of biological structures and their mechanical properties in three dimensions (28). A closely related technique is fluorescence correlation spectroscopy that is widely used currently for measuring biomolecular number density, transport, and association properties in cells (29–32). Our FLTM is a new addition to this class of instruments optimized for measuring cellular rheology over a broad temporal scale.

For rheological measurements, the addition of fluorescence has several unique advantages over white-light schemes. First, because the fluorescent tracer's spectral signature can be distinguished, different targets, such as different cellular membrane receptors, can be studied easily in the same sample. Second, fluorescent tracers can be clearly and readily separated from their cellular background, and their precise localization is less susceptible to optical interference effects than in white-light systems. Third, the development of fluorescent markers of living cells may allow FLTM studies based on exogenous labeling of cellular organelles such as endosomes and lysosomes without introducing exogenous tracer particles. Nevertheless, the use of fluorescence also presents some shortcomings. Since the signal level of fluorescent particles is relatively low, the localization of these tracers is limited by the photon shot noise. Furthermore, long-term monitoring is precluded by photobleaching of the fluorescent tracers.

To resolve both the viscous and elastic properties of samples, we started by enumerating design criteria for the FLTM. First, this FLTM needs to measure the rheological properties of biomaterials using microscopic sample volumes. Second, this FLTM should have molecular and biochemical specificity, which are derived from identifying fluorescence spectral signatures. Third, the FLTM's bandwidth should be broad (∼0.5 Hz–50 kHz), allowing the probing not only of molecular networks that deform at long timescales, but also of the fast bending and twisting fluctuations of single filaments in the cytoskeleton at shorter times (33). By exploiting this large frequency range, the FLTM could help bridge cellular biology and the field of complex fluids by permitting the extensive quantitative comparison between the rheological properties of cells and those of reconstituted networks (34,35). Moreover, this five-decade frequency range incidentally makes numerical treatment of data computationally less demanding (15). Fourth, the spatial resolution of the fluorescent tracer's trajectory should be on the order of a few nanometers to allow the detection of displacements in cytoskeletal networks of shear moduli up to 10³ Pa, a value encountered at high frequencies in many cell types (13,15,36,37).

In this article, we outline the design, fabrication, characterization, and optimization of the FLTM. We further describe the performances of this fluorescence-based microrheometer in glycerol as well as cross-linked polyacrylamide gels. In a companion article, we will study the microrheology of living fibroblast cells by FLTM with nanometer spatial resolution over a five-decade frequency bandwidth extending up to 50 kHz.

METHODS

Preparation of poly(acrylamide) gels

Polyacrylamide gels (PAG) of final total acrylamide concentrations 1.5%, 2%, and 2.5% (weight per volume) were prepared according to Sigma-Aldrich's (St. Louis, MO) standard gel electrophoresis recipe. Briefly, the desired volume of acrylamide/bis-acrylamide 30% stock solution was mixed with lauryl sulfate detergent solution, deionized water, and 1-μm fluorescent polystyrene beads (at a final concentration of 5 × 10⁵ microspheres/ml). Chemical polymerization was initiated with ammonium persulfate (prepared fresh) and catalyzed by tetramethylethylene-diamine. Degassing was enabled and PAG were kept in the dark at room temperature for at least 2 h before starting experiments.

PRINCIPLES OF LASER TRACKING MICRORHEOMETRY

Theory

The viscoelastic properties of a material are usually parameterized by the frequency-dependent complex shear modulus G*(ω) defined in the frequency domain as the ratio of the stress experienced by the material over the strain it undergoes. Both the solid-like (elastic, or energy-storing) and the fluid-like (viscous, or energy-dissipating) characteristics of the material are encompassed by G*(ω) = G′ (ω) + iG″(ω): the storage modulus G′ (ω) is the real part of G*(ω), and the loss modulus G″(ω) is its imaginary part.

To empirically extract G*(ω), passive microrheology exploits the fluctuation-dissipation theorem, which stipulates a relationship between the thermal excitations of a probe particle and the rheology of its environment (16,17). More specifically, the displacements of the probe bead can be specified by its mean-squared displacement (MSD), a time-averaged autocorrelation function given by 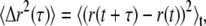where r(t) describes the particle's two-dimensional (2D) trajectory, and τ corresponds to various lag times. Analytically, the motion of a single particle is expressed through a generalized Langevin equation. From the latter and based on the equipartition theorem, a generalized Stokes-Einstein relation (GSER) can thus be derived, whose representation in Fourier space can be written (38)

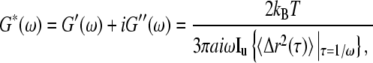where 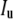{〈Δr²(τ)〉} is the Fourier transform of the MSD, k_B is the Boltzmann constant, T the absolute temperature, a the radius of the probe particle, and i = (−1)^½. To avoid numerical transformation of the data or using functional forms to fit G*(ω) in Fourier space, an algebraic form of the GSER can be yielded by estimating the MSD as a local power law:

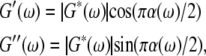(1)

where

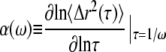(2)

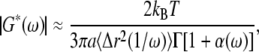(3)

where Γ represents the gamma-function (39). G′(ω) and G″(ω) are dependent on each other and are related by the Kramers-Kronig relations (40). Γ can be also be represented as

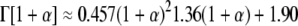(4)

for the range of values of α(ω) spanned by thermally driven spheres (38): α(ω) lies between zero, corresponding to elastic confinement, and one, corresponding to viscous diffusion. The approximations described here give rise to a maximum of 12% correction in G*(ω) where the slope of the MSD varies most rapidly and are thus commonly accepted (38,41).

Recent theoretical work (38,42,43) has looked into the conditions under which the GSER satisfactorily depicts the thermal response of a spherical particle embedded in a viscoelastic medium. The assumptions underlying the GSER are summarized as follows. First, the material surrounding the probe particle is assumed to be a continuum in the sense that the length scale of its microstructure is small relative to the probe's radius a. Second, the probe itself is assumed to be spherical, rigid, and with no-slip boundary conditions at its surface. Finally, the range of validity and accuracy of the GSER lies between two frequency boundaries, ω_u and ω_ℓ. The lower limit, ω_ℓ, is the frequency below which longitudinal, or compressional, modes from the elastic network become significant with respect to the shear modes from the incompressible fluid; this additional contribution needs to be taken into account for ω < ω_ℓ. In the context examined in this article, a typical soft material with an elastic modulus G′ = 1 Pa, a viscosity η = 0.1 Pa.s and a mesh size ξ one-tenth the radius a of the embedded probe, ω_ℓ ∼ G′ξ²/η a² ∼ 0.1 Hz (41). The upper limit, ω_u, on the order of 10 MHz in the current conditions, is the frequency above which inertial effects of the probe particle can no longer be neglected.

These criteria are typically met for FLTM, and using the GSER as a theoretical foundation is well justified: the fluorescent beads of diameter a = 1 μm tracked by the instrument are spherical and rigid, and they are embedded in materials whose typical mesh size ξ is much smaller than a (ξ ∼ 10-100 nm in the cytoskeleton, and ξ ∼ 1–10 nm at the studied concentrations of polyethylene oxide and polyacrylamide gels) (39,44). As a result, our FLTM covers a considerable range of frequencies, ∼0.5 Hz–50 kHz, without extending its scope beyond the limits of validity of the GSER to determine the frequency-dependent complex shear moduli G*(ω) of various samples.

Fluorescence laser tracking experiments

Instrument design

The introduction of fluorescence in a passive microrheology device poses challenges, the most critical of which being the collection of sufficient light to achieve a near-nanometer resolution. Computational simulations were carried out to determine whether the number of photons detected by the system could maintain near-nanometer spatial resolutions at speeds comparable to white-light setups. Assuming the photons emitted by a fluorescent bead can be modeled with a Gaussian distribution, and defining regions L and R on each side of the Gaussian's centroid x_c on a one-dimensional axis, the ratio of the number of photons in the regions L and R could be expressed as

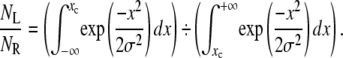The relative uncertainty on this ratio, on the order of (N_L + N_R)^1/2 for a Gaussian distribution, dictates the uncertainty (in nanometers) of x_c, which was therefore calculated using a recursive dichotomy-based algorithm with the software MATLAB (The MathWorks, Natick, MA). It was established that 10⁴ photons per measurement were necessary for the bead's position to be ascertained with ∼4 nanometers of precision (Table 1). The purpose of these preliminary estimates was to serve as a rule of thumb and guide the design of the FLTM; on no account were they meant to replace de facto measurements of the instrument's precision after its assembly.

TABLE 1.

Spatial resolution of the FLTM as a function of the number of photons it detects, per measurement, from a single fluorescent probe

Photons detected per measurement	Uncertainty on NL/NR	Uncertainty on xc (nm)
103	0.033	12.0
104	0.010	4.0
105	0.003	1.2
106	0.001	0.4

The fluorescence emission was modeled by a Gaussian distribution of centroid x_c. The spatial resolution (in nanometers) on the determination of x_c's one-dimensional position was calculated to be dependent on the ratio N_L/N_R (number of photons on both sides of x_c) and thus on the total number of photons detected (per experimental time point, or measurement).

The size of the fluorescent probes is partially dependent upon the minimum photon count determined above. We realized that: i), measurements would be carried out at a rate of 50 kHz for a duration of at least 1 s; ii), 10⁴ photons had to be detected per measurement; iii), FLTM has a photon detection efficiency of ∼2% (45); iv), fluorescent molecules constituting the probe would undergo photobleaching after ∼10⁴ excitations. Therefore, the minimum number of fluorescent molecules required within each bead was estimated to be 5 × 10⁵; hence the minimum bead diameter needed to be 1 μm, which was used for most of the experiments reported in this study.

Since the photon detection rate of 10⁹ photons/s (or ∼10⁴ photons per measurement at 50 kHz) exceeds the linearity limit of single-photon counting circuitry, we opted for analog signal detection, using a high sampling rate analog-to-digital converter (ADC).

Although quadrant photodiodes have been used for fast particle tracking under white-light illumination (46,47), quadrant photomultiplier tubes were used in this research because the high dark current of a photodiode increased the noise level in FLTM applications. Indeed, if photons of wavelength λ_em = 560 nm and of energy E_γ = 3.5 × 10⁻¹⁹ J are detected at a rate Γ_γ = 10⁹ photons/s by a photodiode of sensitivity χ_{560 nm} = 0.35 A/W, this detector is expected to output a current I_diode = Γ_γ × E_γ × χ_{560 nm} ∼ 1 × 10⁻¹⁰ A or 0.1 nA. Since the dark current of a quadrant photodiode is typically ∼0.01 nA (S4349, Hamamatsu, Bridgewater, NJ), the signal current is only 10 times larger than the noise. (It should be noted here that the photon rate considered for these calculations, Γ_γ = 10⁹ photons/s, is certainly not low but, on the contrary, corresponds to the light yielded by a 1-μm fluorescent sphere excited by a high power laser beam, ∼5 × 10⁵ W.m⁻², and hence pertinent for the experiments encompassed in this work.) In contrast, a 2 × 2 multianode photomultiplier tube (PMT) of quantum efficiency QE_{560 nm} = 5%, of cathode radiant sensitivity χ_{560 nm} = 20 mA/W, and of gain G_PMT = 2 × 10⁵ (for a voltage supply of −600 V), yields under the same experimental conditions an anode current per channel I_PMT = Γ_γ × E_γ × χ_{560 nm} ×G_PMT/QE_{560 nm} ∼ 3 × 10⁻⁵ A or 30 μA, whereas its anode dark current per channel is only ∼50 pA (or six orders of magnitude smaller than the signal). The anode saturation current per channel for such a quadrant PMT is ∼100 μA. Thus, a quadrant PMT is better suited for our design.

Instrument setup

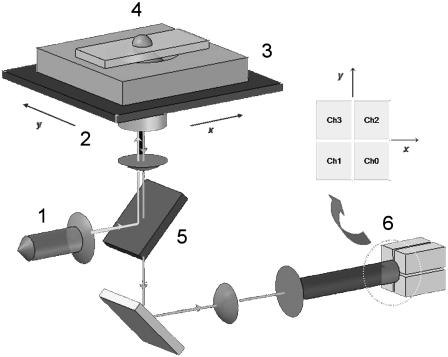
All measurements were performed on vibration-isolating floating optical tables (TMC, Peabody, MA). All samples were ultimately prepared in dishes equipped with a glass bottom coverslip No. 1.0 corresponding to thicknesses between 0.13 and 0.16 mm (MatTek, Ashland, MA). A schematic of the FLTM is presented in Fig. 1: a laser beam (1) (532 nm from a Verdi Nd:YVO₄, Coherent, Santa Clara, CA) was collimated through a custom light path and a 100× NA 1.30 oil objective (2) (Olympus, Melville, NY) and illuminated a 100 μm × 100 μm area of sample positioned on the stage of an Olympus IX71 inverted microscope (3) and mounted on an xy piezoelectric nanopositioning system (Queensgate, Torquay, UK). The photons emitted by the fluorescent beads (4) (of excitation and emission maxima at 540 nm and 560 nm, respectively, orange microspheres from Molecular Probes, Eugene, OR) contained in the excitation volume were filtered by a dichroic mirror-barrier filter combination (5) (Q560LP and HQ585/40m, Chroma Technology, Rockingham, VT) and detected after beam expansion (lenses from Thorlabs, Newton, NJ) by a quadrant photomultiplier tube (6) (PMT, Hamamatsu). The total magnification of the system was of 2250×, so that a 1-μm bead was finally projected on the 18 mm × 18 mm quadrant PMT as a disk of diameter 2.25 mm. Position signals were inferred at the PMT level from the difference in photocurrents between opposing pairs of quadrant elements, which were further amplified into digitized voltages by a 200 kHz 16-bit simultaneous 4-channel ADC (Strategic Test, Stockholm, Sweden). For instance, the x-position of the probe particle was deduced from the signal ratio (Ch0 + Ch2)/(Ch1 + Ch3) (Fig. 1).

FIGURE 1.

Schematic diagram of the FLTM. (Refer to the Instrument Setup section for detailed description.)

Instrument optimization

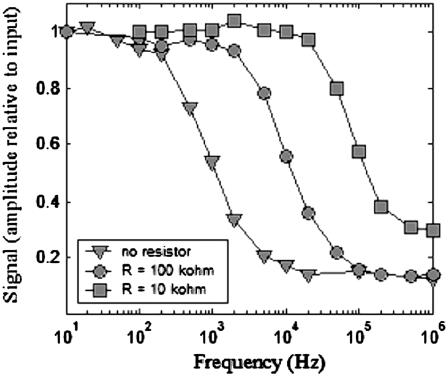
The data acquisition speed and overall resolution of the fluorescence laser tracking microrheometer are governed by parameters that had to be optimized. As far as the instrument's speed is concerned, and as illustrated by Fig. 2, correct detection-circuit design and tuning are crucial to attain 50 kHz data acquisition rates (comparable to the speed achieved by white-light-based setups). The bandwidth of the FLTM is dictated by the ADC data acquisition rate (200 kHz) as well as the transimpedance circuitry at the output of the quadrant PMT. A direct connection of the quadrant PMT anodes to the four ADC channels (Fig. 2, triangles) with an ADC input impedance of 1 MΩ resulted in an acquisition time τ_acq = 1/ω_−3dB ≈ 2.5 × 10⁻⁴ s (or a speed of ∼4 kHz). Inserting a parallel resistor R to ground lowered the transimpedance gain and raised the FTLM's speed to ∼50 kHz (Fig. 2, circles for R = 100 kΩ) or ∼300 kHz (squares for R = 10 kΩ). Although lower resistance values R and a smaller transimpedance gain increased the FLTM's bandwidth, a too-low transimpedance gain would require a second voltage amplification stage to fully utilize the voltage range of the ADC and would introduce additional electronic noise. To conclude, a transimpedance gain of 100 kΩ was a reasonable compromise between system gain and bandwidth.

FIGURE 2.

Influence of the FLTM electronics on its acquisition speed. The three-plotted Bode diagrams were acquired by replacing the sample on the FLTM microscope stage with a very stable light source, a light emitting diode fed with sinusoidal voltages of varying frequencies (10 Hz–1 MHz), and by inserting a simple resistor (squares, R = 10 kΩ; circles, R = 100 kΩ; triangles, no additional component) in the detection circuitry. The amplitude (in volts) of the signal detected by the whole instrument was compared with that of the input sine wave, and this ratio was further normalized to its value at 10 Hz.

In addition to the transimpedance gain, the internal gain of the PMT needed to be optimized. Although the manufacturer typically recommends a supply voltage of −800V for the selected PMT, a trade-off had to be resolved between low-noise high-gain amplification and PMT saturation. Although a PMT at −800 V of supply voltage offered high gain (G_{PMT −800V} = 1.5 × 10⁶) with low electronic noise (three detected photons), it reached saturation when 9 × 10³ photons hit its photocathode (Table 2). In contrast, a supply voltage of −500 V pushed saturation up to 10⁵ photons, detected in the device's linear regime, but with lower gain (G_{PMT −500V} = 6.0 × 10⁴) and higher noise (the level of the electronic noise becomes equivalent to 200 detected photons). The optimal working voltage of −600 V was a reasonable compromise between good PMT gain (G_{PMT −600V} = 2 × 10⁵) and sensitivity (∼30 photons), with a threshold for saturation (6 × 10⁴ photons) above the 10⁴ photons required for each measurement to sustain near-nanometer spatial resolution for the FLTM.

TABLE 2.

Influence of the PMT voltage supply on the photodetector's performance

Voltage supply (V)	PMT gain	Threshold for PMT saturation*	Electronic noise*
−800	1.5 × l06	9 × l03	3
−700	6.5 × 105	2 × l04	8
−600	2.0 × l05	6 × l04	30
−500	6.0 × 104	l × l05	200

The PMT supply voltage, and its resulting internal gain, needed to be optimized to balance amplification capacity and absence of PMT saturation: a supply voltage of −800 V guaranteed low-noise (equivalent to three photons) and high-gain (1.5 × 10⁶) amplification but led to saturation at low signal levels (9 × 10³ photons), whereas −500 V tilted the trade-off satisfactorily.

^*The threshold for PMT saturation and the electronic noise are indicated in equivalent number of photons detected.

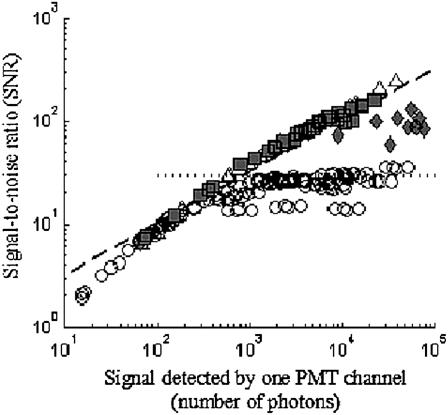
With the detector and electronic components optimized for FLTM, the noise in the fluorescent signal originating from the tracer particle (a 1-μm fluorescent bead) had then to be minimized. Ideally, the emission of photons by fluorophores enclosed in a fluorescent bead should follow a Poisson distribution. For an optical signal consisting of N_γ photons, the intrinsic Poisson noise is equal to the square root of the signal (Noise_Poisson = √N_γ photons), as is the signal/noise ratio (SNR_Poisson = √N_γ). In a log-log plot of SNR versus Signal, an ideal Poisson limited event is epitomized by a straight line with slope of ½. However, this was not observed on the graph generated by our 1-μm fluorescent probes (Fig. 3, circles). This additional noise of the FLTM system was attributed to intensity fluctuations of the laser light source. With the noise of the laser source, Noise_laser, being a fraction α of the laser intensity, and the noise arising from photon emission by the bead, Noise_Poisson, being Poisson-derived, then, assuming proportionality between excitation and emission intensities from the tracer, the signal/noise ratio expected from the bead data could be written

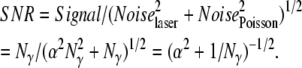FIGURE 3.

FLTM instrument noise can be reduced to its theoretical Poisson limit. As explained in more details in the Instrument Optimization section, an ideal Poisson-limited distribution is characterized by a line of slope ½ in a log-log plot of SNR versus Signal. Before implementing noise cancellation approaches, the fluorescent signal generated by 1-μm microspheres did not follow this rule (open circles). Removing laser noise restored Poisson-like behavior for a uniform rhodamine film (open triangles), but not for 1-μm beads (solid diamonds). Only when the FLTM was effectively isolated from acoustic vibration noises did the signal become shot-noise-limited in all instances (solid squares) and the Poisson line was retrieved.

In other words, whereas the Poisson noise dominated at low signal levels, the laser noise embodied by the parameter α dictated a plateau of the SNR for high values of N_γ. We established that the laser noise dominated at an intensity of 10³ photons, significantly below the 10⁴ photons required for a 5-nm precision in FLTM measurements. A solution to this problem that effectively removed the influence of laser noise was achieved by realizing that all four quadrants of the PMT were subject to the same laser intensity noise. Ratiometric measurement of centroid position therefore effectively removed this common mode noise (Fig. 3, triangles).

Although this scheme attained a Poisson-like behavior for a homogeneous rhodamine film (Fig. 3, triangles), ratioing the PMT signals that originated from the tracer particle still did not lead to Poisson shot noise behavior (Fig. 3, diamonds). The main difference between the rhodamine film and the tracer particle was that the uniform film was completely insensitive to laboratory vibrational noise. The latter had to be removed to ensure optimization of the FLTM's spatial resolution. The dampening of acoustic and mechanical noises was accomplished using a vibration-isolated optical table and suitable acoustic shielding of the microrheometer setup. With the vibration noise removed, the FLTM exhibited near ideal Poisson behavior throughout the relevant light intensity range (Fig. 3, squares).

Data acquisition and instrument calibration

Single fluorescent tracer particles of diameter 1 μm, trapped in viscoelastic samples, were positioned at the center of the quadrant detection zone in three steps. The centering procedure was fully automated by custom LabVIEW (National Instruments, Austin, TX)/ C++/MATLAB programs commanding and coordinating the Queensgate xy stage (for raster-scanning of three successively smaller areas) and the ADC acquisition card (for fluorescent signal detection), and were carried out at very low illumination power (<5 × 10² W.m⁻², or 5 μW for the whole 100 μm × 100 μm excitation area) to avoid photobleaching of the probes. This centering guaranteed that the one bead tracked was located within an ∼1 μm × 1 μm-wide zone where the signals collected from all PMT quadrants were of similar orders of magnitude, and where the positional sensitivity of the detection system was optimal (data not shown).

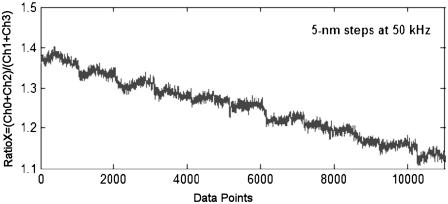
Once the bead was centered, its Brownian motion was monitored by the FLTM for ∼1.5 s, under high illumination power (∼5 × 10⁵ W.m⁻²), at an ADC sampling rate of 200 kS/s. Calibration curves for the FLTM (bead x- or y-position versus ADC signals) were obtained after each experiment for every bead. Calibration consisted in translating the bead along both detection axes (x, then y) with a total of ∼20 10-nm steps from the center position using the high-resolution (0.5 nm) Queensgate xy stage (see Fig. 4 for an example of FLTM calibration curve). Tracking data acquired from the four photodetector quadrants were further analyzed and compared with the calibration data by a custom MATLAB code that established the beads' trajectories, mean-squared displacements, and ultimately the viscoelastic materials' shear moduli G*(ω) using Eqs. 1–4. Only one particle is tracked at a time using the FLTM detection scheme. As far as our instrument is concerned, a constraint on the extent of its motion is imposed by the size of the field of view of the quadrant photodector that is ∼8 μm × 8 μm.

FIGURE 4.

FLTM can discriminate the 5-nm steps of a 1-μm fluorescent bead at a speed of 50 kHz. A 1-μm fluorescent bead, immobile on a coverslip on the microscope stage, was motioned with a 5-nm step size along the x axis of the nanopositioning system. The bead was kept in each position for ∼5 ms (1024 data points) before being moved by 5 nm. The photon signal yielded was recorded by the four quadrants of the multianode PMT, converted into four electron currents, and acquired at a rate of 200 kHz by the four-channel ADC as described in the Principles section. A four-running average was applied to the data to match the FLTM speed of 50 kHz (see Fig. 1 with R = 100 kΩ). The data were plotted as RatioX = (Ch0 + Ch2)/(Ch1 + Ch3) as a function of acquisition time.

RESULTS AND DISCUSSION

Spatial and temporal resolutions of the FLTM

We have developed a fluorescence laser tracking microrheometer to determine rheological features from the statistical analysis of the distribution of displacements of fluorescent microspheres embedded in the material studied. After careful design and optimization, the FLTM has excellent intensity sensitivity and spatial precision, and presents sufficient bandwidth to discriminate, at a speed of 50 kHz, the 5-nm steps taken by a 1-μm fluorescent bead on a piezoelectric platform (Fig. 4, with Fig. 2 attesting to the instrument's speed).

The low-end of the frequency range covered by the FLTM (∼0.5 Hz) was governed by i), the caution not to break down the validity of the core generalized Stokes-Einstein relationship (details in the Theory section), ii), the expediency of the data set size handled by our LabVIEW/C++/MATLAB data processing routines (262,144 time points or ∼10-MB binary files), and importantly iii), the photobleaching of the fluorescent probes. More explicitly, the time constant of the luminosity decay was ∼50 s for a 1-μm fluorescent bead exposed to a laser power of ∼5 × 10⁵ W.m⁻² (excitation level required to achieve adequate signal levels of 10⁴ photons per measurement as explained in the Instrument Design section). Incidentally, this limit of photobleaching was calculated to be far more restrictive than the negligible thermal heating. The maximum temperature rise of the aqueous sample during the ∼1.5-s long data acquisition was estimated to be T ∼ 6 × 10⁻⁴ K, as obtained from the expression of T at the center of the laser beam as a function of exposure time t (48):

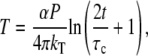where α is the absorption coefficient (α = 5 × 10⁻⁴ cm⁻¹ at λ = 532 nm), P the laser power (P = 5 mW for a Gaussian beam parameter ω₀ ∼ 100 μm), k_T the thermal conductivity (k_T,water = 0.6 W.K⁻¹.m⁻¹), and τ_c the thermal relaxation time (τ_c ∼ 70 ns).

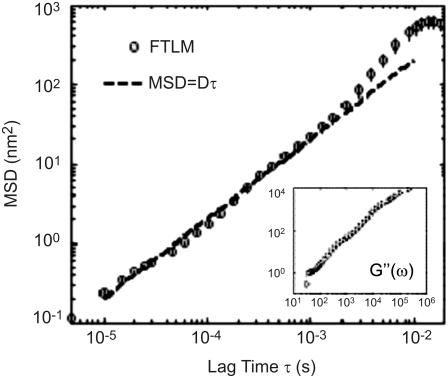
The nanometer spatial and 20-μs temporal resolutions of the FLTM are further substantiated by its performances in glycerol (Fig. 5 and next paragraph) and complex fluids (Fig. 6).

FIGURE 5.

MSD and loss modulus G″(ω) (inset) of a 50% glycerol solution obtained by FLTM.

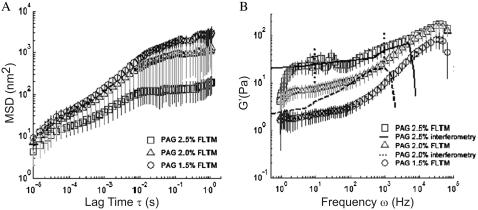
FIGURE 6.

Rheological measurements acquired by the FLTM from PAG of volume fractions 1.5%, 2%, and 2.5%: (A) mean-squared displacements (MSD) and (B) storage moduli G′(ω).

FLTM in glycerol

To test the applicability of the FLTM scheme, we started by applying it to purely viscous solutions of glycerol. Samples consisted of 50 μL of glycerol 100% mixed with 50 μL of 2-μm orange fluorescent spheres diluted in water (1:10³ from 2% solids stock) into a well-slide to prevent surface tension effects. Fig. 5 shows the averaged results obtained from monitoring seven beads (the vertical bars show their spread in terms of standard deviation), and could be reproduced time and again. Purely diffusive Brownian motion is reflected by the linear increase of the MSD at short timescales (20 μs < τ < 10 ms), with a slope given by the diffusion coefficient D = k_BT/(6πaη), where k_B is the Boltzmann constant, T the absolute temperature, a the radius of the colloids, and η the Newtonian viscosity. For a purely viscous 50% glycerol solution, η = 5.5 mPa.s, and D is expected to be 2 × 10⁻¹⁴ m²/s, a value that matches our FLTM experimental data to within experimental noise (∼2%). The measured loss modulus G″(ω), shown in the inset of Fig. 5, corroborates the FLTM's ability to characterize pure fluids; for a freely diffusive particle, frequency-independent viscosity is recovered and G″(ω) = ηω (while G′(ω) is <0.1 Pa).

At long timescales (τ > 10 ms), the motion of the spherical particles is observed to plateau (in terms of MSD), which we attribute to the escaping of the tracked particle from the FLTM field of view (∼8 μm × 8 μm due to a high-magnification optical setup).

Importantly, this first set of findings in simple glycerol solutions constitutes supplementary evidence of the high spatial and temporal resolutions of the FLTM, whose design overcomes the light scarcity inherent in fluorescent-based instrumentation: Granted high signal levels (achieved here by means of larger diameter beads, a = 2 μm), subnanometer movements can be detected at speeds up to 50 kHz (Fig. 5), a performance that surpasses the authors' original goals.

FLTM in PAG

Viscoelasticity measurements acquired with the FLTM were compared to those of established microrheology techniques. Complex fluids were chosen because they exhibit rich linear viscoelastic behavior over the range being tested. Among them, soft materials such as gels or polymer solutions were of particular interest, because they show evidence of different rheological behavior on different time and length scales (39).

We examined a cross-linked polymer system, PAG, close to its gelation threshold to assess cross-linked networks that are similar to those found in the cellular actin cytoskeleton. Fig. 6 A displays the variations of the MSD of 1-μm beads embedded in PAG 1.5%, 2%, and 2.5%, and Fig. 6 B the frequency-dependent storage modulus G′(ω) for these three types of PAG (the plots summarize data from 10 beads in PAG 1.5%, 17 beads in PAG 2%, and 9 beads in PAG 2.5%). On short timescales, the near-nanometer motions of the probe particles are effectively monitored, whereas on longer timescales, the divergence in viscoelastic behavior of the PAGs is successfully uncovered (Fig. 6 A). Solid-like material responses for lag times τ > 0.01 s are manifested through a flattening of the MSD spectra. Although this elastic plateau is apparent for PAG 2.5%, it is barely visible for PAG 2%, and disappears for PAG 1.5%, in conformity with the decreasing degree of cross-linking that accompanies a decrease in polyacrylamide concentration (Fig. 6 A). The absence of long-range diffusion for the beads in all three PAG networks corroborates that all gels are cross-linked at these concentrations, and that a solid mesh has formed from the initial fluid mixtures. The scatter in the data can be attributed to local gel heterogeneities in the PAG of low volume fraction whose gel rigidity varies greatly with concentration.

For the two higher volume fractions of PAG (2% and 2.5%), a comparison between results obtained with the FLTM and results yielded by laser interferometry (49) is given in Fig. 6 B, which confirms the capacity of our FLTM to replicate viscoelasticity data reported using a different measurement method: Schnurr et al.'s data (49) and those of our FLTM display similar trends of the frequency-dependent storage modulus G′(ω) for PAG 2.5% and PAG 2%, particularly the low-frequency elastic plateau, which shrinks as the gel concentration decreases. Even though the overlap of the FLTM and the interferometry plots is not perfect, the FLTM curve likely falls within the error margin of the interferometry data. Schnurr et al. (49) only published the scatter they obtained with 1 μm beads embedded in 2.5% gels, which we indicate in Fig. 6 B by means of dotted vertical segments at frequencies of 1 Hz and 1 kHz. We infer that a relative error similar in scale affected their PAG 2% data, and thereby conclude that a satisfactory agreement between FLTM and interferometry measurements was reached for both PAG 2% and PAG 2.5%. Additionally, the FLTM can distinguish two barely cross-linked polymer networks, PAG 2% and PAG 1.5%, both evidently dominated by viscosity, but whose differences in G′(ω) are identified by our instrument over a five-decade frequency range. The sudden drop in G′ (ω) at 10³ rad/s for 2% gels and at 5 × 10³ rad/s for 2.5% gels observed in Schnurr's study is a data processing artifact due to the limited bandwidth of that laser interferometry system (0.1 Hz–10 kHz) and is not representative of the true material properties. The FLTM, being faster, does not suffer from this limitation and can consequently produce reliable measurements up to frequencies of ∼50 kHz.

FLTM experiments in cross-linked PAG gels yielded frequency-dependent viscoelastic parameters in good agreement with published rheological techniques (Fig. 6), namely laser interferometry (49), and indirectly with a variety of others inspected in this reference (quasi-elastic light scattering, and macroscopic rheometers of either double-wall Couette or cone-and-plate geometries). To the extent that sensitivity of the gelation processes and high local gel heterogeneity are expected to skew the reproducibility of rheological measurements, the FLTM obtains good viscoelastic data in PAG, with an error margin that does not exceed 10% over relevant frequency ranges where the instruments under comparison are both operational. The concentrations selected for the control gels (PAG 1.5%, 2%, and 2.5%) represent a germane range of viscoelasticity to assess a rheometer eventually meant to track particles in biological samples: for instance, the ranges of bead MSD (a few to a few hundred squared nanometers) in gels and fibroblasts overlap (Fig. 6 A in this article, Fig. 3 in the upcoming companion study).

Furthermore, the scrutiny of these polymers networks of PAG validated our choice of particle size. Our fluorescent beads are large enough (1 μm in diameter) to yield enough photons, or signal, yet small enough to be easily endocytosed by cells. They are also well suited to the scrutiny of polymers of mesh size ξ ∼ 1–100 nm, and thus pertinent for biological investigations via the cellular cytoskeleton of similar mesh size. It should be noted the measured rheological properties in complex fluid depends on the size of the probe particle and provides distinct local and bulk information of the particle's surroundings. The tracking of a single micron size particle reveals local rheology over a length scale comparable to the particle diameter, which is on the scale of several microns in our case. In contrast, multiple particle tracking reveals rheological properties over a length scale comparable to the separation of particles and is often a closer match to the bulk rheological measurements using devices such as a cone-plate rheometer.

Comparison of FLTM to other microrheometry techniques

We developed a fluorescence laser tracking microrheometer that can detect with a 5-nm precision the Brownian motion of a 1-μm fluorescent bead embedded in a viscoelastic sample and accordingly compute the rheological properties of this material at a speed of 50 kHz. Drawbacks of the FLTM arise from its reliance on fluorescence: this modality makes the instrument more expensive and optically advanced than its white-light counterparts, and also slightly limits its repeated use on biological samples that are exposed to potentially damaging laser radiation. These downsides are, of course, shared by other fluorescence-based tracking systems (51–54). Nevertheless, the FLTM technical characteristics ensure that the system has comparable properties in terms of spatial discrimination, temporal sensitivity, and frequency range coverage as other microrheometry systems. Table 3 lists the latter specifications for a selection of existing microrheometry techniques as comparison. A trait common to all cataloged active microrheology approaches is their limitation in speed, due either to the actuation of an external forcing device or to the intrinsic speed of the recording camera in the case of video-based detection devices. In more details, the setups of micropipette aspiration (8), microplate manipulation (7), and magnetic tweezers (12) all rely on charge-coupled devices to monitor the cellular responses to their respective mechanical manipulations; this output can therefore only be surveyed up to a 30-Hz frequency (or every 33 ms), with the upside of possibly long acquisition times (several minutes of data have been recorded through the two former techniques). Cameras faster than 30 frames per second are now commonly used, although currently available devices are very limited for high sensitivity fluorescent-based studies because camera read noise increases rapidly at a higher frame rate resulting in images far from the shot noise limit. In contrast, atomic force microscopy allows simultaneous imaging and strain-field mapping of living cells with a spatial resolution of ∼50 nm, and thereby identification of heterogeneities in their dynamic microstructure. Nonetheless, the knowledge thus gained is restricted to mechanics of the cell surface at frequencies constrained by typical cantilever resonance frequency (∼100 Hz) (36). Optical tweezers (55) and twisting magnetocytometry (56) can extract cellular viscoelasticity profiles with a 10-nm precision and up to 500 Hz or 1000 Hz, respectively, above which the actuation of the beam-positioning mirror or the oscillations of the driving magnetic field become challenging. Comparison of our FLTM with other passive microrheometers provides a useful background to understand this new advance. Passive microrheology devices avoid a major drawback that fetter active microrheometry methods and increase measurement accuracy by using models to fit data with no free parameters. Further, passive microrheometers can perform better in terms of instrument speed than active ones. Although video-based multiple particle tracking (possibly based on fluorescent tracers) (51) or single-deflector dynamic light scattering (39) are still limited to speeds <30 Hz, other instruments take advantage of fast photodetectors such as photodiodes (used by laser interferometry and laser tracking microrheology) and photomultiplier tubes (used by FLTM and diffusing wave spectroscopy). White light-based passive microrheology techniques, such as laser interferometry (49), LTM (15), and DWS (39), can achieve higher speeds up to 20 kHz, 30 kHz, and 100 kHz, respectively, with a nanometer spatial resolution. It is worthwhile noting that measurements with a one-nanometer accuracy on the xy-position of a single dye beacon have also been achieved through FIONA, a fluorescence imaging technique based on the two-dimensional Gaussian fit of the fluorophore's point spread function (54,57). This technique has a bandwidth of ∼1 Hz. FLTM reaches spatial and temporal sensitivities of 5 nm and 20 μs (or 50 kHz) and covers a five-decade frequency range (0.5 Hz–50 kHz).

TABLE 3.

Spatial and temporal sensitivities of selected microrheometers

Technique	Spatial resolution (nm)	Temporal resolution (ms)	Frequency range covered (HZ)	Reference
Applied to cell mechanics studies
Micropipette	100	33	10−3–30	(8)
Microplates	100	33	0.001–30	(7)
Magnetic tweezers	10	33	1–30	(12)
*CCD-based MPT	5	33	0.1–30	(51)
AFM	50	10	0.1–100	(36)
Optical tweezers	10	2	0.3–500	(55)
Magnetic twist	10	1	0.01–1000	(13)
LTM	1	0.033	0.5–30,000	(15)
*FLTM	5	0.020	0.5–50,000	this work
Applied to other types of studies
Single scattering	10	22	0.01–30	(39)
Interferometry	1	0.050	0.1–30,000	(49)
DWS	1	0.010	1–100,000	(39)

^*Fluorescence-based systems.

SUMMARY

We presented in this work a fluorescence laser tracking microrheometer capable of quantitatively establishing the viscoelastic properties of a material on micrometer length scales by monitoring the Brownian motion of an embedded fluorescent sphere. First, we listed the successive development stages that finally conferred the FLTM nanometer spatial resolution over a frequency range extending from 1 Hz to 50 kHz: i), determination of the minimum diameter of the fluorescent probe for suitable brightness; ii), choice of a sensitive and low-noise photodetector; iii), expansion of the instrument's bandwidth though manipulation of its detection electronics; and iv), noise characterization and elimination. Then, we gave evidence of the range of applicability of the FLTM by demonstrating its aptitude to capture the rheological features of purely viscous glycerol solutions as well as cross-linked polyacrylamide gels.