The Degree of Redundancy in Metabolic Genes Is Linked to Mode of Metabolism

Abstract

An understanding of the factors favoring the maintenance of duplicate genes in microbial genomes is essential for developing models of microbial evolution. A genome-scale flux-balance analysis of the metabolic network of Saccharomyces cerevisiae has suggested that gene duplications primarily provide increased enzyme dosage to enhance metabolic flux because the incidence of gene duplications in essential genes is no higher than that in nonessential genes. Here, we used genome-scale metabolic models to analyze the extent of genetic and biochemical redundancy in prokaryotes that are either specialists, with one major mode of energy generation, or generalists, which have multiple metabolic strategies for conservation of energy. Surprisingly, the results suggest that generalists, such as Escherichia coli and Bacillus subtilis, are similar to the eukaryotic generalist, S. cerevisiae, in having a low percentage (<10%) of essential genes and few duplications of these essential genes, whereas metabolic specialists, such as Geobacter sulfurreducens and Methanosarcina barkeri, have a high percentage (>30%) of essential genes and a high degree of genetic redundancy in these genes compared to nonessential genes. Furthermore, the specialist organisms appear to rely more on gene duplications rather than alternative-but-equivalent metabolic pathways to provide resilience to gene loss. Generalists rely more on alternative pathways. Thus, the concept that the role of gene duplications is to boost enzymatic flux rather than provide metabolic resilience may not be universal. Rather, the degree of gene duplication in microorganisms may be linked to mode of metabolism and environmental niche.

INTRODUCTION

Microorganisms appear to have multiple strategies to provide resilience to mutations (1–5). One possibility is gene family buffering in which microorganisms carry duplicate genes for the same function. Another approach is pathway buffering, in which distinct sets of enzymes catalyze functionally equivalent metabolic pathways. Although the relative importance of these two strategies has been intensively investigated in eukaryotes, and in particular, Saccharomyces cerevisiae (5–11), there has been less investigation of prokaryotes.

Therefore, we investigated the relative importance of gene family buffering versus pathway buffering in the microorganisms Escherichia coli, Bacillus subtilis, and Geobacter sulfurreducens as well as S. cerevisiae. These organisms were chosen because they inhabit distinct environments and because detailed, constraint-based, genome-scale models of their central metabolism are available (2,12–14). These models not only accurately predict growth under different environmental conditions, but have also successfully predicted the phenotype of strains in which genes have been experimentally deleted (78.7% of 13,750 cases in E. coli (15), 82.6% of 4154 cases in S. cerevisiae (14), 94% of 772 cases in B. subtilis (16) and 78% of 72 cases in G. sulfurreducens (D. Segura, unpublished data). The S. cerevisiae model in particular has been the basis for several studies analyzing the role of gene duplications in metabolic networks (8,17). Furthermore, a suite of methods has been developed for investigating the metabolic capabilities of these genome-scale networks, (18) including the analysis of alternate biochemical pathways (19).

The different habitats of these organisms have selected distinct metabolic strategies. E. coli utilizes a variety of high energy complex substrates and can grow both aerobically as well as anaerobically via mixed acid fermentation (20). In a similar manner, S. cerevisiae metabolizes a variety of substrates aerobically and can grow anaerobically via fermentation that produces ethanol (21). B. subtilis can also grow anaerobically (22,23) and can obtain energy for growth from a broad range of substrates under aerobic conditions (24). In contrast, G. sulfurreducens has low metabolic diversity and specializes in anaerobically oxidizing acetate, a low energy substrate, with the reduction of extracellular electron acceptors such as Fe(III) oxide and electrodes (25,26). Furthermore, E. coli, B. subtilis, and S. cerevisiae can grow rapidly (doubling time ∼20 min), requiring high metabolic flux (8), whereas G. sulfurreducens grows much slower, with a doubling time of ∼8 h on soluble electron acceptors and ∼192 h on its natural electron acceptor, Fe(III) oxide (25).

MATERIALS AND METHODS

Determining essential, conditionally active, and nonessential reactions

Model constraints were based on previously defined constraints for the respective models with the exception that all reactions that represent the substrates available for growth were allowed to be active by setting the appropriate constraints (lower bound −50 mmol/gdw h and upper bound 50 mmol/gdw h). The list of essential reactions was obtained by using the flux balance analysis (FBA) assumption of optimal growth for each of the models (27). The inactive reactions were calculated by utilized the FBA without any additional constraints as outlined in Mahadevan and Schilling (19) and Burgard et al. (28). The reactions that were not essential or inactive are either nonessential or conditionally active reactions. Hence, all reactions can be classified as being either 1), essential or 2), inactive reactions, or 3), conditionally active and nonessential reactions. Some reactions are active only in a specific environment. These reactions are classified as conditionally active reactions. The nonessential reactions are those reactions that can have a nonzero flux, but are not essential for growth. The nonessential reactions can further be classified into 1), reactions with “exact alternates” and 2), those with “suboptimal alternates”. The gene-protein-reaction associations in the metabolic models were used to determine the presence of gene duplicates.

Determining reactions with exact alternates

Equivalent reaction sets were determined using FBA (19). In this approach, the flux through every reaction in the model is maximized and minimized, subject to a constraint that the growth rate is optimal to calculate the range of variation possible in the flux. The reactions with a nonzero range can have different flux values at the same optimal growth rate. Consequently, even if these reactions are deleted, the growth rate does not change as there are alternate biochemical pathways that can be substituted for the deleted reaction without any impact on the growth rate. Such reactions are classified as “reactions with exact alternate”.

Determining reactions with suboptimal alternates

These were defined as the set of reactions, which when deleted lead to a nonzero but suboptimal growth rate relative to the wild-type growth rate. Even though the reactions that substitute for the deleted reaction are not exactly equivalent to the deleted reaction, they do provide a limited degree of buffering. The statistical significance of the differences between the average flux through G. sulfurreducens reactions with and without gene duplicates was also evaluated. For the statistical analysis, the two sided Wilcoxon rank sum test in MATLAB (The MathWorks, Natick, MA) was used. Flux distribution in metabolic networks has been shown to follow the power-law distribution (29), and hence the Wilcoxon rank sum test was used instead of the standard t-test that requires normality. The P-value was calculated to be 0.38, suggesting a lack of statistical significance at a 5% significance level, even though the average flux for the reactions with gene duplicates (4.98 mmol/gdw h, n = 63) was lower than the rest of the reactions (5.4 mmol/gdw h, n = 168).

RESULTS

Metabolic reactions of microorganisms can be categorized as: 1), reactions that are essential under all conditions, 2), condition-specific and nonessential reactions, and 3), reactions predicted to be inactive under all conditions (27,28). The percentage of essential metabolic reactions was much higher for the specialist organism, G. sulfurreducens, than it was for the more metabolically diverse E. coli, B. subtilis, and S. cerevisiae (Fig. 1 a). Methanosarcina barkeri represents another more metabolically specialized organism, converting acetate or hydrogen to methane. Although the constraint-based genome-scale model for the metabolism of M. barkeri (30) has not been as fully evaluated as the other organisms under consideration here, the proportion of essential reactions in this specialist organism is similar to that of G. sulfurreducens (Fig. 1 a). This distribution of essential reactions is consistent with studies that have shown that generalists evolve under varying environments, whereas specialists are selected for in-constant regimes and have a narrower range of metabolic capabilities that are all essential in environments considered (31).

FIGURE 1.

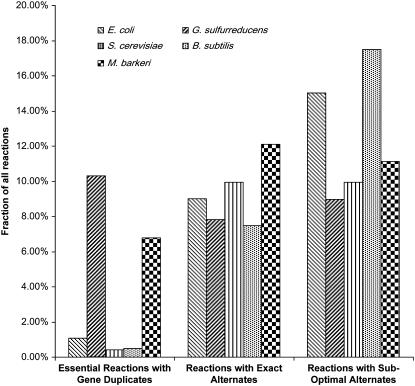
(a) Frequency of predicted essential reactions, conditionally active and nonessential reactions, and inactive reactions in different microbial metabolic networks: 34% of G. sulfurreducens model reactions are predicted to be essential under all growth substrates tested, whereas only 0.4% of the S. cerevisiae reactions are predicted to be essential. (b) Enrichment of gene duplicates in essential reactions of G. sulfurreducens relative to the conditionally active and nonessential reactions, inactive reactions, or all model reactions as compared to other microbial metabolic networks. The role of gene family and biochemical buffering was analyzed by identifying the gene duplicates associated with the essential reactions in all the metabolic networks. The conditionally active and nonessential reactions included those reactions for which either a stoichiometrically and energetically equivalent pathway/reaction (that does not affect the energy yield and is an “exact alternate”) or nonequivalent pathway/reaction (that requires additional energy relative to the original reaction/pathway and is a “suboptimal alternate”) was present in the network. Inactive reactions are those that are predicted to be not active under any condition. More than 30% of the essential reactions in G. sulfurreducens have gene duplicates as compared to 10% in E. coli and 20% (5/20) in S. cerevisiae. However, the S. cerevisiae fraction is partially skewed by the low number of essential reactions under the conditions tested.

Not only do the metabolic specialists, G. sulfurreducens and M. barkeri, have a higher proportion of essential reactions than the generalists, they also have a significantly higher percentage of essential reactions that have gene duplicates (Fig. 1 b). S. cerevisiae also appears to have a relatively high percentage of duplicates in essential reactions, but this result is skewed by the low number of essential reactions in this organism. In contrast, when other classes of reactions or all reactions are considered, there is no significant difference between the specialists and the generalists (Fig. 1 b).

Furthermore, a higher proportion of the metabolic reactions in the specialists are essential reactions that are catalyzed by gene duplicates (Fig. 2). However, the network size and the total number of gene duplicates are different among the organisms. The network size varies from 1176 reactions, of which 231 have gene duplicates in S. cerevisiae, to 524 reactions, of which 111 have gene duplicates in G. sulfurreducens. To normalize for these differences, we calculated the Genetic/Pathway Redundancy Ratio:

where,

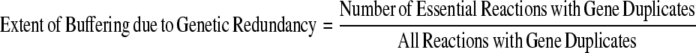and

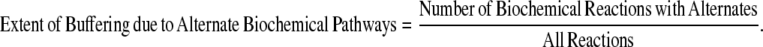FIGURE 2.

Extent of buffering from genetic redundancy and alternate biochemical pathways across different microbial networks. The contribution of alternate biochemical pathways (both optimal and suboptimal) ranges from 7 to 22% in all the networks, whereas the contribution of gene duplicates in providing robustness (as measured by the ratio of essential reactions that have gene duplicates to the total number of reactions) is higher in G. sulfurreducens (10%) and M. barkeri (7%) as compared to other organisms (1% in E. coli and 0.4% in S. cerevisiae).

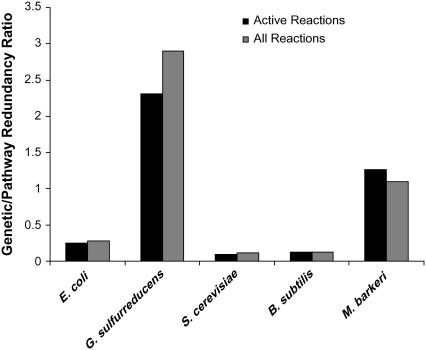
A Genetic/Pathway Redundancy Ratio >1 indicates that the extent of genetic redundancy-based buffering is more significant than the extent of biochemical pathway-based buffering and vice versa. This ratio was calculated for all reactions in the network and for a subset of reactions that can be active in the network. In both the cases, this ratio was much greater for the specialists, G. sulfurreducens and M. barkeri, than for the generalists (Fig. 3).

FIGURE 3.

Relative significance of buffering due to genetic and biochemical pathway redundancy. The Genetic/Pathway Redundancy Ratio is >1 (when either all the reactions or the active subset is considered) for G. sulfurreducens and M. barkeri as compared to the other “generalist” organisms.

Further, the analysis of the magnitude of the flux in the network revealed that in G. sulfurreducens, the flux through the reactions that have gene duplicates, on average, are no higher than the rest of the reaction network. This result suggests that the function of these gene duplicates in G. sulfurreducens is not to boost enzymatic flux and contrasts with the suggested role for gene duplicates in S. cerevisiae (8,11). Specialists appear to have a much higher relative reliance on gene duplicates than alternative pathways to provide resilience to gene mutations.

DISCUSSION

In this study, we have evaluated the extent of genetic and biochemical redundancy in microbial metabolic networks using genome-scale metabolic models. We have shown that the fraction of essential reactions in the different networks clearly distinguishes the metabolic capabilities of the organisms. In generalists such as B. subtilis, S. cerevisiae, and E. coli, <10% of the network is essential, whereas, in contrast, >30% of the network is essential in the specialists G. sulfurreducens and M. barkeri. These differences in the fraction of essential reactions clearly reflect the versatility of the generalists' metabolism as compared to specialists.

Further analysis of the fraction of essential reactions that have gene duplicates clearly points to additional differences between the specialists and the generalists. The generalists with the exception of S. cerevisiae have much lower fraction (<11%) of gene duplicates in essential reactions, whereas the specialists have a higher fraction of gene duplicates (>20%) in essential reactions. In M. barkeri, the fraction of essential reactions with gene duplicates is lower relative to the fraction of inactive reactions with gene duplicates. However, the genome-scale metabolic model of M. barkeri has been recently developed and it has not been reconciled with detailed experimental data. Consequently, there are several gaps in the metabolic network that manifest as reactions that are inactive or blocked reactions. Additionally, the biomass reaction of this organism was constructed based on available literature and the E. coli biomass reaction, and it is possible that the biomass reaction is missing several condition-specific growth components that have not yet been characterized (30). Several of these inactive/incomplete reactions could be required to synthesize such components.

The results also indicate that the specialists have a higher fraction of essential reactions with gene duplicates relative to the generalists, whereas E. coli and B. subtilis have a greater number of reactions that are buffered due to the presence of alternate biochemical reactions (either exact or suboptimal). The normalized ratio of reactions buffered due to gene duplicates relative to those buffered due to alternate biochemical reactions is >1 for specialists. Therefore, specialists appear to rely more on gene duplicates in essential reactions rather than possessing alternate biochemical pathways to maintain metabolic robustness to gene deletions. In contrast, the generalists that have a diversity of metabolic pathways appear to rely more on alternate biochemical pathways by leveraging their metabolic diversity.

These results clearly demonstrate that selection for metabolic strategies in different environments can lead to different approaches to maintain metabolic resilience. Continued analysis of a broader range of microorganisms, as well as experimental evolution studies, may help further define the factors favoring gene duplication versus pathway redundancy as the optimal strategy for maintaining robustness in metabolically diverse organisms.