Characterization of the Resting MscS: Modeling and Analysis of the Closed Bacterial Mechanosensitive Channel of Small Conductance

Abstract

Channels from the MscS family are adaptive tension-activated osmolyte release valves that regulate turgor in prokaryotes and volume in plant chloroplasts. The crystal structure of Escherichia coli MscS has provided a starting point for detailed descriptions of its mechanism. However, solved in the absence of the lipid bilayer, this structure may deviate from a native conformation. In this study, we utilized molecular dynamics simulations and a new iterative extrapolated-motion protocol to pack the splayed peripheral TM1 and TM2 transmembrane helices along the central TM3 shaft. This modification restored the tension transmission route between the membrane and the channel gate. We also modeled the structure of the 26-amino acid N-terminal segments that were unresolved in the crystals. The resulting compact conformation, which we believe approximates the closed resting state of MscS, matches the hydrophobic thickness of the lipid bilayer with arginines 46, 54, and 74 facing the polar lipid headgroups. The pore-lining helices in this resting state feature alternative kinks near the conserved G121 instead of the G113 kinks observed in the crystal structure and the transmembrane barrel remains stable in extended molecular dynamics simulations. Further analysis of the dynamics of the pore constriction revealed several moderately asymmetric and largely dehydrated states. Biochemical and patch-clamp experiments with engineered double-cysteine mutants demonstrated cross-linking between predicted adjacent residue pairs, which formed either spontaneously or under moderate oxidation. The L72C-V99C bridge linking more peripheral TM2 to TM3 caused a shift of channel activation to higher pressures. TM3 to TM3 cross-links through the A84C-T93C, S95C-I97C, and A106C-G108C cysteine pairs were shown to lock MscS in a nonconductive state. Normal channel activity in these mutants could be recovered upon disulfide reduction with dithiothreitol. These results confirmed our modeling predictions of a closed MscS channel featuring a TM3 barrel that largely resembles the crystal conformation though with more tightly packed peripheral helices. From this closed-resting conformation, the TM3 helices must expand to allow for channel opening.

INTRODUCTION

The mechanosensitive channel of small conductance, MscS, is a ubiquitous component of the bacterial osmoregulation system. In bacteria, MscS acts as a tension-activated valve that opens and releases small intracellular osmolytes thus rescuing cells from hypotonic lysis (1). MscS-like channels have been found in fission yeast, alga, and higher plants (2). Two of these MscS homologs in Arabidopsis thaliana have been shown to be critically involved in regulation of chloroplast volume and fission (3). More recently, an MscS homolog was shown to play an important role in maintenance of chloroplasts in Chlamydomonas (4).

Electrophysiological experiments with purified and liposome-reconstituted Escherichia coli MscS have demonstrated that the channel activates in direct response to tension in the lipid bilayer (5,6). Patch-clamp measurements of MscS in native bacterial spheroplasts revealed complex adaptive behaviors in transitions between the resting, open, and inactivated states (7). The slopes of MscS dose-response curves on tension (P_o(γ)), measured in reconstituted and native membranes, implied a substantial in-plane expansion of the protein (8.4 (6) to 18 nm² (7)) associated with opening.

The crystal structure of E. coli MscS was solved by the Rees group to 3.9 Å at pH 7.2 in Foscholine-14 (8). It revealed a nearly symmetric homo-heptameric complex with three transmembrane helices (TM1, TM2, and TM3) per subunit connected to a large hollow cytoplasmic cage formed by all seven C-terminal ends. The crystal structure was postulated to represent the open conformation of MscS and the characteristic ∼30° tilts of TM1-TM2 helical pairs relative to the pore axis were interpreted as a sign of synergistic action of tension and voltage in reaching the open state (8). The upward (toward the periplasm) splaying motion of the peripheral helices (TM1-TM2) carrying positive charges was considered as a mechanism for the voltage sensitivity of MscS-like channel reported in early experiments (9). Later studies, however, demonstrated that the rate of MscS activation is not voltage-dependent (7). Instead, the rate of inactivation was found to be higher under depolarizing voltages (7,10) a trend that was found to be unchanged in mutants lacking a number of positive charges on the TM1 and TM2 transmembrane helices (11).

Although the crystal conformation of MscS was initially deemed to be open (8), several attempts to simulate this conformation, with different force fields and water models, revealed a pore constriction that was largely dehydrated (12–14). Ion permeation through this dry pore was determined to be not possible at physiological voltages (12,13,15), which strongly suggested that the crystal structure represented either a low-conducting or nonconductive state (12). Brownian dynamics simulations demonstrated that even if the crystal pore were fully hydrated, it would still be too narrow to allow for the experimentally observed 1-nS open-state conductance (15,16). These results led to a recent reinterpretation of the MscS crystal structure by its authors (17).

A puzzling feature of the crystal structure is the large tilt of the TM1-TM2 helices shown to create deep crevices on the cytoplasmic side of the transmembrane domain. Attempts to simulate MscS in lipid bilayers using molecular dynamics (MD) (13,14) revealed that the crystal conformation is unstable in a typical lipid environment and suggested that the transmembrane barrel with splayed TM1-TM2 peripheral helices may not represent a native state. A more compact resting state has been discussed by Edwards and co-workers (13,14) and partially supported by chemical cross links (18). It now appears that the splay of the TM1-TM2 pairs, observed by the crystallographers, could be a result of delipidation.

In this article, we sought to address the longstanding questions of what, if any, functional state is represented by the crystal structure and subsequently took the first steps toward elucidating its possible connection to other states in the gating cycle. We have reconstructed a model of the closed-resting conformation of MscS from the crystal structure utilizing a set of novel modeling tools which allowed us to transform the original structure and predict the overall character of the gating transition. We demonstrate that this more compact closed-state model of the complete transmembrane region of MscS is stable in the lipid bilayer and nonconductive within a physiological range of voltages. Finally, we provide biochemical and electrophysiology data testing the predicted helical arrangement of the resting state using disulfide cross links.

Qualitative analysis of MscS crystal structure and the approach to its transformation and analysis of gating

All of the lattice contacts in the MscS crystals were formed between the polar cytoplasmic domains (8). The crystallographic temperature factor (signifying the degree of deviation form the ideal lattice) in the entire structure was found to be highest for the cytoplasmic ends of the tilted peripheral TM1-TM2 helices. The nature of this curious tilt in these helical pairs is not accounted for in an obvious way. There have been several examples of highly tilted helices in membrane proteins such as aquaporin (19,20), CLC channel (21), and the glutamate transporter homolog from Pyrococcus horikoshii (22), but in each of these cases, the helical positions were found to be stabilized by the array of intracomplex interactions. In contrast to those structures, the TM1-TM2 helical pairs of MscS do not participate in intersubunit or crystal lattice contacts and the physical reason of their separation from TM3 helices, which may bear functional significance (23), needs to be clarified.

The structure suggests that the loops connecting the TM1-TM2 pairs with the central TM3 barrel (residues 91–94) are flexible and should not impose fixed angles on the positions of TM1-TM2 relative to TM3. The cytoplasmic end of the TM1-TM2 pair, which forms a charged loop (residues 53–67), may potentially salt-bridge to the TM3b helices forming the roof of the cage (via the D62-R128 pair) (14); however, this interaction is not evident in the crystal state. The observed tilts could also be stabilized by steric clashes between bulky amino-acid side chains, which protrude into the TM2-TM3 gap (residues F80 and L100). In delipidated samples, two factors could potentially increase helical tilts: 1), the absence of an appropriately distributed lateral pressure of lipids around the channel; and 2), the wedging of detergent into the TM2-TM3 gaps, thus stabilizing them. Another consequence of the relaxation of the delipidated barrel into a conical conformation might be increased pressure at the tops of the TM1-TM2 pairs squeezing the N-terminal segments out, which may account for their disordered state in the crystals (8). In concurrence with the previous hypothesis of a more compact resting state (18), we propose that the native resting state, stabilized by the lipid bilayer, should feature the TM1-TM2 pairs in more upright positions, packed closer to the central TM3 shaft.

The question of whether the pore-forming TM3 helices of the MscS channel can be packed more tightly, an idea that has been previously addressed by Edwards and co-workers (24), now requires greater consideration, although this time in the context of the entire structure. Unlike the peripheral TM1 and TM2 helices, the pore-lining TM3a helices show the lowest B factor in the crystals, indicating that these tightly packed core segments forming the gate are in a stable conformation. In these positions, the conducting pore of the crystal structure is too narrow to satisfy the experimentally determined open-state conductance (12,14,16,25) and too hydrophobic to be permanently hydrated (12,13). We contend that the crystal conformation of the pore is nonconductive and, because there appears to be no direct mechanical connection between the tension-receiving peripheral helices and the gate, the structure better satisfies the criteria of the tension-insensitive inactivated state than the criteria of the resting state (26).

Attempts to simulate the crystal structure of MscS in lipid bilayers using MD (13,14) showed that assembling lipids around the transmembrane domain was not straightforward due to its unusual surface topology. A conspicuous discrepancy revealed in these simulations was that the tightly packed assembly of TM3 helices, most stable in the crystal structure, was especially prone to quick kinking and collapse. The obvious factors that could render the crystal structure unstable in simulations were the absence of the N-terminal domains (26 amino acids unresolved on the periplasmic side of the channel), inappropriate positioning of the protein along the Z-coordinate relative to the bilayer, and the splayed orientations of the lipid-facing helices causing stresses and distortion. With regard to this last point, tilting of isolated helices in the bilayer was demonstrated to be energetically costly (27,28); it is therefore plausible that the peripheral helices in the native state of MscS are less tilted and form a more continuous protein interface with the lipid.

To overcome some of these unusual features and tendencies of MscS we chose a different strategy in our MD simulations. In our approach, we first utilized computationally efficient targeted energy minimizations and our new iterative extrapolated-motion technique to quickly refold the crystal conformation in vacuum. The imposed energy gradients in minimizations and the displacements initiating extrapolated motion were directed radially, mimicking lateral stretching (or compressing) force as would be expected in the channels' native environment. The magnitudes of these perturbing factors (forces or displacements) were adjusted to a minimal effective value such that protein motion occurred primarily about hinged regions to preserve all of the existing secondary structure elements. In the next step, we modeled the missing N-terminal segment de novo, attached it to the channel, and tested its compatibility with the closed- and open-like states in multiple cycles of extrapolated expansions and contractions. Having chosen the most favorable conformation of the N-terminal, we then explored the general pathway for reversible barrel expansion permitted by the protein itself. We applied to these trajectories experimentally determined constraints on the amount of in-plane area change and pore diameter (based on conductance), and chose the two end-states roughly approximating the resting and open states of the channel. Seeking to predict the resting state of MscS, we relaxed the most compact conformation of the channel barrel in extended unrestrained MD simulations in the presence of explicit water and lipids. The resultant symmetrized model representing the resting state was then analyzed in terms of critical interhelical interactions and candidate pairs of residues were selected for cysteine substitutions. The generated MscS mutants were then tested for the ability to form disulfide bridges in biochemical and patch-clamp analyses.

MATERIALS AND METHODS

Molecular dynamics simulations

At different stages of structure modification, we utilized targeted energy minimizations as well as molecular dynamics (MD) simulations in equilibrium (unrestrained) mode, steered mode as well as simulations with soft symmetry restraints. All MD simulations were performed using NAMD2 (29) with the CHARMM27 force field (30). VMD (31) was employed for visualization, molecular modifications, and analysis using custom-written Tcl scripts for calculation of in-plane channel area changes, assessment of pore asymmetry, and estimation of the number of water molecules in the constriction region.

The major steps are illustrated in Figs. 1 and 2, whereas many additional technical details of the simulations can be found in the Supplementary Material. Briefly, the initial compacted conformation of MscS was obtained from the crystal structure (PDB ID 1MXM) using targeted energy minimizations (conjugate gradient and line search algorithm) with a gradually increasing harmonic force (0.001–20 kcal/mol/Ų) applied to the protein backbone toward the central axis of the channel. In addition to the purely centripetal force direction, the protocols with a 45° clockwise twisting component were used. The targeted minimizations were performed in vacuum with the charges adjusted according to the dielectric permeability of the implicit medium (lipid membrane or water). Relaxing energy minimizations (with no imposed bias) and symmetry-driven simulated annealing steps under the same simulation conditions followed steered compression of the channel barrel. The resulting compact and symmetric homoheptamer is shown in Fig. 1 C.

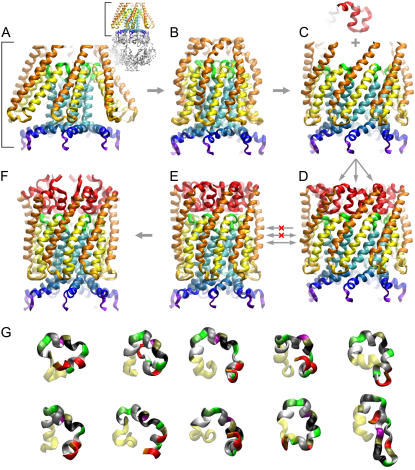
FIGURE 1.

Generation of the complete resting conformation of MscS illustrated as step-by-step transformations of the crystal structure and modeling of the N-terminus. The complete crystal structure is presented as an inset next to panel A with the cytoplasmic cage domain shown in gray. Only the transmembrane pore region is shown in panels A–F. The transformations in panels A–E were performed on the entire protein, with the steering force applied to the transmembrane domain only. (A) The original crystal conformation of the transmembrane domain with splayed TM1 (orange) and TM2 (yellow) pairs of helices. The nearly parallel pore-lining TM3a segments (cyan) are followed by the C-terminal TM3b segments (blue) splayed after a sharp kink near glycine 113. (B) A compact conformation with restored contacts between the lipid-facing TM1-TM2 helices and the pore-lining TM3a helices. The peripheral TM1 helices are slightly bent and the TM1-TM2 loops are distorted due to clashes with splayed TM3b segments. (C) Expanded conformation featuring an open gate and straightened kinks between the TM3a and TM3b (blue) helices. The fragment above the channel (red) represents one of the most probable conformations of the N-terminal domain predicted using the Rosetta algorithm (see G). (D) The complete MscS model of the open state with attached N-terminal segments. Transitions from panels D to E and back represent compaction-expansion cycles performed using the extrapolated motion technique to test for the ability to undergo smooth and reversible transitions between the open and closed states. (F) The relaxed closed-state model representing the transmembrane domain with the adjacent part of the cytoplasmic cage after 8 ns of unrestrained all-atom simulation in the fully hydrated POPC bilayer, followed by symmetric annealing. In contrast to the crystal structure, the closed-state models (E and F) have a straightened kink near G 113, while an alternative kink forms around G121. (G) Ten most probable conformations of the N-terminus (40 residues) predicted by Rosetta. The first 26 residues in these ribbon representations are color-coded by residue name, whereas yellow regions correspond to the resolved helical stretches. The choice of the fragment and its final adjustment were done according to its ability to undergo unhindered transition between the states depicted in panels D and E.

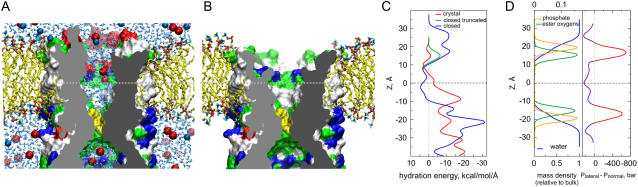
FIGURE 2.

All-atom MD simulation of the modeled resting state and the distribution of polar residues at the protein-lipid boundary. (A) Complete resting state model in the bilayer illustrated by a cross-sectional view captured in the middle of the unrestrained 8 ns simulation (sim2, see also Fig. 3). Shown as solvent-accessible surfaces, polar (green), basic (blue), and acidic (red) residues are exposed to the lipid headgroup regions, whereas nonpolar residues face hydrocarbon. Although the upper hydrophobic chamber is hydrated, neither water (cyan sticks), nor ions (Cl⁻ red or K⁺ blue, spheres) penetrate the dewetted hydrophobic constriction (yellow). (B) The same structure with the N-terminal domain (26 amino acids) removed. Nicks in the channel wall protrude down to the middle of the fatty acid chains and the absence of lipid-facing polar atoms suggests improper anchoring at the periplasmic rim of the channel. Y27 has spontaneously changed its position during the simulation from pore-facing as in the crystal structure, to one that is more peripheral and solvent-exposed. (C) Hydration energy profile for the lipid-exposed surface reveals a balanced distribution of polar groups in the complete resting state model (blue line) with a hydrophobic region near the midplane of the membrane (shown by horizontal dashed line) that is flanked by polar regions at ±16 Å representing the cytoplasmic and periplasmic rims. The model lacking the N-terminus (green line) shows a very small polar region at the periplasmic rim. Positioning the crystal structure (not shown) in the same way produces a maximum of polarity at −8 Å with a highly imbalanced overall distribution along the Z axis (red line). (D) The distribution of polar groups in a POPC bilayer simulated at an area of 64 Ų/lipid matches the distribution of the polar atoms in the closed MscS model. It is consistent with the notion that the route for the transmission of the lateral tension between lipid and protein lies at both the periplasmic and cytoplasmic rims of the channel. The lateral pressure/tension profile is shown in panel D with the red part of the curve representing the tension component. The distributions of lipid groups and pressure across the bilayer are taken from Gullingsrud and Schulten (46).

The resting-state model with the smallest in-plane area, narrowest constriction, and minimal distortions of the secondary structure was simulated in unrestrained mode in a fully hydrated palmitoyl-oleoyl-phosphatidylcholine (POPC) bilayer (220 lipids) with TIP3P water (32) in a flexible hexagonal periodic box. The membrane tension was set at 10 dyne/cm (33). To reduce the size of the system, only the transmembrane domain with the adjacent portion (∼15 Å) of the cytoplasmic cage (residues 1–130, 137–140, 147–154, and 162–175 of each subunit) were included. The number of potassium and chloride ions corresponded to a 200 mM salt concentration. The total system size was ∼100,000 atoms. The entire 15-ns simulation was arranged as a sequence (Fig. 3) of unrestrained simulations interrupted with shorter symmetry-driven simulated annealings. During the annealing stages, all protein atoms were gradually driven toward their continuously updated sevenfold symmetric average positions using harmonic restraints with the spring constant increasing exponentially from 0.001 to 20 kcal/mol/Ų. The rest of the system (lipids, water, and ions) was unrestrained. During the unrestrained simulation stages all the atoms in both the medium and protein were free to move except for the α-carbons of the terminal residues (points where the cytoplasmic domain was truncated) to prevent unnatural drift.

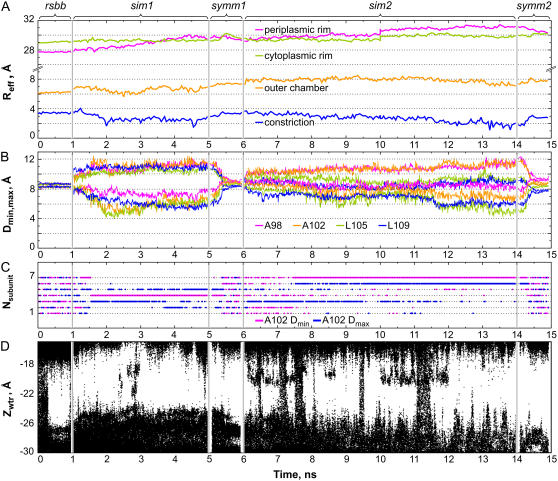
FIGURE 3.

Geometrical parameters of the barrel and the degree of pore hydration in the course of a 15-ns MD simulation. (A) Effective radii of the periplasmic and cytoplasmic rims, outer chamber and of the constriction over the stages of simulation with the restricted backbone (rsbb), first unrestrained simulation (sim1), symmetry-driven annealing (symm1), the second unrestrained simulation (sim2), and the second symmetric annealing (symm2) (estimated every 50 ps). (B) Distances from the pore axis to the closest and the most distant α-carbons of equivalent residues in the heptamer that illustrate the ellipticity of the outer chamber (A98 and A102) and constriction (L105 and L109), estimated every 10 ps. (C) Conformational exchange in the pore illustrated by the radial motion of subunits. Positions of the α-carbons of A102 residues in individual subunits (numbered 1–7) were tracked every 10 ps. Residues closest to the pore axis at a given moment are marked by a magenta dot, whereas those most deviating from the axis are designated by a blue dot. Plots for the residues A98, L105, and L109 (not presented) illustrated the ellipticity of the barrel in the same way as this one for A102. (D) Z-coordinates of water molecules illustrating the degree of hydration of the pore constriction and vestibules scored every 1 ps.

Predictions of the transition pathway using the extrapolated motion protocol

Large-scale motions of the MscS barrel were explored in vacuum by this new iterative protocol. The procedure starts with an initial displacement of a specific domain or all protein atoms in an arbitrary direction. Energy minimization and a short, relaxing, MD simulation follow this step. In the next cycle, atom displacements are calculated as the linear extrapolation of coordinates based on the previous and current positions. After displacement occurs, energy minimization and relaxing MD simulation are repeated (see diagram in Fig. S1, Supplementary Material).

For the transmembrane barrel of MscS, 0.1–1 Å displacements in the radial direction were used to initiate expansion or compression. In each cycle, the extrapolated displacements of atoms were corrected in both absolute value and direction by an initial energy minimization (100 steps, conjugate gradient, and line search algorithm), followed by a 1-ps relaxing MD simulation at 310 K and then by another energy minimization (100 steps) with sevenfold symmetry restraints. When merged into a pseudo-continuous curvilinear trajectory, 50 extrapolation cycles typically produced 5–15 Å of radial displacement of all transmembrane domains also associated with tilting. We found that introduction of amplification coefficient, which slightly increases the absolute value of the coordinate extrapolation vector at every step, expands the range of explored space with the optimal coefficient value between 1.05 and 1.2. Note that extrapolations have a random component due to the Langevin temperature control in the simulations. When repeated from the same starting conformation, independent series were observed to produce varying trajectories, but these trajectories usually displayed similar features.

Modeling of the N-terminal segment

The structure of the N-terminal domain, a 40-residue fragment including the unresolved 26 N-terminal residues, was predicted de novo using the Robetta structure prediction server (34–36) which employs the Rosetta algorithm (37). To provide room for insertion of the unresolved N-terminal domain, the compacted structure (Fig. 1) was expanded (∼4 Å root mean-squared deviation, i.e., RMSD, for the backbone) using the extrapolated motion technique. Seven of the most probable conformations were aligned with the expanded model (using the backbone of residues 27–35) and embedded into the structure. All of the seven selected variants were found to be compatible with the open channel structure and after alignment, all fit into the gaps between the neighboring TM1 helices displaying no structural conflicts with other domains. The embedded N-termini were then tested separately for compatibility in a transition between the closed and open states using the extrapolated motion technique. Some of the tested N-termini failed to follow either the closing or opening transitions, while other moved coherently with the transmembrane helices. The folded variant that revealed the lowest distortions in structure during the transitions was selected as most probable. Extrapolated expansion/compaction was then repeated 50 times with the complete model.

Hydration energy profile calculations and protein positioning within the membrane

For each resulting structure, the hydration energy per atom was calculated using the GETAREA web-based software (38) with the probe radius of 1.4 Å and atomic solvation parameters taken from Wesson and Eisenberg (39). Selection of the atoms on the outer and inner surfaces of the protein separately was permitted through a custom-written algorithm. Selected atoms on the outer surface were grouped in 1 Å slices along the Z axis normal to the membrane plane. Hydration energies for all atoms in each slice were summed, producing the hydration energy density along the axis. The initial profile was smoothed on the assumption of a Gaussian distribution of the Z coordinate for each atom with RMSD = 2 Å. The obtained hydration energy profile was used to position the transmembrane barrel relative to the POPC bilayer for all-atom simulation. The middle of the hydrophobic belt of the barrel (approximately at the level of V40) was aligned with the midplane of the membrane and the stability of this position was tested in unrestrained MD simulations. Matching of hydrophilic belts of residues at the periplasmic and cytoplasmic rims of the channel (located at ±16 Å on the Z coordinate, Fig. 2) to the layers of lipid headgroups was employed as the second criterion for proper protein-lipid assembly.

Estimations of the in-plane area

Area estimations were based on the solvent-accessible surface for a probe of 1.4 Å radius using the CHARMM27 VDW radii for the protein. An area at the selected level was estimated as the area of the surface cross section with a plane normal to the pore axis. The radius of a circle of an area equal to the cross-sectional area was considered as the effective radius at that particular level. Cross sections were spaced every 0.5 Å. For a selected range of slices, an average value for the radius (or area) was estimated as a value for the range. Effective in-plane radii for the periplasmic and cytoplasmic rims of the protein were calculated for the ranges 12.5–17.5 Å and −17.5 to −12.5 Å (relative to the midplane of the membrane with z = 0), respectively. Effective pore radii were calculated in the ranges −13 to −7 Å for the upper hydrophobic chamber and −23 to −17 Å for the pore constriction. Calculations were repeated every 50 ps during the course of the simulations. This automated protocol for area estimations was written in Tcl and run in VMD.

Assessment of pore asymmetry

The degree of the TM3 barrel asymmetry was estimated from the radial distances of the α-carbons of the key pore-lining residues (A98, A102, L105, and L109) to the pore axis. For every group of equivalent residues in the heptameric assembly, a geometric center was determined from the coordinates of the seven α-carbons and the minimal and maximal distances in x-y plane (normal to the channel axis) were calculated every 10 ps throughout the simulation trajectory.

Estimations of channel conductance

Channel conductance (G) was first estimated in a continuum approximation (40,41) taking into account the access and pore resistances in a solution of specific bulk conductivity g. The pore was presented as a stack of cylindrical slices (0.5 Å thick) and the resistances were summed. The ion-accessible cross-sectional area in each slice was determined with the assumption of an average ion radius of 2.83 Å, which includes half of its first hydration shell. The access resistances were determined from the effective radii of the cytoplasmic and periplasmic pore entrances (41) (see Supplementary Material for details).

Estimations of conductance in explicit all-atom MD simulations were done essentially as described by Aksimentiev and Schulten (42,43). In our simulations, the salt concentration in the aqueous phase surrounding the channel was increased to 1500 mM. The protein backbone was restrained softly (0.01 kcal/mol/Ų) to allow for conformational freedom yet prevent large-scale drift. Ion movement was estimated at ±200 and ±500 mV (across the entire simulation cell of 106 Å, with the potential on the cytoplasmic side assigned as zero) for the duration of 4–8 ns (at each voltage). Ion crossing events in the pore were scored using custom-written Tcl scripts in VMD.

Disulfide cross linking of MscS

The PB111 plasmid harboring wild-type (WT) MscS with a C-terminal His-6 tag (5) was used as a template. WT MscS has no cysteines. Single and double cysteine mutations were introduced using the QuikChange mutagenesis kit (Stratagene, La Jolla, CA) and verified using automated sequencing. All mutants were expressed in the MJF465 (mscL⁻, mscS⁻, mscK⁻) E. coli triple knockout strain (1). Cysteine cross-linking and visualization were implemented essentially as described before in Betanzos et al. (44). Briefly, cells from 20 ml of an IPTG-induced cell culture (OD₆₀₀ ∼0.8) were collected, washed in PBS (100 mM NaCl, 30 mM NaPO₄, pH 7.2) and French-pressed. The membranes were collected by centrifugation, resuspended in PBS and aliquoted into separate tubes. Cross-linking reactions were carried out in 1 ml of PBS in the presence of 0.03 mM iodine (I₂) for 10 min at room temperature. After completion of the reaction, membranes were spun for 15 min and resuspended in an iodine-free buffer containing 5 mM n-ethylmaleimide to block unreacted cysteines. Membranes were incubated in n-ethylmaleimide for 10 min, spun again, and dissolved in 50 μl of nonreducing (2×) sample SDS buffer. Proteins were separated on a 4–15% gradient polyacrylamide gel (BioRad Laboratories, Hercules, CA). Bands representing MscS monomers and various multimers were visualized on Western blots with anti-His₆-C-terminal alkaline phosphatase-conjugated antibodies (Invitrogen, Carlsbad, CA). Controls with distant pairs of cysteines are presented in the Supplementary Material (Fig. S2).

Patch-clamp experiments

Preparation of giant E. coli spheroplasts and patch-clamping procedures were conducted as described previously in the literature (7,23). Briefly, WT MscS-His₆ was expressed in MJF465 cells. Channel recording was conducted on excised inside-out patches in symmetrical KCl buffers (7). Mechanical stimuli was applied as negative pressure in the pipette and delivered using a high-speed pressure clamp apparatus (HSPC-1; ALA Scientific, Westbury, NY). For analysis of MscS activity under ambient conditions, spheroplasts were equalized by exposure to air for 1 h on ice before patching. For in situ cross-linking, an oxidizing pipette solution of 0.05 mM iodine in KCl recording buffer was delivered behind a 1 mm plug of 400 mM sucrose bath solution. The effects of iodine in this configuration were delayed by ∼30−60 min to aid in patch-sealing and to take measurements before oxidation. For reduction of disulfides, a solution of 10 mM dithiothreitol (DTT) was prepared in KCl recording buffer. Spheroplasts expressing cysteine MscS mutants were preincubated in 10 mM DTT for 1 h before patching. Alternatively, a 10 mM DTT solution could be perfused into the recording bath by washing the 3 ml chamber with 12 ml of the solution.

RESULTS

Modeling of the compact state

To translate the hypotheses of compact resting state into a structural model, a sequence of transformations was performed with the MscS crystal structure (PDB ID 1MXM) as a starting point (Fig. 1). At each step, a set of structures was generated and then ranked according to compatibility with adjacent states and experimental data. The top-ranked models were then selected for subsequent steps.

The first compaction was achieved using targeted energy minimizations (Fig. 1, A and B) under a centripetal force combined with a clockwise twisting component. After sevenfold symmetrization, the first compact structure acquired some of the predicted features of the closed state, namely a smaller in-plane area and lower and more energetically favorable tilts of the peripheral (TM1-TM2) helical pairs. This refolding of the 21-helix assembly occurred without a collapse or distortion of the central TM3 barrel. The more parallel helical assembly also reestablished the mechanical connection between the peripheral and the pore-lining TM3 helices, which appears to be necessary for the transmission of tension from the lipid bilayer to the gate. The compacted structure was then subjected to symmetry-driven annealing to remove small deviations between the subunit conformations.

In the cytoplasmic half of the resultant compact structure, tips of the TM1-TM2 loops touched the TM3b segments forming the roof of the cage and thus experienced a small bending. The periplasmic half, in turn, featured bent TM1 helices with the tops collapsed inside the barrel (Fig. 1 B). It appears that the latter structural anomaly resulted from the absence of the unresolved N-terminal domain (26 amino acids) in the MscS crystal. Without the N-termini, the transmembrane part of MscS appears to be too short to match the membrane thickness (45) and also featured too few polar contacts with the lipid headgroups that would be necessary to properly connect the barrel with the tension-bearing region of the membrane (46,47). We therefore set out to predict and reintroduce the missing N-terminal segment.

Since the inwardly collapsed N-terminal part of TM1 sterically hindered the insertion of the predicted N-terminus, we transformed the compact state into an open-like conformation using the iterative extrapolated motion protocol. The transition was initiated by a 1 Å radially outward displacement of all atoms from residues 27 to 113, followed by ∼50 steps of extrapolated motion. At intermediate values of amplification coefficient (see Materials and Methods), a meaningful range of the transition could be approximated in a smooth quasicontinuous trajectory between adjacent states. The expansion process was typically terminated when the pore constriction diameter reached 1.6 nm, satisfying a 1.4-ns conductance (6). At this time, the in-plane cross-sectional area of the barrel was observed to have changed from the initial 22 to ∼34 nm² (ΔA = 12 nm²), comparable with the experimentally estimated in-plane protein expansion (6,7). This procedure was repeated 10 times, with each run producing a slightly different conformation but with similar helical tilts, pore diameter, and cross-sectional area. All open conformations featured a spontaneous straightening of the prominent kink near the residue G113 in the crystal conformation. The averaged and minimized expanded structure representing the consensus is shown in Fig. 1 C.

The conformation of the missing N-terminal segment was predicted de novo from the sequence of the first 40 residues of MscS using the Rosetta algorithm. Of predicted conformations, seven were found to be sterically compatible with the expanded heptameric structure (Fig. 1 G). These N-termini were then aligned with N-terminal part of TM1 and attached to the expanded structure as a direct continuation of TM1. The insertion was straightforward because none of the selected variants had significant steric conflicts with neighboring subunits. Each of the variants filled the gap between the neighboring TM1 helices reasonably well and exposed several polar atoms toward the headgroup region of the bilayer on the periplasmic side. This step produced seven possible, and rather similar, conformations of the complete expanded model. One example is shown in Fig. 1 C. In this conformation, the N-terminal extension forms three short helical segments separated by two reverse turns. With the chosen orientation of the N-terminus relative to the existing part of TM1, residue D8 of the extension forms a salt-bridge to residue R88 in the TM2-TM3 loop of the adjacent subunit, which may provide a stabilizing intersubunit interaction. By filling the nicks in the outer rim, the added N-termini also provided structural support for the N-terminal part of TM1 and adjusted the hydrophobic thickness of the barrel to match the surrounding bilayer.

To obtain a closed-state model that would result from a smooth contracting transition, we performed cycles of centripetal extrapolated motions to close the open-like expanded conformation completed with the N-termini (Fig. 1, D and E). Each round of contraction was initiated by a 1 Å inward displacement of all atoms in the transmembrane region. Typically, after ∼50 steps, the pore radius decreased to the values comparable to the crystal-state conformation (2.5–4.5 Å at the constriction), after which the contractile motion slowed, stopped, and often reversed into expansion. Transitions from the open state that were initiated by a random thermal fluctuation (without an initial inward displacement) also lead to closures along similar trajectories illustrating that the trajectory is not particularly sensitive to the direction of the initial shift.

Three complete models (out of seven tested) showed conflict-free motions of N-terminal domains in the course of contraction. In the remaining four models, the N-termini and the adjacent periplasmic parts experienced steric clashes that hindered contraction of the periplasmic part of the protein. These models were discarded as illustrated by a red-crossed, one-way arrow on Fig. 1, E and F.

To test these structures for the ability to expand, selected closed conformations were subjected to an extrapolated transition to the expanded open-like state using the same extrapolated-motion technique. Conformations in which the N-terminal domains were unable to follow the expansion coherently were rejected (Fig. 1, D and E, red crossed-out two-way arrow). Cycles of compaction and expansion were repeated 50 times for closed- and open-state models that were capable of a smooth gating. Our criteria for selecting a closed model (complete with N-termini) were the smallest in-plane area with the narrowest constriction and minimal distortion of the secondary structure. The selected conformation is shown in Fig. 1 E. This new closed-state model features straightened helices (no kinks) between the TM3a and TM3b helices near the residue G113. The tendency to straighten kinks in this location was observed in 82% of the trajectories. It was also observed that an alternative kink often formed at residue G121. In 62% of all transitions, it was present along with the straightened kink at G113, and in 10%, both partially formed kinks were present simultaneously. The relocation of the kink from position 113 to 121 in TM3 allowed more compact packing of the lipid-facing helices without significant distortions of the TM1-TM2 loops which, after initial compaction (Fig. 1 B), clashed with the sharply splayed TM3b segments. We ascribe kink formation at the new location (G121) to the closed resting conformation of MscS, and we also we have strong evidence to attribute the characteristic kink at G113 observed in the crystal structure to the inactivated state. A detailed functional study of the role of alternate kink formation at these two sites is described in a separate publication (26).

MD simulations

All of the above transformations were performed in vacuo for two reasons: 1), to avoid the problem of medium reactions during fast-extrapolated transitions; and 2), to achieve higher computational efficiency. Although the minimization step of the extrapolation protocol ensures structural cohesion of the closed-state model, the stability of this model had to be tested in all-atom MD simulations. The transmembrane region of MscS with the cytoplasmic domain cut at a distance of ∼15 Å from the TM3b helix (see Materials and Methods) was embedded into a fully hydrated POPC bilayer and the α-carbons of the residues at the truncation points were softly restrained. The barrel was subjected to simulations in three different regimes. An initial equilibration period started with a fully hydrated pore and a harmonically restrained backbone. This was followed by two unrestrained periods (4 and 8 ns), each ending with 1-ns periods of symmetry-restrained simulations. During each period, the stability of the protein assembly, its fit to the bilayer, hydration of the pore, and possible ion permeation events were monitored.

The total time of unrestrained barrel simulations in the explicit lipid bilayer was 12 ns. The protein with the mutually equilibrated surrounding lipid bilayer (see hydrophobicity profiles in Fig. 2 B) showed a good match of their hydrophobic surfaces. Belts of tyrosines (Y27 and Y75) were observed to face their preferred layers of glycerols/carbonyls within the lipid bilayer (48). During the unrestrained 8-ns simulation (Fig. 3, sim2) and symmetrization (symm2), the first few residues of the modeled N-terminal domain were observed to slightly uncoil. The presence of three acidic residues in this region indicates that these uncoiled segments could potentially interact with the positively charged choline groups of the lipid headgroups. By the end of simulation, the resultant midplane position of the bilayer relative to the protein stabilized at a level ∼8–10 Å above the position chosen in previous simulations (13,14). The packing of lipids along the straightened peripheral TM1-TM2 helices of the new closed state model caused essentially no distortion of the lipid bilayer; only a minor decrease of the bilayer thickness was observed near the channel boundary. Essentially no net tilting of the lipids was observed near the surface, compared to ∼35° slope expected near the surface of the crystal structure. In previous simulations, tilted conformations of the peripheral helices, with gaps between them, led to substantial distortion of the boundary lipids and apparently contributed to the quick collapse of the TM3 barrel (unrestrained crystal state) into an asymmetric occluded state (13,14).

After initial equilibration, the first 4-ns period of unrestrained simulation was performed (Fig. 3, sim1). To observe the predominant directions of conformational drift and to reveal any propensity toward asymmetric states, the protein backbone was subjected to a 1-ns symmetry-driven annealing (Fig. 3, symm1) before again releasing the restraints. The evolution of the unrestrained system was observed again for the next 8 ns (Fig. 3, sim2) and then subjected to another 1-ns annealing simulation with symmetry restraints (Fig. 3, symm2). The initial, intermediate, and final symmetric states were then compared. The differences between any two conformations, which did not exceed 3.5 Å RMSD for the entire backbone and 0.7 Å for the α-carbons of the gate residues 105 and 109, illustrated that our closed-state model experienced only relatively small relaxation drifts.

On release of the backbone from the initial restraints (Fig. 3 A, rsbb), the periplasmic rim of the barrel first displayed a slow expansion (sim1), which subsequently stabilized during the second unrestrained period (sim2). The effective radii of the cytoplasmic rim, outer chamber, and constriction measured from the in-plane cross-sectional areas of the solvent-accessible surface (see Materials and Methods) remained stable. Fig. 3 B illustrates deviations of the constriction region and the outer chamber from the ideally symmetric state. The trajectories depict mean radial distances from the pore axis to the α-carbons within the rings of A98, A102, L105, and L109. The differences between the smallest and the largest distances illustrate the ellipticity of the pore lumen. After releasing the symmetry restraints, the pore constriction assumed a moderately asymmetric conformation, which remained stable and nonconductive, although sterically unoccluded. The direction of the long axis of the ellipse representing the lumen of the pore fluctuates. The positions of individual residues that are closest to the pore axis or the most distant at a given moment are illustrated in Fig. 3 C. As seen from the trajectories, during sim1, three different subunits visited these extreme points. In sim2, the structure showed some preservation of symmetry for the first 1.5 ns as multiple residues visited the closest point, but then the preference switched toward subunit 7 and the direction of long axis remained relatively stable for the rest of the simulation. Although the statistics of exchange is not large, the observed dynamics suggests that the ellipticity axis switching in the constriction may occur with a characteristic time of ∼5 ns. Environmental factors such as transient nonhomogeneity of the lipid bilayer may act to influence the exchange between asymmetric conformations in the barrel. It is now clear that several equivalent asymmetric conformations exist, occupying a larger conformational space than a single symmetric or asymmetric conformation—thus collectively constituting the nonconductive resting state of MscS. These findings appear to be supported by the recently revised MscS crystal structure (PDB ID 2OAU), which also displays a noticeably asymmetric state of the barrel (17).

During the entire period of simulation, the narrow and most hydrophobic part of the MscS pore remained largely dehydrated. Within the first 300 ps of the initial restrained simulation, water vacated the constriction, and during the course of simulation, it only entered the constriction occasionally, forming small clusters or single strings (Fig. 3 D). The tendency to de-wet the pore constriction was consistent with previous analysis of the vapor-locked state of the crystal structure (12). Ions were not observed to enter the constriction throughout the entire 15 ns of simulation, even though the pathway for water or ions was not sterically occluded since the axis-to-surface distance in the constriction fluctuated between 2 and 4 Å (Fig. 3 A).

To check explicitly whether an applied voltage is able to cause ion permeation through the modeled closed MscS, we performed an additional set of all-atom MD simulations on the structure obtained after symm1. It was previously determined from patch-clamp experiments that MscS conductance is nearly linear in the range of ±50 mV, and at low voltages shows no concentration saturation at least up to a salt concentration of 1.5 M, in which the channel conducts at 5.5 nS (6). Under these conditions, ∼27 ions are predicted to pass through the channel at +200 mV in the course of a 4 ns. In simulations performed without the cytoplasmic cage, the expected number of passing ions should be even higher, as the cage itself is estimated to contribute ∼20% to the total channel resistance (based on the cross-sectional area of the side portals). However, we observed no permeation events at either positive or negative voltage. Even at a much higher voltage (−500 mV, negative on the periplasmic side), no ions were observed to cross the constriction. At + 500 mV, we observed the conduction of two potassium ions which would provide <3% of the measured conductance of the open state. Although statistically insignificant, this result is interesting as the presence of potassium and not chloride in the pore suggests that addition of the N-terminus may have decreased the strong anionic preference observed in previous simulations of the original and expanded MscS crystal structures (13,14). In all other respects our results agree well with previous simulations and indicate that the TM3 barrel, in its compact conformation, is impermeable to ions in a physiological range of voltages becoming permeable only at extremely high voltages (>500 mV) where one is able to force ions to cross the hydrophobic constriction (13,14).

The conformation obtained after symm2 is presented on Fig. 1 F as the final closed-state model. The resultant surface-to-surface diameter of the pore was 4 Å, 40% smaller than that in the crystal structure (6.6 Å). The backbone positions of the TM3a helices forming the gate deviated by 1.3 Å RMSD from the crystallographic coordinates. Fig. 4 shows, superimposed, the backbone of the TM3 helix in the crystal conformation (residues 94–127), and the same segment after our modeling and equilibration. For comparison, also shown is the backbone of the most tightly packed model of TM3a (residues 97–113) previously proposed by Edwards and coauthors (24). These representations illustrate that the deviations between the two models and the crystal coordinates are relatively small. The character of helical packing in the resting state is similar to that in the crystal structure, just slightly tighter. If this type of arrangement remains nearly-symmetrical, it is unlikely that the TM3 helices can be packed in a more compact conformation with the constriction completely occluded by the side chains of L105 and L109, consistent with the current hypothesis of Steinbacher and co-workers (17).

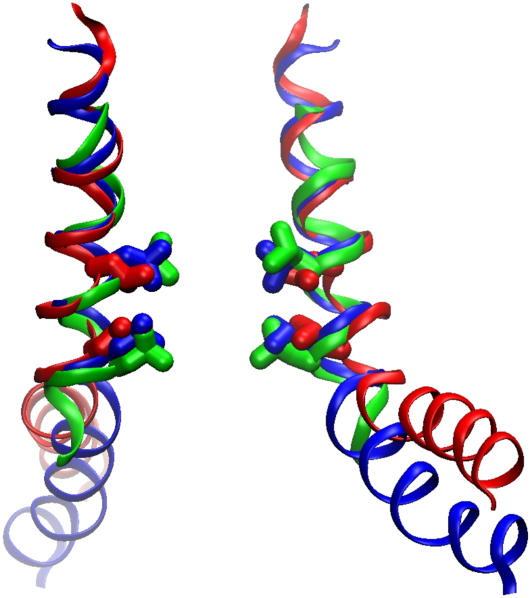
FIGURE 4.

Superimposed representations of the pore-forming helices shown by thin ribbons passing through the α-carbons. Only two opposing helices are shown to illustrate the width of the barrel. TM3 helices in the initial crystal conformation (PDB ID 1MXM) (red), the symmetrized final conformation after an 8 ns simulation (blue), and the most compact state of the TM3 barrel optimized through Monte Carlo simulations (green; depicted from the coordinates kindly provided by J. Bowie) (24). Residues L105 and L109 are shown in stick representation. Note that besides slightly tighter packing of TM3 helices, the major deviation of the modeled resting conformation (blue) from the crystal structure (red) is in the lowered position of the TM3b segment due to the alternative kink at G121 as opposed to G113 in the crystals.

As can be seen from Fig. 4, the main deviation of the TM3 helices of our equilibrated closed-state model from the crystal structure occurs in the most C-terminal TM3b segment. This difference directly reflects the straightened helix near G113 (where the crystal structure shows a characteristic bend) and the presence of the new kink near G121. As a result of alternative kink formation the TM3b segment has shifted down along the pore axis by ∼6 Å, which completely resolved its steric clashes with the TM1-TM2 loops (depicted in Fig. 1 B). This arrangement permitted the most compact alignment of the peripheral helices along the central TM3 shaft. One interesting observation was that after straightening of the G113 kink the Q112 residues of adjacent subunits formed a ring of hydrogen bonds, which apparently stabilize the resting-state packing of the TM3s.

Our simulations of the modeled resting conformation of MscS have revealed considerably higher stability of the TM3 barrel than previously reported for the unmodified crystal structure (13,14). In our assessment, the stabilizing factors appear to be:

1. The parallel packing of the peripheral TM1-TM2 helices bolstering their association with TM3a;

2. An alternate position for the TM3a-TM3b kink (near G121);

3. The new shifted position of the protein relative to lipid bilayer, which is anchored by the newly inserted polar N-termini and also brings the positive charges R46, R54, and R74 to the cytoplasmic surface of the bilayer;

4. An absence of packing conflicts with lipids; and

5. The high probability of the cooperative circular H-bonds within the ring of conserved Q112 residues, converging below the gate from all seven subunits.

Experimental testing of the compact resting conformation with disulfide cross links

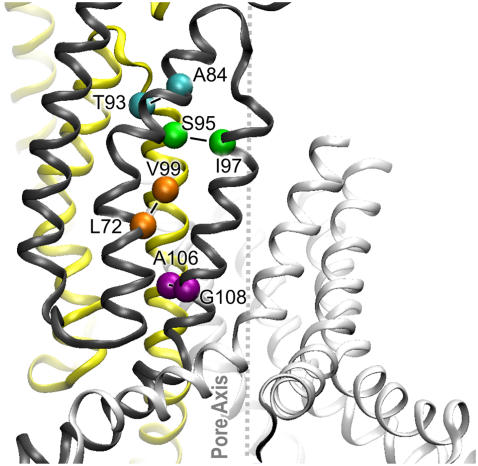
The contact zone between the TM1, TM2, and TM3 helices in two adjacent subunits after simulation is illustrated in Fig. 5. The denoted residues form interhelical contacts between TM2 and TM3 as well as intersubunit contacts of TM3. Residue L72, for instance, is in the proximity of both V99 of the neighboring subunit and G104 of the same subunit. In our model, the position of the backbone of the TM3a segment (residues 98–110) deviates from the original crystal conformation by ∼1.1 Å RMSD (Fig. 4). In this conformation, characteristic contacts between neighboring subunits were formed at the top of the barrel by the A84-T93, and S95-I97 pairs of residues, whereas in the gate region the A106-G108 pair was also observed to be in close proximity.

FIGURE 5.

Intersubunit contacts in the compact bilayer-equilibrated model of the MscS transmembrane domain in the closed state. Two adjacent subunits are shown in ribbon representation (yellow and black). TM1, TM2, and TM3 helices are in order from left to right. The α-carbons of critical residues are shown as spheres.

The distances between all of these pairs of residues in the crystal- and in the relaxed closed-state model are given in Table 1. Cysteines were inserted in corresponding positions, and cross-linking experiments were attempted in native membranes under oxidizing (0.03 mM iodine) or ambient atmospheric conditions. Western blot analysis (Figs. 6 and 7) shows that multimeric bands representing multiple cross links, including complete heptamers, appear with all proximal pairs of cysteines. Single cysteine controls presented also show that, under oxidizing conditions, cross links between equivalent cysteines on different subunits occur at appreciable rates, resulting in primarily dimeric bands and suggesting high flexibility of the complex. Negative controls probing MscS conformations with more distant TM2-TM3 and TM3-TM3 cysteine pairs, illustrating the rate of accidental cross-linking, are presented in the Supplementary Material (Fig. S2). Beyond dimers, relatively little cross-linking was seen in these controls; however, faint bands indicating tri- and even tetramerized protein were observed, suggesting a highly dynamic structure. Pretreatment of all mutant proteins by 10 mM DTT in the reaction buffer produced primarily monomeric bands (data not shown). Despite the appreciable levels of accidental cross-linking, proximal pairs, which were predicted from the model, revealed products of higher order.

TABLE 1.

Distances between the β-carbons of the key contact residues (Fig. 5) in the crystal structure and in the relaxed closed-state models (Å)

Structure	L72C-V99C	A106C-G108C	A84C-T93C	S95C-I97C
1MXM	12.5	2.9	6.0	6.4
2OAU	10.5	3.9	12.8	6.9
Closed model	6.6	2.7	11.5	6.3

The distances were determined after in silico substitutions of these pairs of residues with cysteines. IMXM and 2OAU are the original and revised versions of the crystal structure solved by Rees and co-workers (8,17). Note that, upon opening, the distances for the pairs A84C-T93C, V89C-V91C, and S95C-I97C are predicted to increase to 14.4, 9.8, and 16.2 Å, respectively.

FIGURE 6.

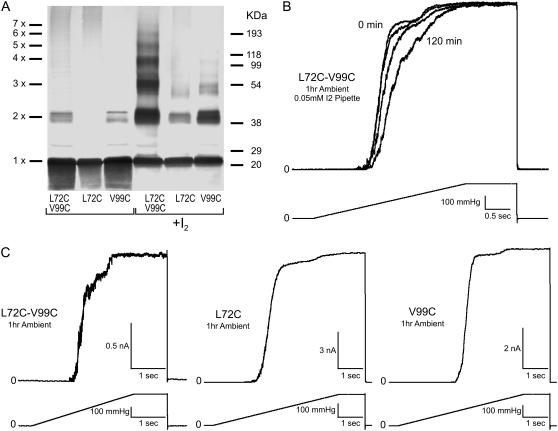
Effects of disulfide cross-link formation in L72C-V99C. Multimerization patterns and functional behavior of mutant channels in patch-clamp. This pair is predicted to link TM2 to TM3 of adjacent subunits. (A) Western blot indicating cross-linking products in the double cysteine mutant separated alongside the products generated in single cysteine controls L72C and V99C under ambient conditions (unmarked) or by adding 0.03 mM iodine (marked +I₂). (B) The effect of adding iodine (0.05 mM) from the patch pipette (periplasm) on the activity of the L72C-V99C mutant. Spheroplasts were preincubated under ambient conditions for 1 h. The data show a strong rightward shift of the activation curves upon exposure to I₂ signifying channel modification by disulfide formation. Current traces were normalized to the maximal observed current to emphasize the pressure shift (see text for details). (C) Activation of the double cysteine mutant and the single cysteine controls (L72C and V99C) by saturating pressure ramps under ambient conditions. Double mutant activation is heterogeneous, displaying at least two populations of channels. Activities of the controls are like WT in agreement with low disulfide formation under ambient conditions shown in Western analysis.

FIGURE 7.

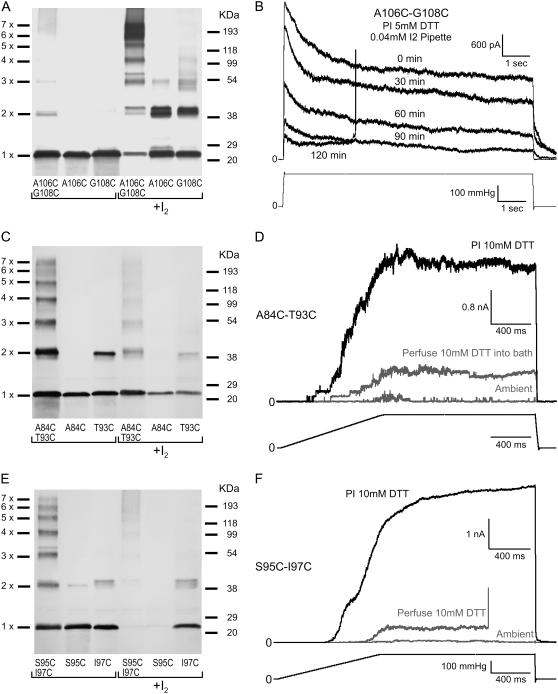
Disulfide cross links between adjacent TM3 helices and their inhibitory effects on channel gating. (A) Cross-linking patterns of A106C-G108C located in the gate region of the pore and corresponding single cysteine mutants. (B) Patch-clamp traces displaying a reduction of the A106C-G108C population current with gradual oxidation as 0.04 mM I₂ reaches the patch through a sucrose plug. (C) Cross-linking patterns of the A84C-T93C and (E) S95C-I97C mutants with their single cysteine controls. These pairs are located in the upper part of the transmembrane barrel and form disulfides spontaneously under ambient conditions. (D and F) Corresponding sets of patch-clamp traces show that under ambient conditions these mutant channels exhibit very low activity (shaded traces). Perfusion of 10 mM DTT into the bath restores a small fraction of activity (shaded), whereas preincubation of spheroplasts with 10 mM DTT for 1 h restores the population current (solid).

The multimerization patterns of the L72C-V99C mutant (Fig. 6 A) were reproduced in four independent membrane preparations, indicating that, in the resting state, TM2 helices are indeed positioned closer to TM3 than in the crystal structure (Table 1).

When tested in patch-clamp experiments under ambient conditions (Fig. 6, B and C), L72C-V99C activities were strongly heterogeneous compared to WT MscS (not shown) or to the single cysteine controls L72C or V99C (Fig. 6 C), displaying faster channel kinetics and at least two distinct populations. Preincubation of the mutant with 10 mM DTT made the activation curve more normal, but no length of incubation could entirely remove the multipopulation behaviors (data not shown). Exposure of L72C-V99C to an oxidizing environment of 0.05 mM I₂ from the pipette resulted in a pronounced shift of the activation curve toward the midpoint of the second population (Fig. 6 B). To emphasize this midpoint shift, currents evoked by the 3-s ramps to saturating pressure were normalized to the maximal observed current. A secondary effect of I₂ exposure was an increase in the rate of channel desensitization, which reduced the observed maximal current under the relatively slow 3-s ramp (data not shown). It was found that a quick pulse (10 ms) to saturating pressure was necessary to activate the full L72C-V99C population under oxidizing conditions, suggesting that the relative positions of TM2 and TM3 helices might shift in the course of opening and that this disulfide bridge somehow restrains the transition, but does not preclude it (data not shown). None of these effects of I₂ exposure on the L72C-V99C mutant channel occurred in WT MscS controls (Fig S3, Supplementary Material).

Other selected TM3-TM3 cysteine pairs exhibited much more efficient cross-linking than the TM2-TM3 pair. All identified pairs at the top of the barrel A84C-T93C and S95C-I97C cross-linked spontaneously under ambient atmospheric conditions, producing the entire spectrum of products from dimers through heptamers (Fig. 7, A, C, and E). The cross-link pair A106C-G108C located in the lower portion of the barrel (i.e., the gate region) produced a strong and thick heptameric band in the presence of 0.03 mM I₂ (Fig. 7 A).

Patch-clamp analysis of the S95C-I97C and A84C-T93C double mutants indicated that spontaneous TM3-TM3 cross-links result in little (∼5%) to no activity in spheroplasts under ambient oxidizing conditions (Fig. 7, D and F, shaded). Perfusion of buffer containing 10 mM DTT into the bath was found to partially restore channel activity (10–30% of normal channel population). Preincubation of spheroplasts with 10 mM DTT for 1 h was more effective in restoring the full activity of the mutant channel population (Fig. 7, D and F, solid). In agreement with the cross-linking pattern in Fig. 7 A, the A106C-G108C mutant was largely active under ambient conditions (data not shown). When the mutant was exposed to 0.04 mM I₂ from the pipette it was observed that the population activity declined, suggesting that this cross link restrains the opening transition (Fig. 7 B).

The successful formation of TM3-TM3 cross links spontaneously or under oxidation between our predicted cysteine pairs clearly indicates that the resting conformation of the TM3 helices in MscS is not far from that depicted in the crystal structure. The fact that these cross links, when formed, restrain channel opening, strongly suggests that the central TM3 shaft must expand from this resting conformation during the gating cycle.

DISCUSSION

Many of the crystal structures of membrane proteins available to date have been solved in detergents that completely replace lipids. The organizing role of lipids has been strongly suggested for transmembrane α-helical proteins (49,50) and therefore every structure obtained in pure detergent should be carefully scrutinized for possible distortions.

Additionally, the crystal conformations of proteins are typically found to be stable in all-atom MD simulations on a nanosecond timescale. The MscS channel, previously simulated with two different force fields (13,14) exhibited a remarkable instability of the pore-forming barrel when inserted into the lipid bilayer. The tapered conformation of the transmembrane domain, which apparently experiences stresses due to unusually packed lipids, did not compact but rather collapsed asymmetrically. To avoid the same outcome, in this study we chose a different strategy in our simulations by first transforming the crystal structure in vacuum, completing it with the missing N-terminus, and only then allowing it to relax in the explicit bilayer.

In pursuing a more compact resting conformation, we performed structural manipulations using targeted minimizations and the new iterative extrapolated-motion protocol. In this procedure, a small initial displacement of the atomic coordinates is adjusted by energy minimizations and short relaxing MD simulations. This new displacement with corrected magnitude and direction is then linearly extrapolated and the minimization-relaxation cycle is repeated. After a few cycles, the system forgets the arbitrary direction of the initial displacement and follows its own trajectory. A judiciously chosen amplification coefficient allowed us to vary the spatial limits of spontaneous transitions while preserving all elements of the secondary structure. Sequences of states created in ∼50 cycles of iterations predict smooth conformational pathways for expansion and compaction permitted by the protein itself. The estimated in-plane area changes and pore conductances in these sequences were compared with experimentally measured parameters, thus allowing us to identify candidate models for the resting and open-like states. These states were subsequently refined in all-atom simulations.

We found that, in the initial compaction of MscS, simply restoring the parallel packing of helices produced steric conflicts at the cytoplasmic side of the barrel and did not solve the problem of compatibility with the outer leaflet of the bilayer. Attachment of a de novo modeled N-terminal segment largely solved these problems by restoring the polar collar at the outer rim of the barrel, which provided support for TM1 helices and multiple sites for interactions with the polar lipid groups. Asparagine-scanning experiments by Yoshimura and co-workers (11) strongly suggested that MscS is sensitive to tension at both periplasmic and cytoplasmic interfacial regions and thus the channel should have comparable polar anchoring at both sides. The complete compact structure with the attached N-termini and a more parallel packing of the TM1-TM2 pairs of helices restored the appropriate hydrophobic matching between the protein surface and the lipid without substantial distortions of the bilayer structure (Fig. 2). Based on the new hydrophobicity profile of the lipid-facing surface (Fig. 2 B) and positions of aromatic residues, the location of the bilayer midplane was shifted 8 Å toward the periplasmic end of the protein compared to the position used in previous simulations (13,14). In this state, arginines 46, 54, and 74 no longer reside in the aliphatic core of the lipid bilayer, as was originally proposed (8), but face the layer of polar headgroups at the cytoplasmic side of the lipid bilayer. The new helical packing restored the physical contacts between the peripheral (tension-receiving) helices and the gate formed by TM3s, thus preparing the channel to respond to membrane tension.

The extrapolated expansion transitions suggested that opening of MscS is likely to be accompanied with complete straightening of TM3 helices, consistent with similar tendencies observed previously in conventional all-atom MD simulations (13,14). This tilted but kink-free conformation of the TM3 helices acts to define the spatial scale of expansion and reasonably satisfies both the experimentally observed conductance and in-plane expansion of the MscS protein (6,7). Repeated compaction transitions revealed alternative kink formation near G121. The presence and importance of kink formation at G121 is supported by its nearly absolute conservation within the family of MscS channels (alignment not shown) and with new experimental data (26). Kink formation at G121 allows for packing of the TM1-TM2 helices along TM3 that is unhindered by steric conflicts between the cytoplasmic TM1-TM2 loops and the TM3b segments. The relocation of the kink from G113 down to G121 was also observed to slightly extend the TM3 barrel to bring conserved Q112 residues together in a hydrogen-bonded ring. The data on mutants with altered flexibilities of the TM3 helix near G113 and/or G121, presented in a parallel publication (26), strongly support the model of the open state with straightened TM3s. The results also suggest that the original kink near G113 is a characteristic feature of the inactivated tension-insensitive state, whereas the alternative kink at G121 forms on channel closing.

The final resting-state structure with TM3s bent near G121 was found to be remarkably stable in extended all-atom MD simulations. In explicit water, the hydrophobic constriction of the channel remained largely dehydrated. The gate-keeping rings of leucines (L105 and L109) oscillated forming elliptic pores with an effective width of 5.4 ± 1.1 Å, slightly smaller than the pore size of an ideally symmetric helical assembly with densely packed helices. This multiplicity of closed states appears to be another stabilizing factor of purely entropic nature. Comparison shows that the TM3 assembly in our equilibrated and symmetrized model of the resting state has a diameter that is an intermediate between the crystal structure and the tightest TM3a bundle optimized by Monte Carlo (24) (Fig. 4). The differences between the three structures, however, are not large and it would be fair to conclude that the TM3a segments in the crystal structure are indeed packed in a near-optimal conformation, consistent with its low B-factor.

The proximities of residues predicted from the model (Fig. 5 and Table 1) suggested disulfide cross links that have been detected in both biochemical and patch-clamp experiments (Figs. 6 and 7). They clearly illustrate that the TM2 and TM3 helices are more proximal in the native resting state than in the crystal structure (Fig. 6). An interesting observation was that the probabilities of the disulfide bond formation with the TM2-TM3 pair (L72C-V99C) were somewhat lower than for the TM3-TM3 pairs, suggesting a more dynamic nature of TM2-TM3 association (Figs. 6 and 7). Spontaneous cross links between the pore-lining TM3 helices of adjacent subunits (Fig. 7) support the idea that in the resting state these helices are in crystal-like positions. Patch-clamp experiments performed under oxidizing or reducing conditions showed that the TM3-TM3 disulfide bridges stabilize the barrel in its nonconductive state, but when reduced, they permit opening. These results strongly suggested, contrary to the initial interpretation (8), that the crystal-like positions of the TM3s cannot represent a conductive state and the helices must move apart to permit conduction. The model illustrated in Fig. 1 D represents our current hypothesis for the conformation of the open MscS channel. The simulated conductive properties of this model correspond well to experimental data, which will be described in detail in a separate publication (unpublished).

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.