Propagation of Mechanical Stress through the Actin Cytoskeleton toward Focal Adhesions: Model and Experiment

Abstract

We investigate both theoretically and experimentally how stress is propagated through the actin cytoskeleton of adherent cells and consequentially distributed at sites of focal adhesions (FAs). The actin cytoskeleton is modeled as a two-dimensional cable network with different lattice geometries. Both prestrain, resulting from actomyosin contractility, and central application of external force, lead to finite forces at the FAs that are largely independent of the lattice geometry, but strongly depend on the exact spatial distribution of the FAs. The simulation results compare favorably with experiments with adherent fibroblasts onto which lateral force is exerted using a microfabricated pillar. For elliptical cells, central application of external force along the long axis leads to two large stress regions located obliquely opposite to the pulling direction. For elliptical cells pulled along the short axis as well as for circular cells, there is only one region of large stress opposite to the direction of pull. If in the computer simulations FAs are allowed to rupture under force for elliptically elongated and circular cell shapes, then morphologies arise which are typical for migrating fibroblasts and keratocytes, respectively. The same effect can be obtained also by internally generated force, suggesting a mechanism by which cells can control their migration morphologies.

INTRODUCTION

Mechanical tension plays a crucial role for the control of cell shape and function, including cell growth and division, migration, differentiation, and apoptosis (1–6). Mechanical tension is also an essential element in the development and maintenance of tissue. For example, tissue cells adapt their mechanical activity as to maintain a constant tension in the tissue (tensional homeostasis) (7), and the spatial distribution of tension in a cell layer has been shown to determine the regions where cells grow and divide (8). A large body of evidence suggests that the shape of adherent tissue cells and their response to internally and externally generated force is closely related to the organization of their actin cytoskeleton (CSK) and its transmembrane linkages to the extracellular matrix, the focal adhesions (FAs) (9–12). Adherent tissue cells are contractile, and it has been found that force and size of single mature FAs, on average, show a linear relation with a stress constant of 5.5 nN/μm² (13,14). External load can be applied to cells in many different ways, including micromanipulators, atomic force microscopy, adherent beads pulled with magnetic or optical tweezers, and magnetic beads twisted with magnetic fields (15). Several studies have shown that application of external stress to FAs leads to their reinforcement by recruitment of additional proteins into the adhesion contact (16–18).

Although force-sensitive growth of FAs is an essential part of the mechanosensitive response of tissue cells, the transduction of mechanical stress toward the FAs is an equally important aspect of this system (16,19,20). In this article, we present a modeling framework which allows us to study the propagation of mechanical stress through the actin CSK toward FAs as a function of different micromechanical determinants of the underlying CSK network, including topology, filament stiffness, and prestrain. Our modeling approach is complemented by experiments in which adherent fibroblasts are externally strained by contacting them with a microfabricated pillar. As the pillar is shifted to the side, additional stress is propagated through the CSK toward the FAs, which adapt to the changed loading by changing their sizes.

Following earlier approaches to provide a simple model for stress propagation inside an adherent cell (21,22), the CSK of a strongly adherent tissue cell is modeled as a two-dimensional network of elastic cables. Networks of elastic springs or equivalent models have been used before to model the elastic properties of red blood cells (23–26). The cable network incorporates the special feature that filaments buckle under compressive load. It has been applied before to discuss experimental results for cell poking, magnetic twisting cytometry, and magnetic bead microrheometry experiments (22). Although the cable network is far from representing the complexity of polymer network mechanics inherent in the actin CSK (27–29), it incorporates some of its essential features. Here we extend this model to describe the effect of external force being applied to a cell which adheres through many adhesion points distributed along its rim. In our study, we used two regular topologies of prestressed cable networks, namely two-dimensional lattices of regular triangles and reinforced squares, respectively. We also implemented a random network topology. The geometric parameters and cable elastic properties were assigned based on data from the literature. The models were homogeneously prestressed to mimic that adherent cells are prestressed by actomyosin contractility.

Our computer simulations showed that the forces which then develop at the FAs depend only weakly on the exact details of the network model, but strongly on the spatial distributions of adhesions. We therefore combined our modeling with experimental data for fibroblasts adhering to a glass substrate through FAs marked by fluorescence markers. Positions and sizes of the FAs were extracted with image analysis software using a threshold-based segmentation algorithm and converted into a computer model for a cable network adhering exactly at these positions. Because experimentally measured sizes can be taken as a measure for the forces acting at single FAs, we then compared FA-size to calculated forces. Indeed a good correlation was found between predicted forces and measured sizes.

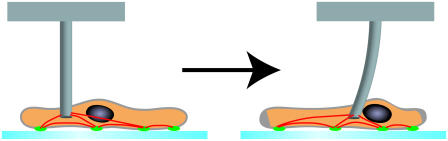
We next used a microfabricated flexible pillar to apply external stress to the adherent cell. The experimental setup is shown schematically in Fig. 1. First, the pillar was approached from the top and contacted for a certain waiting period to allow the establishment of contact. It was then shifted laterally, resulting in an altered stress distribution inside the cell. FAs were then allowed to adjust to the new loading situation and the new FA-sizes were extracted. In the computer simulations, this experiment was modeled by selecting a circular region inside the cell and shifting it to the side. Again, we found reasonable agreement regarding the global distribution of force. If in the computer simulations FAs under large force are allowed to rupture, we obtain different morphologies characteristic for migrating cells, depending on the initial cell shape. This suggests a mechanism by which adherent cells can convert anisotropic intracellular forces into polarized cell morphologies.

FIGURE 1.

Schematic representation of the experiment. The cell is first allowed to spread for at least 30 min. Then a microfabricated pillar is contacted from above and kept there for ∼15 min to ensure stable adhesion between pillar and cell. Culture conditions are chosen such that the actin cytoskeleton (red) is in a homogeneous state (no stress fibers). When the pillar is shifted to the side, the cytoskeleton is strained and the FAs adapt their size to the new loading situation. Typically, this takes 15 min. In the stationary state, the sizes of the focal adhesions (green) are expected to be proportional to the forces transmitted through the cytoskeleton.

EXPERIMENTS

Cell culture and transfection

Rat Embryonic Fibroblast cells (gift from B. Geiger, Weizmann Institute, Rehovot, Israel) stably transfected with YFP paxillin were cultured in Dulbecco's Modified Eagle Medium (Invitrogen, Karlsruhe, Germany) supplemented with 10% fetal bovine serum (Invitrogen) and 1% L-glutamine (Invitrogen) at 37°C in a humidified, 10% CO₂ environment. For some experiments, REF wild-type cells were plated to 80% confluency in six-well-plates and transiently cotransfected with CFP-actin and YPF-zyxin (both provided by B. Geiger, Weizmann Institute) using Lipofectamine (Invitrogen). One microgram of each DNA was used per well, and the serumless transfection medium was replaced with serum-containing Dulbecco's Modified Eagle Medium after 3 h. The cells were used for experiments between 20 and 48 h later.

All measurements were performed in an incubator mounted on an inverted microscope maintained at 36.6°C and 5% CO₂. Before measurements, REF cells were seeded into 60 mm glass bottom petri dishes filled with F-12 + Glutamax medium (Invitrogen) supplemented with 2% fetal bovine serum and 1% Penicillin-Streptomycin solution (Invitrogen) and allowed to spread for at least 30 min so they were able to establish small focal adhesion clusters. The glass bottom was not functionalized at all to slow down cell spreading and adhesion and thus enhance affinity of the cells to the fibronectin-coated micropillars that were to be placed on their dorsal side.

Fabrication and mounting of PDMS micropillars

Prepolymer of poly(dimethylsiloxane) (PDMS; Sylgard 184; Dow-Corning, Midland, MI) was poured over an array of holes in SU-8 (Microchem, Newton, MA) made on silicon wafers via standard photolithography (14,30,31) and cured at 65°C overnight. This resulted in arrays of elastic PDMS micropillars of 5 μm diameter, a height of 11 μm, and a distance of 50 μm. Before experiments, these were treated with Hydrogen plasma (10 s, 0.4 mbar, 150 W in model No. 100-E Plasma etcher; TePla, Corona, CA) and subsequently immersed in 20 μg/ml fibronectin (from bovine plasma; Invitrogen) for 30 min. During the process of molding, they were attached to thin glass plates (0.14 mm × 1 mm × 20 mm). These glass plates were now used to mount the pillars to a micromanipulator. The micromanipulator is connected to an inverted microscope and consists of three micrometer screws, one of them equipped with a piezo unit to allow very fine positioning in z-direction.

Micromanipulation

For experiments, approximately round cells with focal adhesions between 1 μm and 3 μm in size were selected. Round cells can be either circular or elliptical. The roundness selection was done to simplify modeling and understanding of the shearing process. Furthermore, round cells tend to have a less polarized cytoskeleton, thus matching better to the model presented here. Using the z-piezo, a fibronectin-coated micropillar was carefully lowered onto the dorsal side of the cell halfway between its outer edge and its nucleus. It was left at this position for 14–18 min so the cell was able to connect to it and then moved across the cell using a micrometer screw. This way, the cell was sheared and the intracellular stress of the cytoskeleton was redistributed. After approximately another 15 min, the CSK and the FAs have adapted to the new loading situation and a stationary state is reached.

Microscopy and image analysis

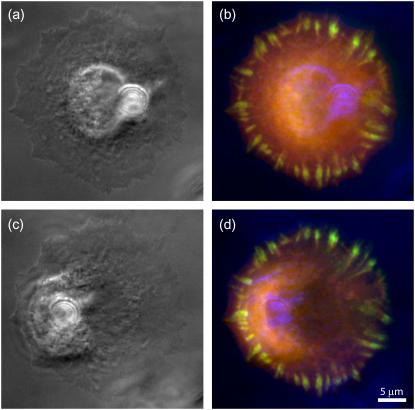
Cells were observed both in phase contrast and fluorescence microscopy through an inverted microscope (Axiovert 100; Zeiss, Oberkochen, Germany) equipped with a halogen and a 100 W mercury vapor lamp (HBO 100; Osram, Munich, Germany) and an environmental chamber. Images were taken through a 63× objective (Plan-Apochromat 63×/1,4 Oil Ph3; Zeiss) and recorded with a digital charge-coupled device camera (ORCA-ER 12-AG; Hamamatsu Photonics, Herrsching am Ammersee, Germany). Typically, one frame was recorded per minute. Fluorescence images were preprocessed in ImageJ (registration and bleach correction). Threshold-based segmentation and evaluation of the focal adhesion areas was performed in MatLab (The MathWorks, Natick, MA). In Fig. 2, we show typical phase contrast and fluorescence images for an experiment on a circular cell right before and right after pulling with the microfabricated pillar. One clearly can see the cellular deformations caused by the pillar shift.

FIGURE 2.

Use of microfabricated pillar. (a and c) Phase contrast showing cell and pillar shortly before and shortly after pulling. (b and d) Same images (now in blue) overlaid with fluorescence data. REF cells are transiently transfected with CFP-actin (red) and YFP-zyxin (green). (c and d) Shortly after pulling, one can discern the large deformations caused by shifting the pillar. However, the focal adhesions had no time yet to adjust their size to the changed loading situation. The images also show that there are no stress fibers present.

MODELING

Network definition

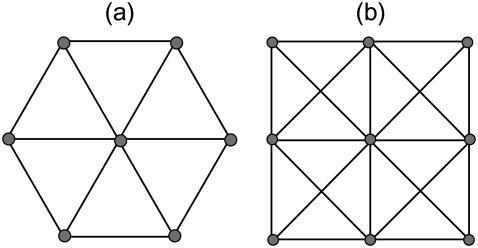
We model the actin CSK as a two-dimensional network of elastic cables (32). The joining points of the cables are called nodes. Two regular geometries of the CSK are considered (see Fig. 3): networks composed of regular triangular lattice and reinforced square lattice, where in the latter case, both nearest and next-nearest-neighbor nodes are directly connected via cables. In the reinforced network, the diagonal cables have no entanglement, i.e., they can pass each other freely. There are six and eight cables going out of a node in the first and second cases, respectively.

FIGURE 3.

Computational network models. (a) A triangular network and (b) a reinforced square network. Each link between two neighboring nodes represents a cable. In the unit cell of the reinforced network, the diagonal cables have no entanglement (no node present).

In the cable model, the force acting on a node due to the deformation of a link to length l reads (22)

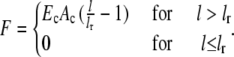(1)

Here E_c is the cable's Young modulus, A_c is its cross-sectional area, and l_r is its resting length. For extension (l > l_r), the cable thus acts like a linear spring, while for compression (l < l_r), it does not show any mechanical resistance.

In the actin cytoskeleton, there is considerable variability of the actin fibers present. The most elementary fiber is a single actin filament with E_c = 2.8 GPa and A_c = 18.8 nm² (22). The largest kind of actin fiber is a stress fiber, which is a bundle of actin filaments which often occurs in mature cell adhesion to a flat and rigid substrate. In this case, E_c = 1.45 MPa and A_c = 314 nm² have been measured experimentally for a typical stress fiber (33). The reduced value for the Young modulus E_c indicates that in a stress fiber, elasticity is determined by the cross linkers (mainly α-actinin), rather than by the actin filaments. Surprisingly, both the case of single filaments and stress fibers give a similar value for the quantity E_cA_c, namely 52.64 nN and 45.7 nN, respectively. In this study, we will consider the CSK to be in a homogeneous state without stress fibers. For our simulations, we will use the value for the actin filaments, because this allows for comparison with Coughlin and Stamenovic (22). Yet it is important to note that in our cable network, links are not meant to represent single actin filaments, but an average fiber in the CSK. As implied by Eq. 1, the actual force transmitted through such a fiber will be somehow less than E_cA_c, because strain ε = |l/l_r − 1| will be less than unity. For example, strain in stress fibers has been found to be of the order of 0.2 (33, 34) and we expect similar, but somehow reduced values for the isotropic CSK studied here. Thus the choice E_cA_c = 52.64 nN agrees with the experimental finding that the typical force at micron-sized FAs is of the order of F₀ ≈ 5.5 nN (13,14).

Before application of external force, the FAs already experience force from actomyosin-generated prestrain in the CSK. In our model, this corresponds to a resting length l_r, which is smaller than the initial fiber length l₀. In the model detailed below, one FA will, on average, carry the load from one network fiber. Thus we can estimate l_r as a function of l₀ by using E_cA_c = 52.64 nN and F₀ ≈ 5.5 nN in Eq. 1. This results in

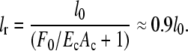(2)

Thus, strain ε = |l/l_r − 1| ≈ 0.1 and the average force per FA ≈ 5.5 nN.

Elastic moduli of the network

Although our model is not expected to behave like a linear isotropic material, to characterize its effective mechanical properties we will make use of the concepts of an effective Poisson ratio σ and an effective two-dimensional Young modulus E_2D, as it is widely done in both modeling and experiments. In a simple square network, the two principal directions decouple and the Poisson ratio vanishes (32). In contrast, in our reinforced square network, the ground-state degeneracy of the square lattice is removed and the Poisson ratio becomes finite. In contrast to the square networks, the triangular network is isotropic due to its sixfold symmetry (32,35,36) (compare Fig. 3).

To determine the elastic properties of the overall network, we follow the procedure from the literature (23,37). In detail, we select a small test region in the middle of a finite sample. Two opposite sides of the sample are clamped and the other two sides are free to move. A deformation of the model network is defined by horizontally stretching one of the clamped edges. In such networks, an elongation along the horizontal causes a contraction along the transverse direction. If ε_x and ε_y are the induced strains along the principal horizontal and transverse directions, the corresponding effective Poisson ratio σ is given by

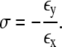(3)

To determine the effective two-dimensional Young modulus E_2D of the network, we calculate the total horizontal force F_x at the nodes located on the edges of length L_y. The two-dimensional Young modulus then follows as

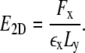(4)

Because our model is parameterized in terms of force, we have to specify values for length to calculate values for the Young modulus. Here we will use l₀ = 100 nm for the typical size between nodes. This value agrees well both with the experimentally observed mesh size in the CSK and with the spatial dimensions of our computer model for cells as shown below.

Evaluating the elastic moduli, several issues may arise due to the discrete nature of the network, e.g., number of nodes in the sample as well as in the test region, size, and position of the network boundary and the degree of deformation. Therefore, rather than working on a single network of fixed dimension, it is more realistic to compute mean values of elastic moduli from a set of networks of variable size.

Fitting experimental data into the model

After extracting the adhesion point coordinates from the experimental data by image processing, they are suitably rescaled to fit into the network model. Because our model assumes pointlike adhesions, the threshold for segmentation has been used in such a way that all FAs obtained are of compact shape—that is, FAs with irregular shapes are split into two neighboring FAs. To make sure that our results are not affected by the network symmetries, the average distance between the adhesion points is taken large compared to the lattice constant. We carried out the simulation on both reinforced square and triangular networks. Keeping the number of adhesion points (≈60) fixed, the system size and the scaling ratios are varied to achieve comparable number of nodes (≈4000) in both cases. Typically, this corresponds to 85 and 90 nodes in the linear dimension for reinforced square and triangular networks, respectively.

Our simulations allow us to derive forces at the single adhesions, while from the experiments, we extract the areas of the single adhesions by image processing. Because it has been shown before that in average, these two quantities show a linear correlation (13,14), here we compare them directly with each other. To quantify the difference between theoretical and experimental results, we define the following root mean-square deviation (RMSD):

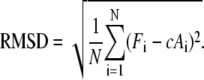(5)

For the data set analyzed below, RMSD is minimal for a conversion factor c = 3.3 nN/μm², which then was used for all other data sets.

Simulation

Since the adhesion points are attached to the substrate, they are immobile and marked to differ from the rest inside the cell which can move freely. After constructing the simulation system, resting length of the cables are reduced step by step until the desired prestress is achieved in the cellular system. Once we have measured the necessary quantities of the prestressed cell, a circular region at the center of the cell is selected. This mimics the contact area of a micropillar placed from above onto the cell. All nodes and cables under the circular face of the pillar are glued to it and move along with the pillar. However, nodes and cables which are outside the periphery of the pillar but directly connected to the nodes under the pillar can move when force is applied to them. In our simulation, the pillar is moved step by step up to 5l₀. During the simulation, equilibrium is established by iteratively solving the equilibrium equation for every node until all of them are simultaneously satisfied. The iterations are terminated once the maximum force on every node becomes smaller than 10⁻⁵ nN. To avoid collapse of the network in regions which are compressed, we introduce a critical length l_c = 0.1l_r, below which nodes are treated as repulsive. This means that if two nodes come closer to each other than the length l_c, they are glued such that they behave like a single node under any compressive load along their joining axis.

Rupture of adhesion points

We also considered a rule to rupture FAs if force rises beyond a certain threshold. Simple models for adhesion cluster stability suggest that there exist a threshold in force F_c beyond which adhesion clusters rupture (38,39). Here we use a rupture threshold of F_c = 6 nN, which is slightly larger than the average force in our parameterization. This value also corresponds well to the order-of-magnitude estimate F_c = T₀w/N = 12 nN which one can derive from the measured peeling tension T₀ = 6 nN/μm for adhering cells (where cell width w = 20 μm and number of adhesions N = 10) (40). As an FA in a high stress region ruptures, force is redistributed onto the remaining ones. Usually this leads to more rupturing events, thus resulting in a rupturing avalanche, as has been investigated in great detail before for material failure under load, for example in the framework of the fiber bundle model (41,42). This avalanche will continue until all the forces on the remaining FAs go below the threshold; otherwise, the whole cell will detach.

As the adhesions rupture, those parts of the network which are no longer sufficiently pinned tend to collapse. The cable network used in this work is a central force network without steric contributions and thus, in general, is prone to collapse (36). In a real CSK, water can flow out of the network only to a certain extent as it is strongly bound to the network due to electrostatic effects. Moreover, other cytoplasmic material and the spatial extension of the network itself will prevent complete collapse. As explained above, in our model this is avoided by an infinite potential below a certain distance between the nodes.

RESULTS

Mechanical properties of the network

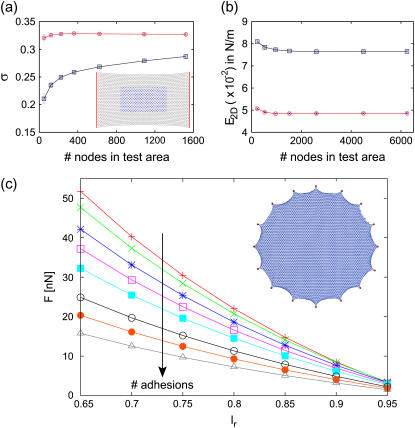
We first characterized the overall mechanical properties of the two regular networks considered in the modeling approach. For both the triangular and reinforced square lattice, we obtained a similar behavior of the Poisson ratio σ and the two-dimensional Young modulus E_2D as a function of the number of nodes in the sample. The strain for each sample is varied from 0.1 to 1. The measured values of the moduli are then averaged as described above. Such measurements are carried out by varying sample nodes from 225 to 4489 and the corresponding number of nodes in the test region from 49 to 1089. We found only a slight difference between measuring the elastic constants on the test region or on the whole sample, thus in the following we report the results from the test region. The results for the triangular network are shown in Fig. 4, a and b (the corresponding results for the reinforced square network are shown as Supplementary Material Fig. 1). For both network topologies, σ first increases while E_2D decreases for small system sizes and finally they saturate for the large systems which we consider for our cellular network. Without prestrain, the average value of σ = 0.328 ± 0.001 and E_2D = 4.87 ± 0.01 × 10⁻² N/m for the triangular lattice. The same quantities for the reinforced square network are σ = 0.73 ± 0.02 and E_2D = 6.7 ± 0.1 × 10⁻² N/m. Prestrain has a marked influence on these values. We set a prestrain in the system by setting l_r = 0.9l₀. Using a similar method to that just described, the average elastic moduli obtained for the triangular network are σ = 0.26 ± 0.02, E_2D = 7.6 ± 0.2 × 10⁻² N/m and for the reinforced square network are σ = 0.4 ± 0.01, E_2D = 8.9 ± 0.1 × 10⁻² N/m.

FIGURE 4.

Mechanical properties of the cable network. (a) Effective Poisson ratio σ and (b) effective two-dimensional Young modulus E_2D for the triangular network as a function of the number of nodes in the test region. In both cases, red and blue curves are for networks without and with prestrain, respectively. (c) Forces at adhesion sites as a function of the resting length l_r, which determines the level of prestress in the network. Different curves correspond to different number of adhesions along a circular contour (8,12, 16, 20, 25, 35, 45, and 60 from top to bottom).

Our values for the two-dimensional Young modulus of ∼10⁻² N/m are in reasonable agreement with experimental results measured for the actin cortex of eukaryotic cells (32). Interestingly, our model predicts that prestrain increases the effective Young module of the CSK (approximately by a factor of 2), but decreases the effective Poisson ratio, thus making the cell effectively more compressible. These effects of prestrain have been found before for a triangular network of elastic springs (32) (for the square network of elastic springs, different effects have been found, but here we use a reinforced square network, which makes it more similar to the triangular case). The agreement between these earlier results for elastic networks and our results for the cable networks might follow from the fact that here we test the cable network mainly for small and tensile strain. The stiffening effect by prestrain has recently been also observed for an in vitro system of actin, myosin, and cross-linkers (43). Increase in effective stiffness due to contractile activity has been discussed before also in the context of effective stiffening of the extracellular environment by cellular contractility (44). The increase of the Young modulus by prestress implies that different culture conditions will significantly change the effective Young modulus through different regulation of contractility.

Contractility of the CSK, which in our model is determined by the resting length l_r, is directly linked to the forces at FAs. To study this relation in a systematic way, we arranged different numbers of FAs around a circular contour and simulated the resulting forces at the FAs as a function of l_r. The results are shown in Fig. 4 c and demonstrate that for a fixed number of contacts, forces at FAs grow with decreasing l_r. Moreover, the force per FA decreases as the number of contacts increases. These results also confirm that l_r = 0.9 is the appropriate choice for the desired force level of 5.5 nN. The corresponding cell shape is shown as an inset in Fig. 4 c.

Prestressed cell: before pulling

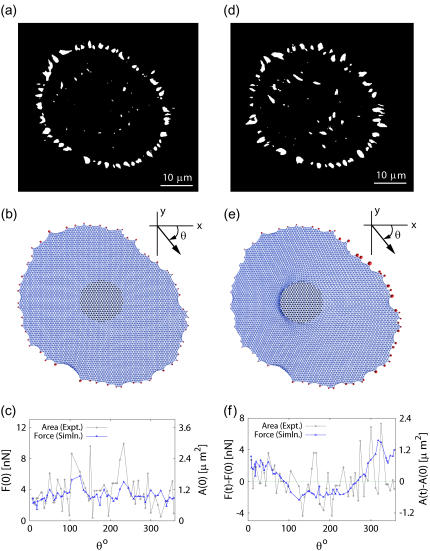
We next considered the prestrained state of our cell model for a configuration extracted from experimental data (the same analysis for two more cell experiments is given in the Supplementary Material). Although we consider both triangular and square networks, in the following all snapshots representing cells are shown for the triangular network only. The desired force levels at the FAs (≈5.5 nN) are obtained by slowly decreasing the resting length l_r of each cable from 1 down to 0.9. In Fig. 5 a we show the experimental image of the FAs of a spread and thus prestressed cell. In Fig. 5 b, we show the corresponding computer simulation with the same adhesion geometry and a triangular lattice. There are 60 adhesion points at the boundary, shown by red circles. The area of the circles corresponds to the force in it. In Fig. 5 c, force distributions over the FAs are plotted as a function of the angle θ measured in the clockwise direction from the axis. At the same time, we plot the areas of the FAs as extracted by image processing. The overall agreement is rather good, suggesting that our model captures the essential aspects of force propagation in the actin CSK of the prestressed cell. The RMSD = 1.89 nN is well below the overall force level and typically is determined by a few regions along the periphery where agreement between model and experiment are somehow perturbed. By combining the results from computer simulations and image processing, we find that the average force per area is 3.8 nN/μm², in good agreement with earlier experimental results (13,14) and thus validating our parameterization. A detailed analysis further shows that a correlation exists between the force at a single FA and the average distance to its two neighbors: the larger this distance, the larger the force on the FA. This is most evident at the two peak values at θ ≈ 120° and θ ≈ 230°, which are present both in the numerical and the experimental data and correspond to spatially isolated FAs. This suggests that the local adhesion geometry is the main determinant of forces at FAs.

FIGURE 5.

Comparison of experiment and model predictions for one set of data. (a and b) Experimental and simulation snapshots of the prestressed cell before pulling, respectively. (c) To compare experiment and simulation, we assume that the size of the experimentally measured FA area is proportional to the pulling force on it. The blue line represents the forces at the adhesions predicted by the computer simulations and the gray line represents the experimentally measured areas of the contacts (RMSD = 1.89 nN). (d–f) Same data but 30 min after the pillar has been laterally shifted to the left. In panel f, the differences in forces and areas are shown relative to the situation before pulling (RMSD = 2.51 nN).

Prestressed cell: after pulling

After we have made the necessary computational measurements on the prestressed cell, a circular region is selected in the cell center and shifted laterally toward the left. The magnitude of the final shift is five lattice spacings, obtained in small steps. Fig. 5, d and e, shows the snapshots from our experiment and simulations, respectively. One sees that both FA areas in the experiment and FA force in the simulations decrease in the direction of pull and increase in the opposite region. There are two reasons for the decrease in the direction of pull: 1), prestrain in the CSK is released; and 2), the cable network does not propagate compression. In contrast, in the direction against the pull, prestrain and additional tension conspire to give high levels of force, leading to proportional growth of adhesions. Although the exact location of the initial pillar position might differ in detail, the simulation results shown here are valid as long as the shifted region is selected in the central region of the cell. A considerable change in the measured forces only occurs when the pillar is attached outside the central region and close to a particular set of FAs. In Fig. 5 f we plot the changes in force and area as a function of the angle θ measured in the clockwise direction (RMSD = 2.51 nN). Both experiment and model show similar changes occurring after the pillar shift. In particular, in both data sets, stress seems to occur mainly in opposite and oblique directions to the pulling direction.

We next investigated the distribution of strain over the whole CSK (compare Supplementary Material Fig. 2). Close to the cell boundary, there are many small domains with varying strains, which reflect the local inhomogeneity very specific to the region. Away from the boundary, the rest of the cell is quite homogeneous, represented by the large domain with a strain level. After pulling, the strain distribution, which was homogeneous before the pillar was shifted, looks completely heterogeneous and composed of many long strips mostly extended from the center of the cell to the periphery. The back of the pulling direction is much more stretched than the front. There is a large population of strips along the oblique periphery, suggesting the presence of large stress in this region.

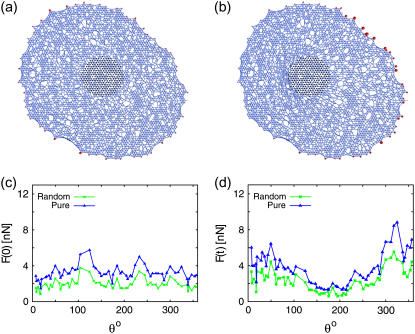
We also investigated how the FA forces are modified when the CSK is constructed out of a disordered lattice. Starting with a regular triangular lattice, a bond (cable between two neighboring nodes) is removed randomly with a probability 1 − p. This process leads to the formation of a inhomogeneous CSK network (see Fig. 6). The distinguishing feature of such an bond-diluted network is the existence of a percolation threshold p_c = 0.5 (45). For p = 1, the system is pure and we choose p = 0.8 (>p_c) for this particular study. Using the same technique as discussed before, we obtained the FA forces before and after the cell is perturbed with the pillar. Comparing with the pure case, we found them in nice qualitative agreement. In the bond-diluted network, the forces are somehow decreased, because the effective spring constant is decreased in a strain-controlled situation. In summary, we found that small variations of the CSK structure at the microscopic level has little influence on the macroscopic FA forces.

FIGURE 6.

Random CSK network on a triangular network for the adhesion geometry from Fig. 5 obtained after bond dilution with bond occupancy p = 0.8. Snapshots showing (a) prestressed CSK and (b) when it is laterally shifted with the pillar. (c) Forces at FAs of the prestressed cell, obtained on a random, and on a pure triangular, CSK network. (d) Same kind of data obtained after the CSK is shifted with the pillar.

Morphologies resulting from FA rupture

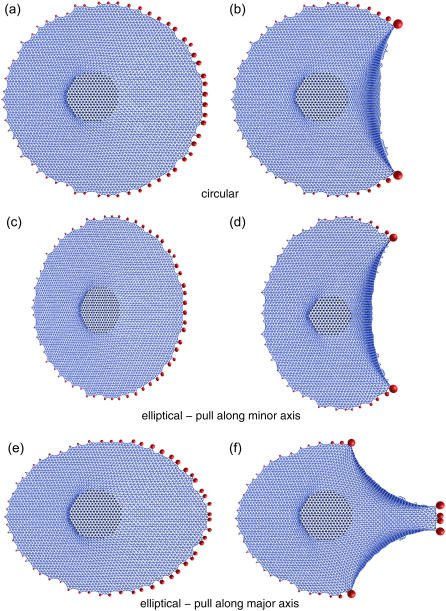
We next addressed the question to which extent the initial shape of a cell determines the distribution of force over the FAs. To answer this question, we simulated cells of two well-defined global geometries, namely circular and elliptical, formed by a triangular mesh and attached to a rigid surface through their FAs (≈60). As we have discussed before, a reduction in the resting length of mesh cables gives rise to a contractility all over the CSK and forces at the FAs. After achieving the desired level of force at the FAs, a circular region is defined in the cell center and shifted to the left (by ≈5 l₀). For the circular cell we observe the maximum stress developed at the FAs exactly opposite to the direction of the pillar shift (see Fig. 7 a). The same is found for an elliptical cell pulled along the short axis (see Fig. 7 c). However, for an elliptical cell pulled along the long axis, the same mechanism generates the maximum stress obliquely opposite to the direction of pull (see Fig. 7 e).

FIGURE 7.

Sequential detachment of FAs opposite to the pulling direction leads to different morphology depending on the initial cell geometry. Each geometry is shown without (a, c, and e) and with rupture (b, d, and f). For initially circular (a and b) or elliptical cells pulled along the minor (short) axis (c and d), a morphology arises which is typical for migrating keratocytes. For initially elliptical cells pulled along the major (long) axis (e and f), we get a morphology that is typical for migrating fibroblasts.

To further evaluate the difference between these two situations, we next implemented a rupture scenario for FAs under force, as described in the Modeling section. We found that rupture of FAs for circular and elliptical cells can lead to two different morphologies which are both well known from studies of cell migration (46). The circular cell takes the shape of a half-moon, which is commonly observed in keratocyte migration (see Fig. 7 b). The same morphology is found for the elliptical cell pulled along the minor (short) axis (see Fig. 7 d). On the other hand, the initially elliptical cell pulled along the major (long) axis forms a long tail at the back, like a fibroblast in motion (see Fig. 7 f). Note that in the computer model, the rupture cascade continues until more or less complete rupture is achieved; in practice, after initial rupture, cells will strengthen their contacts under force and stabilize these morphologies.

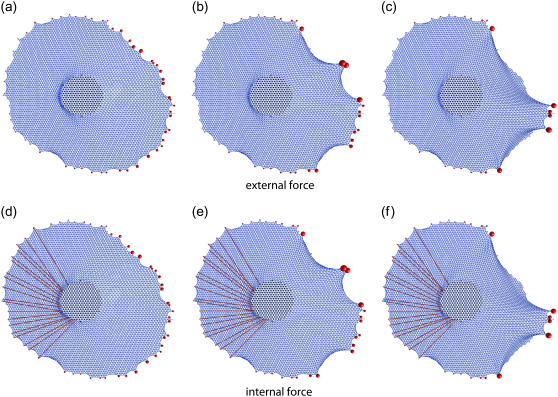
Next, we considered the rupture scenario for the experimental adhesion geometry of the cell shown in Fig. 5. Again FAs are allowed to detach with a force exceeding a threshold F_c = 6 nN. Because this is an elliptical cell, application of external force along the long axis leads to the morphology typical for a migrating fibroblast, as shown in Fig. 8, a–c. In practice, cells are autonomous and do not rely on transfer of external momentum to change into a migration morphology. Instead, this has to be achieved by internally generated force. In particular, in mechanical equilibrium the sum of all forces at the FAs has to be zero. In Fig. 8, d–f, we demonstrate that exactly the same cell shape can be obtained by distributing contractile cables (thick red lines) between the cell boundary at the left and the central regions. These cables should be understood as theoretical representation of actomyosin contractility which is spatially concentrated at the central region and spatially distributed at the left cell boundary, thus avoiding adhesion rupture at the cell front. This mechanical situation could be achieved by the cell by means of regulating the actomyosin system and would indeed ensure complete mechanical equilibrium with no external momentum transfer. This suggests that adhering cells can switch their isotropic morphology into a polarized morphology required for migration by anisotropic generation of internal forces.

FIGURE 8.

Effect of external versus internal force for the experimental adhesion geometry from Fig. 5. (a–c) External force with a threshold value for detachment of F_c = 6 nN. Because the cell is elliptically elongated, a morphology arises which is typical for a migrating fibroblast. (d–f) Exactly the same morphology can be obtained by using internally generated force only. To this purpose, contracting fibers (represented by the thick red lines) are attached between the FAs at the left boundary and the circular area at the center. Their respective contractility is then adjusted in such a way that rupture at the left boundary is avoided, while at the center area, the same overall force is achieved as in panels a–c.

DISCUSSION

To investigate how force is propagated through the actin cytoskeleton toward sites of focal adhesion, here we have introduced a mechanical network model. Such models have been proven very useful before in describing the mechanical properties of various types of cells (21–24,37,47–49). The properties of the models were based upon observations and mechanical measurements from both living cells and individual CSK fibers. The CSK elasticity is assumed to arise from a dense network of interconnected cables, which are average presentations of the load-carrying elements in the actin CSK (possibly small bundles of cross-linked actin filaments). This view is consistent with measurements on different adherent cell types showing that the actin CSK mainly determines the cell mechanical response. The representation of individual filaments in our model as linear elastic cables follows from their observed tensile response (50) and a detailed analysis of their mechanical properties (51). Many actin cross-linking proteins have been identified in a variety of adherent cells, and ultrastructural observations confirm the appearance of a dense, interconnected network permeating the cell cytoplasm. Fixed pin-joints in the model along the periphery represented focal adhesions (FAs) between an adherent cell and the rigid substrate.

Our modeling approach was complemented by experiments on adherent fibroblasts which were laterally sheared using PDMS micropillars. The resulting redistribution of internal stress led to a growth-respective shrinkage of focal adhesion areas. This effect was compared to the force change due to stress propagation predicted by our model. Despite the strong assumptions made in the modeling approach, if cells are selected which are expected to have an isotropic cytoskeleton, the agreement between modeling and experimental results is fairly good. Indeed the same overall trends have been confirmed here for three different data sets (one given in Fig. 5 and two more in the Supplementary Material). The model captures the qualitative features of the FA forces and their evolution in response to the micropillar shift of the adherent cell. The experimentally measured adhesion area of the prestressed cell shows very similar characteristics as obtained from our simulations for the forces at FAs. In the prestressed cell, the model exhibits enhanced stresses at those FAs which are separated by large distances from neighboring adhesion points. When the prestressed cell is laterally shifted by the pillar, the boundary FA forces directly in front of the pillar are reduced while those in the back are enhanced. If the initial cell shape is circular or elliptical with pull along the short axis, one large region of stress results. If it is elliptical with pull along the long axis, two stress regions at oblique directions appear. The simulations also show that the results are largely independent of the topology of the network (reinforced square, triangular, or random).

If the model is complemented by a rupture scenario, we find that circular and elliptically elongated cell shapes lead to morphologies characteristic for migrating keratocytes and fibroblasts, respectively. Keratocytes are a model system for fast moving cells and the half-moon shape is found both for this cell type and for corresponding cell fragments which have lost their nucleus. It has been demonstrated before that keratocyte fragments can be switched from a circular and stationary state to a half-moon and migrating state by mechanical stimulation with flow from a micropipette (52). Our computational results suggest that a similar switch might be induced by internal upregulation of actomyosin contractility at one side of the cell. Note that the proposed mechanism might be used only to establish the migration morphology. It is well known that in the later stage of steady migration, contractile actin bundles and adhesion contacts are arranged in such a way that contraction occurs primarily perpendicular to the direction of locomotion (53,54). The other morphology resulting from our rupture scenario reminds us of migrating fibroblasts. Fibroblasts are a model system for slowly moving cells and in this case, it is well known that actomyosin contractility indeed proceeds along the long axis of the cell and is mainly concentrated at the cell front (55).

In summary, our findings support the notion that the mechanisms determining the model response are present within living adherent cells. This suggests that cable mechanics, prestress in the actin cytoskeleton, and the exact spatial localization of adhesions are the main biophysical determinants for stress distribution in an adherent cell. Although the overall agreement between model and experiment is quite good, when comparing forces and FA-sizes after the shift of the micropillar, one finds that there are regions where the agreement is not perfect, resulting in a typical RMSD of 2 nN. Several reasons might be responsible for this disagreement:

First, existing FAs might move and new FAs might develop after the pillar has been contacted and shifted. However, we repeated the same analysis as presented above with a set of FAs extracted after 30 min, and did not find any considerable change in the comparison between simulations and experiment. Second, in our numerical analysis, we disregarded the FAs in the middle of the cell. However, the experimental snapshots show that, in practice, these FAs grow. Thus, they also carry some amount of force, and might suppress or enhance the force propagation to the FAs at the cell boundary which were the focus of our study. Third, our model does not capture possible three-dimensional effects, including the effect of the cell nucleus, whose position and shape is clearly changed as the pillar is shifted. Fourth, we have assumed a linear relation between force and size of FAs, but this is expected to be valid only on average. Fifth, the model considers the FAs to be pointlike—although, in practice, they are spatially extended. Finally, the model does not consider regulated restructuring of the network after change in loading.

All these effects together or individually can add some perturbation to force propagation through the cytoskeleton to the FAs. In the future, our model might be extended to include these additional aspects. Moreover, it is highly desirable to experimentally measure the forces directly, e.g., on elastic substrates.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.