Summary
Structural studies of large proteins and protein assemblies are a difficult and pressing challenge in molecular biology. Experiments often yield only low-resolution or sparse data which are not sufficient to fully determine atomistic structures. We have developed a general geometry-based algorithm that efficiently samples conformational space under constraints imposed by low-resolution density maps obtained from electron microscopy or X-ray crystallography experiments. A deformable elastic network (DEN) is used to restrain the sampling to prior knowledge of an approximate structure. The DEN restraints dramatically reduce over-fitting, especially at low resolution. Cross-validation is used to optimally weight the structural information and experimental data. Our algorithm is robust even for noise-added density maps and has a large radius of convergence for our test case. The DEN restraints can also be used to enhance reciprocal space simulated annealing refinement.
Introduction
Many experiments on biomolecules only yield low-resolution or sparse structural data; for example, electron cryo-microscopy, small-angle X-ray scattering (SAXS), or fluorescence resonance energy transfer (FRET) measurements. Such data are usually insufficient to completely define the structure of a macromolecule. Even for macromolecular X-ray crystallography and NMR experiments the structure determination problem is often underdetermined, which means the number of parameters exceeds the number of independent experimental observations. It is therefore common to use prior knowledge to provide the missing information needed to reduce over-fitting the data. This is typically done using a molecular mechanics energy function together with the experimental data combined in a hybrid energy function for the structure refinement (Jack and Levitt, 1978) to restrain local geometric quantities such as bond lengths, bond angles, and planarity, which are sequence- and conformation-independent and are therefore known a priori. However, for low-resolution data such general information is insufficient to uniquely determine the structure, and it needs to be complemented by other knowledge about the specific macromolecule. This additional structural knowledge could come from a homology model or from a known structure of the same molecule in a different conformation. Here we assume that all prior structural knowledge is represented by this initial structure. The main task is then to optimally combine the initial structure with the experimental data. In this work we focus on low-resolution density maps obtained from electron microscopy or x-ray crystallography, although the approach presented is general enough to handle many types of experimental structural data.
For density maps obtained from X-ray crystallography or electron microscopy, the over-fitting problem has been addressed before in various different ways, mostly by reducing the dimensionality of the refinement problem. Manual decomposition into domains was used together with subsequent rigid body fitting into an electron density map (Rossmann, et al., 2005; Gao and Frank, 2005; Fabiola and Chapman, 2005). For rigid body fitting into density maps, a number of programs (Wriggers, et al., 1999; Rossmann, 2000; Chacon and Wriggers, 2002; Roseman, 2000; Volkmann and Hanein, 1999; Wu, et al., 2003; Rath, et al., 2003; Ceulemans and Russell, 2004; Ritchie, 2005; Goddard, et al., 2007; Dror, et al., 2007) have been developed. A flexible docking approach has been developed in combination with the Situs program, which defines representative points in the protein and in the density map, and from a correspondence between these points, restraints were derived to be used in molecular dynamics simulation (Wriggers, et al., 2004). Molecular dynamics simulations have also been combined directly with real-space refinement (RSRef/X-PLOR:RSMD) (Chen, et al., 1999; Chen, et al., 2003), but for low-resolution density maps, the rigid domains still need to be defined manually. Low-frequency normal modes of an elastic network model (Tirion, 1996) have been proposed (Delarue and Dumas, 2004; Suhre, et al., 2006; Tama, et al., 2004) and used (Hinsen, et al., 2005; Mitra, et al., 2005; Falke, et al., 2005) to guide global conformational changes during fitting of protein structures to low-resolution electron density maps. A small number of low-frequency normal modes were also used to improve structure refinement in X-ray crystallography (Diamond 1990; Kidera and Go, 1991; Poon, et al., 2007) and in particular enhancing the molecular replacement technique (Suhre and Sanejouand, 2004). Another recent method combines comparative modeling and density fitting to improve the sequence alignment and obtain better homology models (Topf, et al., 2006). For dimensionality-reducing methods in general, it seems reasonable to use only collective low-frequency degrees of freedom to fit a structure into a low-resolution density map, since the map determines only global rearrangements rather than local structural changes. However, in general it is not apparent which degrees of freedom are to be constrained and which are to be released. An increasing number of low-resolution (i.e., 3.5 – 4.5 Å resolution) X-ray crystal structures have been solved and refined (Brunger, 2005; DeLaBarre and Brunger, 2006). However, the process of interpreting low-resolution electron density maps is difficult and highly subjective. A more objective method is required that takes into account already known structural information.
Here we present a new method in order to take previously determined structures into account. The rationale behind our approach is to adapt only those degrees of freedom for which the density map actually provides information, and to keep all other degrees of freedom as close to the initial structure as possible. Cross-validation is used to determine the optimum degree of adaptation (or relative weighting of experimental data and restraints) to prevent over-fitting. We use a Deformable Elastic Network (DEN) as a restraining potential, defined so that at the beginning of the refinement process, the network has its minimum at the initial structure. A very efficient geometry-based conformational sampling algorithm is extended to generate a structural ensemble that is biased by both the restraining potential as well as by the particular density map. It is critical to make this elastic network potential deformable and to carefully adapt it to fit the density map during the refinement simulation. Our DEN approach is devised to deform the elastic network only along those degrees of freedom that are strongly influenced by the density map. For all other degrees of freedom, the elastic network potential remains unchanged and keeps the model close to the initial structure. An important feature of this approach is that there is no need to manually select which degrees of freedom are constrained and which are left free: the elastic network deforms itself to trade off between the initial structure and the density map. In this way, the dimensionality of the system is not reduced; in principle each conformation could potentially be visited. The extent of deformation is controlled by a single parameter γ, for which we show that an optimal value can be estimated by use of cross-validation.
In contrast to high-resolution X-ray crystallography which completely defines a structure, low-resolution data from X-ray crystallography or electron microscopy only provide information about a certain region in conformational space that contains the correct structure. To assess the complete information content of the density map one needs to find in principle the largest ensemble of structures that fit the map. The objective is, thus, not only to find a single best-fitting structure, but rather to determine an ensemble of structures. Our conformational sampling approach allows exploration of a conformational space that fits an experimental low-resolution density map and, thus, yields a whole ensemble of possible solutions. The combined use of the sampling algorithm and the DEN method therefore prevents that the ensemble of possible solution structures contains over-fitted and therefore unlikely structures. This approach is implemented in our program DireX.
In this paper our method is tested using the ribose-binding protein, for which several structures have been solved by X-ray crystallography (Bjorkman, et al., 1994; Bjorkman and Mowbray, 1998) and which is known to undergo a large conformational change upon ligand binding. Starting from an ‘open’ conformation, the goal is to find the ‘closed’ conformation using synthetic density maps computed from the closed conformation at increasingly lower resolutions. We find that our approach is superior to simple rigid-domain fitting. Because of its large radius of convergence and noise-robustness for our test case, we expect our method to be useful in numerous low-resolution structure solution or refinement applications. We also show that DEN restraints can also be implemented in simulated annealing refinement in reciprocal-space, enhancing the convergence of the refinement.
Results and Discussion
Sampling of electron density maps without any elastic network
To obtain a control for comparison to our DEN approach, we first applied our conformational sampling algorithm as a ‘free’ refinement, i.e., without using DEN restraints, but maintaining local geometry, such as bond lengths and bond angles. Synthetic density maps (our ‘experimental’ data) were calculated from the closed conformation (1URP) of the ribose-binding protein (RBP) to dmin = 3, 4, 6, 8, 10, 15, and 20 Å resolution (Figure 1). Starting from the open conformation (2DRI) 1000 steps of the sampling algorithm were performed yielding a trajectory of protein conformations. During the course of the sampling simulation the structure was pulled into the density map to varying degrees. Overall, the structure became more similar to the target structure, which is of course known for this test case.
Figure 1.
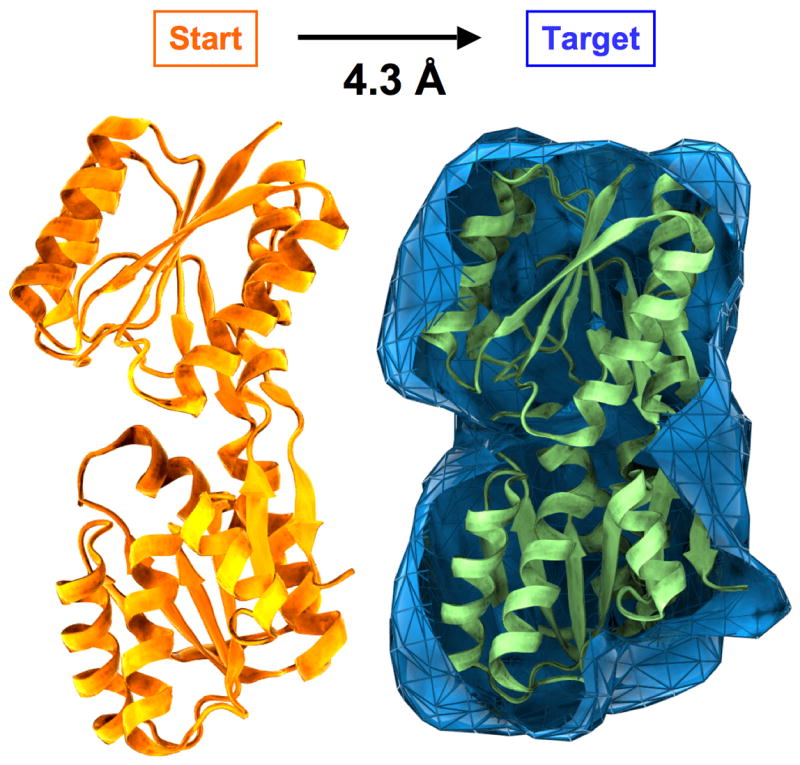
Test case for sampling simulations. The goal is to fit a target electron density map by smoothly deforming a starting structure. The test structure is RBP consisting of 271 amino acid residues for which two different structures have been solved by X-ray crystallography in an open (PDB entry 2DRI, in orange) and a closed (1URP, in green) conformation. The refinement starts from the open conformation, which has a RMSD of 4.3 Å to the closed conformation. Synthetic density maps are calculated at different resolutions (dmin = 3, 4, 6, 8 10, 15, and 20 Å) from the closed conformation and used in our refinement approach as ‘experimental’ data. The density map computed to dmin = 10 Å is shown in blue.
Figure 2 A shows the all-atom root mean square deviation (RMSD) from the target (closed) structure for the density maps computed to different resolutions. In all simulations the RMSD decreased within the first ~ 30 steps, but did not converge to a stable value for any of the simulations. Furthermore, none of the simulations reached structures with an RMSD below 1.5 Å. The RMSD increase that occurred after reaching a minimum value is mainly due to a loss of local structure. This is quantified by the percentage number of residues that maintain the secondary structure of RBP; the number dropped from an initial value of 76% down to a value between 32 and 39%, i.e., about half of the secondary structure was lost in these simulations. At low resolution, the density maps clearly do not provide enough information about local structural features; even the 3 Å density map was not able to sufficiently stabilize the structure during the DireX sampling simulations.
Figure 2.
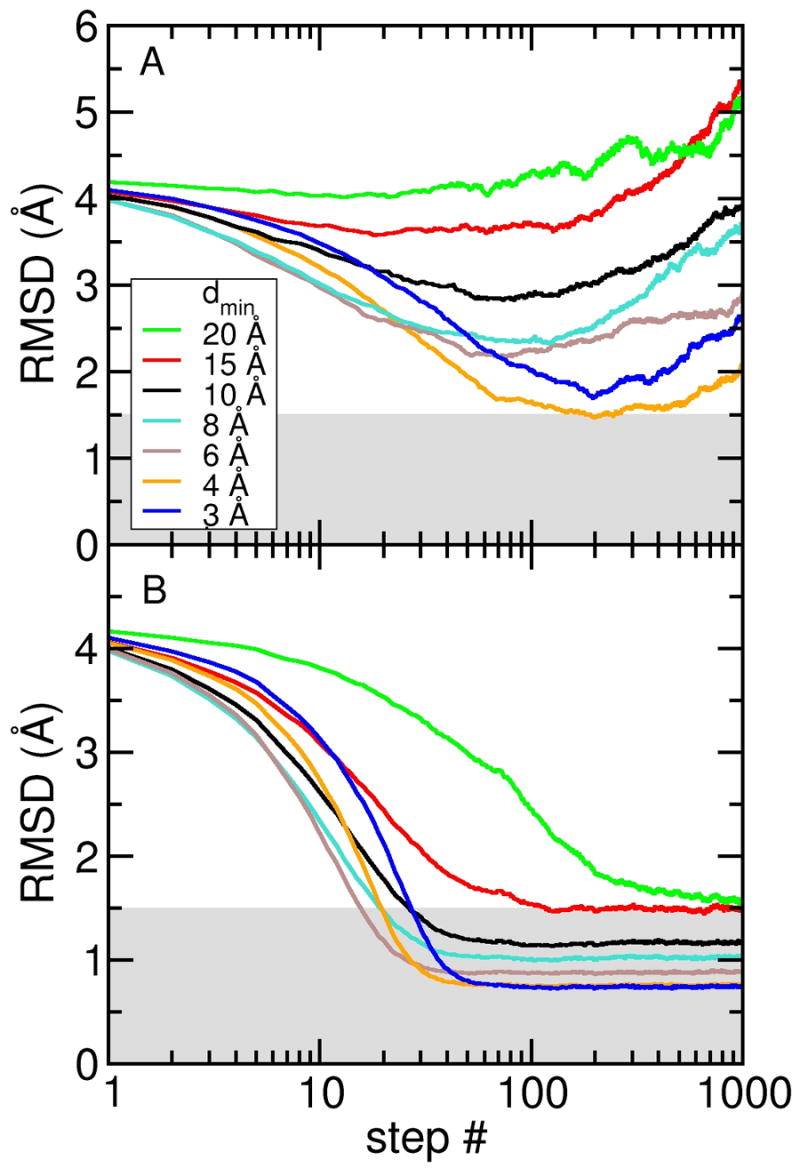
Sampling simulations without and with DEN restraints. All-atom RMSD are computed with respect to the target (closed) conformation of RBP for sampling simulations starting from the open conformation and using electron density maps computed at seven different resolutions (dmin = 3, 4, 6, 8, 10, 15, and 20 Å). (A) Free sampling simulation without DEN. (B) Sampling simulations using the DEN restraints with γ = 0.8. With the DEN restraints, all simulations yielded structures with RMSDs below 1.5 Å (indicated by the grey shaded region).
As a measure of how well the current model fits the ‘experimental’ density map, we calculated the correlation coefficient between the density map derived from the current model and the target map (see Equation 1). During all simulations, the map correlation was monotonically increasing showing that the fit to the data was continuously improving. As expected, the final map correlation, shown in Table 1, is always higher than the map correlation of the starting structure. In addition, the map correlation tends to be higher for lower resolution. This general trend is due to the fact that model errors have a smaller effect on low-resolution maps: to obtain a high map correlation at high resolution, the model needs to be much closer to the correct structure than at low resolution.
Table 1.
Map correlation between target- and model-map for density maps computed at different resolutions obtained from a real-space refinement simulation with DireX.
| Map resolution (Å) | Map correlation
|
||
|---|---|---|---|
| dmin | initial structure | without DEN (free) | with DEN (γ=0.8) |
| 3 | 0.285 | 0.638 | 0.762 |
| 4 | 0.416 | 0.795 | 0.836 |
| 6 | 0.643 | 0.927 | 0.925 |
| 8 | 0.741 | 0.967 | 0.965 |
| 10 | 0.818 | 0.981 | 0.978 |
| 15 | 0.883 | 0.985 | 0.988 |
| 20 | 0.834 | 0.990 | 0.989 |
A general problem in real-space (and also in reciprocal-space) refinement is that the density map information alone is not well suited to move the model towards the correct structure; this is especially true at the beginning of the refinement (Brunger, et al., 1987). Only when the refinement proceeds, do the forces become more effective. For example, for the free simulation with the density map computed to dmin = 3 Å, the structure became heavily distorted (resulting in physically unreasonable local geometry) before a good fit could be reached; the lowest RMSD for the simulation at dmin = 3 Å is 1.69 Å, which is somewhat higher than the 1.47 Å RMSD for the simulation at dmin = 4 Å (Figure 2 A). As the map correlation, i.e. the fit to the data, is improving even though the RMSD increased, the data were being over-fitted and so yielding unusable structures. Application of the deformable elastic network approach is able to overcome this problem, as is shown in the following.
Sampling with DEN
We performed the same simulations as described above, but this time included the DEN restraints (see Experimental Procedures). Figure 2 B shows the RMSD to the target structure for density maps computed to different resolutions, using γ = 0.8, a good compromise at all density map resolutions (discussed further below). Including the DEN restraints has a dramatic and very significant change of the sampling simulation process: for all density maps, the RMSD drops quickly and converges to a constant plateau value, which is, as expected, consistently better (lower RMSD) for higher resolution density maps. The resulting structures are much closer to the correct structure than in the free simulations without the DEN. Specifically, the sampling simulations at dmin =3, 4, 6, 8, 10, and 15 Å all yielded structures with RMSD value at or below 1.5 Å (see shaded area in Figure 2 B). Furthermore, the local structure was very stable: the percentage number of residues that maintain the secondary structure of RBP stays between 72% and 76%, compared to 76% in the target (closed) structure. The Ramachandran statistics depend on the density map resolution: the number of residues in the core region of the Ramachandran plot, as defined by Procheck (Laskowski et al., 1993), decreased from 86% for simulations at dmin = 3 Å to 71% at dmin = 20 Å resolution.
For computational efficiency, bond lengths and angles are only approximately maintained by DireX. Consequently, the corresponding differences to expected equilibrium values are relatively large: 0.12 Å for bond lengths and 0.24 Å for the distance intervals that restrain bond angles. The choice of the width of these intervals is a trade off between precision of coordinates and convergence speed of the algorithm. In high-resolution refinements those distance intervals could easily be further reduced requiring more time for the algorithm to converge. A more efficient approach is to refine the resulting structure with a conventional method, such as reciprocal space minimization or simulated annealing. To illustrate this, we further refined the best structure obtained from the simulation at dmin = 3 Å using the program Crystallography and NMR System (CNS) (Brunger et al., 1998) with the MLHL target function, which refines against both, amplitudes and phases of the structure factors corresponding to the calculated density map of RBP in the closed conformation. During the course of the refinement the free R value dropped from 0.32 to 0.17, and the RMSD dropped from 0.68 Å to 0.20 Å. For comparison, starting the simulated annealing refinement directly from the open conformation was not successful and yielded a structure with an RMSD of 3.2 Å.
The initial RMSD decrease was fastest for the density map calculated at dmin = 8 Å, but slower for higher and lower resolution maps (Figures 2 A and 2 B). The fact that the RMSD decreases slower at low resolution can be understood by the way the sampling method moves the atoms into the density: the force that pulls an atom into the map is proportional to the density values in its vicinity. As the maps are normalized to have a mean value of zero and a standard deviation of one, the maximum density values are lower for low-resolution density maps. Therefore, also the force on the atoms is smaller, which slows down the convergence.
For higher resolution maps one could have expected that the convergence would always be faster, as the experimental information content is higher and should potentially provide better forces. The reason this is not the case, is that the density map at higher resolution is more rugged and, thus, more and higher barriers need to be crossed, slowing down the effective convergence speed. We refer to this effect as the barrier-effect. Due to this barrier-effect, higher resolution sampling simulations may be even more efficient if started at lower resolution before switching to higher resolution after, say, 100 sampling steps. A combination of the DEN approach and simulated annealing may be able to overcome this problem (see below).
The correlation coefficients between the density maps computed from the final structures and the target maps, shown in Table 1, are always higher than the respective correlations at the beginning of the sampling simulation (as also seen in the simulation with no DEN). For the maps computed at dmin = 6 to 20 Å, the map correlations obtained from the DEN simulations are very similar to those from the free simulations. Interestingly, for the 3 and 4 Å maps the map-correlations are significantly better for the DEN simulations, 0.762 and 0.836, than for the free simulations, 0.638 and 0.795, respectively. Thus, although the DEN simulations impose more restraints onto the structure, the fit to the data became better. This suggests that the additional DEN restraints helped to find the correct structure by guiding the fitting process and by stabilizing the structure especially in the beginning of the refinement.
Optimal choice of the γ parameter
In the next step, we systematically varied the γ parameter values between 0 and 1 in steps of 0.l for all seven density map resolutions, leading to a total of 77 simulations. Figure 3 shows the average RMSD (<RMSD>) to the target structure averaged over the last 500 steps, for each of these simulations. At γ = 0, the DEN is not allowed to change at all and therefore behaves like a regular (non-deformable) elastic network. All curves have a minimum at γ between 0.7 and 0.9. The initial decrease of <RMSD> is due to the fact that increasing γ allows the DEN, and therefore also the structure itself, to adapt better to the forces imposed by the electron density. At the same time the influence of the initial structure is weakened.
Figure 3.
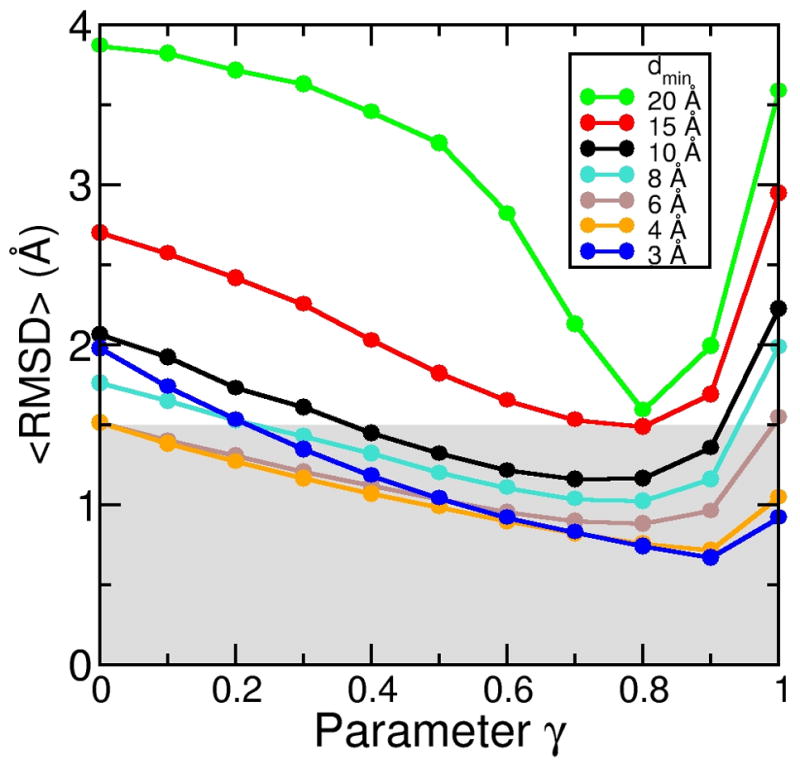
Effect of the γ value on the sampling simulations. For each of the seven density map resolutions, we performed a series of eleven simulations with the γ value (Eqs. 5 and 6) varying between 0 and 1 in steps of 0.1. All-atom RMSD are shown, averaged over the last 500 steps of each refinement simulation (1000 steps total each). The smallest RMSD value that can be achieved depends on the γ value. The optimum choice for γ is different for different resolutions.
For very large γ-values almost no information from the initial structure is used; the target density maps were over-fitted, resulting in an RMSD increase for all values of dmin. In the extreme case of γ = 1.0, none of the simulations converged within 1000 simulation steps, so that after a short initial decrease all <RMSD> values were constantly increasing in a similar manner seen for the free simulation without the DEN (Figure 2 A). In this case there were no restraints present towards the initial structure, and the DEN could potentially deform to any point in conformational space. The ensemble obtained for γ = 1.0 should therefore eventually convergence to the ensemble that is obtained from the free simulation without the DEN.
Obviously, the optimal choice of the γ parameter should yield a minimal <RMSD>. However, in a real application one would of course not know the correct structure, and the <RMSD>, therefore, cannot be used as a suitable criterion for the choice of γ. We will use cross-validation instead to estimate the optimal value for γ.
Cross-validation
The general statement that a structure is better if the fit to the experimental data is better, is only true when the data fully determine the structure. In the case of low-resolution data, where the number of parameters (coordinates of the macromolecular structure) exceeds the number of independent experimental observations, the structure determination problem is underdetermined and over-fitting the data can severely corrupt the structure. The goal, therefore, is to refine a structure just to the point where over-fitting sets in. To detect and prevent over-fitting of experimental data the concept of cross-validation has been introduced to structure determination (Brunger, 1992).
To cross-validate the obtained structures, we generated synthetic structure factors from the closed conformation of RBP and randomly selected 10% of the structure factors, which were defined as the ‘test set’ and were omitted from the calculation of the target density map. Therefore, only the remaining structure factors, which form the ‘working set’, are used for structure refinement. The structure factors from the test set are then used to calculate the free R value, which quantifies the fit to the omitted data and is used to detect over-fitting. The DEN restraints are used to prevent over-fitting and the parameter γ takes on the role of controlling the degree of fitting the data. The optimal choice of γ should yield a minimum free R value.
A series of refinement calculations were performed using the cross-validated density maps at seven different resolutions (dmin = 3, 4, 6, 8, 10, 15, 20 Å) and eleven different γ-values, from 0 to 1 in steps of 0.1, resulting in 77 additional independent simulations. Figure 4 A shows <RMSD>, the RMSD of each simulation averaged over the last 500 steps. The best structures obtained for the sampling simulations at dmin = 3, 4, 6, 8, and 10 Å resolution all reached <RMSD> values below 1.5 Å. In comparison to the simulations without cross-validation (Figure 3), reducing the data set for cross-validation does affect the resulting structures, but the impact is rather small for the high-resolution maps: the best <RMSD> for the 3 and 4 Å maps were shifted by only +3% and −11% respectively. Note that the effect is larger for the lower resolution maps: the best RMSD for the 15 and 20 Å maps are shifted by +61% and +42%, respectively.
Figure 4.
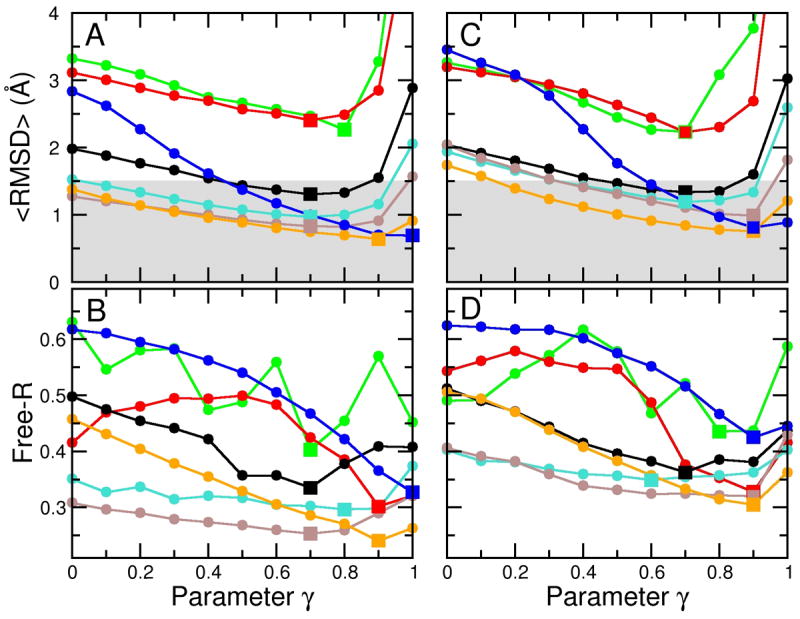
Use of cross-validation data set to determine the optimum value of the γ value. (A), (B) The cross-validation data set is formed by selecting at random 10% of the structure factors that were omitted from the calculation of the density map used to guide the sampling simulations. These omitted structure factors are then used to calculate a free R value (Free-R) that measures the fit between the structure factors calculated from the sampled structure and the omitted structure factors. The curves of <RMSD>, the RMSD averaged over the last 500 steps of each refinement simulation, versus γ differs from those of free R against γ, but the minimum of free R at a particular resolution occurs at a γ value that is close to that which minimizes the <RMSD> value. This provides an approximate method to determine the optimum γ value. In panels (C) and (D) we show how noise effects the variation of <RMSD> with the γ parameter. Adding Gaussian noise with a standard deviation of 40° to the phases of the structures factors has a very small effect at all resolutions. We have marked the minimum values of either <RMSD> or free-R by square symbols to better show the correspondence of the positions.
We described above the barrier-effect typified by the higher values of <RMSD> for the simulation at dmin = 3 Å resolution compared to that at 4 Å or 6 Å (Figure 3). This effect is even more pronounced in Figure 4 A: the 3 Å curve starts much higher for small γ-values than in Figure 3 but still reaches a similar low RMSD for high γ-values. This suggests that the modification of the data set for cross-validation has not changed the position of the minimum of Eρ, but has increased the energy barriers on the path towards the minimum.
Figure 4 B shows the corresponding free R values. The minimum of the free R value should ideally be at a γ-value, for which also the <RMSD> value is at a minimum. This is indeed the case for the higher resolution maps (compare the positions of the square symbols in Figure 4 A and B). At lower resolutions, the curves become noisy. This happens as the number of structure factors is smaller at lower resolutions, and, thus, the statistics for the free R value becomes much less significant. For example, for the 3 Å map there are 24,741 reflections, whereas for the 20 Å map there are only 105. Thus, for cross-validation of the 20 Å data, only 11 reflections were used, causing significant statistical noise. This can be quantified by computing the correlation between RMSD and free R; the average correlation for the simulations at dmin = 3 to 8 Å was 0.928 and for the 10–20 Å was −0.06. However, the minimum of the free R value remained to be a good predictor of the lowest RMSD for all resolutions, which is shown by the fact that the overall correlation between the γ-values at the lowest free R value and the lowest RMSD is 0.70. Complete cross-validation might be used to reduce the noise in the free R values (Brunger, 1993).
Noise
To test our method under more realistic conditions, we added noise to our synthetic data sets. In X-ray crystallography the phases of the structure factors have higher uncertainties than their amplitudes, so we added Gaussian noise with a width of 40° to the phases and computed a density map from these modified phases and the original amplitudes. We are aware that for electron microscopy, a different noise model could be more realistic. We performed simulations (again for seven values of dmin and eleven different γ-values) using the noisy density maps as a target, but otherwise the same simulation parameters as in the previous simulations. The results, shown in Figures 4 C and D, can be directly compared to the noise-free simulations (Figure 4 A and B). The <RMSD> values obtained with noise are only slightly larger, 0.22 Å (+12%) on average, than without noise. The best structures obtained from the simulations at dmin ranging from 3 to 10 Å, again, have an RMSD below 1.5 Å (gray-shaded area). Noise increases the <RMSD> of the best structure at dmin = 3 Å by only 0.12 Å (from 0.69 Å to 0.81 Å). Overall, the resulting structures are very similar to the ones obtained from the noise-free simulations, which means our method is robust against the applied noise.
The previously mentioned barrier-effect at high resolution is even more pronounced in the presence of noise: the simulation at dmin = 3 Å yields an <RMSD> of 3.4 Å for γ = 0, which is even higher than the 3.2 Å RMSD obtained from the simulation at dmin = 20 Å (Figure 4 C). This is expected as the noise creates more and/or higher barriers especially in the high-resolution density maps and further hinders convergence. The free R value is higher for the simulations with noise than for the noise-free simulations; it increased on average by 0.04. In spite of these differences, the γ values for which the free R value is mimimal are very good predictors of the γ values for which <RMSD> is minimal.
Radius of convergence
As we have shown, our method works well when starting from the open conformation of the ribose-binding protein. To assess the radius of convergence of our approach, we generated increasingly difficult test cases. Specifically, we manually opened the open conformation and generated 16 additional conformations with increasing inter-domain angles from 45 and 137° and corresponding RMSDs between 5.4 and 12.7 Å. Three of these conformations are shown in Figure 5 (top). Sampling simulations were started from each deformed structure for the same seven cross-validated density maps calculated at different resolutions, as described above. A γ-value of 0.8 was used for all simulations. Figure 5 (bottom) shows the final RMSD after the sampling simulation versus the initial RMSD of the starting model. Each point is the result of a 1000 step sampling simulation. The fact that all points lie below the diagonal (dashed line) shows that all starting structures were moved closer to the correct (closed) structure. All starting structures with an initial RMSD below about 10 Å could be significantly improved at all tested values of dmin. For example, for starting structures that had an initial RMSD of up to 10 Å, final structures below 1.5 Å RMSD (gray-shaded area) were obtained at dmin = 3 Å, and below 2 Å RMSD at dmin = 10 Å.
Figure 5.
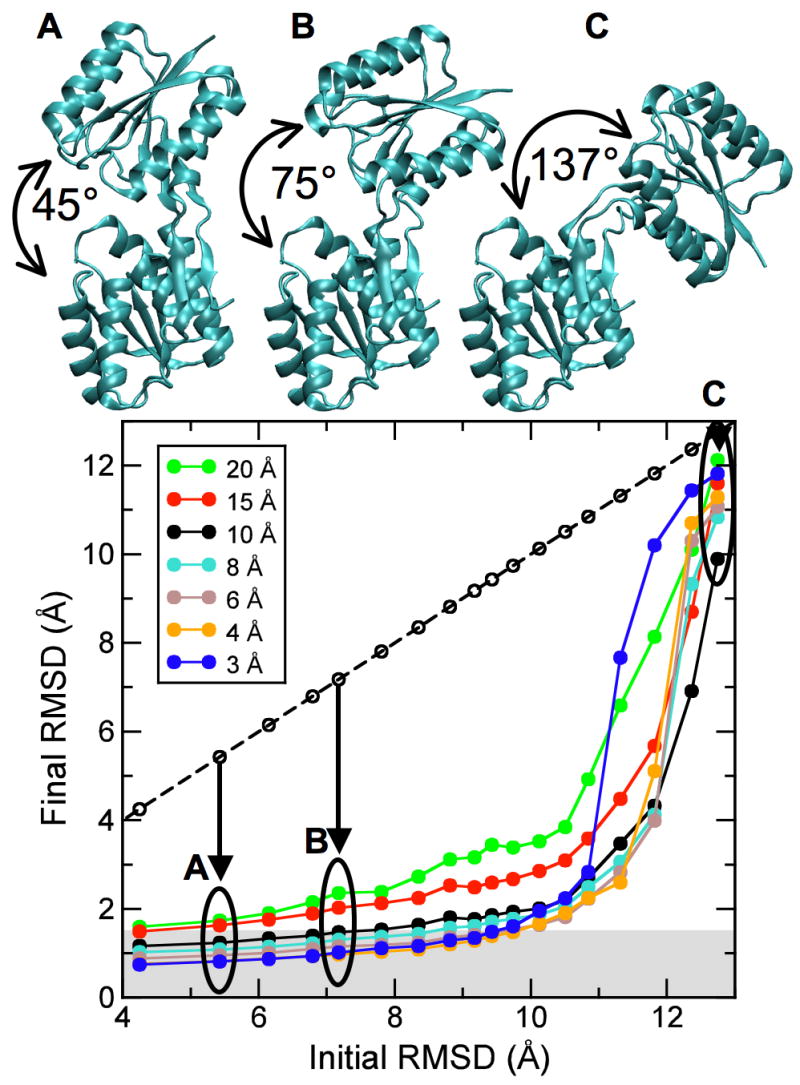
Radius of convergence of DireX as a function of density map resolution. The open conformation of RBP (PDB ID 1URP) has been manually opened to different extents to yield 18 structures with an inter-domain angle of between 41° and 137°, and corresponding RMSD values between 4.3 Å and 12.7 Å, with respect to the closed conformation (PDB ID 2DRI). Three of these different starting structures (A, B, C) with RMSD values of 5.4, 7.2, and 12.7 Å, respectively, are shown. The final RMSD value after the sampling simulation is plotted against the initial RMSD value. Points that lie below the diagonal (dashed line) correspond to starting structures that have been moved closer to the correct structure by sampling simulations against the density map computed to the particular resolution.
Rigid-body refinement
A simple and popular way to reduce the dimensionality of the refinement problem is to manually define rigid domains. Here we use this approach for comparison with our method. We used the program Dyndom (Hayward and Berendsen, 1998) to break the protein into two domains A and B. Dyndom takes two structures and determines rigid domains by comparing and clustering fragments of these two structures. The obtained domain decomposition is an optimum solution that is usually not accessible in a real application, since the target structure would be unknown. The obtained refinement quality is, therefore, an upper limit of what is achievable by rigid-body refinement. According to Dyndom, domain A comprises residues 3 to 100 and 238 to 262, and domain B comprises residues 105 to 232 and 268 to 269. For the structure refinement we used the program CNS with the MLHL target function and the same cross-validation data set as described above (see Figure 4 A and B). The two domains A and B were defined as rigid groups within CNS. All rigid-body refinement calculations were performed using the synthetic structure factor computed to dmin = 3 Å.
In a first attempt, energy minimization starting from the open structure (1URP) did not yield a good solution: the obtained R and free R values were 0.579 and 0.558, respectively, and the resulting RMSD value was high at 1.82 Å. In the next step, a simulated annealing refinement was performed using the standard annealing protocol of CNS, which started at a temperature of 2500 K and decreased it by 25 K every 6 torsional molecular dynamics steps; this yielded a much better structure with R and free R value of 0.189 and 0.174, respectively, and a RMSD value of 0.24 Å. To test the radius of convergence of the rigid-body refinement approach, we used the previously described series of manually opened starting structures. Interestingly, simulated annealing failed even for the least deformed open model, which had an inter-domain angle of 45° and a RMSD of 5.4 Å to the closed structure. A ten times slower cooling protocol did not improve the resulting structure either. Thus, for the case at hand, the radius of convergence for rigid-body refinement with CNS is much smaller than for the method presented here.
Implementation of DEN restraints in reciprocal space simulated annealing refinement
In X-ray crystallography only amplitudes are measured: the phases are unknown and must be determined indirectly. The fastest and most popular method used to solve the phase problem is molecular replacement. If at least part of the structure is already known, or can be modeled by homology modeling, useful approximate phases can potentially be reconstructed from this model. The success of this method strongly depends on the similarity between the starting model and the correct structure. We test here if application of DEN is beneficial to commonly used reciprocal space refinement. Synthetic structure factor amplitudes in the resolution range 100 to 3 Å were computed from the closed structure. The open model, which has a RMSD of 4.3 Å to the closed structure, was taken as the starting (replacement-) model to start simulated annealing refinement.
We implemented the DEN into CNS at the script level, as described in Experimental Procedures. For cross-validation, 10% of the amplitudes were defined as the test set and were not used for the refinement. To assess the impact of the DEN on simulated annealing refinement, two simulated annealing refinement simulations were performed, one with and one without the DEN restraints. For the simulation with DEN, a γ-value of 0.8 and a κvalue of 0.05 were used. In both simulations, the starting temperature was 2000 K, which was lowered by 10 K every 6 torsion-angle molecular dynamics steps (the molecular dynamics time-step was set to 4 fs). The refinement without DEN did not converge to the target structure in that the resulting structure had an RMSD of 3.3 Å to the correct (closed); the R and free R values were 0.57 and 0.58, respectively. In contrast, using the DEN restraints yielded a much better structure with an RMSD of 0.6 Å; the R and free R values of 0.27 and 0.26, respectively.
Conclusions and Future Work
We presented here an approach for flexible fitting and refinement of protein structures into low-resolution density maps obtained by X-ray crystallography or electron microscopy. Our approach consists of two components: the deformable elastic network (DEN) model and the geometry-based sampling algorithm; both are implemented in the program DireX. Our conformational sampling algorithm efficiently generates an ensemble of structures that fit a density map. In the framework of low-resolution data, the DEN acts as a knowledge-based restraint which helps to overcome the over-fitting problem and prevents that the structural ensemble contains over-fitted conformations. DireX can also apply general distance restraints, which makes it also possible to use data obtained from FRET or NMR experiments.
Furthermore we showed that reciprocal space refinement methods benefit from the application of DEN restraints. In particular, we showed that the combination of torsion-angle simulated annealing refinement as implemented in CNS and DEN increases the radius convergence. The simulated annealing helps to improve sampling efficiency by accelerating the crossing of energy barriers while the DEN restraints prevent that the protein explores conformations that are too far from the starting structure, which is typically a homology model.
In addition to fitting protein structures into low-resolution density maps, we expect that our method is able to solve difficult molecular replacement problems, where the replacement model would be relatively far away from the correct structure. The phases obtained from such a model would yield heavily distorted density maps when combined with the observed structure factor amplitudes which poses a considerable challenge to structure refinement. Our conformational sampling algorithm could be particularly powerful in this respect, since it has been shown to be robust for noise-added density maps. An important next step is the application of our approach to structure refinement using real data sets, which is currently in progress.
Experimental Procedures
Test system
The ribose-binding protein (RBP) (Figure 1) is used here as a test case, since it is known to undergo a large conformational change, and several high-resolution crystal structures have been solved. We chose an open and a closed structure from the PDB, 1URP and 2DRI, respectively, and removed any non-protein atoms from the PDB file. These structures each comprise 271 residues (2465 atoms) and differ by an all-atom root mean square deviation (RMSD) of 4.3 Å. Synthetic density maps at seven different resolutions (dmin = 3, 4, 6, 8, 10, 15, and 20 Å) have been computed from the closed structure and serve as our ‘experimental’ data. In all simulations the starting structure was superimposed on the target structure (2DRI) minimizing their RMSD. However, our method is insensitive to the initial position, as tested in trial simulations using an initial center displacement of 10 Å at dmin =10 Å and DEN restraints: the structure refines to an RMSD of 1.17 Å to the target structure, compared to 1.15 Å when the center position of initial structure was superimposed on that of the target structure.
Conformational sampling algorithm
Our conformational sampling algorithm, which is outlined in Figure 6 A, is based on the CONCOORD algorithm (de Groot, et al., 1997) and generates a random walk through the sterically accessible conformational space. The original CONCOORD program was developed to sample conformations around a given structure (usually a crystal structure). The general strategy of CONCOORD is to generate a network of distance restraints from an input structure and to efficiently generate an ensemble of structures that obey these restraints. We use an all-atom description of the protein, except for non-polar hydrogen atoms, which are united with their heavy atom binding partner. The CONCOORD distance restraints are represented as a list of allowed distance intervals. This list contains two different types of restraints: (1) topological restraints, which ensure that the model retains correct stereochemistry, e.g. bond lengths and planar groups, and (2) van der Waals restraints, which prevent atom overlaps and set an upper limit for the allowed conformational change. There are typically about ten times more CONCOORD restraints than atoms. In a next step, the coordinates of the structure are randomly perturbed using a Gaussian distribution with a width of 0.5 Å. Then, the coordinates are iteratively corrected to fulfill the CONCOORD restraints and to eventually produce a new structure. This correction-cycle is the core of the CONCOORD algorithm, which traverses the list of CONCOORD restraints in a random order, and corrects those distances that lie outside their allowed interval. For each violated restraint, the two corresponding atoms are moved along their inter-atomic vector towards a target distance which is randomly picked from within the allowed interval of the particular restraint. Depending on the initial perturbation, usually less than 100 complete correction-cycles are sufficient to correct all CONCOORD restraints.
Figure 6.
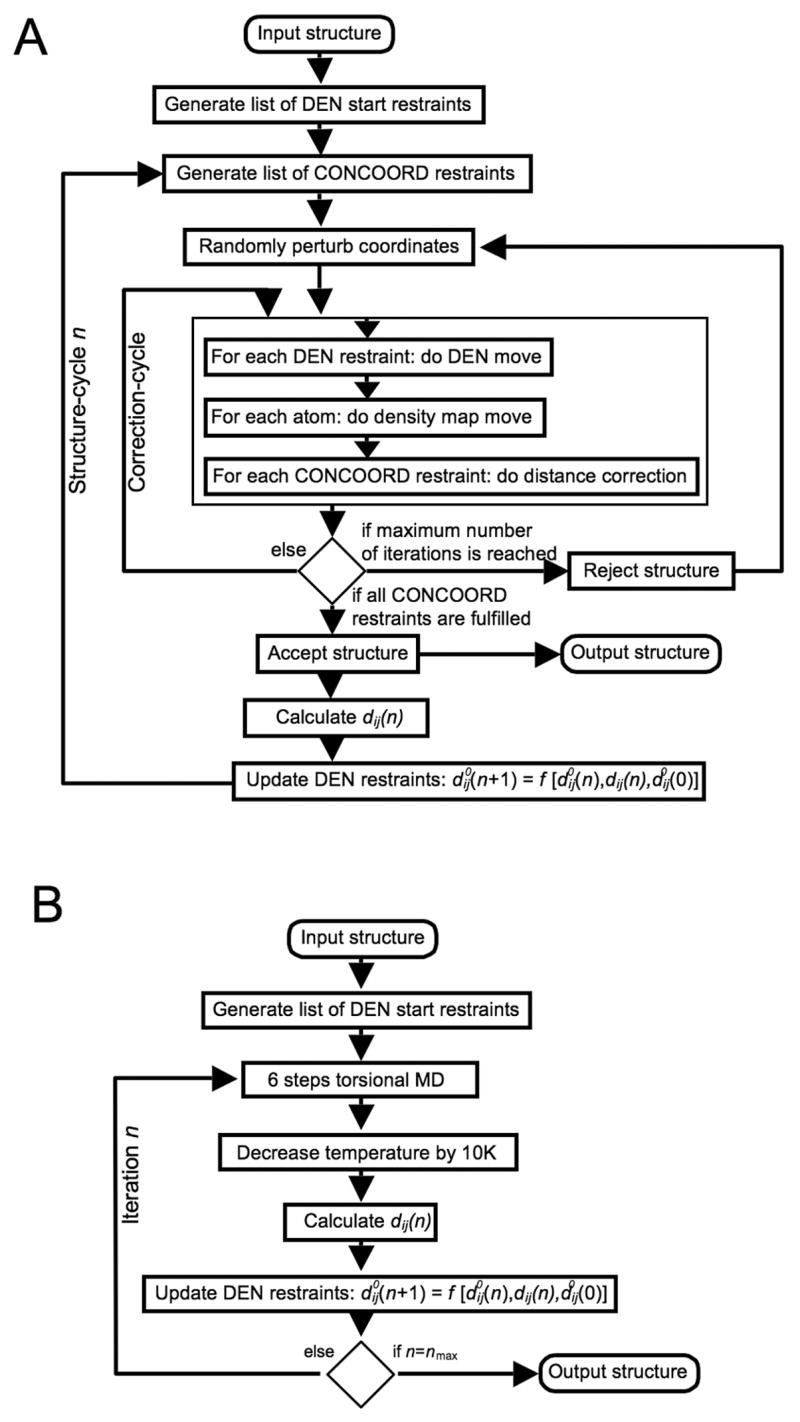
Implementation of DEN. (A) Diagram showing the implementation of DEN in combination with the CONCOORD algorithm in the program DireX. (B) Diagram showing the implementation of DEN in reciprocal space simulated annealing refinement.
Once the structure eventually fulfills all CONCOORD restraints, the next structure-cycle is entered by calculating new CONCOORD restraints from this new structure. However, if the structure does not converge within 500 correction-cycles, a new attempt is made with the same CONCOORD restraints, but with different random perturbations. Without any DEN restraints or forces derived from an electron density map, the typical conformational change of the ribose-binding protein achieved in one structure-cycle is about 0.2 Å and its computation takes about 0.7 seconds on a single Intel PENTIUM 3.0 GHz CPU.
Stochastic gradient of an electron density map
A density map, ρmodel(x⃗), is calculated from the current model at the beginning of each structure-cycle (Figure 6 A). The goal is to refine the model structure such that ρmodel(x⃗) becomes as similar to the experimental density ρexp(x⃗) as possible. In X-ray crystallography, ρexp(x⃗) is obtained using a resolution cutoff (dmin) in reciprocal space. We calculate the model density ρmodel(x⃗) therefore by convoluting the structure with a kernel function that is the Fourier transform of a hollow sphere, as described in Ref. (Chapman, 1995). This choice of the kernel function is most appropriate for applications to X-ray crystallographic data. However, for electron microscopy data other kernel functions might be more suitable. The densities ρmodel(x⃗) and ρexp(x⃗) are shifted and scaled to have a mean value of 0 and a standard deviation of 1, which yields ρ̃model(x⃗) and ρ̃exp(x⃗).
Traditional real-space refinement approaches would typically minimize a pseudo-energy Eρ = 1−CC, where CC is the correlation between ρ̃model(x⃗) and ρ̃exp(x⃗), given by:
| (1) |
where a⃗ijk are the three-dimensional coordinates of the grid points of the density map. Instead, we take an approximate, stochastic approach, which is more efficient and is expected to be more robust with noisy maps. The rationale is to move atoms into regions where the model density does not provide enough density and to push atoms out of regions where the model density is too high. To achieve this, we consider the difference density:
| (2) |
which is computed before the coordinate perturbation step, and is kept fixed during the correction-cycles. The optimal scaling factor λ is found to be 0.6 independent of resolution and this parameter is not expected to be problem-dependent. Each atom is moved during each CONCOORD correction-cycle by adding a vector g⃑i determined by:
| (3) |
where r⃑j are random positions taken from an isotropic Gaussian distribution with a width of 2 Å around the atom position x⃑i. The valueρdiff (r⃗j) is set equal to the value of ρdiff at the closest grid point. Thus, g⃑i is an average over random directions weighted by ρdiff and therefore points in the direction of higher ρdiff values. The scaling factor, v(sc), depends on the correction-cycle step, sc, and is made to decrease linearly from 1 to 0 during the first 90 correction-cycles; this allows the structure generation to converge.
In contrast to calculating the analytical gradient of Eρ which is very sensitive to noise, our approach incorporates information about the surrounding of an atom position to determine its move step g⃑i. Equation 3 in fact computes an approximation to the center-of-mass of the difference electron density weighted by a Gaussian distribution around the given atom.
Deformable Elastic Network (DEN)
The DEN potential or “restraint”, which is key to the present approach, is defined by
| (4) |
where dij (n) is the distance between atom i and j at structure-cycle number n, is the corresponding equilibrium distance, and k is the force constant which typically is 5 kcal/(mol Å2) As our network is deformable, the equilibrium distances of the elastic network are not constant, but instead change after each structure-cycle. A list of 5000 DEN harmonic distance restraints between random atom pairs having a distance between 3 and 12 Å (which excludes bond-lengths and bond-angles), is created from the initial structure (Figure 6 A). The DEN restraints are applied by traversing the list of restraints in random order during each correction-cycle and moving each pair along the inter-atomic vector closer to the equilibrium distance, using a step size proportional to . In this way, the DEN-move of the atoms is similar to applying a harmonic force. Once again, the step size is also scaled by the factor v(sc), as defined above. As soon as a structure obtained from the correction-cycle fulfills all CONCOORD restraints, the equilibrium distances of the DEN are updated using:
| (5) |
| (6) |
where and dij (n) are distances defined above (Equation 4), the damping parameter κ determines the adaptation speed and is set to be smaller than 1; typically 0.05, as determined by trial and error, and γ ∈ [0,1]balances two contributions, an adaptation force, κ [γdij (n)] and a restoring force back to the initial equilibrium value . Figure 7 A illustrates this procedure using a simple two-dimensional example. The adaptation term allows the DEN to slowly follow the structural change so that if a DEN restraint is distorted by forces derived from the density map, it can adapt to these forces by changing the particular equilibrium value.
Figure 7.
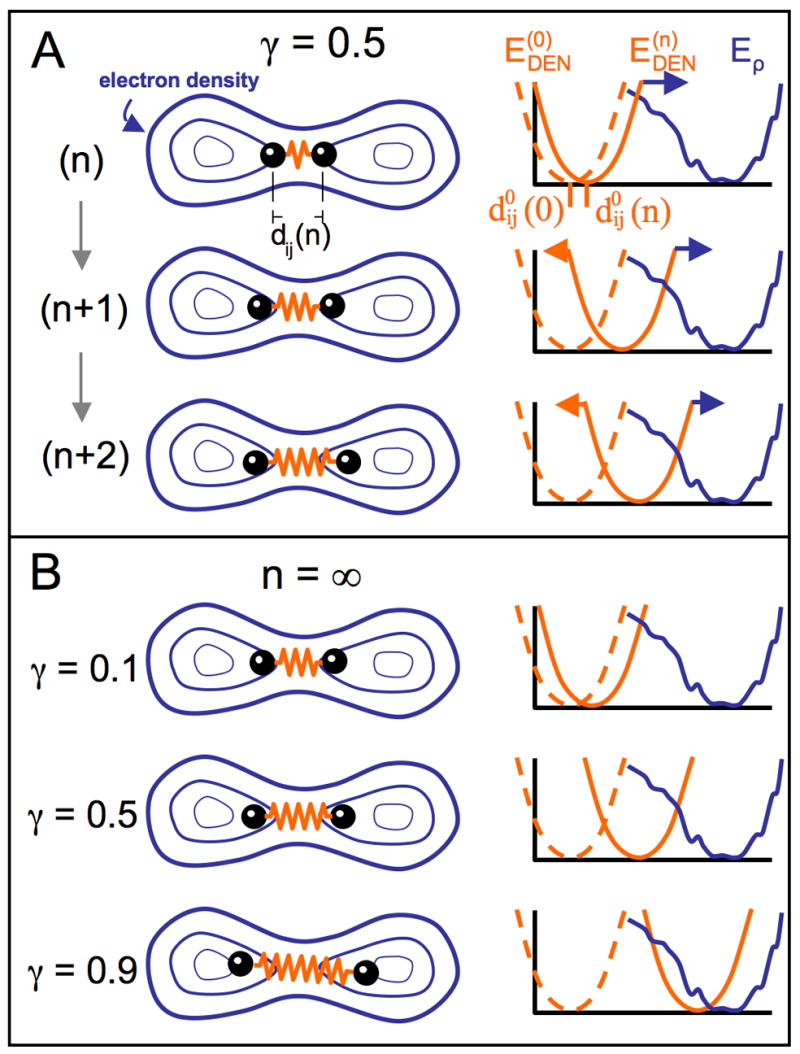
Illustration of DEN for an example with two atoms. The elastic network potential is represented by a spring (orange) between two atoms (black balls) separated by a distance of dij (n) for the atom pair (i,j) at sampling step n. The density map contours are represented by blue iso-contours. The energy terms involved are depicted in the diagrams on the right. The current equilibrium distance of the DEN potential, , can change at each sampling step n. The blue curve shows the rugged pseudo-energy Eρ (see Experimental Procedures), which is minimal for the best fit of the model density to the target density map. At the start of the sampling simulation process, the distance of the atoms in the starting model is at the minimum of the DEN potential, (dashed orange line). As the elastic network deforms by changing the equilibrium distance to , the DEN potential, , also changes (solid orange line). (A) Three steps (n, n+1, and n+2) of a sampling simulation are shown for the parameter γ = 0.5. In the starting model, the two atoms are close to each other. During the sampling simulation the atoms are pulled into higher density regions. The DEN potential adapts to this force up to an extent that is controlled by γ (see Eq. 5 in Experimental Procedures). (B) shows the final converged states of three different sampling simulations for different γ-values (0.1, 0.5, 0.9). The larger the value of γ, the more the DEN is able to adapt to the forces imposed by the density map.
The restoring force, , ensures that the equilibrium distance of the elastic network is pulled back to its initial value when a DEN restraint does not feel a sufficiently strong force from the density map. Thus, the parameter γ controls to which degree the structure can be refined to the experimental data which is shown in Figure 7 B. The more experimental information is available, the closer to 1 should γ be. In extreme cases, γ should be 0 for no data, and 1 for high-resolution data, which completely define the structure. We discuss below how to find an estimate of the optimal γ-value using cross-validation. Note that the effect of γ also depends on the stepsize of the conformational sampling algorithm and the scaling of the gradients derived from the density map. The computation time for one structure-cycle including both DEN restraints and forces from the electron density map, is about 2.5 seconds. The method is implemented in the program DireX, which will be made available through the SimTK website https://simtk.org/home/direx.
Implementation of DEN restraints in reciprocal space refinement
The DEN approach has been implemented into the CNS (Brunger et al., 1998) software package using a modified task file based on the standard CNS simulated annealing task (‘anneal.inp’). Figure 6 B shows a schematic overview of the implementation. N atom pairs that are within a distance range of 3 to 12 Å in the starting structure are randomly selected, where N is the number of atoms. These atom pairs define the list of DEN restraints. The DEN pairs do not include bonds or bond-angles, which are restrained in CNS. The DEN restraints are defined as harmonic NOE restraints in CNS. During the simulated annealing calculation the temperature is lowered by 10 K every 6 steps of torsional-angle molecular dynamics. At the same time the distances between the DEN pairs dij (n) are calculated and the DEN restraints are updated using Equation 5.
Acknowledgments
We thank Pavel Strop and Bert de Groot for stimulating discussions. This work was supported by a postdoctoral fellowship from the Deutsche Forschungsgemeinschaft (DFG) to GFS, by the National Institutes of Health through the NIH Roadmap for Medical Research Grant U54 GM072970, by HHMI to ATB and by NIH award GM-41455 to ML.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Bjorkman AJ, Binnie RA, Zhang H, Cole LB, Hermodson MA, Mowbray SL. Probing protein-protein interactions. The ribose-binding protein in bacterial transport and chemotaxis. J Biol Chem. 1994;269:30206–30211. [PubMed] [Google Scholar]
- Bjorkman AJ, Mowbray SL. Multiple open forms of ribose-binding protein trace the path of its conformational change. J Mol Biol. 1998;279:651–664. doi: 10.1006/jmbi.1998.1785. [DOI] [PubMed] [Google Scholar]
- Brunger AT, Kuriyan J, Karplus M. Crystallographic R factor refinement by molecular dynamics. Science. 1987;235:458–460. doi: 10.1126/science.235.4787.458. [DOI] [PubMed] [Google Scholar]
- Brunger AT. The free R value: a novel statistical quantity for assessing the accuracy of crystal structures. Nature. 1992;355:472–474. doi: 10.1038/355472a0. [DOI] [PubMed] [Google Scholar]
- Brunger AT. Assessment of phase accuracy by cross validation: the free R value. Methods and applications Acta Crystallogr. 1993;D49:24–36. doi: 10.1107/S0907444992007352. [DOI] [PubMed] [Google Scholar]
- Brunger AT, Adams PD, Clore GM, DeLano WL, Gros P, Grosse-Kunstleve RW, Jiang JS, Nilges N, Pannu NS, Read RJ, et al. Crystallography and NMR system (CNS): A new software system for macromolecular structure determination. Acta Crystallogr. 1998;D54:905–921. doi: 10.1107/s0907444998003254. [DOI] [PubMed] [Google Scholar]
- Brunger AT. Low-resolution crystallography is coming of age. Structure. 2005;13:171–172. doi: 10.1016/j.str.2005.01.002. [DOI] [PubMed] [Google Scholar]
- Ceulemans H, Russell RB. Fast fitting of atomic structures to low-resolution electron density maps by surface overlap maximization. J Mol Biol. 2004;338:783–793. doi: 10.1016/j.jmb.2004.02.066. [DOI] [PubMed] [Google Scholar]
- Chacon P, Wriggers W. Multi-resolution contour-based fitting of macromolecular structures. J Mol Biol. 2002;317:375–384. doi: 10.1006/jmbi.2002.5438. [DOI] [PubMed] [Google Scholar]
- Chapman MS. Restrained real-space macromolecular atomic refinement using a new resolution-dependent electron-density function. Acta Crystallogr. 1995;A51:69–80. [Google Scholar]
- Chen Z, Blanca E, Chapman MS. Real-space molecular-dynamics structure refinement. Acta Crystallogr. 1999;D55:464–468. doi: 10.1107/s090744499801097x. [DOI] [PubMed] [Google Scholar]
- Chen JZ, Fürst J, Chapman MS, Grigorieff N. Low-resolution structure refinement in electron microscopy. J Struct Biol. 2003;144:144–151. doi: 10.1016/j.jsb.2003.09.008. [DOI] [PubMed] [Google Scholar]
- DeLaBarre B, Brunger AT. Considerations for the refinement of low resolution crystal structures. Acta Crystallogr. 2006;D26:923–932. doi: 10.1107/S0907444906012650. [DOI] [PubMed] [Google Scholar]
- Delarue M, Dumas P. On the use of low-frequency normal modes to enforce collective movements in refining macromolecular structural models. Proc Natl Acad Sci USA. 2004;101:6957–6962. doi: 10.1073/pnas.0400301101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diamond R. On the use of normal modes in thermal parameter refinement: theory and application to the bovine pancreatic trypsin inhibitor. Acta Crystallogr. 1990;A46:425–435. doi: 10.1107/s0108767390002082. [DOI] [PubMed] [Google Scholar]
- Dror O, Lasker K, Nussinov R, Wolfson H. EMatch: an efficient method for aligning atomic resolution subunits into intermediate-resolution cryo-EM maps of large macromolecular assemblies. Acta Cryst D. 2007;63:42–49. doi: 10.1107/S0907444906041059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fabiola F, Chapman MS. Fitting of high-resolution structures into electron microscopy reconstruction images. Structure. 2005;13:389–400. doi: 10.1016/j.str.2005.01.007. [DOI] [PubMed] [Google Scholar]
- Falke S, Tama F, Brooks CL, III, Gogol EP, Fisher MT. The 13 structure of a chaperonin GroEL protein substrate complex by cryo-electron microscopy. J Mol Biol. 2005;348:219–23. doi: 10.1016/j.jmb.2005.02.027. [DOI] [PubMed] [Google Scholar]
- Gao H, Frank J. Molding atomic structures into intermediate-resolution cryo-EM density maps of ribosomal complexes using real-space refinement. Structure. 2005;13:401–406. doi: 10.1016/j.str.2005.01.004. [DOI] [PubMed] [Google Scholar]
- Goddard TD, Huang CC, Ferrin TE. Visualizing density maps with UCSF Chimera. J Struct Biol. 2007;157:281–287. doi: 10.1016/j.jsb.2006.06.010. [DOI] [PubMed] [Google Scholar]
- de Groot BL, van Aalten DMF, Scheek RM, Amadei A, Vriend G, Berendsen HJC. Prediction of protein conformational freedom from distance constraints. Proteins: Struct Funct Genet. 1997;29:240–251. doi: 10.1002/(sici)1097-0134(199710)29:2<240::aid-prot11>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- Hayward S, Berendsen HJC. Systematic analysis of domain motions in proteins from conformational change: new results on citrate synthase and T4 lysozyme. Proteins. 1998;30:144–154. [PubMed] [Google Scholar]
- Hinsen K, Reuter N, Navaza J, Stokes DL, Lacapère JJ. Normal mode-based fitting of atomic structure into electron density maps: application to sarcoplasmic reticulum Ca-ATPase. Biophys J. 2005;88:818–827. doi: 10.1529/biophysj.104.050716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jack A, Levitt M. Refinement of large structures by simultaneous minimization of energy and R factor. Acta Crystallogr. 1978;A34:931–935. [Google Scholar]
- Kidera A, Go N. Refinement of protein dynamic structure: normal mode refinement. Proc Natl Acad Sci USA. 1990;87:3718–3722. doi: 10.1073/pnas.87.10.3718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laskowski RA, MacArthur MW, Moss DS, Thornton JM. PROCHECK: aprogram to check the stereochemical quality of protein structures. J Appl Cryst. 1993;26:283–291. [Google Scholar]
- Mitra K, Schaffitzel C, Shaikh T, Tama F, Jenni S, Brooks CL, III, Ban N, Frank J. Structure of the E. coli protein-conducting channel bound to a translating ribosome. Nature. 2005;438:318–324. doi: 10.1038/nature04133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poon BK, Chen X, Lu M, Vyas NK, Quiocho FA, Wang Q, Ma J. Normal mode refinement of anisotropic thermal parameters for a supramolecular complex at 3.42-Å crystallographic resolution. Proc Natl Acad Sci USA. 2007;104:7869–7874. doi: 10.1073/pnas.0701204104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rath BK, Hegerl R, Leith A, Shaikh TR, Wagenknecht T, Frank J. Fast 3D motif search of EM density maps using a locally normalized cross-correlation function. J Struct Biol. 2003;144:95–103. doi: 10.1016/j.jsb.2003.09.029. [DOI] [PubMed] [Google Scholar]
- Ritchie DW. High-order analytic translation matrix elements for real-space six-dimensional polar Fourier correlations. J Appl Cryst. 2005;38:808–818. [Google Scholar]
- Roseman AM. Docking structures of domains into maps from cryo-electron microscopy using local correlation. Acta Crystallogr. 2000;D56:1332–1340. doi: 10.1107/s0907444900010908. [DOI] [PubMed] [Google Scholar]
- Rossmann MG. Fitting atomic models into electron-microscopy maps. Acta Crystallogr. 2000;D56:1341–1349. doi: 10.1107/s0907444900009562. [DOI] [PubMed] [Google Scholar]
- Rossmann MG, Morais MC, Leiman PG, Zhang W. Combining X-ray crystallography and electron microscopy. Structure. 2005;13:355–362. doi: 10.1016/j.str.2005.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suhre K, Sanejouand YH. On the potential of normal-mode analysis for solving difficult molecular-replacement problems. Acta Crystallogr. 2004;D60:796–799. doi: 10.1107/S0907444904001982. [DOI] [PubMed] [Google Scholar]
- Suhre K, Navaza J, Sanejouand YH. NORMA: a tool for flexible fitting of high-resolution protein structures into low-resolution electron-microscopy-derived density maps. Acta Crystallogr. 2006;D62:1098–1100. doi: 10.1107/S090744490602244X. [DOI] [PubMed] [Google Scholar]
- Tama F, Miyashita O, Brooks CL., III Flexible multi-scale fitting of atomic structures into low-resolution electron density maps with elastic network normal mode analysis. J Mol Biol. 2004;337:985–999. doi: 10.1016/j.jmb.2004.01.048. [DOI] [PubMed] [Google Scholar]
- Tirion MM. Large amplitude elastic motions in proteins from a single-parameter, atomic analysis. Phys Rev Lett. 1996;77:1905–1908. doi: 10.1103/PhysRevLett.77.1905. [DOI] [PubMed] [Google Scholar]
- Topf M, Baker ML, Marti-Renom MA, Chiu W, Sali A. Refinement of protein structures by iterative comparative modeling and cryoEM density fitting. J Mol Biol. 2006;357:1655–1668. doi: 10.1016/j.jmb.2006.01.062. [DOI] [PubMed] [Google Scholar]
- Volkmann N, Hanein D. Quantitative fitting of atomic models into observed densities derived by electron microscopy. J Struct Biol. 1999;125:176–184. doi: 10.1006/jsbi.1998.4074. [DOI] [PubMed] [Google Scholar]
- Wriggers W, Milligan RA, McCammon JA. Situs: a package for docking crystal structures into low-resolution maps from electron microscopy. J Struct Biol. 1999;125:185–195. doi: 10.1006/jsbi.1998.4080. [DOI] [PubMed] [Google Scholar]
- Wriggers W, Chacon P, Kovacs JA, Tama F, Birmanns S. Topology representing neural networks reconcile biomolecular shape, structure, and dynamics. Neurocomputing. 2004;56:365–379. [Google Scholar]
- Wu X, Milne JL, Borgnia MJ, Rostapshov AV, Subramaniam S, Brooks BR. A core-weighted fitting method for docking atomic structures into low-resolution maps: application to cryo-electron microscopy. J Struct Biol. 2003;141:63–76. doi: 10.1016/s1047-8477(02)00570-1. [DOI] [PMC free article] [PubMed] [Google Scholar]


