A continuous topological change during phase transitions in amphiphile/water systems

Abstract

Amphiphiles are molecules such as surfactants or lipids that have a polar head group (hydrophilic) attached to nonpolar hydrophobic alkyl chains. Because of this characteristic they self-assemble in water and give rise to a wide range of phases with different structures and properties. Aqueous dispersions of amphiphiles are present in every aspect of day-to-day life—e.g., forming biological cell membranes, stabilizing emulsified food, or being used as soap. Time-resolved x-ray diffraction has been used to study the hexadecylhexa(oxyethylene glycol) ether (C₁₆EO₆)/water system, which shows an intermediate phase whose structure depends on the thermal path between lamellar and hexagonal structures. Heating the hexagonal phase from room temperature leads to a lamellar phase via an Ia3d cubic structure. Cooling from the lamellar phase initially leads epitaxially to an intermediate R3̄m before the hexagonal phase is reached. Both cubic and R3̄m phases are formed by very similar rod units, but the overall structures differ because of their spatial distribution and they both bridge morphologically the hexagonal and lamellar phases. The Ia3d does so on heating, whereas the R3̄m does on cooling. The structural path during the phase transitions is determined by topological similarities between the forming phase and the one from which it originates. Although the estimated curvature energies for these two phases are similar, on cooling, kinetics and topology are initial factors determining the path for the phase transitions, whereas on heating energy is the dominant factor.

Aqueous suspensions of nonionic surfactants of the type poly(oxyethylene glycol) alkyl ether, C_nEO_m, are widely used in, e.g., extraction of membrane proteins, oil recovery, and cleaning processes. They show a rich polymorphism governed by the hydrophobic effect (1), forming among others lamellar, hexagonal, and cubic phases. In some cases the cubic phase is replaced by the so-called intermediate (or fluid) phases whose structures are still controversial. Characterization of these structures and their building units is important for the understanding of lyotropism. Moreover, these phases are also believed to occur as intermediate structures during biological processes—e.g., cell fusion (2).

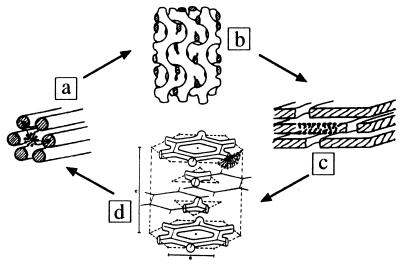
The mesogenic units can have different sizes and shapes, and from their organization different phases originate. They can range from disordered (liquid) to ordered structures in one (lamellar), two (hexagonal), and three dimensions (cubic). The most common cubic phases are formed by bicontinuous networks of rods (3). Gel and lamellar phases are stacked bilayers of amphiphiles and water, as shown in Fig. 1. The transition between these phases can be induced by, e.g., change in temperature or concentration. Most important, during such process there are significant changes in the curvature and morphology of the units (4).

Figure 1.

Different phases formed by the C₁₆EO₆/water system. On heating from the hexagonal phase with two-dimensional (2D) periodicity (a) to lamellar structures with one-dimensional periodicity (c), this system proceeds via an Ia3d cubic structure with three-dimensional periodicity (b), whereas upon cooling from the lamellar phase (c) it proceeds via a rhombohedral phase (d). Modified from refs. and 3 and 21.

From the different amphiphile/water systems studied it has been found that C_nEO_m molecules having long alkyl chains form stable intermediate (or fluid) phases (5–10). The driving forces for their formation remain a subject of debate, particularly because the identification of these structures is difficult. So far, fluid phases have been assigned as disrupted lamellar, L_α^H, in the cases of aqueous mixtures of hexadecylhexa(oxyethylene glycol) ether (C₁₆EO₆) (6) and C₂₂EO₆ (7) systems and rhombohedral in the C₃₀EO₉ (9) systems. The first consists of a random distribution of disruptions, whereas in the latter system the disruptions are regularly arranged. Cesium pentadecafluorooctanoate, CsPFO, forms continuous layers pierced by water-filled holes (11). These disrupted lamellae are stacked layers of amphiphiles containing water-filled intraplanar disruptions. Depending on the amount, size, and shape of these disruptions, different phases can be formed. However, intraplanar curvature is always present within the bilayer. In other cases mixtures of different amphiphiles give rise to phases not formed by the individual components in similar conditions (12). Intermediate phases have been classified according to the fraction of planar interface W present in the amphiphile aggregate (13, 14). A layered structure has W > 0.33, e.g., C₂₂EO₆ (7), while a cubic phase has W = 0 and a rhombohedral structure has W < 0.33 [C₃₀EO₉ (9)].

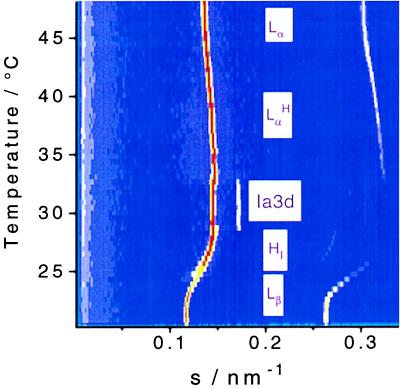
The temperature-dependent phases of the C₁₆EO₆/water system, in the concentration range ≈50 wt % have shown the following sequence (6):

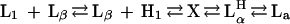(L₁, isotropic micellar solution; L_β, gel; H₁, hexagonal; L_α, lamellar; and L_α^H, a lamellar phase containing water-filled defects). The phase X has been described as cubic V₁ on heating but fluid or intermediate on cooling (6).

In the present paper we investigated the thermal phase sequence of the C₁₆EO₆/water system. We determined the geometrical parameters of the structures observed and discuss the driving force for their formation based on topological and morphological aspects.

METHODS

The surfactant was purchased from Nikko Chemicals (Tokyo) and was used as received. The synchrotron radiation small-angle x-ray scattering measurements were performed at beam-line X-13 of the European Molecular Biology Laboratory, Outstation Hamburg (15), using a linear (16) and a 2D image plate detector. Data were collected by a computer-controlled data acquisition system that also opens and closes a shutter depending on whether data were being registered or not. This procedure eliminates unnecessary exposure of the sample to the beam, minimizing radiation damage. The data were analyzed with in-house programs otoko (17) and scaco. The temperature was controlled by a thermostat interfaced to a computer to vary the temperature at different rates. The reading of a thermocouple close to the sample was input into the data file.

RESULTS AND DISCUSSION

A sequence of time-resolved x-ray diffraction patterns from a 53.6 wt % sample recorded during heating is shown in Fig. 2. In this case lamellar gel, hexagonal, cubic, and a lamellar liquid crystalline phase can be clearly assigned. The hexagonal phase consists of long parallel rods forming a 2D hexagonal lattice. It occurs below 27°C and has a lattice parameter a = 6.7 nm, and the rods have a hydrophobic core radius r_hc = 1.9 nm. Heating this phase leads to a bicontinuous Ia3d cubic phase with a = 14.2 nm (18). It has a body-centered unit cell, and the morphology corresponds to an infinite periodic minimal surface, ipms, of the gyroid type. The rod length and hydrophobic radius are l = 5.0 and r_hc = 1.5 nm, respectively. Upon further heating the cubic phase reaches at 50°C a lamellar L_α phase with interplanar distance d = 6.4 nm. The hydrophobic thickness of these lamellae can be calculated as d_hc = Φ_hc⋅d = 1.9 nm, where Φ_hc is the hydrophobic volume fraction in a sample (6, 7).

Figure 2.

Time-resolved x-ray diffraction patterns of a mixture containing 53.6 wt % C₁₆EO₆ in water, recorded during a heating scan at a rate of 0.25°C/min. It illustrates the phase sequence from lamellar L_β (gel) to hexagonal H_I to cubic Ia3d to disrupted lamellar (L_α^H) and finally to lamellar L_α. At the onset of the cubic phase, one can clearly see that the repeat distance associated with the most intense peaks from H_I and cubic phases have the same value [s = 1/d = (2/λ)sin θ with λ = 0.15 nm and 2θ the scattering angle].

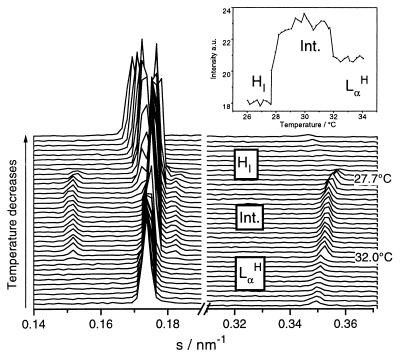
Upon cooling the system from the lamellar phase with a −0.25°C/min scan rate, the system follows another sequence of phases (see Fig. 3). The cubic structure observed on heating has been replaced by a different structure, which can be identified as either rhombohedral R3̄m or tetragonal, formed by stacked arrays of 2D continuous networks (19). Taking into account the dimensions of the unit cells calculated and the morphology of the neighboring phases, we can exclude the tetragonal structure.

Figure 3.

Cooling scan at a rate of −0.25°C/min. It shows the phase sequence from disrupted lamellar (L_α^H) to rhombohedral R3̄m to hexagonal H_I with the respective temperatures of the phase transitions. Several reflections are seen in each phase. It illustrates the need for high-resolution data to solve the structure of the R3̄m phase. The layered periodicity of this phase becomes clear when looking at the integrated intensities (in arbitrary units) of reflections common to the L_α and R3̄m phases at an s range from 0.32 to 0.38 nm⁻¹ (Inset). Note the significant increase in intensity at the onset of the R3̄m phase as well as its decrease once the transition to the hexagonal phase takes place. A common peak at s = 0.18 nm⁻¹ is indicative of the epitaxial relationship between lamellar and rhombohedral phases (21).

Table 1 shows the diffraction peaks observed with a 2D detector, their Miller indices, a qualitative description of their intensities, and the fitting to the R3̄m space group. Taking the cell dimensions determined from the x-ray diffraction patterns, we could estimate the geometrical parameters of the R3̄m phase, considering the network of rods forming hexagons in a single plane. From the value of a we estimate the rod length to be l = a/3^1/2 = 4.8 nm. Knowing that there are 3 independent rods per hexagon, we can calculate the radius of the rods’ hydrophobic core r_hc = a[(d₀₀₃Φ_hc3^1/2)/6lπ]^1/2 = 1.5 nm. For the cubic Ia3d phase the same parameters were calculated according to ref. 20. It is interesting to note the geometrical similarities of the mesogenic units in the cubic and R3̄m phases. Basically, the two structures are formed by similar rods that interconnect themselves in different ways, giving rise to different phases.

Table 1.

Experimental and calculated interplanar distances, the associated Miller indices, and relative intensity characterizing the R3̄ m (space group 166) phase from a sample containing 52.9 wt % surfactant at 30°C

dexp/nm	h	k	l	Relative intensity	dcalc	% error
6.63	1	0	1	0.79	6.60	−0.39
5.70	0	0	3	1	5.70	0.00
5.52	0	1	2	0.81	5.47	−0.557
4.13	1	1	0	0.34	4.13	0.00
3.67	1	0	4	0.42	3.67	−0.08
3.50	0	2	1	0.32	3.50	0.06
3.09	0	1	5	0.40	3.08	−0.20
2.86	0	0	6	0.50	2.85	−0.25
1.90	1	3	1	0.13	1.97	3.55

h, k, and l are the Miller indexes. The calculated Bragg peak positions were obtained according to (1/d_calc)² = (4/3)·(h² + hk + k²)/a² + l²/c², with the condition limiting possible reflections −h + k + l = 3n, with n integer (30). a = b ≠ c are the unit cell parameters and γ = 120° is the angle between a and b forming a plane perpendicular to the direction of c. The unit cell dimensions are a = 2d₁₁₀ = 8.26 nm and c = 3d₀₀₃ = 17.08 nm. The error was estimated by 100(d_exp − d_calc)/d_calc. 

A sequence of time-resolved diffraction patterns during cooling (Fig. 3) clearly shows that lamellar L_α^H and intermediate R3̄m structures have a common reflection, a necessary condition for an epitaxial relationship between these phases (21). The analysis of the integrated intensity of these reflections shows that the corresponding scattering plane is present in both lamellar and fluid phases. Epitaxial relationships involving other phases such as L_α and Ia3d have also been identified in aqueous mixtures of C₁₂EO₆ (22) or C₁₂EO₂ and 1-palmitoyl-2-oleoyl-sn-glycero-3-phospocholine (POPC) (20).

Complementary to x-ray diffraction, differential scanning calorimetry at scan rates of 0.1°C/min was performed to confirm the phase transition and estimate the enthalpies involved. C₁₆EO₆ 48.4 wt % in water showed a complex thermal behavior with clear differences between heating and cooling. On cooling, a peak at 31.8°C with ΔH = 1.47 J/g is observed, corresponding to the transition from disrupted lamellar to rhombohedral, and at 27.8°C the R3̄m to H_I transition is observed. The heating trace at the same scan rate shows a peak with ΔH = 1.42 J/g at 32.2°C, characterizing the transition from cubic Ia3d to L_α^H.

The phase sequence during heating shows an increase in curvature at the interface between the hydrophobic and hydrophilic moieties. However, one should pay attention to the fact that the mean curvature is nonzero in the hexagonal phase and approaches zero in the cubic and lamellar phases. In the Ia3d cubic phase it is zero because there are equal amounts of surfaces with positive and negative curvatures, whereas in the lamellar phase the value is zero because the surface is essentially flat. The cooling sequence shows a decrease in curvature, going from disrupted lamellar (L_α^H) to hexagonal structures.

The relationship between energy and curvature takes into account not only the mean but also the Gaussian curvatures. The free energy per unit area of a monolayer, effectively an energy per surfactant molecule (23–26), is given by

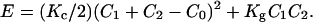K_c and K_g are the rigidity and Gaussian curvature constants, respectively. The curvature is defined as the reciprocal of the radius R_x shown by the surface at each point C_x = 1/R_x, C₀ is the spontaneous curvature, and C₁ and C₂ are the principal curvatures.

We are interested in comparing the relative curvature energies E^R and E^I between the R3̄m and Ia3d phases, respectively, and therefore estimate the ratio between them (E^R/E^I). Knowing that the rods in both phases have the same hydrophobic radius r_hc = R₁ and similar length, we can carry out a simple analysis based on the following considerations:

(i) The spontaneous curvature C₀ can be neglected when the amphiphile bilayer is symmetric (27). This is also supported by the findings of Kléman (28) for this kind of nonionic system, showing that the lamellar phase is expected to have a large range of stability.

(ii) The Ia3d cubic phase has C₁ and C₂ with the same magnitude but opposite signs (27, 29); therefore E^I = −K_gC₁².

(iii) The rods forming the Ia3d and R3̄m phases have the same hydrophobic radius and consequently the same curvature: C₁^I = C₂^I = C₁^R = C₁.

The ratio between the curvature energies of the R3̄m and cubic Ia3d phases can then be reduced to:

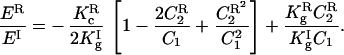This equation shows the contribution of curvature for this energy ratio. Apart from the constants K_c and K_g for both phases,† the relative energy depends on the ratio between the curvature arising from the circle formed by the in-plane array of rods of the R3̄m phase (C₂^R) and the curvature (C₁) due to their radius. Therefore, for rods with the same radius, the curvature energy difference becomes dependent on their length only (longer rods → larger radius of in-plane array → smaller curvature; Fig. 1). Qualitatively we can express the radius R₂ in terms of the rods’ length for both phases and find their ratio, which can be related to the curvature energy. In our case we could estimate that the energy of the cubic phase is about 5% lower.

Why the R3̄m phase forms only upon cooling can be explained by the topology of the neighboring phases. The decrease in curvature from lamellar L_α^H to hexagonal via rhombohedral is a natural sequence to be followed. Organizing the intraplanar disruptions of the lamellae creates a 2D array of mesogenic units. The cooling process increases the hydration of the head groups, inducing lower curvature, therefore forming rods that connect hexagonally in two dimensions (in-plane) leading to the R3̄m intermediate phase. Further cooling induces axial growth of these rods, promoting the formation of the hexagonal phase (Fig. 1). A similar argument can be used to explain the formation of the cubic phase upon heating from the hexagonal: in this case the rods are already present. Heating causes them to interconnect with each other in a three-dimensional network. Note again that the transition from H_I to Ia3d in fact represents an increase in curvature, although the mean value in the Ia3d phase is zero.

The existence of two different paths between lamellar and hexagonal phases upon heating and cooling, respectively, is further supported from experiments at different heating and cooling rates. It was observed that fast cooling of the lamellar phase proceeds initially via the R3̄m phase, which in this case transforms into cubic before reaching the hexagonal phase. This observation indicates that the rhombohedral is in fact a kinetically favored metastable structure. However, once formed and kept at constant temperature it does not convert into cubic. The conversion of cubic into R3̄m has not been unequivocally observed at any heating rate.

The above results are interesting because they show two structures which must have similar energies. One expects the activation energy for the conversion of cubic into R3̄m to be large enough to make this transition unlikely, while the inverse case is relatively easy. It must be noted that the initial formation of the R3̄m phase on cooling is always observed. Its range of stability depends on the cooling rate, but its formation does not.

The similarity of the estimated curvature energies excludes this contribution as definite criteria for the formation of either cubic or rhombohedral phase. It supports the argument that the topology of the phase prior to the transition determines the geometry of the mesogenic units of the forming phase and consequently its structure.

The phase sequence on cooling is therefore determined by an association of topological and kinetic effects. Depending on the rate of heat exchange between the mesogenic units and the environment, the energy factor takes over kinetics, transforming the R3̄m into cubic. However, if the heat exchange is slow the R3̄m phase can form, supercool, and hence transform directly into the hexagonal phase.

Finally, we speculate that the changes in cross-sectional area and curvature of the structures observed in our case should also happen with lipid membranes during biological processes such as membrane fusion, exocytosis, or endocytosis. These processes require extensive morphological changes—at least locally and transiently—to highly curved surfaces (2). We propose that the disruption of lamellar domains (lipid membrane) and the formation of hydrophobic rods together with their change from 2D to 3D network represent a convenient pathway for the formation of these transient states. Their thickness is similar to that of a membrane bilayer of the respective amphiphile, accounting for the curvature imposed on them. The combination of their structural and geometrical properties would make them adequate short-lived intermediates for the above-mentioned processes taking place in living cells.

ABBREVIATIONS

C_nEO_m

poly(oxyethylene glycol) alkyl ether (n carbons in the alkyl group, m oxyethylene units)

2D

two-dimensional