Intrinsic Electrostatic Potential in the BK Channel Pore: Role in Determining Single Channel Conductance and Block

Abstract

The internal vestibule of large-conductance Ca²⁺ voltage-activated K⁺ (BK) channels contains a ring of eight negative charges not present in K⁺ channels of lower conductance (Glu386 and Glu389 in hSlo) that modulates channel conductance through an electrostatic mechanism (Brelidze, T.I., X. Niu, and K.L. Magleby. 2003. Proc. Natl. Acad. Sci. USA. 100:9017–9022). In BK channels there are also two acidic amino acid residues in an extracellular loop (Asp326 and Glu329 in hSlo). To determine the electrostatic influence of these charges on channel conductance, we expressed wild-type BK channels and mutants E386N/E389N, D326N, E329Q, and D326N/E329Q channels on Xenopus laevis oocytes, and measured the expressed currents under patch clamp. Contribution of E329 to the conductance is negligible and single channel conductance of D326N/E329Q channels measured at 0 mV in symmetrical 110 mM K⁺ was 18% lower than the control. Current–voltage curves displayed weak outward rectification for D326N and the double mutant. The conductance differences between the mutants and wild-type BK were caused by an electrostatic effect since they were enhanced at low K⁺ (30 mM) and vanished at high K⁺ (1 M K⁺). We determine the electrostatic potential change, Δφ, caused by the charge neutralization using TEA⁺ block for the extracellular charges and Ba²⁺ for intracellular charges. We measured 13 ± 2 mV for Δφ at the TEA⁺ site when turning off the extracellular charges, and 17 ± 2 mV for the Δφ at the Ba²⁺ site when the intracellular charges were turned off. To understand the electrostatic effect of charge neutralizations, we determined Δφ using a BK channel molecular model embedded in a lipid bilayer and solving the Poisson-Boltzmann equation. The model explains the experimental results adequately and, in particular, gives an economical explanation to the differential effect on the conductance of the neutralization of charges D326 and E329.

INTRODUCTION

Large-conductance Ca²⁺ voltage-activated K⁺ (BK) channels have the largest single channel conductance of all K⁺-selective channels (250–300 pS in symmetrical 150 mM KCl; Pallotta et al., 1981; Latorre et al.,1982; Latorre et al., 1989; Hille, 2001). BK channels are ubiquitously expressed in different tissues such as neurons, smooth muscle, endocrine and exocrine glands, and kidney tubules. The large BK single channel conductance may be an asset in, for example, K⁺-secreting cells where they can provide the large K⁺ efflux from the cell to the lumen. BK channels have a tetrameric structure, with four α subunits constituting the functional channel (Shen et al., 1994). Additionally, all K⁺ selective channels have in the selectivity filter a conserved signature sequence −TVGYG (Heginbotham et al., 1994). Why, then, is the conductance of BK channels is so high? Brelidze et al. (2003) and Nimigean et al. (2003) compared the sequence of BK channels to lower-conductance K⁺ channels. This alignment revealed that BK channels have a ring of eight negatively charged glutamate residues at the entrance of the intracellular vestibule. By decreasing the local concentration of K⁺ in the vestibule through an electrostatic mechanism, neutralization of this ring of charges halves the conductance of BK channels for outward currents, results in inward rectification, and weakens block by Mg²⁺ and polyamines (Brelidze et al., 2003; Zhang et al., 2006). Thus, the internal ring of negative charges accounts only partially for the high conductance of BK channels. The conductance of the neutralization BK channel mutant is still about sixfold larger than the single channel conductance of, for example, the Shaker K⁺ channel.

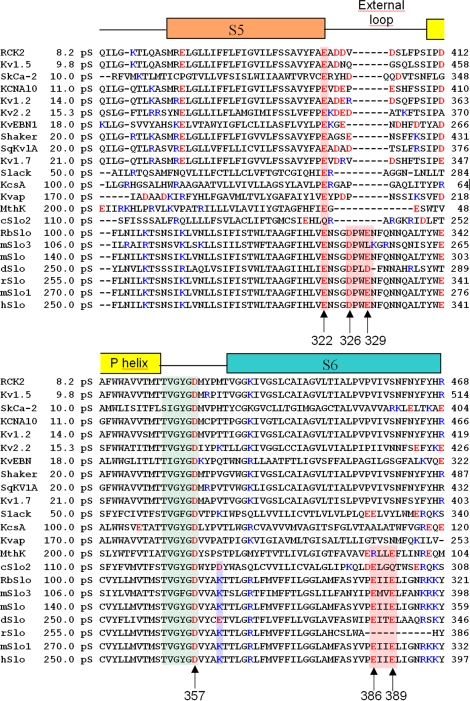
The aim of the present study was to further analyze the role of charged amino acids in the pore region of BK channels. As shown in the multiple alignments (Fig. 1), the external loop (turret) between S5 and the P-helix of BK channels contains several amino acid residues more than the other K⁺ channels analyzed. In this loop there are two negative charges, while in the other K⁺ channels, at least one of these charges is always absent. We hypothesized that the outer ring of negative charges increases the local K⁺ concentration in the outer vestibule of the pore and contributes to increase channel conductance. To test this hypothesis, we constructed mutants D326N, E329Q, and D326N/E329Q, and measured their single channel conductance expressed in Xenopus oocytes. Our results revealed that mutations D326N, E329Q, and D326N/E329Q only have marginal effect on single channel conductance. In order understand why these charges have such a small effect compared with those induced by neutralization of charges located in the internal vestibule, we built a molecular model for the open BK channel using MthK (Ca²⁺-gated K⁺ channel from Methanobacterium autotrophicum) as template. We performed continuum electrostatic calculations (Poisson-Boltzmann; Honig and Nicholls, 1995; Im et al., 1998) on the molecular model embedded in a lipid bilayer. 3D electrostatic potential maps were calculated for the wild-type (WT) model and for neutralization mutations of the inner and outer vestibule negative charges. We found that the electrostatic potential at the inner vestibule and at the selectivity filter is significantly affected by the ring of eight negative charges located on the inner vestibule. This result is consistent with the direct measurement of the single channel currents of BK mutants (Brelidze et al. 2003). Calculations on BK channel neutralization mutants (D326N, E329Q, and D326N/E329Q) revealed that the ring of eight negative charges in the outer vestibule has very little effect on the electrostatic potential on the outer vestibule and at the selectivity filter. This result is also consistent with our single channel measurements. Our electrostatic calculations allow us to make predictions about the importance of other negatively charged residues in the neighborhood of the BK conduction system in determining BK single channel conductance, and go beyond naive arguments based on screened Coulomb law, whereby one considers only the direct distances of charged residues to the selectivity filter. This was tested experimentally by determining the effect of neutralizing glutamate 322 located in the C-terminal end of S5 on the ion channel conductance.

Figure 1.

Multiple alignment of the primary structure of potassium channel pores from 21 different species computed using Clustalw (http://www.ebi.ac.uk/clustalw/, European Bioinformatics Institute). The signature sequence TVGYGD on the selectivity was used as reference for the alignments. The segments S5, External loop, and P-helix were assigned using prediction of transmembrane helices and topology of protein software (HMMTOP, Hungarian Academy of Sciences, http://www.enzim.hu/hmmtop/). Residues from the beginning of segment S5 to the end of S6 were included in the alignment. RCK2 (Kv1.6), Rattus norvegicus (GI:116435); Kv1.5, Mus musculus (GI:2493594); SkCa-2, Homo sapiens (GI:37955868); KCNA10, Homo sapiens (GI:5031819); Kv1.2, Oryctolagus cuniculus (GI:9652317); Kv2.2, Homo sapiens (GI:27436974); KvEBN1, Homo sapiens (GI:2801452); Shaker, Drosophila melanogaster (GI:288442); SqKv1A, Schistosoma mansoni (GI:510098); Kv1.7, Homo sapiens (GI:14485555); Slack, Rattus norvegicus (GI:11177892); KcsA, Streptomyces lividans (1K4C); KvAP, Aeropyrum pernix (1ORQ); MthK, Methanothermobacter thermautotrophic (1LNQ); cSlo2, Caenorhabditis elegans (GI:71986737); RbSlo, Oryctolagus cuniculus (GI:46396500); mSlo3, Mus musculus (GI:86990444); mslo, Mus musculus (GI:347144); dSlo, Drosophila melanogaster (GI:62472831); rSlo, Rattus norvegicus (GI:58339363); mSlo1, Mus musculus (GI:111607492); hslo, Homo sapiens (GI:46396283).

MATERIALS AND METHODS

Mutagenesis and Channel Expression

The cDNA coding for BK α-subunit (KCNMA) from myometrium (GenBank/EMBL/DDBJ accession no. U11058) was provided by Dr. Ligia Toro (University of California, Los Angeles, CA). The mutations were made in hSlo1 cDNA in pBsta vector (ZM4). All were performed by PCR-based techniques of site-directed mutagenesis by overlapping extension (Sambrook et al., 2001), with PfuTurbo DNA Polymerase (Stratagene). Primers were designed based on the sequences of hSlo's cDNA and ordered from Integrated DNA Technologies, Inc. (IDT Inc.). The PCR products were purified by agarose gel electrophoresis (Sigma-Aldrich), phosphorylated using T4 polynucleotide kinase, and ligated using T4 DNA ligase (Fermentas International Inc.).

Competent Escherichia coli cells, XL1 Blue, were transformed with the ligation products (Stratagene). The transformed colonies were selected by resistance to ampicillin (100 μg/ml) in Luria-Bertani (LB) agar plates and then grown in liquid LB medium with the same antibiotic. The DNA was extracted by QIAprep Spin Miniprep Kit (QIAGEN GmbH) and sequenced by oligo extension. DNA samples with the correct sequences were linearized using the restriction enzyme NotI (Fermentas) and transcribed in vitro using T7 RNA Polymerase (mMessage Machine; Ambion). Transcriptions were performed at 37°C in 10 μl, following the manufacturer's instructions. cRNAs produced were precipitated with LiCl, washed with ethanol 70%, and resuspended in 5 μl water from the kit (Ambion). The final RNA concentration was 2 μg/μl.

RNAs were expressed in Xenopus laevis oocytes. Oocytes were injected with 50 nl RNA solution (100 ng/μl or 10 ng/μl) and stored in ND96 solution at 18°C. Xenopus were purchased from Nasco International Inc. The protocol used to isolate Xenopus laevis oocytes received institutional approval and followed rules and regulations from National Institutes of Health and of the Chilean Servicio Agrícola y Ganadero.

Electrophysiological Recordings and Solutions

1–3 d after cRNA injection, potassium currents were recorded from the oocyte membrane using the inside-out configuration of the patch-clamp technique. All recordings were performed at room temperature (20–22°C). The internal solution contained (in mM): 110 K-MES, 30 mM K-MES, or 1 M K-MES depending on the experiment, 10 HEPES, 2 KCl, different concentrations of free Ca⁺² ranging from 1 to 100 μM, and adjusted to pH 7.4 with methanosulfonic acid. Free calcium was buffered using EGTA, HEDTA, or NTA. In some experiments 60 μM GdCl was added to block native mechanosensitive channels. The external solution and the solution in the patch pipette had the same basic composition; either no calcium was added or it was adjusted with HEDTA to 3 μM. Single channel current was measured from all points current histograms obtained with voltages ranging from −150 to +100 mV, on patches containing one, two, or three active channels.

TEA⁺ blockade experiments were performed in outside-out configuration. The pulse protocol for the TEA⁺ external blockade was as follows: holding potential, 0 mV; prepulse, −100 mV; test pulse, +70 mV, and tail, −100 mV (Thompson and Begenisich, 2003a). The pipette solution contained the same composition described above but with 96 μM Ca²⁺. Barium blockade experiments were performed in inside out configuration (Diaz et al., 1996) with 20 μM Ca²⁺ estimated in bath solution. Charybdotoxin blockade was performed in outside-out configuration. The pulse protocol was as follows: HP, 0 mV; prepulse, −80 or −100 mV, test pulse, +50 mV; and tail, −60 mV. The pipette solution was the same described above and the [Ca²⁺ _i] = 96 μM.

Molecular Model for the BK Pore

Multi alignment of the hSlo sequence with several K⁺ channels was performed as a first step to build a molecular model for the BK channel pore (Fig. 1). This alignment was achieved using CLUSTALW software (Higgins et al., 1994). The model for the human BK pore was built using the primary sequence read from Gene Bank (GI:46396283) and the crystallographic data for KcsA channel (K⁺ channel from Streptomyces lividans; PDB:1K4C) and MthK channel (PDB:1LNQ) as structural references. Following the procedure outlined by Jogini and Roux (2005), we displaced the inner and out helices of KcsA until the backbone atoms superimposed with the equivalent residues of MthK. The result is an open KcsA structure. A homology model of the BK pore was obtained using the program ICM (Abagyan et al., 1994) using the open KcsA x-ray structure as template. Since the extracellular loop of BK is longer than that of KcsA, we performed an extensive conformational sampling of this region using the module Sampling Loop (Monte Carlo) implemented in ICM program. From this, the 112 structures with the lowest energy were analyzed as tentative models of the external loop. For each model the protein hydrogen atoms were added using the HBUILD module of CHARMm version c31b1 (Brooks et al., 1983). Tautomeric states of histidine residues in the model were assigned according to the local environment. Then, the electrostatic potential perturbation generated by the residues D326 and E329 in the external loop was calculated numerically for each structure using the finite-difference Poisson-Boltzman solver of the PBEQ module of CHARMm31. To select the probable structure of the external loop we compared calculated electrostatic potentials with those measured experimentally using TEA⁺ block. From this analysis just one of these conformations was compatible with the experimental data.

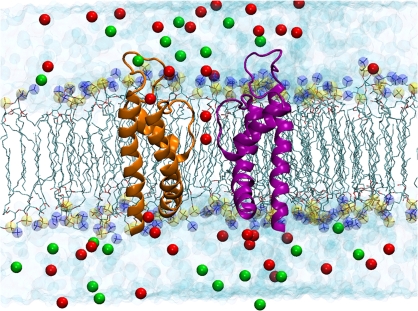
This selected structure was oriented in space to align the symmetry axis of the transmembrane pore with the z axis, and embedded into a preequilibrated phosphatidyl oleoyl phosphatidylcholine (POPC) bilayer oriented parallel to the xy plane in a periodic boundary condition box (103 × 103 × 88 Å) with preequilibrated TIP3P (Jorgensen et al., 1983) water molecules. Two K⁺ ions were associated to the model in positions S1 and S3 of the selectivity filter and a water molecule was placed in site S2. 39 potassium ions were added to the aqueous phase to make it 110 mM K⁺. 23 chloride ions were added to make the system electro-neutral, as it is shown in Fig. 2. The initial configuration of the system was first optimized using energy minimization followed by an equilibration using a molecular dynamics (MD) simulation at 300 K for 500 ps. The system was further equilibrated for 1 ns in the NPT ensemble using progressively decreasing harmonic restraints of 5, 2, and 0.5 kcal/mol Ų applied to the backbone atoms, respectively. The total time for relaxation was 3 ns. All molecular dynamic simulation was performed using the NAMD program (Phillips et al., 2005). The electrostatics interactions were computed with no truncations using the particle mesh Ewald (Essmann et al., 1995) algorithm under periodic boundary conditions. Structures of the protein were saved every 10 ps from the MD trajectory and the electrostatic potential was calculated using the Poisson-Boltzmann (PB) equation. This approach considers several conformations to account for the effect of thermal fluctuations of the lateral chains on the calculated electrostatic potential (Allen et al., 2004).

Figure 2.

Molecular representation of the atomic model of the open BK pore embedded in an explicit POPC phospholipid membrane bathed in a 110 mM KCl aqueous salt solution after 1 ns of MD. The extracellular aqueous phase is on top of the bilayer and the intracellular phase is below the bilayer. The structure embedded into the bilayer was obtained by homology using the 3D structures of KcsA and MthK as templates. The extracellular loop that is into the extracellular aqueous phase was modeled using Loop Search. Potassium ions in the selectivity filter (red spheres) are located in sites S1 and S3. Two opposing monomers of BK are shown using ribbon representation for the secondary structure of the protein. Phospholipid hydrocarbon chains are shown as green sticks. Phosphate atoms are shown as yellow spheres and nitrogen atoms of the phospholipds are shown as blue spheres. Water molecules are drawn as light blue spheres, chloride ions are the green spheres, and the red spheres represent the potassium ions.

Electrostatic Potential Calculations

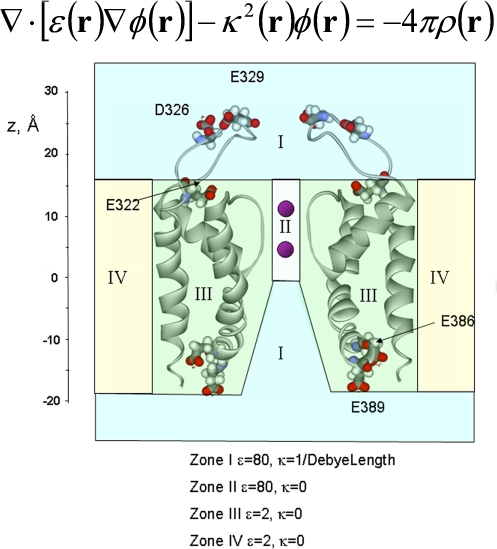
The electrostatic potential, φ(r), was calculated by solving the PB equation (Fig. 3) using the finite-difference method (Warwicker and Watson., 1982). The model of the BK pore was oriented with the pore along the z-axis relative to the membrane (which extends in the xy plane). The negative z-axis corresponds to the intracellular side and the positive z-axis corresponds to the external side of the channel. The geometric center of the protein is at x = y = 0, z = 5 Å, and the membrane was situated between −18.0 < z < 17.0 Å. This z interval adequately covered the transmembrane regions of the model. The channel with all its explicit atoms is embedded into a low dielectric planar slab 35 Å thick with a dielectric constant of 2 representing the hydrocarbon core of the membrane (see Fig. 3). We used a 35-Å hydrocarbon slab since BK channels display the maximum conductance in bilayers of this thickness (Yuan et al. 2004). The aqueous solution, including the water-filled vestibules, was represented as a uniform continuum media with a dielectric constant of 80. To make sure that the proper dielectric constant is assigned to the interior of the pore and the inner vestibule of the channel, a cylinder of radius r = 12 Å and a dielectric constant of 80 was cut out from the membrane slab before the channel structure was overlaid onto it. A water probe of 1.4 Å in radius was used to define the molecular surface corresponding to the dielectric boundary. κ(r), the position-dependent ionic screening constant (Fig. 3) was used when φ(r) was calculated between 17.0 < z < 35 Å and −0.5 < z < −30 Å to account for the ionic strength of the bulk solution. All PB calculations were performed with a cubic grid of 180³ points, with a grid spacing of 0.5 Å and using the PBEQ module (Nina et al., 1997; Im et al., 1998), which is implemented into the biomolecular simulation program CHARMm (Brooks et al., 1983). Residues topologies and atomic partial charges were taken from CHARMM27 force field (MacKerell et al. 1998). The dielectric interface of the protein was set using optimized atomic Born radii (Nina et al., 1997). The protein dielectric constant was set to 2 to be consistent with previous reports (Jogini and Roux, 2005). The electrostatic potential contribution for a particular residue (Δφ_E) was calculated along the z axis at 0.5-Å intervals turning off the all system charges and leaving on the charges of the residue of interest.

Figure 3.

Calculation of the electrostatic potential, φ(r) by solving the PB equation. In the PB equation ε(r) and κ²(r) are the position-dependent dielectric constant and ionic screening constant, respectively, and ρ(r) is the total atomic charge distribution in the system. κ(r) is 0 in zones II, III, and IV, and it is 1/9.8 A⁻¹ for zone I. Internally located residues E386 and E389 and externally positioned residues E322, D326, and E329 are represented as CPK space-filling mode. In solving the PB equation the bilayer was considered a continuum with a dielectric constant of two, the protein as a continuum with a dielectric constant of two and the solutions a continuum with a dielectric constant of 80.

Data analysis and curve fitting were done using LABFIT by Silva, W.P., and Cleide M. Silva. LABORATORY Fit Curve Fitting Software (Nonlinear Regression and Treatment of Data program) V 7.2.36 (1999–2007) was obtained online at www.labfit.net.

Online Supplemental Material

In the supplemental material (available at http://www.jgp.org/cgi/content/full/jgp.200709862/DC1) the model for the human BK pore built using the crystallographic data for KcsA channel (PDB:1K4C) and MthK channel (PDB:1LNQ) as structural references is described in detail.

RESULTS

Single Channel Conductance Measurements in BK Neutralization Mutants

Multiple alignment of the primary structure of BK with other potassium channels shows that BK has a longer S5-P-helix linker segment as compared with KcsA, KvAP, MthK, or Shaker (Fig. 1). Prediction of the transmembrane segments and topology of the protein places this loop on the extracellular side of the membrane, creating an extended turret in BK channels. This turret contains two negatively charged residues: Asp326 and Glu329 (Figs. 1 and 3). The other K⁺ channels studied have only one negative amino acid residue or none. Since BK has the largest single channel conductance, it is possible that the electrostatic potential caused by the extra negative charges concentrate K⁺ ions, enhancing the single channel conductance. To evaluate the effect of fixed charges near the conduction pore of the BK channel, we measured the single channel conductance in mutants where these charges were neutralized. We measured single channel currents induced by the mutant channels E329Q and D326N and the double mutant E329Q/D326N using the patch clamp technique in the inside out configuration. In the E329Q and D326N mutant we neutralized a total of four negative charges, and in the double mutant eight negative charges were neutralized in the outer vestibule of the channel.

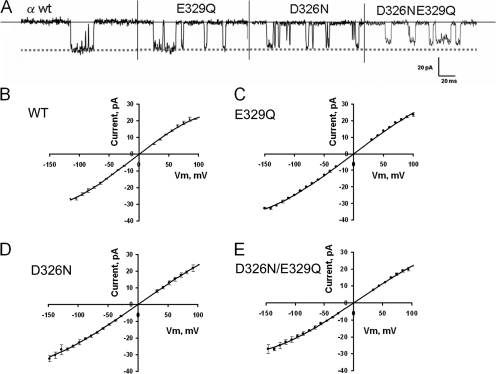
Fig. 4 A shows samples of WT BK and mutant single channel records obtained at −100 mV, respectively. The single channel sample records show only a marginal decrease of the current due to the charge neutralization. Histograms of potassium current were constructed from current records taken at different voltages under symmetric 110 mM K⁺ to construct current–voltage curves. Single channel current was measured from the difference of the peaks in the current amplitude histograms. Fig. 4 (B–E) shows the current–voltage curves obtained for the WT BK and the neutralization mutants. The data points were collected at 15–20 different voltages on at least three different experiments for each different channel. A total of 50–85 histograms were collected for each mutant. Since there is a clear sublinearity in the I-V relations, the data points were fitted using a third degree polynomial to estimate the expected current for each voltage. A correction on the voltage axis was introduced to let the polynomial intersect the current axis at V = 0, as expected for symmetric K⁺ solutions. Fig. 4 B is the I-V relationship for the WT channel. The zero-voltage conductance is 270 ± 8 pS (mean ± 95.4% confidence limit). For the E329Q channel this conductance is 270 ± 5 pS (Fig. 4 C), a value not differing from the conductance obtained for the WT BK channel. For the D326N mutant the zero-voltage conductance is 232 ± 7 pS, which is significantly lower than the control (Fig. 4 D). The double neutralization mutant shows a slight outward rectification and the zero-voltage conductance is 229 ± 8 pS (Fig. 4 E). In conclusion, the two different mutations (D326N or E329Q) used to remove four negative charges do not reduce the single channel currents to the same extent, suggesting that these sites are not equivalent in their effects on the conductance.

Figure 4.

Negatively charged amino acids located in the external loop have a marginal effect on single channel conductance. (A) Samples of single channel current fluctuations induced by the WT BK channel and the neutralization mutants and recorded at −100 mV in symmetric 110 mM K⁺. Current–voltage relationship for WT (B) and neutralization BK channel mutants (C–E). Single channel current was measured from the peaks of all-points histograms of the current intensity records of membranes containing 1, 2, or 3 channels. (C) Current–voltage relationship for the E329Q mutant. (D) Current–voltage relationship for the D326N mutant. (E) Current–voltage relationship for the D326N-E329Q double mutant. Experiments were performed at room temperature, 20–22°C.

Differences between WT and Neutralization Mutants Channels Are Explained by an Electrostatic Mechanism

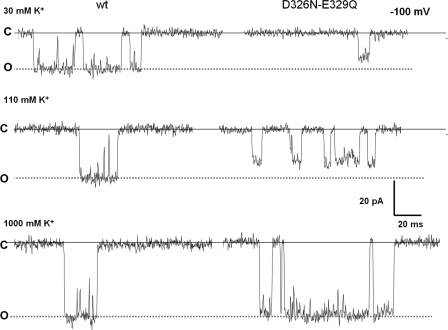
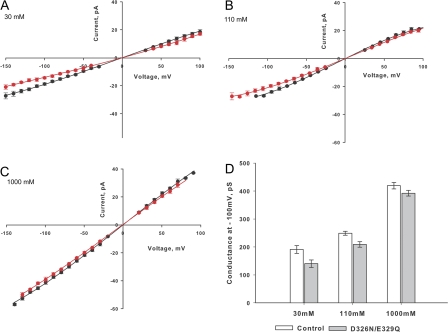
To investigate the mechanism underlying the decrease in single channel conductance measured in the neutralization mutants, we measured conductance at three different salt concentrations. It can be seen in Fig. 5 that the differences in single channel current between WT BK and the D326N-E329Q mutant are negligible at 1 M symmetrical K⁺ and then increase as the K⁺ concentration decreases. In Fig. 6 (A–C) we show the I-V relationships at 30, 110, and 1,000 mM K⁺, respectively. The single channel conductance at −100 mV measured from the I-V curves determined for each concentration and processed as those of Figs. 4 (B–E) are displayed in the bar plot depicted in Fig. 6 D. For the WT BK these are 188 ± 6, 249 ± 12, and 419 ± 8 pS at 30, 110, and 1,000 mM, respectively. On the other hand, single channel conductances for the double mutant are 141 ± 5, 208 ± 11, and 392 ± 8 pS at 30, 110, and 1000 mM, respectively. Such an effect is expected for an electrostatic mechanism since the negative potential induced by the negatively charged residues increases as the ionic strength is lowered. Thus, from a microscopic point of view it may concluded that the rate of enhancement of the differences in single channel conductance between WT and neutralization mutants BK channels is a consequence of an increase in the local K⁺ concentration. Also, as expected from a purely electrostatic mechanism, we observed that the outward rectification became more pronounced with decreasing ionic strength (Fig. 6, compare A and C). These results clearly show that the effect of neutralizing the charges contained in the external loop is much weaker than that promoted by decreasing the number of negative charges contained in the internal vestibule of the BK channel (Brelidze et al., 2003).

Figure 5.

Comparison of single channel currents fluctuations of the D326-E329Q double mutant with WT BK channel recorded at different K⁺ concentrations. Samples of single channel current fluctuations at −100 mV induced by the WT BK channel and the neutralization mutant D326N-E329Q at 30, 110, and 1,000 mM symmetrical K⁺.

Figure 6.

Current–voltage relationship for the D326N-E329Q mutant and WT BK channel at different K⁺ concentrations. (A) I-V relation obtained in symmetrical 30 mM K⁺ for the WT (solid black circles) and the D326N-E329Q mutant (solid red circles). Points are the mean of three to five different experiments ± SD. (B) I-V relation obtained in symmetrical 110 mM K⁺ for the WT (solid black circles) and the D326N-E329Q mutant (solid red circles). Points are the mean of two to five different experiments ± SD. (C) I-V relation obtained in symmetrical 1,000 mM K⁺ for the WT (solid black circles) and the D326N-E329Q mutant (solid red circles). Points are the mean of three to six different experiments ± SD. (D) Bar graph of single channel conductance at different K⁺ for the mutant and for WT. *, P < 0.05; **, P < 0.005.

Determination of the Electrostatic Potential Using Ion Blockers

An electrostatic mechanism as the one describe above should affect the block induced by positively charged external blockers such as TEA⁺ and charybdotoxin. Under the assumption that mutations do not induce structural changes in the blocker binding sites, the whole effect of neutralizing the negative charge at the channel vestibules on the equilibrium blocker binding should be a decrease in the blocker on rate constant (k_on; Toro et al., 1994). In other words, the concentration of the positively charged blocker in the neighborhood of the conduction machinery of the channel should be higher in the WT BK channel than in the neutralization mutants. The observed ratio between the zero-voltage second rate-order rate constant k_on^mut/k_on^WT and, therefore, the blocker zero-voltage dissociation equilibrium constant ratio, K^mut_D/K^WT_D is expected to vary as a Boltzmann distribution with respect to the blocker net charge, z, and the electrostatic potential at the blocking site, Δφ, produced by the presence of the negatively charged residues at the channel entrances:

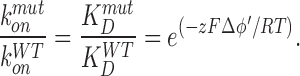(1)

BK channels are blocked by TEA⁺ and show a high affinity for this quaternary ammonium ion (Blatz and Magleby, 1984; Vergara et al., 1984; Yellen, 1984). The kinetics of block by TEA⁺ are rapid (Villarroel et al., 1988) and TEA⁺ appears to reduce the observed channel current. Because of this effect, the open probability is modified by the presence of the blocker according to the relation:

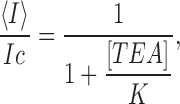(2)

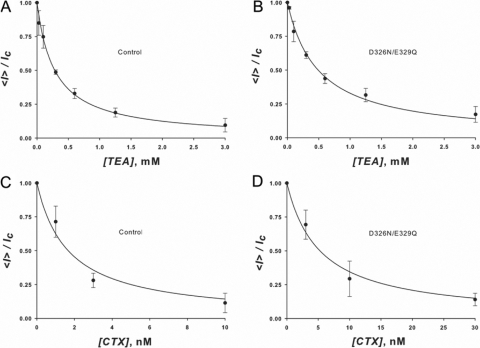
where <I> is the current in the presence of the blocker, I_C the current obtained in its absence, and K the dissociation constant of the blocking reaction. Fig. 7 A illustrates the dependence of the macroscopic BK currents on TEA⁺ concentration at +70 mV. The solid line is a fit to the data using Eq. 2 with K^WT_TEA = (2.9 ± 0.3) × 10⁻⁴ M. The double mutant D326N/E329Q data, on the other hand, is well fitted using Eq. 2 and a K^mut _TEA = (4.9 ± 0.3) × 10⁻⁴ M (Fig. 7 B). From the ratio of these two experimentally obtained dissociation constants and using Eq. 1, we obtain a Δφ' = 13 ± 2 mV. This is the change of surface potential in the outer vestibule caused by the mutation D326N/E329Q, measured at 110 mM K⁺.

Figure 7.

(A and B) TEA⁺ blockade. The figures are plots of the macroscopic current measured at +70 mV on outside out patches at various outside TEA⁺ concentrations normalized by the current measured in the absence of TEA⁺. (A) Control wt BK channels. (B) D326N/E329Q BK mutant channels. Data points represent the average and standard deviation of the normalized current measured in three membranes. TEA⁺ dissociation constants are 1.9 ± 0.3 × 10⁻⁴ M for the control channels and 4.9 ± 0.3 × 10⁻⁴ M for the double mutant channels. From the effect of the mutation on the TEA⁺ dissociation a constant surface potential difference of 13 ± 2 mV was calculated using Eq. 1. (C and D) CTX blockade. The figures are plots of the relative macroscopic current measured on outside out patches at various outside CTX concentrations normalized by the current measured in the absence of the blocker. (C) Control channels. (D) D326N/E329Q BK mutant channels. Data points represent the average and standard deviation of the normalized current measured in three membranes. CTX dissociation constants are 1.7 ± 0.3 × 10⁻⁹ M for the control channels and 5.3 ± 0.3 × 10⁻⁹ M for the double mutant channels. From the effect of the mutation on the CTX dissociation constant, a surface potential difference can be calculated using Eq. 1. Δφ' is 28.8 mV for z = 1 and 4.8 mV for z = 6. Assuming that the actual surface potential difference is that measured using TEA⁺, the apparent z of CTX is 2.1.

Charybdotoxin, a potent inhibitor of BK channels (Miller et al. 1985), contains seven positively and one negatively charged amino acid. An electrostatic mechanism (e.g., Eq. 1) predicts that the neutralization of the external charges should have a much larger effect on the blockade induced by this polyvalent cation than on TEA⁺. The charybdotoxin dose–response curves for the WT BK channel and the D326N/E329Q double mutant are shown in Fig. 7, C and D, respectively. Relative macroscopic currents were plotted against charybdotoxin concentration and fitted with an equation similar to Eq. 2 with K ^WT _CTX = (1.7 ± 0.3) × 10⁻⁹ M and K ^mut _CTX = (5.3 ± 0.3) × 10⁻⁹ M. The ratio K^mut_CTX/K^WT_CTX = 3.3, and as an electrostatic mechanism demands, this ratio is larger than K^mut_TEA/K^WT_TEA = 1.75. Assuming z = 6 for CTX and using Eq. 1 we obtain a Δφ' ∼5 mV, a value much lower than the one obtained when using TEA⁺ as a reporter of the electrostatic potential. Charged peptides, however, due to their large size, cannot be considered as point charges as they exert a smaller effect on the potential than that predicted by the classical screening theory (e.g., Alvarez et al., 1983). In fact z for CTX can be obtained using Eq. 1 and the Δφ' obtained using TEA⁺ as the blocker ion. Using the electrostatic potential obtained from the TEA⁺ experiments, the ratio K^WT_CTX/K^mut_CTX, and Eq. 1, the effective valence of CTX, z = 2.1.

Barium Block

Barium ions block BK channels when present in the intracellular solution (Vergara and Latorre, 1983). We used Ba²⁺ block to estimate the electrostatic potential induced by the ring of negatively charged glutamate residues located at the entrance of the channel internal vestibule. Negative charge neutralization is expected to decrease the local Ba²⁺ concentration of and therefore decrease the rate of Ba²⁺ block. Since Ba²⁺ block is voltage dependent, we measured the relaxation of the current after a voltage step from 0 mV to various positive voltages. At 0 mV the BK channels are open but not blocked; when the membrane is further depolarized, Ba²⁺ blocks the open channels and the macroscopic current relaxes from an initial current, I_o, to a lower steady-state current, I_ss, following an exponential time course characterized by a time constant, τ. In this case I_ss/I₀ and the time constant τ are given by the relations:

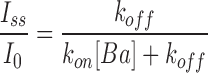(3)

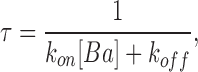(4)

where k _on is the on rate constant, [Ba] is the local barium concentration, and k _off is the off rate constant. From the analysis of the current relaxation, the product k _on[Ba] and k _off were obtained. We limited analysis of the current relaxation curves to those where I_ss/I₀ was 0.2 or less in order to get an accurate determination of the time constant τ of I_ss/I₀. The relaxation constant is dominated by k _on[Ba] in this interval, therefore estimation of k _off less accurate than k _on[Ba]. For this interval we found that k _off rate constants were independent of voltage and Ba²⁺ concentration, and averaged 0.82 ± 0.48 s⁻¹ for the WT channels and 0.55 ± 0.29 s⁻¹ for the E386N/E389N channels. The range of k _on[Ba], on the other hand, extended up to 27 s⁻¹. We checked that k _on[Ba] was indeed a linear function of [Ba]_o the bulk Ba²⁺ concentration when measured at a constant voltage. k _on[Ba] changes exponentially with voltage and is significantly smaller when measured on E386N/E389N mutant channels as compared with WT channels. This is because the local Ba²⁺ concentration is smaller in the charge neutralization mutants than in the WT, compared at equal bulk Ba²⁺ concentration. We calculate the local electrostatic potential from this decrease in k _on[Ba]. Local Ba²⁺ concentration, [Ba], depends on the bulk Ba²⁺ concentration, [Ba]_0, and a Boltzmann factor determined by the electrostatic potential φ: [Ba] = [Ba]₀ e ^{−2φ F / RT}. The voltage-dependent rate constant is the zero-voltage rate constant k _on,0, multiplied by a Boltzmann factor on the membrane potential 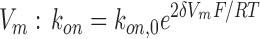. Therefore,

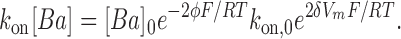(5)

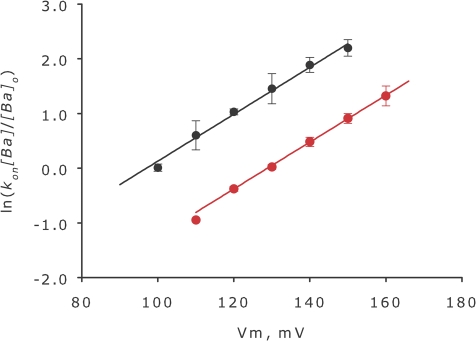
The factor 2δ accounts for the voltage dependency of the rate constant, while F, R, and T have their usual meaning. In Fig. 8 we use a linear form of Eq. 5 to display our results for the WT and E386N/E389N mutant.

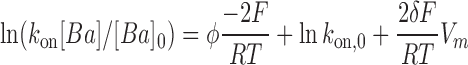(6)

The data are described well by two parallel straight lines with slopes 2δF/RT and intercepts at V_m = 0 that depends on the surface potential, φ and k _on,0 . The lines in Fig. 8 are parallel and the vertical distance between them is proportional to Δφ, the difference in surface potential between the WT and E386N/E389N mutant.

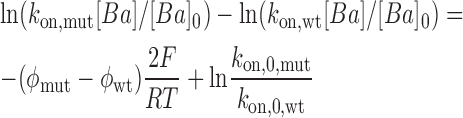(7)

We assume here that charge neutralization of distant residues does not change the structure of the Ba²⁺ binding site and, therefore, k _on.0.mut = k _on.0.wt. Under this assumption the value of Δφ is 17 ± 2 mV. We argue that this is a reasonable assumption since the k _off rate constants are essentially unmodified by neutralization of residues E386 and E389 and probably this argument is also valid for the TEA⁺ blockade as well. This is the change of surface potential measured at 110 mM K⁺ in the inner vestibule caused by the mutation E386N/E389N.

Figure 8.

Ba²⁺ blockade. On rate constant of Ba²⁺ blockade as a function of membrane potential. The product of barium block on rate constant times the local barium concentration, k_on[Ba], was calculated from the relaxation experiments. Since barium block is voltage dependent the kinetics of barium entry to the blocking site can be examined using voltage jump experiments and observing the decay of the current as channels are blocked. Constants k _on[Ba] and k _off were calculated from the extent of the blockade and the time constant according to Eqs. 3 and 4. In this figure, the logarithm of the on rate constant standardized to 1 μM bulk barium concentration is plotted as a function of membrane potential for the WT channels (black symbols) and the E386N/E389N double mutant BK channels. The vertical distance of the two straight lines is Δφ times 2F/RT according to Eq. 7, where Δφ is 17 ± 2 mV.

Barium and potassium may compete for the binding site in the selectivity filter and the impact of this effect on the estimate Δφ is unknown. It is possible, however, to make an educated guess by equating degree of site occupancy with conductance. Since the single channel conductance of E386N/E389N channels is about half the conductance of the WT channels, we can assume that the fraction of time the binding site remains empty is larger in the mutant by a factor of 2. If this is so, then k _on,0,mut is twice k _on0,wt. Introducing this correction, Δφ would increase to 26 mV.

The BK Pore Molecular Model

We measured a 13 ± 2 mV change in electrostatic potential at the TEA⁺ binding site located in the outer vestibule caused by mutation D326N/E329Q. For this neutralization mutant the single channel conductance was 18% lower the control. We measured a 17 ± 2 mV change in electrostatic potential at the Ba²⁺ binding site located in the inner vestibule caused by mutation E386N/E389N. Single channel conductance for this mutant is only 50% that of the WT, as measured by Brelidze et al. (2003). We conclude that the electrostatic potentials induced by the ring of charges formed by residues D326/E329 and E386/E389 are not very different. However, the conductance changes caused by these neutralization mutants are clearly dissimilar. These findings appear to conflict with the notion that the effects of these charge mutations on single channel conductance are purely electrostatic in origin, though one has to be careful in relying on naive and simplified considerations solely based on distances and shielded Coulomb interaction in the interpretation of the experimental data. In an attempt to resolve this discrepancy, we decided to calculate the electrostatic potential along the full length of the intracellular and extracellular vestibules using the Poisson-Boltzmann equation on a realistic molecular model of the pore. While continuum may be good for the wide aqueous vestibules, detailed all-atom MD is necessary for a realistic treatment of ions and water inside the narrow filter (Berneche and Roux, 2001). However, our interest is limited to the wider parts of the pore, and we did not examine the electrostatic potential inside the narrow filter proper where a continuum dielectric representation would be inaccurate anyway.

The molecular model of the BK pore was built using homology modeling taking the structure of the KcsA and MthK channels as templates following the procedure of Jogini and Roux (2005) (Fig. 2). The pore model includes segments S5 through S6 of the BK channel. Two other channels, KvAP and Kv1.2, have been crystallized in an open state (Jiang et al., 2003; Long et al., 2005) and they show narrower internal vestibules when compared with the internal vestibule of the MthK channel. Our decision in choosing the MthK channels as template for the BK channel pore is based on the following prior observations: first, Li and Aldrich (2004) concluded, on the basis of the characteristics of quaternary ammonium block, that BK channels show an enlarged inner vestibule compared with other K⁺ channels; and second, the geometry of the inner cavity was probed by testing the effect of sugars of different sizes on the single channel current (Brelidze and Magleby, 2005). The results obtained using this experimental strategy suggest an effective diameter for the entrance to the inner vestibule of ∼20 Å, a value close to that found for the inner vestibule of MthK channels. Also we note here that as in MthK channels, BK channels show the presence in S6 of a highly conserved glycine residue that in MthK serves as a gating hinge where the inner helices are sharply bent away from the central axis when the channel opens. Furthermore, BK channels do not contain in the S6 helix the PVP motif present in Shaker, Kv1.2, and other voltage-dependent K⁺ channels (see Fig. 1). In Kv1.2, the open channel shows that the S6 inner helices curve at the PVP motif with these running almost parallel to the membrane near the intracellular interface (Long et al., 2005).

A gap in the KcsA and MthK sequences was introduced in order to align the structure with hSlo. This gap corresponds to the extracellular loop connecting S5 with the P-loop. It is in this loop where the residues forming the extracellular ring of charges are located. Since there is no homologous structure to copy from, we had to model this loop using a conformational space search procedure. Since the method used yielded many probable structures, we selected the conformation that was consistent with our experimentally determined electrostatic potentials.

Electrostatic Potential Calculations on the Molecular Model of the BK Pore

Electrostatic potential calculations were performed using the Poisson-Boltzmann equation on a BK model embedded in a lipid bilayer considered as a continuum with a dielectric constant of 2 (Fig. 3). We use the Poisson-Boltzmann equation assigning the appropriate dielectric constant to the various phases: protein, bilayer, and water, and letting the distribution of the density of the freely movable charges to comply with electrostatic constraints (Fig. 3). Charges in the aqueous phase were placed to simulate a 110 mM K-MES solution.

The results of the electrostatic potential differences for each residue, Δφ, calculated along the pore axis (x = 0, y = 0, −30 < z < 35 Å) are displayed in Fig. 9. The electrostatic potential caused by residue j at location z, was calculated by turning off all the charges in the system but not those of residue j. This procedure is correct because the PB continuum electrostatic equation is linear as discussed in depth by Jogini and Roux (2005). The data shown on Fig. 9 are the result of this calculation multiplied by −1 in order to obtain a positive number representing the change in electrostatic potential expected when the negative charge of residue j is turned off Δφ(z,j). Values of Δφ(z,j) are the average and standard deviation calculated over 100 structures obtained by MD where the backbone of the protein was under a harmonic restraint of 5 kcal mol⁻¹ and the lateral chains of the residues were free to move.

Figure 9.

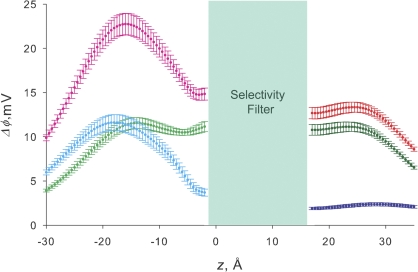
Electrostatic potential difference along the axis of the pore. Ordinate represents the change in local electrostatic potential, in mV, observed when the charge of the different residues is turned off. Error bars are the standard deviation of the potential calculated over 100 different structures sampled during a 1-ns MD simulation. Abscissa is the z coordinate in Angstrom units. z = 5 is defined as the geometric center of the selectivity filter. The entrance of the extracellular mouth of the pore is at z = 17 Å and the intracellular mouth is at z = −15.5 Å. The magenta line describes the electrostatic potential differences calculated for the neutralization of the acidic amino acids located at the inner opening of the channel. The light green line is the calculation for the neutralization of residue Glu386. The cyan line is the result of the neutralization of Glu389. The red line is the electrostatic potential associated with turning off the charges of residues Asp326 and Glu329. Green and blue lines represent the individual contributions of Asp326 and Glu329, respectively.

Fig. 9 shows the electrostatic potentials calculated along the z axis. Each curve represents the change in electrostatic calculated when turning off the charge of the indicated residues. Electrostatic calculations on the external vestibule are based on a conformation of the external loop able to account for the experimental results as described in Materials and methods. We measured the position of residues 326 and 329 and calculated the electrostatic potentials at the external opening of the selectivity filter on 112 possible conformations of the turret. D326 distance ranged from 13 to 313 Å and the electrostatic potential change associated to the charge neutralization range was 1 to 35 mV. For E329 these figures were 9 to 35 Å and 2 to 127 mV. The electrostatic potential change calculated,Δφ, for the double neutralization of Glu329 and Asp326 is 13 mV in the external vestibule near the selectivity filter (z = 17 Å; Fig. 9, red line). This value of Δφ is the same we measured using TEA⁺, such that the structure of the external loop we have chosen quantitatively explains this experimental result. The structure also explains the differential effect on single channel conductance of neutralization of residues Asp326 and Glu329. The electrostatic potential change calculated for neutralization of Asp326 in is on the average 11 mV (Fig. 9, green line). Fig. 9 also shows that the electrostatic potential induced by Glu329 is negligible (2 mV, blue line). This result explains the reduction of the single channel conductance observed for the mutant D326N and the lack of effect of the neutralization mutation E329Q. We conclude that the conformation of the external loop proposed is consistent with our experimental results. In this model, charged residues Asp326 and Glu329 are submerged into the external solution, and Asp326 is closer to the axis of the pore than Glu329. Asp326 carboxyl oxygen atoms are located in a 14-Å radius ring centered at the pore axis, and those of Glu329 in a 21-Å radius ring We computed the radial distribution function of the carboxyl oxygen atoms around x, y, z = 0, 0, 17, and the TEA⁺ binding site on 100 structures sampled during the MD with the backbone atoms under a 5 kcal mol⁻¹Å⁻² harmonic restraint. Radial distribution function peaks at 16.2 Å (range 15.8–20.0) for Asp326 and 23 Å (range 21.6–24.2) for Glu329. The details of the conformation of the external loop are still unknown because the structure became unstable under unconstrained MD.

Electrostatic calculations on the inner vestibule, on the other hand, are based on a structure constructed using a homology modeling procedure that is independent of our single channel conductance or Ba²⁺ block experimental results, with this structure being stable under unconstrained MD. Radial distribution function of the carboxyl oxygen atoms of Glu386 around x, y, z = 0, 0, −2, the Ba²⁺ binding site (Jiang and MacKinnon, 2000), is centered at 20.2 Å and extends from 18.4 to 20.7 Å. For Glu389 the radial distribution function peaks at 22.4 Å and ranges from 21.0 to 23.5 Å. Electrostatic potential difference is 15 mV at z = −2 Å was calculated for Glu386 and Glu389 double neutralization (Fig. 9, magenta line). The Δφ value is in good agreement with that determined experimentally using Ba²⁺ block. The contributions to the electrostatic potential of E386 and E389 are 11 and 4 mV, respectively (Fig. 9, light green and cyan lines, respectively). This result was unexpected since these two charges have the same effect on single channel conductance (Brelidze et al., 2003). As seen on Fig. 9, the Δφ values change dramatically with distance and peak to 22 mV at z = −15.5 Å, the mouth of the inner vestibule. At this distance the Δφ values are the same for Glu386 and Glu389. This finding demonstrates that these residues form a low potential energy for potassium at the inner entrance of the pore where potassium ions are concentrated, allowing high conduction rate. The existence of such potassium binding site in the Shaker channel was demonstrated by Thompson and Begenisich (2003b). Our PBEQ calculation shows that inversion of the charge substituting acidic amino acids by positively charged residues (Brelidze et al. 2003; E321K/E324K) on the intracellular mouth of the pore adds 43 mV to the electrostatic potential at the mouth of the inner vestibule (unpublished data).

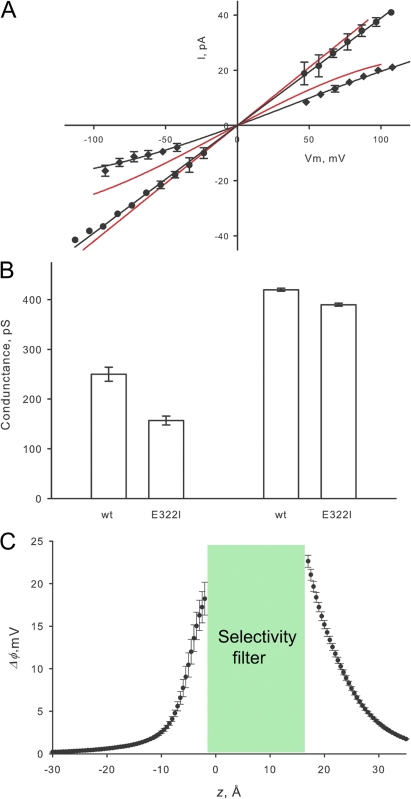
A well-conserved charge in most K⁺ channels is a glutamate located in position 322 in BK. In Shaker this negative charge corresponds to E418 (Fig. 1). In our homology model glutamate 322 is located inside the membrane as shown in Fig. 3. The distance measured from Glu322 to the TEA binding site is 17 Å. We speculated that charge neutralization of Glu322 should have an electrostatic effect of potassium conductance larger than the electrostatic effect of Asp326. This is because Glu322 is placed in a low dielectric constant region (Region III in Fig. 3) while Asp 326 is in a high dielectric constant region. (Region I in Fig. 3) To test this prediction we made the neutralization mutant E322Q but it did not express potassium currents. Mutation E322I expressed potassium currents in Xenopus oocytes, and we were able to measure single channel currents in 110 mM K-MES. The result is shown in Fig. 10. Single channel currents measured in 110 mM K-MES on E322I are lower than those of the WT at all voltages, and the I/V curve reveals an outward rectification: inward currents are lower than outward currents at the same absolute voltage (Fig. 10 A). E322I single channel conductance measured at −100 mV is 157 ± 9 pS, significantly lower than that of the WT, 250 ± 14 pS (Fig. 10 B). To check whether or not the effect of neutralization of Glu322 is due to an electrostatic mechanism, we measured single channel conductance in 1 M K-MES. We found, as an electrostatic mechanism demands, that the single channel currents in 1 M K-MES of the mutant were very close to those of the WT. Conductance was 390 ± 3 pS for E322I and 420 ± 3 pS for the WT channels (Fig. 10 B). We calculated the contribution to the electrostatic potential of residue Glu322 on the homology model using the Poisson-Boltzmann equation. Fig. 10 C shows that the differences Δφ(z,j) promoted by the mutation neutralization of Glu322, Δφ(E322) is maximal at the entrances of the selectivity filter and decays with distance along the vestibules. We calculated 23 ± 1 mV for the external entrance and 18 ± 2 mV for the internal entrance. This latter figure is even larger than Δφ(E386)+ Δφ(E389), the residues of the inner ring of eight negative charges (Brelidze et al. 2003). The result of the Poisson-Boltzmann calculation suggests that the electrostatic potential effect propagates from residue Glu322 located on the extracellular side of the channel to the intracellular vestibule. To check this point we measured the electrostatic potential on the intracellular vestibule using Ba²⁺ block. In contrast to the calculated contribution of this residue to the electrostatic potential using the Poisson-Boltzmann equation, Ba²⁺ block reported that the mutation E322I caused no change in the electrostatic potential of the internal vestibule. Therefore, the experimental evidence indicates that there is not transmembrane propagation of the electrostatic potential produced by Glu322. We do not have an explanation for these findings but a possible problem of the electrostatic calculation using the Poisson-Boltzmann equation may reside in the assumption of a continuous dielectric (ε = 2) for the whole protein milieu (zone III, Fig. 3).

Figure 10.

Removing the ring four negative charges (Glu322) in the external mouth of the BK channel induces outward rectification. (A) Single channel current measured as a function of membrane potential for mutant E322I (black dots and solid line) compared with the WT channels (red line) measured in symmetrical 110 mM K-MES and 1 M K-MES. (B) Column plot of the average single channel conductance measured at −100 mV for the control and double mutant channels at 110 mM K-MES and 1 M K-MES. (C) Electrostatic potential calculated associated with turning off the charges of residue Glu322.

DISCUSSION

The crystal structure of K⁺ channels revealed a highly conserved selectivity filter adjoining a shallow external vestibule and a deep internal vestibule that is wide for the open channel and narrow for the closed channel (Doyle et al., 1998; Jiang et al., 2002, 2003; Kuo et al., 2003; Long et al., 2005). At physiological concentrations of K⁺, the selectivity filter is occupied by more than one ion and ion–ion interactions ensure a high ion throughput. This structure implies that nature has optimized ion channels to conduct ions given that the selective steps in ion transport are circumscribed to the short (∼12 Å) selectivity filter. On the other hand, the conductance of a channel depends on the concentration of permeant ions located near the entrance to the selectivity filter. This concentration is determined by the bulk ion concentration and the local electrostatic potential. The latter is a function of channel geometry and the density, location, and sign of the fixed charges located in the pore vestibules. The role played by fixed charges in controlling ion permeation has been previously investigated assuming the geometry and charge distribution for the vestibules (Dani, 1986; Jordan, 1987; Cai and Jordan, 1990; Naranjo et al., 1994; Wilson et al., 2000; Nadler et al., 2004). In these cases, the Poisson-Boltzmann equation was solved for the particular geometry chosen for the vestibule. The importance of strategically located charged groups in providing an electrostatic potential that dominates cation conductance is exemplified in the case of the acetylcholine receptor (AChR) channel. In this channel a ring of aligned glutamate residues lining the internal entryway enhances the conduction of K⁺ and increases affinity of the pore-blocker Mg²⁺ (Imoto et al., 1988). More recently, Wilson et al. (2000), by replacing glutamates with glutamines, were able to show that the intrinsic electrostatic potential in the intracellular end of the AChR channel is almost entirely due to this ring of charge and determines the channel conductance to alkali cations.

The x-ray structure of KcsA K⁺ channel reveals the channel in its closed configuration (Doyle et al., 1998). The crystallography of the bacterial Ca²⁺-activated K⁺ channel MthK (Jiang et al., 2002), on the other hand, provided an insight into the structure of an open channel and this structure can be used as a template to infer the molecular characteristics of other K⁺ channels. This in turn allows solving the Poisson-Boltzmann equation using a realistic geometry based on structural foundations to determine the electrostatic potential landscape along the conduction machinery of the channel (e.g., Jogini and Roux, 2005). In particular, since conduction and block in BK channels are known to be affected by surface charges (MacKinnon and Miller, 1989a; MacKinnon et al., 1989; Toro et al., 1994; Brelidze et al., 2003, Haug et al., 2004; Zhang et al., 2006), it is of particular interest to obtain a detailed electrostatic potential profile along the BK channel pore.

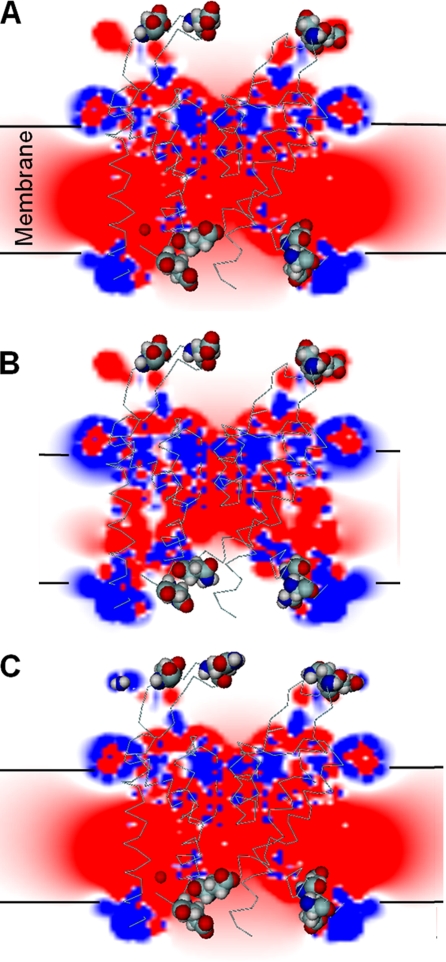
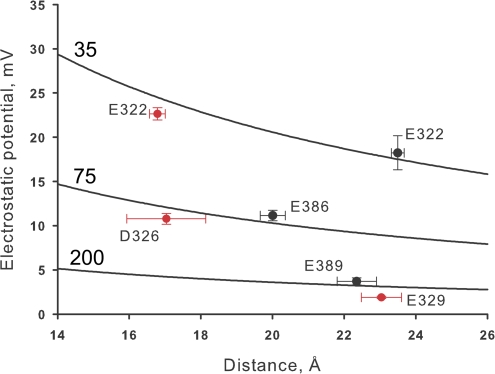
We have shown here that the contribution to the electrostatic potential of the external side of the channel is quite different to that of the charges located on the inner side of the channel. We conclude that the internal ring of charges is able to modulate BK single channel because they are located in a region of the protein surrounded by the lipid bilayer. This situation is analogous to the large electrostatic effect of the pore α helices of the KcsA channel induced by the surrounding low dielectric constant medium (Roux and MacKinnon, 1999; Roux et al., 2000). In this case the dipoles of the α helices are able to stabilize a K⁺ ion positioned in the pore central cavity. What is notable is that this stabilization occurs even though the center of the cavity is located 8 Å from the nearest carbonyl oxygen at the C terminus of the helices. This result is contrary to expectations since the 50 waters molecules contained in the cavity are expected to shield the electric field of the α-helix. The long-range electrostatic effect of the pore α helices in the pore cavity is due to an amplifying effect induced by the low dielectric bilayer environment. On the other hand, our electrostatic calculations predict a very low electrostatic effect on the channel conductance mediated by the external ring of charges. These negative charges are screened out by the external solution. The differential effect of the internal and external negative charges on the electrostatic potential landscape is illustrated in Fig. 11. Fig. 12 plots of the electrostatic potential contribution of a given residue against the distance measured from the residue to the corresponding mouth of the selectivity filter. The figure shows that the electrostatic potential cannot be described using a simple 1/distance function. The lines on the plot are functions of the electrostatic potential calculated from Coulomb's law equation using different dielectric constants: 35, 70, and 200. These large dielectric constants reflect the shielding of the fixed charges by the freely moving ions in the solutions bathing the channel.

Figure 11.

Electrostatic potential maps (EPMs). The figures show in pseudo colors the electrostatic potential obtained solving the Poisson-Boltzmann equation. The map corresponds to the electrostatic potential on the plane x = y = 0. The extracellular space is represented on the top of each figure and the intracellular space is below the bilayer. In blue are shown the positive potential (>20 mV) and in red are shown the negative potential (<−20 mV). The map was merged with a 3D representation of the α carbon trace of the BK protein. Amino acids Asp326, Glu329, Glu386, Glu389 are shown in CPK space-filling mode. Calculations were performed using the PBEQ module of CHARMM28, and figures were drawn using the program DINO: Visualizing Structural Biology (2002), http://www.dino3d.org. (A) The EPM for the WT hSlo structure. The plane cuts through the bilayer, the protein, and the water-filled vestibules. The electrostatic potential inside the protein and the lipid bilayer is negative (red) and neutral on the bulk of the aqueous phase (white). The water-filled vestibules of the channel have negative electrostatic potential (red to pink color). (B) The EPM for the neutralization mutant E386N/E389N, in this mutant the intracellular vestibule is no longer at negative potential (white). (C) The EPM for the mutant D326Q, E329N. Neutralization of these external negative charges produces only marginal changes in the electrostatic potential map of the BK pore.

Figure 12.

Calculated electrostatic potentials are not a simple functions of distance. Electrostatic potentials are plotted in the vertical axis and the distances to the carboxyl group in the horizontal axis. Electrostatic potentials calculated at the internal end of the selectivity filter are represented with black symbols, the coordinates of this site are x = 0, y = 0, z = −2 Å. Electrostatic potentials calculated at the internal end of the selectivity filter (x = 0, y = 0, z = 17) are represented with red symbols. Error bars on the horizontal axis are the distance ranges read from the radial distribution function computed of 100 snapshots of an MD simulation where the protein backbone atoms were under a 5 kcal per angstrom square harmonic restraint. The three lines drawn represent the electrostatic potential as a function of distance calculated using 35, 75, or 200 as dielectric constants.

Alignment of the S5 transmembrane domains for different K⁺ channels shows the presence of a conserved glutamate (E322) near the C-terminal end (Fig. 1). The structural model we obtained for the BK pore indicates that E322 is embedded in a hydrophobic environment close to the lipid–solution interface where it makes a hydrogen bond with the protein backbone. The long-range electrostatic effect of this residue is due, as is the case of the pore helices and the negatively charged residues located in the internal vestibule, to an amplifying effect induced by the low dielectric bilayer environment. In this study, we show that BK channels double their conductance at negative potentials by using a ring of four negative charges located near the external entrance of the selectivity filter without much effect on channel gating. In Shaker, neutralization of this glutamate residue (E418Q) causes a 20% decrease in single channel conductance (from 13.4 to 10.6 pS in the voltage range of 0–60 mV) favors C-type inactivation and destabilizes the open state of the channel (Ortega-Sáenz et al., 2000). Glutamate 322 is also known to have a strong influence on the electrostatic binding of positively charged toxins to the K⁺ channels (MacKinnon and Miller, 1989b; Goldstein et al., 1994). Our molecular model explains the strong electrostatic effect of E322 charges on the selectivity filter in terms of its location on a low dielectric constant medium.

The electrostatic potential calculation made by solving the finite difference Poisson equation was also applied to the Kir2.1 channel. In this case the crystal structure of KirBac1.1 was used as template (unpublished data). This channel has three negatively charged residues located near the extracellular entrance of the channel that were mutated to cysteines (E125C, D152C, and E153C; D'Avanzo et al., 2005). Surprisingly, D'Avanzo et al. (2005) found that only neutralization of E153 was able to modify the channel conductance. Our calculation of the electrostatic potential along the Kir2.1 conduction machinery gives a simple explanation of these results: only E153 contributes to the negative electrostatic potential in the channel external entrance whereas E125 and D152 are shielded by the aqueous external environment.

Although there is a clear electrostatic tuning of channel conductance, the mechanism for the large BK channel conductance is not completely understood. The rings of negative charges located at the inner and outer mouth contribute only partly. It is clear, however, that comparison of the electrostatic potential profile between different channels indicates that the pore of BK channels, especially in the neighborhood of the selectivity filter, has a much more pronounced negative electrostatic potential. For example, our calculations indicate that the electrostatic potential of the internal vestibule of BK in the neighborhood of amino acids E386 and E389 is ∼140 mV more negative than in Kv1.2 channels. As suggested by Li and Aldrich (2004) and Brelidze and Magleby (2005) another factor that may improve the BK channel conductance is the larger dimensions of its internal vestibule compared with other K⁺ channels. A larger inner pore would imply a smaller access resistance and, therefore, permeation of K⁺ ions may be less restricted by the inner pore approaching the diffusion limit.