Organization of mammalian locomotor rhythm and pattern generation

Abstract

Central pattern generators (CPGs) located in the spinal cord produce the coordinated activation of flexor and extensor motoneurons during locomotion. Previously proposed architectures for the spinal locomotor CPG have included the classical half-center oscillator and the unit burst generator (UBG) comprised of multiple coupled oscillators. We have recently proposed another organization in which a two-level CPG has a common rhythm generator (RG) that controls the operation of the pattern formation (PF) circuitry responsible for motoneuron activation. These architectures are discussed in relation to recent data obtained during fictive locomotion in the decerebrate cat. The data show that the CPG can maintain the period and phase of locomotor oscillations both during spontaneous deletions of motoneuron activity and during sensory stimulation affecting motoneuron activity throughout the limb. The proposed two-level CPG organization has been investigated with a computational model which incorporates interactions between the CPG, spinal circuits and afferent inputs. The model includes interacting populations of spinal interneurons and motoneurons modeled in the Hodgkin-Huxley style. Our simulations demonstrate that a relatively simple CPG with separate RG and PF networks can realistically reproduce many experimental phenomena including spontaneous deletions of motoneuron activity and a variety of effects of afferent stimulation. The model suggests plausible explanations for a number of features of real CPG operation that would be difficult to explain in the framework of the classical single-level CPG organization. Some modeling predictions and directions for further studies of locomotor CPG organization are discussed.

1. Half-center organization of the central pattern generator

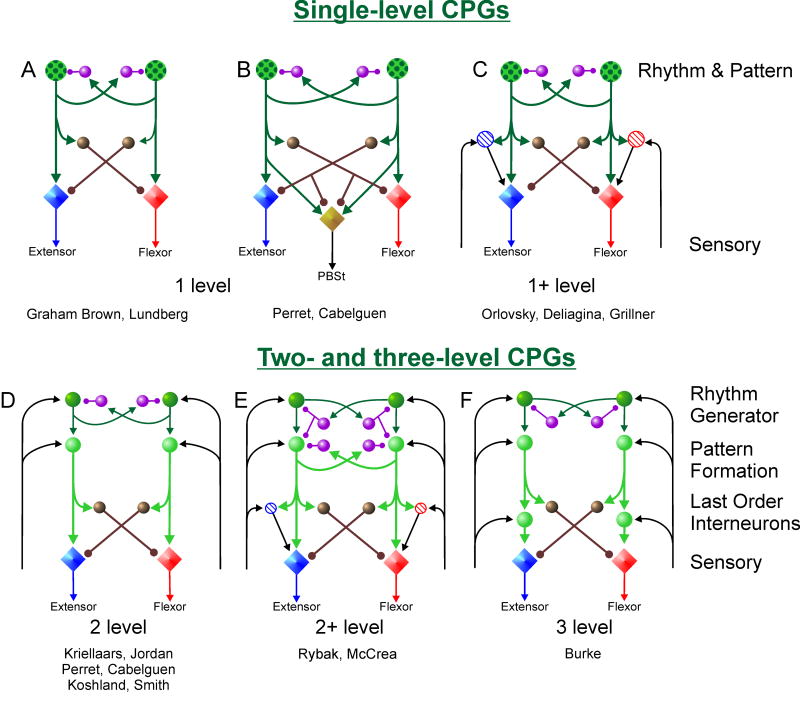
More than 90 years ago, T. Graham Brown (1911) demonstrated that the cat spinal cord can generate a locomotor rhythm in the absence of input from higher centers and afferent feedback. These and later investigations led to the widely accepted concept of central pattern generators (CPGs) which reside within the central nervous systems of invertebrates and vertebrates and control various rhythmic movements. Graham Brown (1914) also proposed a general schematic for the spinal CPG generating rhythmic alternating activity of flexor and extensor motoneurons during locomotion, the “half-center” model. His ideas were later embraced by Lundberg and colleagues in their description of how spinal interneurons involved in flexion reflexes could serve as the basic building block of the circuitry responsible for mammalian locomotion (Jankowska et al., 1967a, b; Lundberg, 1981). The key points of the half-center CPG organization shown in Fig. 1A are: 1) Each limb is controlled by a separate CPG. 2) Each CPG contains two groups of excitatory interneurons (i.e. the half-centers) that directly project to, and control the activity of, flexor and extensor motoneurons respectively. 3) Mutual inhibitory interconnections between the half-centers ensure that only one center can be active at a time. 4) An undefined “fatigue” process gradually reduces excitation in the active half center. 5) Phase switching occurs when the reduction in the excitability of one half center falls below a critical value and the opposing center is released from inhibition. 6) Inhibition of antagonist motoneurons is tightly coupled to the excitation of agonists.

Fig. 1. Schematic representations of half-center CPG models.

Circles represent spinal interneuron and diamonds represent motoneuron populations. Excitatory and inhibitory connections are shown by lines ending with arrow heads and small filled circles, respectively. A,B,C. Single-level half-centre models in which rhythm generation is produced by two excitatory interneuron populations (green stippled populations) interconnected by reciprocal inhibition (purple). The same interneurons excite the corresponding motoneuron populations as well as inhibitory interneurons responsible for rhythmic inhibition of motoneurons during locomotion. A. Classical half-center scheme. B. More complex patterns of motoneuron activity can be produced by connections from both half centers to some motoneuron populations (PBSt, posterior biceps semitendinosus). C. Motoneurons receive excitation during locomotion from interneurons with sensory input (hatched circles) as well the half-centres. D,E,F. Two-and three-level CPG architectures with separate rhythm generator (dark green circles) and pattern formation (light green) circuitry. E. As in C, a portion of motoneuron excitation during locomotion is mediated by interneurons with sensory input. There is reciprocal inhibition at both the rhythm generator and pattern formation levels. F. A three level CPG organization in which all locomotor excitation of motoneurons is mediated by interneurons with sensory input. See text for details.

The attractiveness of the half-center hypothesis for control of locomotion includes corroborating evidence on the organization and activity of lumbar interneurons during locomotor-like flexor and extensor motoneuron activity. Systemic administration of the noradrenergic precursor, L-DOPA, evokes spontaneous alternating activity of flexors and extensors (see Grillner 1969; Grillner and Zangger 1979). Intracellular motoneuron recordings during L-DOPA induced locomotion revealed strong mutual inhibitory interactions between interneuronal pathways to flexors and extensors (Jankowska et al., 1967a). Interneuron recordings showed a strong reciprocal organization of interneurons that were rhythmically active in the absence of sensory stimulation and were also part of the reorganization of flexion reflexes that occurs in these preparations (Jankowska et al., 1967b). A key feature of the half-center hypothesis is that there is an intrinsic spinal organization of interneuron populations with strong (mutual) inhibition between them. Alternating activity in flexor and extensor motoneurons results from alternating activity in interneurons that can also be activated by a variety of sensory afferents (see also Lundberg, 1981).

One general problem with the original half-center architecture is that it accommodates only a strictly alternating pattern of flexor and extensor activity with all motoneurons divided into these two groups. During locomotion, however, some motoneuron pools display activity during both the flexion and extension phases of the step cycle and there are differences in the onset and offset of activity in individual flexor and extensor pools (see Rossignol 1996). Originally it was suggested that proprioceptive afferent input was responsible for converting simple alternating flexor and extensor activity into a more complex pattern (Engberg and Lundberg 1969). The persistence of more complex activity patterns following bilateral deafferentation of the hindlimbs in decerebrate cats, however, led Grillner and Zangger (1975) to conclude that the locomotor CPG “… does not simply generate an alternate activation of flexors and extensors but a more delicate pattern that will sequentially start and terminate the activity in the appropriate muscles at the correct instance”. Their ideas were further developed in a proposal for a CPG architecture in which separate “modules” or unit burst generators (UBG) controlled subsets of motoneurons (see Grillner 1981). However, despite the attractiveness of this proposal, the UBG model has not yet provided explicit solutions for the generation of complex motoneuron activity patterns.

The existence of mixed-synergy motor patterns, e.g., the co-activation of some extensors with the ankle flexors during paw shake in the cat (Carter and Smith, 1986a,b; Koshland and Smith, 1989; Pearson and Rossignol, 1991), has also been raised as evidence against a simple half-center organization of the locomotor CPG (see Stein and Smith, 1997; Stein 2005). Paw shake is a specialized reflex in which cutaneous stimulation (e.g., water or tape on the paw or other parts of the limb) evokes a fast rhythm (the shake) in that limb. Paw shake movements can be incorporated into ongoing CPG operation and when elicited during walking, locomotor activity in other limbs is modified to minimize any destabilisation that might occur (Smith et al., 1985; Carter and Smith, 1986a; Pearson and Rossignol, 1991). Paw shake can be elicited in deafferented (Koshland and Smith, 1989) as well paralyzed preparations (i.e., fictive paw shake, Pearson and Rossignol, 1991). During both fictive and real paw shake there is a brief period of overlapping activity in extensors and the ankle flexor, tibialis anterior. This period of co-contraction has been called a “mixed synergy” (see Koshland and Smith, 1989). Measured from the EMG during real paw shake the overlap is about 40 ms for vastus lateralis activity and about 15 ms for ankle extensors within a cycle period of about 100ms (see Koshland and Smith 1989). But without direct comparison of the degree of overlap in the activities of flexors and extensors during locomotion, it remains unclear whether the mixed paw shake synergy differs from that occurring during locomotion. One difficulty in extrapolating from the motoneuron activity observed during paw shake to an understanding of the underlying organization of central neuronal circuitry is that there are no intracellular recordings during this behavior. With this in mind, let us consider another specialized cutaneous reflex, the stumbling corrective reaction, for which intracellular records have been obtained as the reflex is evoked during fictive locomotion without the influence of sensory feedback (Quevedo et al., 2005a,b).

The stumbling correction reaction is evoked by contact between the dorsum of the paw and an obstacle (e.g., Forssberg, 1979). During forward walking this contact would usually occur during the swing phase when limb extensors are inhibited. Contact results in a hyper-flexion of the limb to lift the paw over the obstacle. The reflex response includes a mixed synergy in which a brief activation of ankle extensors helps to move the paw away from the obstacle. Intracellular recordings from motoneurons show, however, that this mixed synergy is not due to the activation of extensor CPG circuitry during the flexion phase. Rather it results from an excitatory cutaneous reflex directed to ankle extensor motoneurons (Forsberg 1979, Quevedo et al, 2005a,b). Cutaneous reflex excitation overcomes the swing phase-related inhibition produced by the CPG and activates ankle extensors (Quevedo et al., 2005b). The point here is that not all motoneuron activity occurring during locomotion necessarily involves the locomotor CPG. The stumbling correction reaction highlights the general difficulty in making conclusions about CPG organization and function without a full understanding of the underlying events. It is plausible that like in stumbling correction, cutaneous input during paw shake activates excitatory reflexes and central circuits that overcome the inhibitory locomotor drive to extensors during the swing phase and cause an advanced onset of extensor activity onset resulting in a flexor-extensor co-contraction. Therefore, it may be premature to conclude that the “mixed” synergy during paw shake represents a deviation from the alternating activity of a half-center based locomotor CPG.

Another issue raised against the half-center hypothesis concerns the inhibitory mechanisms between the half-centers. The question is whether the reciprocal inhibition between the half-centers is necessary to produce the locomotor rhythm. For example, it was shown that synchronized rhythmic discharges of flexor and extensor motoneurons can be evoked after blocking inhibitory synaptic transmission (e.g., with strychnine or bicuculline; references in Kiehn, 2006). This finding has also been used as an argument (see Kiehn et al., 1997; Rossignol et al., 2006) against the half-center concept. As articulated recently, “… excitatory networks are responsible for rhythm generation in the mammalian spinal cord and exclude a half-center organization” (Kiehn, 2006). A related issue is the apparently independent cycling of the flexor and extensor portions of the CPG during fictive locomotion that led to the suggestion that flexor and extensor portions of the CPG can generate independent rhythms (Burke et al., 2001). Since the half-center hypothesis predicts an important role of reciprocal inhibition in the strict coupling of activity, these observations appear to disprove a half-center CPG organization.

However, the above observations do not necessarily contradict the half-center concept. Rather they provide important information about intrinsic rhythmogenic properties that may be present within each half-center. Because of the intrinsic rhythmogenic properties, each half-center can solely generate oscillations under certain conditions, e.g. when inhibition is blocked. We suggest that the flexor-extensor synchrony that follows the suppression of inhibition results from excitatory interconnections between the half-centers (Rybak et al., 2006a). Such connections might be analogous to those between excitatory CPG neurons in the lamprey (see Cangiano and Grillner, 2005). It is questionable, however, whether the synchronous rhythm is the locomotor rhythm. The fact that the fundamental locomotor process of flexor and extensor alternation disappears when inhibition is removed is actually a strong argument for the critical role of inhibition in mammalian locomotion. Intrinsic rhythmogenic properties of the half-centers may be necessary but not sufficient for the generation of the locomotor rhythm and pattern. Reciprocal inhibition between the half-centers appears to be another essential component. The essential role of inhibition is supported by the tight coupling of extensor and extensor activities in both fictive and real locomotion under normal conditions and during various perturbations and deletions (see Guertin et al., 1995; Lafreniere-Roula and McCrea, 2005). In addition, the independent cycling of flexor and extensor half-centers (Burke et al., 2001) and continued rhythmic activity of some motoneurons when activity in antagonist pools fails (Lafreniere-Roula and McCrea, 2005) during fictive locomotion are predictable consequences of certain types of deletions and not evidence for independent flexor and extensor rhythm generation (discussed below and in Lafreniere-Roula and McCrea, 2005). We are in agreement with Orlovsky et al. (1999) that the half-center organization remains a viable hypothesis of how the fundamental locomotor pattern of alternating flexor and extensor activity is produced. Other models of CPG organization are discussed in Orlovsky et al. (1999) and will not be considered here.

2. Single level half-center models of the CPG

Although the half-center formulation remains an attractive basis for locomotor CPG organization, it has several limitations. For example, while a half-center organization could produce alternating activity with one flexor and one extensor burst per cycle, it cannot not easily generate the two bursts per cycle exhibited by some motoneuron pools during locomotion (e.g., posterior biceps and semitendinosis; see Perret et al., 1988). Proponents of the half-center architecture have clearly recognized the need for additional circuitry and processes to supplement basic CPG operation (see Lundberg, 1981). Figure 1B illustrates one such proposal in which additional circuitry shapes the biphasic, half-center derived, alternating pattern into one with more complex motoneuron activity patterns (Perret et al., 1988). Along similar lines, additional intermediate circuitry has been proposed to explain the more complex locomotor activity of other hindlimb motoneurons such as flexor digitorum longus (Burke et al., 2001).

There is, however, a deeper problem with the original half-center organization. A common feature of simple half-center organizations is that the excitatory interneurons generating locomotor rhythm are connected directly to motoneurons. Consequently, any changes in excitability of the half-centers should simultaneously affect both cycle timing and motoneuron activity. This is an obvious disadvantage when independent regulation of motoneuron activity (i.e., muscle force) and step cycle timing is required, e.g., when marching up and down inclined surfaces. This intertwining of cycle timing and motoneuron activation within a single-level CPG architecture has prompted suggestions for a more complex organization.

In the scheme in Fig. 1C, additional neurons act in parallel to the main “half-center” excitatory neurons and assist in the activation of motoneurons (Orlovsky et al., 1999). These additional populations (small hatched circles in Fig. 1C) provide afferent-dependent motoneuron excitation gated by the phase of the locomotor step cycle. Since motoneuron recruitment is controlled in part by neurons not involved in rhythm generation per se, the level of motoneuron activation can be partially modulated without affecting locomotor timing. At the same time, because neurons involved in rhythm generation in Fig. 1C also directly influence motoneurons, cycle timing cannot be regulated independently of motoneuron activity. Therefore this scheme can be considered a “1+ level” organization.

While a 1+ level architecture improves on the flexibility of the half-center CPG to regulate motoneuron activity, it fails to explain certain observations on the sensory control of the locomotor CPG. There is now a large body of evidence that group Ia muscle spindle and group Ib tendon organ afferents (collectively referred to group I afferents) evoke a powerful control of extensor motoneuron activity and step cycle timing (see McCrea, 2001; Donelan and Pearson, 2004; Rossignol et al., 2006). One important observation during fictive locomotion in the cat is that sensory stimulation can prolong the ongoing extensor phase without changing step cycle period (Guertin et al., 1995; Fig. 3B2, discussed below). In such cases extensor phase prolongation is compensated by a complementary reduction in the duration of the following flexor phase. Such a separation of the control of phase transition timing and phase duration cannot be easily reconciled within a basic half-center organization since cycle period and phase duration are linked together by the excitability of the half-centers.

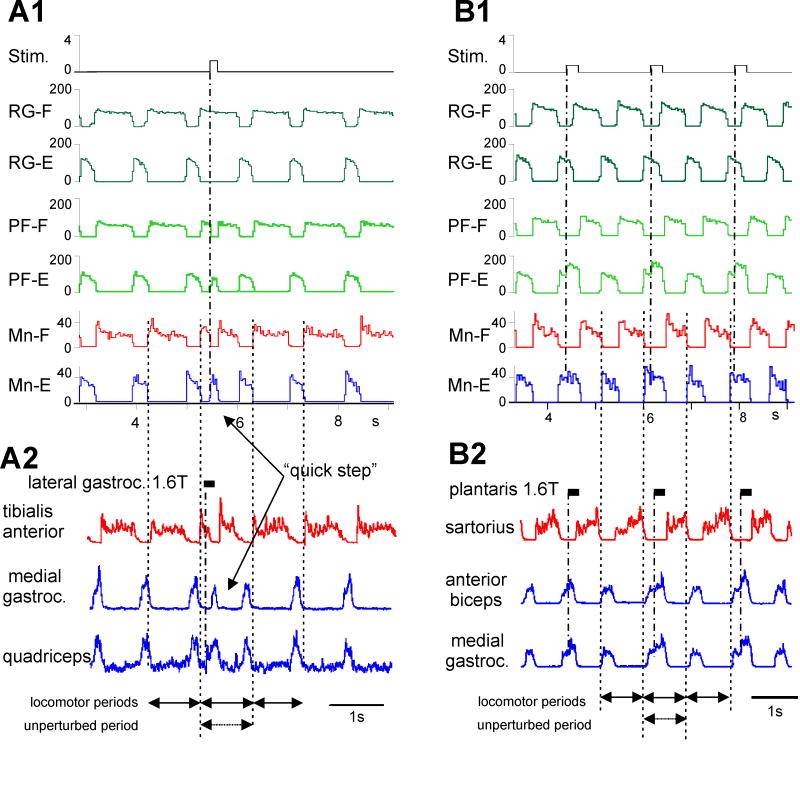
Fig. 3. Sensory control of the CPG by extensor group I afferents.

A1, B1, Simulations of the effects of stimulation of extensor group I afferents delivered during the flexion phase (A1) and the extension phase (B1). The top traces show the stimulus delivery (arbitrary units). The other traces show the average activity of RG and PF interneuron populations and flexor (Mn-F) and extensor (Mn-E) motoneurons (ordinate in spikes /s, abscissa in seconds). A2, B2. Rectified-integrated nerve recordings from decerebrate cats during MLR-evoked fictive locomotion. Vertical dashed lines indicate the step cycle period without sensory stimulation. In A2, a train of shocks (black rectangle) delivered to extensor group I afferents (lateral gastrocnemius nerve at 1.6 times threshold, T) during the flexion phase produced a premature onset of extension (rectified, integrated electroneurograms from knee extensors, quadriceps, and the ankle extensor, medial gastrocnemius) and terminated the ongoing flexion phase (see tibialis anterior activity). In A1 (and similar to A2) stimulation applied during flexion in the model also produced a short extensor burst followed by a shortened flexion phase. This “quick step” of activity was created by the increased activity at the PF level and inserted into the ongoing rhythm which did not change (see RG activities and arrows at the bottom). In B2 Stimulation of extensor group I afferents (plantaris, 1.6T) during the extension phase of fictive locomotion increased the size and duration of extensor motoneuron activity (anterior biceps and medial gastrocnemius) and shortened the duration of the following flexor phase (see sartorius activity). In B1 (and similar to B2) extensor phase group I stimulation increased PF-E population activity that enhanced and prolonged extensor motoneuron activity without changing the locomotor period (see equal length arrows at the bottom). From Rybak et al. (2006b).

An even more problematic issue for simple half-center schemes is providing an explanation for non-resetting deletions. During fictive locomotion (e.g., Grillner and Zangger 1979; Jordan, 1991; Turkin and Hamm, 2004; Lafreniere-Roula and McCrea 2005) and treadmill locomotion (Duysens, 1977) in the cat and during the scratch reflex in the turtle (Stein 2005) and the cat (Lafreniere-Roula and McCrea 2005), rhythmic bursts of motoneuron activity can be absent (deleted) for a few cycles. During these deletions activity fails simultaneously in multiple synergist motoneuron pools and becomes tonic in multiple antagonists. This suggests that deletions reflect changes in the excitability of a network common to all motoneurons, like the CPG, and are not simply the result of direct inhibition of a few motoneurons. An important finding has been that rhythmic motoneuron bursts often reappear after a time interval equal to an integer multiple of the pre-deletion cycle period (Lafreniere-Roula and McCrea 2005). Such deletions have been classified as “non-resetting” since rhythmic motoneuron activity reappears without phase shift in the locomotor cycle (Lafreniere-Roula and McCrea 2005). The most reasonable explanation is that the CPG controlling each limb contains a structure that maintains the timing of the cycles during failures of rhythmic motoneuron activity. Another, but in our opinion less likely possibility, is that rhythm is maintained during non-resetting deletions by CPGs operating in other limbs. Although no attempt has been made to record activity in all four limbs during non-resetting deletions, the phase of oscillation is maintained during fictive locomotion without contralateral hindlimb activity (Rybak et al 2006a) and during fictive scratch with minimal or no rhythmic activity in all other limbs (Lafreniere-Roula and McCrea 2005). Thus we think it more likely that some central structure performs the “clock function” and can “remember” the timing of the cycle. It is difficult to imagine how a single-level CPGs like those illustrated in Fig. 1A-C, could maintain the phase of the locomotor rhythm during and after deletions. If a single network were responsible both for both rhythm generation and motoneuron excitation, one would expect that disturbances affecting the CPG would generally be accompanied by changes in the phase of the locomotor rhythm following the deletion. Therefore, it appears that single-level CPGs (like those shown in Fig 1A-C) cannot explain non-resetting deletions nor the effects of sensory stimulation that alter phase duration without affecting cycle period (discussed below).

3. Two-level half-center CPG models

Several investigators have suggested that in order to overcome some of the disadvantages of the classical half-center organization, the single-level half-center model in Fig. 1A should be replaced with a more complex organization. In the two-level CPG depicted in Fig. 1D, rhythm generation and motoneuron recruitment are carried out by separate neural populations. Such an organization was suggested to explain the independence between changes in burst duration and cycle timing during paw shake (Koshland and Smith, 1989; Stein and Smith 1997). A similar separation of CPG function was suggested to explain how sensory stimulation could alter locomotor cycle timing without altering the level of motoneuron activity (Kriellaars et al., 1994). In the latter scheme the CPG was divided into a half-center rhythm generator and “reciprocity modules” each of which was responsible for the depolarization and hyperpolarization of subsets of motoneurons (Jordan, 1991). Perret and colleagues also clearly recognized the importance of sensory input in determining motoneuron activity during locomotion and the need to have separate control of motoneuron recruitment and timing (e.g., Orsal et al., 1990). A two-level CPG has been suggested as an explanation of how some sensory stimulation can affect cycle timing while other stimulation affects only motoneuron activation in the turtle (Lennard, 1985). Burke and colleagues (Burke et al., 2001) also stressed the critical role of sensory input in separate control of motoneuron output and CPG operation during locomotion. In their scheme (see the representation in Fig. 1F) all of the last order interneurons exciting motoneurons receive sensory input. Accordingly, this might be considered a three-level CPG organization.

Our studies had shown that non-resetting deletions were quite common during fictive locomotion and scratch in the decerebrate cat (Lafreniere-Roula and McCrea, 2005). The simple explanation was that some circuitry separate from that involved in rhythm generation was responsible for the rhythmic depolarization and hyperpolarization of motoneurons. A similar conclusion about separation of rhythm and motoneuron activation duties arose from intracellular studies of deletions of scratch reflex activity in the turtle (Robertson and Stein, 1988). Our observations on deletions and on the ability of sensory stimulation to alter phase switching within the ongoing step cycle without changing the phase of the post stimulation rhythm (e.g., Guertin et al., 1995; Perreault et al., 1995; Stecina et al., 2005) led to the proposal for a two-level CPG (Lafreniere-Roula and McCrea, 2005; Rybak et al., 2006a). It was recently suggested that a single-level CPG could produce non-resetting deletions if there were a powerful control mechanism that could regulate synaptic transmission between excitatory CPG interneurons and motoneurons (Kiehn, 2006). Such a mechanism would allow for reduced motoneuron activation without changes in cycle timing in a single-level network such as that in Fig. 1A. However, it is difficult to imagine a plausible mechanism for such modulation of synaptic transmission. Such transmission control would have to be very powerful since intracellular recordings show that the excitatory drive to motoneurons is not only reduced during deletions but is often completely eliminated (Lafreniere-Roula and McCrea, 2005). Moreover, a failure of motoneuron activation during deletions is usually accompanied by active motoneuron hyperpolarization to the same level that occurs during normal locomotion (Lafreniere-Roula and McCrea, 2005). This strongly suggests that locomotor excitation has not just been reduced during deletions but rather it has been replaced by the same inhibitory pathways that normally operate during the inactive, hyperpolarized phase. Finally, a regulatory scheme affecting synaptic transmission would have difficulty accounting for the independent control of rhythm and motoneuron recruitment. The rhythm can be slowed or accelerated by sensory stimulation without altering the level of motoneuron activity (e.g., Kriellaars et al., 1994) and motoneuron activation can be altered without affecting cycle timing (Perreault et al., 1995; Guertin et al., 1995; Stecina et al., 2005) As discussed below, a two-level CPG can explain both the sensory control of locomotion and the occurrence of resetting and non-resetting deletions.

4. Implementation of a two-level CPG model

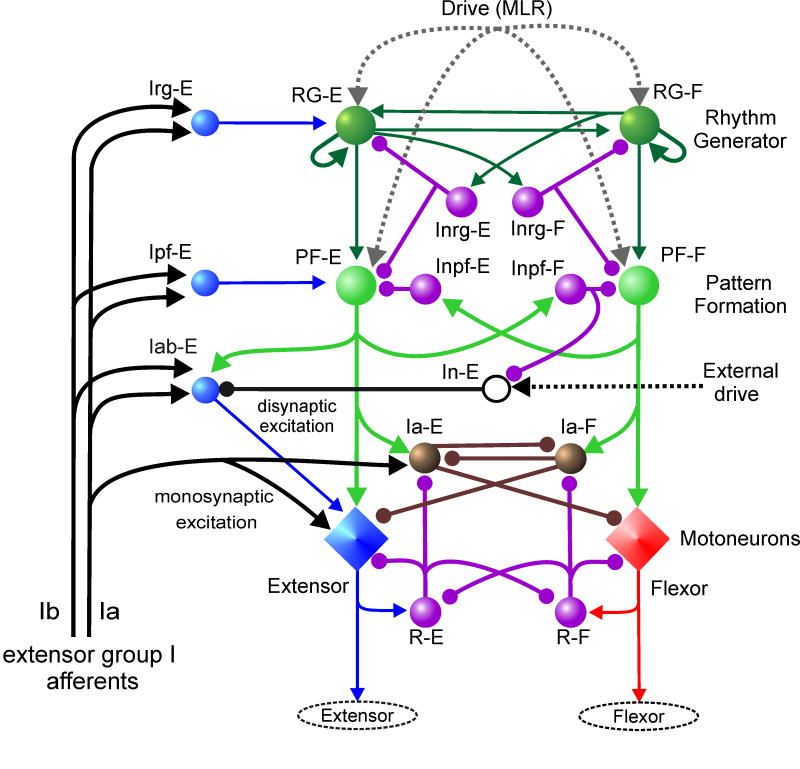
We recently proposed (Rybak et al., 2006a,b) a two-level CPG architecture (Fig. 1E) that shares some features of the networks in Fig 1C and 1D. In this model the CPG contains a half-center rhythm generator (RG) and a pattern formation (PF) network. The latter is controlled by the RG and projects to flexor and extensor motoneuron populations. In addition there is a phase-dependent, sensory driven, component of motoneuron excitation (akin to that in Fig. 1C) which provides phase-dependent disynaptic activation of extensor motoneurons during the extensor phase of locomotion (see McCrea 2001; Angel et al., 2005). Figure 2 shows a more detailed schematic of the model including the neural pathways providing sensory control by extensor group I afferents of both the RG and PF levels of the CPG. The effects of other sensory inputs to the model are presented elsewhere (Rybak et al., 2006b).

Fig. 2. Rybak-McCrea CPG model.

Detailed schematic of a computational model of the of the spinal circuitry with the two-level CPG. Rhythm Generator (RG) and Pattern Formation (PF) networks representing the two levels of the CPG are labelled on the right. The excitatory RG populations reciprocally inhibit each other via the inhibitory Inrg populations. The PF populations reciprocally inhibit each other through the Inpf inhibitory populations. The RG-E and RG-F populations have recurrent excitatory connections and excitatory connections between the half-centers. Locomotion is initiated by a tonic excitatory drive (MLR) to both the RG and PF populations. The locomotor rhythm and the durations of flexor and extensor phases are determined by the RG network which controls the activity of the PF network by a combination of direct excitation and inhibition mediated by the Inrg populations. PF population activity produces a phase-specific activation of the corresponding group of synergist motoneuron pools. Phase-dependent inhibition of motoneurons is produced by the Ia-E and Ia-F populations whose activity is regulated by excitation from the PF network and inhibition from Renshaw cells (R-E and R-F) as well as mutual inhibitory connections between the Ia populations. Afferent input from extensor muscle spindle (Ia) and tendon organ (Ib) afferents to the spinal circuits are shown on the left. Activity in Ia afferents evokes monosynaptic excitation of synergist (extensor) motoneurons and disynaptic inhibition of antagonists. During locomotion, extensor group Ia and Ib afferents access the CPG at the RG and PF levels through the Irg-E and Ipf-E populations, respectively. Extensor motoneurons also receive a phase-dependent excitation from the Iab-E population whose activity is augmented by group I sensory input during the extensor phase. The Iab-E population is inhibited at rest by tonic drive from the In-E population. This inhibition is removed during the extension phase by inhibition from the Inpf-F population. Further details in Rybak et al. (2006 a, b).

The model describes interacting populations of interneurons and motoneurons modeled in the Hodgkin-Huxley style with 20-50 neurons per population. The RG contains a homogeneous population of excitatory interneurons with mutual excitatory interconnections. These neurons are divided into two populations, RG-E and RG-F, representing the half-centers of the RG. Reciprocal inhibition between the RG half-centers is mediated by inhibitory interneuron populations, Inrg-E and Inrg-F. The PF network is similarly organized but has a lower capacity for rhythmogenesis (Rybak et al., 2006a). It also contains excitatory interneuron populations coupled by reciprocal inhibition (via Inpf-E and Inpf-F). The PF populations PF-E and PF-F operate under control of the RG by receiving strong inhibitory inputs from Inrg-E and Inrg-F and weak excitation from RG-E and RG-F, respectively. The PF populations project directly to motoneuron populations and are responsible for the phasic excitation of motoneurons during locomotion. Phasic inhibition of motoneurons during locomotion is provided by an additional set of inhibitory interneurons, Ia-E and Ia-F, also driven by the PF network. These interneurons are also responsible for reciprocal inhibition of antagonists during the stretch reflex. The model incorporates appropriate connections between and among the inhibitory Ia interneurons, Renshaw cells and motoneurons (see Jankowska, 1992).

The model has been developed to simulate motoneuron activity recorded during fictive locomotion evoked by continuous electrical stimulation of the mesencephalic locomotor region (MLR) in the decerebrate cat. Locomotion in the model is initiated and stopped by the application and removal of excitatory tonic (“MLR”) drives to the RG and PF networks (Rybak et al., 2006a,b). The excitatory RG drive generates a biphasic rhythm with alternating bursts of RG-E and RG-F populations. The rhythmogenic mechanism operating in the RG is based on a combination of intrinsic cellular properties (activation of the slowly inactivating persistent sodium current, I_NaP) and reciprocal inhibition between the RG-E and RG-F half-centers. During normal locomotor operation, the onset of firing bursts in the model is determined mostly by the activation of the intrinsic I_NaP-dependent excitatory mechanism whereas burst termination is determined by the reciprocal inhibition. Alternating bursting activity in the PF network follows that in the RG and produces phasic excitation of the corresponding motoneuron pools. The full description of the model can be found in Rybak et al. (2006a).

An important feature of the model is the ability to differentially regulate locomotor speed at the RG level and the level of motoneuron activity at the PF level. By changing MLR drive to the RG half-centers, locomotor phase durations and step cycle periods can be independently regulated (see Rybak et al., 2006a; McCrea and Rybak, 2007) over ranges that encompass those occurring during fictive locomotion in decerebrate cats (Yakovenko et al., 2005) and during treadmill locomotion in intact cats (e.g., Halbertsma, 1983). Since the PF populations have their own MLR input, the degree of motoneuron activation can be controlled independently of RG activity.

In addition to the two level arrangement of the CPG, three levels of reciprocal inhibition distinguish our CPG model. The first level is the mutual inhibition between the RG half-centers. Like earlier half-center models, our model relies on mutual inhibitory interconnections between half-centers to generate the alternating locomotor pattern. This reciprocal inhibition defines the termination of flexor and extensor bursts and an increase in this inhibition prolongs step cycle period (i.e., slows down the locomotor rhythm) (Rybak et al. 2006a). Similar to experimental findings (see above) blocking inhibition in the model switches its operation to generating synchronous flexor and extensor bursts (Rybak et al. 2006a). These synchronous oscillations result from a combination of the intrinsic rhythmogenic properties of RG neurons and mutual excitatory connections between the RG populations (see Fig. 2 and Rybak et al., 2006a). During these oscillations, the synchronized bursts in both RG populations are terminated by the slow inactivation of the persistent sodium channels in RG neurons which does not require inhibition. It is important to note that the intrinsic, I_NaP-dependent mechanism is critically involved in burst initiation in both the locomotor and synchronous rhythms. However, in contrast to the synchronized rhythm, the termination of flexor and extensor bursts in the locomotor rhythm is defined by the reciprocal inhibition between the RG half-centers, which also provides alternation of flexor and extensor activities without intervening quiescent periods.

The second level of reciprocal inhibition in the model is that operating within the PF network (via Inpf-E and Inpf-F populations, see Fig. 2). Incorporating this reciprocal inhibition allows the model to reproduce experimental findings on deletions and the effects of afferent stimulation (discussed below and in Rybak et al. 2006a,b) which would be difficult or impossible to explain without PF-level reciprocal inhibition.

The third level of reciprocal inhibition in the model is the rhythmic inhibition of motoneurons during locomotion via the Ia interneuron populations, Ia-E and Ia-F. Excitatory PF input excites agonist motoneurons as well as Ia inhibitory interneurons projecting to the antagonist motoneuron pool. This configuration ensures that antagonist motoneuron inhibition is closely linked to agonist recruitment in a “reciprocity module” (Jordan 1991). Previous studies have shown that such reciprocal Ia inhibitory interneurons are rhythmically active during fictive locomotion and contribute to the rhythmic inhibition of motoneurons during locomotion (Feldman and Orlovsky, 1975; McCrea et al, 1980; Pratt and Jordan, 1987). Other, as yet unidentified, interneurons may also contribute to the rhythmic inhibition of motoneurons during locomotion (Gosgnach et al., 2006).

As Fig. 2 shows, our CPG model is symmetrical for generation of flexor and extensor activities. Based on observations in walking thalamic cats, it has been argued that flexor motoneuron activity is more directly controlled by the CPG (Duysens 1977). In this “flexor burst generator” scheme, extensor activity occurs as a consequence of flexor activation. Gelfand et al. (1988) have also proposed an asymmetrical drive to flexor and extensor portions of the CPG for locomotion and scratch (discussed in Orlovsky et al., 1999). However, evidence for an asymmetrical CPG organization is underwhelming (Duysens et al., 2006). The important argument for the symmetrical organization is that both flexor and extensor deletions occur during fictive locomotion. Moreover, we found that the shorter duration (flexor or extensor) phase is subject to more frequent deletions during fictive locomotion and scratch. Thus flexor deletions occur frequently in those fictive locomotion preparations in which extensor activity dominates and extensor deletions occur more frequently in preparations showing a longer flexor phase (Lafreniere-Roula and McCrea, 2005). A flexor generator organization cannot easily explain non-resetting deletions in which extensor activity continues when flexor activity falls silent. While we support the idea that descending and sensory drive to the CPG can result in asymmetrical CPG operation (see Rybak et al. 2006a), more evidence is needed before concluding that the organization of rhythm generation in the CPG is asymmetrical (c.f. Brownstone and Wilson, 2007).

5. Features of the two-level CPG: The role of the pattern formation network

As mentioned in section 2, single-level CPG architectures are unable to explain non-resetting deletions which occur without rhythm resetting or shifting the phase of the post-deletion rhythm (Lafreniere-Roula and McCrea 2005). A two-level CPG model which separates cycle timing and motoneuron activation offers a simple explanation for these deletions (see Fig. 2 and Rybak et al., 2006a). An important feature of the suggested architecture is that alterations in the excitability of neural populations at the PF level that do not affect RG performance do not perturb the locomotor rhythm. Using our computational model we demonstrated that either an increase or a decrease in excitability of one of the PF populations can produce non-resetting (period maintaining) deletions but these deletions will have distinctive characteristics (Rybak et al., 2006a). Specifically, a decrease in the excitability of the extensor-related population (i.e., PF-E, see Fig. 2) can cause a deletion of extensor motoneuron activity for the duration of the disturbance. However because of continuing rhythmic activity in the RG, flexor motoneurons will remain rhythmically active and the pre-deletion rhythm and phase will be preserved during a PF-level inhibition. We suggest that this activity might be responsible for the independent cycling of some motoneuron groups during fictive locomotion (Burke et al., 2001) (discussed in Lafreniere-Roula and McCrea 2005; Rybak et al., 2006a).

If instead of a decrease, the excitability of one PF population (e.g., PF-E) is increased, there can be sustained activity in the agonist (e.g., extensor) motoneurons. At the same time the opposing PF-population (e.g., PF-F) will be strongly inhibited by the PF-level, mutual-inhibitory connections. This inhibition will result in a deletion in which tonic activity of agonists is accompanied by tonic inactivity of antagonist motoneurons. Again, operation of the RG will remain unchanged during and after the deletion. Following the disturbance, alternating bursts of flexor and extensor activity will reappear without phase shift relative to the pre-deletion rhythm. Thus both increases and decreases in PF-level excitability will produce non-resetting types of deletions. In contrast, changes in excitability at the RG level will produce deletions in which the cycle period is perturbed (Rybak et al., 2006a). In the spinal cord intact, fictive locomotion, preparation, the majority of deletions are of the non-resetting type (Lafreniere-Roula and McCrea 2005). We consider the common occurrence of non-resetting deletions to be strong evidence for the ability of the CPG to maintain locomotor phase and consequently strong support for a two-level organization of the CPG controlling each limb.

An important point for the development of our model was the realization that afferent stimulation can affect (delay or advance) the ongoing phase transition without affecting the post-stimulation locomotor rhythm (timing the following cycles). A more complete explanation of these observations can be found elsewhere (Rybak et al., 2006b). In the case of extensor group I afferents, we suggest that they have access to both the RG and PF networks. The hypothetical Irg-E and Ipf-E interneuron populations have been included in the model (see in Fig. 2A) to mediate the effect of these afferents on RG and PF respectively. Accordingly, the model suggests that sensory stimulation may alter cycle period if it changes the excitability of the RG. However, because both single- and two-level CPGs organizations can accommodate phase-resetting sensory stimulation (or deletions) they are of less interest for the present discussion. Let us consider, therefore, the effects of afferent stimulation at the PF level that does not perturb the RG.

In Fig. 3A2, extensor afferent stimulation (lateral gastrocnemius) during the flexion phase produced a premature switch to extension (see the “quick step” in the extensors medial gastrocnemius and quadriceps) and the early termination of the ongoing flexor burst in tibialis anterior. Note, however, that the duration of the next flexion phase was shortened so that neither the total cycle period nor the phase of the post-stimulus rhythm was changed (Guertin et al., 1995). In Fig. 3B2, extensor afferent stimulation was applied during extension (Guertin et al., 1995). This stimulation prolonged ongoing extensor activity and delayed transition to the flexion phase. The duration of the delayed flexion phase was also shortened so that the timing of the subsequent phase transition did not change. The ability of afferent stimulation to affect phase switching without affecting the phase of poststimulus rhythm is difficult to explain within the framework of a single-level CPG organization but easily reproduced with the two-level CPG architecture.

Our hypothesis is that extensor group I input is more heavily weighted to the PF level. Consequently, with moderate levels of sensory stimulation the effects will be largely produced at the PF network. The simulation in Fig. 3A1 shows that sensory input to the PF-E population during flexion overcomes the flexion-phase-related inhibition and activates PF-E. This produces both the early switch to extension (the “quick step” in extensor motoneurons) and, via the PF-level reciprocal inhibition (Inpf-F), the termination of ongoing flexor motoneuron activity. This PF-E activity is short lived because the unchanged activity in RG-F (top trace) quickly quenches PF-E excitation (via Inrg-E). Consequently, the PF-F population is released from inhibition and generates a shortened burst of flexor motoneuron activity. Subsequent flexor bursts occur at the “expected” time (Fig. 3A1, vertical dashed lines) because the sensory stimulation had little effect at the RG level. This simulated behavior closely reproduces the effect of extensor afferent stimulation observed during fictive locomotion (Fig. 3A2).

Figure 3 B1 shows a similar effect of phase maintenance following extensor afferent stimulation during extension. The stimulus (top trace) increased PF-E activity but the intensity was insufficient to reset the RG. This increased PF-level activity delayed the switch to flexion. As a result, the firing activity of extensor motoneurons was enhanced and prolonged. However, as in the previous case, the next flexion phase was shortened and the timing of subsequent step cycles did not change (Fig. 3B1, vertical dashed lines). This simulation closely reproduces the experimentally observed effect of extensor stimulation shown in Fig. 3B2. Thus when sensory-evoked excitation is limited to the PF network, the timing of the next phase transition within the ongoing step cycle can be altered without shifting or resetting the locomotor rhythm.

In both examples in Fig 3, reciprocal inhibition at the PF-level is critical for phase switching during the ongoing step cycle. During these sensory stimulations and non-resetting deletions (see Rybak et al., 2006a), PF network activity does not strictly follow that of the RG. Example simulations reproducing other types of sensory control of CPG operation are shown in Rybak et al. (2006b). In summary, our modeling studies have demonstrated that a simple two-level CPG organization with separate rhythm generator and pattern formation networks can provide a plausible explanation for a number of features of real CPG network operation. We believe that a CPG with separate PF and RG networks creates a flexible substrate for sensory (and descending) control of locomotion.

6. Can the two-level CPG and UBG architectures complement each other?

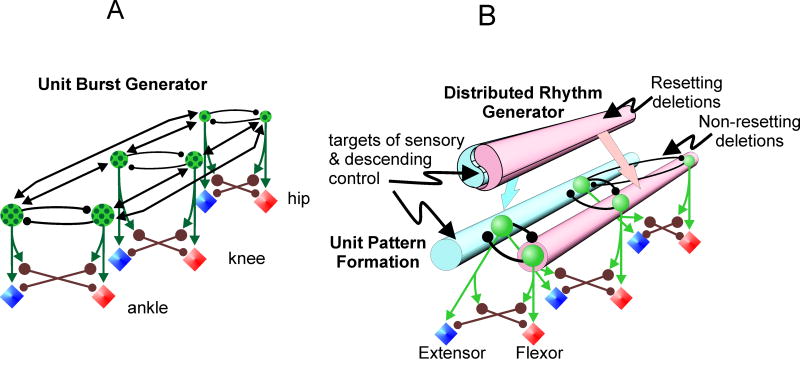
While afferent input plays a critical role in controlling and shaping CPG operation, it is also clear that the spinal cord circuitry can generate specific profiles of motoneuron activity in the absence of sensory input (Grillner and Zangger, 1984). Such observations led to suggestions for more complicated architectures for the locomotor CPG. One such architecture is the unit burst generator (UBG) scheme (Grillner, 1981) in which the locomotor CPG consists of multiple coupled oscillators (Fig. 4A). Each unit (oscillator) in this scheme has a half-center organization and controls the activity of a subset of motor pools. Activity between the units is regulated by excitatory and inhibitory synaptic connections. While under many conditions the outputs of the units would be similar, each unit could differentially control the activity of groups of motoneurons when needed (see Stein and Smith, 1997). However, despite the potential for flexibility and for generating particular activity in individual motor pools, the UBG scheme remains a single-level architecture. Cycle period is determined by the combined excitability of the individual units as well as the interactions between them. These interactions must be strong enough to synchronize the units so that they act in concert.

Fig. 4. Extending the CPG to multiple motoneuron pools.

A, In the unit burst generator (Grillner, 1981) interconnected half-centers generate the rhythm and control the activity of functional groups of motoneurons. B, Rhythm generation and pattern formation are separated in this architecture with a single RG and multiple, unit pattern formation modules.

Let us consider a UBG scheme of the CPG in the context of the non-resetting deletions described above. Assume first that each UBG has equal rhythmogenic capacity and strongly influences the other units. In this case, a deletion-producing perturbation affecting one UBG would affect the excitability of all other units. In this “democratic” organization, cycle timing would be perturbed because there is nothing in the network that could serve as the “master clock” and maintain the phase of the common rhythm. Therefore, all deletions would be of the resetting type. Let us now imagine a UBG organization in which one UBG (e.g., the hip unit) is the “master” RG responsible for synchronizing activity in all other units. In this case, as long as deletion-producing perturbations do not affect the master UBG, deletions would be of the non-resetting type. This implies that during non-resetting deletions at least one unit should be spared and rhythmic activity in the motoneurons controlled by this unit should continue during the deletion. As mentioned, this suggestion is not supported by the experimental data. Non-resetting deletions can occur simultaneously in any motoneuron group and, importantly, in all motoneuron groups within the limb (Lafreniere-Roula and McCrea, 2005). Therefore, the existence of non-resetting deletions provides a strong argument against the single-level aspect of the UBG architecture with or without a “master” UBG. Furthermore, without separation of RG and PF duties, it is difficult to explain effects of sensory stimulation like those shown in Fig. 3A2,B2. It should be noted that previous discussions of the UBG hypothesis did not consider non-resetting deletions nor CPG responses to sensory stimulation.

Finally, let us consider a modification of the UBG architecture in which an additional structure performs the function of the rhythm generator and controls and synchronizes network activity in all UBGs. In order to accommodate the observation that activity in any motoneuron group can fail and then be restored after the deletion without phase shift, this additional RG unit should not directly excite motoneurons and should not receive strong connections or feedback from other units. This modification converts the single-level UBG schematic to the two-level hierarchical architecture illustrated in Fig. 4B.

In the proposed elaboration of our CPG model (Fig 4B; see also Lafreniere-Roula and McCrea, 2005; Rybak et al. 2006a), a single rhythm generator network controls the activity of multiple, unit pattern formation modules connected to sub-populations of motoneurons. The suggestion of a common RG is not in conflict with an extensive distribution of rhythmogenic capabilities (e.g., Kjaerulff and Kiehn 1996; Cowley and Schmidt 1997) providing that strong propriospinal connections create a single functional entity within the circuitry controlling motoneurons in the limb. In our terminology the CPG consists of a single, distributed, Central Rhythm Generator (CRG) network controlling several Unit Pattern Formation (UPF) modules (Lafreniere-Roula and McCrea 2005; Rybak et al., 2006a). For the control of quadrupedal locomotion, the architecture in Fig. 4B would be replicated in all four limbs with additional networks providing gait-dependent CPG coordination. Two fundamental disadvantages of the UBG scheme in comparison with the two-level CPG are its lack of hierarchy and the use of the same neurons for rhythm generation and motoneuron activation. We believe that the incorporation of multiple UPF modules into the two-level architecture would allow the model to maintain the advantages of the UBG organization in generating a variety of motoneuron activity patterns and to be consistent with experimental observations on deletions and sensory control of the CPG.

We have not yet modeled the full CPG with multiple UPF modules. As indicated in Fig. 4B, we expect that the control of flexors and extensors may not be completely symmetrical. The locomotor activity of flexors can differ markedly with different locomotor gaits and under different conditions (see Stein and Smith, 1997; Rossignol, 1996). In addition, the sensory control of the CPG from hindlimb flexor afferents is more complex than that from extensors. Flexor afferent stimulation produces a variety of preparation-dependent effects that can show variability between stimulus trials (examples and references in Stecina et al., 2005). Extending our model to include multiple UPF networks will also involve incorporating asymmetries analogous to those providing coupling between UBGs in the UBG schematic (see Stein and Smith, 1997). However, we believe that these asymmetries should be primarily at the PF layer and not at the level of the RG.

The inclusion of individual pattern formation networks for locomotion is in accord with a broader view of the spinal organization of movement control. There is general consensus that descending control and proprioceptive regulation of many motor behaviors involves activation of groups of muscles (synergies) performing elementary movements rather than activation of individual muscles (Bernstein, 1967; Lundberg et al., 1987; McCrea, 1992; Bizzi et al. 2000). This suggests that the spinal cord should contain networks of interneurons each of which activates select motoneuron populations to produce a particular muscle synergy. It would make eminent sense for such interneurons to be major targets for descending control and proprioceptive regulation and to be part of the substrate for muscle synergies. Local inhibitory interactions among these interneurons may allow descending signals to dynamically select the most appropriate behavior from the available repertoire (McCrea, 1992). We suggest that these networks can be engaged in motor tasks other than locomotion. Some synergies would include activation of motoneuron pools acting at different joints of the limb. Accordingly, elementary units or sub-modules operating at the PF level should not necessarily be organized strictly on a joint basis as proposed in the original UBG network.

In summary, we believe that a combination of the hierarchical two-level CPG architecture, separating rhythm generation and pattern formation functions, with the UBG flexibility employed at the PF level provides a useful framework for further investigation and understanding of neural mechanism responsible for control of locomotion and other movements.

Abbreviations

CPG

central pattern generator

MLR

midbrain locomotor region

RG

rhythm generator

PF

pattern formation

UBG

unit burst generator

UPF

unit pattern formation