A more unified picture for the thermodynamics of nucleic acid duplex melting: A characterization by calorimetric and volumetric techniques

Abstract

We use a combination of calorimetric and volumetric techniques to detect and to characterize the thermodynamic changes that accompany helix-to-coil transitions for five polymeric nucleic acid duplexes. Our calorimetric measurements reveal that melting of the duplexes is accompanied by positive changes in heat capacity (ΔC_P) of similar magnitude, with an average ΔC_P value of 64.6 ± 21.4 cal deg⁻¹ mol⁻¹. When this heat capacity value is used to compare significantly different transition enthalpies (ΔH^o) at a common reference temperature, T_ref, we find ΔH_Tref for duplex melting to be far less dependent on duplex type, base composition, or base sequence than previously believed on the basis of the conventional assumption of a near-zero value for ΔC_P. Similarly, our densimetric and acoustic measurements reveal that, at a given temperature, all the AT- and AU-containing duplexes studied here melt with nearly the same volume and compressibility changes. In the aggregate, our results, in conjunction with literature data, suggest a more unified picture for the thermodynamics of nucleic acid duplex melting. Specifically, when compared at a common temperature, the apparent large differences present in the literature for the transition enthalpies of different duplexes become much more compressed, and the melting of all-AT- and all-AU-containing duplexes exhibits similar volume and compressibility changes despite differences in sequence and conformation. Thus, insofar as thermodynamic properties are concerned, when comparing duplexes, the temperature under consideration is as important as, if not more important than, the duplex type, the base composition, or the base sequence. This general behavior has significant implications for our basic understanding of the forces that stabilize nucleic acid duplexes. This behavior also is of practical significance in connection with the use of thermodynamic databases for designing probes and for assessing the affinity and specificity associated with hybridization-based protocols used in a wide range of sequencing, diagnostic, and therapeutic applications.

Thermodynamic studies of nucleic acids have produced data of both fundamental and practical importance. On the fundamental side, such studies have provided insight into the nature and strength of the forces that stabilize nucleic acids in the myriad of structural states they can assume (1–7). On the practical side, such studies have produced databases that are used to predict the stability and selectivity of hybridization events required in a broad range of nucleic acid-based diagnostic and therapeutic protocols (3, 8–11, 19, 42–44).

Three aspects of the current nucleic acid thermodynamic library that are conspicuously deficient are values for the heat capacity change(s), ΔC_P, the volume changes, ΔV, and the compressibility changes, ΔK_s, which accompany nucleic acid conformational transitions. These deficiencies are of particular concern because ΔC_P, ΔV, and ΔK_s provide unique insights into the role of solvent in duplex stabilization (12–15) and because quantitative knowledge of ΔC_P is required to compare thermodynamic properties of nucleic acids at a common reference temperature (16–18). This latter capacity is of specific practical value because thermodynamic databases reported at a given temperature often are used to predict hybridization properties at a different temperature as part of various diagnostic and therapeutic protocols (19). Without a significant body of directly measured heat capacity values, this parameter generally has been assumed to be zero for the melting of duplex structures to their component single strands (1–3). In this paper, we use a new generation of highly sensitive differential scanning calorimeters to demonstrate that this assumption is false. In fact, we measure ΔC_P to be positive, with an average value of 64.6 ± 21.4 cal⋅deg⁻¹⋅mol⁻¹, a value that we find to depend somewhat on base composition and sequence. We use this ΔC_P value to compare the transition enthalpies, ΔH, of different duplexes at a common reference temperature, T_ref. This comparison yields duplex transition enthalpies at T_ref, ΔH_Tref, which depend significantly less on duplex type, base composition, or base sequence than previously believed on the basis of the conventional assumption of a near-zero value for ΔC_P. We also present volumetric data (ΔV and ΔK_s) on nucleic acid duplexes that we derive from acoustic and densitimetric measurements (14, 15, 20). These volumetric data reveal a similar decrease in the dependence of duplex thermodynamic properties on the conformation, composition, and/or sequence of the duplex. Besides the fundamental importance of and insights derived from these ΔC_P, ΔV, and ΔK_s data, they also allow us to resolve duplex interactions into two general categories: those that depend primarily on duplex conformation, composition, and/or sequence (so-called “duplex-specific” interactions) and those that are relatively independent of conformation, composition, and sequence; that is to say, those that are common to all duplexes (so-called “duplex-nonspecific” interactions).

In the aggregate, our heat capacity and volumetric results, in conjunction with literature data, suggest a more unified picture of duplex melting thermodynamics in which, at a common temperature, the thermodynamic similarities between duplexes are greater than the thermodynamic differences induced by disparities in duplex conformation, base composition, and/or base sequence. In other words, insofar as thermodynamic properties are concerned, when comparing duplexes, the temperature under consideration is as important as, if not more important than, differences in the conformations, base compositions, or base sequences of the duplexes being compared. This general behavior has significant implications for our basic understanding of the forces that stabilize nucleic acid duplexes. This behavior also is of practical significance, as noted above, because thermodynamic databases are used to design probes and to assess the affinity and specificity associated with hybridization-based protocols used in a wide range of sequencing, diagnostic, and therapeutic applications.

MATERIALS AND METHODS

Materials.

The synthetic single-stranded polymers poly[d(A)], poly[d(T)], poly[r(A)], poly[r(U)], and double-stranded polymers poly[d(AT)]⋅poly[d(AT)], poly[d(A)]⋅poly[d(T)], poly[d(AC)]⋅ poly[d(GT)], poly[d(GC)]⋅poly[d(GC)], and poly[d(IC)]⋅ poly[d(IC)] are of the highest grade commercially available and were purchased from Amersham Pharmacia-LKB. All ultrasonic velocimetric and densimetric measurements were performed in a pH 6.8 buffer consisting of 10 mM cacodylic acid-sodium cacodylate, 20 mM NaCl, and 0.1 mM Na₂EDTA. The differential scanning calorimetric experiments were performed in the same basic buffer containing variable amounts of NaCl ranging from 20 to 200 mM. All solutions were exhaustively dialyzed at 4°C against the same buffer by using tubing with a molecular weight cutoff of 1,000 (Spectrum Laboratories, Houston).

Preparation of Double-Helix Solutions and Concentration Determinations.

Equal amounts of complementary single strands were mixed in buffer to obtain the poly[d(A)]⋅poly[d(T)], poly[r(A)]⋅poly[r(U)], poly[d(A)]⋅poly[r(U)], and poly[r(A)]⋅ poly[d(T)] duplexes.

The concentrations of all single- and double-stranded polynucleotides were determined spectrophotometrically by using the following molar extinction coefficients: poly[r(A)], ɛ₂₅₈ = 9,800 M⁻¹ cm⁻¹ (per base); poly[r(U)], ɛ₂₆₀ = 9,350 M⁻¹ cm⁻¹ (per base); poly[d(A)], ɛ₂₅₇ = 8,600 M⁻¹ cm⁻¹(per base); poly[d(T)], ɛ₂₆₄ = 8,520 M⁻¹ cm⁻¹(per base); poly[r(A)]⋅poly[r(U)], ɛ₂₅₇ = 14,000 M⁻¹ cm⁻¹ (per base pair); poly[d(A)]⋅poly[d(T)], ɛ₂₆₀ = 12,000 M⁻¹ cm⁻¹(per base pair); poly[d(AT)]⋅poly[d(AT)], ɛ₂₆₀ = 13,300 M⁻¹ cm⁻¹ (per base pair); poly[d(A)]⋅poly[r(U)], ɛ₂₅₇ = 13,000 M⁻¹ cm⁻¹ (per base pair); poly[r(A)]⋅poly[d(T)], ɛ₂₅₇ = 13,800 M⁻¹ cm⁻¹ (per base pair); poly[d(AC)]⋅poly[d(GT)], ɛ₂₅₈ = 13,000 M⁻¹ cm⁻¹ (per base pair); poly[d(GC)]⋅poly[d(GC)], ɛ₂₅₄ = 16,800 M⁻¹ cm⁻¹ (per base pair); poly[d(IC)]⋅poly[d(IC)], ɛ₂₅₁ = 13,800 M⁻¹ cm⁻¹(per base pair). These values were either provided by the manufacturer or taken from the literature (21). For all calorimetric, densimetric, and ultrasonic velocimetric experiments, polynucleotide concentrations were between 1 and 2 mM in base pair.

Ultrasonic Velocimetry.

For the poly[d(A)]⋅poly[d(T)], poly[r(A)]⋅poly[r(U)], poly[d(A)]⋅poly[r(U)], and poly[d(AT)]⋅ poly[d(AT)] duplexes, the solution sound velocities between 20 and 70°C were determined at a frequency of 7.5 MHz with a precision of ±10⁻⁴% by using previously described ultrasonic resonator cells and a differential mode of measurement (20, 22). The characteristic of a solute derived from ultrasonic measurements is the relative molar sound velocity increment, [U], which is equal to (U − U₀)/(U₀C), where C is the molar concentration of a solute, and U and U₀ are the sound velocities in the solution and in the “pure” solvent buffer, respectively.

Ultrasonic velocimetric titrations of 3 mM poly[r(A)] with 12 mM poly[r(U)], at 20, 30, and 40°C, were performed as previously described (23–26).

Densimetry.

The solution densities of the poly[d(A)]⋅ poly[d(T)], poly[r(A)]⋅poly[r(U)], poly[d(A)]⋅poly[r(U)], poly[r(A)]⋅poly[d(T)], and poly[d(AT)]⋅poly[d(AT)] duplexes were measured between 20 and 70°C with a precision of ±1.5 × 10⁻⁶ g/cm³ by using a vibrating tube densimeter (DMA-60, Anton Paar, Graz, Austria). The partial molar volumes, V^o, of each polynucleotide duplex were calculated by using the well known relationship (13):

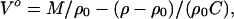1

where M is molecular weight of the DNA and/or RNA duplex (average per nucleotide) and ρ and ρ₀ are the densities of the solution and the solvent (buffer), respectively.

Densimetric titrations of 3 mM poly[r(A)] with 12 mM poly[r(U)], at 20, 30, and 40°C were performed as previously described (23, 24).

Determination of the Partial Molar Adiabatic Compressibility.

The relative molar sound velocity increments, [U], determined as described above, were used in conjunction with the partial molar volume, V^o, data to calculate the partial molar adiabatic compressibility, K_S^o, of polynucleotides by using the relationship (27, 28):

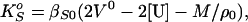2

where β_S0 is the coefficient of adiabatic compressibility of the solvent.

Differentiating Eq. 2 yields the expression

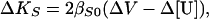3

where ΔK_S, ΔV, and Δ[U] are, respectively, the changes in adiabatic compressibility, volume, and relative molar sound velocity increment accompanying the helix-to-coil transitions of each polynucleotide.

Differential Scanning Calorimetry.

Calorimetric melting profiles of the heteropolymeric poly[d(IC)]⋅poly[d(IC)], poly[d(AT)]⋅poly[d(AT)], poly[d(AC)]⋅poly[d(GT)], and poly[d(GC)]⋅poly[d(GC)] duplexes and the homopolymeric poly[d(A)]⋅poly[d(T)] duplex were determined by using either a model 5100 NanoDSC (CSC, Provo, UT) differential scanning calorimeter with nominal cell volume 0.9 ml, or a model 6100 NanoDSCII (CSC) differential scanning calorimeter with nominal cell volume 0.3 ml. Results for both instruments were indistinguishable within the error of the experiment (>±3%). For each polynucleotide/salt condition, several denaturation/renaturation scans were performed, and the denaturation scans were averaged. This approach was justified as the repeat scans were indistinguishable, provided the sample was not heated to high temperatures. Appropriate buffer vs. buffer baselines were determined before and immediately after the polymer vs. buffer scans and were averaged. After subtraction of the (averaged) buffer scan, the (averaged) polymer scan was normalized for concentration and analyzed as follows. The heat capacity difference, ΔC_P, was determined from the difference in the pre- and posttransition baseline at the midpoint of the transition; the calorimetric enthalpy, ΔH_cal, was determined by integration of the area enclosed by the transition curve and the pre/posttransition baseline; and the melting temperature, T_m, was determined as the midpoint of the melting transition.

RESULTS AND DISCUSSION

Nucleic Acid Duplex Melting Is Accompanied by a Positive ΔC_P, with an Average Value of 64.6 ± 21.4 cal⋅deg⁻¹⋅(mol per base pair)⁻¹.

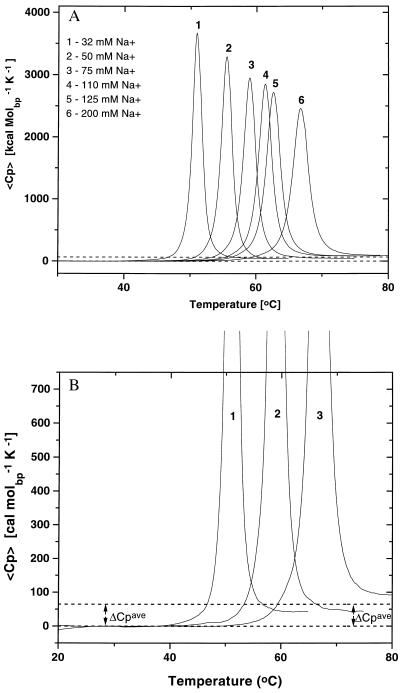
Fig. 1A shows the family of heat capacity curves we have measured as a function of salt [Na⁺] concentration for the melting of the poly[d(AT)]⋅poly[d(AT)] duplex. Fig. 1B shows three of these curves with an expanded y-axis to facilitate visualization of the positive change in heat capacity. We observe similar heat capacity changes for the other four duplexes (not shown).

Figure 1.

(A) Excess heat capacity profiles for the poly[d(AT)]⋅poly[d(AT)] duplex at different salt concentrations ranging from 32 mM Na⁺ (curve 1) to 200 mM Na⁺ (curve 6). The difference in the pre- and posttransition baselines reflects a positive heat capacity change, ΔC_P, for the denaturation of the polynucleotide duplex. (B) Expanded scale representation of the excess heat capacity profiles of poly[d(AT)]⋅poly[d(AT)] at three of the salt concentrations to facilitate visualization of the heat capacity change. The average ΔC_P measured for all polynucleotides [ΔC_P = 64.6 ± 21.4 cal⋅K⁻¹⋅(mol of base pair)⁻¹] is indicated by the dotted lines.

In addition to the poly[d(AT)]⋅poly[d(AT)] curves shown in Fig. 1A, we have also measured the heat capacity profiles for the poly[d(A)]⋅poly[d(T)] and poly[d(IC)]⋅poly[d(IC)] duplexes as a function of salt concentration, between 32 mM and 200 mM [Na⁺]. Analysis of each of these 20 curves yields T_m, ΔH_Tm, and ΔC_P data. In Table 1, we list in the second and third columns the T_m and ΔH_Tm data at 32 mM Na⁺, whereas in the fourth column we list the ΔC_P data averaged over the entire salt range studied. Note that the average ΔC_P values are not zero, as often has been assumed (1–3), but rather are positive. Further note that although similar in magnitude, the ΔC_P values are somewhat different for different duplexes and even appear to exhibit a small dependence on Na⁺ concentration and/or temperature (see footnote to Table 1). However, given the experimental uncertainty associated with measuring ΔC_P, we focus here on the average ΔC_P value of 64.6 ± 21.4 cal⋅deg⁻¹⋅mol⁻¹ that we measure across duplexes and across Na⁺ concentration.

Table 1.

Thermodynamic parameters for polynucleotides in 32 mM Na⁺ buffer

Polymer	Tm, °C	ΔHTm, kcal/molbp	ΔCP*, cal/molbp K	ΔCP†, cal/molbp K	ΔHTref‡, kcal/molbp
Poly[d(IC)]⋅poly[d(IC)]	44.7	8.76  ±  0.26	31.2  ±  16.4	96.7	7.48  ±  0.49
Poly[d(AT)]⋅poly[d(AT)]	50.9	8.06  ±  0.24	61.3  ±  18.3	42.6	6.38  ±  0.60
Poly[d(A)]⋅poly[d(T)]	58.2	9.36  ±  0.28	101.7  ±  24.5	54.5	7.21  ±  0.76
Poly[d(AC)]⋅poly[d(GT)]	79.9	9.62  ±  0.28	40.0§	—	6.06  ±  1.21
Poly[d(GC)]⋅poly[d(GC)]	103.8	12.10  ±  0.36	78.2§	—	7.00  ±  1.72

^*Measured ΔC_P derived from the difference in pre- and posttransition baseline averaged over all salt concentrations (32 mM, 50 mM, 75 mM, 105 mM, 125 mM, and 200 mM). 

^†ΔC_P derived from a plot of ΔH_Tm vs. T_m. 

^‡ΔH_Tref (at 25°C) calculated by using the average ΔC_P = 64.6 cal deg⁻¹ mol⁻¹ (see text). 

^§ΔC_P value derived from a measurement at a single salt concentration (32 mM Na⁺). 

Comparison with Literature Data.

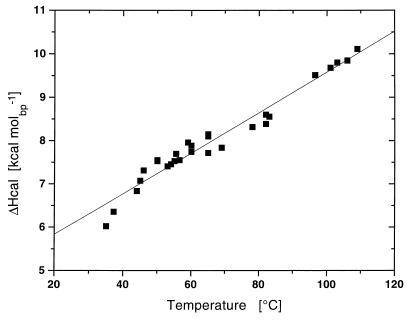
Armed with our calorimetrically measured average ΔC_P value of 64.6 ± 21.4 cal⋅deg⁻¹⋅mol⁻¹ for nucleic acid duplex melting, we surveyed the literature for published calorimetric ΔH^o data on duplex melting over a range of temperatures (2, 3, 9). This survey revealed that the most extensive compilation of calorimetric T_m and ΔH data on polynucleotides is that of Klump (3, 9). Because the published calorimetric studies were conducted on a variety of polymeric duplexes over a range of solution conditions, they yield different T_m values over which ΔH^o is reported. Fig. 2 shows a plot of these ΔH^o values vs. the duplex melting temperature, primarily on the basis of the data of Klump (3, 9). Within the experimental uncertainty, these data yield a straight line with a slope (ΔC_P) of 47 cal⋅deg⁻¹⋅(mol per base pair)⁻¹, a value within the range of our directly measured average ΔC_P value of 64.6 ± 21.4 cal⋅deg⁻¹⋅(mol per base pair)⁻¹.

Figure 2.

Comparison of the published calorimetric enthalpy values for all RNA/RNA, RNA/DNA, and DNA/DNA polynucleotide duplexes plotted against their melting temperatures. The experimental data in Fig. 2 (■) are taken from the extensive collection of polynucleotide thermodynamic data compiled by Klump (3, 9). The solid line corresponds to the best fit straight line to these values. This line has a slope, ΔH/T_m (=ΔC_P), equal to 47 cal⋅ K⁻¹⋅(mol of base pair)⁻¹.

The Average Heat Capacity Change of 64.6 ± 21.4 cal⋅deg⁻¹⋅mol⁻¹ That We Derive from the Difference in the Pre- and Posttransition Baselines Agrees with the Value We Calculate from the Salt Dependence of the Calorimetrically Measured Transition Enthalpies.

As noted above, we have measured heat capacity curves as a function of salt concentration for three of the duplexes studied here. Because increasing the salt concentration also increases the melting temperature (29, 30), we obtain the transition enthalpy as a function of temperature as well. The slopes of these plots (not shown), which correspond to ΔC_P, are listed in column 5 of Table 1. The average ΔC_P value of 64.7 cal⋅deg⁻¹⋅mol⁻¹ derived from these data is in excellent agreement with the average of 64.6 ± 21.4 cal⋅deg⁻¹⋅mol⁻¹ derived from the directly measured values determined from the difference in the pre- and posttransition baselines of the experimental heat capacity curves. Although the near identity of these two average values is undoubtedly fortuitous, the good agreement lends credence to both the quality of our measurements and our data analysis. These two average ΔC_P values also are in good agreement with the few early estimates in the literature (31–36).

In the sections that follow, we use our average heat capacity value of 64.6 ± 21.4 cal⋅deg⁻¹⋅mol⁻¹ to make comparisons between duplex properties at a common reference temperature. As previously stated, we judge the use of an average heat capacity value to be justified given the experimental uncertainties in this parameter. However, it is important to note that the general nature of our observations and conclusions remains unaltered when we use the individual heat capacity values listed in Table 1 in our analysis.

When ΔC_P Is Used to Compare Duplex Transition Enthalpies at the Same Temperature, the Apparent Composition/Sequence-Dependent Differences Becomes Much Less Pronounced.

We used our average calorimetrically measured ΔC_P value to extrapolate and compare at a common reference temperature, T_ref, the disparate transition enthalpies at T_m that we and others have measured (3, 9). These data are listed in column 6 of Table 1 for T_ref equal to 25°C. Note the substantial compression of the generally accepted strong dependence of transition enthalpy on duplex composition and sequence. The ΔH_Tm values measured at the various T_m values (column 3 in Table 1) range from 8.06 to 12.10 kcal/mol⁻¹ (ΔΔH_Tm = 4.04 kcal/mol⁻¹). However, when ΔC_P is used to extrapolate these ΔH values at T_m to a common reference temperature, T_ref (e.g., 25°C), the thermodynamically more appropriate comparison reveals the ΔH_Tref values to range only from 6.06 to 7.48 kcal/mol⁻¹ (ΔΔH_Tref = 1.42 kcal/mol⁻¹). In other words, the apparent strong dependence of the transition enthalpy on duplex type, base composition, and base sequence becomes far less significant (more compressed) when the ΔH values are compared at a common reference temperature. In fact, when we use our average ΔC_P value to compare existing nucleic acid transition enthalpies at a common reference temperature, all duplexes studied to date (2, 3, 9) exhibit ΔH_Tref values that differ by a ΔΔH_Tref of only 1.3 kcal/mol⁻¹, despite possessing major differences in base composition and sequence. By comparison, the transition enthalpies at T_m (ΔΔH_Tm) differ by 4.09 kcal/mol⁻¹. One interpretation of this result suggests that on average about 70% of the transition enthalpy results from duplex nonspecific general interactions.

Superficially, the above conclusion may appear to conflict with literature reports that different duplexes melt with dramatically different transition enthalpies, ΔH_Tm, at their melting temperatures, T_m, an observation consistent with an apparent dependence of the transition enthalpy on duplex conformation/composition/sequence (1–3). However, unless ΔC_P is zero (a common assumption that we show here to be erroneous), such direct comparisons of ΔH_Tm are inappropriate because they generally refer to different temperatures. In short, our results suggest that, insofar as the enthalpy is concerned, duplex-nonspecific general interactions contribute more substantially to duplex energetics than previously assumed. An alternative complementary framing of this same point states that insofar as the enthalpy is concerned, duplex-specific interactions contribute less to duplex energetics than previously assumed.

Minor Differences in the Small Duplex-Specific Contributions to the Transition Enthalpy Can Yield Substantial Shifts in T_m.

In the paragraphs above, we have shown that all nucleic acid duplexes calorimetrically studied to date exhibit nonzero positive heat capacity changes of similar magnitudes. Further, when these ΔC_P values are used to extrapolate duplex transition enthalpies to a common temperature, we find ΔH_ref to depend less on composition, sequence, and conformation than previously believed. We attribute these observations to the strong contribution of duplex-nonspecific interactions to ΔH^o and its temperature dependence. Nevertheless, it is an experimental fact that, under identical solution conditions, duplexes with different base compositions and base sequences exhibit significantly different T_max or T_m values (37). We propose that this difference in thermal stability derives from differences in the duplex-specific contribution to ΔH^o, which, because of its logarithmic relationship to the equilibrium constant, translates into a significant shift in T_m, despite being a less significant fraction of the overall ΔH^o than previously assumed (1–3).

If the observations of conformation/composition/sequence-independent and dependent contributions to duplex melting energetics described above are general, then they also should be reflected in other thermodynamic observations, including volumetric changes associated with duplex melting. To make this assessment, we have used a combination of densimetric and acoustic techniques to determine the change in volume, ΔV, and compressibility, ΔK_S, accompanying the melting and/or formation of several nucleic acid duplexes. The resulting data, which are listed in Tables 2 and 3, are presented and discussed below.

Table 2.

Changes in the relative molar volume, ΔV, sound velocity increment, Δ[U], and adiabatic compressibility, ΔK_s, accompanying the thermally induced helix-to-coil transitions of polynucleotide duplexes

Polymer	Tm, °C	ΔV, cm3⋅molbp−1	Δ[U], cm3⋅molbp−1	ΔKS × 104, cm3⋅molbp−1·bar−1
Poly[d(A)]⋅poly[r(U)]	30.5  ±  0.5	−10.6  ±  2.0	20.0  ±  2.0	−27.0  ±  4.0
Poly[r(A)]⋅poly[r(U)]	48.0  ±  0.5	0  ±  2.0	14.0  ±  2.0	−13.0  ±  4.0
Poly[d(AT)]⋅poly[d(AT)]	51.0  ±  0.5	8.0  ±  2.0	10.0  ±  2.0	−2.0  ±  4.0
Poly[r(A)]⋅poly[d(T)]	55.0  ±  0.5	0  ±  2.0	12.0  ±  2.0	−11.0  ±  4.0
Poly[d(A)]⋅poly[d(T)]	56.5  ±  0.5	2.0  ±  2.0	10.0  ±  2.0	−7.0  ±  4.0

Table 3.

Changes in the relative molar volume, ΔV, sound velocity increment, Δ(U), and adiabatic compressibility, ΔK_S, accompanying the helix-to-coil transitions of poly[r(A)]⋅poly[r(U)] duplex resulting from the addition of single-strand poly[r(U)] to single-strand poly[r(A)] at 20, 30, and 40°C

	20°C	30°C	40°C
ΔV, cm3·molbp−1	−9.6  ± 2.6	−8.0  ± 2.6	−4.0  ± 3.0
Δ[U], cm3·molbp−1	42.2  ± 1.6	31.2  ± 1.6	20.0  ± 2.0
ΔKS × 104 cm3·molbp−1 ·bar−1	−47.2  ± 4.0	−34.6  ± 4.0	−20.3  ± 4.0

Volume Changes Accompanying Helix-to-Coil Transitions of Polynucleotide Duplexes.

In general, the partial molar volume, V^o, of a solute can be represented by a sum of the intrinsic volume, V_M, occupied by the solute molecule itself and the hydration-induced changes in the solvent volume, ΔV_h:

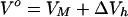As previously discussed (33), the overall volume change, ΔV, which accompanies helix-to-coil transitions of biopolymers, can be expressed as the sum of the intrinsic and hydration contributions.

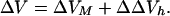4

Transition-induced structural changes in the polynucleotide strands are reflected in the ΔV_M term in Eq. 4, whereas the hydration changes are reflected in the ΔΔV_h term. It should be noted that the ΔΔV_h term also reflects changes in the amount and nature of counterion and free ion hydration (29, 30).

In this work, we have measured the volume changes, ΔV, which accompany the helix-to-coil transitions of several of the polynucleotide duplexes studied here, in two different ways: (i) volume changes at T_m were measured for the thermally induced denaturations of the poly[d(A)]⋅poly[r(U)], poly[r(A)]⋅poly[r(U)], poly[d(AT)]⋅poly[d(AT)], poly[r(A)]⋅poly[d(T)], and poly[d(A)]⋅ poly[d(T)] duplexes, and (ii) volume changes at 20, 30, and 40°C were measured for duplex formation of poly[r(A)]⋅poly[r(U)] by addition of the poly[r(U)] single strand to the poly[r(A)] single strand.

Table 2 presents the T_m (second column) and ΔV (third column) data we have measured for the thermally induced helix-to-coil transitions of the five duplexes. Our T_m values (obtained at pH 6.8 and a total Na⁺ concentration of 28 mM) are in good agreement with previous reports (3, 21). Table 3 shows the ΔV data for the isothermal duplex formation of poly[r(A)]⋅poly[r(U)] at 20, 30, and 40°C.

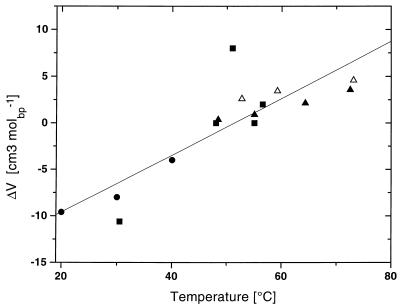
Fig. 3 shows a plot of temperature vs. volume changes, ΔV, accompanying the helix-to-coil transitions of the five polynucleotide duplexes. Note that when two transition temperatures are close, the ΔV values for the corresponding duplexes nearly coincide. For example, the poly[d(A)]⋅poly[r(U)] and the poly[r(A)]⋅poly[r(U)] duplexes at about 30°C or the poly[d(A)]⋅poly[d(T)] and the poly[r(A)]⋅poly[d(T)] duplexes at about 55°C exhibit nearly identical ΔV values. In other words, the volume change, ΔV, associated with the helix-to-coil transitions of these all-A/T and all-A/U duplexes depends primarily on the transition temperature, although it is rather insensitive to the type of the duplex, which for these duplexes corresponds to quite different helical types based on their CD spectra. This volumetrically based observation parallels our assessment of the calorimetric data; that is to say, the value of either ΔV or ΔH^o for the melting of all-A/T- and all-A/U-containing duplexes depends primarily on the temperature, although it is less dependent on the base sequence and/or duplex conformation. Consequently, at a common reference temperature, all the AT- and AU-containing duplexes studied here exhibit similar values for ΔH^o and ΔV.

Figure 3.

The dependence of volume change (ΔV) on temperature for the poly[d/r(A)]⋅poly[d/r(T/U)] system. Solid squares (■) correspond to the values listed in Table 2 determined by thermal denaturation of the polynucleotides; solid circles (●) correspond to values derived from the titration of poly[rA] with poly[rU] (Table 3); triangles correspond to published ΔV values reported by Wu and Macgregor (39) for poly[d(AT)]⋅poly[d(AT)] (▴) and poly[d(A)]⋅poly[d(T)] (Δ).

This duplex-independent temperature-specific ΔV observation is supported further by comparison of our densimetric data with the results of Wu and Macgregor (39), which are represented in Fig. 3 by the symbols ▴ and ▵. These investigators calculated ΔV values for the heat-induced helix-to-coil transitions of the poly[d(AT)]⋅poly[d(AT)] and poly[d(A)]⋅poly[d(T)] duplexes from the change in T_m when the ambient hydrostatic pressure is increased from its atmospheric value to 2,000 bar (39). In their high-pressure experiments, Wu and Macgregor used a Tris⋅HCl buffer (as opposed to our cacodylic buffer) and NaCl concentrations of 20 mM to 1 M (39). In Fig. 3, Wu and Macgregor’s “high-pressure” volume changes, ΔV, are plotted vs. T_m values that correspond to atmospheric pressure [these T_m values were altered by changing the NaCl concentration (39)]. Note that Wu and Macgregor’s “high-pressure” data on poly[d(A)]⋅poly[d(T)] and poly[d(AT)]⋅poly[d(AT)] are in excellent agreement with our densimetric data. In the aggregate, the data in Fig. 3 reveal that, between 20 and 70°C, ΔV for all the A/U and A/T duplexes studied here increases linearly from negative values below 50°C to positive values at higher temperatures. The slope, ΔΔV/ΔT, is equal to 0.30 ± 0.05 cm³mol⁻¹K⁻¹. This value represents the change in thermal expansibility, ΔE, that accompanies the helix-to-coil transitions of the A/U and A/T duplexes. To our knowledge, this determination of ΔE_hc represents the first such measurement of nucleic acids.

As noted above, our data reveal that A/T and A/U duplexes exhibit very similar volumetric temperature dependencies, ΔV(T), which, within experimental uncertainty, do not depend on the method of measurement, the buffer, the salt concentration, or the duplex type. We offer below one possible interpretation of this observation. We present this interpretation only as a basis for further discussion because clearly other possibilities exist.

The volume change, ΔV, accompanying the helix-to-coil transitions of nucleic acids can be expressed as the sum of specific, ΔV_spec, and nonspecific, ΔV_non, contributions:

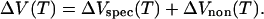5

The striking similarity of the observed temperature dependencies, ΔV(T), for all the A/T- and A/U-containing duplexes shown in Fig. 3 suggests that the duplex-nonspecific contribution, ΔV_non(T), overwhelms the duplex-specific contribution, ΔV_spec(T). One interpretation of this observation is that, at least for the helix-to-coil transitions of A/T- and A/U-containing duplexes, the intrinsic and hydration volumetric changes are predominantly nonspecific; that is to say, they do not strongly depend on the specific type of duplex, the arrangement of the component bases, or the structure of the sugar ring.

The significant general observation concerning the ΔV data presented above is that for diverse AT- and AU-containing duplexes, the value of ΔV, like that of ΔH⁰, depends primarily on temperature, although it depends less on duplex conformation, base composition, or base sequence than previously assumed (40, 41).

Adiabatic Compressibility Changes Accompanying Helix-to-Coil Transitions of Polynucleotide Duplexes.

Analogous to the treatment of the volumetric data noted above (see Eq. 4), and as previously discussed (15), the changes in adiabatic compressibility, ΔK_S, that accompany biopolymer transitions can be expressed as the sum of intrinsic (K_M) and hydration (K_h) contributions:

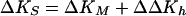6

Using Eq. 3 from Materials and Methods, we have calculated changes in adiabatic compressibility, ΔK_S, by combining our data on the changes in volume, ΔV, and the relative molar sound velocity increment, Δ[U], listed in Table 2. The fourth and fifth columns in Table 2 list the changes in Δ[U] and ΔK_S, respectively, for the thermally induced helix-to-coil transitions of the duplexes studied here. Table 3 lists the corresponding Δ[U] and ΔK_S data for the isothermal duplex formation of poly[r(A)]⋅poly[r(U)] at 20, 30, and 40°C.

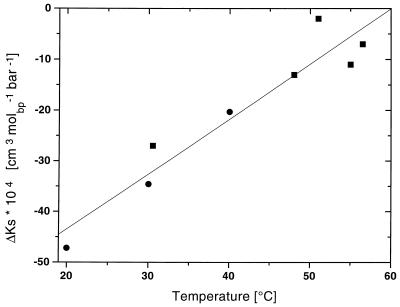
Fig. 4 shows a plot of the adiabatic compressibility changes, ΔK_S, vs. T_m that we have measured for the duplexes studied here. Inspection of this plot reveals that, independent of the type of the duplex or the means of duplex disruption/formation, ΔK_S linearly increases with temperature. In other words, analogous to ΔV and ΔH^o, we find the magnitude of the temperature dependence of ΔK_S to be relatively insensitive to the type of duplex.

Figure 4.

The change in adiabatic compressibility (ΔK_s) with temperature for the poly[d/r(A)]⋅poly[d/r(T/U)] system. Solid squares (■) correspond to the values listed in Table 2 determined by thermal denaturation of the polynucleotides; solid circles (●) correspond to data derived from the titration poly[r(A)] with poly[r(U)] at various temperatures (Table 3).

This observation, as in the case of ΔH^o and ΔV, can be rationalized by defining the observable as the sum of specific, ΔK_spec, and nonspecific, ΔK_non, contributions to ΔK_S:

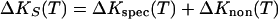7

The similarity of the observed temperature dependencies, ΔK_S(T), for A/T and A/U duplexes shown in Fig. 4 suggests that the nonspecific contribution, ΔK_non(T), overwhelms the specific contribution, ΔK_spec(T). This observation also is consistent with our early suggestion that, for the A/T and A/U duplexes, intrinsic and hydration changes accompanying helix-to-coil transitions are predominantly nonspecific, i.e., they do not strongly depend on the specific type of duplex.

Given the volumetric results described above, it is instructive now to revisit the heat capacity data presented earlier.

Dissection of the Helix-to-Coil Transition Enthalpies for the Polynucleotide Duplexes.

Recall that Fig. 2 shows a plot of calorimetrically determined ΔH^o values vs. T_m for all combinations of A/U, A/T, G/C, and I/C-containing DNA, RNA, and DNA/RNA hybrid polymeric duplexes studied to date. Note that the A/U- and A/T-containing duplexes, as well as the G/C- and I/C-containing duplexes, exhibit similar linear temperature dependencies for ΔH^o(T), with a standard deviation of ±0.3 kcal⋅mol⁻¹ per base pair. Analogous to our analysis of the ΔV and ΔK_S data (see Eqs. 5 and 7), we also can represent ΔH^o(T) as a sum of conformation/composition/sequence specific and nonspecific contributions:

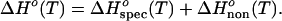8

We propose that the similarity in the magnitude of the observed temperature dependence of ΔH^o [ΔH^o(T)] for all polymeric duplexes studied to date (Fig. 2) suggests that, relative to specific enthalpic contributions, ΔH^o_spec(T), nonspecific enthalpic contributions, ΔH^o_non(T) contribute more than previously assumed. In other words, those interactions that are common to all duplexes are more significant contributors to ΔH^o(T) than those that are different from one duplex to another. Simply stated, the similarities between duplexes exceed the differences.