Atomic levers control pyranose ring conformations

Abstract

Atomic force microscope manipulations of single polysaccharide molecules have recently expanded conformational chemistry to include force-driven transitions between the chair and boat conformers of the pyranose ring structure. We now expand these observations to include chair inversion, a common phenomenon in the conformational chemistry of six-membered ring molecules. We demonstrate that by stretching single pectin molecules (1 → 4-linked α-d-galactouronic acid polymer), we could change the pyranose ring conformation from a chair to a boat and then to an inverted chair in a clearly resolved two-step conversion: ⁴C₁ ⇄ boat ⇄ ¹C₄. The two-step extension of the distance between the glycosidic oxygen atoms O₁ and O₄ determined by atomic force microscope manipulations is corroborated by ab initio calculations of the increase in length of the residue vector O₁O₄ on chair inversion. We postulate that this conformational change results from the torque generated by the glycosidic bonds when a force is applied to the pectin molecule. Hence, the glycosidic bonds act as mechanical levers, driving the conformational transitions of the pyranose ring. When the glycosidic bonds are equatorial (e), the torque is zero, causing no conformational change. However, when the glycosidic bond is axial (a), torque is generated, causing a rotation around C—C bonds and a conformational change. This hypothesis readily predicts the number of transitions observed in pyranose monomers with 1a-4a linkages (two), 1a-4e (one), and 1e-4e (none). Our results demonstrate single-molecule mechanochemistry with the capability of resolving complex conformational transitions.

Atomic force microscope (AFM) manipulations of single polysaccharide molecules have recently expanded conformational chemistry (1) to include force-driven transitions between the chair and boat conformers of the pyranose ring structure (2). The application of a force to a single molecule will deform it elastically and also induce conformational transitions. Although it is easy to understand the origin of an elastic deformation, the mechanics of the conformational transition is less clear.

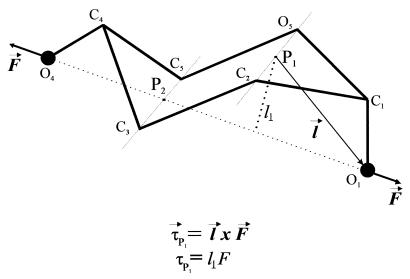
Pyranose-based sugars have two distinct chair conformations, ⁴C₁ and ¹C₄ (3), separated by an energy barrier of ≈11 kcal/mol (4). In addition to the chair conformers, pyranoses have intermediate conformers corresponding to the boat conformation, whose energy is ≈5–8 kcal/mol above the energy of the ⁴C₁ chair (5). Thermally driven transitions do occur between these conformers. However, in the absence of an applied force, the most stable conformation of a pyranose is that of the ⁴C₁ chair (4–9). Application of a force of ≈200 pN to polymers of α-d-glucopyranose such as amylose drives a conformational change in the pyranose ring that is evident as a sudden elongation of the molecule, marking a prominent enthalpic component of the elasticity of the molecule (2, 10). This enthalpic component results from an increase in the distance between glycosidic oxygen atoms caused by a force-induced transition between the chair and boat conformations of the pyranose ring (2, 11). The glycosidic bonds of amylose are disposed in the C1-O1 [axial (a)] and C4-O4 [equatorial (e)] configuration. Inspection of this configuration reveals that a stretching force (whose direction coincides with the direction of the line passing through the backbone oxygen atoms) applied to the axial glycosidic oxygen O1 has a large lever arm relative to the C2-O5 axis and therefore produces torque about this axis, promoting the transition to the boat conformation. The line of action of the force applied to the equatorial oxygen atom O4 passes in the vicinity of the C3-C5 axis and therefore the C4-O4 bond does not produce significant torque about this axis. Fig. 1 illustrates this concept. Typically, ab initio calculations are required to predict the path of the conformational changes of the pyranose ring. However, the simplified mechanical schematic of Fig. 1 does make useful predictions. It is evident from this picture that axial linkages generate torque, whereas equatorial linkages do not. We propose that the torque generated by forces applied to the glycosidic linkages does the rotational work necessary to flip the linkage to an extended conformer. To examine the validity of this hypothesis, we compare the extensibility of three different pyranose-based polymers with 1–4 glycosidic linkages: pectin (1a-4a), amylose (1a-4e), and cellulose (1e-4e). We find that, as predicted, the number of conformational transitions reported in force-extension curves of these polymers correlates with the number of glycosidic linkages in the axial orientation.

Figure 1.

A simplified mechanical model of the pyranose ring. An external force (F) is applied to the ring through the oxygen atoms O₁ and O₄ as in an (1a → 4e)-linked polysaccharide chain (e.g., amylose). The direction of F coincides with the direction of the residue vector O₁O₄. The force applied to the axial oxygen O₁ has a large torque τ_P1 relative to the pivot point P₁ (P₁ lies on the imaginary axis of rotation passing through C₂ and O₅) and promotes a transition of the ring to the boat conformation. The axial bond C₁O₁ works as a lever arm. The force applied to the equatorial oxygen O₄ has a negligible torque relative to P₂ (P₂ lies on the imaginary axis of rotation that passes through C₃ and C₅) because its line of action passes in the vicinity of P₂. Therefore the equatorial bond cannot mediate a conformational transition; however, a force applied to it will strain the ring. (Inset) Definition of torque as the cross product between the distance vector l and the force vector F.

MATERIALS AND METHODS

Single-Molecule AFM.

Our custom-made AFM apparatus, as well as its mode of operation, is identical to those that we have recently described (2, 12); it is capable of measuring the extensibility of individual molecules. The spring constant of each individual AFM tip was calibrated in solution, by using the equipartition theorem as described by Florin et al. (13). This method gives values for the spring constant of the cantilever that are within 20% of the values obtained by other methods (13).

Polysaccharides.

The polysaccharides used were: pectin (14), a partially methoxylated α-(1 → 4)d-galactouronan (from citrus fruits; Sigma; galactouronic acid content ≈80%, methoxyl content ≈9%); amylose, an α-(1 → 4)d-glucan (Type III: from potato; Sigma); and methylcellulose, a partially methoxylated β-(1 → 4)d-glucan (degree of substitution, 1.5–1.9; Sigma). Amylose and methylcellulose are linear homopolymers of glucopyranose, whereas in pectin the galactouronan chain is interrupted by short sequences of α-l-rhamnopyranosyl units linked (1 → 2) and contains small amounts of neutral sugar side chains (15). Pectin and methylcellulose were dissolved in water at a concentration of 0.1–1% (wt/vol). Amylose was solubilized by wetting with ethanol (100 mg/ml), followed by treatment with sodium hydroxide (10%) and heating. The final concentration of amylose was 0.2–1% (wt/vol). A layer of polysaccharide molecules was created by drying a drop of these solutions onto glass coverslips followed by extensive rinsing. This procedure leaves a monolayer of polysaccharide molecules tightly adsorbed to the glass surface (16). The measurements were carried out in water or in PBS buffer (pectin).

For ring cleavage, the polysaccharide samples were treated with 5 mM sodium metaperiodate (Sigma) for up to 180 min. We cannot exclude the possibility that, on cleavage, the dialdehyde groups react further to form a seven-membered ring. This reaction would occur by the addition of water to one of the carbonyls and the subsequent addition of one of the formed hydroxyl groups to the other aldehyde carbonyl. Another possibility is that an aldehyde carbonyl forms a new six-membered ring by reacting with the free carboxyl group of pectin. However, our experimental observations show that after periodate oxidation, dissimilar polysaccharides such as dextran, amylose, and pectin all show similar force-extension curves with a large decrease in their Kuhn length, to the size of a single bond (2). Hence, it is unlikely that after ring cleavage, new cyclization reaction makes a permanent contribution to pectin elasticity.

To pick polysaccharide molecules, an AFM tip was pressed down onto the sample for 1–3 sec and at forces of several nN. A subsequent force-extension measurement typically revealed a complex pattern with many overlapping force peaks. By manipulating the polysaccharide concentration and the force and duration of the tip-sample contact, it was possible to regularly obtain single polysaccharide force-extension curves.

Ab Initio Calculations of the Galactouronic Acid Ring Conformations.

Different conformations of the galactopyranuronic acid ring were generated by the published procedure (2), with the exception that in the present work the B3LYP/6–31G* method (17) was used to consider the electron correlation effect. Length of the residue vector in the relaxed state of galactouronan (no external force) was obtained from the distance between the two consecutive glycosidic oxygen atoms (O₁O₄) in the most stable pyranose conformer (⁴C₁ chair). The corresponding lengths of the residue vector in the boat and inverted chair conformations were optimized by ab initio calculations (Table 1).

Table 1.

Ab initio calculation of the separation of glycosidic oxygen atoms during chair inversion in galactouronic acid

Method	4C1	Boat*	1C4	4C1 → boat	Boat → 1C4	4C1 → 1C4
	l1, Å	l2, Å	l3, Å	(l2 − l1)/l1, %	(l3 − l2)/l2, %	(l3 − l1)/l1, %
HF/6-31G*	4.462	5.044	5.435	13.0	7.8	21.8
B3LYP/6-31G*	4.522	4.891	5.492	8.2	12.3	21.5
AFM data	4.500	4.901	5.405	8.9 ± 0.8†	10.3 ± 0.7†	20.1 ± 0.9†

^*This is a symmetrical boat with the “flagpole” hydroxyl at positon C2 and the “flagpole” hydrogen at position C5 (not shown). 

^†Standard error of the mean (n = 8).  

RESULTS AND DISCUSSION

Stretched Pectin Monomers Undergo a Two-Step Chair Inversion Reaction.

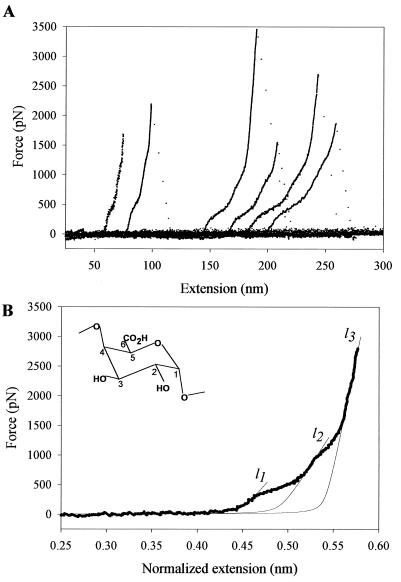
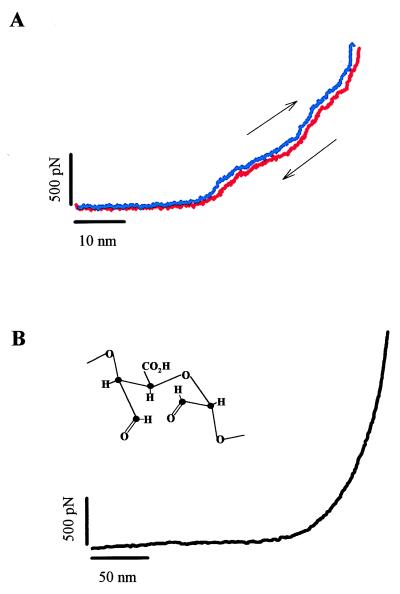
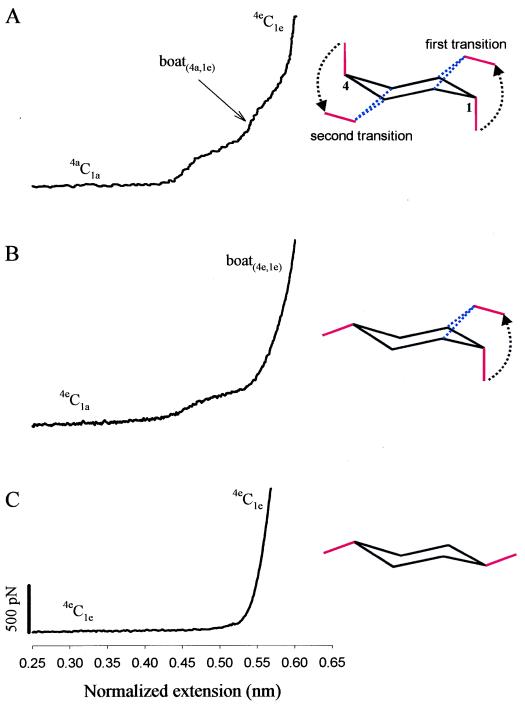
We begin by studying the elasticity of single pectin molecules, which has not been characterized before. In Fig. 2A we show a family of force-extension curves obtained from pectin molecules. The force-extension curves for pectin deviate from the shape predicted for a simple entropic freely jointed chain (FJC) (2, 10, 16, 18–21), and they display two enthalpic extensions at an average force of ≈300 and ≈800 pN. The curves superimpose well after being normalized by the length of the molecule, indicating that we stretched single molecules. Both enthalpic extensions are fully reversible (Fig. 3A) and disappear on cleavage of the pyranose rings with periodate (Fig. 3B) (22), confirming the view that they correspond to two separate force-driven transitions of the pyranose ring (2). We characterized these transitions by fitting the data to the modified FJC model of polymer elasticity (10, 20), as exemplified in Fig. 2B, where l₁, l₂, and l₃ correspond to the normalized contour length (monomer size; see Fig. 2 legend) of the polymer before the first transition, after the first transition, and after the second transition, respectively. The first transition was observed at a force of ≈300 pN and elongated the molecule by 0.042 nm/monomer, (l₂−l₁)/l₁ corresponding to 9.3% of its total length. The second transition was resolved at ≈900 pN and elongated the molecule by 0.049 nm/monomer, (l₃−l₂)/l₂, corresponding to 10% of its total length (for average values, see Table 1). Ab initio calculation of the length of the residue vector O₁O₄ of the different pectin ring conformers show that a ⁴C₁ → boat transition elongates the molecule by 0.037 nm/monomer (8.2%, B3LYP/6–31G* method; see Table 1) and that chair inversion (23) further elongates the monomer by 0.06 nm (12.3%, B3LYP/6–31G* method; see Table 1). The ab initio calculations are in good agreement with our experimental observations, suggesting that the two transitions observed in pectin correspond to a sequential chair inversion reaction ^4aC_1a ⇄ boat ⇄ ^1eC_4e. The total elongation of the monomer determined experimentally, 20.1%, is slightly shorter than the elongation calculated ab initio: 21.5%. This difference is consistent with the fact that the pectin chain contains a small amount of α-l-rhamnopyranosyl units linked (1 → 2) (15), which do not undergo a transition to elongated conformers. Significantly, the first transition in pectin occurs at the force that was found to trigger a chair-to-boat transition of the pyranose rings in amylose (2). Hence, our AFM measurements clearly resolve a chair inversion reaction, as a two-step conformational transition within the pectin pyranose rings.

Figure 2.

Force-extension curves for single-pectin molecules reveal a two-step transition. (A) The shape of the curves obtained from short and long molecules clearly deviates from the shape expected for a FJC. The curves reveal two enthalpic extensions that occur at ≈300 and ≈800–900 pN. (B) High-resolution plot of the force-extension relationship for a single pectin molecule. The extension, x, was normalized: x_norm = 0.45x/l₁^c, where 0.45 nm corresponds to length of the residue vector O₁O₄^chair in the relaxed state of the polymer (chair ⁴C₁; see Table 1), and l₁^c the contour length of the molecule determined from the FJC fit to the nonnormalized data before the first transition (l₁^c = 69.97 nm for this recording). Thin lines are the local fits of the FJC model modified to include the extensibility of the monomers (segment elasticity S_E; 10, 16, 20). l₁ = 0.45 nm (by definition); S_E1 was found to be 17,000 pN/nm; l₂ was determined to be 0.492 nm (it corresponds to O₁O₄^boat); S_E2 was determined to be 24,000 pN/nm; l₃ was found to be 0.541 nm (it corresponds to O₁O₄^inv-chair), whereas S_E3 was found to be 83,000 pN/nm. The length of the Kuhn segment l_K was determined from the low force region fit to be 1.81 nm. (Inset) Structure of the α-d-galactouronic acid (the pectin monomer). Note that in contrast to α-d-glucopyranose that has the C4—O4 bond in the equatorial position, α-d-galactopyranuronic acid has the C4—O4 bond in the axial position.

Figure 3.

Force-extension curves for native (A) and periodate-oxidized pectins (B). In A, we demonstrate that the conformational transitions underlying the enthalpic components of pectin elasticity are reversible. The blue trace represents the recording obtained on stretching and the red trace, on relaxing a single pectin. The recording did not show any hysteresis and was separated only to reveal the forward and backward traces. Pulling speed, 0.5 nm/ms. (B) The force-extension curve of periodate-oxidized galactouronan (Inset) does not reveal any significant enthalpic elasticity and represents the extensibility of a FJC of very short (l_K = 0.19 nm) and rigid (S_E = 70,000 pN⋅nm⁻¹) segments.

The Number of Axial Glycosidic Bonds Determines the Number of Force-Induced Conformational Transitions.

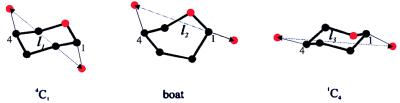
We can now compare the mechanics of the different glycosidic attachments to a pyranose ring. Fig. 4 compares the three types of linkages. It is clear that forces applied to the 1(equatorial)(e)-4(e) molecule (methylcellulose; Fig. 4C) will not generate any torque about the C2-O5 and C3-C5 axes of rotation (see Fig. 1). By contrast, a force applied to the oxygen O1 in the 1(axial)(a)-4(e) molecule generates torque about the C2-O5 axis of rotation (see Fig. 1) and triggers a single type of conformational transition ^4eC_1a ⇄ boat, as observed experimentally (Fig. 4B). By contrast, forces applied to O1 and O4 in the 1(a)-4(a) molecule (pectin, Figs. 2 and 4A) generate torques about both the C2-O5 and C3-C5 axes, triggering the two transitions observed experimentally and identified as a chair inversion reaction. These data support the view that, depending on their bond orientation, the glycosidic linkages act as levers generating the torque that does the work necessary to complete conformational transitions of the pyranose ring. However, the precise way in which the work done by the levers is distributed between bond stretching and conformational energy is unknown. We anticipate that through the use of steered molecular dynamics simulations, it will be possible to predict the energy surface describing the pyranose ring transitions that then can be contrasted with the forces measured by AFM.

Figure 4.

A comparison of elastic characteristics of pyranose-based polysaccharides that exploit both glycosidic bonds in the axial position (galactouronan, A), one axial and one equatorial bond (amylose, B) and both equatorial bonds (methylcellulose, C). (Right) Conformational transitions that are responsible for the enthalpic extensions of the polymers. The dominant conformers of the pyranose ring are indicated along different fragments of the force extension curves. The extensions in A and B were normalized in the same way as in Fig. 2B (O₁O₄^chair for amylose is also equal to 0.45 nm; ref. 2); in C the extension was normalized: x_norm = 0.542x/l^c nm, where 0.542 nm corresponds to the length of the residue vector O₁O₄^chair for the β-d-glucopyranose monomer of cellulose (2), and l^c is the contour length of methylcellulose determined from the FJC model fit to the data in the whole force region (not shown).

Furthermore, our work shows that by finely calibrating the applied force, it is possible to selectively populate the different conformers allowed by the pyranose ring.

Force-Induced Conformational Transitions as Switching Signals.

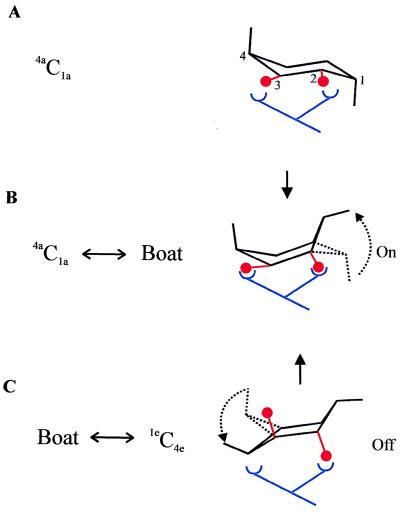
It is likely that the force-driven conformational changes of the pyranose ring have biological significance. For example, pectin ring conformers that are accessible by force could serve as off-on-off switches that modulate biological functions (Fig. 5). Our results contrast the widespread view that the pyranose ring serves as a rigid scaffold for ligand binding. Furthermore, the range of forces required to trigger conformational changes of the pyranose ring are similar to those commonly found in many cellular systems, such as the bacterial and plant cell walls that accommodate high tensile stresses generated during changes in turgor pressure (24, 25). The cell wall is now known to play an active role in the signaling that coordinates plant growth and other functions (26).

Figure 5.

The pyranose ring as an elastic switch. We model the receptor–ligand interaction as a bivalent contact where a forced deformation of the ligand (e.g., pectin monomers) changes the affinity of the interaction. In our example, the balls (oxygen atoms O2 and O3) represent epitopes on pectin recognized by a receptor. (A) At zero applied force, the pectin ring is in the ⁴C₁ chair conformer and interacts at low affinity with the receptor. The low affinity results from the mismatch between the binding sites and O2-O3 (equatorial and spaced by 2.9 Å, derived from ab initio). (B) A force of ≈300 pN converts the ring into the boat conformation (“On”) with O2 in the axial position. The O2-O3 distance increases to 3.2 Å, favoring high-affinity binding. (C) At higher forces (≈800 pN), the ring changes its conformation to an inverted chair, ¹C₄, moving O3 to the axial position and further increasing the O2-O3 separation to 3.6 Å. This results in bond failure (“Off ”).

Hydroxyl and other functional groups attached to the pyranose ring coordinate the binding of lectins (27, 28). The selectivity of lectin binding to polysaccharides is largely determined by the position of the hydroxyl groups of the pyranose ring (28). Our ab initio calculations of the pyranose conformers show that a chair inversion reaction will change the spacing and the orientation of the hydroxyl groups in positions 2 and 3 (Fig. 5). As shown, a forced chair inversion reaction would increase the O2-O3 distance by 0.7 Å and also would change the orientation of the hydroxyls from equatorial to axial. It is very likely that these changes will have a large effect on the affinity of lectin binding (28). Hence, pectin and other polysaccharides may serve as detectors that send biological signals in a narrow force range.

Conclusions.

Our results support the hypothesis that the conformational transitions of the pyranose ring are driven by the glycosidic bonds that act as mechanical levers. The torque generated by these levers determines the conformers that can be reached by an applied force and hence the number of transitions during the elongation of the molecule. Our experiments also demonstrate the capability of the AFM to manipulate the conformation of single molecules and of resolving complex conformational transitions, opening up the new field of single molecule mechanochemistry.

ABBREVIATIONS

AFM

atomic force microscope

FJC

freely jointed chain

e

equatorial

a

axial