A Quantitative Model for the Dynamics of Serum Prostate-Specific Antigen as a Marker for Cancerous Growth

Abstract

Prostate-specific antigen (PSA) is an enzyme produced by both normal and cancerous prostate epithelial cells. Although PSA is the most widely used serum marker to detect and follow patients with prostatic adenocarcinoma, there are certain anomalies in the values of serum levels of PSA that are not understood. We developed a mathematical model for the dynamics of serum levels of PSA as a function of the tumor volume. Our model results show good agreement with experimental observations and provide an explanation for the existence of significant prostatic tumor mass despite a low-serum PSA. This result can be very useful in enhancing the use of serum PSA levels as a marker for cancer growth.

Prostate-specific antigen (PSA) is a proteolytic enzyme that is used widely as a tumor marker for the diagnosis of prostate cancer and for monitoring patients with prostatic adenocarcinoma. PSA is produced by normal human prostate secretory epithelial cells and by virtually all prostatic adenocarcinomas. 1-3 The serum concentration of PSA correlates with the age of the patient, with the size of the prostate in men without demonstrable prostate carcinoma, with the volume of carcinoma in men with both primary and metastatic prostate carcinoma, 1 and with the stage of prostate cancer. 3,4 The presumed mechanism for the observation that serum PSA levels in men with prostate carcinoma are significantly higher, on average, than levels in men without carcinoma demonstrable by prostate needle biopsies is that PSA leaks from malignant cells and glands into the interstitium and thence into the blood instead of being confined to the ductal excretory system.

However, the correlation between serum PSA and the volume of cancer is poor and the variance is high in patients with prostate carcinoma. Because of the high variance, several modifications have been proposed to improve the diagnostic accuracy of serum PSA levels. These modifications include the use of age-specific reference ranges, PSA density, PSA velocity, and assays that specifically measure the different molecular forms of PSA. 3,5 PSA density is the serum PSA value divided by the ultrasound-determined volume of the prostate. 6 PSA velocity is the rate of increase in serum PSA concentrations throughout time. 7,8 The molecular forms of PSA that are produced in different ratios in patients with prostate cancer than in those without demonstrable cancer include complexed PSA and free PSA. However, the prospect that these modifications of PSA assays would provide more reliable markers of prostate cancer than a simple serum PSA assay has not yet been convincingly demonstrated. 6,8

One approach to understanding the contribution of potential independent variables to predict the serum PSA concentrations in individual patients would involve correlation of the volume of prostate carcinomas with serum PSA values throughout time. This approach would entail measuring the volume of carcinoma in prostates in men in vivo. Unfortunately, the volume of carcinoma in the human prostate cannot be accurately measured in vivo. Imaging techniques such as ultrasound were first thought to be tools that could identify carcinoma in vivo. This prospect has not been realized. The correlation coefficient between ultrasound-determined volume of cancer and pathologically measured volume is as low as 0.1. 9 The difficulty of determining the volume of prostate cancer is also reflected in the correlation between location and volume of cancer in needle biopsies and in the radical prostatectomy specimen. Sampling of individual prostates by needle biopsies is too poor to provide an accurate assessment of cancer volume in individual prostates; correlation coefficients as low as 0.5 have been reported. 10

We hypothesized that differences in growth rates of prostate cancers could help explain the variance in correlations of serum PSA concentrations with tumor size. Because the volume of human prostate cancer cannot be determined in patients with accuracy, we worked with xenografts of human prostate cancers in immunocompromised mice. We developed a mathematical model that accounted for the contribution of independent variables to the size of the xenograft and the serum level of PSA.

Methods

To better understand the relationship between serum PSA and the rate of tumor growth, we have developed a mathematical model for serum PSA dynamics that is based on studies of xenografts of human prostate carcinoma implanted in severe combined immunodeficiency (SCID) mice.

Development of Xenografts

Details of the xenografts and the method for generating them have been previously published. 11 In brief, the LuCaP 23 series of prostate carcinoma xenografts came from a 63-year-old white male donor diagnosed with advanced prostate cancer. 2,11 The patient was treated with external beam radiation therapy to the pelvis, chemotherapy, and hormone therapy. 2,11 The tumor progressed after hormone ablation therapy. Samples of tumor were removed in a sterile manner from two lymph nodes and a liver metastasis and implanted into SCID mice. Three distinct sublines of these xenografts have been established and serially passaged through at least three generations of SCID mice. These xenografts, which have distinctive functional properties, are termed LuCaP 23.1, 23.8, and 23.12, respectively. Histologically, all three xenografts are adenocarcinomas. They differ with respect to growth rate in both androgen-deprived and androgen-supplemented host mice.

PSA Assays

Serum PSA and xenograft volume data were collected weekly. To measure the concentration of human PSA in the blood of mice with xenografts, 0.2 ml of whole blood were removed from the tail vein by capillary pipette. After centrifuging to separate the serum from the blood cells, the serum sample was analyzed for PSA using an indirect enzyme-linked immunosorbent assay. This assay is specific for human PSA. The blood of mice lacking xenografts of human prostate tissue, either benign or malignant, have no detectable PSA. This assay detects concentrations of PSA as low as 0.05 μg/ml. 11

Anatomy of Xenografts

Being located subcutaneously as spherical tumor masses, the size of xenografts can readily and accurately be measured using calipers opposed to the skin on either side of the xenograft. Histologically, the structure and cell composition of different xenografts is virtually identical, regardless of the size, growth rate, or androgen sensitivity of the xenograft. The majority (>95%) of cells are prostate carcinoma. Host mouse inflammatory, stromal, and vascular cells represent ≤5% of cells in the tumors.

Results

Mathematical Model

Our mathematical model for serum PSA dynamics can be written, in words, as the conservation equation: the rate of change of PSA equals the source of PSA from benign cells plus the source of PSA from cancer cells minus the loss of PSA from the blood.

To introduce the relevant parameters, we write the model mathematically as

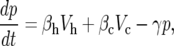where p(t) is the serum PSA level at time t, V_h and V_c are the volumes of benign and cancerous PSA-producing cells, respectively. Initially, at time t = 0, we assume the serum PSA level is p₀. We assume that PSA is produced by benign and cancerous cells at the rate β_h and β_c, respectively. Cancer cells leak much more PSA than benign cells so β_h is much smaller than β_c: β_h ≪ β_c. We assume that PSA is metabolized and cleared from the blood of both humans and mice with xenografts at approximately the same constant rate γ.

For our analysis, we assume that the total volume of benign (noncancerous) PSA-producing cells is constant (V_h = constant) in men with prostate carcinoma and that the total tumor cell population increases exponentially in both patients and in tumor xenografts. Because we will compare the model results to experimental data received from xenografts in mice, we assume that an initial tumor volume V₀ is implanted in the mouse and that at some future time, t, the total tumor volume V_c is defined by the equation V_c(t) = V₀ e^ρt where ρ is the tumor growth rate such that ln (2)/ρ is the tumor doubling time. Because we are considering data from mice, we assume that the initial serum PSA level, p₀, is zero.

Figure 1 ▶ shows the range of behavior that is possible under the proposed mathematical model. Given exponential tumor growth (dotted line), serum PSA levels (solid lines) can either increase concurrently with the tumor volume as in Figure 1a ▶ or appear delayed until significant tumor volume has accrued as in Figure 1b ▶ . The parameter differentiating these two scenarios is μ, the ratio of the PSA loss rate, γ, to the tumor growth rate, ρ. When μ is large, the serum PSA level increases with tumor volume (Figure 1a) ▶ . Otherwise, there is an apparent lag between tumor growth and elevated serum PSA levels (Figure 1b) ▶ .

Figure 1.

Range of behavior of PSA production given exponential tumor growth. The PSA level (solid line) can either increase significantly in sequence with tumor growth (a, dotted line) or appear delayed depending on the parameter μ defined as the ratio of the loss rate of PSA, γ, and the growth rate of the cancer mass, ρ (b).

Figure 2 ▶ shows serum PSA level predicted by the model for a tumor of given volume V versus the tumor growth rate. For any given tumor volume V, the serum PSA level varies with the growth rate. Two tumors diagnosed at the same volume (V) can manifest very different serum PSA levels depending on the length of time it took them to grow to volume V.

Figure 2.

Serum PSA level, p, for a fixed tumor volume V versus the tumor growth rate ρ. For a given tumor volume, a wide range of serum PSA levels can be observed depending on the length of time it took the tumor to grow to volume V.

Comparison with Experimental Data: LuCap 23

Extensive analysis of the three different xenografts of LuCaP 23 in laboratory mice by Ellis and colleagues 11 provides experimental results for comparison with our model predictions.

Untreated Tumor Growth and Serum PSA Levels

The LuCaP 23 xenograft cell sublines were implanted into 10 male (nude) mice. Tumor volume and serum PSA data are shown in Figure 3 ▶ as previously reported by Ellis and colleagues. 11 The circles in Figure 3 ▶ represent the mean experimental values at each time point with standard deviations defined by the bars attached to the data points. Linear regression analysis of the log of tumor volume versus time revealed tumor growth rates ρ of 0.0655, 0.0504, and 0.0487 (1/day) for LuCaP 23.1, 23.8, and 23.12, respectively. The fit of the exponential growth curves to the experimental data are given in Figure 3 ▶ ; a, c, and e.

Figure 3.

Experimental observations of LuCaP 23 tumor volume (mm³) and serum PSA levels (ng PSA per ml of serum) in xenografts with model predictions versus time (in days). a, c, and e: Tumor volumes for LuCaP 23.1, 23.8, 23.12, respectively. b, d, and f: Serum PSA levels for LuCaP 23.1, 23.8, 23.12, respectively.

To predict the serum PSA levels as a function of time given the tumor growth characteristics of a specific subline, we need estimates of the PSA loss rate, γ, and the production rate of PSA per unit volume of cancerous cells per unit time, β_c. We do not need to know the production rate of PSA per unit volume of normal human prostate cells per unit time β_h because there are no normal human PSA-producing prostate cells in the mice with xenografts.

Ellis and colleagues 11 cite a mean PSA half-life of 12.9 hours for the LuCaP 23 studies described above. We convert this half-life to a PSA decay rate as γ = log(2)/12.9 hours = 0.0537/hour = 1.2896/day. To calculate the production of PSA per unit volume of tumor tissue per unit time, β_c, we consider Figure 4 ▶ suggesting that the ratio of the serum PSA (p) to the tumor volume (V_c) is asymptotic to a constant for large tumor volumes:

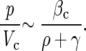Ellis and colleagues 11 term this ratio of the serum PSA level, p, and the tumor growth rate ρ the PSA index and cite estimates of 1.27, 1.63, and 5.21 ng/ml/mm 3 for LuCaP 23.1, 23.8, and 23.12, respectively. We then obtain estimates for β_c by the formula

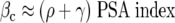We tabulate the LuCaP 23 series parameter estimates in Table 1 ▶ . Using these estimates, we plot serum PSA levels predicted by the model in Figure 3, b, d, and f ▶ . Note that although the serum PSA level seems to increase exponentially with tumor volume (V_c) for later times, the solution to Equation 1 for the xenograft case (V_h=0,p₀=0):

has a biexponential form that manifests a small bump near t = 0 in the plots of the serum PSA levels in Figure 3, b, d, and f ▶ .

Figure 4.

PSA index, the ratio of the serum PSA level, p, to the tumor volume, V_c, versus the tumor volume, V_c.

Table 1.

Parameter Estimates for the LuCaP 23 Experiments

Parameter	Symbol	LuCaP 23.1	LuCaP 23.8	LuCaP 23.12	Units
Tumor growth rate	ρ	0.0655	0.0504	0.0487	1/day
Normal PSA production	βh	0	0	0	ng/mm3/day
Cancer PSA production	βc	1.7210	2.1841	6.9722	ng/mm3/day
Decay rate of PSA (loss)	γ	1.2896	1.28966	1.2896	1/day
Implanted tumor volume	V0	20–25	20–25	20–25	mm3
Volume of benign PSA-producing cells	Vh	0	0	0	mm3

Discussion

The mathematical model suggests that there could be an apparent delay between tumor growth and PSA production as illustrated by Figure 1 ▶ . The model suggests that this delay depends on the parameter μ defined as the PSA decay rate γ normalized by the tumor growth rate ρ. When μ is small, the tumor growth rate is large compared to the PSA decay rate and a large tumor could yield a low serum PSA level, at least for a short time. Alternatively, when μ is large, the serum PSA level can increase significantly in sequence with tumor growth.

Virtually invariably, serum PSA levels will increase to clinically significant values for each tumor, assuming, of course, that the patient survives sufficiently long for the tumor to reach that critical volume. Because the serum PSA level that is considered clinically significant is standardized by convention at 4 ng/ml, but the net proliferation rate of the tumor cells is quite variable, the model suggests that there can be a large difference in the size of tumors when using serum PSA levels as a screening assay.

To understand the distinction between the two cases of μ small or large, consider two tumors of volume V. Tumor 1 grows quickly and has attained its present volume V in 1 unit of time. Alternatively, tumor 2 grows more slowly and has taken 10 units of time to attain volume V. A cell in slowly growing tumor 2 has been producing PSA for at most 10 units of time. This is 10 − 1 = 9 units of time more than any cell in tumor 1. This increased opportunity for a cell in tumor 2 to produce PSA augments the serum PSA level. Although the tumor 1 is the more rapidly growing tumor, tumor 2 has been leaking PSA for a longer period of time. The more slowly growing tumor 2 has an increased opportunity to produce significant levels of PSA.

From the experimental data presented in Figure 3 ▶ , we see that PSA levels are related to tumor growth. We also observed that a wide range of PSA levels is observed for different cancers. There are, however, limitations to our modeling approach. We have restricted our discussion to the experimental data available from subcutaneous xenografts. These data presumably only approximate tumor growth within the human prostate. Additionally, the amount of tumor necrosis, cellular growth rates, and PSA kinetic rates of xenografts could significantly differ from values for these parameters in patients with primary prostate carcinomas. Furthermore, in limiting our study to the three available different sublines of prostatic tumors that were derived from a single patient, we may not be modeling the full range of clinical manifestations of prostate cancer that occur in different patients.

Despite the numerous limitations, this model has led to a better understanding of PSA chemistry and observations of temporal changes of serum PSA values in men with prostate carcinoma that do not seem intuitive on first reflection. Clinically, the fact that patients with large, rapidly growing tumors often have low levels of serum PSA has been perplexing. Our model has devised a possible explanation for the experimentally and clinically observed disparity between tumor volume and serum PSA level.

This is a significant result because our model provides validation that serum PSA does not predict tumor volume, but is dependent to a significant degree on the growth rate of the tumor. In Figure 2 ▶ we see that the serum PSA level for a tumor with volume V can extend over a wide range of possible values, depending on the net growth rate of the tumor. That prostate cancers may differ markedly in their growth rate has been demonstrated in patients. Although the rate of growth of primary tumors in patients cannot be measured directly because they cannot be imaged, as discussed above, 9 surrogate measures of growth show wide variance among primary prostate carcinomas of the same stage. For example, the percentage of cells in the S phase of the cell cycle ranges from 0 to 15%. 12 The percentage of cells in the cell cycle, which is a value that is obtained by counting the fraction of cells immunohistochemically expressing the cell cycle marker Ki67, ranges from 0 to 33%. 13 There is a comparably wide range of rates of tumor cell death in different tumors. Between 0.25 and 5.25 cells per day per cc undergo apoptosis in different primary prostate carcinomas. 14

We have developed a mathematical model to describe a possible mechanism for serum PSA levels as a function of tumor volume. In fact, our simple model has suggested why a rapidly growing tumor does not predictably lead to an increased PSA level. We are optimistic that further mathematical modeling will help quantify these results and assist in determining the best measurement of PSA to be used to indicate tumor growth.