Method for Optimizing Pulsed-Field Gel Electrophoresis Banding Pattern Data

Abstract

The genomic DNA of 47 strains of TSST-1 toxin-producing Staphylococcus aureus were cleaved with SmaI restriction endonuclease and resolved in an agarose gel by pulsed-field gel electrophoresis (PFGE). An algorithm was designed to standardize the band weights or brightness (trace quantity) produced to a bounded region between 0 and 1 regardless of DNA fragment size while simultaneously reducing gel-to-gel variability. The algorithm allows for classification of isolates by band intensity as well as DNA mobility without a numerical hierarchy of band intensity that is caused by ranging DNA fragment lengths. On analysis many isolates were classified as separate entities on the basis of DNA co-migration only. Isolates differing by only DNA co-migration were subjected to a second digestion with restriction enzyme SacII. These isolates were characterized similarly to the standardized trace quantity analysis of SmaI PFGE patterns. The standardization method proposed in this article permits characterization of isolates on the basis of band differences, regardless of DNA co-migration, thus increasing the discriminatory power (0.79 to 0.89) of PFGE by increasing band-associated information. An established unbiased approach to the partitioning of data were also explored.

Pulsed-field gel electrophoresis (PFGE) has been one of the most useful developments in molecular epidemiology for the past few decades and is now regarded as the gold standard for molecular typing of microorganisms. 1^, 2^, 3^, 4 PFGE is capable of resolving large fragments of DNA with a practical range of 10 kb to ∼7 Mb. 1^, 5 Highly discerning endonuclease-treated Staphylococcus aureus genomic DNA resolved by PFGE generates a high degree of discrimination. 3^, 4^, 6^, 7^, 8^, 9 Traditionally, band velocity or relative front (Rf), the distance a band travels in a lane divided by the total lane length, is the determining variable used to discriminate band type. The band is then designated as present or absent, indicated by a 1 or 0, respectively (a form of data standardization). Pattern recognition methods are then used to identify groups of isolates with similar banding patterns. This method of numerically reducing PFGE pattern data, although quite successful, overlooks much of the diversity present in PFGE banding patterns. PFGE, like many other methods of sieving molecules, separates only by size, isoelectric potential, or topology. 5 Because DNA fragments of similar lengths are likely to resolve to the same Rf during electrophoresis, a band is produced that is more intense or broader than other bands of similar migration distance; a phenomenon called “DNA co-migration.” Band typing by Rf alone does not recognize the difference between a band produced in this way and a band produced by a single fragment. One method used in an attempt to prevent DNA co-migration is to run longer gels. This effectively increases the resolving power of electrophoresis, allowing similar, but not identical, lengths of DNA to form discrete bands. Unfortunately, the use of longer gels also results in a greater dispersion of DNA fragments within the gel during the molecular sieving process; bands produced by smaller DNA fragments disappear as the gel length increases. Clearly, the limitations of the resolving power of PFGE illustrate a need for alternative methods of increasing discrimination between closely related restriction patterns.

This study presents a classification algorithm that increases the sensitivity of current PFGE techniques in detecting pattern differences despite the potential for DNA co-migration. The algorithm is not intended to illustrate the biological relevance of subtle PFGE pattern differences per se, but rather to provide an unbiased approach for detecting their existence using current PFGE methods. An established method of partition recognition (stopping rule) was also evaluated.

Materials and Methods

S. aureus Strains

Forty-seven TSST-1 toxin-producing strains of S. aureus were acquired from nasal, anal, or vaginal swabs taken from women living in various geographic locations including, Ohio, Florida, Arizona, and New Jersey in the United States, and Manitoba in Canada. Strains were isolated as part of a large epidemiological study to determine rates of S. aureus carriage and occurrence of TSST-1 toxin-producing strains. TSST-1 toxin-producing isolates obtained from women living in one geographical location were selected to illustrate the standardization algorithm described in this article. Standard microbial techniques were used for isolating S. aureus. Briefly, swabs from each subject were streaked onto mannitol salt agar plates (PML Microbiologicals, Tualatin, OR) and incubated for 48 hours at 37°C. Isolated colonies were then streaked for purity onto tryptic soy agar plates with 5% sheep blood (PML Microbiologicals) and incubated for 24 hours at 37°C. A gram stain, catalase test, and a rapid S. aureus-specific latex agglutination test (Staphaurex; Remel, Lenexa, KS) were performed to confirm the identity of isolates as S. aureus. Isolates so identified were grown in brain heart infusion broth overnight at 37°C and the supernatant was evaluated for the presence of the TSST-1 toxin via a competitive enzyme-linked immunosorbent assay. 10 TSST-1 toxin-producing S. aureus isolates were then stored at −80°C for later analysis.

Preparation of DNA for PFGE

S. aureus isolates were incubated overnight on an orbital shaker at 37°C in brain heart infusion broth. After incubation, 200 μl of the cell culture were harvested and washed with cell suspension buffer [10 mmol/L Tris, pH 7.2, 20 mmol/L NaCl, 50 mmol/L ethylenediaminetetraacetate (EDTA)] and resuspended in 100 μl of fresh cell suspension buffer. Two μl of RNase A stock (10 mmol/L Tris Base, 0.1 mmol/L EDTA, ribonuclease A 1.25 mg/ml; Sigma, St. Louis, MO) was added to the suspension, which was warmed in a 50°C water bath. The preparation was mixed with 100 μl of 2% CleanCut agarose (Bio-Rad, Richmond CA), vortexed lightly, and cast in disposable plug molds (Bio-Rad). The plugs were then placed into a lysis solution containing 237 μl of lysozyme buffer (10 mmol/L Tris, pH 7.2, 50 mmol/L NaCl, 0.2% sodium deoxycholate, 0.5% sodium lauryl sarcosine; Bio-Rad), 10 μl of lysozyme stock (25 mg/ml, Bio-Rad), and 2.5 μl of lysostaphin stock (100 mmol/L Tris base, 40 mmol/L magnesium sulfate, 0.8 mol/L sucrose, pH 7.6, lysostaphin 10 mg/ml; Ambi Inc.) and incubated at 37°C for 4 hours. The plugs were then washed briefly with 1× wash buffer (20 mmol/L Tris, pH 8.0, 50 mmol/L EDTA; Bio-Rad) and incubated overnight at 50°C in 250 μl of proteinase K reaction buffer (100 mmol/L EDTA, pH 8.0, 0.2% sodium deoxycholate, 1% sodium lauryl sarcosine; Bio-Rad) with 10 μl of proteinase K stock (>600 U/ml, Bio-Rad). These plugs were then washed four times with 1× wash buffer; the second and third wash were treated with 10 μl of phenylmethyl sulfonyl fluoride stock (100 mmol/L phenylmethyl sulfonyl fluoride in 100% isopropanol) and stored at 4°C for later enzymatic treatment.

Restriction Enzyme Digestion and PFGE

Plugs were cut to size (5 × 1.5 × 2.5 mm) and digested in 100 μl of restriction buffer (10 mmol/L Tris-HCl, 50 mmol/L KCl, 7 mmol/L MgCl₂, 1 mmol/L dithiothreitol, pH 7.75) with 40 U SmaI (Promega Corp., Madison, WI) overnight at 24°C. The plugs were then washed in 1× wash buffer, equilibrated in 0.5× TBE buffer (45 mmol/L Tris, 45 mmol/L borate, 1.0 mmol/L EDTA, pH 8.3), and loaded into a 1.2% pulsed-field certified agarose (Bio-Rad) gel with the samples flanked by bacteriophage λ DNA concatemers CI857Sam7 (Roche Molecular Biochemicals, Indianapolis, IN). All gels were electrophoresed in 0.5× TBE buffer at 5.1 V/cm for 36 hours at 14°C with a pulse duration of 1 to 85 seconds ramped linearly in a CHEF-DR II system (Bio-Rad).

Data Acquisition

Gels were stained with ethidium bromide, destained in distilled water, and photographed with a Gel Doc 2000 (Bio-Rad). Data were obtained from the digital image using the Diversity Database software (Bio-Rad). This included band typing by Rf and trace quantities, with trace quantity defined as the integration of the signal intensity over the width and height of a particular band in the image. Thus, a trace quantity directly reflects the band intensity or brightness. Band assignment was determined by Rf values plus or minus 5% error. Data standardization and classification were performed using Minitab for Windows (Minitab Inc., State College, PA).

Standardized Trace Quantity (STQ)

Standardized data can be obtained by dividing values of all trace quantities from all bands produced by a given isolate by the sum of those intensities from that isolate to produce adjusted trace quantities (e1_a) and then dividing the resulting values by the maximum adjusted trace quantity of all like band types produced by all samples (e1_b) . This can be written in mathematical terms as a two-part algorithm ( e1_a then e1_b ):

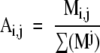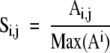where M is a matrix representing the entire raw data set and i and j represent the band-type IDs (ie, DNA mobility) and sample index, respectively. The values in S can be interpreted as the standardized relative percentage of the brightest like band (eg, of the same band type) of all isolates. Thus, the brightest band of each band type is represented by 1, and all other like band intensities become a standardized fraction of the brightest band for a given band type.

Assumptions

The basic assumptions for this algorithm are: 1) a given DNA fragment is the product of two restriction sites; 2) DNA digestion by restriction enzyme is complete; 3) DNA band intensity, in a PFGE gel stained with ethidium bromide, is proportional to the quantity of DNA present; 4) the genome size for evaluated isolates compared are similar; and 5) an appreciable amount of the total genomic DNA is represented. These assumptions are well suited to large population studies of the same organism and for suspected nosocomial outbreaks requiring an objective analysis of banding patterns that demonstrate DNA co-migration.

Typing

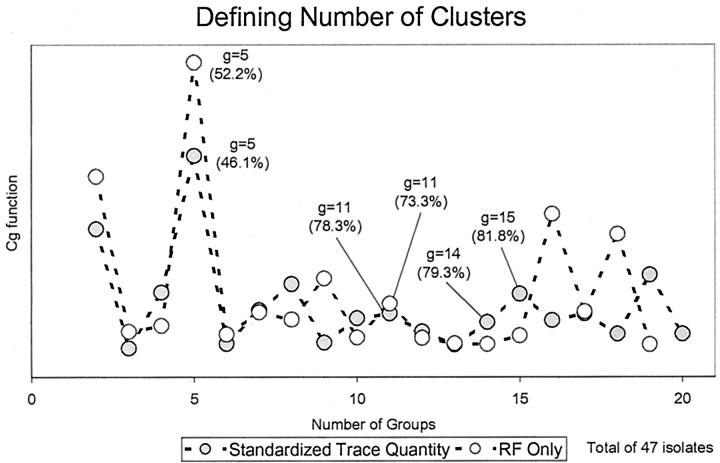
Cluster analysis was performed by first applying the Ward’s hierarchical linkage method on squared Euclidean distances of Rf or STQ data at an 80% similarity cut-point, followed by MacQueen’s k-means partitioning method starting with the cluster partition produced by the Ward’s hierarchical linkage. 11 The number of clusters determined using percent similarity was closely scrutinized or corroborated by the successive difference criterion function C_g (e4) . This utilizes the total within-cluster sum-of-squares, minimized by the Ward’s linkage method objective function (e2) , where x̄_j denotes the centroid vector of cluster c_i and g is the number of groups. The maximum of C_g was then used as the stopping rule, where m is the number of variables and g is the number of groups. The optimum number of groups g is defined as the value of g that maximizes C_g. 11^, 12^, 13 For subtyping, a local maximum of C_g was found to estimate the optimum number of subgroups (see Figure 1 ). For details of why the C_g function was chosen see Wolfgang Vogt and colleagues. 11

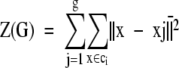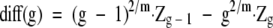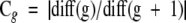Figure 1.

The C_g criterion function (e4) , which illustrates data partitions by using the within-group total sum-of-squares (TSS) of Ward’s method. The feasible number of partitions is represented by a maximum of C_g. Values in brackets are the smallest similarity cut-points required to produce the indicated number of partitions. It is not unreasonable to expect superimposition of partitions; therefore, local maxima should indicate subtyping.

Subtyping and Mean Band Difference (MBD)

The groups determined by the model were evaluated for band differences (BDs). To calculate the BDs between two or more subtypes, all possible pairs of isolate patterns in all subtypes within a group were evaluated using (e5) .

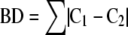where C_i is a vector for the ith isolate and BD represents the total BD between the i^th and i^th+1 isolate. The minimum, mean, and maximum BDs between a group of isolates was also found by applying (e5) to all possible pairs of isolate vectors for that group (see Figure 3 ). The mean is an average estimate of genetic variance representing BDs between isolates within a group and is called the MBD. BD is a useful variable because it is a measure of genetic divergence. 2^, 9 In this study a target maximum BD cut-point of 6, which generally corresponds to two genetic events at most (ie, insertions, deletions, and rearrangement 2^, 9 ), was considered an ideal break-point for defining a group. BD values equal to or less than this value would suggest a close genetic relationship. Sensitivity to these relationships can be tailored to a desired maximum genetic divergence by adjusting the number of possible groups. It should be noted that the C_i vectors are derived from absolute band presence/absence data. Trace quantity or STQ data could not be used for this purpose because of its continuous nature. Deciding at what numerical value a band produced in PFGE is derived from one, two, or even three DNA fragments is purely arbitrary and therefore not practical. Based on the need for equation (e5) to consider all trace quantity or STQ values equally, a concession was made. It was assumed that one band was the product of one DNA fragment source. Arguably this is consistent with current methods of PFGE pattern evaluation and therefore more comparable to current convention. Short of a complete sequence of genomic and extra-genomic DNA for a group of organisms, a procedure can only estimate the true genetic diversity for that group.

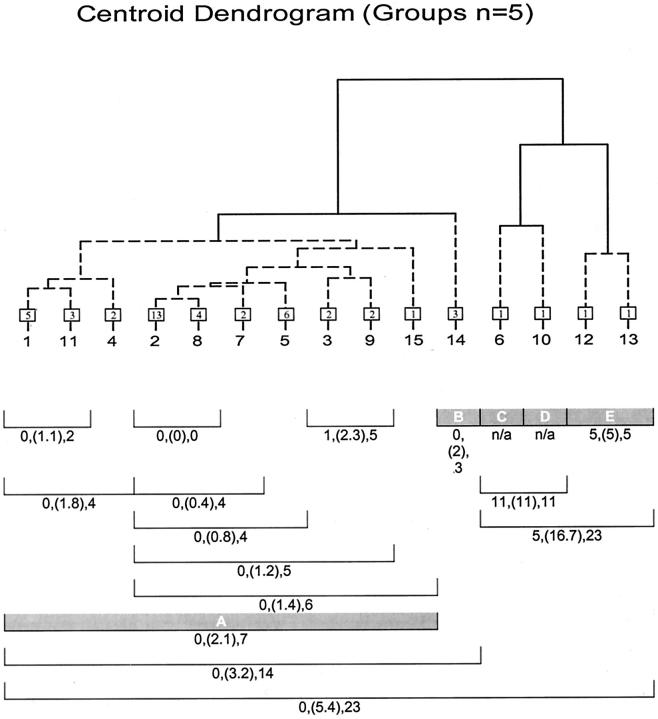
Figure 3.

Dendrogram of subtype centroids and between-isolate within-group statistics, including minimum, mean (in parentheses), and maximum BDs. Numbers in box represent the isolates per subtype (centroid), and shaded bars represent the final partition as determined by the C_g criterion. Note that the maximum number of BDs corresponds well with final partition.

Results

General

For the 47 isolates used to assess STQ analysis, there were 20 unique banding patterns based on band position only. When a clustering algorithm was applied at an 81.8% similarity cut-point (as determined by C_g), and band position was the only variable taken into account, 11 clusters were produced. When band intensity was considered, 15 clusters were produced. C_g determined an optimal partitioning of 5 clusters (Figure 1) from both Rf-only and STQ data. The isolate memberships determined by the two methods were identical for these 5 clusters (Table 1) . With the use of the hierarchical partitioning methods described above, the percent similarity cut-point that was required to produce 5 clusters as determined by C_g was (52.2%) and (46.1%) for Rf only and STQ data, respectively. This partitioning would not have been found by simply applying a similarity cut-point of 70 or 80% with either Rf-only or STQ data. The subtype partition g = 15 for STQ data are not as clearly defined as the C_g-determined partitions for typing. Figure 1 show many different and sometimes conflicting local maximum values between Rf-only and STQ analysis methods ranging from 8 to 16 clusters. It became clear that a common structure between the two methods may or may not be represented by C_g local maximum values at the same number of partitions, but isolate membership should be identical (Table 1) . This occurred at a common similarity index of 81.8%.

Table 1.

Relating Subtypes between Analysis Methods

Rf-only subtypes	Rf-only types	STQ types	STQ subtypes
1	A	A	1, 3
2	A	A	2, 7, and 8
3	A	A	4
4	A	A	5, 9
5	C	C	6
6	D	D	10
7	A	A	11
8	E	E	12
9	E	E	13
10	B	B	14
11	A	A	15

Rf-only typing is determined by band migration only. STQ typing is determined by the STQ analysis method, where both band migration and band intensities are considered. Note that the two middle lanes, which correspond to the optimal partitioning of their respective data types, are identical.

Rf-Only and STQ Subtyping

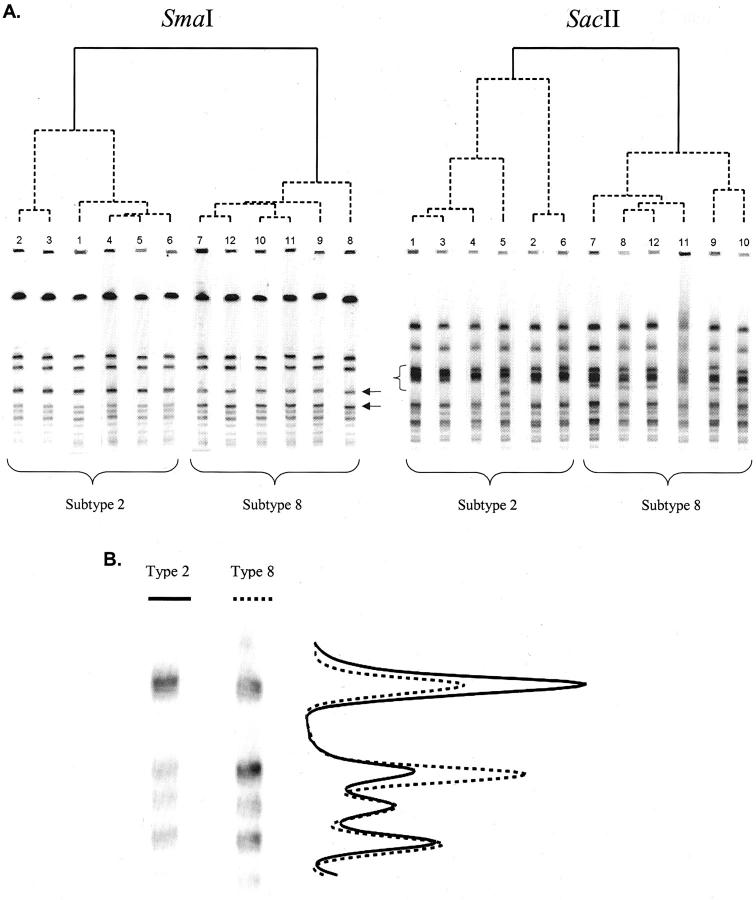
The use of both band intensity and position produced more subtypes than the use of band position alone (Table 1) . Rf-only subtypes 1 and 4 were each cut into two partitions by the STQ analysis, where the difference was primarily a single band. Rf-only subtype 2 was cut into three partitions based on Rf or band intensity differences. The differences based on band intensity alone were considered most interesting, and the isolates were therefore subjected to a different endonuclease enzyme and PFGE resolution. Twelve isolates, six each belonging to subtypes 2 or 8 as determined by STQ analysis, yet considered identical by Rf-only analysis, were digested using SacII endonuclease enzyme and resolved by PFGE using the same parameters as described above (Figure 2) . From the diagram, one can see subtle differences between subtypes 2 and 8; where SmaI digestion shows only band-intensity differences, the SacII digestion shows band-Rf differences. Although these isolates are clearly subtypes of a related strain, these gels and dendrograms nevertheless illustrate the subtle differences between them, which the STQ analysis method is able to resolve.

Figure 2.

Two PFGE gels with identical isolates digested with different enzymes and their associated dendrograms. A, Left: Subtypes 2 and 8 are defined by the STQ analysis method. Differences are based on band intensity only (arrows). A, right: The same isolates digested with a different enzyme. Differences are based on band position (bracket). The two methods grouped subtypes 2 and 8 similarly. B: Two representative isolates from SmaI-digested isolates and a graph of the average band intensity values for all six isolates.

Human Eye

The characterization by STQ analysis was in high agreement with analysis by human eye (45 of 47 isolates, 96%), where Rf-only was lower (38 of 47 isolates, 81%). This was established by printing the PFGE patterns of the 47 isolates and pasting them in a grouped manner to a board, with only the human eye used to compare them. Band brightness was taken into account, and isolates were grouped accordingly. Final assignments were agreed on by two reviewers with no previous knowledge of PFGE pattern origin. The result was then compared with computer-generated partitioning determined by Rf-only and STQ analysis. The only differences noted between human and STQ analysis methods were the result of marginal PFGE patterns that could have been put into one of two clusters (assigned by human or computer), depending on which bands were considered important (data not shown).

Band Differences (BDs)

The optimum number of groups determined by the C_g criterion produced a maximum level of within-partition BDs ranging from 5 to 7 (Figure 3) . This theoretically corresponds to (on average) one or two genetic events separating the most divergent subtypes within defined groups. These results suggest that the number of partitions defined by C_g is plausible.

Discussion

For the purpose of analysis one fragment of DNA resolved by PFGE should be assigned some constant value (X) regardless of the fragment size. When two co-migrating fragments are detected, the value should become 2X, and so on. Associated numbers then become proportional to the number of DNA fragments. This relates directly to the number and position of endonuclease enzyme recognition sites throughout the bacterial genome. However, variations ranging from DNA loading and purity, enzyme selection, staining technique, and gel-to-gel variability make assigning discrete numbers representative of DNA fragment count impossible. Resolution of these issues required some form of band-intensity standardization that compensates for the concentration of DNA loading as well as other variables. In STQ data, band variables remain continuous as deciding at what values STQ data should be considered two or more fragments of DNA required arbitrary rules to be introduced to the pattern evaluation.

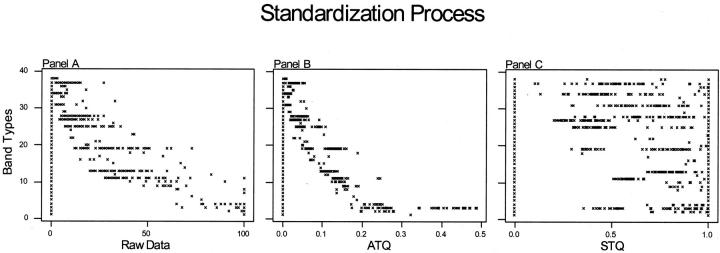
Nearly all clustering linkage methods require a scale-invariant data set. 11 Typical PFGE-banding patterns inherently have a hierarchy of band intensity; that is, the bands produced by larger fragments of DNA are more intense than the bands produced by smaller DNA fragments. As a result, the values representing the band intensities of larger fragments of DNA exhibit an exaggerated role in typical cluster analysis methods when these values are used directly (Figure 4A) . Standardizing PFGE band intensity data using parametric methods is not plausible. PFGE data have many zero designations that represent the absence of bands; and the PFGE data distribution is bounded, two factors that confound any chance of normality, a requirement of parametric analysis methods.

Figure 4.

Illustrating the standardization process. A: Raw data, where the band-type axis represents band characterization determined by ±5% (Rf) tolerance and the raw data axis is the unstandardized trace quantity of each band. B: Adjusted trace quantities (ATQ), where each isolates trace values (raw data) for all bands produced by that isolates is divided by the sum of those values (standardize for gel loading). C: Standardized trace quantities, where each ATQ of all isolates is divided by the maximum respective ATQ. Note that hierarchy of band intensity is removed while retaining a standardized form of band intensity. Note also the bimodal distributions in the STQ values, particularly band types 19 and 25.

The STQ method of standardization converts band patterns to a scale-invariant data set by first dividing trace quantities by the sum of those band intensities, producing what were earlier referred to as adjusted trace quantities (Figure 4B) . This mathematical procedure will standardize trace quantities between all isolates regardless of DNA loading or gel-to-gel variability (within reason), provided that assumptions regarding proportionality of DNA staining and similarity of genome size are met. However, the problem of band hierarchy (scale-variant data) still exists. Dividing all like band-intensity values by the brightest or largest numerical value will result in a number no larger than 1 and no smaller than 0 for any given band. Performing this operation for all band-intensity values results in a standardized data set that is practical for cluster analysis (Figure 4C) . Underlying patterns otherwise masked by the inherent noise of PFGE are revealed.

Under rare conditions, one isolate could possess an unusually high number of multiple co-migrating DNA fragments, producing a very bright band. After standardization and cluster analysis, the isolate producing such a band would still be characterized as different from the other isolates, as this would be considered a large disparity. However, when used as a common denominator, the value associated with this band would reduce those numbers associated with similar bands of other isolates, thus reducing the role they play in characterization (ie, a mathematical weighted effect). In practice, however, this weighted effect does not appear to be detrimental to the ability of the standardized data set to be representative of the PFGE patterns. Two limitations of the STQ analysis are all isolates must be represented in the database before analysis (because of the standardization process) and that very large data sets (>10,000) may be impractical, as the standardization process for such a large matrix would be time-consuming.

The Criterion Function

Data set partitioning based on a similarity index poses several concerns. The value of the cut-point is an external arbitrary index required before data analysis, and this value needs to be adjusted in accordance with the number of isolates evaluated. This is related to the structure of the data set. For an example, if the structure in a group of isolates is well defined (exists), additional samples can in effect fill in the gaps between disparate groups. This does not change the original groups or their relationship to each other but it does require adjusted similarity indices to maintain an analysis outcome for that relationship. Of course larger sample populations are more statistically significant and are encouraged but are not always practical. Another concern posed by hierarchical linkage methods is that groups will be defined even when there are none. Among the numerical classification community there is little consensus regarding the best stopping-rule methods. In fact, one of the few points of consensus that does exist among authors is that clustering algorithms are inherently data-dependent. Hence, prudent use of any analytic method is necessary. Unlike a similarity index in hierarchical linkage methods, C_g should not define partitions where there are none. In application, this assumption holds. 12 The C_g function should fluctuate around one when analysis is performed on randomly generated ungrouped data. 12 Therefore, if a peak occurs, particularly at the same value g, while using different forms of data representing the same phenomenon, one can be reasonably assured that an intrinsic pattern exists in the data set. Although the C_g function as described by Krzanowski and Lai 12 is certainly not the only stopping-rule available, based on the data presented here, it does appear to be superior to percent similarity index cut-points at determining the optimum number of clusters. Its most attractive attributes are that its approach to determining the optimum number of partitions is unbiased and its compatibility with the objective function used in the Ward’s hierarchical linkage algorithm. 11 Where the similarity cut-point is an external arbitrary parameter needed in advance, C_g takes the data set as a whole into consideration, finding the maximum successive difference between k and k + 1 partitions of the total sum-of-squares for each possible number of groups. Therefore, no user input is required for estimating the number of groups present in an experimental data set.

Practical Use of STQ Analysis

The STQ analysis method is ideally suited for the evaluation of nosocomial outbreak stains and population studies of same species organisms using PFGE. Standardized band intensity as a marker for isolate disparity, and indirectly DNA co-migration, is the purpose of this algorithm. Other source data may include polymerase chain reaction-based patterns such as random amplification of polymorphic DNA or whole cell protein patterns such as that produced by sodium dodecyl sulfate-polyacrylamide gel electrophoresis. In every case STQ analysis is designed to increase associated descriptive data for each evaluated banding pattern, allowing a finer partitioning of the samples where investigators may use discretion as to how discriminatory the analysis should be. Using a stopping-rule such as the one described above provides an unbiased approach to determining inherent data structure, if in fact it exists, and at what level groups are interconnected.

This algorithm could easily be implemented into any available software product as an optional method of data standardization. Analysis thereafter would be identical to existing methods. Stopping-rules and methods of visualization also would vastly improve any tools currently used by investigators. Optionally, this algorithm is simple enough that calculations could be done in a spreadsheet before cluster analysis using most statistical software packages.

The primary benefit of the STQ analysis algorithm over current protocols found in software products such as BioNumerics/GelCompar (BioSystematica, UK) and Diversity Database (Bio-Rad) is cost. Combined with programs such as ImageJ, a free public domain Java image-processing program inspired by NIH Image, a statistical package capable of multivariate analysis such as MiniTab or Statistica, and a spreadsheet program, STQ can facilitate band pattern analysis at a significant cost reduction over commercial packages. Additionally the band-weighting analysis method used by Diversity Database introduces a hierarchical effect of band brightness. That is, larger and brighter bands are given more importance than smaller bands in the pair-wise comparison of patterns. This results in an unusual partitioning of the data set.

Significance of DNA Co-Migration

DNA co-migration is an important characteristic of PFGE patterns. If one isolate has co-migrating fragments of DNA and another does not, the two isolates in all probability are genetically different (Figure 2) . Incorporating DNA co-migration as an attribute can improve the discriminatory power of PFGE by increasing the amount of information available for analysis. Cluster subtypes 2 and 8, determined by analysis of STQ data set, in this study illustrate that point well. The additional information found in band types 19 and 25 between the two clusters are enough for the Ward’s linkage method to separate the isolates into two entities at a minimum similarity cut-point of 79.2%. This and other further partitioning by STQ analysis increased the index of discriminatory power in this study from 0.79 to 0.89 compared with Rf-only analysis. Use of the STQ PFGE band-pattern standardization methods described here permits consideration of DNA co-migration, often found in PFGE patterns, during analysis. In addition, the C_g criterion function offers an unbiased tool for determining the optimum number of partitions for an experimental data set.