Molecular Analysis of the Putative Inactivation Particle in the Inactivation Gate of Brain Type IIA Na⁺ Channels

Abstract

Fast Na⁺ channel inactivation is thought to involve binding of phenylalanine 1489 in the hydrophobic cluster IFM in L_III-IV of the rat brain type IIA Na⁺ channel. We have analyzed macroscopic and single channel currents from Na⁺ channels with mutations within and adjacent to hydrophobic clusters in L_III-IV. Substitution of F1489 by a series of amino acids disrupted inactivation to different extents. The degree of disruption was closely correlated with the hydrophilicity of the amino acid at position 1489. These mutations dramatically destabilized the inactivated state and also significantly slowed the entry into the inactivated state, consistent with the idea that F1489 forms a hydrophobic interaction with a putative receptor during the fast inactivation process. Substitution of a phe residue at position 1488 or 1490 in mutants lacking F1489 did not restore normal inactivation, indicating that precise location of F1489 is critical for its function. Mutations of T1491 disrupted inactivation substantially, with large effects on the stability of the inactivated state and smaller effects on the rate of entry into the inactivated state. Mutations of several other hydrophobic residues did not destabilize the inactivated state at depolarized potentials, indicating that the effects of mutations at F1489 and T1491 are specific. The double mutant YY1497/8QQ slowed macroscopic inactivation at all potentials and accelerated recovery from inactivation at negative membrane potentials. Some of these mutations in L_III-IV also affected the latency to first opening, indicating coupling between L_III-IV and channel activation. Our results show that the amino acid residues of the IFM hydrophobic cluster and the adjacent T1491 are unique in contributing to the stability of the inactivated state, consistent with the designation of these residues as components of the inactivation particle responsible for fast inactivation of Na⁺ channels.

introduction

Voltage-gated Na⁺ channels initiate the action potential in most excitable cells. Na⁺ channels open in response to depolarization, resulting in Na⁺ influx through an Na⁺-selective pore. Within a few milliseconds after opening, the channels convert to a nonconducting, inactivated state, from which they recover only after repolarization. The rat brain Na⁺ channel consists of three glycoprotein subunits: α (260 kD), β1 (36 kD), and β2 (33 kD) (reviewed in Catterall, 1992; 1995). The α subunit is composed of four homologous domains (I-IV) each with six transmembrane segments (S1-S6; Noda et al., 1984; 1986a ; Auld et al., 1988). Expression of the cloned α subunit in mammalian cells (Scheuer et al., 1990; West et al., 1992b ) or Xenopus oocytes (Goldin et al., 1986; Noda et al., 1986b ; Stühmer et al., 1987) yields functional channels, although co-expression of β1 and β2 accelerates activation and inactivation in oocytes (Isom et al., 1992; Patton et al., 1994; Isom et al., 1995).

Treatment of the intracellular surface of Na⁺ channels with proteolytic enzymes specifically blocks inactivation, indicating that intracellular parts of the channel are involved in inactivation (Rojas and Armstrong, 1971; Armstrong et al., 1973; Armstrong, 1981). Studies using site-specific antibodies and site-directed mutagenesis indicated that the intracellular loop between homologous domains III and IV (L_III-IV)¹ is critically involved in inactivation (Vassilev et al., 1988; Stühmer et al., 1989; Vassilev et al., 1989). Transfer of this loop of the Na⁺ channel to the NH₂ terminus of a noninactivating K⁺ channel restores inactivation (Patton et al., 1993). Naturally occurring mutations in L_III-IV of the skeletal muscle Na⁺ channel α subunit affect Na⁺ channel inactivation and cause various forms of paramyotonia (reviewed in Barchi, 1995; Hoffman et al., 1995; Cannon, 1996), and deletion of three amino acids in this loop of the heart Na⁺ channel α subunit causes one form of the long QT syndrome (Wang et al., 1995).

In L_III-IV of the rat brain type IIA α subunit, mutation of F1489 in the center of a cluster of three hydrophobic amino acids, IFM (isoleucine-phenylalanine-methionine), to glutamine almost completely removed inactivation (West et al., 1992a ), and the analogous amino acid residue in the cardiac (Hartmann et al., 1994; Bennett et al., 1995) and skeletal muscle (Lawrence et al., 1996; Nuss et al., 1996) Na⁺ channels is also critical for fast inactivation. By contrast, neutralization of the charged residues in L_III-IV has only small effects (Moorman et al., 1990; Patton et al., 1992), indicating that these charged residues do not play a critical role in Na⁺ channel inactivation. Peptides containing the IFM motif block open Na⁺ channels, consistent with the IFM cluster serving as an inactivation particle which enters the intracellular mouth of the pore and blocks it during inactivation (Eaholtz et al., 1994). The strong effects of mutations of F1489 suggest that this residue may be primarily responsible for this binding interaction.

In this report, we describe the functional effects of site-directed mutations which change the structure and hydrophobicity of amino acid residues within and adjacent to the IFM cluster and amino acid residues within two other hydrophobic clusters in L_III-IV. The hydrophobicity of the amino acid substituted at position 1489 dictated the strength of the interaction of IFM with its putative receptor and determined the stability of the inactivated state of the channel. Placement of the critical F residue at positions 1488 or 1490 did not restore normal inactivation to a mutant lacking F1489. Mutation of T1491 on the COOH-terminal side, but not of D1487 on the NH₂-terminal side, of the IFM cluster strongly disrupted inactivation. Screening other hydrophobic clusters for effects on inactivation confirmed the unique importance of F1489 compared to other hydrophobic residues. Mutation of the hydrophobic cluster MVF near the COOH-terminal end of the loop had no effect. Mutations of a pair of tyrosine residues in the center of the loop slowed inactivation but did not impair the stability of the inactivated state at depolarized membrane potentials, indicating that these residues are not required for stable inactivation of open brain Na⁺ channels.

materials and methods

Site-directed Mutagenesis

Mutations were introduced in a 2,128-bp EcoRV DNA fragment excised from the rat brain type IIA Na⁺ channel α subunit (Auld et al., 1988; 1990) in M13mp18/RV and confirmed by DNA sequencing as described (West et al., 1992a ). The full-length, mutant Na⁺ channel was produced by subcloning the mutant cassette into Zem-RVSP6-2580 containing the remainder of the Na⁺ channel and a bacteriophage RNA polymerase promoter.

Na⁺ Channel Expression

RNA encoding wild-type (WT) and F1489C mutant Na⁺ channel α subunits and WT β1 subunits was synthesized in vitro using the Ambion mMessage mMachine kit (Ambion Inc., Austin, TX). Isolation, preparation, and maintenance of Xenopus oocytes was done as described (McPhee et al., 1995). Healthy stage V and VI oocytes were pressure injected with 50–100 nl of a solution containing a 1:1 ratio of α and β1 subunits at a concentration of 10– 200 ng/ml. Electrophysiological recordings were carried out 2–8 d after injection.

Electrophysiological Recording

Two-electrode voltage-clamp recordings were obtained from injected oocytes using a Dagan CA-1 voltage clamp (Dagan Corp., Minneapolis, MN). The amplitude of expressed Na⁺ currents was typically 1–5 μA. The bath was continuously perfused with Frog Ringer (115 mM NaCl, 2.5 mM KCl, 1.8 mM CaCl₂, 10 mM HEPES, pH 7.2). Recording electrodes contained 3 M KCl and had resistances of <0.5 MΩ. Pulses were applied, and data were acquired using a personal computer based data acquisition system (Basic-Fastlab; Indec Systems, Sunnyvale, CA). Maximal possible series resistance compensation was used to avoid errors due to relatively large Na⁺ currents and to maximize resolution of their rapid kinetics. Capacity transients were partially cancelled using the internal clamp circuitry. The remaining transients and leak were subtracted using the P/4 procedure (Armstrong and Bezanilla, 1974).

The cell-attached configuration of the patch-clamp technique was used to obtain both macropatch and single channel data. Before recording, the vitelline layer was removed as described (Methfessel et al., 1986). Oocytes were then transferred to a solution containing 10 mM NaCl, 90 mM KCl, 1 mM MgCl₂, 10 mM EGTA, and 10 mM HEPES, pH 7.4, to depolarize the membrane potential. Microelectrode measurement of oocyte membrane potential after incubation in this solution gave a value of −0.7 ± 0.4 mV (n = 10). Pipettes were pulled from 75 μl micropipette glass for macropatches (VWR Scientific, Seattle, WA) or Corning 7052 for single channel patches (Garner Glass Co., Claremont, CA), coated with Sylgard, and fire-polished before filling with Frog Ringer. Currents were recorded with a List EPC-7 patch clamp amplifier and filtered at 8 (macropatch currents) or 5 (single channel currents) kHz before digitization at 30 kHz.

Data Analysis

Normalized conductance-voltage curves were fit with A/{1 + exp[(V − V _1/2)/k]}, and inactivation curves with A/{1 + exp[(V − V _1/2)/k]} + B where V was the test pulse voltage (for activation) or prepulse voltage (for inactivation), V _1/2 was the midpoint of the curve, k was a slope factor, A was the amplitude of the voltage-dependent component, and B was the amplitude of the noninactivating component of current in inactivation curves. The percentage of noninactivating current in two-electrode voltage-clamp experiments was calculated as [(current at the end of a 30-ms long pulse/peak current) × 100] at the potential where peak current was maximal. The time course of recovery from inactivation was fit with (A − B) × {1 − exp[−(t − d)/τ]} + B, where A was the amplitude of total current, B the amplitude of the current which did not inactivate during the first depolarizing pulse, d the delay, and τ the time constant of recovery. Least-squares fitting was done with Sigma-Plot (Jandel Scientific, San Rafael, CA). The voltage dependence of gating parameters was shifted negatively in cell-attached macropatches compared to two-electrode voltage-clamp measurements and patch-to-patch variation in macropatch experiments was greater than the cell-to-cell variation seen in two-electrode voltage-clamp experiments. Gating parameters listed in Tables I and II are derived from two-electrode voltage-clamp measurements. Statistical significance of differences between parameters was determined by t test (P < 0.05; Sigma Plot).

Table I.

Voltage-dependent Gating Parameters of Macroscopic Currents from Mutant and WT Na⁺ Channels

		Peak conductance								Fast inactivation
		V 1/2(mV)		k (mV)		sustained current (%)		n		V 1/2 (mV)		k (mV)		n
F1483Q		−22		−4.5		4		1		−50 ± 1		7.6 ± 0.4		3
D1487A		−17 ± 1		−5.6 ± 0.7		1 ± 0		3		−51 ± 4		5.3 ± 0.1		3
D1487N		−16 ± 3		−7.3 ± 1.3		1 ± 0		3		−56 ± 1*		5.3 ± 0.1		3
F1489A		−21 ± 2		−4.9 ± 0.3		41 ± 8*		5		−30 ± 1*		4.3 ± 0.3		5
F1489C		−17 ± 5		−6.4 ± 0.8		22 ± 3*		4		−36 ± 1*		5.9 ± 0.3		4
F1489D		−19 ± 2		−4.2 ± 0.2		82 ± 8*		3
F1489H		−18 ± 2		−5.1 ± 0.3		26 ± 3*		4		−30 ± 1*		4.2 ± 0.0		4
F1489I		−19 ± 2		−6.1 ± 0.5		18 ± 2*		4		−33 ± 2*		4.8 ± 0.1		4
F1489K		−21 ± 1		−3.9 ± 0.1		93 ± 2*		5		−26 ± 3*		3.5 ± 0.3		5
F1489L		−22 ± 5		−5.4 ± 0.4		3 ± 1		7		−46 ± 2		5.4 ± 0.5		5
F1489M		−20 ± 3		−5.2 ± 0.1		7 ± 1*		6		−41 ± 1*		5.6 ± 0.1		5
F1489Q		−22 ± 3		−4.6 ± 0.4		85 ± 2*		4		−28 ± 4*		3.8 ± 0.5		4
F1489S		−21 ± 3		−4.7 ± 0.3		72 ± 2*		3		−27 ± 3*		4.2 ± 0.2		3
F1489T		−20 ± 1		−5.1 ± 0.2		35 ± 2*		4		−31 ± 0*		4.8 ± 0.2		4
F1489V		−21 ± 2		−4.3 ± 0.3		45 ± 3*		5		−27 ± 1*		3.7 ± 0.2		5
F1489W		−26 ± 1*		−5.0 ± 0.5		11 ± 1*		4		−49 ± 3		5.1 ± 0.2		4
F1489Y		−22 ± 3		−5.8 ± 0.3		6 ± 1*		4		−37 ± 3*		4.5 ± 0.1		4
I1488F/F1489Q		−24 ± 4		−5.2 ± 0.4		58 ± 4*		8		−30 ± 2*		3.4 ± 0.2		6
F1489Q/M1490F		−26 ± 5		−3.7 ± 0.3		98 ± 2*		9		−29 ± 6*		3.2 ± 0.6		7
T1491D		−19 ± 3		−4.9 ± 0.2		13 ± 3*		9		−32 ± 4*		4.9 ± 0.2		7
T1491M		−20 ± 2		−5.3 ± 0.2		24 ± 1*		3		−38 ± 1*		4.2 ± 0.1		3
T1491V		−16 ± 1*		−6.5 ± 0.3		13 ± 1*		3		−38 ± 2*		4.3 ± 0.1		3
Y1497Q		−12 ± 1*		−7.9 ± 0.3		2 ± 1		4		−43 ± 1*		5.1 ± 0.2		4
Y1498Q		−16 ± 2		−6.3 ± 0.3		2 ± 2		3		−44 ± 2		5.3 ± 0.3		3
YY1497/8QQ		−15 ± 1*		−7.2 ± 0.4		3 ± 1		4		−44 ± 2*		7.2 ± 0.8		3
MVF1523-5QQQ		−15 ± 3*		−6.6 ± 0.5		2 ± 2		3		−52 ± 1		6.4 ± 0.1		3
WT		−20 ± 3		−5.5 ± 0.3		2 ± 1		8		−50 ± 4		6.2 ± 0.2		7

Values for V _1/2, the voltage of half activation or inactivation, and the slope factor, k, derived from Boltzmann fits to activation and inactivation curves (see materials and methods); n, number of cells studied. Prepulse duration in steady-state inactivation protocols was 100 ms. All data are from two-electrode voltage-clamp experiments.  

^*Significantly different from WT (P < 0.05).  

Table II.

Recovery from Inactivation in Two-electrode Voltage-clamp Experiments

		τ−60mV (ms)		n		τ−90mV (ms)		n		τ−120mV (ms)		n
F1483Q		18.28		1		2.98 ± 0.07		3
D1487A		14.63 ± 0.59		3		2.26 ± 0.28		3		0.80 ± 0.08		3
D1487N		15.14 ± 0.17		3		2.95 ± 0.16		3		0.78 ± 0.05		3
F1489A		2.47 ± 0.36*		3		0.87 ± 0.10*		3		0.37 ± 0.04*		4
F1489C		4.30 ± 0.11*		3		0.89 ± 0.01*		3		0.43 ± 0.01*		3
F1489H		2.70 ± 0.09*		4		0.74 ± 0.02*		4		0.35 ± 0.02*		4
F1489I		4.32 ± 0.29*		4		1.00 ± 0.06*		4		0.39 ± 0.04*		4
F1489L		14.28 ± 1.06		4		1.88 ± 0.28		4		0.64 ± 0.06		4
F1489M		8.38 ± 0.31*		3		1.49 ± 0.10*		3		0.56 ± 0.04*		3
F1489Q		1.19 ± 0.06*		3		0.57 ± 0.02*		3
F1489S		1.91 ± 0.13*		3		0.69 ± 0.07*		3
F1489T		2.83 ± 0.12*		3		0.90 ± 0.04*		3		0.39 ± 0.02*		3
F1489V		2.41 ± 0.16*		2		0.76 ± 0.03*		4		0.35 ± 0.03*		2
F1489W		13.33 ± 0.35*		4		2.06 ± 0.18		4		0.65 ± 0.09		4
F1489Y		9.89 ± 0.76*		4		1.69 ± 0.10*		4		0.58 ± 0.04*		4
I1488F/F1489Q		1.17 ± 0.12*		3		0.46 ± 0.04*		3		0.28 ± 0.01*		4
T1491D		3.41 ± 0.16*		5		0.95 ± 0.06*		5		0.39 ± 0.01*		5
T1491M		2.32 ± 0.11*		4		0.63 ± 0.03*		4		0.27 ± 0.01*		4
T1491V		2.74 ± 0.11*		3		0.71 ± 0.01*		3		0.28 ± 0.01*		3
Y1497Q		8.09 ± 0.36*		3		1.66 ± 0.06*		3		0.71 ± 0.10		3
Y1498Q		8.27 ± 0.61*		3		1.44 ± 0.12*		3		0.63 ± 0.10		3
YY1497/8QQ		3.39 ± 0.15*		3		0.84 ± 0.01*		3		0.36 ± 0.02*		3
MVF1523-5QQQ		11.76 ± 0.67*		3		2.04 ± 0.06		3		0.76 ± 0.05		3
WT		17.66 ± 1.42		4		2.51 ± 0.22		4		0.72 ± 0.03		4

The time course of recovery from inactivation at the potentials indicated was measured after a 15-ms depolarization to 0 mV and fitted with an equation including a single exponential component and a delay (see materials and methods).  

^*Significantly different from WT (P < 0.05)  

Single channel openings were detected using standard half-amplitude threshold analysis after digital filtering at 2 kHz (Colquhoun and Sigworth, 1995). Events which were truncated by the end of the pulse were omitted from the analysis. Errors due to truncation of long closed times were estimated by simulation using scheme SI (Kellenberger et al., 1996) and corrected time constants were used for estimating k _off if the estimated error was >10%. Except for F1489Y and T1491M the error was considerably lower than 20% for all channels analyzed. Patches contained one to four channels. Channel number was estimated from the maximum number of overlapping openings at potentials where the probability of opening was high. Open times, closed times, and first latencies were analyzed from the binned data (Sigworth and Sine, 1987) with durations >100 μs, using PSTAT (Axon Instruments, Foster City, CA). Overlapping openings were omitted from analysis. Only single channel patches were used for closed time and burst analysis. The cut off for burst durations was determined from the fast and slow time constants of closed times as described by Colquhoun and Sakmann (1985). First latency distributions were fitted with the double exponential equation P = f × {1 − exp[−(x − d)/a]} + (P _max − f) × [1 − exp(−x/b)], where P is the probability, P _max is the maximal cumulative probability, f is the fraction of the fast component, d is the delay, and a and b are the time constants of the fast and slow components, respectively. The first exponential term which contains the delay describes the steps in the activation pathway that lead directly to channel opening. The delay approximates the multiple transitions in the direct activation pathway that occur before channel opening which is fit by the exponential. Consecutive null sweeps (>3 in a row) are most likely due to slow inactivation and were omitted from the first latency analysis. The errors in time constants derived from single channel data due to missed events were estimated from model simulations (Kellenberger et al., 1996). Although this approach is more model dependent than correction of the original data, the remaining error is too small to influence our conclusions. In the case of mutants with long openings, open duration time constants were overestimated due to missed short closings. For the calculation of k _on, corrected values for open duration time constants were used if the estimated error was >10%. The corrections were 25% (F1489Q), 20% (F1489A), and 18% (T1491M). Averaged data are presented as mean ± SEM, except for fits to single channel data which are given as mean ± SD.

Scheme I.

results

The Position of F1489 in L_III-IV Is Critical for Its Function

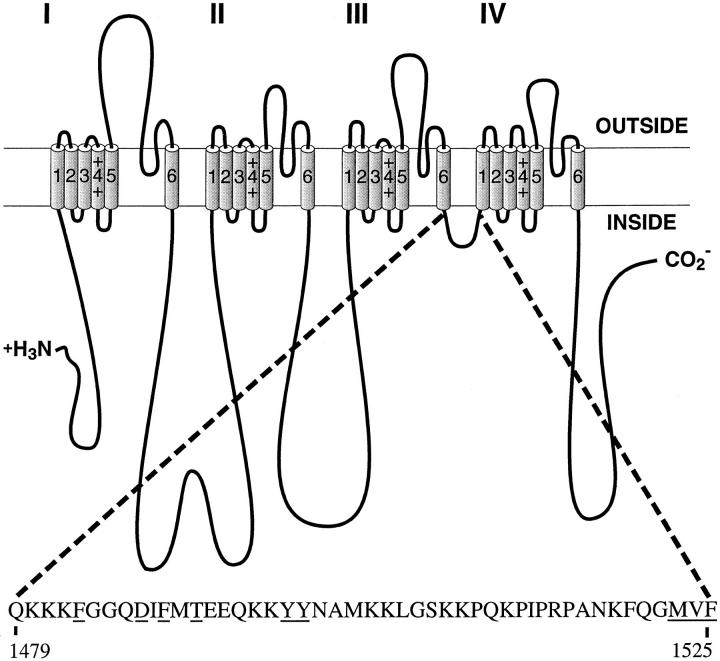
Fig. 1 illustrates the position of the inactivation gating loop L_III-IV in the Na⁺ channel structure and the amino acid sequence of this intracellular segment. Amino acid residues which were analyzed in this study are underlined. WT and mutant Na⁺ channel α subunits were co-expressed with Na⁺ channel β1 subunits in Xenopus oocytes and analyzed by two microelectrode voltage clamp recording. Macroscopic Na⁺ currents through the F1489Q mutant channel are almost noninactivating during 30-ms depolarizations compared to the rapid and complete inactivation of WT within 2 ms (Fig. 2).

Figure 1.

Schematic representation of the brain Na⁺ channel α subunit and the location of the inactivation gate. The amino acid sequence of the inactivation gate is shown for the rat brain IIA α subunit, and amino acids which were mutated in this study are underlined.

Figure 2.

Effects of shifting F1489 one amino acid residue in either direction. Two-electrode voltage-clamp recordings from Xenopus oocytes expressing either WT, the single mutant F1489Q, or the double mutants I1488F/F1489Q and F1489Q/M1490F. The currents were elicited by step depolarizations from a holding potential of −90 mV to test potentials of −30 to +10 mV in 10-mV increments. The vertical calibration bars are 1,000 nA; the horizontal calibration bars are 5 ms.

Of the single-residue mutations that have been studied to date, mutations of F1489 cause the most slowing of inactivation and the largest fraction of sustained current, indicating that the native F1489 is critical for inactivation (West et al., 1992a ). Mutations were designed to test whether the exact position of this residue in L_III-IV was critical for its function. Using F1489Q as a background to produce a channel with little inactivation, phe was substituted for the flanking residues I1488 or M1490 to produce mutants I1488F/F1489Q and F1489Q/M1490F. Thus, F1489 has been shifted by one position in the NH₂-terminal or the COOH-terminal direction in these two double mutants. Introduction of a phe residue at these positions in the F1489Q background would partially restore inactivation if this portion of L_III-IV was flexible enough to allow the displaced residue to bind stably to its receptor. Inactivation was not effectively restored in either of the mutant channels (Fig. 2). Inactivation was significantly more effective for I1488F/F1489Q (58 ± 4% sustained current, n = 8) than for F1489Q (85 ± 2% sustained current, n = 4), but even less effective for F1489Q/M1490F (98 ± 2% sustained current, n = 9) than for F1489Q. Thus, the I1488F mutation can stabilize the inactivated state of the F1489Q mutant channel to a small degree whereas it is further disrupted by mutation M1490F. Perhaps F1488 in the I1488F/F1489Q channel can partially interact with a suitable receptor whereas F1490 in the F1489Q/M1490F channel cannot. Nevertheless, the inactivated state of the I1488F/F1489Q mutant channel is still far less stable than that of the WT channel, indicating a requirement for precise positioning of F1489 for fast inactivation.

The Nature of the Interaction between F1489 and Its Receptor

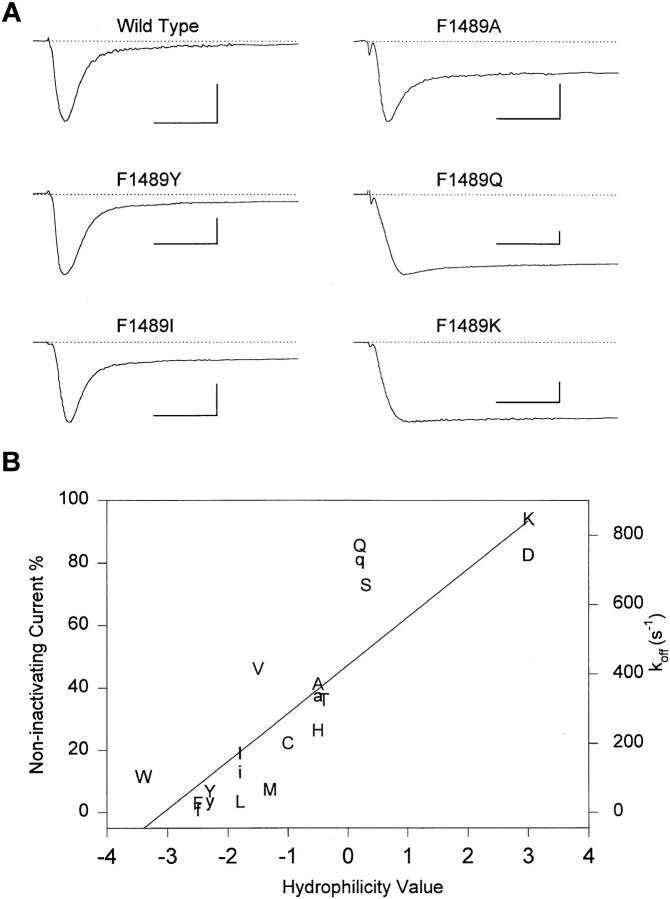
A series of amino acids was substituted for F1489 to examine the nature of the interaction between this critical residue and its putative receptor. Fig. 3 A shows current traces from WT and some of these mutants for depolarizations to −10 mV. These mutations caused a variable increase in the fraction of current which was not inactivated at the end of a 30-ms depolarizing pulse. This fraction is plotted for each amino acid versus a scale of amino acid hydrophilicity (Hopp and Woods, 1981) in Fig. 3 B. This measure of amino acid hydrophilicity is well-correlated with the fraction of noninactivating current.

Figure 3.

Effects of mutations of F1489 on inactivation. (A) Two-electrode voltage-clamp recordings from WT and the indicated mutant channels during depolarizations to −10 mV. The vertical calibration bars are 1,000 nA; the horizontal calibration bars are 5 ms. (B) Correlation of the fraction of noninactivating current (left hand ordinate) and the hydrophilicity of the amino acid at position 1489 in WT and mutant channels. The substituted amino acid is indicated in upper case single letter code. Hydrophilicity values are from Hopp and Woods (1981). k _off values (right hand ordinate) calculated from corrected closed duration time constants in single-channel experiments are plotted in lower case single letter code.

For macroscopic Na⁺ currents recorded during strong depolarizations, the process of inactivation can be adequately described by Eq. 1:

1

where O and I represent channels in the open and inactivated states, respectively, k _on is the rate constant governing the transition from the open to the inactivated state, k _off is the reverse rate constant, and the fraction of sustained current is approximately equal to k _off/(k _off + k _on). As shown below, mutations of F1489 primarily affect k _off. An increase in k _off reflects a decrease in the stability of the inactivated state. We can therefore use the fraction of noninactivated current as an indicator of the degree of disruption of inactivated state stability. Replacement of F1489 with amino acids of increasing hydrophilicity produces channels with an increasingly less stable inactivated state. This indicates that F1489 forms a hydrophobic interaction with its putative receptor in the inactivated state.

Mutations of F1489 had only small effects on the voltage dependence of activation (Table I). In contrast, they shifted the midpoint of steady-state inactivation positively by up to 24 mV and increased the steepness of the steady-state inactivation curve (Table I). The degree of shift in the midpoint of steady-state inactivation increases steeply with mutations causing small increases in the fraction of noninactivating current and saturates at a net shift of about +20 to +24 mV for mutants having a fraction of noninactivating current that is >20%. These mutations also increased the rate of recovery from inactivation after repolarization to negative membrane potentials (Table II). As for steady-state inactivation, the acceleration of recovery from inactivation by the mutations of F1489 is more sensitive to substitution of hydrophilic residues than the increase in the fraction of sustained current, and the voltage dependence of recovery from inactivation (Table II) was shifted similarly to the midpoint of steady-state inactivation. The saturation of the voltage shift with only small increases in sustained Na⁺ currents is expected because the voltage shift is a logarithmic function of the underlying change in the stability of the inactivated state (Tang et al., 1996). Steady-state inactivation and recovery from inactivation at negative membrane potentials reflect the inactivation and the reversal of inactivation of closed Na⁺ channels. Thus, mutations of F1489 impair inactivation of both closed and open Na⁺ channels.

Single Channel Properties of F1489 Mutant Channels

To directly measure the rates of binding and unbinding of the inactivation gate and its receptor, single channel experiments were carried out with selected mutants which disrupted inactivation to differing extents. The simple kinetic model shown in scheme SI has been used successfully to describe the gating of single Na⁺ channels during depolarizations to −30 mV or more positive membrane potentials (Armstrong and Bezanilla, 1977; Aldrich et al., 1983; Horn and Vandenberg, 1984; Scanley et al., 1990; Kellenberger et al., 1996).

Upon depolarization, Na⁺ channels undergo voltage-dependent transitions through multiple closed states (states C₁ through C₃), open (state O), and then inactivate (state I). Channels can also pass directly from one (or more) closed states to inactivated states as illustrated. For WT channels at depolarized potentials, the inactivated state is functionally absorbing since transitions out of the inactivated state are rare on the millisecond time scale.

Fig. 4 shows representative traces and the corresponding ensemble averages (last traces in each column) at −20 mV from patches containing single WT, F1489Y, F1489I, F1489A, or F1489Q mutant channels. The ensemble averages of the analyzed single channel traces are similar in time course to the corresponding macroscopic currents (Figs. 3 A and 4; Tables II and III), indicating that the single channel behavior analyzed is sufficient to produce the macroscopic behavior. In response to a 40-ms depolarization to −20 mV, WT Na⁺ channels opened once or twice at the beginning of the depolarization but then inactivated and did not reopen until the membrane patch was repolarized (Fig. 4). Single mutant channels opened repeatedly during the 40-ms depolarizations. With increased hydrophilicity of the amino acid at position 1489, the number of reopenings per pulse increased, the mean open time became longer, and the closed times between openings became shorter (Fig. 4).

Figure 4.

Single-channel records and ensemble averages of WT and F1489 mutant channels. Traces of single-channel activity and ensemble averages (last trace in each column) from cell-attached patches. The arrows indicate the beginning of 40-ms depolarizations to −20 mV from a holding potential of −140 mV. The vertical calibration bar is 1 pA for single-channel traces and 0.5 pA for ensemble averages. The number of channels in the patches for the single-channel traces shown were two for WT and one for each mutant. The dotted ensemble averages are normalized WT data for comparison.

Table III.

Inactivation Time Course in Cell-attached Macropatches at +30 mV

		τh(+30 mV)		n				τh(+30 mV)		n
F1483Q		0.21 ± 0.01		6		F1489Y		0.48 ± 0.02		6
D1487A		0.22 ± 0.01		6		T1491M		1.51 ± 0.24		4
D1487N		0.22 ± 0.02		3		Y1497Q		0.33 ± 0.07		3
F1489A		0.95 ± 0.05		6		Y1498Q		0.20 ± 0.02		5
F1489I		0.46 ± 0.02		5		YY1497/8QQ		0.55 ± 0.04		8
F1489Q		1.32 ± 0.13		3		WT		0.16 ± 0.01		13

τ_{h(+30 mV)} was derived from single exponential fits to the inactivation time course. τ_{h(+30 mV)} was significantly different from WT (P < 0.05) for all mutants tested.  

Open times for F1489Y and F1489I channels were similar to WT, but they were significantly longer for F1489A and F1489Q mutant channels (Figs. 4 and 5 A). Open time distributions for all mutants of F1489, except for F1489A, were well-fit by a single exponential, consistent with a single open state (Fig. 5 A). The time constants at −20 mV were 0.39 ms for WT, 0.58 ms for F1489Y, 0.46 ms for F1489I and 1.80 ms for F1489Q. The two time constants for F1489A were 2.00 and 0.58 ms (Table IV). The second open state found in the F1489A mutant might be due to switching between different gating modes, or alternatively this open state might be present but rarely visited in WT channels due to intact fast inactivation. Two open states have previously been described for squid Na⁺ channels at positive potentials (Correa and Bezanilla, 1994a , b ). For WT Na⁺ channels, the single channel open time at strong depolarizations gives a good estimate of the rate of channel entry into the inactivated state because the transition to the inactivated state (O → I) is rapid and, thus, is more likely than transition to closed states (O → C) (scheme SI; Armstrong and Bezanilla, 1977; Armstrong, 1981; Aldrich et al., 1983; Vandenberg and Horn, 1984). The estimated inactivation rate for WT channels at −20 mV, calculated as 1/τ_{open duration}, is 2,577 s⁻¹. For the F1489 mutants, the transition O → I is slowed, and a substantial fraction of openings is ended by a transition back to closed states (O → C₃). Therefore, calculation of the O → I transition rate from the open times alone gives an overestimate for these mutations. We have calculated the rate O → I (g in scheme SI) as the reciprocal of the time the channels spend on average in the open state during bursts before inactivation occurs, as {(mean number of openings per burst) × [τ(open duration)]}⁻¹ (Hoshi et al., 1990). For this calculation, open duration time constants were corrected for the error due to missed events by simulation of scheme SI (see materials and methods and Kellenberger et al., 1996). Inactivation rates determined by this method are 1,479 s⁻¹ for F1489Y, 1,733 s⁻¹ for F1489I, and 410 s⁻¹ for the predominant (longer) open state of F1489A. The inactivation rate could not be calculated by this method for F1489Q channels since closures due to inactivation and closures due to transitions to closed states could not be distinguished. The inactivation rate for F1489Q calculated from open times was 625 s⁻¹. Assuming that the closing rate for F1489Q was similar to that for F1489A, a corrected inactivation rate of 408 s⁻¹ was obtained for F1489Q. Thus, the rate of entry into the inactivated state (k _on) was about half of the k _on value of WT channels for F1489Y and F1489I mutant channels and 1/6 of WT for the predominant open state of F1489A channels and for F1489Q channels.

Figure 5.

Single-channel properties of WT and F1489 mutant channels. Data are from two patches for WT, F1489Y, F1489I and F1489Q channels, and from three patches for F1489A channels. (A) Single-channel open time histograms at −20 mV. Patches containing one to two channels were used for the open time analysis. The solid lines are fits of single exponentials (WT, F1489Y, F1489I, F1489Q) or the fit to the sum of two exponentials (F1489A) to the log binned data. The time constants derived from the fits are shown in Table IV. The dotted lines are single exponentials with the WT time constant. Mean open times for individual patches at −20 mV were 0.38 and 0.41 ms (WT), 0.65 and 0.51 ms (F1489Y), 0.62 and 0.44 ms (F1489I), 1.54 and 1.11 ms (F1489A), and 2.02 and 1.87 ms (F1489Q). (B) Closed time histograms for depolarizations to −20 mV. Only closed times occurring after the first opening of a depolarization were analyzed to exclude first latencies and only data from single-channel patches were used. The solid lines are single exponential fits (F1489Q) or fits of the sum of two exponentials (WT, F1489Y, F1489I, F1489A) to the log binned data. Time constants derived from the fits are given in Table IV. (C) Cumulative first latency distributions at −20 and −40 mV for the indicated mutants. Distributions were corrected for the channel number (Patlak and Horn, 1982). Data are from patches with one channel (F1489Y, F1489Q), one to two channels (F1489I, F1489A), or two channels (WT). Parameters for fits to the sum of two exponentials (see materials and methods) are shown in Table V.

Table IV.

Single Channel Properties of Wild-type and Mutant Na⁺ Channels

		WT		F1489Y		F1489I		F1489A		F1489Q		T1491M
−40 mV
open times
τ1, (ms) (A)		0.32 ± 0.04		0.45 ± 0.06		0.39 ± 0.06		0.46 ± 0.21 (0.51)		1.50 ± 0.24		—
τ2, (ms) (A)		—		—		—		1.59 ± 0.00 (0.49)		—		—
No. of events		1,469		3,074		3,388		5,417		3,875		—
closed times
τ1, (A)		—		0.21 ± 0.06 (0.41)		0.42 ± 0.23 (0.33)		0.25 ± 0.04 (0.53)		0.28 ± 0.07 (0.34)		—
τ2, (A)		—		1.33 ± 3.18 (0.27)		7.80 ± 0.00 (0.67)		3.44 ± 0.66 (0.48)		2.08 ± 0.79 (0.66)		—
τ3, (A)		—		17.08 ± 2.75 (0.32)		—		—		—		—
No. of events		—		1,826		1,044		3,783		3,420		—
−20 mV
open times
τ1, (ms)		0.39 ± 0.04		0.58 ± 0.10		0.46 ± 0.06		0.58 ± 0.00 (0.33)		2.12 ± 0.15		0.57 ± 0.00 (0.40)
τ2, (ms) (A)		—		—		—		2.00 ± 0.65 (0.67)		—		1.45 ± 1.70 (0.60)
No. of events		2,427		5,173		7,141		6,930		15,350		8,934
closed times
τ1, (A)				0.21 ± 0.06 (0.31)		0.37 ± 0.13 (0.23)		0.27 ± 0.06 (0.32)		1.38 ± 0.49		0.13 ± 0.00 (0.38)
τ2, (A)				18.76 ± 0.00 (0.69)		7.76 ± 0.00 (0.77)		3.02 ± 0.00 (0.68)		—		12.89 ± 0.77 (0.62)
No. of events				2,404		2,832		7,849		13,567		2,517
0 mV
open times
τ1, (ms)		0.36 ± 0.04		0.51 ± 0.10		0.47 ± 0.07		0.56 ± 0.36 (0.42)		2.26 ± 0.20		1.40 ± 0.30
τ2, (ms)		—		—		—		1.92 ± 0.00 (0.58)		—		—
No. of events		1,123		1,373		5,334		5,603		8,669		3,239
closed times
τ1, (A)		—		0.08 ± 0.00 (0.28)		0.25 ± 0.07 (0.25)		0.07 ± 0.02 (0.29)		0.20 ± 0.05 (0.33)		0.12 ± 0.01 (0.50)
τ2, (A)		—		14.49 ± 0.71 (0.72)		5.54 ± 0.00 (0.75)		1.96 ± 0.37 (0.71)		1.46 ± 0.79 (0.67)		12.08 ± 0.79 (0.50)
No. of events		—		768		1,638		3,208		7,377		2,119

τ1, τ2, and τ3 (ms), time constants of exponential fits to open and closed time distributions. Open time distributions were constructed from patches containing one to two channels, and closed time distributions were constructed from patches containing one channel. A, relative amplitudes of individual fit components. The errors indicated are values for SD estimated by the fitting routine. 

According to scheme SI, the Na⁺ channel can leave the open state by two pathways, entry into the inactivated state or closure to state C3. Closed time distributions of F1489 mutant channels (Fig. 5 B) had two principal resolvable components. The largest component of the closed time distributions arose from closure to a state that was not in the activation pathway since it was longer than the latency to first channel opening (τ_fast in Table V; Hoshi et al., 1994). According to scheme SI the inactivated state is the only closed state not in the activation pathway. Fits of two exponentials to closed time distributions yielded time constants for the component with the longer duration of 18.8 ms for F1489Y, 7.8 ms for F1489I, 3.0 ms for F1489A, and 1.4 ms for F1489Q (Table IV). For F1489Q channels the time constants of the two components were similar and could not be separated at −20 mV. The longer closed time constant is a direct measure of the stability of the inactivated state at this potential and is the reciprocal of k _off in Eq. 1, approximately equal to f + h in scheme SI. The k _off values for the F1489 mutants analyzed on the single channel level correlated well with the hydrophilicity of the amino acid at position 1489 in these mutants (Fig. 3 B, lower case letters). This indicates that the hydrophobic interaction indeed determines the stability of the inactivated state.

Table V.

Fit Parameters for First Latency Distributions

		WT		F1489Y		F1489I		F1489A		F1489Q		T1491M
−40 mV
τfast (A)		1.17 ± 0.01 (0.68)		1.26 ± 0.01 (0.59)		2.00 ± 0.03 (0.48)		0.65 ± 0.02 (0.58)		0.20 ± 0.01 (0.60)		—
delay		0		0.23 ± 0.01		0.17 ± 0.01		0.26 ± 0.01		0.20 ± 0.01		—
τslow (A)		—		11.20 ± 0.06 (0.27)		12.50 ± 0.10 (0.32)		9.60 ± 0.12 (0.27)		4.40 ± 0.05 (0.32)		—
No. of events		1,048		1,440		925		784		368		—
−20 mV
τfast (A)		0.21 ± 0.01 (0.52)		0.41 ± 0.01 (0.80)		0.95 ± 0.01 (0.76)		0.41 ± 0.00 (0.82)		0.12 ± 0.00 (0.86)		1.18 ± 0.01 (0.60)
delay		0.32 ± 0.00		0.26 ± 0.00		0.26 ± 0.00		0.18 ± 0.00		0.22 ± 0.00		0.19 ± 0.01
τslow (A)		19.4 ± 0.44 (0.04)		15.5 ± 0.21 (0.10)		9.95 ± 0.10 (0.17)		3.15 ± 0.04 (0.15)		2.04 ± 0.02 (0.14)		12.5 ± 0.08 (0.30)
No. of events		2,316		4,312		1,650		802		1,443		2,664
0 mV
τfast (A)		0.32 ± 0.00 (0.50)		0.14 ± 0.00 (0.67)		0.34 ± 0.00 (0.72)		0.24 ± 0.01 (0.57)		0.08 ± 0.00 (0.90)		0.35 ± 0.01 (0.73)
delay		0.26 ± 0.00		0.40 ± 0.00		0.29 ± 0.00		0.18 ± 0.01		0.22 ± 0.00		0.30 ± 0.00
τslow (A)		21.0 ± 0.22 (0.03)		15.0 ± 0.14 (0.19)		9.3 ± 0.07 (0.17)		6.5 ± 0.06 (0.33)		1.98 ± 0.04 (0.10)		15.3 ± 0.10 (0.21)
No. of events		1,111		987		945		685		742		1,420

τ_fast, τ_slow, relative amplitudes, A, and the delay, all in ms, are derived from a two-exponential fit to the cumulative first latency distribution (see materials and methods). The difference between the sum of the relative amplitudes, A, and 1 yields the fraction of null sweeps. The errors indicated are values for SD estimated by the fitting routine.  

For WT channels, the inactivated state is far more stable since reopenings occur only rarely during the 40-ms test pulses (Fig. 4). To estimate the stability of the inactivated state in the WT channel at −20 mV, the frequency of reopening was determined for all of the depolarizations analyzed at this potential. The number of openings occurring after the first 5 ms of depolarization was 130 per 1,690 sweeps and 217 per 1,802 sweeps, respectively, in two different patches, each containing two WT channels. Occasional sweeps in which the channel is in a different gating mode where inactivation appears to have failed completely (0.1% of total sweeps) were excluded from this analysis. The number of reopenings during the 40-ms pulses are a function of k _off. To estimate the time constants of closed durations that would produce this rate of reopenings, channel behavior was simulated according to scheme SI (Hoshi et al., 1994; Kellenberger et al., 1996). Time constants producing the observed frequency of reopenings were 580 or 380 ms, respectively, for the two patches. Using these values for WT and the corrected measured closed times for the mutants (see materials and methods), rates of return from the inactivated state were 2.2 ± 0.5 s⁻¹ (WT), 28 s⁻¹ (F1489Y), 110 s⁻¹ (F1489I), 331 s⁻¹ (F1489A), and 725 s⁻¹ (F1489Q). This represents a 13-fold increase in the rate of return from inactivation for F1489Y, a 50-fold increase for F1489I, a 150-fold increase for F1489A, and a 329-fold increase for F1489Q. The disruption of inactivation by the F1489Q mutant corresponds to a difference in binding energy, ΔΔG, of 4.4 kcal, as calculated from k _on and k _off rates of WT and F1489Q channels.

The latency to first opening after depolarization gives information about the rate of transitions among the nonconducting states traversed by a channel before opening. First latency distributions from single WT rat brain type IIA Na⁺ channels are characterized by a rapid time course and a substantial number of sweeps in which no opening occurs (null sweeps), because the channel inactivates before it opens (Fig. 5 C; WT). In mutants with destabilized inactivation, the null sweeps disappear and are replaced by a slower component of the first latency distribution due to channels which inactivate from a closed state and then open (McPhee et al., 1994; 1995). Distributions of first latencies at −40 and −20 mV for WT and mutant channels were corrected for the number of channels in the patch (Patlak and Horn, 1982) and plotted as cumulative probability density distributions (Fig. 5 C). First latency distributions were well fit with two exponentials and a delay (see materials and methods). The faster component of the first latency distribution describes the steps in the activation pathway directly leading to channel opening. We expected that the F1489 mutations, which disrupt steps in inactivation that occur after opening of the channel, would not affect these early transitions. The slower component of the first latency distribution appears in the mutant channels and its time constant is largely determined by the time the channel spends in inactivated states before opening. Therefore, we expect to see a decrease in the time constant of the slow component for mutants with more severe disruption of inactivation. As expected, the first latency distributions of the mutants with destabilized inactivation had an increased maximum open probability relative to WT and displayed a second, slower component with time constants decreasing with decreasing stability of the inactivated state (Fig. 5 C, Table V). In contrast to our expectations, the time constants of the fast component also varied among mutations. The fast time constant was similar for WT, F1489Y and F1489A, but was faster for F1489Q and slower for F1489I (Fig. 5 C, Table V). These differences were most apparent at −40 mV. This indicates that two mutations of F1489 in the inactivation gate, F1489I and F1489Q, affect a transition in the activation pathway occurring before channel opening and before inactivation. This result is consistent with the idea that channel activation and inactivation are coupled (O'Leary et al., 1995) so that changes in the structure of the inactivation gate can affect activation. Additional evidence for this coupling is presented in the following paper on mutations of gly and pro residues in the inactivation gate.

Effects of Mutation of Amino Acid Residues that Flank the IFM Motif

The IFM cluster is flanked by D1487 on the NH₂-terminal side and by T1491 on the COOH-terminal side. Mutation D1487Q did not produce measurable current in a previous study (Patton et al., 1992). Mutations D1487A and D1487N, however, expressed large currents in Xenopus oocytes. The kinetics and the voltage dependence of gating were very similar to WT (Tables I). Therefore, these mutants were not investigated further.

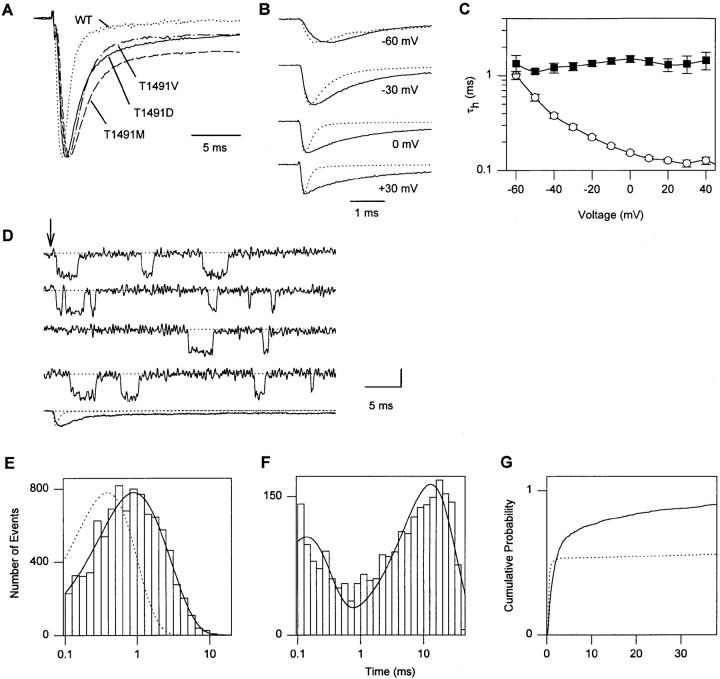
A naturally occurring mutation of the thr residue analogous to T1491 to met in the skeletal muscle Na⁺ channel α subunit causes paramyotonia congenita, a disorder characterized by an impairment of muscle relaxation (for review see Barchi, 1995; Hoffman et al., 1995; Cannon, 1996). We have mutated T1491 to met, val, and asp in the brain type IIA Na⁺ channel α subunit. These mutations cause slowed and incomplete macroscopic inactivation (Fig 6 A). The fraction of sustained current at the end of a 30-ms pulse was 13 ± 3% (n = 9) for T1491D, 13 ± 1% (n = 3) for T1491V, and 24 ± 1% (n = 3) for T1491M in two-electrode voltage-clamp experiments. The voltage dependence of activation was unaffected (Table I). The midpoint of steady-state inactivation was shifted positively by 18 mV for T1491D and by 12 mV for T1491M and T1491V (Table I). Recovery from inactivation was accelerated by all three mutations (Table II). The time constant for recovery at −90 mV, τ_rec-90, was 0.95 ± 0.06 ms (n = 5) for T1491D, 0.63 ± 0.03 ms (n = 4) for T1491M, and 0.71 ± 0.01 ms (n = 3) for T1491V, compared to 2.51 ± 0.22 ms (n = 4) in WT. The extent of acceleration of recovery from inactivation was greater than would have been predicted by the shift in the voltage dependence of inactivation.

Figure 6.

Effects of mutations of T1491. (A) Two-electrode voltage-clamp recordings from oocytes expressing WT and mutant channels. Normalized current traces in response to depolarizations to 0 mV for the indicated mutants are shown. Panels B–G show experiments with mutant T1491M. (B) Averaged current traces from cell-attached macropatches in response to pulses to the indicated potentials from a holding potential of −140 mV. Each trace is an average of normalized traces from different experiments for WT (dotted line, n = 13 experiments) and T1491M (solid line, n = 4). (C) Voltage-dependence of macroscopic inactivation. τ_h was determined from single exponential fits to the current decay in macropatch experiments from WT (○; n = 4) and T1491M (▪; n = 3) Na⁺ channels studied in the same batch of oocytes. (D) Single-channel records and an ensemble average (last trace) from a cell-attached patch containing a single channel. The dotted ensemble average is WT normalized for comparison. The arrow indicates the beginning of 40-ms depolarizations to −20 mV from a holding potential of −140 mV. The vertical calibration bar is 1 pA for single-channel traces and 0.5 pA for the ensemble average. (E) Open time histogram at −20 mV. Three patches containing one to two channels each were used for open time analysis. The solid line is a fit to the sum of two exponentials to the log binned data. The time constants from the fit are 1.45 and 0.565 ms (Table IV). The dotted line is a single exponential with the WT time constant. Mean open times for individual T1491M patches at −20 mV were 1.02, 0.96, and 1.23 ms. (F) Histogram of closed times excluding first latencies at −20 mV. Only single-channel patches were used for closed time analysis. The solid line is the fit of the sum of two exponentials to the log binned data. The time constants derived from the fit are 0.13 and 12.89 ms (Table IV). (G) Cumulative first latency distributions for WT (dotted line) and T1491M (solid line) at −20 mV. Distributions were corrected for the channel number (Patlak and Horn, 1982). Data are from patches with one to two channels (T1491M) or two channels (WT). Parameters for fits to the sum of two exponentials (see materials and methods) are shown in Table V.

Since T1491M produced the strongest disruption of inactivation during depolarizations, it was selected for a detailed analysis. The kinetics of macroscopic inactivation of T1491M were analyzed using cell-attached macropatch recording (Stühmer et al., 1987). Fig. 6 B shows current traces from macropatches at four different test potentials. Each trace is an average of records from several individual experiments as described in the figure legend. Time constants of macroscopic inactivation (τ_h) are plotted versus voltage in Fig. 6 C. Macroscopic inactivation was dramatically slowed relative to WT at potentials more positive than −60 mV (Fig. 6 B and C, Table III). Single T1491M channels show markedly increased open times and several reopenings during a 40-ms depolarizing pulse (Fig. 6 D). The open time distribution at −20 mV was best fitted with two time constants, 1.45 and 0.57 ms, which were both longer than the WT time constant (Fig. 6 E, Table IV). The inactivation rate calculated from bursting properties (Hoshi et al., 1990; see above) was 686 s⁻¹ for the predominant (longer) open state. The closed time distribution had two components (Fig. 6 F). The large, slower component, which describes dwell times in the inactivated state, had a time constant of 12.9 ms at −20 mV. Thus, the T1491M mutation slows entry into the inactivated state to a similar extent as F1489A and destabilizes the inactivated state similarly to F1489Y. These two effects sum to produce macroscopic currents with more sustained current than F1489Y due to the longer open times but less than F1489A due to the more stable inactivated state (Table I).

In addition to its effects on transitions occurring after channel opening, the T1491M mutation slowed the fast component of the first latency distribution and substantially increased the maximum probability of opening (Fig. 6 G). The slowing of the fast component of the first latency indicates that the T1491M mutation slowed the early gating transitions preceding opening of the channel similarly to the F1489I mutation. The substantial increase in the maximum probability of activation indicates that the inactivated state is destabilized sufficiently to allow most channels to open within 40 ms after inactivation.

Voltage Dependence of Open and Closed Times in F1489 and T1491M Mutant Channels

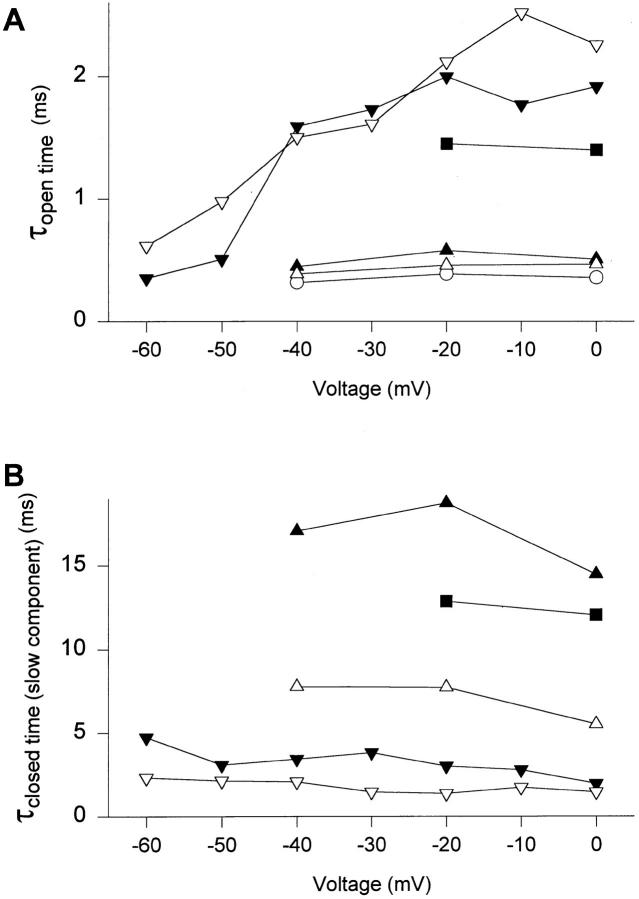
According to scheme SI, the open times are determined by the rates of the two transitions for leaving the open state, the transition to the last closed state (C3 in scheme SI) and entry into the inactivated state. The rate of inactivation from the open state in neuronal Na⁺ channels is thought to be voltage independent (Armstrong and Bezanilla, 1977; Armstrong, 1981; Aldrich et al., 1983) or to increase slightly with depolarization (Vandenberg and Horn, 1984) whereas the transition rate from the open to closed states decreases substantially with depolarization. To examine whether mutant Na⁺ channels behaved in a manner that was consistent with this scheme, we examined single channel properties of some of the mutants at a range of membrane potentials. In Fig. 7 A, the time constants of open times of WT and selected mutant channels are plotted versus the test pulse voltage. Open times of WT channels were independent of voltage. In WT channels at strong depolarizations, inactivation of open channels is thought to be rapid relative to channel closure at all potentials and the constant open times reflect the voltage-independent inactivation rate (Fig. 7 A). For mutants F1489Y and F1489I, the open times were also voltage independent and similar to WT from −40 to 0 mV, consistent with their inactivation rate being rapid relative to channel closing and unaffected by the mutation over this voltage range. In contrast, open times of mutants F1489A, F1489Q, and T1491M were increased relative to WT (Fig. 5 A) and voltage dependent (Fig. 7 A; Table IV). Such voltage-dependent open times are expected from scheme SI when the rates of inactivation and closing become similar so that many openings are terminated by transitions to closed states. The observed voltage dependence of open times is consistent with the conclusion that these mutations slow inactivation enough to unmask the underlying voltage dependence of the rate governing the transition from open to closed states.

Figure 7.

Voltage-dependence of open and closed time constants. Time constants from fits to the pooled open times (A) and the slow component of closed times (B) at different voltages, as described for −20 mV in the legend to Figs. 5 and 6. WT (○), F1489Y (▴), F1489I (▵), F1489A (▾), F1489Q (▿), and T1491M (▪). For F1489A, where open time distributions at potentials more positive than −50 mV were best fit with the sum of two exponentials, the time constant of the longer component is shown. Similarly, T1491M open times at −20 mV were fit with the sum of two exponentials, and the time constant of the longer component is shown.

The slower component of the closed time histogram represents the inactivated state. The time constant of the slow component of closed times which describes inactivation was nearly voltage independent for each mutant, although the absolute value of the closed time varied between mutants (Fig. 7 B). This finding is consistent with the slow component of the closed time histogram reporting sojourns in a voltage-independent inactivated state that is disrupted in the mutants.

Effects of Mutation of Two Other Clusters of Hydrophobic Amino Acids

There are two other conserved clusters of hydrophobic amino acids besides IFM in L_III-IV of the Na⁺ channel α subunit (Fig. 1), YY1497/8 in the center and MVF1523-5 at the COOH-terminal end. These hydrophobic clusters could in principle play similar roles in inactivation to IFM1488-90, although a different role for YY1497/8 has been postulated in the heart Na⁺ channel (O'Leary et al., 1995). To examine the role of these hydrophobic amino acid clusters in the brain Na⁺ channel, Y1497 and Y1498 were mutated individually (Y1497Q and Y1498Q) and in combination (YY1497/8QQ) to glutamine, which is uncharged but polar. M1523, V1524, and F1525 were all mutated to glutamine in a single construct (MVF1523-5QQQ). Fig. 8 A shows families of whole-cell Na⁺ currents from wild type (WT) and the mutant channels YY1497/8QQ and MVF1523-5QQQ. WT and mutant channels show a typical pattern of rapid voltage-dependent activation followed by inactivation in response to depolarization. No differences in time course between the WT and mutants could be resolved by two-electrode voltage-clamp. Furthermore, the fraction of noninactivating current at the end of a 30-ms depolarization was unchanged in the mutant channels, 3 ± 1% (n = 4) for YY1497/8QQ and 2 ± 2% (n = 3) for MVF1523-5QQQ, compared to 2 ± 1% (n = 8) for WT (Table I). Thus, mutations YY1597/ 8QQ and MVF1523-5QQQ do not disrupt inactivation in the manner observed with mutations of F1489 (West et al., 1992a; Fig. 3).

Figure 8.

Effects of mutations of hydrophobic amino acids YY1497/8 and MVF1523-5 to Gln. (A) Two-electrode voltage-clamp recordings from Xenopus oocytes expressing either WT, YY1497/ 8QQ, or MVF1523-5QQQ mutant channels. The currents were elicited by step depolarizations from a holding potential of −90 mV to test potentials of −30 to +10 mV in 10-mV increments. (B) Steady-state inactivation curves in response to 100-ms prepulses. Data are averages of three to seven two-electrode voltage-clamp experiments (Table I) with WT (○), Y1497Q (▴), Y1498Q (▾), YY1497/8QQ (♦), and MVF15-23-5QQQ (•). Solid lines are least-square fits of the Boltzmann equation to the data. (C) Voltage-dependence of the time constant of recovery from inactivation, τ_rec. The recovery time course at each voltage was fitted by one exponential (see materials and methods). Data are from three to four experiments with WT (○), Y1497Q (▴), Y1498Q (▾), YY1497/8QQ (♦), and MVF1523-5QQQ (•).

These mutations did affect the voltage-dependent properties of the channel. Mutation MVF1523-5QQQ shifted the midpoint of activation 5-mV positively (Table I) but did not affect the voltage dependence of inactivation (Table I, Fig. 8 B). Mutations Y1497Q, Y1498Q, and YY1497/8QQ each shifted the midpoints of activation (Table I) and inactivation (Table I, Fig. 8 B) positively by 5–8 mV and speeded recovery from inactivation (Fig. 8 C, Table II). The time constant for recovery at −90 mV, τ_rec-90, was 0.84 ± 0.01 ms (n = 3) for YY1497/8QQ, 1.66 ± 0.06 ms (n = 3) for Y1497Q, and 1.44 ± 0.12 ms (n = 3) for Y1498Q, in comparison to 2.51 ± 0.22 ms (n = 4) for WT. The effect on recovery from inactivation is not secondary to the shift in the voltage dependence of gating kinetics, because a positive shift of about 30 mV would have been necessary to produce the acceleration of recovery from inactivation observed in YY1497/8QQ (Fig. 8 C). This indicates that mutations of Y1497 and Y1498 increase the rates of leaving inactivated states at negative potentials after repolarization, even though they do not impair the stability of the inactivated state at depolarized potentials.

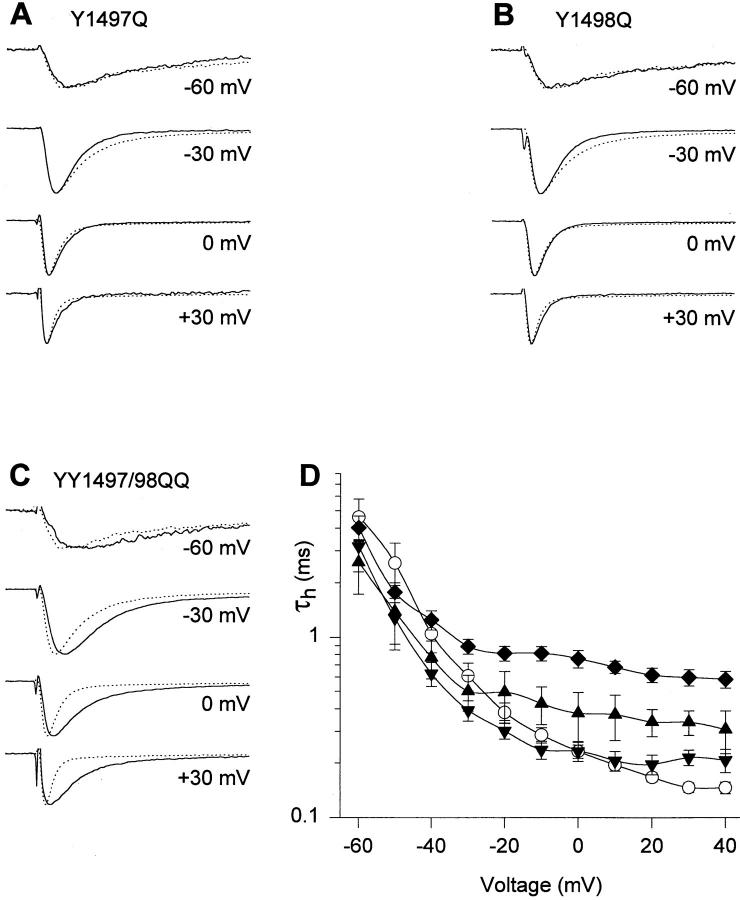
To examine Na⁺ current kinetics at higher resolution, currents conducted by channels with mutations of Y1497 and Y1498 were analyzed by recording from cell-attached macropatches (Fig. 9). For Y1497Q and Y1498Q, macroscopic inactivation was actually faster than WT at potentials more negative than −30 mV but was similar to WT at more positive potentials (Fig. 9 A, B, and D). The effects of the double mutation YY1497/8QQ (Fig. 9 C and D) were more substantial. This mutation slowed the rates of macroscopic activation and inactivation but did not cause sustained Na⁺ currents (Fig. 9 C and D, Tables I and III). Together with the results of whole cell voltage clamp studies above, these characteristics indicate that the YY1497/98QQ mutation slows the rates of activation and entry of the channel into the inactivated state, and destabilizes the inactivated state at negative, but not at positive, membrane potentials.

Figure 9.

Time course of macroscopic inactivation of channels with mutations of Y1497 and Y1498. (A–C) Current traces from cell-attached macropatches from Xenopus oocytes. Currents were elicited from a holding potential of −140 mV to the potentials indicated. Each trace shown is an average of normalized traces from different experiments for WT (dotted line, n = 13) and mutants, shown as solid lines, Y1497Q (n = 2), Y1498Q (n = 4), and YY1497/8QQ (n = 9). (D) Voltage dependence of macroscopic inactivation. τ_h was determined from a single exponential fit to the current decay in macropatch experiments of WT (○), Y1497Q (▴), Y1489Q (▾), YY1497/8QQ (♦).

discussion

Hydrophobic Interactions of F1489 in the Inactivated State

An important role in fast inactivation for L_III-IV (Vassilev et al., 1988; Stühmer et al., 1989; Vassilev et al., 1989) and specifically for IFM1488-90 has been established previously (see introduction). Within IFM1488-90, F1489 plays by far the most important role (West et al., 1992a ), and it has been proposed that it interacts with the putative inactivation gate receptor to keep the inactivation gate closed once the channel has inactivated (Catterall, 1992; Patton et al., 1992; West et al., 1992a ; McPhee et al., 1994; 1995). We have investigated the nature of the interaction of F1489 with the inactivation gate receptor by site-directed mutagenesis. Substitution of 14 different amino acids for F1489 showed that hydrophilic amino acids disrupt the interaction of F1489 with its putative receptor, whereas amino acids with aliphatic and aromatic side chains stabilized the interaction nearly as effectively as F1489. The fraction of noninactivating current correlated well with the hydrophilicity of the amino acid at position 1489. This indicates that the mutations affected a hydrophobic interaction, causing disruption of inactivation. Thus, the hydrophobicity or aromaticity of the amino acid at position 1489 defines the stability of the inactivated state.

Multiple scales of hydrophilicity/hydrophobicity have been compiled which are based on different experimental and theoretical criteria (Cornette et al., 1987). We have used the scale of Hopp and Woods (1981) that is based on solubility properties of each amino acid and is optimized to predict antigenic determinants on protein surfaces from amino acid sequences. This scale seems most relevant for analysis of the Na⁺ channel inactivation process in which a hydrophobic amino acid residue is thought to be buried in the protein structure. Using this scale for hydrophilicity/hydrophobicity, the unbranched aliphatic residue leu was more effective relative to its hydrophobicity than phe, tyr, or trp, while the branched aliphatics ile and val were comparable or less effective than the aromatic residues relative to their hydrophobicity (see Fig. 3). The weaker interaction with the branched aliphatic residues may reflect their inability to fit well into a site that is optimal for a planar aromatic moiety. Since a flexible unbranched aliphatic residue is more effective relative to hydrophobicity than the aromatic residues in stabilizing the inactivated state, our results are most consistent with the conclusion that hydrophobicity is more important than aromaticity in this interaction.

Effects of Mutations of Other Hydrophobic Residues

F1489 is unique among the hydrophobic amino acid residues in L_III-IV. In contrast to F1489, mutation of the nearby residue F1483 (West et al., 1992a , Table I), the pair of tyr residues at positions 1497/8, and the MVF cluster at positions 1523–5 to less hydrophobic residues does not cause an increase in sustained Na⁺ current and therefore does not impair the stability of the inactivated state at depolarized membrane potentials. Mutation of the pair of tyr residues at positions 1497/8 accelerates recovery from inactivation at negative membrane potentials and shifts steady-state inactivation to more positive membrane potentials, suggesting that this mutation does destabilize the inactivated state at negative membrane potentials. The mechanism of these effects is considered further in the accompanying paper.

F1489 Forms a Structurally Specific Hydrophobic Interaction

The exact position in L_III-IV of F1489 is critical for inactivation since the phe was much less effective when displaced one amino acid position toward the NH₂ or COOH terminus from position 1489. Hydrophobic interactions are often not highly structurally specific because they result from the apposition of two hydrophobic surfaces without precise complementarity. For example, serum albumin can bind a wide range of hydrophobic ligands to a site containing a hydrophobic interaction surface (Koch-Weser and Sellers, 1976). Our results support the idea that the interaction of F1489 with the putative inactivation gate receptor is structurally specific, resembling a specific ligand-binding interaction, because the phe side chain must be precisely positioned to make an effective interaction.

T1491 Also Is Required for Normal Inactivation

T1491, adjacent to IFM1488-90, also participates in inactivated state stability. Mutations at this position disrupted inactivation in the same manner as the mutations of F1489, but to a smaller extent. Mutations of T1491 to different amino acids all produced slowed macroscopic inactivation and an increase in the fraction of noninactivating current. These inactivation-disrupting mutations of T1491 also caused a positive shift in the voltage dependence of steady-state inactivation and accelerated recovery from inactivation at negative membrane potentials. Mutation of T1491 disrupted inactivation to a greater extent than mutation of any other residue in L_III-IV except for F1489, consistent with the idea that it also interacts with the inactivation gate receptor and stabilizes the inactivated state.

Mutations of F1489 and T1491 Specifically Destabilize the Inactivated State

Single-channel analysis of WT and four mutant channels in which F1489 was converted to Y, I, A, and Q allowed the direct measurement of the rate constants governing the closing (k _on) and opening (k _off) of the inactivation gate. k _on was reduced 1.5- to 6-fold compared to WT by these mutations, and k _off was increased 13- to 329-fold. For each of these mutations, the change in k _off was more than sevenfold greater than the change in k _on, indicating that the hydrophobic interaction of F1489 mainly determines the stability of the inactivated state and to a lesser extent the rate of inactivation. Our previous studies showed that during inactivation F1489 moves from a solvent accessible position to a position in which it is inaccessible to hydrophilic reagents (Kellenberger et al., 1996). Hydrophobic interactions require close enough contact to displace water molecules from the interacting surfaces (Tanford, 1980). Thus, hydrophobic interaction cannot be the driving force for this longer range movement. Instead, the hydrophobic interaction has the function of a “latch” that keeps the inactivation gate closed. The decrease in k _on is probably due to slowed association of the inactivation gate and its receptor after the major movement of the gate has occurred and they are in close proximity.

Single-channel recordings from the T1491M mutant also allowed the determination of on- and off-rates of the inactivation gate. The T1491M mutation decreased k _on 3.5-fold and increased k _off 24-fold over WT. Thus, the predominant effect of this mutation, like those of F1489, is to destabilize the stability of the inactivated state, consistent with the conclusion that T1491 also interacts directly with the inactivation gate receptor.

Comparison to Cardiac and Skeletal Muscle Na⁺ Channels

Mutations of the phe residues homologous to F1489 to gln in cardiac (Hartmann et al., 1994; Bennett et al., 1995) and skeletal muscle (Lawrence et al., 1996; Nuss et al., 1996) Na⁺ channels had normal activation voltage dependence, a large positive shift in the midpoint of steady-state inactivation, and 30 or 37% noninactivating Na⁺ current, respectively. This compares to 85% noninactivating Na⁺ current in the present study of the brain type IIA Na⁺ channel. Mutation of the whole IFM cluster to gln residues in the cardiac channel (Hartmann et al., 1994) completely abolished detectable inactivation, much as it did in the brain channel (West et al., 1992a ). Open times of the corresponding F/Q mutant were increased twofold in cardiac and fourfold in skeletal muscle channels. The smaller increase in the fraction of noninactivating current by the mutation in the cardiac and skeletal muscle channels compared to the brain channel is partially due to the smaller increase in open times in these mutants. Inactivation is different in cardiac, skeletal muscle, and brain Na⁺ channels (for review see Fozzard and Hanck, 1996). Macroscopic inactivation of heart and skeletal muscle Na⁺ channels at depolarized potentials is several-fold slower than for brain Na⁺ channels. The differences in inactivation seen between channels originating from different tissues are not due to differences in L_III-IV, because this loop is highly conserved. Replacement of L_III-IV in the human heart α subunit with L_III-IV of the brain type IIA α subunit has no effect on inactivation (Hartmann et al., 1994). Therefore, these differences in inactivation properties are most likely due to differences between inactivation gate receptors of these channels or to differences in the coupling of activation to inactivation.

The homologous mutation to T1491M occurs in vivo in skeletal muscle Na⁺ channels, causing the disorder paramyotonia congenita. Macroscopic currents from this mutant in recombinant human (Yang et al., 1994) and rat (Hayward et al., 1996) skeletal muscle Na⁺ channels had slowed macroscopic inactivation. Increased sustained current was seen only with the rat isoform. Single-channel Na⁺ currents from cultured muscle cells from a patient carrying the T → M mutation had increased reopening frequency during depolarizations, indicating a destabilized inactivated state, in addition to a mean open time that was two- to threefold increased over WT (Tahmoush et al., 1994). The latter effects are qualitatively similar to effects of this mutation in the brain Na⁺ channel reported here, but like the mutation of the F1489Q mutation are weaker. Overall, the previous studies of these naturally occurring mutations in differing types and species of Na⁺ channels are consistent with the results of our studies of brain type IIA Na⁺ channels presented here.