Control of Maximum Sarcoplasmic Reticulum Ca Load in Intact Ferret Ventricular Myocytes

Abstract

In steady state, the Ca content of the sarcoplasmic reticulum (SR) of cardiac myocytes is determined by a balance among influx and efflux pathways. The SR Ca content may be limited mainly by the ATP-supplied chemical potential that is inherent in the gradient between SR and cytosol. That is, forward Ca pumping from cytosol to SR may be opposed by energetically conservative reverse pumping dependent on intra-SR free [Ca]. On the other hand, SR Ca loading may be limited by dissipative pathways (pump slippage and/or pump-independent leak). To assess how SR Ca content is limited, we loaded voltage-clamped ferret ventricular myocytes cumulatively with known amounts of Ca via L-type Ca channels (I_Ca), using Na-free solutions to prevent Na/Ca exchange. We then measured the maximal resulting caffeine-released SR Ca content under control conditions, as well as when SR Ca pumping was accelerated by isoproterenol (1 μM) or slowed by thapsigargin (0.2–0.4 μM). Under control conditions, SR Ca content reached a limit of 137 μmol·liter cytosol⁻¹ (nonmitochondrial volume) when measured by integrating caffeine-induced Na/Ca exchange currents (∫I_NaCaXdt) and of 119 μmol·liter cytosol⁻¹ when measured using fluorescence signals dependent on changes in cytosolic free Ca ([Ca]_i). When Ca-ATPase pumping rate was slowed 39% by thapsigargin, the maximal SR Ca content decreased by 5 (∫I_NaCaXdt method) or 23% (fluorescence method); when pumping rate was increased 74% by isoproterenol, SR Ca content increased by 10% (fluorescence method) or 20% (∫I_NaCaXdt method). The relative stability of the SR Ca load suggests that dissipative losses have only a minor influence in setting the SR Ca content. Indeed, it appears that the SR Ca pump in intact cells can generate a [Ca] gradient approaching the thermodynamic limit.

introduction

In cardiac myocytes, many properties of the Ca-induced Ca release (CICR) and excitation–contraction coupling (ECC) processes depend on the quantity of Ca stored in the sarcoplasmic reticulum (SR).¹ Among these are the gain or efficacy (Janczewski et al., 1995) and related factors such as the fraction of stored Ca released during twitches (Han et al., 1994; Bassani et al., 1995c ), the amount of Ca-dependent negative feedback on Ca influx through L-type Ca channels (Sipido et al., 1995; Grantham and Cannell, 1996), and the probability of local or propagated spontaneous Ca release events (Cheng et al., 1993; Satoh et al., 1997). Secondary to changes in CICR or ECC are, for example, inotropy with increased SR Ca loads (e.g., in phospholamban knockout mice; Wolska et al., 1996; Li et al., 1997), as well as rest potentiation or decay related with load changes (Bassani and Bers, 1994). Accordingly, mechanisms setting and otherwise controlling the maximum SR Ca load are of interest.

A particular SR Ca load is maintained in steady state when influx and efflux of Ca from the SR are equal. The maximal SR Ca load could be set by the limiting chemical potential gradient of free [Ca] between the SR lumen and the cytosol, ΔG_SR = 2RT ln ([Ca]_SR/ [Ca]_i). Efflux from the SR could be mediated by a combination of reverse pump flux (regenerating ATP; Makinose and Hasselbach, 1971) and dissipative leakage. In isolated rat SR vesicles, with dissipative leak through ryanodine receptor/release channels blocked, Shannon and Bers (1997) found a gradient of 7,000, corresponding to an apparent efficiency of 74%, based on ΔG_ATP = 58.9 kJ/mol (Allen et al., 1985). Under this limiting condition, the flux balance should be set mainly by the forward and backward pump rates, and the energy cost incurred due to incomplete reversibility of the Ca-ATPase (Inesi and de Meis, 1988) should be minimal (Takenaka et al., 1982; Feher and Briggs, 1984).

In contrast, in intact cells, Ca must also leak from the SR through ryanodine receptors, dissipating the SR [Ca] gradient. One aim of this study was to determine whether enough Ca leaks from the SR in intact myocytes to reduce the steady state SR Ca load below the limit set by ΔG_SR. If sufficient, leak flux, rather than reverse pumping, would be the main factor opposing forward pumping (SR uptake) and thereby determining steady state SR Ca load.

In intact cells, existing estimates of SR Ca pump and leak rates should help predict SR Ca loading, but appear disparate. Pump parameters estimated from cytosolic [Ca]_i transients (K _m ≈ 0.27 μmol·liter cytosol⁻¹ and V_m ≈ 210 μmol·liter cytosol⁻¹·s⁻¹; Sipido and Wier, 1991; Balke et al., 1994; Bassani et al., 1994a ) predict a forward rate of 27 μM·s⁻¹ at cytosolic [Ca]_i = 100 nM. By contrast, direct estimates of unidirectional Ca leak from the SR of ventricular cells of rabbit and rat with normal loads amount to only 0.3 μmol·liter cytosol⁻¹·s⁻¹ (Bassani and Bers, 1995). Since this Ca pump independent leak is much slower than the unidirectional SR Ca uptake, pump backflux may limit SR Ca content in intact cells, as appears to be the case in permeabilized myocytes with leak blocked as described above (Shannon et al., 1997).

Ca leak from the SR may increase with increasing SR Ca load (Bassani and Bers, 1995). Consistent with this, and consistent with the view that the ryanodine receptors are the source of the leak, Ca spark frequencies increase when SR Ca load is increased; e.g., by high external [Ca] or isoproterenol (ISO) treatment (Cheng et al., 1993; Gómez et al., 1996; Satoh et al., 1997). In intact rat cells, high SR Ca loading is associated with spontaneous waves that may indicate a sharply accelerating leak rate (Cheng et al., 1996; Diaz et al., 1997).

To assess the importance of leak in limiting SR Ca load, we loaded voltage-clamped cells cumulatively with known amounts of Ca via L-type Ca channels (I_Ca). During loading, Na-free solutions were used to prevent Na/Ca exchange current (I_NaCaX). We then measured the maximal resulting caffeine-released Ca content of the SR, using both Na/Ca exchange currents and fluorescence-based measurements of cytosolic free Ca ([Ca]_i). We perturbed SR Ca pumping by accelerating it with ISO (1 μM; Tada et al., 1974) or slowing it (blocking it partially) with thapsigargin (TG; 0.2–0.4 μM; Sagara and Inesi, 1991; de Meis and Inesi, 1992; Hove-Madsen and Bers, 1993b ). If Ca leak is minimal, stimulation or inhibition of the SR Ca pump rate should not alter maximal SR Ca load, but only change the time required to attain it. If leak is important in setting the SR Ca load, the load should change substantially when the pump rate is changed.

Under control conditions, SR Ca content reached a limit of 137 μmol·liter cytosol⁻¹ (nonmitochondrial volume) when measured via ∫I_NaCaXdt and 119 μmol·liter cytosol⁻¹ when measured using fluorescence. When Ca-ATPase pumping rate was slowed 39% by TG, the maximal SR Ca content decreased by 5% (∫I_NaCaXdt method) or 23% (fluorescence method); when the pumping rate was increased 74% by ISO, SR Ca content increased by 10% (fluorescence method) or 20% (∫I_NaCaXdt method). These modest changes indicate that leak flux has only a minor influence on maximal SR Ca content in intact ventricular myocytes.

materials and methods

Cell Preparation

Cells were isolated from adult ferret hearts by approved methods as previously described (Bassani et al., 1994a ). Animals were anesthetized with pentobarbital (50 mg/kg) and killed by exsanguination. Hearts were excised, rinsed of blood, mounted on a standard Langendorff apparatus, and retrogradely perfused at 30–70 mmHg with Ca-free Tyrode solution for 5 min, after which collagenase (0.5–0.8 mg/ml) and neutral protease (0.02–0.05 mg/ml) were added. When the heart was somewhat flaccid, it was removed, rinsed in Ca-free Tyrode solution, and the tissue was cut and teased to yield free cells. After washing, cells were put in MEM with 2 mM Ca, plated onto laminin-pretreated recording chambers, and secured to the stage of a Nikon TMD microscope equipped for epifluorescence (Photon Technology, Inc., South Brunswick, NJ).

Fluorescence Measurement of [Ca]_i

Cells were incubated in a normal Tyrode solution containing (mM): 140 NaCl, 6 KCl, 1 MgCl₂, 1 CaCl₂, and 10 HEPES, with pH 7.4 using NaOH. Dye loading with Indo-1/AM (10 μM, 20 min, 20°C) was done in this same solution, after which 30 min in dye-free solution was allowed for deesterification. In some cells, instead of Indo-1/AM, K₅-Indo (50 μM) was loaded through the patch pipette (see below). Indo-1 fluorescence was excited at 365 nm, detected at 405 ± 10 and 485 ± 10 nm by photomultipliers with current-to-voltage converters and recorded using PClamp6 software (Axon Instruments, Foster City, CA), which also acquired the voltage clamp data (see below) and controlled the application of bathing solutions. Autofluorescent background at each wavelength, measured each day in separate cells that were not dye loaded, was adjusted for apparent surface area of each cell and subtracted from the corresponding total fluorescence. In a few cells, a time-dependent trend for individual fluorescence signals at 405 and 485 nm to decrease was removed; detrending slightly reduced variability in the calculated [Ca]_i (see below) but did not affect any conclusions.

Electrophysiology

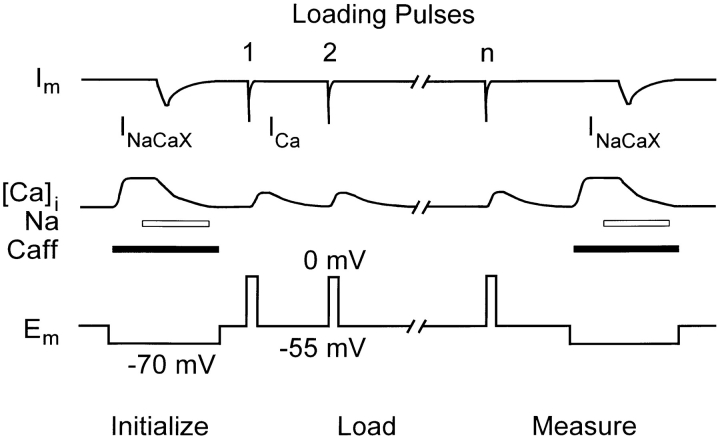
Perforated patch voltage clamp was used for most cells to record I_Ca or I_NaCaX. Recording electrodes of resistance 1–2 MΩ were tip-filled with (mM): 40 CsCl, 80 Cs-methanesulfonate, 0.1 EGTA, 1 MgCl₂, and 10 HEPES, with pH 7.2 using CsOH. The same solution, with amphotericin added at 120 μg/ml, was used to backfill the electrodes. In a few cells, ruptured patch recording was used, in which case K₅-Indo-1 (50 μM), Mg-ATP (5 mM), and Li-GTP (0.3 mM) were added to the pipette solution, and EGTA and amphotericin were omitted. During recording, cells were bathed in a standard solution containing (mM): 140 TEA-Cl, 4 CsCl, 1 MgCl₂, 10 HEPES, and 2 CaCl₂, with pH 7.4 using CsOH. Bathing solutions were substituted during appropriate periods by means of a fast switching device under computer control as set by the experimental protocol (see below and Fig. 1).

Figure 1.

Experimental protocol showing voltage and solution changes applied to priorly Na_i-depleted cells. The sequence of initially emptying the SR, loading, and then measuring the load was repeated on each cell for various numbers of pulses, first in control condition, and then after application of TG or ISO.

Experimental Protocol

Cells were maintained in the Na-free Ca-containing solution described above, so that I_Ca could be recorded without interference from I_NaCaX. To prevent cells from Ca overloading via reverse Na/ Ca exchange in this solution, they were initially depleted of Na_i before experiments were begun. This was accomplished by incubating for 15 min in K-containing Na- and Ca-free solution containing (mM): 140 LiCl, 6 KCl, 1 MgCl₂, 1 EGTA, and 10 glucose, with pH 7.4 using LiOH.

As shown in Fig. 1, a cell was first initialized to deplete the SR Ca load by applying caffeine. Next, to Ca-load the cell progressively, we evoked I_Ca by depolarizing repeatedly from V_hold (−55 mV) to 0 for 200 ms, at 0.25 Hz. The number of pulses was 1, 2, 5, 10, 20, or 40. Finally, the resulting SR Ca load was measured. Caffeine was applied in Na-free solution to release the SR Ca load. The initial increase in [Ca]_i was sustained long enough to use as a first measure of SR Ca load, the only routes for Ca to leave the cytosol being extrusion on the sarcolemmal Ca pump and/or uptake into mitochondria (Bassani et al. 1994a ). 2 s after the start of caffeine application, caffeine-containing standard solution with 140 mM NaCl instead of TEA-Cl was substituted, which rapidly activated inward Na/Ca exchange current (I_NaCaX) and also caused [Ca]_i to decline steeply. After 10 s, caffeine-free standard solution was restored. During caffeine applications, V_hold was reset to −70 mV to enhance I_NaCaX. Integration of I_NaCaX provided data for a second measure of SR Ca content (Callewaert et al., 1989; Varro et al., 1993). This initialization, loading, and measurement sequence was repeated for the various numbers of loading pulses, in random order. Thereafter, we added either ISO (1 μM; sustained application) or TG (0.2–0.4 μM, 1–2 min application), and repeated the entire set of sequences (again with 1, 2, 5, 10, 20, or 40 pulses in random order) on the same cell.

Calculations

Cumulated molar Ca influx via I_Ca in each loading sequence was calculated by integrating I_Ca and summing over all pulses during the sequence. Since the depolarization for I_Ca was to 0 mV (eliminating leak current) and since K and Na were absent, all current was considered to be due to I_Ca, and the baseline for integration was set to 0. The molar influx was divided by the nonmitochondrial cytosolic volume to get Ca concentration influx. Cytosolic volume was found by dividing the cell's capacitance by the ratio of capacitance to cytosolic volume for ferret myocytes (7.96 pF/ pl cytosol; Satoh et al., 1996).

Fluorescence transients recorded as the ratio (R) of background-corrected fluorescence at 405 vs. 485 nm during Ca loading and subsequent release of SR Ca were converted to [Ca]_i according to [Ca]_i = K _dβ(R − R_min)/(R_max − R) (Grynkiewicz et al., 1985). Limiting ratio parameters R_min (corresponding with [Ca] < 10⁻⁹ M) and R_max (corresponding with [Ca] = 2 mM) were measured in vivo, separately for Indo-1/AM and K₅-Indo, as described in Bassani et al. (1995b). The value of β, the ratio of free ([Ca] < 10⁻⁹ M) to bound ([Ca] at saturation) Indo-1 fluorescence measured in vitro at 485 nm, was 3.0. The dissociation constant (K _d) for intracellular Indo-1 was taken as 750 nm (reflecting higher K _d values seen in vivo vs. in vitro; see Hove-Madsen and Bers, 1992; comparable with Bassani et al., 1995b ). [Ca]_i was used to follow the time course of SR Ca uptake during loading. To measure SR Ca content, resting [Ca]_i after loading but before caffeine application and peak [Ca]_i, which occurred during the first 2 s of caffeine applications, were converted to total cytosolic Ca ([Ca]_T). The difference between these [Ca]_T values (Δ[Ca]_T) was taken to indicate the added SR Ca load, referred to the cytosolic volume. [Ca]_T was determined from [Ca]_i using [Ca]_T = [Ca]_i + 232 μM/[1 + (455 nM/[Ca]_i)] + 50 μM/[1 + (750 nM/[Ca]_i)], in which the second term reflects passive cellular Ca buffering (Bers and Berlin, 1995; based on data in Hove-Madsen and Bers, 1993a ), and the third term accounts for Ca buffering by Indo-1.

Fluorescence-based SR Ca content measurements depend on numerous parameters, including those for cytosolic Ca buffering (K _d and B_max) and for calibration (R_min, R_max, K _d, and β), and could be affected by non–Ca-related background fluorescence. We assessed the sensitivity of SR Ca content to these factors by putting typical observed values in the defining equations and noting how much the apparent SR Ca content changed when we varied each parameter ±20% around its typical value. B_max for cytosolic Ca binding affects apparent content quite strongly (±19.6% for ±20% change), compared with cytosolic binding K _d (±3.6%). However, these parameters are well established (Berlin et al., 1994; Hove-Madsen and Bers, 1993a ). Apparent SR Ca content is sensitive to changes in background fluorescence (±1–10%). Although we could not measure the background for each individual cell, we did base our background correction on 10 or more cells each day with compensation for cell size. SR Ca content was relatively less sensitive to changes in Indo-1 AM calibration parameters R_max (±8%), K _dβ (±4.6%), and R_min (±4.4%).

SR Ca content was also calculated by integrating the current that flowed during caffeine application after Na was added (∫I_NaCaXdt method; Varro et al., 1993; Terraciano and MacLeod, 1994; Delbridge et al., 1996). We believe this current is entirely I_NaCaX because no change in current flow occurs in association with caffeine applications when Na is absent. To measure the amount of Ca added to the SR during loading, the I_NaCaX integral should run until [Ca]_i has decayed to the resting value it had attained at the completion of SR Ca loading. Even after [Ca]_i has returned to this resting value, I_NaCaX can be nonzero because [Ca]_i is still determined by a balance among Ca transport processes (excluding the SR Ca-ATPase). To predict resting I_NaCaX, we first subtracted the leakage current flowing at the start of caffeine application before Na was added. We used linear regression (with zero asymptote) to predict how I_NaCaX depended on [Ca]_i, selecting only the decaying part of the caffeine-evoked [Ca]_i transient. A linear dependence of I_NaCaX on [Ca]_i applies when [Na]_i (= 0), [Ca]_o, and [Na]_o are constant, as applies here (Kimura et al., 1987; Barcenas-Ruiz et al., 1987). Using as a baseline the predicted I_NaCaX at resting [Ca]_i, we directly integrated the rising and decaying phases of the current. In some cases, especially where I_NaCaX was small, the later part of the decaying phase was affected by noise or by transient changes in seal leakage during contraction (downward deflections in the I_NaCaX record in Fig. 2 D). Since our linear model could predict the entire decaying portion of the I_NaCaX record, we replaced any uninterpretable late segments of the actual I_NaCaX record by the prediction, before integrating. The direct integral always included at least the first few seconds (sometimes all) of the I_NaCaX decay, and accounted for 87 ± 4% (SEM, n = 117) of the total integral. The integral was divided by 0.75 to correct for the parallel removal of cytosolic Ca by slow transport processes (mitochondrial uptake and sarcolemmal Ca pump extrusion) in the ferret (Bassani et al., 1994b ) and also by 0.65 to exclude the fraction of total cell volume occupied by mitochondria (Page et al., 1971), yielding content in micromoles·liter cytosol⁻¹.

Figure 2.

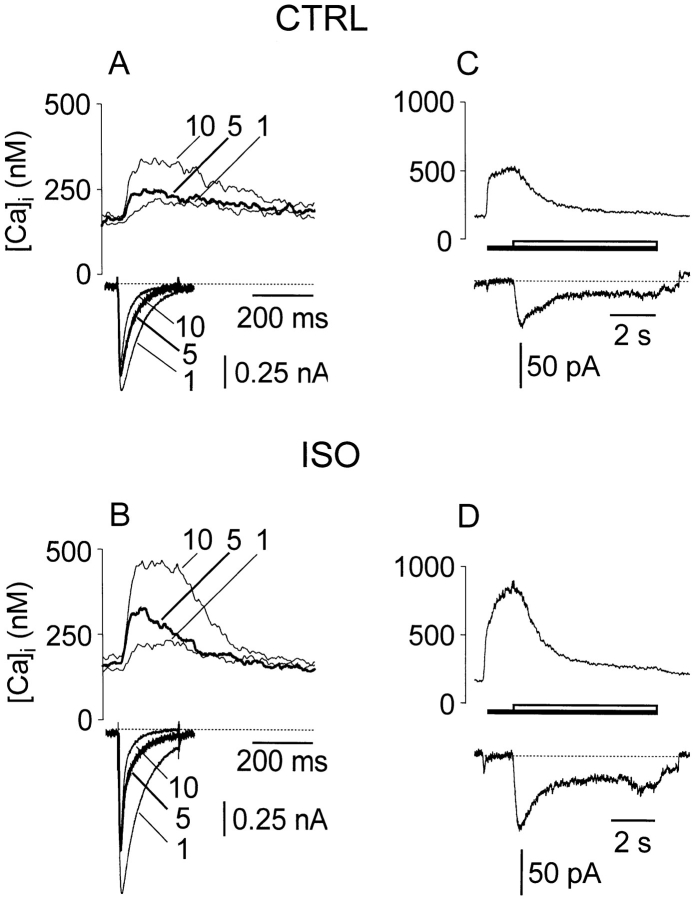
I_Ca was larger, while corresponding [Ca]_i transients were larger and decayed faster with ISO treatment. (A and C) Control; (B and D) ISO, 1 μM. (A and B) I_Ca and corresponding [Ca]_i transients during moderate Ca loading of the SR by a sequence of 10 pulses. Dotted line marks 0 current level. Only pulses 1, 5, and 10 shown. (C and D) Corresponding responses to caffeine after loading. Dotted line marks nonexchange (leakage) current flowing during Na-free portion of caffeine application.

The Δ[Ca] _T- and ∫I_NaCaXdt-based SR Ca content estimates are complementary. In our case, they are not truly independent because the baseline value for integration of I_NaCaX and in some cases parts of the integrals themselves were determined from [Ca]_i. However, the respective calculations have independent bases: Δ[Ca]_T estimates rely on prior knowledge of cytosolic Ca binding but not on knowledge of Ca removal by non-I_NaCaX processes, and vice versa for the ∫I_NaCaXdt-based estimates.

results

Ca Loading and SR Ca Content Data

Fig. 2 (left) shows I_Ca and corresponding fluorescence transients recorded during moderate Ca loading of the SR by a sequence of 10 pulses. For clarity, only pulses 1, 5, and 10 are shown. A shows control records, while B shows the loading of the same cell after ISO treatment. I_Ca was larger with ISO. I_Ca became progressively smaller and decayed faster from its peak as loading progressed in both control and ISO cases. However, the decay rate changed more within the first few pulses in the ISO case. The twitch [Ca]_i transient amplitude increased as loading progressed, but in the ISO case it also declined faster than in control.

Fig. 2 (right) shows the corresponding responses to caffeine after loading with 10 pulses. With the moderate total Ca influx during 10 pulses, the SR Ca load was higher in ISO (D vs. C), whether measured from the Ca transient or the integral of I_NaCaX. In this example, caffeine-evoked [Ca]_i increased during the interval in Na- and Ca-free solution. In most records, however, [Ca]_i was stable or decreased slightly during this period. On average, SR Ca content measured at the start of Na application was 0.916 ± 0.014 (SEM, n = 142) of the content at the peak of the [Ca]_i transient, which occurred 442 ± 56 ms (SEM) earlier. This slight loss of content was very similar in control, TG, and ISO conditions.

The effects of TG treatment on loading I_Ca and [Ca]_i transients were complementary to those of ISO. Although I_Ca still decayed faster with loading in TG-treated cells, the progression rate of this change was drastically reduced with TG. That is, the decay rate changed less after a given number of pulses after TG treatment than in control. Similarly, the [Ca]_i transient amplitude increased as loading progressed, but in the TG case this increase was smaller, and the loading transients were as a group smaller and decayed much more slowly with TG.

Decay of I_Ca and [Ca]_i Transients During Loading

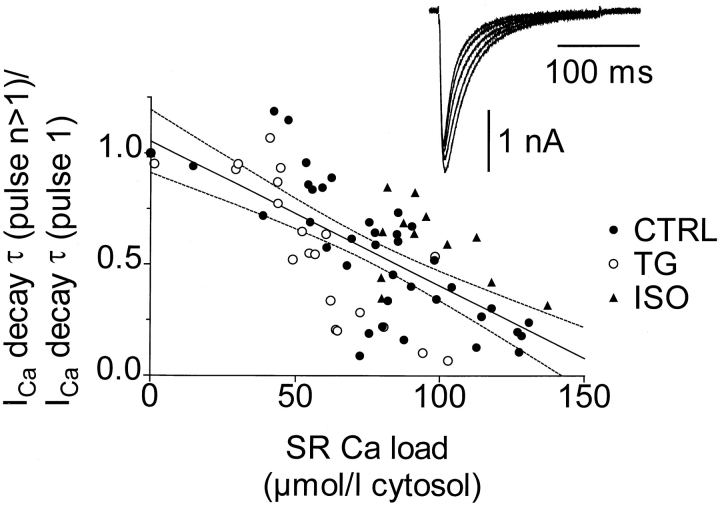
Fig. 3 shows that the I_Ca decay time constant τ (single exponential fit) shortened as SR Ca loading increased. This is presumably caused by Ca-dependent inactivation. For this illustration, τ values were measured for cells under each treatment at numbers of pulses where corresponding measurements of the SR Ca load were available. For example, the SR Ca load before the first loading pulse was 0, the load associated with pulse 2 was that measured after a single pulse, and so on. In a given cell, at each number of pulses, any repeated measurements of either I_Ca decay τ or SR load were averaged. The single regression line was fitted to all of the data. For this illustration, SR Ca loads were calculated using the Δ[Ca]_T method. I_Ca was larger and decayed faster with ISO (not shown), even before SR loading. This may explain why data points with ISO fell above the regression line (and conversely for TG).

Figure 3.

Decay time constant τ of Ca current (single exponential fit) shortened as SR Ca loading increased. τ was first measured for I_Ca at pulse 1, for which the previously existing SR Ca load was 0. τ was then measured for Ca currents evoked by 2, 3, 6, and 11 pulses, for which just previous SR Ca load measurements were available (at 1, 2, 5, and 10 pulses, respectively). τ was also measured for I_Ca evoked by 20 and 40 pulses, but since load measurements were not done at 19 or 39 pulses and the SR Ca load was close to steady state, the respective SR Ca load measurements for 20 or 40 pulses were those made just afterward. τ for the various numbers of pulses were normalized to τ of the first (0 load) pulse and plotted against the corresponding SR Ca loads. A single regression line was fitted to all the data.

Degree of SR Ca Pump Alteration by ISO and TG

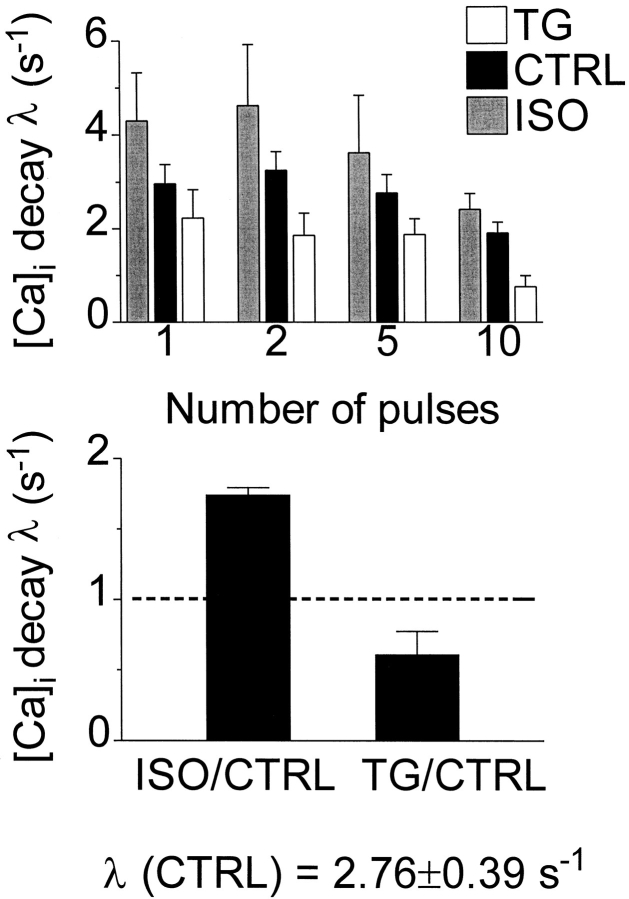
We selected conditions (ISO and TG application) either to stimulate or partially inhibit the SR Ca-ATPase rate. In Fig. 4, the relative changes in SR Ca pump rates are assessed by evaluating rate constants of twitch [Ca]_i decline under ISO and TG. These rate constants were calculated from half-decay times of fluorescence ratios (using λ = 1/τ = ln(2)/t _1/2). Fig. 4 A shows that the rate of [Ca]_i decline slowed with loading and was slower with TG and faster with ISO, relative to control. As each cell was studied successively under control and treatment, paired comparisons of the decay rate constants are appropriate. Fig. 4 B shows these comparisons for the five-pulse-loading case. Decay was 39 ± 16% (SEM, n = 5) slower in TG or 74 ± 5% (SEM, n = 5) faster in ISO. These changes in Ca transient decay rate correspond approximately with changes in the SR pump rate, since SR uptake is the dominant process reducing [Ca]_i during loading. We infer that the concentrations of TG and ISO we used nearly halved and nearly doubled, respectively, the SR Ca pumping rate.

Figure 4.

TG and ISO modulated the SR Ca pumping rate effectively. (top) Decay rates (λ = 1/τ = ln 2/t _1/2, where t _1/2 was obtained from straight line fits) for [Ca]_i transients during loading decreased with increasing number of loading pulses and were longer with TG or shorter with ISO than in control. (bottom) Paired comparisons of λ before and after treatment, 5-pulse loading. Decay was 74 ± 5% (SEM, n = 5) faster in ISO or 39 ± 16% (SEM, n = 5) slower in TG. SR uptake is the dominant process reducing [Ca]_i during loading.

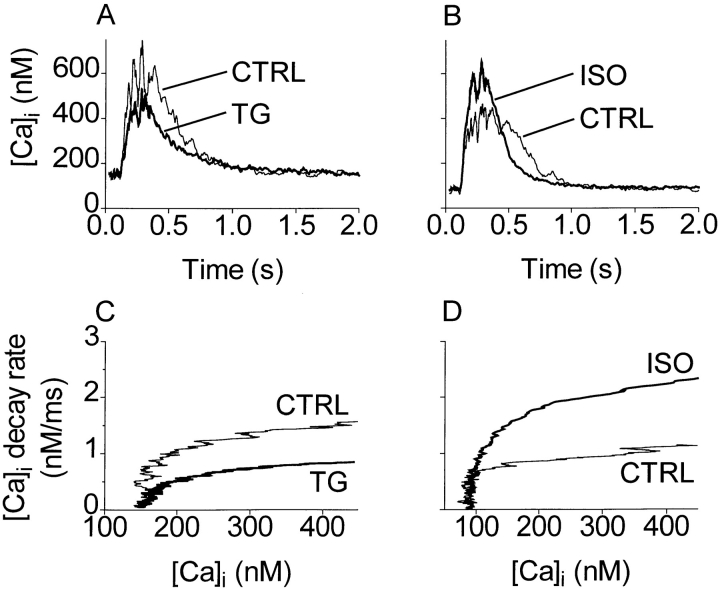
Changes in decay rate do not always indicate changes in SR Ca pumping properties, because the pump rate depends intrinsically on [Ca]_i. It may increase, as found by Bers and Berlin (1995) or decrease (as discussed further below). Fig. 5 shows that TG - and ISO-dependent decay rate changes were not artifacts of simultaneous changes in [Ca]_i. Fig. 5 (top) shows [Ca]_i transients recorded during the 10th loading pulse, with control and TG records from the same cell compared in A and control and ISO records from a different cell compared in B. Fig. 5 (bottom) shows how the decay rates of [Ca]_i depend on [Ca]_i. TG slowed the decay rate (C) and ISO sped the decay rate (D), relative to the respective rates in the control condition, for all [Ca]_i above rest.

Figure 5.

TG - and ISO-dependent rate changes were not artifacts of simultaneous changes in [Ca]_i. (A) Loading [Ca]_i transients, control and TG conditions, from one cell. (B) Loading [Ca]_i transients, control and ISO conditions, from another cell. Each transient was the last evoked in a 10-pulse sequence. (C and D) d[Ca]_i/dt as dependent on [Ca]_i corresponding with A and B, respectively. TG slowed the decay rate at all [Ca]_i above rest; correspondingly, ISO sped the decay at all [Ca]_i. Noise in the rate plots was reduced by fitting the decaying phase of each transient in A and B to a single exponential before differentiating.

[Ca]_i Changes during Loading

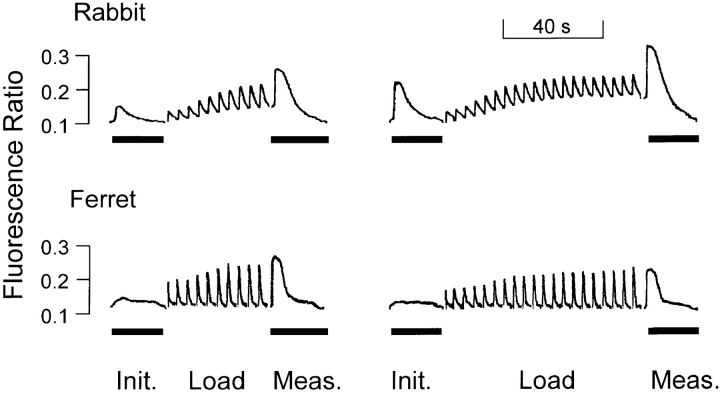
Ca entering the cell in Na-free conditions must distribute between the cytosol and the SR, although some may be transported into mitochondria or extruded by sarcolemmal Ca pumping. In Fig. 6, original records of fluorescence ratio show that diastolic [Ca]_i increases substantially during our loading protocol in a rabbit ventricular myocyte (representative of n = 4). A much smaller corresponding increase of diastolic [Ca]_i is apparent in the ferret, which was used for all analysis in this study. This greater recovery of [Ca]_i may be due to the unusually high sarcolemmal Ca-ATPase-dependent Ca removal flux in this species (Bassani et al., 1995a ). In fact, diastolic [Ca]_i increased in ferret myocytes during loading by only 0.12 ± 0.018 nmol/μmol added Ca, resulting in a typical increase of only 50 nM after moderate to large loadings. Sarcolemmal Ca extrusion or mitochondrial uptake may limit our ability to account for the fate of all entering Ca in SR or cytosol. However, the relatively small variations of diastolic [Ca]_i represent nearly constant driving conditions for the SR Ca pump, even with varying numbers of loading pulses and under control, ISO, or TG conditions. Further, the increase in [Ca]_i with loading, though small, means that sufficient Ca has entered cells to load the SR to maximal capacity.

Figure 6.

Diastolic [Ca]_i increases during loading in ventricular myocytes of both species, but less so in ferret than in rabbit. Original chart records of fluorescence ratio during execution of protocol in Fig. 1. Solid bars mark caffeine applications.

SR Ca Load Reaches a Maximum

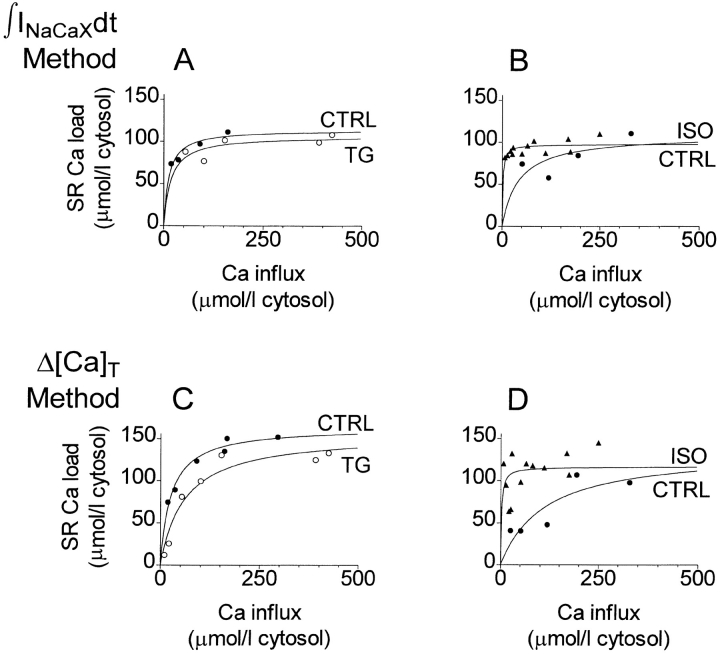
Fig. 7 shows how SR Ca loading depends on added Ca for two different cells recorded in ruptured patch with K₅-Indo, one treated with TG (A and C) and the other with ISO (B and D). The SR Ca content data were fitted to single-site binding (Michaelis-Menten) isotherms for descriptive purposes. In these single experiments, the maximal SR Ca contents, although different between cells, were unaffected by treatment: using the ∫I_NaCaXdt method, the SR Ca content was 114.7 ± 8.7 μmol·liter cytosol⁻¹ (control, 2 df) vs. 107.2 ± 9.3 (TG, 3 df, Fig. 7 A), and 108.4 ± 31.1 (control, 2 df) vs. 97.6 ± 3.0 (ISO, 10 df, Fig. 7 B). Using the Δ[Ca]_T method, corresponding values were 164.0 ± 6.8 μmol·liter cytosol⁻¹ (control, 4 df) vs. 156.2 ± 14.8 (TG, 5 df, Fig. 7 C), and 136.1 ± 47.5 (control, 3 df) vs. 116.4 ± 10.9 (ISO, 10 df, Fig. 7 D). The error tolerances represent the standard errors of the estimates of parameter B_max and are shown with the corresponding number of degrees of freedom in the fits.

Figure 7.

SR Ca content grows quickly with added Ca for small Ca influxes but reaches a limiting value below proportionality for large additions. Ruptured patch recording (K₅-Indo) from one cell treated with ISO (A and C showing ∫I_NaCaXdt and Δ[Ca]_T methods, respectively), and from a different cell treated with TG (B and D showing ∫I_NaCaXdt and Δ[Ca]_T methods, respectively). Symbols show individual measurements; solid lines show least squares fits to the purely descriptive function [Ca]_SR(total) = B_max/(1 + K _1/2/∫I_Cadt). B_max was practically unaffected by treatment (for values see text).

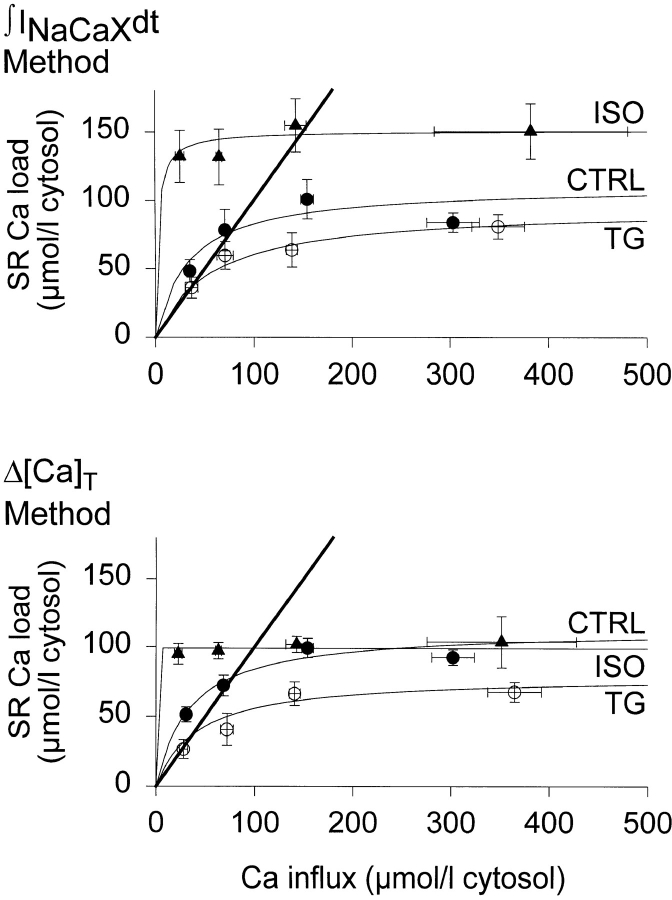
Fig. 8 A shows how the SR Ca load measured using the ∫I_NaCaXdt method depended on the cumulated amount of Ca added, for a set of several perforated patch experiments (n = 6, TG; n = 4, ISO). Fig. 8 B shows results from the same cells with SR Ca load measured from the increase in peak fluorescence (Δ[Ca]_T method) early during caffeine application. To show the data more clearly, observed loads were grouped within Ca influx ranges of 0–50, 51–100, 101–200, and >200 μmol·liter cytosol⁻¹, respectively.

Figure 8.

Composite data from several cells showing how SR Ca load saturated as cumulated amount of Ca added increased. (top) ∫I_NaCaXdt method (n = 6, TG; n = 4, ISO). (bottom) Peak fluorescence (Δ[Ca]_T) method (n = 6, TG; n = 4, ISO). For clarity, data points were grouped in influx ranges of 0–50, 51–100, 101– 200, and 201–500 μmol·liter cytosol⁻¹, but curves were fit to individual data. Parameters of fits appear in Table I. Heavy lines mark unity slope that would result if all added Ca were accounted for in the SR.

Fits to the purely descriptive function [Ca]_SR(total) = B_max/(1 + K _1/2/∫I_Cadt), presented as curves in Fig. 8 and as numeric values in Table I, were made to pooled raw (not grouped) data. Under control conditions, the fitted maxima were 110.4 ± 17.5 μmol·liter cytosol⁻¹ (n = 10, ∫I_NaCaXdt method) and 113.1 ± 8.3 μmol·liter cytosol⁻¹ (n = 8, Δ[Ca]_T method). Parameter K _1/2 is increased by TG and decreased by ISO. Although this K _1/2 does not measure a physical characteristic of the SR Ca-ATPase, it changes with TG or ISO, as would be expected from the corresponding changes in the pump's ability to compete for cytosolic Ca against the other Ca transport systems.

Table I.

Parameters of Fits Predicting Maximum SR Ca Load

		∫INa/Ca dt method				Δ[Ca]T method
		SR[Ca]max		K1/2		SR[Ca]max		K1/2
ISO		150.7 ± 14.9		2.8		98.9 ± 4.9		∼0
CTRL		110.4 ± 17.5		33.5		113.1 ± 8.3		34.9
TG		94.6 ± 16.6		56.6		78.7 ± 10.0		41.2

All values given in micromoles·liter cytosol⁻¹. 

Under the hypothesis that SR Ca loading is limited mainly by chemical potential and not by leakage, fitted SR Ca loads under all conditions must reach similar maxima. In Fig. 8 A, with the ∫I_NaCaXdt method, ISO increased B_max by 36% and TG decreased it by 14%. With the Δ[Ca]_T method ISO decreased B_max by 12.6% and TG decreased it by 30%. Although it is not possible to combine analytically the content measurements made by the two methods, the overall pattern of the curve fits is consistent with a modest increase under ISO treatment and a modest decrease with TG.

In Fig. 8, the loading clearly increased progressively as Ca influx increased, under each treatment condition. To measure TG or ISO effects, data from each experiment, under each condition, would ideally be fit separately and the parameters compared pairwise. However, the raw data had some scatter, and as a result load in some experiments did not increase monotonically with increasing influx, leaving individual fitting difficult. To reduce uncertainty, we therefore compared pairwise the absolute maximum loads in each cell, regardless of stimulation history, with and without TG or ISO treatment.

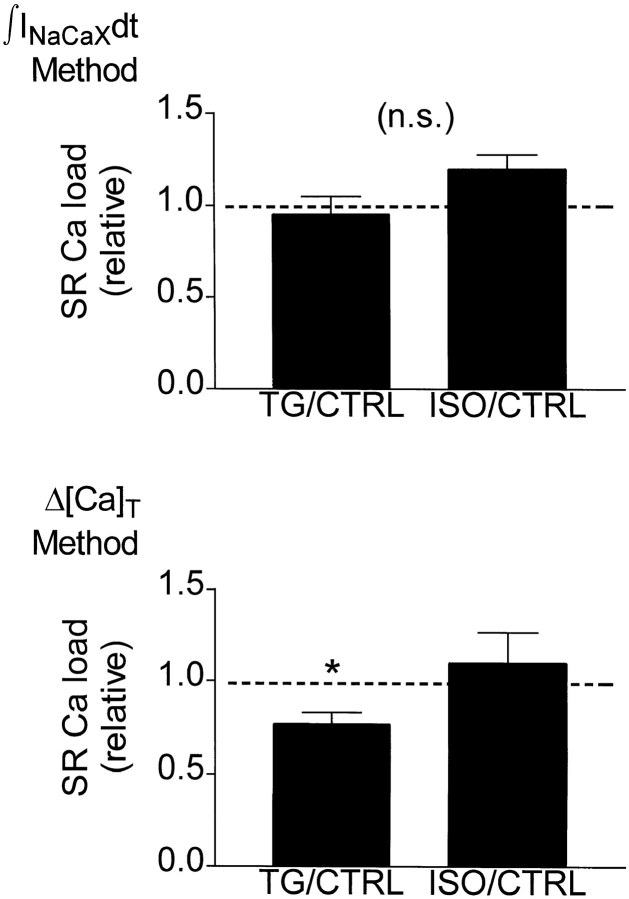
Fig. 9 shows how ISO and TG affected maximal SR Ca load. For illustration, loads under ISO and TG were normalized to the corresponding control loads in the particular cells. Absolute loads appear in Table II. Using the ∫I_NaCaXdt method, the SR Ca load with TG was 95.3% of control, and the load with ISO was 119.4% of control. The load with TG was 76.7% of the control load, while the load with ISO was 110.0% of control, using the fluorescence method. In paired t test comparisons of the loads (before normalization) before and after treatment, the deficit with TG was significant (P < 0.05, Δ[Ca]_T method only), but the increment with ISO was not (either ∫I_NaCaXdt or Δ[Ca]_T method). When maximum loads under TG and ISO treatment were compared (unpaired t tests before normalization, either method), the difference was also insignificant.

Figure 9.

Absolute maximum SR Ca loads, regardless of stimulation history, with and without TG or ISO treatment, were similar. (top) ∫I_NaCaXdt method; (bottom) Peak fluorescence (Δ[Ca]_T) method. *Load with TG was significantly lower (P < 0.05) in paired comparisons with control data. For illustration, maximum load with ISO or TG treatment was expressed as a fraction of the maximum load in same cell before treatment.

Table II.

SR Ca Load: Absolute Maxima and Relative Changes

		Δ[Ca]T method		∫INa/Ca dt method
		*SR[Ca]max		*SR[Ca]max		n
CTRL		124.2 ± 8.49		118.4 ± 14.82		6
TG		94.5 ± 9.10‡		108.3 ± 8.88		6
TG/CTRL		0.767 ± 0.062		0.953 ± 0.095		6
CTRL		110.4 ± 6.03		164.0 ± 27.46		4
ISO		118.8 ± 14.63		198.4 ± 37.67		4
ISO/CTRL		1.100 ± 0.169		1.194 ± 37.67		4

^*Values given in micromoles·liter cytosol⁻¹.  

^‡ P < 0.05. 

To clarify the paired comparisons, loads under control conditions are shown separately in Table II for cells later treated with ISO or with TG. As noted in the abstract and discussion, the average control load for all cells was 118.7 ± 5.8 μmol·liter cytosol⁻¹ (∫I_NaCaXdt method) or 136.7 ± 15.1 μmol·liter cytosol⁻¹ (Δ[Ca]_T method). We conclude from the data in Figs. 7–9 and Tables I and II that there were at most modest differences in maximum SR Ca load among ISO, TG, or control conditions. The main difference among conditions was in the number of pulses needed to reach maximum load, which corresponds with the K _1/2 values in Table I.

Model for Steady State SR Ca Loading Characteristics

A simple theoretical model may make clear how our experimental alterations in SR pump function would be expected to change maximal SR Ca content. In accord with the ability of the SR Ca-ATPase to translocate Ca bidirectionally with minimal dissipative loss (Makinose and Hasselbach, 1971; Takenaka et al., 1982; Feher and Briggs, 1984; Inesi and de Meis, 1988), pumping by the SR Ca-ATPase is assumed to behave as a reversible enzymatic reaction, in which the net pump rate V_pump is defined as (Segel, 1976; Shannon and Bers, 1997):

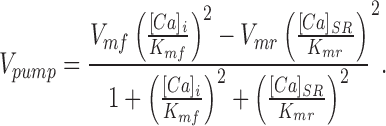1

In this equation, V_mf and V_mr are the forward and reverse maximum velocities, and K _mf and K _mr are the forward and reverse affinities, respectively. [Ca]_i and [Ca]_SR are the free Ca in cytosol and SR, respectively. If the pump reaches a thermodynamic steady state and there is no leakage, then the net flux V_pump is 0. We assumed, in accord with Takenaka et al. (1982), that the maximum possible forward and backward rates are equal; i.e., V_mf = V_mr ≡ V_m. This V_pump = 0 condition reduces Eq. 1 to K _mr/K _mf = [Ca]_SR/[Ca]_i.

Assuming that the SR pump can generate a maximum gradient ([Ca]_SR/[Ca]_i) of 7,000 in the absence of leak (based on data of Shannon and Bers, 1997), then K _mr = 7,000 · K _mf.

In intact cells, Ca must leak from the SR, and in steady state, V_leak = V_pump. Defining V_leak as an independent variable and substituting 7,000 · K _mf for K _mr, we can make Eq. 1 explicit for free [Ca]_SR:

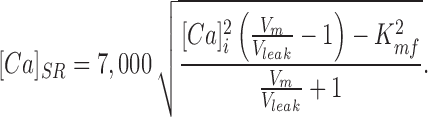2

Under control conditions, we assume V_m = 210 μmol·liter cytosol⁻¹·s⁻¹ and K _mf = 270 nM (Bassani et al., 1994a ). With the SR loaded, we found [Ca]_i = 150 nM, so that, in the absence of leak, [Ca]_SR = 1,050 μM.

The relationship between free [Ca]_SR and total SR Ca ([Ca]_SRT), determined predominantly by calsequestrin binding, is (Shannon and Bers, 1997):

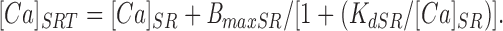3

Using for convenience [Ca]_SRT = 100 μmol·liter cytosol⁻¹, taking SR volume as 3.5% of the cytosolic volume (Page et al., 1971), and setting K _dSR = 600 μmol/ liter SR (Shannon and Bers, 1997), B_maxSR is calculated as 1.3 mmol/liter SR when binding is at thermodynamic equilibrium.

Addition of TG is simulated by a 50% reduction of both forward and reverse V_m, to 105 μmol·liter cytosol⁻¹·s⁻¹; i.e., a complete blockage of 50% of the pumps. ISO treatment is simulated by reducing both forward and backward K _m by 50% to 135 nM and 945 mM, respectively. This is in accord with data of Kirchberger and Wong (1978) and leaves the energy efficiency unchanged and the maximal gradient at 7,000.

Fig. 10 shows how maximum SR Ca load is expected to decrease with increasing leak rates, as predicted by Eqs. 2 and 3. In Fig. 10 A, the leak rate is expressed as a fraction of the forward pump rate. When leak is expressed this way, the loss in SR Ca content as leak rate increases is the same in control, TG, and ISO conditions. For instance, a loss of 25% of the SR Ca content requires a leak rate that is 59% of the forward rate, regardless of treatment condition. Under control conditions, this leak would be ∼15 μmol·liter cytosol⁻¹·s⁻¹, 50× as high as the value actually observed, 0.3 μmol·liter cytosol⁻¹·s⁻¹ (Bassani and Bers, 1995).

Figure 10.

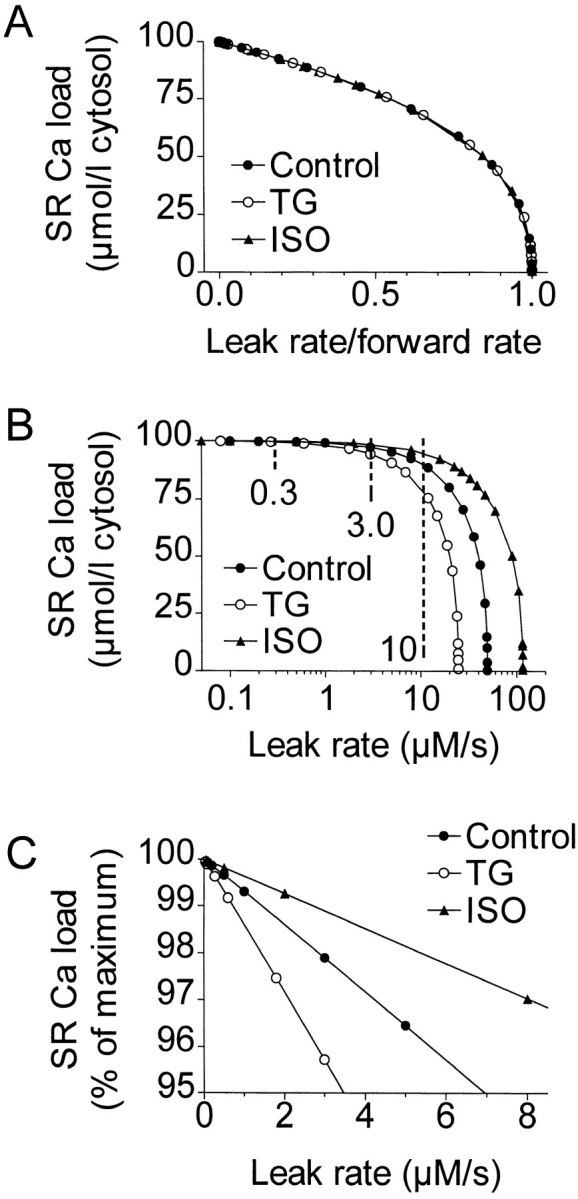
Model based predictions of changes in SR Ca load with TG or ISO due to leakage. Maximum SR Ca load decreases with increasing leak flux, but at the experimentally observed leak rate of 0.3 μmol·liter cytosol⁻¹ · s⁻¹, the effect is minor. (A) Loss of SR Ca load as leak is increased, with leak rate expressed as a fraction of forward pump rate. (B) Same, expressed using absolute leak rate, log scale. (C) Normalized and expanded version of B. The forward pump rate stays relatively constant as V_leak increases, but the reverse rate decreases, maintaining V_forward − V_reverse − V_leak = 0.

SR Ca content relative to absolute leak rate is shown in Fig. 10 B. For each condition, the model is defined at leak rates up to the forward pump rate, at which the SR Ca content is 0. Fig. 10 B shows that for a given leak rate, the calculated steady state SR Ca content is higher with ISO and lower with TG, compared with control. At the physiological leak flux, 0.3 μmol·liter cytosol⁻¹·s⁻¹, TG, or ISO treatment are predicted to leave the SR Ca content virtually unchanged. Even with a leak flux 10× higher (3 μmol·liter cytosol⁻¹·s⁻¹), there is only a modest variation in SR Ca load, and it is not until the leak is 30–50× the observed value, well beyond the physiological range, that the model predicts substantial changes. Fig. 10 C shows an expanded view of the likely physiological range of leak flux. Even with a leak of 3 μmol·liter cytosol⁻¹·s⁻¹, the SR Ca content remains 95% of maximum.

Reverse pump flux is critical to the model. Since in the steady state, V_forward − V_reverse − V_leak = 0, V_leak = V_forward must hold in the absence of reverse flux. In fact, to obtain a total [Ca]_SR of 100 μmol·liter cytosol⁻¹ with a model neglecting V_reverse, V_leak would need to be 63.7 μmol/liter cytosol⁻¹·s⁻¹, an unreasonable amount, inconsistent with observation.

discussion

SR Ca Content Reaches a Limit

Using a cumulative loading protocol, we saw that under control conditions SR Ca content in ferret ventricular myocytes reached a maximum that we estimated as 118.7 ± 5.8 μmol·liter cytosol⁻¹ from ∫I_NaCaXdt measurements and 136.7 ± 15.1 μmol·liter cytosol⁻¹ from Δ[Ca]_T (fluorescence) measurements. The steady state load in the SR must be determined by a balance among influx and efflux pathways that include both conservative (forward and reverse pumping) and dissipative (pump slippage and/or pump-independent leak) pathways (Inesi and de Meis, 1988). When TG slowed the SR Ca-ATPase pump rate by 39 ± 16% or ISO increased the rate by 74 ± 5%, the perturbations in maximum SR Ca load were systematically smaller. These minor perturbations are consistent with a minimal influence of dissipative losses on SR Ca content.

Origin and Amount of Leak Flux

Under steady state SR Ca loading, influx and efflux of Ca from the SR are equal. The maximal SR Ca load could be set by the limiting chemical potential gradient of free [Ca] between luminal and cytosolic compartments, ΔG_ATP = 2RT ln ([Ca]_SR/[Ca]_i), but some Ca must leak from the SR through the ryanodine receptors, dissipating the SR Ca gradient. Experimentally, the question of whether enough Ca leaks from the SR in intact myocytes to reduce the steady state SR Ca load below the chemical potential-dependent limit can be answered by perturbing the SR Ca uptake rate. If leakage, rather than reverse pumping, is the dominant factor opposing forward pumping (SR uptake), steady state SR Ca load will change when the forward rate is perturbed as we have done.

Leakage from the SR may be due to infrequent spontaneous openings of ryanodine receptors, which are manifest as Ca sparks (Cheng et al., 1993). The rate of spark occurrence is consistent with the low leak rate observed by Bassani and Bers (1995). Some dissipative loss of Ca from the SR could also result from normal slippage of the Ca-ATPase (Wolosker and de Meis, 1985).

If the leak flux from the maximally loaded SR of ferret cells is comparable to the flux measured directly in rabbit and rat ventricular cells with a normally loaded SR, 0.3 μmol·liter cytosol⁻¹·s⁻¹ (Bassani and Bers, 1995), then modifying the SR pump rate with ISO or TG should hardly perturb the maximum SR Ca content at all. Considering the data at varying loads, we found that perturbations were very minimal in particular cells (Fig. 7), though readily detectable in the fits to the pooled data (Fig. 8). In the data at absolute maximum loads, the finding of significant variations in load depended on the particular method and statistical test used (see Fig. 9, legend). In summary, leak rates in our cells may have been several times higher than observed previously, but they are not comparable to the forward rate. This supports the idea that backflux, rather than leak, mainly limits SR loading.

Using [Ca]_i transient decay data, Balke et al. (1994) calculated a much larger SR leak flux in rat ventricular myocytes, 18 μmol·liter cytosol⁻¹·s⁻¹, than did Bassani and Bers (1995). The model of Balke et al. (1994) considered the forward SR uptake rate to be balanced entirely by leakage, not pump-mediated backflux.

How Ca Influx from Outside the Cell Affects SR Ca Loading

All Ca added to a cell must distribute among cytosolic, SR, and mitochondrial compartments or be extruded. Initially, nearly all Ca added to the cell goes into the SR. This corresponds with the lines of unity slope on Fig. 8. The SR Ca content reaches a limiting value below proportionality for large additions. It is not surprising that almost all Ca initially enters the SR, since the SR Ca-ATPase is the transporter of highest capacity and its most effective competitor, the Na/CaX, is inoperative. As the SR fills progressively, the net uptake rate will decline as reverse flux increases (see Fig. 4 and Eq. 1; Shannon et al., 1997). Then, more of the entering Ca is transported by the slow systems; e.g., mitochondria and the sarcolemmal Ca-ATPase. This may account for the deviation below unity slope in Fig. 8 as load increases.

Mitochondria may sequester some of the Ca that does not end up in the SR or cytosol. However, we have recently measured SR Ca content in rabbit myocytes using the same protocol described here, and could discern no difference in experiments done with and without a mitochondrial Ca uptake blocker, RU360, a kind gift of Dr. Abdul Matlib, University of Cincinnati (Cincinnati, OH; unpublished observations). Even in cells having substantial SR Ca loads and both SR Ca uptake and Na/CaX-mediated Ca extrusion blocked, redistribution of Ca into mitochondria appears very minimal, although detectable (Bassani et al., 1994a ).

Some Ca will be extruded on the sarcolemmal Ca pump. We have predicted the cumulated sarcolemmal pump-mediated Ca efflux during loading over the duration (80 s) of the 20-pulse sequences in Fig. 6. From [Ca]_i, measured at each sample point, and using sarcolemmal Ca pump parameters estimated by Bassani et al. (1994a , 1995a) for rabbit and ferret myocytes, we calculated an integrated Ca efflux of 45–100 μmol·liter cytosol⁻¹. Cumulated sarcolemmal pump extrusion seems only partially to explain the fate of Ca, which enters neither SR nor cytosol at high cumulative loads. However, slow Ca efflux via this route does have the capacity to maintain low diastolic [Ca]_i even with Na absent and SR function suppressed (Lamont and Eisner, 1996). SL Ca efflux could be accelerated manyfold by calmodulin or by ISO-mediated PKA activation (Dixon and Haynes, 1989). If this happened, we might not detect increases in SR pumping capacity (and hence loading) with ISO. Since initial Na-free caffeine-induced [Ca]_i transients do not decay any faster with ISO present (see Fig. 2, legend), SL pumping may already be at maximum under control conditions.

Although we cannot trace the fate of all admitted Ca in our cells, we do not believe any other cytosol-related processes have worked to limit SR loading in our experiments. In the ruptured patch experiments, the patch pipette also sinks Ca from the cell cytoplasm. This loss appears insignificant, as SR Ca contents measured in ruptured and perforated patch experiments were close. Ca efflux on an active Na/CaX could limit SR loading, but our use of Na-free solutions eliminates this possibility (contrast Ginsburg and Bers, 1996; Trafford et al., 1997; Bassani et al., 1995c ) and so better drives the cells toward a maximal SR Ca load.

With ISO treatment, the SR Ca content often exceeded the Ca influx as measured by ∫I_Cadt; that is, it fell above a line of unity slope in Fig. 8, particularly for small influxes. One possible explanation is leakage of Ca into the cell (Lamont and Eisner, 1996). SR Ca reloading without stimulation has been seen previously (Trafford et al., 1997), but is not expected in the absence of internal Na. In a 30-pl cell, each picoampere of leakage carried by Ca would add 0.16 μmol·liter⁻¹·s⁻¹ to the total cell Ca content. For a worst-case 40-pulse loading sequence of duration 160 s, 1 pA could increase the SR Ca content by ≈23 μmol·liter cytosol⁻¹ in the absence of removal processes (see Eq. 1). Under low Ca loading conditions, the SR Ca pump can compete quite effectively with other Ca transport processes, especially when K _m is reduced by ISO. For example, with external Ca absent, the SR can recover Ca from mitochondria without raising [Ca]_i (Bassani et al., 1993).

Another possible explanation for the supralinear Ca content in ISO is potential Ca loading via Na/Ca exchange. Since K was absent, Na entering cells during caffeine/Na measurements of load via I_NaCaX was not rapidly extruded via the sarcolemmal Na/K-ATPase. In a typical caffeine/Na record, 100 μM Ca was extruded by I_NaCaX, which could correspond to 0.3 mM Na gain/ trial. Even this small growth of [Na]_i would, however, be opposed by ongoing Na/H exchange (since external Na is absent except during the short periods that caffeine-induced I_NaCaX flows) and by diffusion into the patch pipette. This maximum change in [Na]_i would also not be expected to significantly activate Ca entry via Na/Ca exchange because the exchanger's K _m for Na is 30 mM (Reeves and Philipson, 1989).

Decline of I_Ca and Increase of [Ca]_i

Larger SR Ca loads corresponded with a faster I_Ca decline. We infer that this was caused by Ca-dependent inactivation after SR Ca release since the SR is a major source of inactivating Ca (Sham et al., 1995; Grantham and Cannell, 1996; Sipido et al., 1995). SR Ca load was a good predictor of the fractional decline of τ during successive loading pulses, since increased loads lead to greater fractional Ca release. Ca admitted via I_Ca would also be expected to enhance I_Ca inactivation, as was seen by Hadley and Hume (1987) and Yuan and Bers (1995). Between no-load and maximum-load conditions, resting [Ca]_i increases, though variable, were on average 50 nM. This gradual increase in the average [Ca]_i may have enhanced [Ca]_i-dependent I_Ca inactivation and limited peak I_Ca as load progressed (Fig. 2). We assume that the I_Ca inactivation at pulse 1 (with no SR Ca load) was almost entirely due to Ca influx through the Ca channel. Since I_Ca decline was accelerated four- to fivefold with SR Ca loading (Fig. 3), we infer that ∼75% of the Ca-dependent inactivation is due to SR Ca release. Together, these observations suggest that Ca originating from I_Ca, SR Ca release, and average diastolic [Ca]_i all contribute to Ca-dependent inactivation.

Comparison with Previous Measures of SR Ca Content

Our estimates of the SR Ca load (either ∫I_NaCaXdt or Δ[Ca]_T method) agree well with most previous estimates. Our preliminary Na/Ca exchange–based estimate in ferret, which was based on steady state loading in Na-containing solutions was somewhat higher (170 μmol·liter cytosol⁻¹; Ginsburg and Bers, 1996). In saponin-treated ferret ventricular muscle strips, maximal SR Ca content with [Ca]_i = 100 nM was 260 μmol·liter cytosol (Kawai and Konishi, 1994). Previous ∫I_NaCaXdt-based estimates have varied somewhat with the species used (rat: 185 μmol·liter⁻¹ cytosol, Varro et al., 1993; 115 μmol·liter cytosol⁻¹, Terraciano and MacLeod, 1997; 169 μmol·liter cytosol⁻¹, Diaz et al., 1997; rabbit: 87 μmol·liter cytosol⁻¹, Delbridge et al., 1996; guinea pig: 58.8 μmol·liter cytosol⁻¹, Terraciano and MacLeod, 1997). Our fluorescence-based content measures are quite comparable with other fluorescence-based measures from our own laboratory in ferret (91 μmol·liter cytosol⁻¹; Bassani et al., 1995c ), rat (114 μmol·liter cytosol⁻¹; Bassani and Bers, 1995), and rabbit (106 μmol·liter cytosol⁻¹; Bassani and Bers, 1995). For comparison, these measurements have been adjusted where needed to refer to nonmitochondrial cell volume (Page et al., 1971); however, not all previous measurements were made under conditions that maximized loading.

We combined both ∫I_NaCaXdt and Δ[Ca]_T methods, for which calculations differ somewhat, to evaluate SR Ca load. The initial exposure to caffeine in 0 Na/0 Ca solution is valuable in the Δ[Ca]_T method because it prevents snubbing of the peak of the [Ca]_i transient (Bassani et al., 1994a ). A minor potential disadvantage of the ∫I_NaCaXdt procedure is that any removal of Ca by the sarcolemmal Ca-ATPase (possibly boosted during ISO treatment) will have progressed somewhat by the time Na is added. We found, however, that the average loss of SR Ca content between peak [Ca]_i and the start of Na application was under 10% in each condition.

Modeling

Backflux via the SR Ca pump (Inesi and de Meis, 1988; Takenaka et al., 1982; Feher and Briggs, 1984) is an essential feature of our SR loading model, which has not been included in previous related models (Negretti et al., 1993; Balke et al., 1994). It allows us to explain the apparent disparity between previous measurements of forward pumping (Sipido and Wier, 1991; Balke et al., 1994; Bassani et al., 1994a ) and backward leak fluxes (Kawai and Konishi, 1994; Bassani and Bers, 1995).

Physiological Implications

Some implications of a limiting SR Ca load have been discussed previously (Bassani et al., 1995c ). As SR Ca content increases, the fraction that is free [Ca]_SR increases, amplifying the inotropic tendency of increased loads. A limit to loading mitigates this factor, providing an additional control point that may help to optimize twitch force so as to maintain efficient excitation–contraction coupling.

Ca leak from the SR can be presumed to increase with increasing SR Ca load (Bassani and Bers, 1995) as Ca spark frequencies increase when SR Ca load is increased; e.g., by high external [Ca] or ISO treatment (Cheng et al., 1993; Gómez et al., 1996; Satoh et al., 1997). Leak may increase in proportion to the SR Ca content (rate constant 0.0027 s⁻¹ or 16% min⁻¹, Bassani and Bers, 1995; 0.005 s⁻¹, Kawai and Konishi, 1994). However, as we noted in the introduction, rat myocytes undergo spontaneous SR Ca release at high SR loads (Cheng et al., 1996; Diaz et al., 1997), indicating that leak from the SR, and hence [Ca]_i, may increase disproportionately with increasing SR Ca load. [Ca]_i might then reach triggering threshold more often during random fluctuations. It is somewhat surprising that we seldom saw spontaneous SR Ca release or waves in these ferret cells even as they approached the maximum SR Ca load. This might be related to the particularly strong sarcolemmal Ca-ATPase in ferret ventricular myocytes (Bassani et al., 1995a ).

A potentially important pathophysiological implication of our results is that ΔG_ATP changes due to energetic compromise in ischemia or heart failure would reduce the maximal SR Ca load. Any loss of the maximal [Ca]_SR/[Ca]_i gradient would reduce both the amount of SR Ca available for release and the fraction of that Ca released (Bassani et al., 1995c ). These factors could thus contribute to systolic cardiac dysfunction in various pathophysiological states.