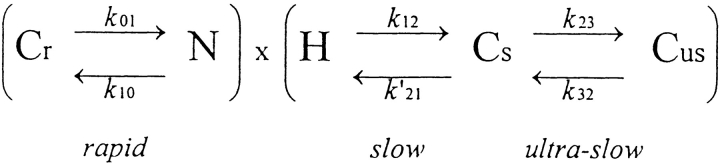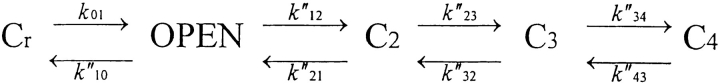Idiosyncratic Gating of HERG-like K⁺ Channels in Microglia

Abstract

A simple kinetic model is presented to explain the gating of a HERG-like voltage-gated K⁺ conductance described in the accompanying paper (Zhou, W., F.S. Cayabyab, P.S. Pennefather, L.C. Schlichter, and T.E. DeCoursey. 1998. J. Gen. Physiol. 111:781–794). The model proposes two kinetically distinct closing pathways, a rapid one favored by depolarization (deactivation) and a slow one favored by hyperpolarization (inactivation). The overlap of these two processes leads to a window current between −50 and +20 mV with a peak at −36 mV of ∼12% maximal conductance. The near absence of depolarization-activated outward current in microglia, compared with HERG channels expressed in oocytes or cardiac myocytes, can be explained if activation is shifted negatively in microglia. As seen with experimental data, availability predicted by the model was more steeply voltage dependent, and the midpoint more positive when determined by making the holding potential progressively more positive at intervals of 20 s (starting at −120 mV), rather than progressively more negative (starting at 40 mV). In the model, this hysteresis was generated by postulating slow and ultra-slow components of inactivation. The ultra-slow component takes minutes to equilibrate at −40 mV but is steeply voltage dependent, leading to protocol-dependent modulation of the HERG-like current. The data suggest that “deactivation” and “inactivation” are coupled through the open state. This is particularly evident in isotonic Cs⁺, where a delayed and transient outward current develops on depolarization with a decay time constant more voltage dependent and slower than the deactivation process observed at the same potential after a brief hyperpolarization.

introduction

In the previous paper (Zhou et al., 1998), we described in a microglial cell line, MLS-9, a K⁺ conductance resembling that generated by the human ether--à-go-go- related gene (HERG)¹ in most respects. Two notable differences include an almost complete absence of outward current during depolarizing pulses in symmetrical K⁺ salines and the existence of very slow gating around −40 mV. Here we describe a simple kinetic model that describes the data reasonably well.

The model postulates two kinetically distinct closing pathways, one favored by hyperpolarization leading to closed states that equilibrate slowly with the open state, and the other favored by depolarization that equilibrates rapidly with the open state. Because the slowly equilibrating closed states behave like classical absorbing inactivated states, it is convenient to consider these channels to be in a resting state at depolarized potentials and to activate and then inactivate upon hyperpolarization. Overlap in the voltage dependence of these two closing pathways leads to a standing window current between −50 and +20 mV that may be important for microglial biology. In addition, equilibration of inactivated states appears to take minutes at potentials around the peak of the window current yet occurs much more rapidly at more positive and negative potentials. This gating behavior leads to steady state levels of HERG-like current that are not simply voltage dependent but also dependent on prior voltage history. Our model thus predicts that oscillations in microglial membrane potential can have frequency- or use-dependent effects if the frequency of oscillation is faster than the slow gating steps (see MacDonald et al., 1991; Jassar et al., 1993).

The predictions of our sequential model are contrasted with those of an uncoupled model that assumes independent activation and inactivation. Although such a model can account for steady state behavior and rapid gating of the current, under certain conditions the two models diverge and the experimental data supports the coupled sequential model. This is particularly evident in isotonic Cs⁺, where a delayed and transient outward current develops on depolarization with a decay time constant more voltage dependent and slower than the deactivation process observed at the same potential after a brief hyperpolarization.

We also compare our model to another coupled sequential model developed recently by Wang et al. (1997) to describe gating of HERG channels expressed in oocytes. Although steady state inactivation appears similar in the two models, steady state activation in oocytes appears to have a half-maximal potential that is 40 mV more positive. This difference accounts for the substantially greater outward current component observed in symmetrical K⁺ salines with HERG expressed in oocytes compared with the HERG-like current in microglia. A hybrid model constructed with activation kinetics modified to generate a 40-mV shift in the voltage– activation curve and inactivation kinetics identical to the model of Wang et al. (1997) predicts steady state currents that overlap reasonably well with our observed data. However, this hybrid model does not predict the observed slow gating phenomena such as hysteresis in the availability curves.

materials and methods

Experimental results.

Experimental results reported here were obtained with the same cells and experimental techniques described in the previous paper (Zhou et al., 1998).

Simulations.

The simulated responses were generated using a commercially available software package called Axon Engineer (Aeon Software, Madison, WI). Details are described elsewhere (Pennefather and DeCoursey, 1994).

Theory

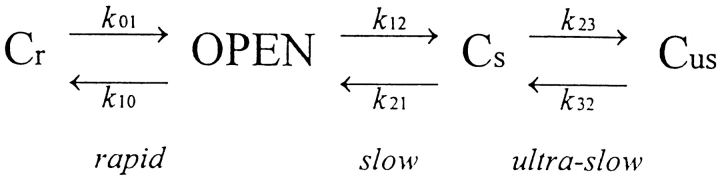
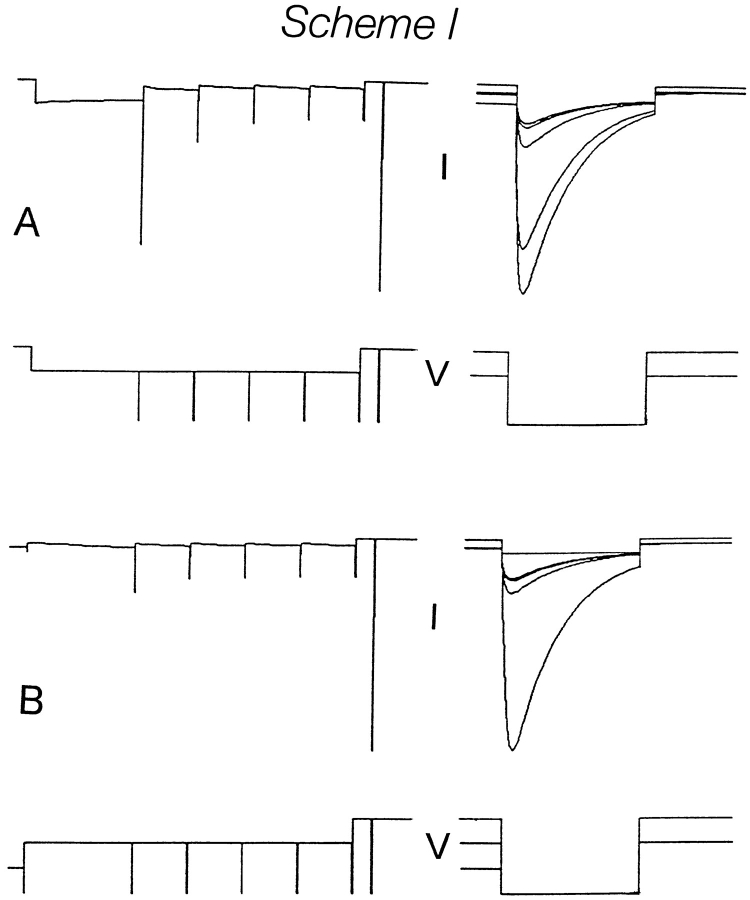
Various terminologies have been used to describe HERG and HERG-like K⁺ currents. In describing our results (Zhou et al., 1998), we define activation as the fast onset of current with hyperpolarization, and inactivation as the slower closing that follows this opening. The term, deactivation, is used to describe the fast closing that occurs at depolarized potentials. We will show below that our data is well described by Scheme SI. Scheme SI postulates two kinetically distinct pathways of channel closing: a rapidly equilibrating pathway leading to C_r, a closed state favored by depolarization, and a slowly equilibrating pathway leading sequentially to slowly and ultra-slowly equilibrating closed states (C_s and C_us) favored by hyperpolarization. At −80 mV, most of the channels reside in the slowly gating closed states that behave functionally like inactivated states. On depolarization after inactivation, they revert back to the open state from which they rapidly deactivate to state C_r. As a result, little or no tail current is generated during the depolarizing pulse. However, on repolarization, those channels that have had an opportunity to convert to state C_r activate rapidly before slowly converting back to state C_s.

Scheme I.

In showing that Scheme SI adequately describes our data, we have not engaged in systematic parameter optimization strategies. Rather, we have simply used our experimental data to suggest approximate values for the rate constants and their voltage dependence and have shown that these nonoptimized parameters predict responses that are close to what are observed. The rate constants used in our simulations of Scheme SI and the experimental measurements used in constraining them are listed in Table I. The rate constants k ₀₁, k ₁₀, k ₁₂, and k ₂₁ are anchored by current relaxations at a voltage range where the model predicts that the major determinant of the current relaxation after a voltage jump is one of those rate constants. The voltage dependence of the change in measured time constant of the current relaxation in that voltage range (determined as described in Zhou et al., 1998) is used to extrapolate the rate constant into ranges of potential where the particular rate constant is not the prime determinant of gating kinetics.

Table I.

Rate Constants Used in Simulation of Schemes I–III

Scheme SI (coupled model)

k 01 = 110 exp[−1.0(F/RT) (V + 120)] s−1

(τact, −120 to −80 mV; see Fig. 7, Zhou et al., 1998)

k 10 = 66/{1.0 + exp[−0.70(F/RT) (V + 20)]} s−1

(τtail, −20 to 80 mV; see Fig. 7, Zhou et al., 1998)

k 12 = 10 exp[−1.5(F/RT) (V + 120)] s−1

(τi, −120 to 80 mV; see Fig. 8, Zhou et al., 1998)

k 21 = 4 exp[1.0(F/RT) (V − 40)] s−1

(τrecovery, 40 to 0 mV; see Fig. 8, Zhou et al., 1998)

k 23 = 0.005 exp[−1.7(F/RT) (V + 30)] s−1

(use dependent inactivation, hysteresis)

k 32 = 0.005 exp[3.0(F/RT) (V + 30)] s−1

(use dependent recovery, hysteresis)

Scheme SII (independent model)

k 01, k 10, k 12, k 23, k 32 (same as Scheme I)

k′21 = 4 exp[1.0(F/RT) (V) s−1

Scheme SIII (modified from Wang et al., 1997)

k 01 (same as Scheme I)

k″10 = 2*30.8266 exp[0.64(F/RT) (V)] s−1

(double values uses by Wang et al., 1997)

(All other rate equations shifted by −5 mV)

k″12 = 0.0689 exp[−1.1(F/RT) (V + 5)] s−1

k″21 = 13.733 exp[1.0(F/RT) (V + 5)] s−1

k″23 = 36.778 s−1

k″32 = 23.761 s−1

k″34 = 47.002 exp[−1.6(F/RT) (V + 5)] s−1

k″43 = 22.348 exp[0.3(F/RT) (V + 5)] s−1

V is membrane potential in millivolts, F is Faraday's constant, R is the gas constant, T is temperature. 

The information enclosed in brackets beside the rate equations listed in Table I indicate the relaxation time constant, the range of potentials, and the data set used to define the rate equations. These first four rate constants (k ₀₁, k ₁₀, k ₁₂, k ₂₁) are the prime determinants of gating observed with standard protocols used to define activation and deactivation (see Fig. 2 A), and inactivation and recovery from inactivation (see Fig. 2 B) of the HERG-like current. The rate constants of ultra-slow inactivation are based on the hysteresis observed in measuring normal inactivation. These rates, k ₂₃ and k ₃₂, were established by adjusting them so that simulated results roughly matched the experimental observations.

Figure 2.

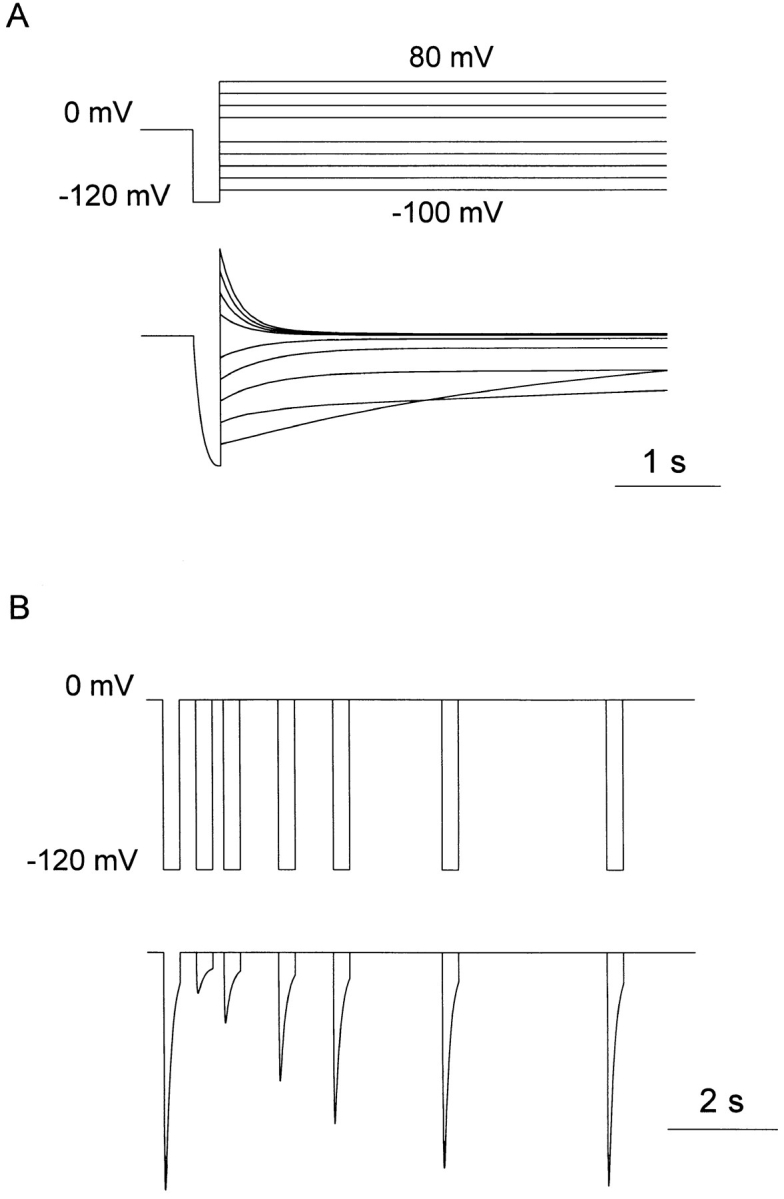
(A) Simulation of the experiment illustrated in Fig. 5 A of Zhou et al. (1998). A brief 25-ms step from a holding potential of 0 to −120 mV is followed by 500-ms steps to test potentials that increased in 20-mV increments from −100 to +80 mV (omitting 0 mV). (B) Simulation of the experiment illustrated in Fig. 7 of Zhou et al. (1998). A 300-ms step from 0 to −120 mV is followed at increasing intervals by an identical test step. The recovery of the response to the second step reflects recovery from inactivation.

For comparison, we have considered a gating model (Scheme SII) in which deactivation and inactivation are independent. In that case, the open probability is defined as the product of the proportion of channels that are neither deactivated (N) nor inactivated (H) and the time course of current relaxation at a particular potential reflects whichever transition process is rate limiting at that potential.

Scheme II.

We use the same rate equations to define Scheme SII as Scheme SI, except that k ₂₁ is shifted by 40 mV to compensate for the lack of coupling between activation and inactivation implicit in Scheme SI, giving k′₂₁ (see Table I). The appropriateness of this modification is shown in Fig. 1, where the steady state proportions of inactivated, open, and deactivated channels predicted by Schemes I–III are plotted. The shift in k ₂₁ to k′₂₁ in Scheme SII allows the curve describing steady state inactivation to superimpose almost exactly with the curve predicted by Scheme SI.

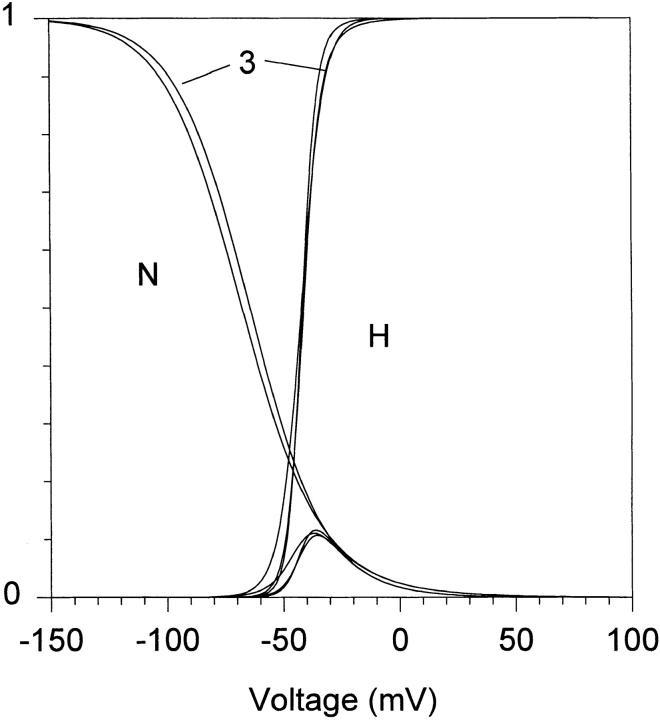
Figure 1.

Simulation of steady state inactivation, activation, and deactivation predicted by the three kinetic schemes. The curves that decline with depolarization represent the proportion of channels (N) that at steady state are open, in the absence of inactivation. The curves that ascend represent the proportion of channels (H) that at steady state are not in inactivated (C_s states), and are available to open. The bell-shaped curves, which are significant between −50 and +20 mV, represent the steady state open probability that is manifested as window current. The lines leading from the numeral 3 point to curves predicted by Scheme SIII.

Scheme SIII is based on kinetic parameters derived by Wang et al. (1997) to describe HERG currents expressed in Xenopus oocytes. The behavior of HERG-like currents in microglia could be mimicked with fairly minor adjustments to their parameters, with the exception of the opening rate k ₀₁. Apparently, the steady state activation curve is shifted negatively ∼40 mV in microglia, primarily as the result of a slower and more voltage-dependent activation rate. Scheme SIII thus incorporates our value for the activation rate constant k ₀₁. This hybrid model predicts steady state behavior similar to that of the other two models (Fig. 1).

Scheme III.

The rate equations describing this scheme are listed in Table I.

results

The simulations illustrated in Fig. 2 A are driven by the same protocol used to obtain the data in Fig. 5 A of Zhou et al. (1998). The K⁺ conductance was activated by a brief pulse to −120 mV from holding potential, V_hold = 0 mV, followed by a step to a range of potentials. The test current at most potentials decayed rapidly as channels closed, in terms of our model, predominantly into state C_r. The time constant of decay, τ_tail, was moderately voltage dependent, becoming faster at large positive potentials. At moderately negative potentials, the current no longer decayed completely, consistent with a window current existing in this voltage range. At larger negative potentials, the current decayed anomalously slowly, and the simulations show that this is due to channels entering the inactivated or slowly equilibrating C_s states, rather than the C_r or resting state. The turn-on of current during the brief hyperpolarizing step defines τ_act, this becomes faster as the hyperpolarizing step is made more negative, but the size of the outward tail seen upon repolarization is not increased since activation is maximal by −120 mV (data not shown).

Figure 5.

Simulation of history dependence of availability. Scheme SI predicted results (A and B) that were quite similar to those shown in Fig. 4, E and J, respectively. On the left, the full protocol is shown, while on the right the responses to the test pulses are superimposed and plotted on an expanded time base. The voltage commands are plotted below the current traces. In A, V_hold = 0 mV. After a 60-s step to −40 mV, availability is tested by a 300-ms step to −120 mV. This test step is repeated four times at 30-s intervals. The membrane voltage is then returned to 0 mV, and 10 s later a command to −120 mV measures maximal availability. In B, V_hold = −80 mV. Again, after 60 s at −40 mV, availability is tested by a 300-ms step to −120 mV, which is repeated four times at 30 s intervals. The membrane voltage is then returned to 0 mV, and 10 s later a command to −120 mV measures maximal availability.

The simulations illustrated in Fig. 2 B are driven by the protocol used to generate the data in Fig. 7 of Zhou et al. (1998). A hyperpolarizing pulse to −120 mV from 0 mV is paired with a second pulse of the same type with an incrementing interval. The decline of the current during the 300-ms hyperpolarizing pulse reflects inactivation of the channels that activated rapidly after the voltage step. The time constant of this inactivation (τ_i) increases with hyperpolarization and at −120 mV is determined primarily by k ₁₂. That the channels are inactivated in the classic sense defined by Hodgkin and Huxley (1952) and not simply resting is demonstrated by the fact that little current can be activated by the second hyperpolarizing pulse after short delays. The time constant of recovery from inactivation (τ_recovery) is monitored by the increase in activatable current with increasing delays between the paired pulses. At 0 mV, this recovery time course is dominated by k ₂₁.

Figure 7.

Simulation of hysteresis in measurement of quasi– steady state inactivation and window currents (Fig. 4 of Zhou et al., 1998) using Schemes I and III. The entire experimental voltage pulse sequence is condensed (top), and the calculated responses for Schemes I and III are plotted in A and B, respectively. The responses to the test pulses are plotted in the positive direction as open probabilities rather than inward currents, as in the real data. The smaller, slowly changing current between these responses gives rise to the “window” current. (C) The peak open probabilities “measured” in the simulated experiment in A are plotted in the same way the real data were plotted (Fig. 4 C of Zhou et al., 1998). In the illustrated sequence in A, V_hold was initially 40 mV and was made progressively more negative (□). The reverse sequence in which V_hold was made progressively more positive, starting as −80 mV, is also shown (•). The curves show Boltzmann fits, with fitted parameters V _1/2 = −44.1 mV and k = 6.56 mV (□), and V _1/2 = −24.4 mV and k = 5.89 mV (•) for Scheme SI. (D) The analogous simulated data plotted for Scheme SIII, with V _1/2 = −41.6 mV and k = 10.1 mV (□), and V _1/2 = −40.8 mV and k = 10.1 mV (•). (E) Window currents (in arbitrary units) generated by Scheme SI, measured after 20 s at each V_hold just before the test pulse was applied. A linear leak current was added to resemble that in the experiment in Fig. 4 D of Zhou et al. (1998). (F) The window currents generated by Scheme SIII exhibit almost no hysteresis.

Because the rate equations defining ultra-slow inactivation were based on limited types of data, we explored how sensitive the simulated currents were to changes in these parameters. In addition, it is useful to know how the existence of an ultra-slow inactivation mechanism would manifest itself in experimental data. Arbitrarily multiplying k ₂₃ and k ₃₂ by a factor of four had little detectable effect on simulations driven by the protocols illustrated in Fig. 2 (data not shown). However, a second ultra-slow inactivation state must then be postulated to account for hysteresis and use dependence observed in certain protocols (see below). There is little difference in the predictions of the coupled or the independent models of activation and inactivation (Schemes I and II) for protocols such as are illustrated in Fig. 2 (data not shown). However, differences become apparent in the presence of Cs⁺, and under other conditions that accentuate the idiosyncratic gating properties of HERG-like currents.

Gating in the Presence of High [Cs⁺]_o

The peculiar gating behavior previously observed in Cs⁺ solutions for HERG channels exogenously expressed in Xenopus oocytes (Schönherr and Heinemann, 1996) also occurs in microglia cells. When V_hold was 0 mV, small time-dependent inward Cs⁺ currents were seen in isotonic Cs⁺ saline, which were ∼5–10% of the amplitude of K⁺ currents in the same cell in K⁺ saline (data not shown). This suggests that Cs⁺ permeability is 10% that of K⁺, a conclusion supported by the observed reversal potential with 160 mM Cs⁺ outside and 160 mM K⁺ inside. As a result of this change in reversal potential, outward currents are more apparent.

Fig. 3 A shows that when V_hold was −80 mV, outward currents were observed at positive potentials, evidently reflecting K⁺ efflux from the cell. These outward currents develop with a voltage-dependent delay and show a steeply voltage-dependent decay phase. Both the rising and falling phases become markedly faster at more positive potentials. By the end of the 1-s depolarizing pulses, most of the channels had closed. After a brief step to −80 mV to reopen a large proportion of channels, steps back to positive potentials elicited normal tail currents, which decayed much more rapidly than did the currents during the first depolarization.

Figure 3.

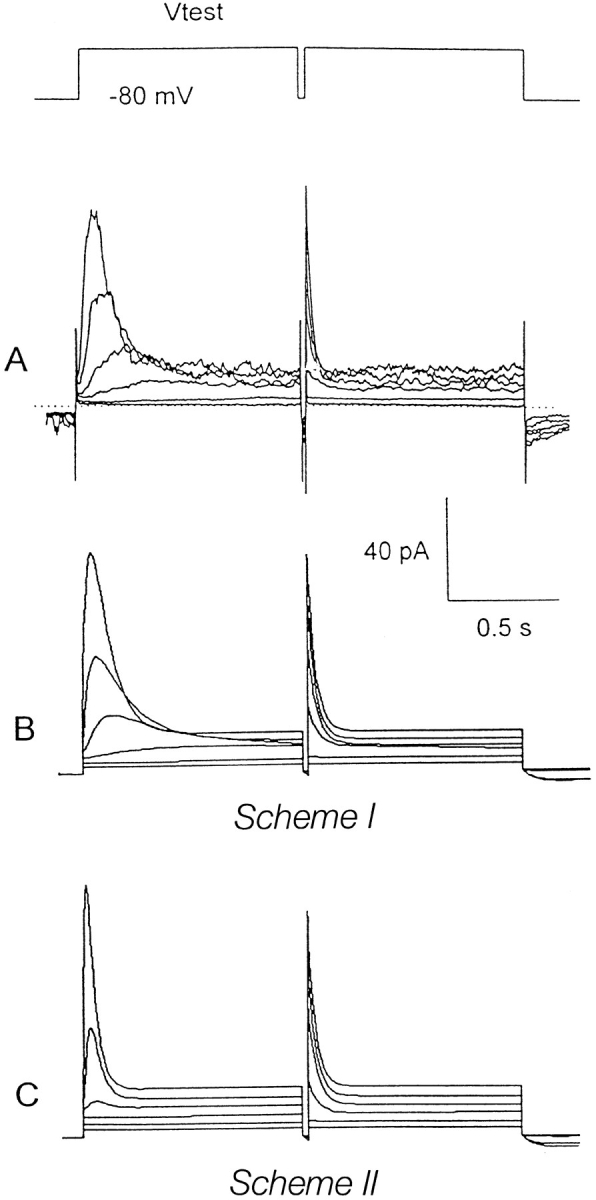
(A) Idiosyncratic gating in the presence of Cs⁺. The bath contained K⁺-free Cs⁺ saline, and the pipette contained KMeSO₃. Pairs of identical 1-s depolarizing pulses were applied from V_hold = −80 mV, separated by a 20-ms repolarization to −80 mV, to –20 through +80 mV in 20-mV increments (nominal voltages). (B) Simulation of gating in the presence of Cs⁺. The same parameters as in other simulations were used, except that [K⁺]_o was reduced to 10 mM to mimic the reduced permeability of Cs⁺, and activation and deactivation rates were halved. Voltages in the simulation were corrected −7 mV for liquid junction potentials. Note the steeply voltage-dependent decay rate during the first pulses in A and B, but not in C.

Fig. 3 B shows that this behavior is well described by the coupled gating model (Scheme I). The presence of the weakly permeant Cs⁺ was modeled by reducing extracellular K⁺ to 10 mM and the rates of activation (k ₀₁) and deactivation (k ₁₀) were reduced by a factor of two while retaining the same voltage dependence, as was found experimentally (data not shown); otherwise, the same parameters were used as in the previous simulations. A small leak current is included to facilitate comparison with the real data in Fig. 3 A.

In terms of Scheme SI, the rapid deactivation of the second transient outward current is a simple tail current reflecting conversion from state O to C_r and is dominated by rate constant k ₁₀. The decay phase of the first transient outward current is a convolution of the latency for channel recovery from inactivation and k ₁₀ (see Aldrich et al., 1983). Entry into the deactivated C_r state occurs in a coupled sequential fashion such that the channel must pass through several intermediate states (including the open state) while recovering from inactivation. As a result, there is a delay in the development of the transient outward current during the first pulse, and the outward current decays much more slowly than expected from τ_tail measured at the same potential (i.e., during the second pulse).

In our simulations, this delayed transient outward current was prominent only when conversion between the inactivated states (C_s, C_us) and the resting state (C_r) was constrained to pass through the open state (i.e., a linear-coupled system). If rapid closing and slow closing were assumed to be uncoupled and independent (Scheme SII; compare Faravelli et al., 1996), the transient outward current was also observed but showed little delay and had a final rate of decay that was simply dominated by k ₁₀ much like the decay of the second pulse (Fig. 3 C). Because the slower gating process is more steeply voltage dependent than the faster one, coupling imparts this steep voltage dependence to the rate at which outward current decays during the first pulse (Fig. 3, A and B). The uncoupled model, Scheme SII, predicts that this decay rate will exhibit the same modest voltage dependence of the fast process (Fig. 3 C). Therefore, in subsequent simulations we consider only coupled sequential models (Schemes I and III).

Use Dependence of Current Availability

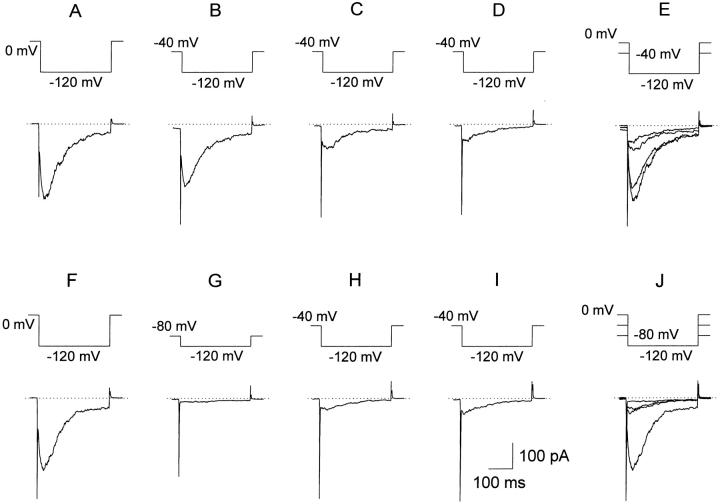
The experiment depicted in Fig. 4 illustrates the necessity of postulating a second inactivated state and suggests an explanation for hysteresis observed in the availability measurements (Fig. 4 E; Zhou et al., 1998). Identical test pulses to −120 mV were applied from different V_hold, as labeled. When V_hold was initially 0 mV (Fig. 4 A) or more positive, the conductance was fully available; i.e., all channels were in the rapidly equilibrating resting state C_r and the test current during the pulse to −120 mV was maximal. 1 min after V_hold was changed to a moderately negative potential (−40 mV), the test current evoked by stepping to −120 mV was still large (Fig. 4 B). During subsequent pulses (Fig. 4, C and D), the test current was attenuated by >80%. These four records are superimposed on the right (Fig. 4 E). In contrast, when V_hold was initially −80 mV where all of the channels were in inactivated states C_s and C_us (Fig. 4 G), the test current 1 min after changing V_hold to −40 mV was quite small (H). During a subsequent pulse, the test current increased somewhat (Fig. 4 I). Again, the four records are superimposed at the end of the row in Fig. 4 J.

Figure 4.

History dependence of the availability of current. Currents recorded during test pulses to −120 mV from different V_hold (as labeled) are plotted in the order obtained. When V_hold was 0 mV (A) or more positive, the conductance was fully available (i.e., the test current was maximal). 1 min after V_hold was changed from 0 to −40 mV, the current during the first test pulse was still large (B), but the current during two subsequent test pulses, each after a 30-s interval, was attenuated greatly (C and D). Returning V_hold to 0 mV for 1 min fully restored the test current (F). Shifting V_hold to −80 mV for 30 s reduced the availability of channels to near zero (G). When V_hold was then changed to −40 mV, the test current after 1 min was still quite small (H). After a further 30 s, the test current had increased slightly (I) and was similar to the test current in D. Thus, equilibration of the system at −40 mV requires well over 1 min if no pulses are applied to open the channels. The capacity transient at the end of the test pulses has been truncated. In E and J, the four records in the corresponding row are superimposed.

The key observation is that when V_hold was changed to −40 mV from the positive voltage range, in which C_r predominates, there was very little decrement of availability even after 1 min (Fig. 4, A vs. B). There are two implications: (a) conversion to C_s states (i.e., inactivation) proceeds exceedingly slowly at −40 mV (see also Fig. 6 in Zhou et al., 1998); and (b) inactivation develops in a sequentially coupled fashion from the open state (conversion from C_r to C_us occurs through O and C_s). Although some channels are open at −40 mV, as can be seen from the distinct inward window current in Fig. 4 B, the open probability is low. The observed time constant of equilibration under these circumstances will be slowed by a factor approximately equal to the inverse of the open probability (i.e., P _open ⁻¹) (Bernasconi, 1976; MacDonald et al., 1991). The same argument holds for equilibration between C_s and C_us. A single hyperpolarizing test pulse opens many channels, “short-circuiting” this slow equilibration so that a pseudo-equilibrium can be reached much more rapidly.

Figure 6.

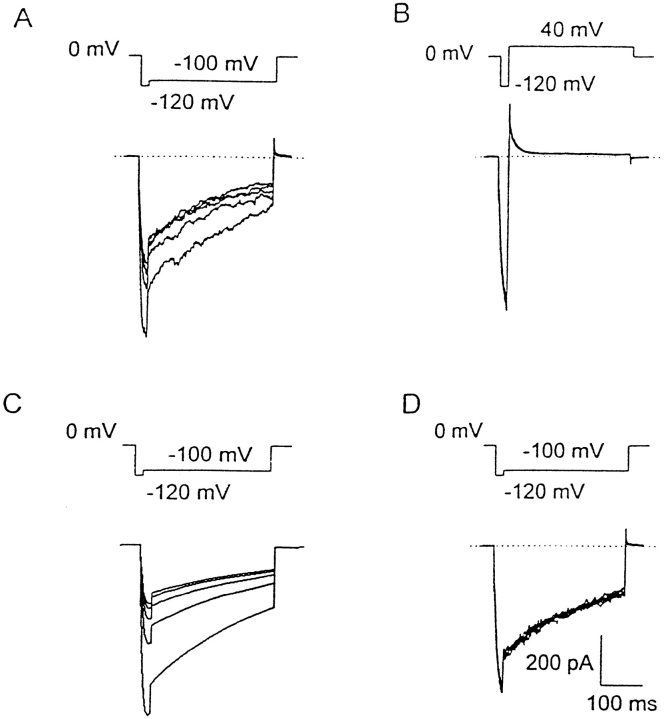
Use-dependent inactivation. A voltage pulse protocol (above each set of records) like that used to elicit tail currents in Fig. 2 A (and Fig. 5 A in Zhou et al., 1998) was repeated and the first five current records are plotted. With a test pulse to 100 mV repeated at 0.91 Hz, there was substantial accumulation of inactivation (A). This result is qualitatively mimicked in our simulations (C ). When the rapid 0.91-Hz rate was used with a test pulse to +40 mV, no accumulation of inactivation was observed (B). In D, the voltage protocol in A was repeated at a slower rate (0.1 Hz) and no build up of inactivation was observed. This result was also mimicked by simulations using Scheme SI (not shown). The calibration bars in D also apply to A and B.

The predictions of Scheme SI for this protocol are shown in Fig. 5. The model reproduces the use dependence fairly accurately. At least two C_s states were needed to reproduce the very slow equilibration observed at −40 mV, as well as the kinetics and voltage dependence observed at more negative and positive potentials. Indeed, the interaction between test pulse frequency and the establishment of the steady state response places important constraints on the rate equations defining the equilibration between C_s and C_us. Subtle differences remain between experimental and simulated results (for example, in Fig. 5 B the first response in the train is slightly bigger than subsequent responses while the reverse is true in the experimental results), suggesting that there may be more than two inactivated states. Nevertheless, the simple model described by Scheme SI is remarkably robust in predicting the responses of the HERG-like current to diverse voltage protocols.

During standard tail current measurements, anomalously slow closing at large negative potentials was observed (Fig. 5 A in Zhou et al., 1998). The idea that this slow decay was due to inactivation is explored in the experiment depicted in Fig. 6. A brief 20-ms command to −120 mV from a holding potential of 0 mV, followed by a 180-ms command to a given test potential is repeated with a frequency of 1 Hz. When the tail current was measured at −100 mV (where it decayed anomalously slowly, see Fig. 2 A), there was a use-dependent build up of inactivation during repeated pulses (Fig. 6 A). In contrast, when the pulse sequence eliciting a tail current at +40 mV was repeated at ∼1 Hz (Fig. 6 B), there was little or no accumulation of inactivation. When the protocol in Fig. 6 A was repeated with a longer interval between pulses (10 s), the use dependence was greatly reduced (Fig. 6 D). The use dependence seen in Fig. 6 A is mimicked by our model (Fig. 6 C), as is the lack of use dependence for the protocols in Fig. 6, B and D (data not shown).

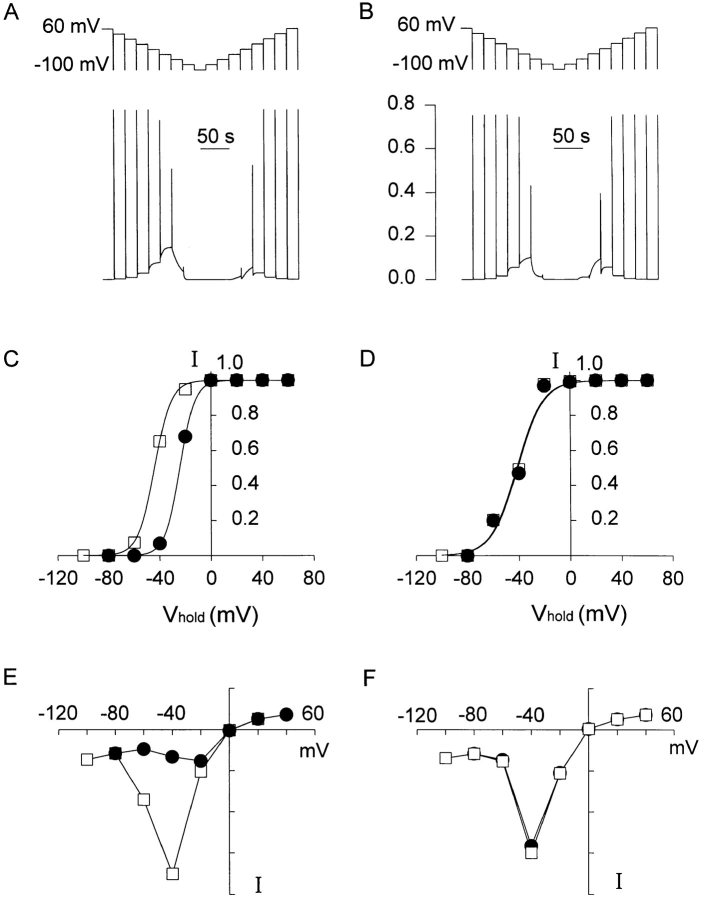
Hysteresis in Steady State Availability and Window Current Measurements

The voltage dependence and magnitudes of the rates governing ultra-slow inactivation were deduced from the use-dependent protocols (Figs. 4 and 6). Scheme SI, incorporating these parameters, predicted the observed hysteresis of availability measurements obtained with incrementing or decrementing conditioning commands 20 s in duration. This result is shown in Fig. 7, A and B, respectively, where the predictions of Scheme SI and the hybrid Scheme SIII (based on the model of Wang et al., 1997) are compared. Starting from +60 mV, a series of decrementing 20-mV steps in V_hold lasting 20 s were applied with availability measured at the end of each step by a 300-ms pulse to −100 mV. The peak test currents from these simulations are plotted in Fig. 7, C and D (Schemes I and III, respectively), for comparison with the actual data in Fig. 4 C of Zhou et al. (1998). On the decrementing course of this protocol, both schemes predict similar results. Availability remains constant until the command potential drops below 0 mV and becomes negligible by the time the steps reach −80 mV. However, the predictions of the two schemes diverge for the incrementing limb. With Scheme SIII, no hysteresis is seen, while Scheme SI predicts hysteresis comparable with that observed experimentally. For Scheme SI, the midpoint of a Boltzmann distribution (V_1/2) was 20 mV more positive on the way up and the slope was somewhat steeper than on the way down.

The calculated window currents, derived from P _open at the end of each 20-s sojourn at V_hold (including a linear leak to facilitate comparison with Fig. 4 D) are plotted in Fig. 7, E and F (Schemes I and III, respectively). Once again, on the decrementing course of this protocol, both schemes predict similar results: the apparent steady state current at V_hold increases to a peak at −40 mV and disappears at −80 mV. On the way up, Scheme SI predicted substantial hysteresis, and with Scheme SIII there was no hysteresis.

The parameters used in our simulations to obtain this match were derived by trial and error. However, our simulations predict that greater constraints on ultra-slow inactivation could be obtained by varying the duration of the test pulses. This has not yet been attempted. It is notable that a similar degree of hysteresis was observed with Scheme SII, which proposes independent activation and inactivation.

discussion

HERG gating is state and use dependent (fast and slow closing are coupled via a common open state).

Although many previous models of HERG (or HERG-like) channel gating assumed independent activation and inactivation (Shibasaki, 1987; Faravelli et al., 1996; Ho et al., 1996), there is strong evidence suggesting coupling between these kinetic pathways, and a linear-coupled model has been considered by a number of authors (Snyders and Chaudhary, 1996; Wang et al., 1997). In particular, the behavior of HERG channels in isotonic Cs⁺ solutions can be explained most economically if the two types of closing are mutually exclusive and the channels must pass through intermediate states such as the open state to interconvert. In high [Cs⁺]_o, both HERG (Schönherr and Heinemann, 1996) and HERG-like channels in microglia (Fig. 3 A) close much more slowly at positive potentials if they are first inactivated by a prolonged hyperpolarizing prepulse. This phenomenon closely parallels the model of Armstrong (1969) explaining block of K⁺ channels by internal quaternary ammonium ions, and the observations of Aldrich et al. (1983) on the coupling of activation and inactivation in Na⁺ channels. The inactivation of HERG channels that develops at negative potentials must be reversed before the channels can undergo fast closing at positive potentials.

A shift in the voltage dependence of activation explains the absence of outward currents in microglia.

We compared our model with a previous model of HERG expressed in oocytes (Wang et al., 1997) by constructing a “chimeric” model (Scheme SIII) in which our rate constants for activation/deactivation are combined with their parameters for the slower gating processes (inactivation/recovery). This exercise revealed that to describe our data the voltage dependence of steady state activation (or deactivation) had to be shifted negatively by 40 mV. The practical effect of this shift is that the overlap between activation and inactivation is much smaller in microglia, and this greatly reduces the size of outward currents seen when depolarizing pulses are applied from a large negative V_hold in symmetrical K⁺ salines. The almost complete absence of outward currents is the main observable difference in the properties of HERG-like currents in microglia and HERG currents in other cells. This phenomenological difference also explains why HERG-like currents are often described as inactivating inward rectifiers. It is difficult to describe a K⁺ channel as a depolarization-activated delayed rectifier when depolarizing pulses elicit little or no observable outward current.

HERG-like currents in microglia are influenced by an ultra-slow inactivation process.

Comparison of our model with others revealed another difference. To explain several aspects of our data, it was necessary to postulate the existence of an ultra-slow inactivation process. Manifestations include incomplete recovery from inactivation and pronounced hysteresis in the measurement of quasi–steady state inactivation and window current. The existence of an absorbing closed state with extremely slow equilibration in the voltage range near or slightly positive to a normal resting potential range would have significant effects on the physiological behavior of these channels. The slow kinetics of the inactivation process effectively introduces a lag in the feedback between voltage and gating. At a large negative potential, all of the channels are inactivated and recover very slowly with moderate depolarization. However, the steep voltage dependence of the recovery kinetics means that a strong depolarization would greatly enhance the availability of HERG-like channels and facilitate repolarization. The slow and incomplete inactivation at moderately negative potentials would permit sustained K⁺ current that would persist tens of seconds even at physiological membrane potentials, which in these cells appears to be ∼−40 mV.

Nomenclature

The HERG channel has been described either as a depolarization-activated K⁺ channel with anomalously rapid inactivation at positive potentials (Shibasaki, 1987; Trudeau et al., 1995; Spector et al., 1996; Smith et al., 1996), or a channel that activates and then inactivates upon hyperpolarization (Bauer et al., 1990; Dousmanis and Pennefather, 1992; Arcangeli et al., 1995; Trudeau et al., 1995; Bauer et al., 1996; Ho et al., 1996; Hu and Shi, 1997; Weinsberg et al., 1997). The former terminology stems from the finding that HERG underlies a component of I _Kr (Sanguinetti et al., 1995), a “delayed rectifier” current in cardiac muscle. As pointed out by Faravelli et al. (1996), these two viewpoints are specular—they use different terms to describe identical phenomena, hence the choice of nomenclature is semantic. The fast gating mechanism opens the channels upon hyperpolarization. The slow mechanism opens channels upon depolarization. In the steady state, the channels close at either extreme of voltage. In their original description of the phenomena of activation and inactivation, Hodgkin and Huxley (1952) defined “inactivation” as the slower gating process. Because the Gestalt of HERG-like currents in symmetrical K⁺ solutions is of a channel conducting large inward currents and only small outward currents, HERG-like currents in various cells have invariably been described as inactivating inward-rectifier currents. Nevertheless, several rationales have been presented for describing the rapidly equilibrating closed state as the inactivated state and designating HERG channels as outward rectifiers.

Analogy of properties.

Tetraethylammonium (TEA⁺) effects can be used to distinguish between N- and C-type inactivation (Choi et al., 1991), the former inhibited by internal and the latter by external TEA⁺. Because external TEA⁺ slows fast closing of HERG channels at positive potentials, this closing has been considered analogous to C-type inactivation (Smith et al., 1996). However, internal quaternary ammonium ions interfere with the closing of delayed-rectifier channels at negative potentials (Armstrong, 1969); thus, the effect of external TEA⁺ is precisely what one would predict if HERG, like KAT1 (Anderson et al., 1992; Cao et al., 1995; Hoshi, 1995), were a K⁺ channel with functionally inverted gating machinery. The slowing of HERG closing by increased [K⁺]_o (Wang et al., 1996) is at first reminiscent of both delayed rectifiers and inward rectifiers, in which closing is slowed by increased [K⁺]_o. However, because both closing and inactivation of depolarization-activated delayed-rectifier K⁺ channels are slowed by elevated [K⁺]_o, this property cannot be used to distinguish between these gating processes.

HERG channels lack an inactivation process like other K⁺ channels. The possibility of N-type inactivation has been ruled out by mutagenesis studies (Schönherr and Heinemann, 1996; Spector et al., 1996; Smith et al., 1996). A hallmark of C-type inactivation of K⁺ channels (as well as Na⁺ channels) is that inactivation is essentially voltage independent and derives its apparent voltage dependence from coupling to activation. Both gating processes of HERG channels are distinctly voltage dependent (Wang et al., 1996; Zhou et al., 1998) and, therefore, neither can reasonably be described as C-type inactivation. These differences from known mechanisms of inactivation suggest that a distinct mechanism exists for HERG channels, and that terminology may as well be based on function.

Which gating process is more labile?

Traditionally, inactivation is thought of as being more labile than activation. The rapid channel closing at positive potentials (here called deactivation) can be removed by substitution of a single amino acid presumed to be in the outer vestibule of the pore (Schönherr and Heinemann, 1996). Similarly, the stability of the open state of the closely related eag channel is greatly enhanced by a single amino acid substitution, resulting in an effectively voltage independent (and open) channel (Tang and Papazian, 1997). Both gating mechanisms therefore exhibit molecular lability.

The inactivation (slow closing) of HERG-like channels at negative potentials is labile in its native molecular state as well. Arcangeli et al. (1995) remarked on the heterogeneity in the steady state inactivation of HERG-like currents in neuroblastoma cells, with V_1/2 ranging from −40 to 0 mV. We observed lability in this process as well, with a few cells exhibiting much slower and less pronounced inactivation during hyperpolarizing pulses. Complete removal of extracellular divalent cations removes inactivation of HERG-like currents in neuroblastoma cells (Faravelli et al., 1996) and slows inactivation of I_kr in rabbit SA node cells (Ho et al., 1996). Both gating mechanisms of HERG-like channels are rather labile, and thus this property is not particularly enlightening.

Structural comparisons.

There are some similarities in the primary amino acid sequence and proposed secondary structure of HERG and depolarization-activated K⁺ channels. However, there is just 15% homology with Shaker channels and slightly higher with KAT1 (Warmke and Ganetzky, 1994). Both HERG channels and depolarization-activated K⁺ channels have six putative membrane-spanning domains, but so does the hyperpolarization-activated inward-rectifier K⁺ channel (KAT1) in plants (Anderson et al., 1992; Cao et al., 1995). Although clearly distinct from the animal inward rectifier family, HERG functionally resembles plant inward rectifiers. Regardless of structural considerations, there is no unique molecular definition of activation and inactivation beyond simply whatever mechanism is found to be responsible for gating processes that were already named on the basis of function. Several radically different mechanisms have been found to account for inactivation. Likewise, activation may arise from a variety of molecular mechanisms in different types of channels. In the absence of compelling reasons to do otherwise, we prefer to use the classical Hodgkin-Huxley definitions and describe HERG-like channels in microglia as existing in a resting state at depolarized potentials, and as activating and inactivating on hyperpolarization.

Abbreviation used in this paper

HERG

human ether-à-go-go-related gene (erg) and its product