Human Ether-à-go-go–related Gene K⁺ Channel Gating Probed with Extracellular Ca²⁺

Abstract

Human ether-à-go-go–related gene (HERG) encoded K⁺ channels were expressed in Chinese hamster ovary (CHO-K1) cells and studied by whole-cell voltage clamp in the presence of varied extracellular Ca²⁺ concentrations and physiological external K⁺. Elevation of external Ca²⁺ from 1.8 to 10 mM resulted in a reduction of whole-cell K⁺ current amplitude, slowed activation kinetics, and an increased rate of deactivation. The midpoint of the voltage dependence of activation was also shifted +22.3 ± 2.5 mV to more depolarized potentials. In contrast, the kinetics and voltage dependence of channel inactivation were hardly affected by increased extracellular Ca²⁺. Neither Ca²⁺ screening of diffuse membrane surface charges nor open channel block could explain these changes. However, selective changes in the voltage-dependent activation, but not inactivation gating, account for the effects of Ca²⁺ on Human ether-à-go-go–related gene current amplitude and kinetics. The differential effects of extracellular Ca²⁺ on the activation and inactivation gating indicate that these processes have distinct voltage-sensing mechanisms. Thus, Ca²⁺ appears to directly interact with externally accessible channel residues to alter the membrane potential detected by the activation voltage sensor, yet Ca²⁺ binding to this site is ineffective in modifying the inactivation gating machinery.

introduction

Human ether-à-go-go–related gene (HERG)¹ encoded K⁺ channel isoforms exist in a number of cell types including neurons, glia, cardiac myocytes, and tumor cells (Warmke and Ganetzky, 1994; Trudeau et al., 1995; Faravelli et al., 1996; Arcangeli et al., 1997; Shi et al., 1997; Bianchi et al., 1998). HERG channels may be involved in neuronal spike frequency adaptation and tumor cell growth (Warmke and Ganetzky, 1994; Chiesa et al., 1997; Bianchi et al., 1998). In the heart, HERG K⁺ channel subunits mediate a delayed rectifier K⁺ current (I_Kr) that aids cellular repolarization (Sanguinetti and Jurkiewicz, 1991; Sanguinetti et al., 1995). Mutations of the HERG gene or drugs that suppress cardiac I_Kr cause the congenital and acquired forms of human long QT syndrome, respectively (Sanguinetti et al., 1995; Sanguinetti et al., 1996; Spector et al., 1996a).

Despite homology to the Shaker family of voltage gated K⁺ channels, HERG K⁺ channels exhibit distinctive gating behavior. Voltage-dependent channel activation is much slower than channel inactivation, giving rise to the characteristic rectification-like behavior of this channel (Trudeau et al., 1995; Smith et al., 1996; Spector et al., 1996b). There is also evidence that HERG channel inactivation has intrinsic voltage dependence (Wang et al., 1996, 1997), unlike N- and C-type inactivation in the Shaker family K⁺ channels (Hoshi et al., 1991; Zagotta and Aldrich, 1990).

Divalent cations have often been used to probe ion channel function, and Ca²⁺ has been implicated as a modulator of K⁺ channel gating (Frankenhaeuser and Hodgkin, 1957; Gilly and Armstrong, 1982; Armstrong and Matteson, 1986; Armstrong and López-Barneo, 1987; Armstrong and Miller, 1990; Mazzanti and DeFelice, 1990; Clay, 1995). Interaction between Ca²⁺ and a distinct region of the channel protein could cause a specific effect on its function, or Ca²⁺ could nonspecifically associate with diffuse charged moieties on the membrane surface, effectively neutralizing charges and leading to a global change in the transmembrane potential perceived by all membrane molecules. Both mechanisms of modulation have been proposed to explain the effects of divalent cations on ion channels (Frankenhaeuser and Hodgkin, 1957; Gilly and Armstrong, 1982; Green and Andersen, 1991).

In the squid axon, elevation of extracellular Ca²⁺ leads to a decrease in the rate of K⁺ channel activation (Gilly and Armstrong, 1982; Armstrong and Matteson, 1986; Armstrong and López-Barneo, 1987). Complete removal of extracellular divalent cations and K⁺ causes loss of selectivity and gating in the squid axon K⁺ channel, resulting in channels that are constitutively open. Recombinant K⁺ channels from Drosophila melanogaster, including Shaker and EAG, are affected by divalent cations in much the same way as the squid K⁺ channel (Armstrong and Miller, 1990; Spires and Begenisich, 1994; Ludwig et al., 1994).

Unlike invertebrate K⁺ channels, guinea pig ventricular I_Kr channels appear to retain gating and selectivity in the absence of extracellular Ca²⁺ and K⁺ (Sanguinetti and Jurkiewicz, 1990, 1992). However, Ca²⁺ and Mg²⁺ have been suggested to serve critical roles in the gating of K⁺ channels from both rabbit sinoatrial node and neuronal cell lines, and these channels are functionally similar to HERG K⁺ channels (Faravelli et al., 1996; Ho et al., 1996). To gain further insight into the gating behavior of HERG K⁺ channels, we have examined the effect of external Ca²⁺ on HERG channels under conditions in which the extracellular K⁺ concentration was in the normal physiological range (4 mM).

materials and methods

Plasmid cDNA Constructs

The HERG cDNA was obtained from Dr. Mark Keating (University of Utah, Salt Lake City, UT). HERG was ligated into the pSI mammalian expression plasmid (Promega Corp.). The CD8 antigen gene in the EBO-pcD Leu2 vector was kindly provided by Dr. Richard Horn (Thomas Jefferson Univ. Medical College, Philadelphia, PA). CD8 is a human T-lymphocyte surface antigen and was used to visually identify transfected cells using CD8 antibody–coated polystyrene microbeads.

Cells

Chinese hamster ovary K1 (CHO-K1) cells were obtained from the American Type Culture Collection and maintained in HAMS F-12 media (Gibco Laboratories) supplemented with 1 mM l-glutamine, and 10% heat-inactivated fetal bovine serum (Gibco Laboratories) in a humidified, 5% CO₂ incubator at 37°C.

Transfection

CHO-K1 cells were cotransfected with the HERG and CD8 plasmids in a ratio of 4:1. Transfection was accomplished using the Lipofectamine transfection reagents and method (Gibco Laboratories). Immediately before patch clamping, cells were labeled with commercially prepared microbeads conjugated to CD8 antibodies (DynaBeads; Dynal) to identify transfected cells. Cells that displayed CD8 on their surface bound DynaBeads, indicating successful transfection (Jurman et al., 1994).

Solutions

The intracellular recording solution for all experiments was (mM): 110 KCl, 5 K₂ATP, 5 K₄BAPTA, 2 MgCl₂, 10 HEPES, pH 7.2. The control extracellular recording solution was (mM): 145 NaCl, 4 KCl, 1.8 CaCl₂, 1 MgCl₂, 10 HEPES, 10 glucose, pH 7.35. Solutions with elevated divalent cation concentrations were made by adding an appropriate amount of 1 M aqueous chloride salt solution to the control extracellular solution. The 2 mM EGTA extracellular solutions in Fig. 4 A was the same as control except that CaCl₂ and MgCl₂ were omitted and 2 mM EGTA was added. For the Ca²⁺ dose response in Fig. 4 B, contaminant Ca²⁺ was assumed to be 25 μM. MgCl₂ was omitted and, for Ca²⁺ concentrations ≥100 μM, the appropriate concentration of Ca²⁺ was added to the solution without a Ca²⁺ buffering agent. At concentrations <100 μM, 1 mM EGTA was used to buffer the Ca²⁺. The amounts of Ca²⁺ and chelator needed to obtain a desired concentration of free Ca²⁺ were determined using Sliders MaxChelator software with the BERS.CCM constants (Chris Patton, Stanford University, Stanford, CA).

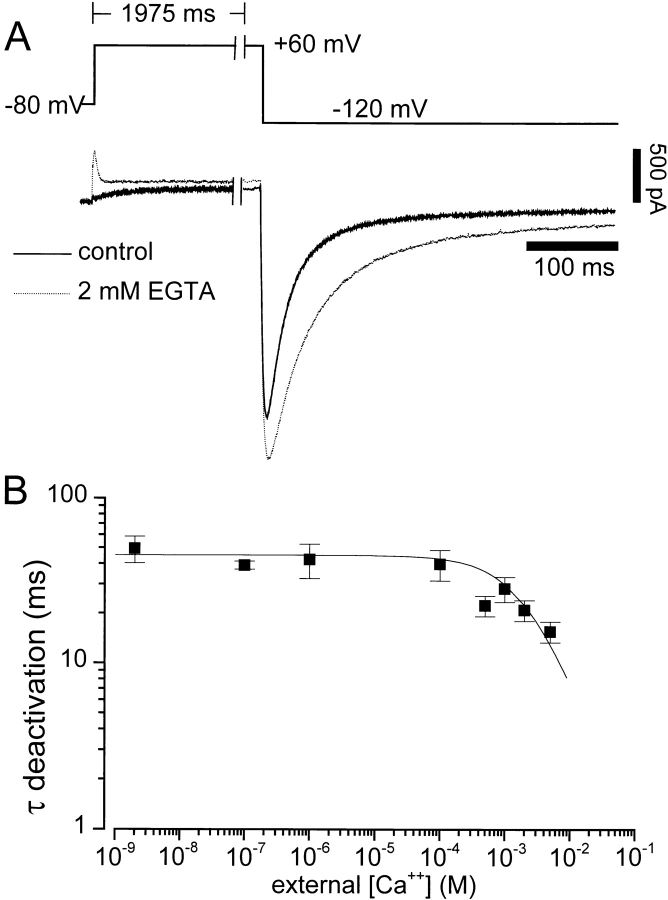
Figure 4.

The effect of removal of divalent cations from the extracellular solution on HERG channel gating. (A) The voltage clamp protocol is shown at the top. The membrane potential was held at −80 mV, then stepped to +50 mV for 2 s before hyperpolarizing to −120 mV. Two recordings from the same cell are shown in control (1.8 mM Ca²⁺ and 1 mM Mg²⁺, dark solid line) and divalent free solutions (2 mM EGTA, dashed line). Similar results were obtained in four additional cells. (B) Deactivation persists in very low extracellular Ca²⁺ concentrations, and the deactivation rate is independent of Ca²⁺ concentration over five orders of magnitude. The voltage clamp protocol in A was used to measure deactivation. A monoexponential function was then fit to the deactivating tail current recorded at −120 mV. The resulting time constants are plotted versus extracellular Ca²⁺ concentration. The concentrations tested were: 5 mM (n = 5), 2 mM (n = 6), 1 mM (n = 5), 500 μM (n = 4), 100 μM (n = 2), 1 μM (n = 2), 100 nM (n = 4), and no added divalent cations that are estimated (see methods) to be 2.5 nM Ca²⁺ (n = 5). The error bars represent SEM. The solid curve was generated with a logistic equation with an IC₅₀ value of 2.5 mM. Mg²⁺ was omitted from all the external solutions used in B. Ca²⁺ concentrations were calculated as described in methods.

Electrophysiology

The whole-cell patch clamp technique was used to assay HERG channel function (Hamill et al., 1981). Cells were patch clamped 36–60 h after transfection at a temperature of 20–25°C. HERG currents in transiently transfected CHO-K1 cells are very stable. We observe no rundown during whole cell voltage clamp over the lifetime of the cell, which can be well over 1 h. All recordings were made using an Axopatch 200A patch clamp amplifier in conjunction with a Digidata 1200 interface (Axon Instruments). Patch pipettes were fabricated from capillary glass (1.1 mm outside diameter, #3-00-2-3-G/X; Drummond Scientific Co.; or 1.2 mM outside diameter starbore, #001812; Radnotti) using a Flaming/Brown micropipette puller (P-97; Sutter Instruments, Co.). Patch pipette resistances were 1–2 MΩ. Cell and pipette capacitances were nulled and series resistance was compensated (85– 95%) before recording. Data were acquired using pCLAMP programs (6.03; Axon Instruments). Data were analyzed and plotted using a combination of pCLAMP, Origin (Microcal Software), and SigmaPlot 4.0 (Jandel Scientific). In all figures featuring raw current recordings, the bottom of the current scale bar indicates the zero current level.

A HERG Model with Voltage-dependent Activation and Inactivation

We adopted a simple multistate Markov kinetic model from the literature (Scheme I; Wang et al., 1997). Our purpose was not to uniquely identify a model of HERG K⁺ currents, but to test whether a simple voltage shift in one or more parameters of the published model could account for the data. Multistate Markov gating models have been successfully used for modeling voltage-gated ion channels and interpreting experimental observations (Hille, 1992; Sigworth, 1994; Zagotta et al., 1994).

In the model, only the O state conducts ionic current. C states are closed states primarily occupied at negative membrane potentials. The I state is a closed state primarily occupied during membrane depolarization. The transitions along the activation pathway (see Terminology) are governed by voltage-dependent rate constants (a ₁, a ₋₁, a ₃, and a ₋₃) and voltage-independent rate constants (a ₂ and a ₋₂). Transitions to and from the inactivated states are governed by two additional voltage-dependent rate constants (a ₄ and a ₋₄) (as used by Wang et al., 1997). The rate constants were limited to a maximum value at extreme membrane potentials by applying the following: a _n = [(1/a _n) + (1/a _max)]⁻¹, where a _max (s⁻¹) is the limiting value of the rate constant (a _1max = 100, a _3max = 25, and a _4max = 400). The simulations were carried out using ModelMaker (Cherwell Scientific). The rate constants for the forward and reverse transitions were calculated according to Eqs. 1 and 2 (Stevens, 1984; Patlak, 1991).

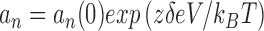1

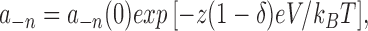2

where a _n and a _−n represent the forward and reverse transition rate constants between the nth state and the n + 1 state in units of s⁻¹, k _B = 1.3807 × 10⁻²³ V C K⁻¹ (Boltzmann constant), T = 293.15°K, e = 1.6022 × 10⁻¹⁹ C (electronic charge in Coulomb). Each rate constant is defined by two terms. One term is the rate constant in the absence of a membrane potential, [a _n(0) and a _−n(0)], and the other term is membrane potential dependent [zδeV/(k _B T)]. The effective charge on the “gate” is z, the fraction of the electrical field sensed is δ, and the membrane potential is V. The same equations with changes in a _n(0) and z were used for the other rate constants. The parameters for each of the transition rate constant pairs were as follows: a ₁, a ₋₁:δ₁ = 0.40, z ₁ = 1.80, a ₁(0) = 6.963 s⁻¹, a ₋₁(0) = 11.481 s⁻¹; a ₂, a ₋₂:δ₂ = 0.00, z ₂ = 0.00, a ₂(0) = 8.172 s⁻¹, a ₋₂(0) = 42.977 s⁻¹; a ₃, a ₋₃:δ₃ = 0.40, z ₃ = 1.98, a ₃(0) = 11.481 s⁻¹, a ₋₃(0) = 0.094 s⁻¹; a ₄, a ₋₄:δ₄ = 0.5, z ₄ = 0.82, a ₄(0) = 116.824 s⁻¹, a ₋₄(0) = 14.023 s⁻¹; V = V_clamp − V_shift.

V_clamp is the voltage clamp potential applied. V_shift is the apparent change in membrane potential caused by Ca²⁺ binding and was set to zero except to simulate elevation of external Ca²⁺. We found that applying the same V_shift to all rate constants could not simulate the observed data. A shift in a ₄ and a ₋₄ also altered simulated inactivation, inconsistent with our data. Therefore when simulating elevated Ca²⁺ (10 mM) V_shift for a ₁, a ₋₁, a ₃, and a ₋₃ was set to +23 mV so that only the voltage dependence of the activation rate constants were affected, and V_shift for a ₄ and a ₋₄ was set to 0 mV. Rate constants a ₂ and a ₋₂ are voltage independent.

HERG K⁺ currents measured with the voltage clamp protocols described in the results were used for adjusting the model parameters to approximate the data obtained in 1.8 mM Ca²⁺. The model K⁺ currents were scaled to fit the data sets using a linear open channel current–voltage relationship and a K⁺ channel reversal potential of −90 mV to correspond with the experimentally determined value. The HERG open channel current–voltage relationship has been described as linear in several studies (Sanguinetti et al., 1995; Smith et al., 1996).

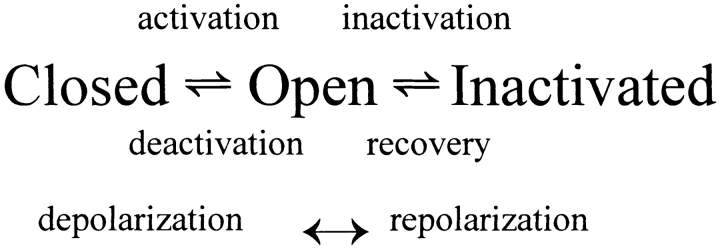
Terminology

The simple model of HERG gating described above can be further simplified to facilitate the discussion of the experimental current measurements. There are three main classes of kinetic states needed for the discussion: closed, open, and inactivated states (Scheme II).

C (closed) and I (inactivated) are both nonconducting states. Only the O (open) state conducts ionic current. Channels are primarily in closed states at negative voltages. Membrane depolarization predisposes the channels to move toward the open and inactivated states. Repolarization allows channels to return to the closed state. It is important to note that in this model, as in the more complicated model described above, inactivated channels may close only after recovering through the open state.

HERG channel gating has been described as a depolarization-activated channel with slow activation, and fast inactivation gating (Scheme I), in accordance with the previous description of I_Kr gating (Shibasaki, 1987; Sanguinetti et al., 1995; Smith et al., 1996; Spector et al., 1996b; Wang et al., 1997). However, it is also possible to describe this channel as a hyperpolarization-activated channel where channel activation is more rapid than inactivation (Pennefather et al., 1998; Zhou et al., 1998a). This distinction is semantic and we will discuss our data using the terminology indicated in the scheme above.

results

Ca²⁺ Decreases HERG Current Amplitude and Shifts the Isochronal Activation Curve

Fig. 1 shows the effects of elevated external Ca²⁺ on HERG channel currents. Increasing the external Ca²⁺ concentration from 1.8 to 10 mM decreased the current amplitude and enhanced the rate of decay of tail currents at −50 mV (compare Fig. 1, A and B). Plotting the maximal current during the test step versus the test potential results in the bell-shaped current–voltage relationship characteristic of HERG channels seen in Fig. 1 C (Trudeau et al., 1995; Sanguinetti et al., 1995). The decrease in the current–voltage relationship at positive potentials is due to voltage-dependent channel inactivation (Smith et al., 1996; Spector et al., 1996b). Elevating the external Ca²⁺ concentration increased the degree of depolarization required to activate HERG currents (Fig. 1, C and D). However, at membrane potentials greater than +40 mV, current amplitudes during the test pulse were nearly the same in 1.8 or 10 mM Ca²⁺ (Fig. 1 C). Plotting the peak tail current amplitude measured at a constant potential (−50 mV) as a function of the preceding test potential resulted in a sigmoidal curve that described the voltage dependence of channel opening (Fig. 1 D). Elevation of external Ca²⁺ from 1.8 to 10 mM shifted the midpoint of this tail current curve by +22.3 ± 2.5 mV (n = 3), in agreement with the shift in voltage dependence of currents measured during the test step (Fig. 1 C). Ca²⁺ also decreased the maximum tail current amplitude, but the slope factors of the tail current curves were not significantly different between 1.8 (8.8 ± 0.2 mV, n = 3) and 10 (9.0 ± 0.4 mV, n = 3) mM Ca²⁺. To understand the nature of these Ca²⁺ effects, the changes in activation and deactivation kinetics were characterized in greater detail.

Figure 1.

External Ca²⁺ modifies HERG current. Representative families of HERG currents recorded in 1.8 (A) and 10 (B) mM extracellular Ca²⁺. The scale bars at bottom left of A and the voltage clamp protocol shown at the top right apply to both A and B. Cells were held at −80 mV, and then stepped to test potentials between +50 and −70 mV in 10-mV increments for 2 s before repolarizing to −50 mV. The symbols above the recordings indicate the approximate time of measurement for the current– voltage relationships in C and D. In C and D, the symbols represent mean and SEM from three cells. Filled symbols indicate 1.8 mM Ca²⁺; open symbols indicate 10 mM Ca²⁺. Squares indicate peak tail current at −50 mV; circles indicate measurement at the end of the test voltage step. Normalization before averaging was accomplished by fitting a Boltzmann curve to the tail current in 1.8 mM Ca²⁺ for each cell, and then normalizing all measurements (C and D) in that cell to the limit of the Boltzmann fit.

Ca²⁺ Slows the Rate of HERG Channel Activation

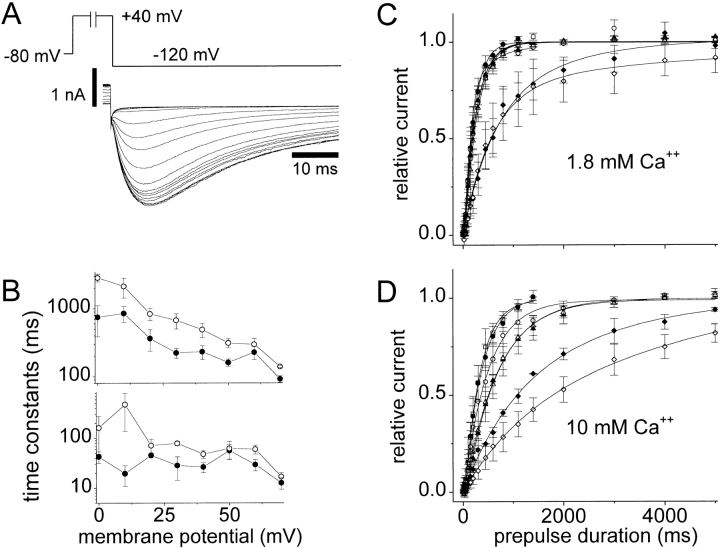
Because HERG inactivates very rapidly (relative to activation) at most membrane potentials, the rate of activation cannot be observed accurately during a single voltage clamp step (Smith et al., 1996; Spector et al., 1996b; Wang et al., 1996). The time course of the K⁺ current observed during a test pulse reflects the rates of both activation and inactivation (Sanguinetti et al., 1995; Schönherr and Heinemann, 1996; Smith et al., 1996; Wang et al., 1997). To estimate the rate of channel opening at positive potentials, we took advantage of the channel's rapid recovery from inactivation (compared with deactivation). This allowed determination of the rate of activation using the method shown in Fig. 2 A (Wang et al., 1997). A variable duration prepulse is used to drive channels into the open and/or inactivated state before stepping to a negative potential (−120 mV), which allows rapid recovery from inactivation (see Scheme II, the current measured at −120 mV is inward since the K⁺ reversal potential was −90 mV). Measuring the time course at different prepulse potentials allowed determination of the voltage dependence of the rate of activation. Comparison of these rates in 1.8 mM extracellular Ca²⁺ (Fig. 2 C) and 10 mM Ca²⁺ (D) shows that activation was slower in the presence of 10 mM Ca²⁺. Elevated Ca²⁺ decreased the rate of HERG activation at all potentials measured (+60 to 0 mV). This can be seen in Fig. 2 B, which shows activation time constants determined by fitting a second order exponential equation to the data (see legend for details). The slow time constant of activation was significantly increased (P < 0.05) by elevating extracellular Ca²⁺ from 1.8 to 10 mM for all test potentials between +50 and 0 mV. The fast time constant of activation was significantly increased (P < 0.05) for test potentials +50, +40, +30, and 0 mV.

Figure 2.

The effect of Ca²⁺ on the rate of activation of HERG channels. (A) Representative voltage-clamp protocol and current traces for measuring HERG activation time course in 1.8 mM Ca²⁺. The membrane potential is stepped to the test potential (in this case +40 mV) for a variable duration before stepping to −120 mV. (B) Large (top) and small (bottom) time constants of activation in 1.8 (•) and 10 (○) mM extracellular Ca²⁺ are shown. The time constants were determined by fitting a two-exponential equation to activation data like that in C and D. The peak tail current after repolarizing to −120 mV is plotted as a function of the test pulse duration in 1.8 (C) and 10 (D) mM Ca²⁺ for voltages: 0 mV (⋄; n = 6 in 1.8 mM, n = 5 in 10 mM), +10 mV (♦; n = 3 in 1.8 mM, n = 3 in 10 mM), +20 mV (▵; n = 4 in 1.8 mM, n = 4 in 10 mM), +30 mV (▴; n = 3 in 1.8 mM, n = 4 in 10 mM), +40 mV (○; n = 4 in 1.8 mM, n = 5 in 10 mM), +50 mV (•; n = 5 in 1.8 mM, n = 4 in 10 mM), and +60 mV (□; n = 3 in 1.8 mM, n = 4 in 10 mM). The smooth lines in C and D are two-exponential fits of the mean values at each voltage. Each set of raw data points was fit with a two-exponential equation and then normalized to the limiting amplitude of that fit before averaging data from multiple cells. Error bars in B–D indicate SEM and are shown for each point.

Ca²⁺ Speeds HERG Channel Deactivation

Deactivation kinetics were examined by measuring the voltage dependence of the time course of the K⁺ current decay upon stepping to different membrane potentials as shown in Fig. 3. Time constants of deactivation were determined by fitting a monoexponential equation to the initial current decay. The initial phase of deactivation is well fit by a monoexponential allowing a simple quantitation of the change in deactivation rate upon elevation of extracellular Ca²⁺. Time constants determined in this manner were plotted as a function of the test potential to obtain the curves in Fig. 3 D. Increasing external Ca²⁺ from 1.8 to 10 mM increased the rate of channel deactivation at every potential measured (P < 0.05), resulting in smaller measured time constants (Fig. 3 D).

Figure 3.

The effects of elevated extracellular Ca²⁺ on HERG deactivation. A and B are families of current recordings measured in 1.8 and 10 mM Ca²⁺, respectively, using the voltage-clamp protocol shown at top right. The membrane potential was stepped from a holding potential of −80 to +50 mV for 2 s before stepping to the test potential between −130 and +20 mV. Traces in C are super-imposed tail currents measured at −60 mV taken from the records shown in A and B and scaled to the peak current level. The time constants shown in D were measured by fitting a monoexponential function (y = Ae ^−(t/τ) + c) to the initial segment of the tail currents at the indicated membrane potentials in 1.8 (•) or 10 (○) mM Ca²⁺. Time constants were not obtained at potentials less than −80 mV or greater than −105 mV due to the difficulty in fitting the small currents close to the K⁺ reversal potential. Each point represents the mean and SEM for three to four cells. The time constants were significantly different between 1.8 and 10 mM Ca²⁺ with P < 0.05 at all voltages tested.

Neither External Ca²⁺ nor Mg²⁺ Are Required for Channel Closing

Under physiological conditions, Ca²⁺ is always present in the extracellular environment, and it is conceivable that extracellular Ca²⁺ is required for gating (Armstrong and López-Barneo, 1987; Armstrong and Miller, 1990; Ho et al., 1996). Voltage-dependent block of the open channel could be a mechanism of channel deactivation, as has been suggested for I_K in rabbit sinoatrial node (Ho et al., 1996). Fig. 4 A shows that HERG channels continued to gate when bathed in a solution with no added Ca²⁺ or Mg²⁺ and buffered with 2 mM EGTA. Removal of extracellular divalent cations increased the K⁺ current immediately upon solution exchange. Channels opened more rapidly upon membrane depolarization leading to a transient current peak that rapidly decays with the onset of inactivation. Channels also closed more slowly upon repolarization, but channels continued to gate. These effects were rapidly and completely reversible upon the return of control extracellular solutions. These results are consistent with the effects of raising extracellular Ca²⁺ seen in Figs. 1–3, where opposite effects are seen. Fig. 4 B shows the Ca²⁺ concentration dependence of the time constant of deactivation at −120 mV. If channel closing results from block by external divalent cations, then gating should cease in the absence of divalent cations. This is not the case. Fig. 4 B shows that gating persists at extremely low extracellular Ca²⁺ concentrations. In fact, the rate of deactivation approaches a limiting value (time constant ∼50 ms) for Ca²⁺ concentrations below 100 μM. Thus, divalent cation pore block cannot be the mechanism of deactivation gating for HERG channels, nor are these ions absolutely required for gating.

Ca²⁺ Is Not a Fast Voltage-dependent Blocker of HERG Channels

Fig. 1 indicates that raising extracellular Ca²⁺ results in decreased outward K⁺ currents. Fig. 4 shows that time-dependent block of the channel by divalent cations is not the mechanism of the channel deactivation since deactivation occurs even in the absence of Ca²⁺ and Mg²⁺. To determine whether the Ca²⁺ effect is due to a rapid voltage-dependent block of open HERG channels, the method of Gilly and Armstrong (1982) was modified to accommodate HERG inactivation behavior. The instantaneous current–voltage relationships were measured in 1.8 and 10 mM external Ca²⁺ (Fig. 5, A and B). Increasing external Ca²⁺ from 1.8 to 10 mM did not alter the shape of the open channel current– voltage relationship. The K⁺ current was decreased in 10 mM Ca²⁺ by ∼20% at all potentials measured (Fig. 5 C), indicating that the Ca²⁺ effect was independent of membrane potential. This finding is not consistent with the idea that the positively charged Ca²⁺ is acting as a rapid voltage-dependent blocker of the channel (Gilly and Armstrong, 1982). Therefore, neither slow nor fast voltage-dependent block is the mechanism of the Ca²⁺ effect. We next investigated the possibility that the apparent Ca²⁺-induced decrease in conductance was due to the observed changes in channel gating.

Figure 5.

Lack of rapid voltage-dependent open-channel Ca²⁺ block. (A and B) Instantaneous current measurements through open HERG channels in the presence of 1.8 and 10 mM external Ca²⁺, respectively. The voltage clamp protocol is shown at the top right. The membrane potential was stepped from a holding potential of −80 to +50 mV The potential was then stepped to −100 mV, before stepping to the test potential between +100 and −140 mV. The membrane potential was first stepped to +50 mV for 1,975 ms to fully activate channels, and then stepped to −100 mV for 12.5 ms to allow recovery from inactivation. This allows most channels to recover from the inactivated state into the open state, but does not allow time for most channels to return to the closed state. The membrane potential was then stepped to the test potential (plotted on the abscissa in C). The resulting current was fit with an exponential curve that was then extrapolated to the moment of transition to the test potential for test potentials of −100 mV. This extrapolation was done to correct for current that inactivates during the capacitance transient. At potentials less than −100 mV, the initial current level after the step to the test voltage was measured. The currents in 1.8 (•) and 10 (○) mM Ca²⁺ were then plotted on the ordinate in C. The curves in C were corrected for deactivation during the recovery step (12.5 ms at −100 mV) by estimating the time course of deactivation at −100 mV in each condition. A monoexponential was fit to the initial deactivation as depicted by the dashed fit in E. Extrapolation of this fit estimates the K⁺ current in the absence of inactivation (E, lower arrow). Dividing this extrapolated current by the current observed 12.5 ms after the step to −100 mV (the length and potential of the recovery step in A and B) allowed estimation of the fraction of channels still open. This measurement was made three times for each cell and the average ratio was used for the subsequent correction. For example, the ratios for the cell shown in the figure were 1.25 in 1.8 mM Ca²⁺ and 1.52 in 10 mM Ca²⁺. Multiplying the current measured in 1.8 mM Ca²⁺ by 1.25 and the current measured in 10 mM Ca²⁺ by 1.52 results in the corrected currents seen in D. Similar results were obtained in two additional cells.

Increasing extracellular Ca²⁺ slowed the rate of HERG activation and accelerated deactivation (Figs. 1, 3, and 4). We therefore examined whether these kinetic changes could account for the Ca²⁺-induced reduction of HERG current seen in Fig. 5 C. The protocol for measurement of this instantaneous current–voltage relationship contains a 12.5-ms step to −100 mV that was required to allow the channels to recover from inactivation. Thus, in elevated Ca²⁺, accelerated deactivation (Fig. 3) might result in more channels deactivating during the 12.5-ms recovery step, before the measurement of current. This would result in fewer open channels at the time of the test step and hence would reduce the instantaneous K⁺ current measured upon stepping to +30 mV.

Therefore, we measured the rate of deactivation at −100 mV and used this information to estimate the deactivation that occurred before measurement. This estimation was used to scale instantaneous current–voltage curves for the deactivation that occurs during the 12.5-ms recovery step at −100 mV (see Fig. 5 legend for details). Exact determination of the degree of deactivation that occurs during the recovery step is not possible if channels must recover from inactivation before deactivating (Schemes SI and SII). Nonetheless, because deactivation at −100 mV is more than an order of magnitude slower than recovery from inactivation (see Figs. 2 and 7), it is possible to estimate the fraction of channels that have deactivated during the 12.5-ms recovery step using the method in Fig. 5 (adapted from Smith et al., 1996). When the enhanced rate of deactivation induced by 10 mM Ca²⁺ was accounted for, the apparent decrease in current was eliminated (Fig. 5 D). This resulted in instantaneous current–voltage relationships in 1.8 and 10 mM Ca²⁺ that superimpose. This analysis illustrates that the reduction of HERG K⁺ current observed in elevated extracellular Ca²⁺ concentrations results from the kinetic changes caused by Ca²⁺.

Scheme I.

Scheme II.

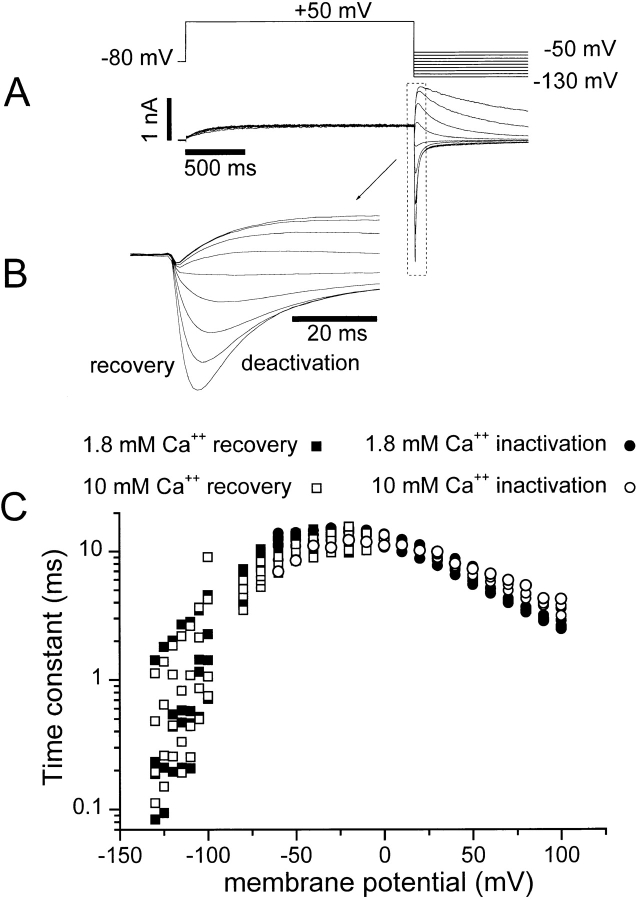
Figure 7.

The voltage dependence of the rate of inactivation in 1.8 and 10 mM external Ca²⁺. The voltage-clamp protocol used to measure the transition into the inactivated state is shown in Fig. 5 B. The voltage clamp protocol at the top of this figure (A) was used to measure the rate of recovery from inactivation. HERG current was inactivated by a 2-s step to +50 mV. The membrane potential was then stepped to the test potential between −130 and −50 mV to measure the rate of recovery. Holding potential was −80 mV. Representative current tracings are shown below. B is an expansion of the recording in A to illustrate the recovery phase. The current scale bar in A also applies to B. The initial increase of the current after stepping to the test potential was fit with a monoexponential equation to determine a time constant for the recovery process at the test potentials. The time constants are plotted versus test potential in C for 1.8 (▪) and 10 (□) mM external Ca²⁺. The time constants of the inactivation process at potentials between −40 and +100 mV were determined using the voltage clamp protocol in Fig. 5 B. The time course of inactivation of the open channels was observed as the decay of current during the third step. A monoexponential equation was fit to the decay of the current upon stepping to the test potential. Time constants measured in this fashion for 1.8 (•) and 10 (○) mM external Ca²⁺ are shown in C. Each point represents a measurement from an individual cell. Measurements were repeated in three to six cells at each membrane potential.

Ca²⁺ Acceleration of Deactivation Alters the Apparent Voltage Dependence of Activation

With this information on the influence of deactivation on the instantaneous current–voltage curves in Fig. 5 C, the decrease in outward current seen in the isochronal activation curve with 10 mM Ca²⁺ in Fig. 1 D was reexamined. To test whether this decrease in current might also be due to the observed changes in gating kinetics, a three-pulse protocol (Fig. 6) was used to measure the voltage dependence of isochronal activation (Smith et al., 1996). Deactivation at −100 mV was measured in each test solution immediately after measurement of the voltage dependence of isochronal activation in Fig. 6 B. The activation curves observed with the three-pulse protocol and the curves scaled to account for deactivation are shown in Fig. 6, B and C, respectively. This scaling for deactivation removed the observed reduction in HERG peak tail currents, leaving only a parallel shift of the curve to more positive membrane potentials.

Figure 6.

Correction of activation curves for Ca²⁺ induced acceleration of deactivation. The three-pulse protocol at the top of A was used. The membrane potential was held at −80 mV, and then stepped to a test potential of +50 to −70 mV for 3 s. A step to −100 mV for 12.5 ms allowed recovery from inactivation. The final step to +30 mV was 35 ms in duration. A representative family of current recordings in A is shown on a split time scale for clarity. The time scale bar applies only to the portion of the recording after the break. (B) Current measured at the immediate beginning of the third pulse plotted as a function of the test pulse potential in 1.8 (•) and 10 (○) mM Ca²⁺ is shown. (C) Current measurements from B after correction for deactivation that occurred during the 12.5-ms recovery step to −100 mV are shown. The correction was made as in Fig. 5.

If the observed reduction of K⁺ current results from enhanced deactivation of the channels before measurement, then the decrease should become greater if a longer recovery period allows the degree of deactivation to increase. We analyzed data from protocols using 12.5-, 25-, and 50-ms recovery periods as an internal control for this method of analysis (data not shown). Increasing recovery duration results in progressive decreases in measured current (due to increasing contamination from deactivation). Likewise, increasing the length of recovery increases the amount of current suppression by addition of 10 mM Ca²⁺. In each case, this decrease could be removed by accounting for deactivation. This analysis illustrates that the reduction in observed outward current in 10 mM Ca²⁺ (Figs. 1 D and 6 B) is not due to channel block by Ca²⁺. The data in Figs. 4 and 5 also demonstrate that Ca²⁺ does not block HERG directly. Instead, Ca²⁺ appears to interact with or influence the channel voltage sensor(s) and alter the apparent membrane potential sensed by the channel gating machinery.

A common way in which multivalent cations have been found to influence ion channel gating is through screening of diffuse negative surface charges (Frankenhaeuser and Hodgkin, 1957; Cole, 1969; Gilbert and Ehrenstein, 1969; McLaughlin et al., 1971; Århem, 1980; Green and Andersen, 1991; Hille, 1992; Elinder et al., 1996). This can cause shifts in the membrane potential sensed by a membrane protein, such as a voltage-gated K⁺ channel. This type of nonspecific surface charge screening should affect all channel parameters that depend on membrane potential (Gilly and Armstrong, 1982). To determine whether all voltage-dependent channel parameters are equally affected by external Ca²⁺, the inactivation of HERG currents in the presence of 1.8 and 10 mM Ca²⁺ was examined.

Ca²⁺ Does Not Affect the Rate of Inactivation

The rate of channel inactivation was measured in 1.8 and 10 mM external Ca²⁺ over a range of membrane potentials and under conditions designed to isolate the inactivation process. Two voltage-clamp protocols were used to determine the voltage dependence of inactivation and recovery from inactivation (Figs. 5 B and 7 A). A three-pulse protocol (see Fig. 5 B) was used to measure the rate of inactivation at membrane potentials more positive than −60 mV (Smith et al., 1996). Monoexponential curves were fit to the rapidly declining current during the step to the test potential, and the time constants obtained from these fits are plotted versus membrane potential in Fig. 7 C (circles, right side). Fig. 7 C shows that, surprisingly, the voltage-dependent rate of inactivation was almost unaffected by elevation of extracellular Ca²⁺ from 1.8 to 10 mM. The large shift in voltage-dependent gating behavior observed for activation and deactivation was not present. At membrane potentials more negative than −60 mV, it was difficult to accurately measure inactivation by the three step method described above. Therefore, a two-pulse protocol, described in Fig. 7 A, was used to measure the rate of recovery from inactivation between −130 and −50 mV. In this case, the channels were activated and inactivated by a 2-s pulse to +50 mV. Then, stepping to the test potential results in a rising phase of the tail current that is largely due to recovery from inactivation (Smith et al., 1996). The rate of recovery was estimated by fitting a monoexponential function to the rising recovery phase, and the time constant obtained was plotted as a function of the test potential in Fig. 7 C (squares, left side of curve) along with the time constants obtained for inactivation with the three-pulse protocol (Fig. 7 C, circles, right side). As observed for the rate of inactivation, the rate of recovery from the inactivated to the open state was largely unaffected by increasing the Ca²⁺ concentration to 10 mM. These findings support the hypothesis that there are separate voltage sensors for channel activation and inactivation gating (Wang et al., 1997; Zou et al., 1998) and indicate that external Ca²⁺ affects them differently.

Voltage Dependence of Availability Is Ca²⁺ Independent

The very slow activating and fast inactivating phenotype of HERG currents prevents traditional determination of a steady state inactivation (h_∞) curve (Hodgkin and Huxley, 1952; Hille, 1992; Smith et al., 1996; Schönherr and Heinemann, 1996; Spector et al., 1996b; Wang et al., 1997). The voltage dependence of the distribution of channels between the open and inactivated states can be tested by the method illustrated in Fig. 8 (Smith et al., 1996; Zou et al., 1998).

Figure 8.

Voltage dependence of channel distribution between the open and inactivated states in 1.8 and 10 mM external Ca²⁺. Measurements were made using the voltage-clamp protocol shown at the top of A. Note the difference in time scales before and after the break. The cell was stepped from a holding potential of −80 to +70 mV for 3 s to maximally inactivate the channels. The membrane potential was then stepped to the test potential for 12.5 ms to allow channels to recover into the open state. The membrane potential was then changed to +30 (where the K⁺ driving force is greater) to estimate the fraction of open channels. A representative current record measured in 1.8 mM Ca²⁺ is shown. Peak K⁺ currents at +30 mV were used to generate the voltage-channel availability curves in B. The decrease for test potentials less than −100 mV is due to deactivation at these potentials (see Fig. 3). Each point in B and C represents paired measurements in both conditions for four cells. Filled symbols indicate 1.8 mM Ca²⁺; open symbols indicate 10 mM Ca²⁺. Correction of the curves measured in B for deactivation gives the sigmoid curve in C. The correction was accomplished as for Figs. 5 and 6 with the exception that deactivation correction ratios were determined for each corrected potential. Only potentials of −40 mV or less were corrected. At more positive voltages, there is little deactivation, making this correction unnecessary. Normalization was accomplished by fitting a Boltzmann curve to the corrected current in 1.8 mM Ca²⁺ for each cell (C). All four curves illustrated in B and C were then normalized to the limit of the Boltzmann fit of the corrected current in 1.8 mM Ca²⁺. Error bars show the SEM for each point. The smooth curve in C is a Boltzmann fit of the mean corrected data in 1.8 mM external Ca²⁺. The midpoint for the fit was −74 mV and the slope factor was +24 mV.

A three-pulse protocol was used and the instantaneous current measured in the third step to +30 mV was plotted as a function of the test membrane potential (Fig. 8 B). Note that these curves (Fig. 8 B) largely superimpose except at potentials less than −80 mV, indicating that 10 mM Ca²⁺ had no effect on the voltage dependence of this relationship. The decrease in K⁺ current observed for test steps more negative than −100 mV is again due to channel deactivation at these membrane potentials. Accounting for the enhanced rate of deactivation eliminates this decrease (Fig. 8 C). Correction was accomplished in the same manner as was described for Figs. 5 and 6, with the exception that the fraction of current lost due to deactivation must be determined for each test potential. Thus, both the corrected and uncorrected data indicate that Ca²⁺ affects only deactivation and does not affect the voltage dependence of inactivation. A decrease in current measured with this voltage clamp protocol due to accelerated deactivation is also predicted by the model discussed below.

Small Changes in External Ca²⁺ Alter HERG K⁺ Current During an Action Potential Clamp

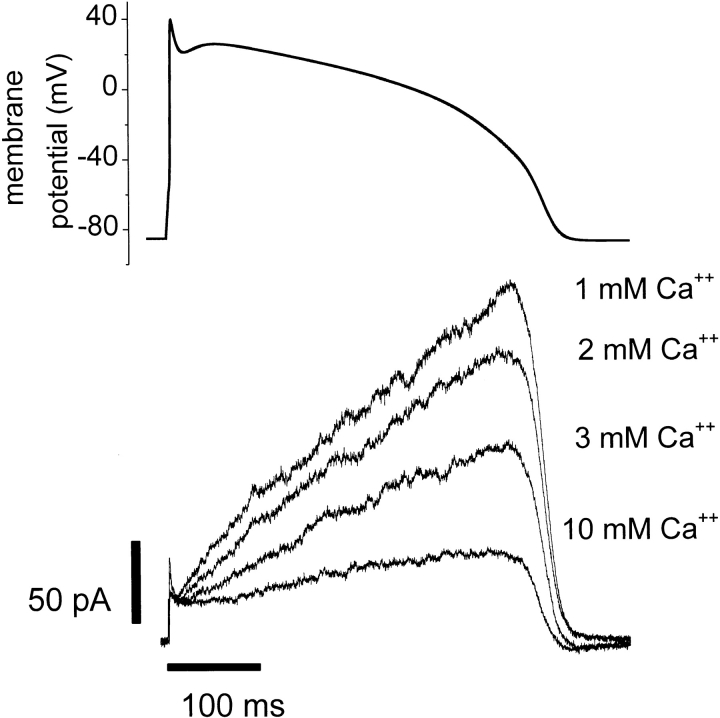
To determine whether changes in external Ca²⁺ near the physiological range impact HERG K⁺ currents during the time course of a cardiac action potential, we used a voltage-clamp protocol with the shape of an action potential (Fig. 9). A similar protocol has been used to study HERG current stably expressed in HEK-293 cells (Zhou et al., 1998b). Human total serum Ca²⁺ concentrations range between 1.5 and 4.25 mM (average ∼2.5 mM), ∼50% of which is in the free ionized form (Guyton, 1991). Fig. 9 illustrates how Ca²⁺ modulation of HERG gating results in changes in current during an action potential clamp. The action potential clamp protocol was applied to a cell expressing HERG K⁺ channels in solutions containing 1, 2, 3, or 10 mM external Ca²⁺. Relatively little outward K⁺ current was apparent during the peak of the action potential clamp, but as the cell membrane potential decreases (at the end of the action potential), HERG current rises sharply. HERG currents during this voltage clamp protocol were highly sensitive to changes in extracellular Ca²⁺ concentration between 1 and 3 mM. Note that, although our experiments were at room temperature, the action potential duration used (∼400 ms) is appropriate for a human ventricular myocyte at 37°C. As a consequence, these experiments may underestimate the impact of Ca²⁺ on the currents during an actual action potential. Changing external Ca²⁺ from 1 to 3 mM resulted in a 50% reduction of the maximum outward K⁺ current during this action potential voltage clamp protocol. For comparison with the concentrations used in the biophysical characterization of the Ca²⁺ effect, 10 mM Ca²⁺ was applied to the cell and caused an 80% reduction of the maximum current under these conditions.

Figure 9.

A voltage clamp waveform in the shape of a ventricular action potential (A) was applied to a HERG expressing CHO-K1 cell at 25°C. The waveform was computed from a published model (Beeler and Reuter, 1977). Superimposed K⁺ current traces measured in 1–3 or 10 mM extracellular Ca²⁺ from a single cell are shown in B. Each trace represents the average of five whole cell voltage clamp sweeps in each condition. Similar results were obtained in two other cells.

discussion

Mechanisms of Ca²⁺ Modulation

Our data suggest an intimate association of Ca²⁺ with the HERG channel protein that alters the voltage dependence and kinetics of channel activation gating, while having little effect on inactivation gating. Figs. 1–3 show that increasing extracellular Ca²⁺ from 1.8 to 10 mM had at least two effects on HERG currents. The voltage dependence of channel activation was shifted to more depolarized membrane potentials and the current amplitude was decreased at membrane potentials less than +50 mV. Several simple mechanisms could potentially explain these effects of Ca²⁺. First, voltage-dependent block of the channel might decrease HERG current at potentials less than +50 mV, producing an apparent shift in the voltage-dependent activation of the channels. Relief of block at positive potentials could then account for the lack of block at potentials +50 mV. This possibility was ruled out by two interdependent findings. Removing external divalents does not remove deactivation (Fig. 4), eliminating the possibility that slow voltage-dependent block by divalent cations causes HERG deactivation. It is impossible to assure that all divalent cations have been removed from the external solution, but by omitting them from the solution and adding the chelator EGTA, we can assure that the concentration is extremely low (∼2.5 nM). We also showed (Fig. 4 B) that the time constant of HERG deactivation reaches a maximum (∼50 ms) in 100 μM Ca²⁺ and does not increase for lower concentrations of Ca²⁺ over five orders of magnitude. The shape of the open channel current–voltage relationship is not changed by elevating external Ca²⁺ (Fig. 5 C); a voltage-dependent open channel blocker would change the shape of this curve (Gilly and Armstrong, 1982). A second possible mechanism for Ca²⁺ modulation is through charge screening of negative membrane surface charges, resulting in a change in the membrane potential sensed by the channel (Green and Andersen, 1991). Such a screening could be nonspecific, resulting from association with diffuse charged moieties like membrane phospholipid head groups, or it could occur through specific interaction with the channel protein. Nonspecific surface charge screening would cause a global change in the membrane potential (V) perceived by the entire channel protein, and therefore all voltage-dependent parameters of the channel would be shifted in a parallel manner along the voltage axis by the change in perceived membrane potential (V = V_clamp − V_shift). The fact that the voltage dependence of activation gating was shifted by elevated external Ca²⁺ (Figs. 1–4 and 6) while inactivation gating was not (Figs. 7 and 8) indicates that nonspecific charge screening inducing a change in the membrane potential sensed by the entire channel cannot be the mechanism of Ca²⁺ modulation. Ca²⁺ association with a specific channel residue(s) could cause more selective effects on channel function since it need not result in a global change in the potential sensed by the channel protein. The observation of differential modulation of the voltage dependence of activation and inactivation greatly constrains the possibilities for the nature of the channel voltage sensing machinery. Both HERG activation and inactivation gating appear voltage dependent (Figs. 2, 3, and 7; Sanguinetti et al., 1995; Trudeau et al., 1995; Smith et al., 1996; Schönherr and Heinemann, 1996; Spector et al., 1996b; Wang et al., 1996, 1997; Zou et al., 1998). However, it is possible that inactivation derives its apparent voltage dependence from coupling to voltage-dependent channel activation, as is true for Shaker potassium channels (Zagotta and Aldrich, 1990; Hoshi et al., 1991). In this case, any effect on the activation voltage sensor would also alter the apparent voltage dependence of inactivation, contrary to our data (Figs. 1–3, 7, and 8) and previous observations of K⁺ modulation of HERG (Liu et al., 1996; Wang et al., 1996, 1997). Alternatively, both processes could be intrinsically voltage dependent, but use the same voltage-sensing machinery. This possibility is also excluded by the specificity of the Ca²⁺ effect. If the same voltage sensor controlled both activation and inactivation, Ca²⁺ shielding of that sensor should affect both gating processes, contradicting the data. Our data seem to indicate that there are at least two voltage-sensing regions involved in HERG channel gating: one governing channel activation and another for inactivation. Furthermore, these distinct sensors can detect different local values of membrane potential and be differentially screened by Ca²⁺.

To test the feasibility of this idea, we used a simplified HERG channel gating model to determine whether our observations could be predicted by a voltage shift in only the voltage dependence of the rate constants that govern channel activation (see methods for details). The model simulates the major features of our own data and is consistent with data from the literature (Trudeau et al., 1995; Sanguinetti et al., 1995; Smith et al., 1996; Schönherr and Heinemann, 1996; Wang et al., 1997). In the model, both activation and inactivation are voltage dependent (Wang et al., 1997). Fig. 10 A illustrates simulated currents for the voltage-clamp protocol in Fig. 1. Elevated Ca²⁺ was simulated (Fig. 10 B) by including a +23-mV bias in the rate equations for the activation rate constants (a ₁, a ₋₁, a ₃, a ₋₃). As seen in Fig. 10, this change alone accounts for a decrease in K⁺ currents and an increase in the rate of deactivation (compare with Fig. 1, A and B). Fig. 10 C plots the simulated outward current after 2 s at the test potential, and D shows the peak tail current (compare with Fig. 1, C and D, respectively). Fig. 10 E indicates that the simple shift of voltage-dependent activation rate constants in the model also results in an apparent decrease in the open channel current–voltage relationship (compare with Fig. 5 C). Furthermore, the modeled voltage shift does not affect the voltage dependence of the equilibrium between the open and inactivated states (Fig. 10 F). The model also predicts the Ca²⁺-induced decrease in K⁺ current measured at negative test potentials with this protocol (compare Figs. 10 F and 8 B). This occurs because the rate of deactivation is accelerated in elevated extracellular Ca²⁺ (Fig. 3). Therefore, at test potentials more negative than the threshold for channel activation, the faster deactivation in 10 mM extracellular Ca²⁺ allows more channels to make the transition from the open to the closed state. As a result, 10 mM Ca²⁺ exaggerates the decrease in the channel availability curve measured at negative potentials in Fig. 8 B, as is simulated in the modeled data (Fig. 10 D). Thus, a simple shift in the membrane potential felt by the activation process, but not the inactivation process, explains the effects experimentally observed upon elevation of extracellular Ca²⁺. Such an effect can be envisioned if we assume Ca²⁺ binds to a region of the HERG protein near the region that controls activation voltage sensing and alters the membrane potential sensed by amino acids in the vicinity of the binding site. Voltage shifts applied to both activation and inactivation rate constants in the model failed to qualitatively reproduce the experimental observations (not shown). Although we cannot definitively rule out the possibility that Ca²⁺ causes an allosteric change in HERG channels that mimics a specific association near the activation voltage sensor, our data are consistent with a simple Ca²⁺-induced change in membrane potential sensed specifically by the activation process.

Figure 10.

Simulated kinetics and voltage dependence of K⁺ current generated from the model (see methods) using the voltage-clamp protocols shown to simulate data in Figs. 1, 5, and 8. Simulated currents are shown for a series of membrane potential steps ranging from −80 to +70 mV in 10-mV steps. A +23-mV shift was applied to the equations for the activation rate constants to simulate 10 mM [Ca²⁺]_out. (A) K⁺ currents generated from a control simulation (1.8 mM [Ca²⁺] = no shift in activation rate constants). (B) K⁺ currents generated during simulated elevated external Ca²⁺ [10 mM] (i.e., a +23-mV shift in activation rate constants). Note the reduction of current and the increase in deactivation rate in simulated 10 mM [Ca²⁺]_out. (C) Outward currents during the membrane potential steps to the potential shown on the abscissa. Isochronal values were taken after 2 s at the test potential. Closed symbols in C–F indicate values taken from the control simulation; open symbols are values from the activation shift simulation. (D) Tail currents during the membrane potential steps to −50 mV plotted versus the test pulse potential. Values were taken at the peak of the tail. (E) Reduction in “instantaneous” current due to the change in the deactivation rate (see Fig. 5). The same shift in the voltage dependence of the activation rate constants (see above) leads to the decreased current measured in this voltage clamp protocol. The reduction in current is explained entirely by a change in the rate of deactivation that occurs during the brief step to −100 mV. (F) Voltage dependence of the open–inactivated state transitions. Currents were generated from the model using the voltage-clamp protocol shown to simulate data in 1.8 mM Ca²⁺ (compare Fig. 8). The model was equilibrated at +70 mV for 3.01 s. The membrane potential was changed to a value between +60 and −130 mV for 12.5 ms, and then changed to +30 mV. This placed the channels in the inactivated (0.98) or open (0.02) state. Stepping to potentials between +60 and −130 mV probes the equilibration between the open and inactivated states at these potentials. The step to +30 mV reveals the channels in the open state. The model accurately simulates the decrease in K⁺ current at negative potentials due to enhanced deactivation, and reveals that there is no shift in the voltage dependence of this relationship when the voltage dependence of the activation rate constants were shifted. Simulated currents used to generate the curve in E were “normalized” to the maximum possible current based upon the K⁺ driving force and the scale factor used to generate the currents.

Comparison with Previous Studies

Ca²⁺ is critical in the gating of some voltage-gated channels. HERG belongs to the family of six transmembrane domain voltage-gated K⁺ channel genes such as Shaker, EAG, and the mammalian Kv channels. The effects of Ca²⁺ have been most thoroughly characterized in the squid delayed rectifier K⁺ channel and the recombinant Shaker K⁺ channel; both require divalent cations to stabilize the closed channel and maintain channel selectivity (Armstrong and Matteson, 1986; Armstrong and López-Barneo, 1987; Armstrong and Miller, 1990). Unlike these channels, we find that HERG channels do not absolutely require Ca²⁺ for selectivity and gating, though even control extracellular Ca²⁺ concentrations cause a shift relative to the gating behavior in their absence (Fig. 4). These results agree with data for I_Kr recorded from guinea pig ventricular myocytes in high K⁺ (Sanguinetti and Jurkiewicz, 1992). Our data show that the voltage dependence of the HERG activation curve was shifted by +22.3 ± 2.5 mV upon raising extracellular Ca²⁺ from 1.8 to 10 mM. This shift was accompanied by slowed channel activation, and enhancement of the rate of channel deactivation, even in physiological concentrations of external permeant cations (4 mM K⁺). Deactivation of I_K in rabbit sinoatrial node myocytes is sensitive to external divalent cations, and block by the extracellular divalent cations Ca²⁺ and Mg²⁺ has been proposed to be the primary determinant of voltage-dependent deactivation gating of that current (Ho et al., 1996). Our data indicate that HERG K⁺ channels retain deactivation gating even in the absence of external divalent cations (Fig. 4). Furthermore, the apparent decrease of current through open HERG channels was not voltage dependent (Fig. 5). This indicates that Ca²⁺ does not experience the transmembrane field when interacting with HERG channels. Thus, neither a time-dependent nor -independent voltage-dependent block of open HERG channels can explain the effect of extracellular Ca²⁺. The observed decrease in HERG K⁺ currents upon elevation of external Ca²⁺ was completely explained by modulation of gating. Correction of the current amplitudes for these Ca²⁺-induced changes in gating removed the apparent current suppression (Figs. 5, 6, and 8). Thus, external divalent cations modulate, but do not cause, HERG deactivation gating. This is in contrast with the conclusions that divalent cations cause deactivation gating of rabbit I_K (Ho et al., 1996).

There are several possible explanations for this discrepancy. It is conceivable that native rabbit sinoatrial node K⁺ channels interact with divalent cations in a fundamentally different manner than heterologously expressed HERG channels due to differences in structure or subunit composition. However, there is considerable similarity in the behavior of rabbit sinoatrial node I_K and HERG (Shibasaki, 1987; Trudeau et al., 1995; Sanguinetti et al., 1995; Ho et al., 1996). A more likely explanation involves the differences in the external ionic conditions between the two studies. Our study was performed in 4 mM external K⁺, while studies in rabbit sinoatrial node were performed in the presence of high extracellular K⁺ (140 mM). Elevated external K⁺ was necessary in part because the native currents are small in physiological K⁺ (Ho et al., 1996). Both HERG K⁺ currents and I_Kr are modulated by external K⁺(Sanguinetti and Jurkiewicz, 1992; Trudeau et al., 1995; Sanguinetti et al., 1995; Schönherr and Heinemann, 1996; Smith et al., 1996; Wang et al., 1996, 1997; Yang et al., 1997). Elevated extracellular K⁺ slows inactivation and deactivation gating of HERG. Slow deactivation kinetics induced by high K⁺ could make deactivation in the absence of extracellular divalent cations difficult to observe. This difficulty is exacerbated by the apparent competition between external K⁺ and Ca²⁺ (Ho et al., 1998). Elevated extracellular K⁺ (20 mM) decreases the shift in the HERG channel isochronal current–voltage curve caused by Ca²⁺ (Ho et al., 1998). This functional interaction was interpreted as a competition for a binding site within the channel pore (Ho et al., 1998). Since our data indicate that Ca²⁺ does not directly occlude the permeation pathway of HERG channels, this competition between external K⁺ and Ca²⁺ is most likely at a site outside the pore, or it may be a functional result of the two ions exerting antagonistic effects on channel gating at distinct sites.

The specificity of Ca²⁺ for HERG activation gating is further evidenced by the identity of K⁺ current at membrane potentials +10 mV in Fig. 1 C. This lack of current suppression could be interpreted as relief of Ca²⁺ block by positive membrane potentials (Ho et al., 1998). However, Figs. 4 and 5 illustrate that Ca²⁺ is not a voltage-dependent blocker of HERG currents. HERG outward currents are determined by both activation and inactivation controlling channel open probability. Outward currents during depolarization to intermediate potentials are suppressed because a shift of the voltage dependence of channel opening to more positive potentials leads to a decrease in channel open probability (Figs. 1 and 6). At membrane potentials greater than +10 mV, activation approaches a maximal level, and therefore channel inactivation is the primary determinant of HERG channel open probability at these voltages. HERG inactivation is much less sensitive to external Ca²⁺ than is activation (Figs. 7 and 8). Therefore at potentials greater than +10 mV, where inactivation largely determines HERG open probability, there is no Ca²⁺-induced decrease in current. Still another illustration of the specificity of the Ca²⁺ effect on activation gating is seen in Fig. 4 A. The current recorded in divalent cation–free solution showed a distinct inactivating phase during depolarization to +50 mV. This is because the rate of activation was increased upon removing Ca²⁺. Increased Ca²⁺ slowed activation (Fig. 2, B and C), but complete removal of divalent cations increased the rate of activation, while the rate of inactivation was little affected by changes in external Ca²⁺ (Figs. 7 and 8). The result is that a significant fraction of the channels were activated before the onset of inactivation, and a portion of the current inactivation could therefore be directly observed (Fig. 4 A).

Implications for the Nature of HERG Inactivation

It has been suggested that the inactivation of HERG K⁺ channels is mechanistically related to the C-type inactivation identified in Shaker K⁺ channels (Hoshi et al., 1991; Schönherr and Heinemann, 1996; Smith et al., 1996). Indeed, HERG inactivation shares several characteristics with C-type inactivation. For example, the rate of HERG inactivation is sensitive to extracellular K⁺ and TEA, but insensitive to intracellular TEA (Choi et al., 1991; Smith et al., 1996). The rate and voltage dependence of HERG inactivation are also dependent upon the identity of the amino acid present at position 631, analogous to Shaker residue 449, which in part determines the rate of C-type inactivation in those channels (López-Barneo et al., 1993; Schönherr and Heinemann, 1996; Zou et al., 1998). Unlike C-type inactivation in Shaker channels, HERG inactivation occurs more rapidly than activation at some potentials and has been suggested to have its own independent voltage sensor (Liu et al., 1996; Wang et al., 1996, 1997). Our data support this conclusion. Neither N- nor C-type inactivation of Shaker K⁺ channels have significant inherent voltage sensitivity. The apparent voltage dependence at positive potentials occurs through coupling to the voltage dependence of activation gating (Zagotta and Aldrich, 1990; Hoshi et al., 1991). However, it is now clear that, for HERG channels, mutation of serine 631 to alanine causes a shift in the voltage dependence of channel inactivation without shifting the voltage dependence of activation (Zou et al., 1998). The selectivity of the effect of Ca²⁺ on the activation gating process provides further support for the idea that HERG-type inactivation has a distinct voltage sensor and is therefore fundamentally different from C-type inactivation in Shaker-like channels.

Implications for HERG Function In Vivo

Fig. 9 shows that raising external Ca²⁺ from 1 to 3 mM reduced the HERG current maximum by 50% during an action potential voltage clamp. This large effect may seem surprising, but it is actually quite consistent with the biophysical characterization of the Ca²⁺ effect. The characteristic slow activating, fast inactivating behavior of HERG channels results in outward currents during the action potential clamp that are largest near the midpoint of the voltage-dependent activation curve. Hence, Ca²⁺-induced shifts in the midpoint of the activation curve greatly affect the current level during an action potential clamp. HERG currents recorded with a voltage clamp protocol of this type at 35°C display more current during the plateau phase of the action potential waveform due to the temperature dependence of the activation process (Zhou et al., 1998b). As a result, calcium effects could be even larger at physiological temperatures than they are in our study. Our results demonstrate how even modest changes in external Ca²⁺ concentration could significantly change the fraction of HERG channels available to participate in cellular repolarization in vivo.

Conclusions

We conclude that elevation of extracellular Ca²⁺ interacts specifically with channel activation voltage sensing, and does not act as a direct blocker of the open pore. This interaction is likely mediated by the association of Ca²⁺ with distinct, possibly negatively charged, channel residues near a voltage sensor. Voltage-dependent inactivation gating was nearly unaffected by elevating external Ca²⁺. The differential effect of external Ca²⁺ on the voltage dependence of activation and inactivation indicates that these two processes sense different values of transmembrane potential and are therefore probably physically separated in space. Further studies will be needed to elucidate the specific channel residues that are responsible for this interaction.

Abbreviations used in this paper

CHO

Chinese hamster ovary

HERG

human ether-à-go-go–related gene

I_Kr

delayed rectifier K⁺ current