Kinetic, Mechanistic, and Structural Aspects of Unliganded Gating of Acetylcholine Receptor Channels

Abstract

The spontaneous activity of adult mouse muscle acetylcholine receptor channels, transiently expressed in HEK-293 cells, was studied with the patch-clamp technique. To increase the frequency of unliganded openings, mutations at the 12′ position of the second transmembrane segment were engineered. Our results indicate that: (a) in both wild type and mutants, a C ↔ O kinetic scheme provides a good description of spontaneous gating. In the case of some mutant constructs, however, additional states were needed to improve the fit to the data. Similar additional states were also needed in one of six patches containing wild-type acetylcholine receptor channels; (b) the δ12′ residue makes a more pronounced contribution to unliganded gating than the homologous residues of the α, β, and ε subunits; (c) combinations of second transmembrane segment 12′ mutations in the four different subunits appear to have cumulative effects; (d) the volume of the side chain at δ12′ is relevant because residues larger than the wild-type Ser increase spontaneous gating; (e) the voltage dependence of the unliganded gating equilibrium constant is the same as that of diliganded gating, but the voltage dependences of the opening and closing rate constants are opposite (this indicates that the reaction pathway connecting the closed and open states of the receptor changes upon ligation); (f) engineering binding-site mutations that decrease diliganded gating (αY93F, αY190W, and αD200N) reduces spontaneous activity as well (this suggests that even in the absence of ligand the opening of the channel is accompanied by a conformational change at the binding sites); and (g) the diliganded gating equilibrium constant is also increased by the 12′ mutations. Such increase is independent of the particular ligand used as the agonist, which suggests that these mutations affect mostly the isomerization step, having little, if any, effect on the ligand-affinity ratio.

INTRODUCTION

The acetylcholine receptor channel (AChR) is a synaptic receptor ion channel (Karlin and Akabas 1995) whose activation can be understood in the framework of thermodynamic cycles with spontaneous gating and two ligand-binding events as the elementary steps (Monod et al. 1965; Jackson 1989; Edelstein and Changeux 1998). Accordingly, the equilibrium properties of unliganded gating determine those of liganded gating. For example, a recombinant AChR engineered to have a more favorable spontaneous opening reaction will also have a higher tendency to be open when diliganded.

In wild-type AChRs, as in any other allosteric protein, the gating equilibrium constant of the unliganded receptor is finely tuned to ensure the appropriate response both in the presence and absence of the ligand (Jackson 1989). Mutations that increase the gating equilibrium constant of unliganded AChRs have been shown to cause disease (Zhou et al. 1999a). It is thus of considerable importance to investigate the molecular mechanisms of unliganded gating.

There have been only a few studies of AChR spontaneous gating (Brehm et al. 1984; Jackson 1984, Jackson 1986; Jackson et al. 1990). In wild-type receptors, the paucity and brevity of unliganded openings make the characterization of this activity difficult. In addition, in cultured muscle cells, the precise molecular identity of the AChRs under study is not known with certainty because the presence of receptors having unusual subunit stoichiometries, in patches usually containing thousands of channels (Jackson 1986), is almost impossible to rule out. AChRs formed with only the α, β, and δ subunits exhibit more frequent spontaneous openings than complete α₂βδε receptors, but their respective mean open life times and single-channel conductances are indistinguishable (Jackson et al. 1990; Zhou et al. 1999b). Therefore, the extent to which these defective channels contribute to the “wild-type” unliganded activity remains an unsolved issue. This is, however, less of a concern when dealing with recombinant receptors expressed in HEK-293 cells, the system used in this paper. The small number of AChRs per patch makes the identification of ε/γ-less receptors, in the presence of ACh and at the single-channel level, unequivocal (Zhou et al. 1999b).

The frequency of unliganded openings has been shown to increase as a result of several different mutations, most notably in the second transmembrane segment (M2) (Ohno et al. 1995; Auerbach et al. 1996; Engel et al. 1996; Milone et al. 1997). Thus, we decided to study M2-mutant AChRs as a means of magnifying this otherwise almost intractable aspect of the channel's function. We chose the 12′ position (a Ser in δ, and Thr in α, β, and ε), which is near the middle of the M2 segment, for three reasons. First, it was known that a mutation at this position of the ε subunit increases spontaneous activity (Ohno et al. 1995; Auerbach et al. 1996). Second, this position is one of the very few M2 positions conserved among the entire superfamily of nicotinoid receptors (Table ). Finally, two naturally occurring mutations at this position have been shown to cause a slow-channel congenital myasthenic syndrome (α12′ T→I, Croxen et al. 1997; ε12′ T→P, Ohno et al. 1995). Cysteine-scanning mutagenesis studies suggested that the 12′ residues of the α and β subunits do not face the channel conduction pathway (Akabas et al. 1994; Zhang and Karlin 1998), while affinity-labeling experiments with snake α-neurotoxins suggested that, in Torpedo, δ12′ is accessible from the extracellular side (Machold et al. 1995a).

Table 1.

M2 Sequence Alignment of the Members of the Superfamily of Nicotinoid Receptors

Subunit	1′	2′	3′	4′	5′	6′	7′	8′	9′	10′	11′	12′	13′	14′	15′	16′	17′	18′	19′
m/hAChRα	M	T	L	S	I	S	V	L	L	S	L	T	V	F	L	L	V	I	V
tAChRα	M	T	L	S	I	S	V	L	L	S	L	T	V	F	L	L	V	I	V
m/hAChRβ	M	G	L	S	I	F	A	L	L	T	L	T	V	F	L	L	L	L	A
tAChRβ	M	S	L	S	I	S	A	L	L	A	V	T	V	F	L	L	L	L	A
m/hAChRδ	T	S	V	A	I	S	V	L	L	A	Q	S	V	F	L	L	L	I	S
tAChRδ	M	S	T	A	I	S	V	L	L	A	Q	A	V	F	L	L	L	T	S
m/hAChRγ	C	T	V	A	T/I	N	V	L	L	A	Q	T	V	F	L	F	L	V/L	A
tAChRγ	C	T	L	S	I	S	V	L	L	A	Q	T	I	F	L	F	L	I	A
m/hAChRε	C	T	V	S	I	N	V	L	L	A	Q	T	V	F	L	F	L	I	A
hAChRα2	I	T	L	C	I	S	V	L	L	S	L	T	V	F	L	L	L	I	T
hAChRα3	V	T	L	C	I	S	V	L	L	S	L	T	V	F	L	L	V	I	T
hAChRα4	I	T	L	C	I	S	V	L	L	S	L	T	V	F	L	L	L	I	T
hAChRα5	I	C	L	C	T	S	V	L	V	S	L	T	V	F	L	L	V	I	E
hAChRα6	V	T	L	C	I	S	V	L	L	S	L	T	V	F	L	L	V	I	T
hAChRα7	I	S	L	G	I	T	V	L	L	S	L	T	V	F	M	L	L	V	A
chAChRα8	I	S	L	G	I	T	V	L	L	S	L	T	V	F	M	L	L	V	A
hAChRα9	V	S	L	G	V	T	I	L	L	A	M	T	V	F	Q	L	M	V	A
hAChRβ2	M	T	L	C	I	S	V	L	L	A	L	T	V	F	L	L	L	I	S
hAChRβ3	L	S	L	S	T	S	V	L	V	S	L	T	V	F	L	L	V	I	E
hAChRβ4	M	T	L	C	I	S	V	L	L	A	L	T	F	F	L	L	L	I	S
h5-HT3A	V	S	F	K	I	T	L	L	L	G	Y	S	V	F	L	I	I	V	S
h5-HT3B	I	V	F	K	T	S	V	L	V	G	Y	T	V	F	R	V	N	M	S
m/hGlyRα1-4	V	G/A	L	G	I	T	T	V	L	T	M	T	T	Q	S	S	G	S	R
hGlyRβ	V	P	L	G	I	F	S	V	L	S	L	A	S	E	C	T	T	L	A
hGABAAα1-6	T	V	F	G	V/I	T	T	V	L	T	M	T	T	L	S	I	S	A	R
hGABAAβ1-3	V	A	L	G	I	T	T	V	L	T	M	T	T	I	S/N	T	H	L	R
r/hGABAAγ1-3	T	S/A/T	L	G	I	T	T	V	L	T	M	T	T	L	S	T	I	A	R
hGABAAδ	V	S	L	G	I	T	T	V	L	T	M	T	T	L	M	V	S	A	R
hGABAAε	T	S	L	G	I	T	S	V	L	T	M	T	T	L	G	T	F	S	R
hGABAAπ	T	C	I	G	V	T	T	V	L	S	M	T	T	L	M	I	G	S	R
hGABACρ1	V	P	L	G	I	T	T	V	L	T	M	S	T	I	I	T	G	V	N
hGABACρ2	V	S	L	G	I	T	T	V	L	T	M	T	T	I	I	T	G	V	N

M2 residues are usually referred to by following a numbering system that ranges from 1′ at the intracellular end to 19′ at the extracellular one. Residues occupying the 12′ position are bolded. The sequences of all subunits were taken from the SWISS-PROT Protein Sequence Database with the exception of AChRα8 (Schoepfer et al. 1990) and 5-HT_3B (Davies et al. 1999). Whenever possible, the human (h) sequences are given; otherwise, the sequences of either chicken (ch), mouse (m), or rat (r) are indicated. The M2 sequences of the human α, β, δ, and ε AChR subunits are identical with those of mouse (the clones used in this paper). Torpedo (t) sequences are also included.

Here, we show that the unliganded activity of M2 12′ mutants largely resembles that of AChRs from embryonic cultured mouse muscle (Jackson 1984, Jackson 1986). The higher frequency of the mutants' spontaneous openings allowed us to extend our understanding of this phenomenon by addressing issues that bear not only on the kinetics but also on the structural and mechanistic aspects of unliganded gating.

METHODS

Mutagenesis and Expression

Mouse cDNA clones were generously provided by Dr. S.M. Sine (Department of Physiology and Biophysics, Mayo Foundation, Rochester, MN), who had obtained them from the late Dr. J. Merlie and Dr. N. Davidson (α, β, and δ subunits), and Dr. P. Gardner (ε subunit, Gardner 1990), in the CMV-based expression vector pRBG4 (Lee et al. 1991; Sine 1993). The α subunit had a background mutation in M4 (V433A), which does not significantly affect the gating behavior of diliganded AChRs (Salamone et al. 1999). εT264P, αY93F, αY190W, and αD200N cDNAs in pRBG4 were generously provided by Dr. Sine. Mutations αT254S, βT265S, δS268A, δS268C, δS268I, δS268N, and δS268Y were engineered using the QuikChange™ Site-Directed Mutagenesis Kit (Stratagene Inc.) protocol. Mutations αT254P, βT265P, δS268P (Chen and Auerbach 1998), δS268T, and εT265S were engineered by overlap PCR (Higuchi 1990). All constructs were confirmed by dideoxy sequencing.

Human embryonic kidney fibroblast cells (HEK 293) were transiently transfected using calcium phosphate precipitation (Ausubel et al. 1992). A total of 3.5 μg of cDNA per 35-mm culture dish in the ratio 2:1:1:1 (α:β:δ:ε) was applied to the cells for ∼20 h, after which the medium was changed. Electrophysiological recordings started ∼30 h later.

Patch-Clamp Recordings

Recordings were performed in the cell-attached patch configuration (Hamill et al. 1981) at ∼22°C. The bath solution was Dulbecco's phosphate-buffered saline containing (mM): 137 NaCl, 0.9 CaCl₂, 2.7 KCl, 1.5 KH₂PO₄, 0.5 MgCl₂, and 8.1 Na₂HPO₄, pH 7.3. The pipette solution contained (mM): 142 KCl, 5.4 NaCl, 1.8 CaCl₂, 1.7 MgCl₂, 10 HEPES/KOH, pH 7.4. Patch pipettes pulled from borosilicate capillaries were coated with Sylgard (Dow Corning Corp.) and fire-polished. Pipette resistances ranged between 7.5 and 12.5 MΩ. Pipettes outside this range were discarded in an attempt to exert some control on the area of patched membrane. Unless otherwise stated, the potential of the patch pipette was held at +65 mV, which corresponds to an estimated membrane potential of approximately −100 mV. The membrane potential was estimated based on the amplitude of the single-channel currents and the single-channel conductance. Single-channel currents were recorded using an Axopatch 200B (Axon Instruments) at a 100-kHz bandwidth, digitized at a frequency of 94.4 kHz (VR-10B, f_c = 37 kHz; Instrutech Corp.), and stored on videotape. For analysis, the recordings were transferred to a PC via a digital interface (VR111; Instrutech Corp.) at a sampling frequency of 94.4 kHz.

Some of the mutants studied exhibited high levels of spontaneous activity, but some of them did not. For the latter, it was critical to distinguish between low activity and low expression levels. Rather than relying on the expression of a reporter gene, we identified AChR-expressing cells by making seals, with 5-μM ACh in the pipette, on cells having the typical morphological alterations of cells that are expressing the transfected DNA. Only those cells displaying activity in the presence of ACh were further patched using another pipette that did not contain ACh. In some cases, series of up to six seals on the same cell, alternating the presence and the absence of the agonist, were performed. Only those series displaying activity whenever ACh was present in the pipette were considered for analysis. To prevent contamination of ACh-free solutions with ACh, the pipette electrode (i.e., the Ag/AgCl wire connected to the headstage) was extensively washed with distilled water after each time it came in contact with the agonist. Separate filling needles were used throughout.

Data Analysis

The QUB suite of programs was used (www.qub.buffalo.edu). Single-channel recordings were inspected visually (program PRE) and segmented into ∼1.5-s–long stretches of data. Noisy sections and those containing simultaneous openings of two or more channels were excluded. Typically, >98% of the original recording was retained for the kinetic analysis. The data were further filtered digitally (Gaussian filter; effective bandwidth: ∼18 kHz) and idealized (program SKM) by using a hidden-Markov modeling procedure (recursive Viterbi algorithm) known as the “segmental k-means” method (Rabiner et al. 1986). Current amplitudes were also estimated during this idealization process.

The list of dwell times generated with SKM was used to obtain kinetic parameters in two different ways. One method consisted of estimating the mean duration of detected closures and openings (here referred to as τ_c and τ_o, respectively) by averaging the corresponding idealized dwell times. This calculation is what a maximum likelihood approach would perform when applied to a two-state, C ↔ O model without correction for missed events. The reciprocal of τ_c was taken as an estimate of the opening frequency which, as long as openings are brief, is a good approximation. Because the number of channels in the patch was not known, this parameter is a measure of both the opening frequency per channel and the number of channels in the patch. The open probability was calculated as τ_o/(τ_o + τ_c) and, because it is not a measure of the single-channel open probability, we refer to it as “patch open probability”. The second procedure (program MIL; Qin et al. 1996, Qin et al. 1997) was used for kinetic modeling of the dwell-time series to find the model and rate constants that fit the data best. It consists of an interval-based full-likelihood algorithm (Horn and Lange 1983; Chay 1988) that includes a correction for missed events based on a first-order approximation (Roux and Sauvé 1985). A fixed resolution was imposed on the open and closed times (the same for both) by considering all dwell times shorter than a given value (“dead time”) as belonging to the conductance of the flanking sojourns. The average dead time was 26 μs and in most cases it was 18 μs. Standard errors of the rate-constant estimates were calculated from the curvature (second derivative) of the likelihood surface at its maximum.

In the case of currents elicited by saturating concentrations of choline (20 mM) or acetylthiocholine (2 mM), clusters of single-channel openings were defined as a series of openings separated by closures shorter than a critical time (τ_crit). For every patch, different τ_crit values were tested and the corresponding idealized intracluster dwell-time series were analyzed with MIL (f_c = 18 kHz; dead time ≅ 30 μs). Because diliganded gating is very likely to proceed from a single closed diliganded state, the longest τ_crit defining clusters whose kinetics of closed durations were still best modeled by a single closed state was chosen. To discriminate between models with one or two closed states, we compared the corresponding maximum log-likelihood values. The two extra free parameters of the model with two closed states were penalized by subtracting two units from its maximum log-likelihood value (asymptotic information criterion; Korn and Horn 1991). The mean open time of each cluster was calculated and compared with those of the other clusters in the same patch. Only those clusters whose mean open times were within ±2 SD of the overall mean of the corresponding patch were retained for further analysis.

RESULTS

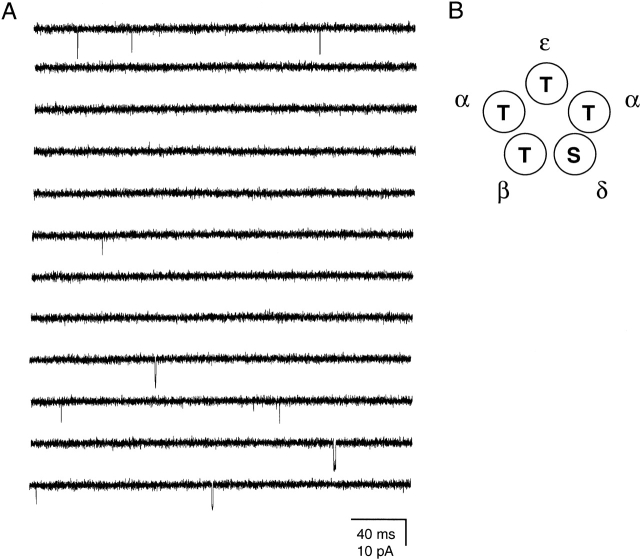
In the absence of ligand, wild-type AChRs open rarely and briefly. Fig. 1 shows a continuous stretch of data illustrating the spontaneous activity of recombinant, adult muscle AChRs transiently expressed in HEK-293 cells. Some kinetic parameters are listed (see Table and Table ).

Figure 1.

Wild-type unliganded gating. (A) Continuous single-channel traces of spontaneous openings recorded at an estimated membrane potential of −120 mV. For display purposes, f_c ≅ 6 kHz. Openings are downward deflections. (B) Schematic representation of the residues occupying the M2 12′ position in wild-type receptors. The ordering of the subunits, as seen from the extracellular side, is as suggested by Machold et al. 1995b.

Table 2.

Kinetic Properties of Unliganded Gating in M2 12′ Mutants

	12′ residue
AChR	α	β	δ	ε	Opening frequency	τo	P o	n
					s−1	ms
Wild type	T	T	S	T	1.46	0.209	3.02 × 10−4	6
δS268T	T	T	T	T	23.85	0.555	1.45 × 10−2	5
εT264S	T	T	S	S	1.41	0.081	1.11 × 10−4	4
βT265S	T	S	S	T	5.23	0.143	7.48 × 10−4	1
αT254S	S	T	S	T	*	*	*	>10
δS268T + εT264S	T	T	T	S	15.86	0.984	1.51 × 10−2	4
δS268T + βT265S	T	S	T	T	24.40	1.120	2.68 × 10−2	3
δS268T + αT254S	S	T	T	T	5.00	0.054	2.51 × 10−4	3
δS268A	T	T	A	T	8.73	0.405	3.45 × 10−3	2
δS268C	T	T	C	T	1.98	0.111	2.62 × 10−4	4
δS268N	T	T	N	T	6.02	1.46	8.78 × 10−3	1
δS268I	T	T	I	T	6.77	0.672	4.55 × 10−3	1
δS268Y	T	T	Y	T	6.11	0.802	5.86 × 10−3	2
δS268P	T	T	P	T	14.80	0.594	8.23 × 10−3	3
βT265P	T	P	S	T	12.20	1.162	1.29 × 10−2	2
εT264P	T	T	S	P	9.59	0.454	3.58 × 10−3	2
αT254P	P	T	S	T	137.41	0.108	1.20 × 10−2	2

The displayed values of unliganded opening frequency, mean duration of detected openings (τ_o), and patch open probability (P _o) are the corresponding mean values for the indicated number of patches (n). *No openings were detected.

Table 4.

Kinetic Modeling of Unliganded Gating in M2 12′ Mutants

	Rates								Openings per burst*		Kinetic model
AChR	k 01	k 10	k 02	k 20	k 03	k 30	k 34	k 43		n‡
	s−1	s−1	s−1	s−1	s−1	s−1	s−1	s−1
Wild type	1.6	10176	—	—	0.7	1112	235.6	13825	1.2	812	B
δS→T	37.5	6547	9.2	1416	2.8	111.8	53.3	2683	1.5	4226	A
δS→T + εT→S	16.0	13102	—	—	1.2	163.4	36.4	4510	1.2	3623	B
δS→T + βT→S	11.1	11590	3.3	3266	1.2	95.8	43.6	1843	1.5	928	A
δS→A	4.1	4484	—	—	1.1	1006	102.9	8497	1.1	2085	B
δS→N	5.4	6533	—	—	0.5	72.6	55.4	3434	1.8	2742	B
δS→I	5.7	9205	—	—	1.2	356.0	49.4	3034	1.1	2633	B
δS→Y§	6.1	13398	4.0	1496	0.9	101.5	35.0	22130	1.3	4752	G
δS→P	9.4	22154	—	—	3.7	701.0	65.6	11419	1.1	969	B
βT→P	6.7	9876	—	—	1.8	185.6	16.8	8141	1.1	1600	B
εT→P	4.1	11325	1.9	3825	0.2	99.1	40.9	1261	1.4	1408	A
αT→P§	318.8	32698	0.8	836.1	6.3	859.5	6908	6750	9.0	88242	G

Transition rates were estimated using a full-likelihood algorithm that includes a correction for missed events (program MIL; Qin et al. 1996, Qin et al. 1997). The values in each row correspond to one example patch per construct. The values given here for k ₀₁, k ₀₂, and k ₀₃ depend on the number of channels in the patch and are not true rate constants. However, k ₄₃, which corresponds to the reopening rate within bursts, and all the closing rates, is a true rate constant. *Calculated as 1 + k ₃₄/k ₃₀. ^‡Number of shut and open intervals in the idealized dwell-time series after imposing a fixed resolution (“dead time”). ^§The data were fitted better to G than to A. To allow for a comparison of the opening rates of these two mutants with those of the wild type and the other mutants, the rates indicated here as k ₀₁, k ₀₂, and k ₀₃ are values calculated as: k _0i k ₅₀/(k ₅₀ + k ₀₅), where i is either 1, 2, or 3 (see Fig. 3 G). These apparent opening rates are the reciprocal of the mean time spent in C₅ ↔ C₀ interconversions weighted by the proportion of openings to O₁, O₂, or O₃.

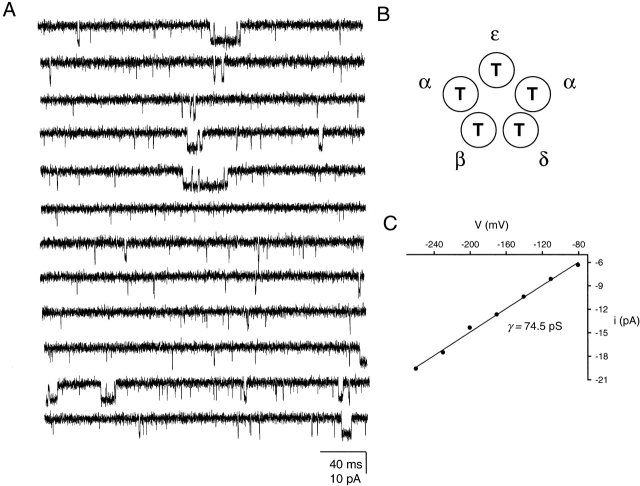
Fig. 2 illustrates the effect of the M2 12′ δS→T mutation at the single-channel level. Both the frequency and average duration of spontaneous openings are considerably increased by the mutation. In four of five patches, multiple closed and open components were apparent, with the longest (and least frequent) type of openings occurring in bursts. However, in all patches, short-lived isolated openings accounted for the majority of events. Estimates of the opening frequency, mean duration of detected openings (τ_o), and patch open probability are displayed in Table .

Figure 2.

δS→T AChR unliganded gating. (A) Continuous single-channel traces of spontaneous openings recorded at approximately −100 mV. Note the multiplicity of closed- and open- time components. Display f_c ≅ 6 kHz. Openings are downwards. (B) Schematic representation of the residues occupying the M2 12′ position in δS→T receptors. (C) I-V curve under cell-attached conditions and least-square fit with a straight line.

We next tested the effect of T→S single mutations in the 12′ positions of the other subunits. The results in Table suggest that T→S substitutions in the β or ε subunit exert little (if any) effect, while this mutation in both α subunits decreases the spontaneous activity of the wild type to undetectable levels. We then expressed combinations of mutant subunits to generate AChRs that, like the wild type, have a Ser in only one type of subunit. As expected from mutational effects that are cumulative (if not additive; Wells 1990), double-mutant AChRs having a single S in β or ε display high spontaneous activity, comparable with the sum of the effects of the single mutants. Likewise, adding the T→S mutation in both α subunits to δS→T receptors reduces unliganded activity, as it does when added to the wild type. We conclude that the residues occupying the 12′ position of the different subunits make asymmetric contributions to unliganded activity, the δ subunit playing the most prominent role. Also, since the mutational effects do not seem to deviate from additivity, we conclude that the five subunits are likely to make independent contributions to gating.

Estimates of opening frequency, mean duration of detected openings, and patch open probability of different δ12′ mutants and of the Pro mutants in the four subunits are also listed in Table . The very large “opening frequency” of α12′ T→P receptors resulted, at least in part, from an increased number of openings per burst, as analyzed below.

A Kinetic Model

The parameters in Table do not fully reflect the differences between the spontaneous activity of wild-type and mutant receptors that are clear from even a cursory examination of the recordings. Particularly, the multiplicity of open states is not represented at all in Table , where all open durations were averaged into a single value. We therefore sought to characterize the behavior of unliganded gating in terms of rate constants. It is worth noting that the occurrence of bursts of openings was not always observed. In the δS→T mutant, these bursts were recorded in four of five patches, while in the wild type they were detected in only one of six patches, even with cells corresponding to the same transfection batch. The other constructs, however, displayed this component in either all, or none, of the patches. The kinetic analysis below was performed on single-channel records from patches that exhibited these bursts. With the exception of noisy sections and those containing simultaneous openings of two or more channels, which typically represented <2% of the original data, the recordings were analyzed in their entirety.

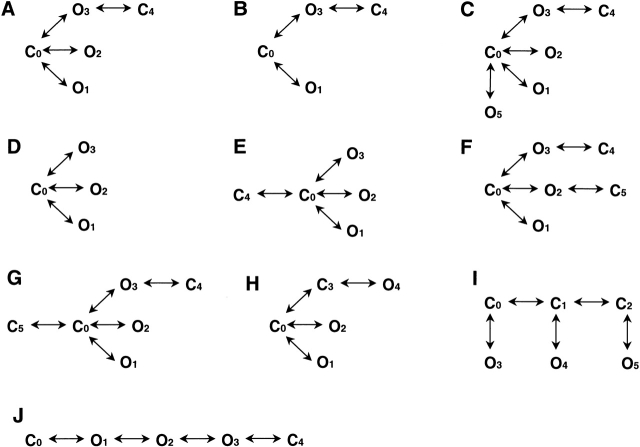
What follows is an example of model discrimination applied to a particular dwell-time sequence (4,226 events) obtained from a patch of a cell expressing the δS→T mutant. Fig. 3 shows all the kinetic models tested, and Table displays the corresponding maximum likelihood values expressed as log-likelihood ratios (LLRexp), taking A as the reference (i.e., maximum log-likelihood value for model i – maximum log-likelihood value for A, where model i is any model from B to J). A comparison of the LLRexp values leads to the rejection of B, D, and E, which suggests that at least two closed and three open states are needed to describe the kinetics of the data, and that the second closed state has to be connected to one of the open states (compare A and E). Sojourns in this additional closed state (C₄) account for the population of brief closures present within bursts of openings. The best fit to the data always connected this short-lived closed state to the slowest open state (with the exception of the αT→P mutant), in agreement with the observation that openings within a burst are longer than isolated openings. Both A and H satisfy these conditions and LLRexp = 0. C and F were rejected because the rates leading to O₅ (C) and C₆ (F) were negligibly small and, therefore, sojourns in these states are very rare.

Figure 3.

Set of reaction schemes used for kinetic modeling according to a full-likelihood approach. C, nonconductive; O, open. Whether these models represent different closed–open transitions of individual receptors or the gating activity of heterogeneous receptors in the patch is not known.

Table 3.

LLR-based Discrimination among Kinetic Models of Unliganded Gating for δS→T AChRs

Model	LLRexp	LLRi	LLRA
B	−48	0	−25
C	+6	+7	+7
D	−141	+2	−134
E	−114	+36	−121
F	+2	+2	0
G	+2	+4	+3
H	0	+7	+4
I (unconstrained)	+2	+11	+5
I (constrained)*	−2	+9	+1
J	−11	+1	−3

Example of model discrimination applied to a particular dwell-time series of the 12′ δS→T mutant (patch 1). Log-likelihood ratio values (LLR) between i (B to J) and A (Fig. 3) were computed from the experimental data (LLRexp) and from simulated data (program SIMU, QUB suite) according to i (LLRi) or A (LLRA). A dead time of 18 μs was used throughout. The rate constants used for simulation were the rate-constant estimates obtained by maximum-likelihood fitting of the experimentally derived dwell-time series to either model. If the models made very different predictions, LLRi would be a positive number, whereas LLRA would be a negative number (because LLR values are calculated with A as reference). Assuming that the variables LLRi and LLRA are normally (Gaussian) distributed and that their standard deviations are similar, comparison of the LLRi and LLRA values in any given row with the corresponding LLRexp should lead to a decision (Korn and Horn 1991). Only one dwell-time sequence per model was simulated and used for the calculation of the LLRi and LLRA values. *k ₀₁ was constrained to be twice k ₁₂, and k ₂₁ was constrained to be twice k ₁₀ (Fig. 3), as if two equivalent conformational rearrangements separated C₀ from C₂.

Throughout this procedure, only large LLR values were taken into account to discriminate between models and, thus, application of penalties for excess free-parameters did not affect the decisions. The LLRexp values and rate constants corresponding to Fig. 3G, Fig. I, and Fig. J, however, did not allow a clear decision to be made. Therefore, we simulated noise-free single-channel event lists (containing approximately the same number of events as the original data) according to each model in Fig. 3. Analysis of the simulated data (Table ) and comparison with the LLRexp values confirms that G, I, and J cannot be ruled out as appropriate kinetic schemes for spontaneous gating.

We conclude that, for the δ S→T mutant, A, G, H, I, and J in Fig. 3 are all plausible, with A, H, I (constrained), and J being the most parsimonious. Simulating dwell-time sequences containing ∼10× more intervals revealed that I (constrained) and J could have been distinguished from A and H if more data had been collected. As expected, however, A and H could not have.

The maximum log-likelihood value obtained with Fig. 3 A was then compared with that obtained from fitting the experimental data to a fully connected model with the same number of closed and open states. In such a model, all connections between states (regardless of their conductances) are allowed, the corresponding maximum-likelihood value being the highest possible for the given number of closed and open states (for a related approach, see Rothberg and Magleby 1998). The LLR between these two models was zero, indicating that no other model with two closed and three open states can describe the data better. The rate-constant estimates to A for this example patch (No. 1) are shown in Table for comparison with other mutants, and in Table for comparison with three other δS→T patches (Nos. 2–4) where the three types of openings were present. A model discrimination analysis of these three other patches supports all the conclusions above for patch No. 1.

Table 5.

Patch-to-Patch Variation in the Kinetic-Parameter Estimates of δS→T AChR Unliganded Gating

	Rates
Patch	k 01	k 10	k 02	k 20	k 03	k 30	k 34	k 43	n
	s−1	s−1	s−1	s−1	s−1	s−1	s−1	s−1
1	37.5 ± 1.8	6547 ± 335	9.2 ± 1.5	1416 ± 229	2.8 ± 0.4	111.8 ± 13.5	53.3 ± 7.5	2683 ± 436	4226
2	35.2 ± 1.5	6263 ± 217	3.2 ± 1.1	1827 ± 814	1.5 ± 0.5	240.2 ± 46.6	44.0 ± 10.0	2054 ± 1147	6317
3	6.8 ± 0.8	10057 ± 1164	2.9 ± 0.8	2975 ± 460	0.17 ± 0.06	52.7 ± 17.8	19.3 ± 10.8	3254 ± 1874	802
4	5.1 ± 0.7	13267 ± 2244	1.5 ± 0.5	3739 ± 707	0.18 ± 0.07	164.2 ± 66.9	138.8 ± 50.1	1980 ± 822	462

Fig. 3 A was used as the kinetic model. The smaller number of intervals detected in patches 3 and 4 mainly resulted from the slower opening rates k ₀₁, k ₀₂, and k ₀₃. Variation of these values between patches reflects differences in both the opening rate constants and the number of channels in the patch. The total duration of the recordings in the four cases were similar but not equal. Dead times were (μs): 18, 45, 44, and 46 for patches 1–4, respectively. Standard errors were calculated from the curvature of the likelihood surface at its maximum. n, number of intervals.

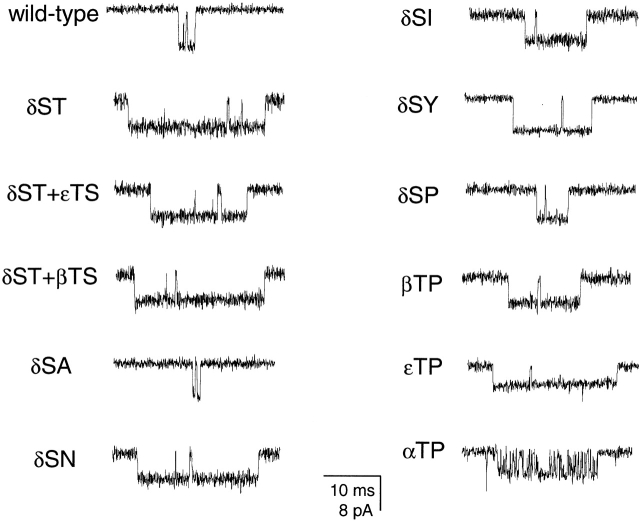
A similar procedure was applied to all other constructs that exhibited multiple open and closed components. Fig. 4 shows the dwell-time histograms and the superimposed density functions of example patches, and Table shows the corresponding rate constants. The kinetics of the δS→T + βT→S and εT→P constructs, like those of the δS→T mutant, were best described by Fig. 3A, Fig. G, Fig. H, Fig. I, and Fig. J. The corresponding rate-constant estimates to A are shown in Table . For the wild type and the mutants δS→T + εT→S, δS→A, δS→N, δS→I, δS→P, and βT→P, Fig. 3 B (with only two open states) was superior. In these seven cases, the intermediate open state was of doubtful existence, a fact that could be related to its lifetime being close to (and thus difficult to distinguish from) that of either the fastest or slowest type of openings, rather than to a genuine mechanistic difference between mutants. Finally, the mutants δS→Y and αT→P were fitted best to G. Again, we think that this difference may reflect some data heterogeneity rather than a different gating mechanism. For any given mutant, the rank order of the models was the same for all patches.

Figure 4.

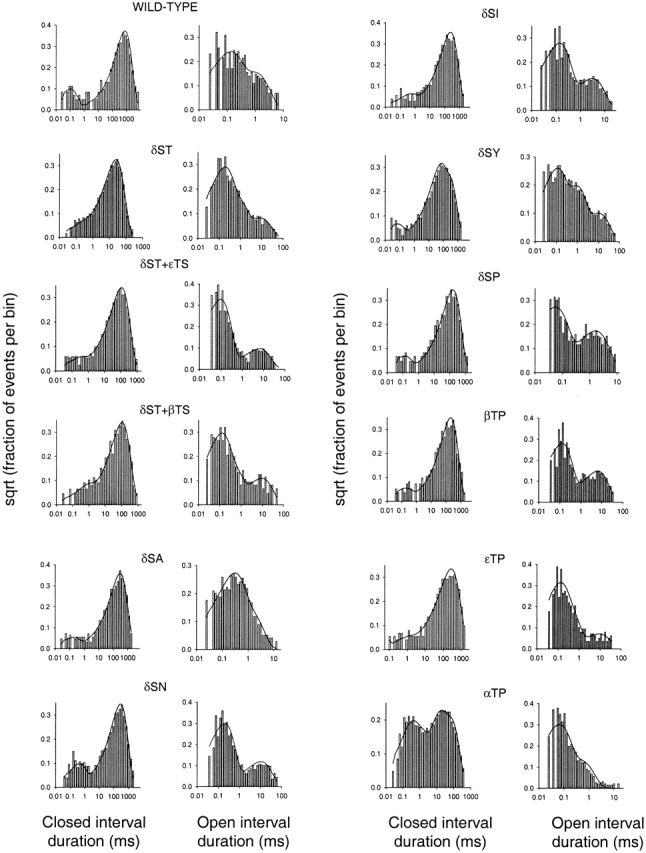
Dwell-time histograms and superimposed density functions corresponding to wild-type and M2 12′ mutant AChR unliganded gating. The kinetics of δS→T, δS→T + βT→S, and εT→P receptors were fitted to Fig. 3 A. Those of the wild-type and δS→T + εT→S, δS→A, δS→N, δS→I, δS→P, and βT→P receptors were fitted to Fig. 3 B. Those of δS→Y and αT→P receptors were fitted to Fig. 3 G. The corresponding rate constant estimates are listed in Table . Each histogram corresponds to data recorded in one example patch for each construct.

Other than the opening rates, which in our case depended on the number of channels in the patch, the rate constants varied little between constructs. However, two noteworthy differences were present. First, δS→A and wild-type AChRs have larger k ₃₀ values, which make their longest-lived openings shorter than those of the other mutants (Fig. 5). Nevertheless, as k ₃₄ values are also increased, these openings still occur in bursts with a “regular” number of openings. Second, αT→P AChRs have a much larger k ₃₄, which greatly increases the number of openings per burst and reduces the duration of these openings to as little as ∼150 μs (Fig. 5). If, for example, Fig. 3 H were used instead (where the bursting behavior is modeled by a C ↔ C→O scheme), an increase in two rate constants, k ₄₃ and k ₃₄, would be needed to account for the same finding.

Figure 5.

Example bursts of unliganded openings of wild-type and M2 12′ mutant receptors. Display f_c ≅ 6 kHz. The different current amplitudes most likely reflect differences in the membrane potential. This is most evident in the case of the εT→P mutant, where a somewhat detached patch could have decreased the cell's membrane potential. Openings are downwards.

If we assume that the multiple kinetic components arise from the activity of individual channels, then, in bursty patches, the unliganded AChR can access three different open conformations with mean lifetimes of ∼100 μs (>75% of the total openings), ∼500 μs, and ∼5 ms. From the rate-constant estimates, it can be calculated that the longest openings are grouped in bursts of, on average (and excluding the αT→P mutant), ∼1.29 openings separated by brief (∼150 μs) gaps. In other words, ∼60% of these openings occur as isolated events, ∼27% occur as pairs of openings separated by a brief gap, ∼9% form triplets separated by two gaps, and so on. Fig. 5 shows examples of such bursts for different constructs, including the wild type. In all the cases where multiple open components were not observed, only brief isolated openings, indistinguishable from the fast predominant component described above, were recorded.

The fact that short-lived openings dominated the unliganded activity clearly suggests that these represent the main allosteric transition of wild-type gating. This is the reason why we focused on this kinetic component to study the effects of voltage and binding-site mutations on spontaneous activity (see below). It is not clear, however, what the diliganded counterpart of the longest-lived, less-frequent type of openings is.

Voltage Dependence

It has been known for several decades that the equilibrium constant of AChR-diliganded gating is voltage dependent (Magleby and Stevens 1972). A reversible cyclic model with only gating and (voltage insensitive) binding steps requires that the voltage dependence of gating be the same regardless of the number of agonists bound to the receptor (0, 1, or 2). The study of the voltage dependence of unliganded gating in recombinant AChRs has been hampered, however, by the low frequency of openings in the case of wild-type AChRs, and by the low expression levels in the case of certain M2 mutants. We therefore explored the voltage dependence of unliganded gating in the 12′ δS→T mutant.

The voltage dependence of the opening and closing rate constants was studied in a patch that displayed only the brief type of openings (i.e., the data were fitted best to a C ↔ O model). The zδ parameters were obtained from fits of rate-versus-voltage plots to the Boltzmann equation [k = k _o exp(−zδF V/RT)] (Fig. 6). Their values were 0.363 ± 0.024 for the opening and 0.011 ± 0.023 for the closing rate constant. Thus, in this patch, the unliganded gating equilibrium constant increased e-fold with an ∼70-mV hyperpolarization, a change that was entirely due to the increase in the opening rate constant. In diliganded AChRs, Auerbach et al. 1996 found that the gating equilibrium constant increases e-fold with an ∼66-mV hyperpolarization, but that this change is mainly due to the decrease in the closing rate constant. We conclude that the voltage dependence of the gating equilibrium constant is the same in un- and diliganded gating, but that the voltage dependences of the gating rate constants are opposite.

Figure 6.

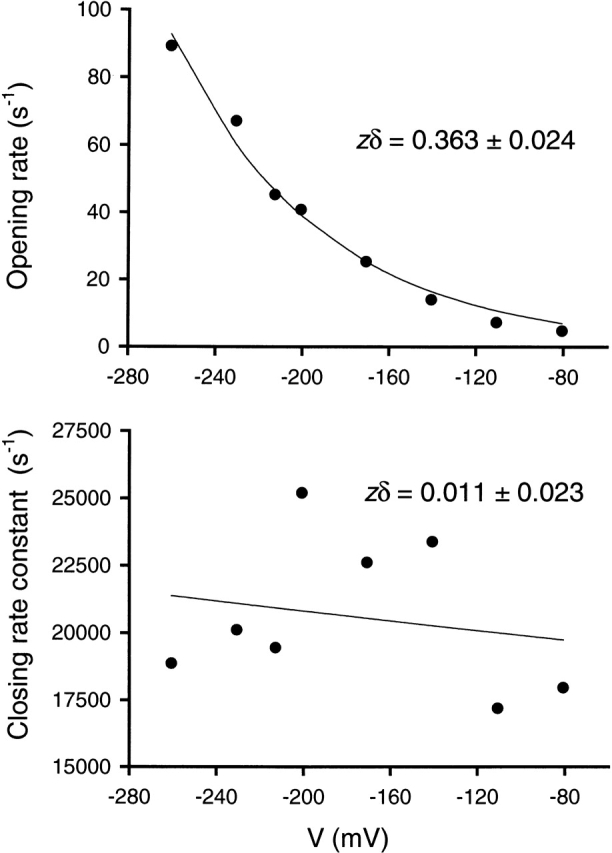
Voltage dependence of 12′ δS→T AChR unliganded gating. Solid lines are fits to the Boltzmann equation for voltage dependence. Because only the brief type of openings was recorded in this patch, the full-likelihood approach was applied to a C ↔ O scheme. The opening rate is assumed to be the product of the opening rate constant and the number of channels in the patch. The particular value of the latter does not affect the zδ estimate.

Effect of Binding-Site Mutations

According to the constraints imposed by a cyclic model with only binding and isomerization steps, unliganded gating must involve a conformational rearrangement in both the pore and the transmitter binding sites, just like during liganded gating. However, the increased spontaneous activity often recorded from recombinant ligand-gated ion channels has been interpreted as arising from the uncoupling of the binding sites from the gate (Auerbach et al. 1996; Neelands et al. 1999). This interpretation implies that, in the absence of ligand, the pore can act autonomously, regardless of the affinity state of the binding sites. In principle, this mechanism of spontaneous gating does not seem unreasonable insofar as most point mutations leading to an increased unliganded activity occur in M2; namely, in the pore domain and ∼50 Å away from the binding sites (Valenzuela et al. 1994; Miyazawa et al. 1999). Moreover, if such a mechanism turned out to be the case, it would be interesting to know to what extent it contributes to the spontaneous activity of wild-type receptors, for which a strictly coupled mechanism has been hypothesized (Jackson 1989, Jackson 1994).

To distinguish between such coupled and uncoupled mechanisms of unliganded gating, we transfected HEK-293 cells with cDNA encoding for 12′ δS→T, 12′ εT→S, β wild type, and either αY93F, αY190W, or αD200N. The combination of both 12′ mutations was shown, above, to yield receptors with high spontaneous activity. The three binding-site mutations in the α subunit have been shown to decrease the diliganded gating equilibrium constant by, mainly, slowing down the channel's opening rate (Chen et al. 1995; Akk et al. 1996; Auerbach et al. 1996). We reasoned that if spontaneous activity arose from a local deformation of the pore, then co-expression with the binding-site mutants would have no effect on unliganded activity. Fig. 7 shows that these three binding-site mutations substantially decreased (>15-fold) the frequency of unliganded openings when coexpressed with the 12′ mutations. This suggests that there is a binding-site rearrangement upon unliganded gating.

Figure 7.

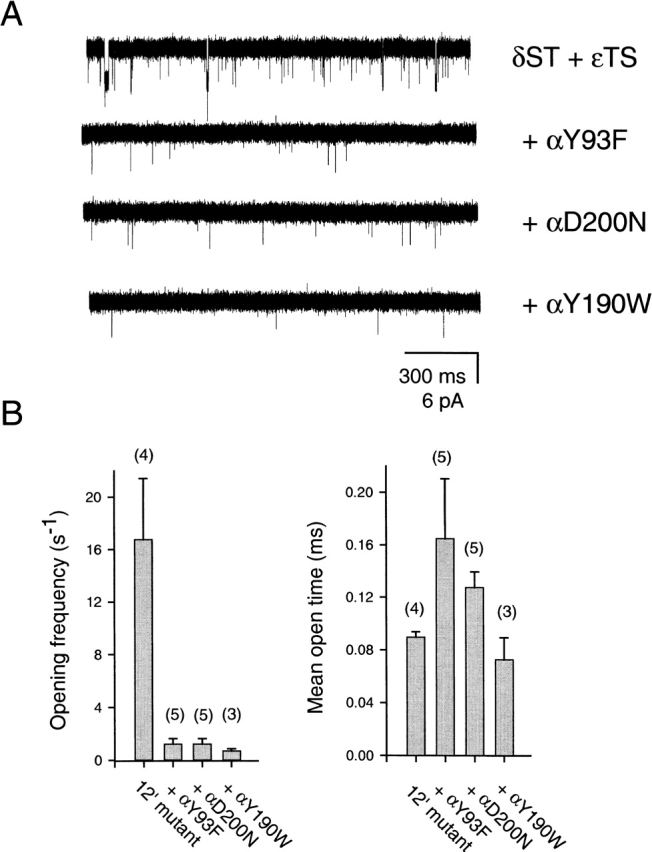
Effect of binding-site mutations on unliganded gating. (A) Representative single-channel traces in the absence of ligand. Display f_c ≅ 6 kHz. Openings are downwards. The background receptor on which the binding-site mutations were engineered was the double mutant 12′ δS→T + εT→S. (B) Bar representation of opening frequencies, mean open times, and the corresponding standard errors for the four constructs. The number of analyzed patches in each case is indicated in parentheses. The constructs having the binding-site mutations displayed only one type (the briefest one) of openings. However, the kinetics of the 12′ δS→T + εT→S mutant alone were best described by two open states (Fig. 3 B) with mean open times of 89.7 μs (88% of the total openings) and 4.66 ms (n = 4). In this case, only the rates associated with the briefest component were considered for comparison with the other three constructs. While the binding-site mutations greatly reduced the frequency of brief openings, little effect was exerted on their mean duration. “Opening frequencies” are the opening rates. Mean open times were calculated as the reciprocal of the closing rate constants, and the corresponding standard errors were calculated using and 2 in the companion paper.

Diliganded Gating in Channels with Increased Unliganded Activity

The results presented in the above section suggest that both unliganded and diliganded gating result from the same global conformational change, even though, as suggested by the voltage-dependence experiments, the particular pathway followed in each case may differ. This supports the application of thermodynamic cycles to model the AChR's activity, according to which:

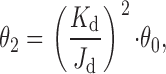1

where K _d and J _d are the microscopic dissociation equilibrium constants from the closed and open states respectively, and θ₀ and θ₂ are the gating equilibrium constants for the unliganded and diliganded AChR, respectively. predicts that an increase in θ₀ (caused, for example, by a pore mutation) has to be accompanied by the same increase in θ₂ as long as the affinity ratio (K _d/J _d) is not affected.

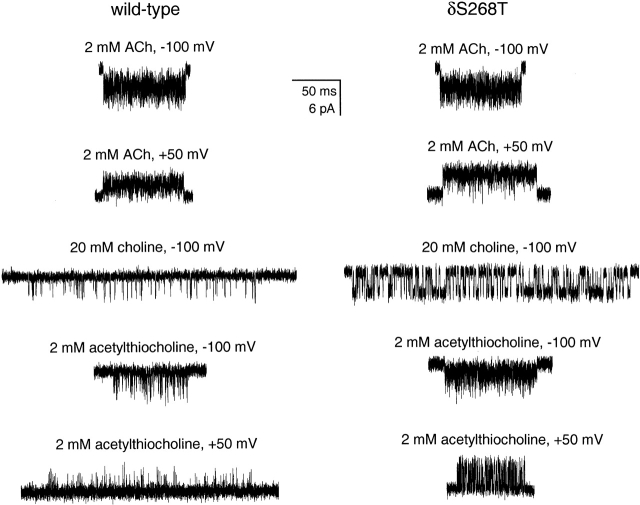
θ₂ values were estimated as the ratio between the opening (β₂) and closing (α₂) rate constants from clusters of single-channel currents elicited at saturating concentrations of agonist (Grosman and Auerbach 2000). Fig. 8 shows that, in the presence of 2 mM ACh, it is difficult to detect any increase in θ₂ upon the 12′ δS→T mutation. This is because the wild-type's θ₂ value is already near the upper limit of reliable estimation. However, such an increase is readily apparent in the presence of choline or acetylthiocholine (the thioester counterpart of ACh), two slowly opening, low-efficacy agonists (Fig. 8). The δ12′ mutation increases θ₂ by a factor of 14.5 when the AChR is occupied by choline and by a factor of 13.1 when it is occupied by acetylthiocholine (Table ). The increase in θ₂ thus appears to be independent of the particular agonist used, suggesting that the 12′ δS→T mutation mainly affects θ₀, leaving the K _d /J _d ratio almost unchanged.

Figure 8.

Effect of the 12′ δS→T mutation on diliganded activity. Display f_c ≅ 6 kHz. In addition to inward currents (approximately −100 mV), outward currents (approximately +50 mV) were also recorded in the presence of 2 mM ACh or 2 mM acetylthiocholine to relieve fast blockade by the agonist itself. This was not necessary in the presence of 20 mM choline because the increase in open-channel noise due to fast blockade was much lower (Grosman and Auerbach 2000). Openings are downward deflections at −100 mV and upward deflections at +50 mV. The higher amplitude of the δS→T currents in the presence of 2 mM ACh at +50 mV, as compared with that of the wild type, is most likely due to the slower closing rate constant of the mutant.

Table 6.

Effect of the δ12′ S→T Mutation on Diliganded Gating

AChR	Agonist	Voltage	θ2	n	θ2 increase
Wild type	20 mM choline	−100 mV	0.054 ± 0.010	5
12′ δS→T	20 mM choline	−100 mV	0.783 ± 0.059	7	14.5 ± 2.9
Wild type	2 mM acetylthiocholine	+50 mV	0.038 ± 0.003	3
12′ δS→T	2 mM acetylthiocholine	+50 mV	0.496 ± 0.080	2	13.1 ± 2.3

Saturating concentrations of agonist were used to isolate gating from agonist-binding steps. In the presence of 20 mM choline or 2 mM acetylthiocholine, gating was modeled best by a C ↔ O reaction scheme. θ₂ values for each patch were estimated as the ratio of the opening rate constant and the closing rate (Grosman and Auerbach 2000), and the values displayed here are the mean ± SEM for the indicated number of patches (n). The excess open-channel noise in the presence of 2 mM acetylthiocholine (due to fast block by the agonist) was conveniently reduced by depolarizing the patch to approximately +50 mV. Standard errors of the θ₂ increase were calculated using and 2 in the companion paper.

DISCUSSION

Kinetic Aspects

In both wild type and M2 12′ mutants, a two-state C ↔ O kinetic scheme provides a good description of spontaneous gating. In the case of some 12′ mutants, however, additional states were needed to improve the fit to the data and similar extra states were needed in one of six patches containing wild-type AChRs. Multiple kinetic components during unliganded gating have also been observed for a number of slow-channel congenital myasthenic syndrome (SCCMS) mutants in M2 (εT264P, Ohno et al. 1995; βV266M and εL269F, Engel et al. 1996; αV249F, Milone et al. 1997), suggesting that these additional kinetic components may be associated with M2 mutations in general. In a few patches of cultured embryonic mouse skeletal muscle, Jackson 1986 described the existence of additional, longer-lived components in the open-time distribution of unliganded gating. Furthermore, heterogeneous kinetics have been reported for liganded gating in both native (Auerbach and Lingle 1986) and recombinant (Gibb et al. 1990; Naranjo and Brehm 1993) wild-type AChRs.

There are a number of possible explanations for the multiplicity of kinetic states that we observed during unliganded gating. A trivial explanation is that trace concentrations of ACh (or some other cholinergic ligand) were present and resulted in a small number of liganded openings. We consider this to be unlikely because precautions were taken to avoid such contamination. A second possibility is that the patches contained a set of heterogeneous receptors. Under our experimental conditions, these could have arisen from alternative assembly patterns and/or different extents of post-translational modifications. However, neither of these are likely to be affected by mutations in δM2 (Verrall and Hall 1992; Eertmoed and Green 1999; Swope et al. 1999) and hence the degree of molecular heterogeneity of the mutants studied here is not expected to be any greater than that of recombinant wild-type AChRs. A third clear possibility is that the complex kinetic activity represents an intrinsic property of individual AChRs, which is unveiled by the M2 mutations. The finding that, for some constructs, the complex kinetic behavior was recorded in some, but not all, patches may be attributed to modulation by cellular processes, based on the observation that protein kinase A–catalyzed phosphorylation of Torpedo AChRs increases the proportion of long over short unliganded openings (Ferrer-Montiel et al. 1991). In conclusion, although our experiments do not allow us to definitively distinguish between molecular heterogeneity and complex kinetics, the observation that M2 mutations increase the complexity of unliganded gating leads us to suspect that the multiplicity of kinetic states is a property of individual AChRs.

Structural Aspects

Our results suggest that the M2 12′ position of each subunit makes an asymmetric and independent contribution to unliganded gating. We showed that this is also true during diliganded gating (Grosman and Auerbach 2000). Other mutational studies of the M2 domain also support the idea of an uneven contribution to function made by residues occupying homologous positions in different subunits. This has been shown, in the presence of agonist, for the 2′ (Villarroel et al. 1992), 9′ (Kearney et al. 1996), 12′ (Chen and Auerbach 1998; Grosman and Auerbach 2000), and 17′ (Chen and White 1999) positions. In all these cases, it is the δ subunit that stands out. Whether this reveals differences in the dynamics of the subunits during gating or results from an asymmetric orientation of the five subunits in the pore of the pentameric complex is still unclear.

Voltage Dependence

There is a discrepancy in the literature about the voltage dependence of the unliganded gating rate constants. Although Jackson 1986 showed evidence that the opening rate constant is voltage dependent, the results of Auerbach et al. 1996 suggested that it was not. In the latter case, even though M2 mutations were used to increase spontaneous activity, the observed frequency of openings was so low (<1.5 s⁻¹, presumably due to poor expression levels) that only a few events were usually collected. This limitation could well have been the source of the difference between both reports.

With the 12′ mutants, we were able to record higher frequencies of openings. One remaining problem, however, was that a complex kinetic scheme was generally needed to fit the data. To make the analytic procedure more reliable and the interpretation of the results more straightforward, we analyzed the voltage dependence of unliganded gating in a patch that only displayed the fast class of openings (which, even in the kinetically most complex patches, accounts for the majority of openings). We found clear evidence that the opening rate constant increases as the membrane is hyperpolarized, in agreement with the results of Jackson 1986. We also found that the closing rate constant is not voltage dependent, as shown by Auerbach et al. 1996. Interestingly, the voltage dependence of the whole reaction is very close to that found for diliganded gating; i.e., ∼70-mV/e-fold (Neher and Steinbach 1978; Auerbach et al. 1996). Thus, the unliganded and diliganded gating equilibria seem to have the same voltage dependence, as expected from a cyclic model with voltage-independent binding steps. The voltage dependences of the rate constants are, however, exactly opposite. Therefore, the relative position along the gating-reaction coordinate (i.e., closed-like versus open-like) of the structural elements that define voltage dependence, measured at the transition state, differs depending on whether the channel is bound or vacant (Grosman et al. 2000). We do not know whether these differences extend to other regions of the receptor. However, that the corresponding position of the transmitter binding site does not change with the number of bound ligands, is one of the assumptions of the use of linkage relationships to predict the rate constants of un- and monoliganded gating based on the (measured) rate constants of diliganded gating (Edelstein et al. 1996).

Coupling between Binding Sites and Pore

The results in Fig. 7 indicate that the binding-site mutations αY93F, αY190W, and αD200N impair unliganded gating. This can be interpreted as an indication that there is a conformational rearrangement around these binding-site residues during unliganded gating, whose manifestation at the pore is the opening–closing of the channel. This suggests that spontaneous openings do not arise from the autonomous activity of the M2 region.

This interpretation relies on the assumption that binding-site mutations can only cause local perturbations that do not reach the distant gate. We cannot rule out, however, the possibility that a local perturbation at the binding sites could propagate to the “autonomous gate” and affect its behavior. Nevertheless, crystallographic data of proteins shows that structural changes are usually greater near the sites of mutation and fall off rapidly with increasing distance (Skinner and Terwilliger 1996). It could be argued that the AChR, being an allosteric protein, is “designed” to propagate local conformational changes from the binding sites to the pore region. For that reason, we tested three different binding-site positions, and the mutations were designed to be conservative in an attempt to minimize the magnitude of the local perturbation and the extent of its propagation. Therefore, it is likely that, regardless of local differences caused by the bound agonist (Kyte 1995), the end points of the binding-site rearrangement during unliganded and diliganded gating are globally the same. This concept lends full support to the use of thermodynamic cycles to model the AChR's activity.

Control of the Isomerization Step by Binding-Site Residues

There are two ways a binding-site mutation can reduce θ₂: it can reduce the ligand-affinity difference between the open and closed states (the affinity ratio), or it can interfere with the low affinity → high affinity conformational change that accompanies channel opening (θ₀). Here, we showed that the decrease in θ₂ caused by the binding-site mutations αY93F, αY190W, and αD200N (Chen et al. 1995; Akk et al. 1996; Auerbach et al. 1996) is due, at least in part, to a decrease in θ₀ (). Thus, the use of spontaneously opening mutants as the background receptors on which other mutations are engineered constitutes a useful tool to identify binding-site residues that contribute to gating in forms other than by binding the agonist with different affinities in the open versus closed state. It is very likely that these residues, in addition to making contact with the ligand (at least in the case of αY93 and αY190), also participate in protein–protein interactions that change upon gating. This distinction between effects on θ₀ or the affinity ratio would have been difficult to make if the background receptor had been the wild-type channel.

It seems that the gating conformational change of AChRs is controlled in opposite directions by residues at the pore and the binding sites. With the exception of αG153S (Zhou et al. 1999a), we are not aware of binding-site mutations that increase spontaneous activity, nor are we aware of M2 mutations that substantially decrease it. Whether this reflects a fundamental aspect of the channel's design or just the paucity of mutational-analysis data remains to be ascertained.

Diliganded Activity

In the absence of a solid estimate of the number of channels per patch, we cannot estimate θ₀. As a consequence, it was impossible to determine directly whether the increase in θ₂ caused by the 12′ mutations arises exclusively from an equal increase in θ₀ or there is a contribution from a change in the affinity ratio as well. To solve this issue, we took an indirect approach reasoning that it is unlikely for a mutation that alters the affinity ratio of a receptor to do so to the same extent for different ligands. According to , it is clear that a mutation that increases θ₀ without affecting the affinity ratio causes the same increase in θ₂ for different agonists. Here we suggest that the reverse is also true: the same increase in θ₂ for different ligands can be taken as an (indirect) evidence that the mutation in question only affects θ₀. By comparing the responses of wild-type and δS→T AChRs to two agonists (choline and acetylthiocholine), we concluded that the δS→T mutation mainly affects θ₀.

As shown in Fig. 8, we cannot directly measure the effect of the δ12′ S→T mutation on ACh-activated AChR gating. However, from the average increase in θ₂ for choline and acetylthiocholine (∼13.8×), we can predict that θ₂ for ACh would be ∼380, which is 13.8× the θ₂ value for the wild-type AChR (calculated to be ∼27.5 at −100 mV, from data in Salamone et al. 1999). Further, based on the observation that opening (and closing) activation-free energies of δ12′ mutants are linearly correlated with the corresponding gating equilibrium free-energy changes, and that the slope of such relationship (Φ) is ∼0.3 for choline or acetylthiocholine (Grosman and Auerbach 2000; Grosman et al. 2000), we can also predict the gating rate constants of ACh-bound receptors. This “linear free-energy relationship” (Leffler and Grunwald 1963) implies that β_2mut/β_2wt = (θ_2mut/θ_2wt)^Φ [and, therefore, α_2mut/α_2wt = (θ_2mut/θ_2wt)^(Φ − ¹⁾]. Thus, the diliganded opening rate constant of δ12′ S→T receptors should be 13.8^0.3 ≅ 2.2 times that of wild-type AChRs, or ∼110,000 s⁻¹, and the closing rate constant should be 13.8^−0.7 ≅ 0.16 times that of wild-type AChRs, or ∼300 s⁻¹ (at −100 mV).

In the following paper, we make extensive use of choline as a slowly opening, low-efficacy agonist to investigate the effect of 12′ pore mutations on diliganded gating.