Rapid Induction of P/C-type Inactivation Is the Mechanism for Acid-induced K⁺ Current Inhibition

Abstract

Extracellular acidification is known to decrease the conductance of many voltage-gated potassium channels. In the present study, we investigated the mechanism of H⁺ _o-induced current inhibition by taking advantage of Na⁺ permeation through inactivated channels. In hKv1.5, H⁺ _o inhibited open-state Na⁺ current with a similar potency to K⁺ current, but had little effect on the amplitude of inactivated-state Na⁺ current. In support of inactivation as the mechanism for the current reduction, Na⁺ current through noninactivating hKv1.5-R487V channels was not affected by [H⁺ _o]. At pH 6.4, channels were maximally inactivated as soon as sufficient time was given to allow activation, which suggested two possibilities for the mechanism of action of H⁺ _o. These were that inactivation of channels in early closed states occurred while hyperpolarized during exposure to acid pH (closed-state inactivation) and/or inactivation from the open state was greatly accelerated at low pH. The absence of outward Na⁺ currents but the maintained presence of slow Na⁺ tail currents, combined with changes in the Na⁺ tail current time course at pH 6.4, led us to favor the hypothesis that a reduction in the activation energy for the inactivation transition from the open state underlies the inhibition of hKv1.5 Na⁺ current at low pH.

INTRODUCTION

In the heart, an interruption in the normal flow of blood to the myocardium is quickly accompanied by tissue acidification (Eisner et al., 1989; Orchard and Kentish, 1990; Yan and Kléber, 1992). Experimentally, such extracellular acidification has been shown to result in an inhibition of the Kv1.5 potassium current (Steidl and Yool, 1999; Jäger and Grissmer, 2001; Kehl et al., 2002), as it does in some other voltage-gated K⁺ channels, including Shaker (Perez-Cornejo et al., 1998), Kv1.4 (Claydon et al., 2000), and Kv1.2 (Ishii et al., 2001). It has been suggested that the causative mechanism is an increased open-state inactivation rate in the presence of lowered pH that results in an accumulation of channels in the C-type inactivated state (Steidl and Yool, 1999). Since an inhibition of voltage-gated K⁺ channel activity is well known to be associated with action potential prolongation, it is important to understand the mechanisms by which acid pH inhibits K⁺ currents. In Kv1.5 and Kv1.4 general agreement has been reached that protonation of a histidine residue in the outer pore mouth acts as a sensor for the pH-dependent reduction of the macroscopic channel conductance (Claydon et al., 2002; Jäger and Grissmer, 2001; Kehl et al., 2002). However, although it has been suggested that this induces an acceleration of C-type inactivation during depolarization (Steidl and Yool, 1999), other evidence suggests that a change in the time course of C-type inactivation does not itself account for the reduced availability of channels (Kehl et al., 2002).

In this study, we took advantage of Na⁺ permeation through the inactivated state of Kv channels to monitor the number of inactivated channels at acid and normal pH. Na⁺ conduction through the inactivated state(s) is reflected as a typically small sustained current during prolonged depolarization, and comparatively much larger and slower (compared with control) tail currents on deactivation (Starkus et al., 1997; Wang et al., 2000; Wang and Fedida, 2001). Although the amount of sustained Na⁺ current through inactivated channels on depolarization varies depending on the channel type, a consistent feature of the inactivated channels is a large Na⁺ conductance on repolarization to negative potentials. This generates slow Na⁺ tail currents with a very prominent initial rising phase followed by a slow relaxation process that reflects the deactivation of Na⁺-conducting inactivated channels to closed-inactivated states in Shaker channels (Starkus et al., 1997) and in Kv1.5 (Wang et al., 2000).

We found that acid pH inhibited the current through the open state without significantly altering the size of the slow Na⁺ tail current through inactivated channels. Our data showed that channels appeared to be inactivated as soon as they were opened, but that outward Na⁺ currents through high Na⁺-conducting states were absent. When interpreted using our existing models of Kv1.5 activation-inactivation gating, these data were more simply explained if inactivation occurred much faster than previously thought when channels were activated at low pH.

MATERIALS AND METHODS

Cell Preparation

Wild-type and R487V mutant human (h) Kv1.5 channels were studied in a human embryonic kidney cell line (HEK293) as reported previously (Wang and Fedida, 2001). Cells were dissociated for passage by using trypsin-EDTA and were maintained in MEM, 10% fetal bovine serum, penicillin-streptomycin, and 0.5 mg ml⁻¹ geneticin at 37°C in an atmosphere of 5% CO₂ in air. All tissue culture supplies were obtained from Invitrogen.

Recording Solutions

To record K⁺ currents, the bath solution contained (in mM) 135 NaCl, 2 CaCl₂, 1 MgCl₂, 10 glucose, and its pH was adjusted to 7.4 with 10 mM HEPES as buffer, or pH 6.4 with 10 mM MES as buffer instead of HEPES. The pipette solution contained (in mM) 135 KCl, 5 EGTA, 10 HEPES, and 1 MgCl₂ and was adjusted to pH 7.2 with KOH. To record Na⁺ currents, the bath solution was usually unchanged. For experiments of the type illustrated in Fig. 1 B, NaCl was reduced to 5 mM and the rest of the NaCl was replaced by 130 mM NMG⁺. The pipette solution contained, in mM, 130 NaCl, 1 MgCl₂, 10 EGTA, and 5 HEPES and was adjusted to pH 7.2 with NaOH. To record both K⁺ and Na⁺ currents, 1 mM KCl was added to the Na⁺ bath solution described above, and an N-methyl-D-glutamine (NMG⁺)-based pipette solution was used. This contained, in mM, 140 NMGCl, 1 MgCl₂, 10 HEPES, 10 EGTA and was adjusted to pH 7.2 with HCl. Chemicals were from Sigma-Aldrich.

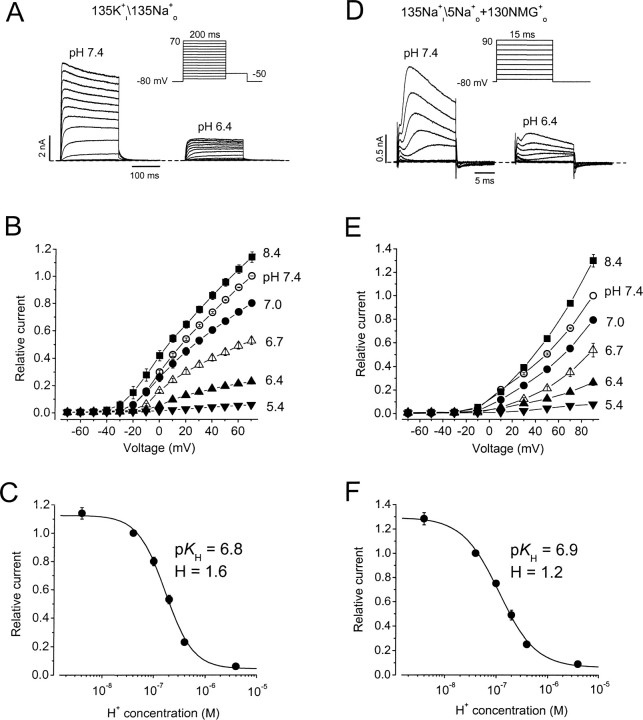
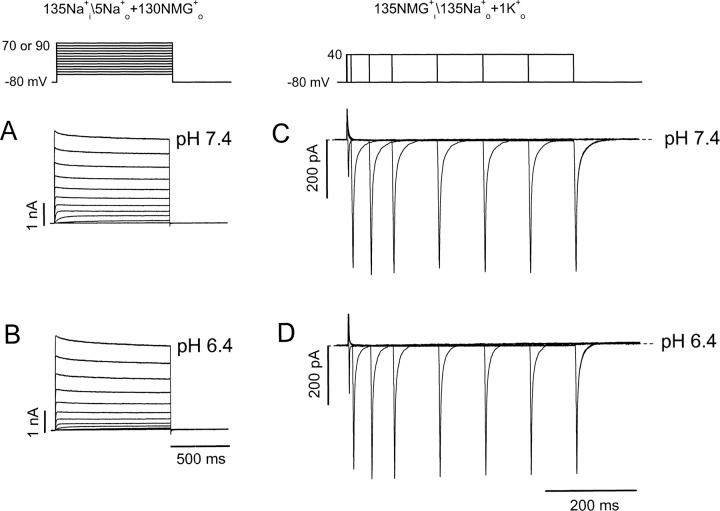
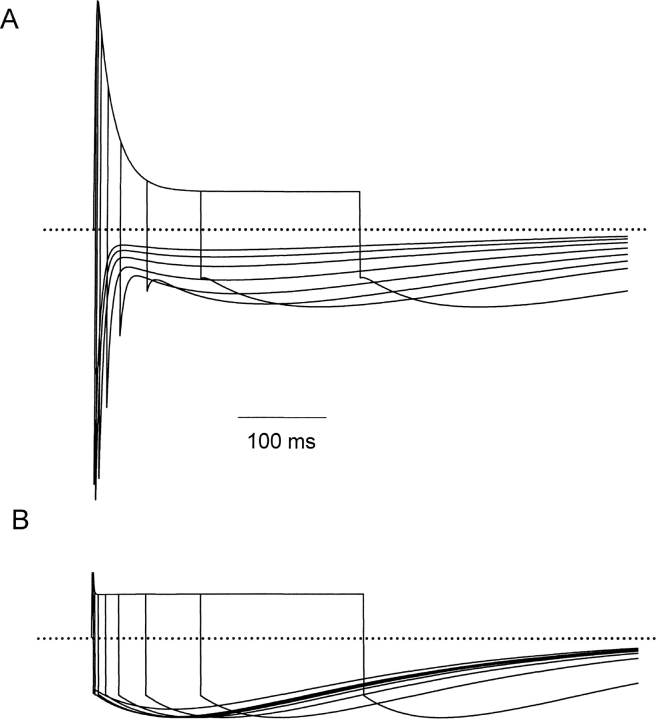
Figure 1.

Extracellular acidification inhibits hKv1.5 K⁺ and Na⁺ currents. (A–C) pH effects on K⁺ currents. A, hKv1.5 currents in response to a step voltage protocol at pH 7.4 or pH 6.4 from the same cell in nominally K⁺ _o-free medium. Internal\external solution composition is shown above A and D. (B) Normalized mean peak I-V relationships at different pH from 3–5 cells. Data were normalized to peak outward current at 70 mV, pH 7.4. (C) Peak current amplitude at 70 mV normalized to the value at pH 7.4, and plotted versus pH. The K _d was 166 nM, pK _H was 6.8, and the Hill coefficient was 1.6. (D–F) As for A–C except that the pipette and bath solutions contained Na⁺ as the permeant ion, as indicated above D. In F the K _d was 114 nM, pK _H was 6.9, and the Hill coefficient was 1.2. No significant difference was detected between the values at the two pHs (P > 0.1). Lines through points in C and F are Hill fit lines, whereas those in B and E are to connect the points only.

Signal Recording

Coverslips containing cells were removed from the incubator before experiments and placed in a superfusion chamber containing the control bath solution at 22–23°C. The bath solution was constantly flowing through the chamber and the solution was exchanged by switching the perfusates at the inlet of the chamber, with complete bath solution changes taking ∼10 s. Whole-cell current recording and data analysis were done using an Axopatch 200A amplifier and pClamp6 software (Axon Instruments, Inc.). Patch electrodes were fabricated using thin-walled borosilicate glass (World Precision Instruments) with electrode resistances of 1–2 MΩ. Capacitance and series resistance compensation, typically 80%, were routinely used. Data were filtered at 10 kHz and sampled at 50 kHz for all protocols. Leak subtraction was not used. Data are shown as mean ± SEM. The statistical significance of differences between means was determined using the unpaired Student's t test.

Data Analysis and Modeling

To quantify the effects of H⁺ ions on Na⁺ currents, tail currents were recorded at −80 mV after a depolarizing prepulse. Peak tail current amplitudes were normalized to the maximum current amplitude at pH 7.4, and the data points were fitted to a single Boltzmann function:

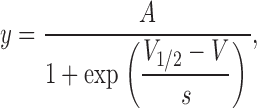(1)

in which y is the tail current normalized with respect to the maximal value at pH 7.4, and A is the best fit value for the normalized maximal response and ideally has a value of unity at pH 7.4. V _1/2 is the half-activation potential, V is the voltage during the prepulse, and s is the slope factor, in mV, reflecting the steepness of the voltage dependence of gating.

Concentration-response data for H⁺ were fitted to a modified Hill equation to account for the fact that the data points were normalized to the response at pH 7.4.

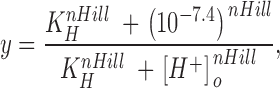(2)

in which y is the proportion of the control g _max, K _H is the equilibrium dissociation constant for H⁺ binding, and n _Hill is the Hill coefficient reflecting the number of H⁺ ions binding per channel. pK _H is defined as the negative logarithm of K _H.

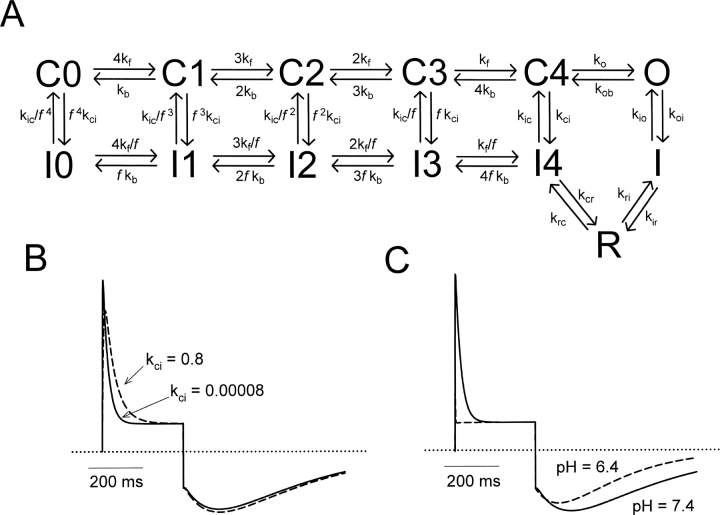
A model of Kv1.5 gating was constructed using ScoP and ScoPfit (version 3.51, Simulation Resources), and was based on an allosteric model of inactivation proposed previously (Wang et al., 2000; Kurata et al., 2001). The number of channels moving between different states was described by a series of first-order differential equations and solved numerically. Except for transitions between the upper and lower rows of the gating scheme in Fig. 8 A, transitions in Fig. 8 A were exponential functions of voltage of the form: rate = k_o · exp[z_i · e₀ · V/k_BT], where k_o represents the rate at 0 mV, z_i refers to the valency for the transition, and i, e₀, V, k_B, and T have their usual meanings; at 20°C, k_BT/ e₀ ≈ 25 mV.

Figure 8.

Kinetic model describing Na⁺ permeation through WT Kv1.5. (A) All rate constants in the activation pathway were governed by exponential functions of voltage (see materials and methods), and were taken from a previously published model of Kv1.5 inactivation (Kurata et al., 2001). At 0 mV, the rate constants were (in ms⁻¹) k_f = 0.4, k_b = 0.065, k_o = 0.31, and k_ob = 0.017, with associated valences of z_f = 1.4, z_b = −0.35, z_o = 0.60, and z_ob = −0.70. Closed-state inactivation and recovery transitions were voltage independent, but were allosterically coupled to transitions in the activation pathway. Rate constants were (ms⁻¹) k_ci = 0.00008, k_ic = 0.000055, and the allosteric factor f was 0.64. Rate constants in the recovery pathway to simulate currents at pH = 7.4 were (ms⁻¹) k_io = 0.00125, k_oi = 0.05, k_ri = 0.0072, k_ir = 0.000323, k_cr = 0.185, k_rc = 0.00855. Transitions between I, R, and I4 were exponential functions of voltage with equivalent valences for z_ri= 0.55, z_ir = −0.65, z_cr = 0.05, and z_rc = −0.05. The relative conductances γ of the open, inactivated states and R states were 1.0, 0.1, and 1.0, respectively. (B) Rate k_ci was increased from 0.00008 ms⁻¹ to 0.8 ms⁻¹, to simulate channel inactivation occurring primarily from closed states. (C) Rates k_io and k_oi were accelerated 50-fold to simulate the currents observed at pH = 6.4.

Online Supplemental Material

The gating pathways by which Kv1.5 channels inactivate and recover from inactivation are described diagrammatically online at http://www.jgp.org/cgi/content/full/jgp.20028760/DC1.

RESULTS

Extracellular Acidification Inhibits hKv1.5 K⁺ and Na⁺ Open-state Currents

We confirmed that hKv1.5 K⁺ currents, like many other Kv channel currents, are inhibited by extracellular acidification. This is shown in the left panels of Fig. 1, A–C . The channels activate at approximately −10 mV, and the current increases and activates more rapidly as the step depolarization increases. Only mild channel inactivation is seen during a 200-ms pulse. Changing pH from 7.4 to 6.4 significantly inhibits the currents recorded during step depolarizations. Fig. 1 B shows that the effect on peak outward current is dependent on the concentration of H⁺ _o. For B, the peak current amplitudes during depolarizing steps were normalized to the current amplitude at 70 mV at pH 7.4 and plotted versus the depolarizing voltage at pH 8.4, 7.0, 6.7, 6.4, and 5.4. To fit the data to a Hill equation, the relative current amplitude at 70 mV at each pH is plotted against H⁺ concentration (Fig. 1 C). H⁺ blocks the current with a K _d of 166 nM (pK _H = 6.8) and a Hill coefficient of 1.6 ± 0.2, and these values are similar to those we have obtained previously (Kehl et al., 2002), confirming the high sensitivity of Kv1.5 channels to block by protons.

Na⁺ currents through the open state of the hKv1.5 channel are similarly inhibited by extracellular acidification as illustrated in Fig. 1, D–F. The advantage of using Na⁺ currents to study the mechanism of action of H⁺ _o is that Na⁺ can pass through both the open and inactivated states of the channel (Starkus et al., 1997; Wang et al., 2000). To focus on the open state current, a short 15-ms depolarizing pulse is used. Na⁺ currents are shown between −70 and 90 mV in 20-mV steps. In comparison to K⁺ current, Na⁺ current inactivates more quickly for reasons related to the relative mean dwell time of the ions at binding sites within the pore (Kiss et al., 1998, 1999). Despite this much faster reduction, the action of H⁺ on Na⁺ currents is very similar to that observed on K⁺ currents. There is significant current inhibition over a range of pH from 8.4 to 5.4 (Fig. 1, D and E). In Fig. 1 E, the peak current amplitudes during depolarizations are shown normalized to the current amplitude at 90 mV at pH 7.4 in each cell and the corresponding I-V relationships at pH 8.4, 7.0, 6.7, 6.4, and 5.4 are plotted. The normalized currents at 90 mV at each pH, fitted to the Hill equation give a calculated K _d of 114 nM, or pK _H value of 6.9, and a Hill coefficient of 1.2 ± 0.15 (Fig. 1 F). Since these values are not significantly different (P > 0.1) from those obtained for K⁺ current (Fig. 1 C), it appears that H⁺ _o modulation of open hKv1.5 channels occurs with the same potency no matter whether K⁺ or Na⁺ is used as the charge carrier.

Extracellular Acidification has Little Effect on hKv1.5 Inactivated State Na⁺ Current

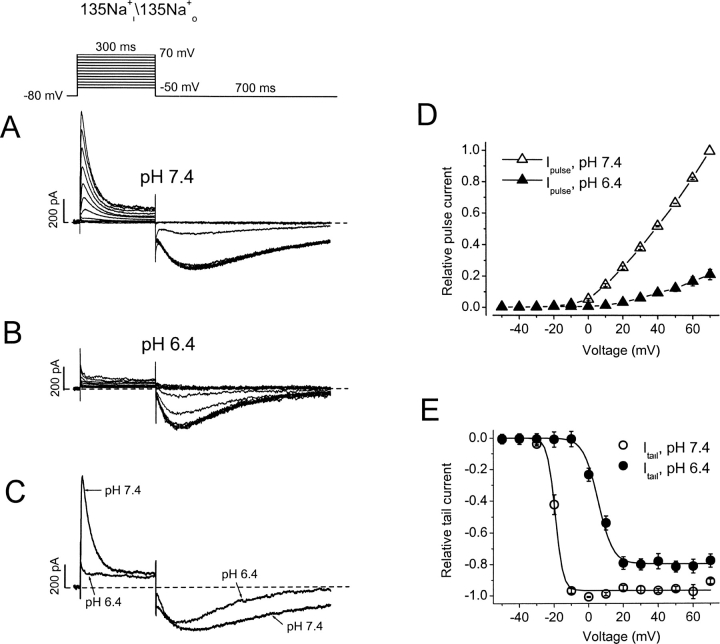
As reported from our laboratory previously (Wang et al., 2000), when bath and pipette K⁺ is substituted by symmetrical 135 mM Na⁺ _i/o, hKv1.5 currents conduct Na⁺ through the open as well as the inactivated state. We have used this property in the present experiments to investigate the fate of the channels at low pH. Our hypothesis is that the fall of Kv1.5 conductance at pH 6.4 is the result of channels populating inactivated states. Na⁺ conduction allows us to interrogate the state dependence of this action. At pH 7.4, hKv1.5 Na⁺ currents are rapidly inactivating, showing a small, sustained phase of current during maintained depolarizations due to Na⁺ passing through inactivated channels (Fig. 2 A). A second, more Na⁺-conductive inactivated state (R of Fig. 8 A) visited in the recovery pathway accounts for the large inward and slowly developing Na⁺ tail currents, on repolarization to −80 mV. These tail currents then relax to the baseline as channels close while remaining inactivated. Thus, in symmetrical Na⁺ conditions, the tail currents show a rising phase and slow decay, all the time reflecting conduction through inactivated channels (Fig. 2 A). In brief, during a current trace, the transient outward currents reflect Na⁺ passing through the open channels, while the inward currents on repolarization track current through inactivated channels. Changing extracellular pH from 7.4 to 6.4 virtually eliminates the transient outward Na⁺ current at all depolarizing voltages, without substantially reducing the slow inward Na⁺ tail current (Fig. 2 B). There is also an interesting change in the time course of the Na⁺ tail current at low pH (Fig. 2 C). At pH 6.4 the tail current peaks earlier and decays more rapidly than it does at pH 7.4. Average I-V data from six cells indicates that at pH 6.4 the transient outward Na⁺ current was inhibited by 79% at 70 mV (Fig. 2 D). In contrast, acidification caused a 27.4 mV rightward shift of the mid-point (V _1/2) for the normalized peak Na⁺ tail current amplitude, but decreased the maximum current at −80 mV by only 19% (Fig. 2 E).

Figure 2.

Differential effects of extracellular acidification on Na⁺ currents through open versus inactivated hKv1.5 channels. (A and B) Na⁺ currents from the same cell in response to the step voltage protocol shown above the current traces at pH 7.4 and pH 6.4. Currents are shown for 10-mV steps. The interpulse interval was 10 s. (C) Comparison of current traces at 70 mV from A and B. (D and E) I-V relationships normalized to current at 70 mV and pH 7.4 for the peak outward current on depolarization and peak tail currents on repolarization. Note that acidification dramatically reduced the outward Na⁺ current without substantially affecting the tail currents. With extracellular acidification the peak current at 70 mV decreased by 78.8 ± 3.3% (n = 6, P < 0.01), whereas the maximal Na⁺ tail current was reduced by 18.5 ± 4.4% (n = 6, P < 0.01). Acidification caused a rightward shift of the voltage (V _1/2) for the half maximal Na⁺ tail current amplitude by 24.7 mV from −19.3 ± 0.4 to 5.4 ± 0.6 mV. Lines through points in E are Boltzmann fit lines, whereas those in D are to connect the points only.

Extracellular Acidification Promotes hKv1.5 Channel Inactivation

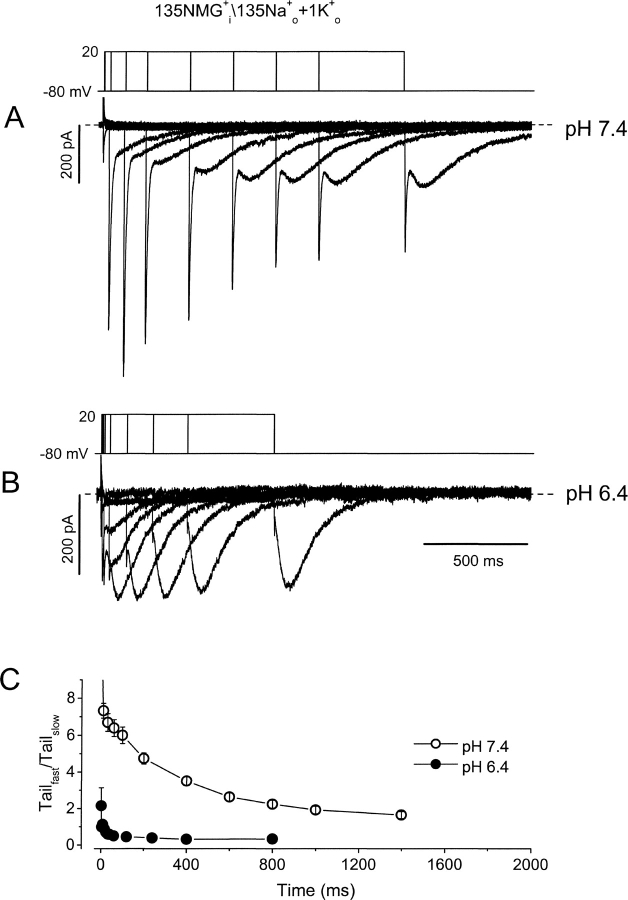
The data presented in Fig. 2 show that although open-state (pulse) hKv1.5 current is strongly reduced by acidification, inactivated-state (tail) current is little affected. This agrees with previous speculation that H⁺ _o inhibits hKv1.5 current by promoting channel inactivation. Of course, this inactivated state is not evident with K⁺ as the charge carrier since K⁺ does not permeate inactivated Kv1.5 channels. The time course of the Na⁺ tail currents at pH 7.4 and 6.4 (Fig. 2, A and B) shows that although the channel is inactivated, it appears to close normally while remaining inactivated. In an attempt to observe the time-dependence of the passage of channels into this inactivated state at low pH we used an “envelope of tails” voltage protocol that allowed us to monitor both open and inactivated channels (Fig. 3 , top). In the experiment shown, only NMG⁺ is present in the pipette solution, to prevent outward currents, but the inclusion of a small concentration of K⁺ in the bath medium (1 mM) with 135 mM Na⁺ permits study of rapidly deactivating K⁺ tail currents through open hKv1.5 channels as well as the Na⁺ tail currents through inactivated channels. Data in Fig. 3 A show the superimposed tail currents during the envelope protocol at pH 7.4. Depolarizations from the −80-mV holding potential to 20 mV are given for variable durations, so that at the end of each depolarization, some channels are in the open state and others are in the inactivated state. Upon repolarization to −80 mV the fast component of tail current reflects K⁺ current deactivation from the open state, while the slow tail current reflects Na⁺ current through inactivated states of the channel. As the duration of depolarization is increased more channels enter the inactivated state, consequently the amplitude of the slow tail current increases while that of the fast tail current decreases. It can be seen in Fig. 3 A that inactivation is not complete even after the longest depolarization shown here, as evidenced by the maintained presence of a fast tail current and the still-increasing size of the slow Na⁺ tail current.

Figure 3.

Extracellular acidification promotes inactivation. (A and B) Superimposed tail currents after depolarizations of varying duration at pH 7.4 and pH 6.4. Pipette contained NMG⁺ as the major intracellular cation, and the bath solution contained 135 Na⁺ _o + 1 mM K⁺ _o. On the first pulse the membrane was depolarized from −80 to 20 mV for 2 ms at pH 7.4, and 1 ms at pH 6.4. For subsequent pulses the protocol was repeated every 10 s for increasing durations, 10, 30, 60, 100, 200, 400, 600, 800, 1,000, and 1,400 ms at pH 7.4; and 4, 8, 16, 24, 32, 40, 60, 120, 240, 400, and 800 ms at pH 6.4. Tail currents are composed of a fast component, reflecting deactivation from the open state, and a slow component reflecting Na⁺ current through inactivated channels. (C) The ratio of peak transient inward current amplitude versus the peak slow tail current is plotted against the duration of depolarization at 20 mV at pH 7.4 (○) and pH 6.4 (•).

With external acidification (pH 6.4), the tail currents change dramatically (Fig. 3 B). Although currents are recorded from the same cell as in Fig. 3 A, three features are obviously different at pH 6.4, compared with pH 7.4. First, the fast tail current is essentially eliminated, as it cannot be convincingly resolved from the capacity transient; second, the slow tail current reaches its peak amplitude much more rapidly—in fact as soon as the depolarizing prepulses are long enough to activate all the channels; and, third, the slow Na⁺ tail current is larger at pH 6.4 than at pH 7.4. The absence of a clear fast tail current suggests that channels have inactivated before the pulse, and/or inactivate extremely rapidly once activated. This idea is supported by the relatively constant amplitude of the slow Na⁺ tail currents once channels have had time to fully activate. These observations are supported by the mean amplitude ratios of fast inward current to slow tail current at pH 7.4 (○) and pH 6.4 (Fig. 3 C, •).

Extracellular Acidification has No Effect on hKv1.5-R487V Na⁺ Currents

If promotion of channel inactivation is the mechanism of current inhibition, removal of channel inactivation by mutagenesis should abolish the pH sensitivity of the current amplitude. Mutation of arginine 487 to valine removes P/C-type inactivation of Na⁺ currents through hKv1.5 (Wang et al., 2000), and data in Fig. 4, A and B , show the effect of pH 7.4 (A) and pH 6.4 (B) extracellular solutions on hKv1.5-R487V currents during step depolarizations. Obviously, inactivation of hKv1.5 Na⁺ currents is prevented by the mutation, and changing the pH to 6.4 does not affect the Na⁺ current amplitude once the gating shift is taken into account. Furthermore, tail currents recorded using the envelope protocol described for Fig. 3 reveal that repolarization yields only fast tail currents at both pH 7.4 and 6.4 (Fig. 4, C and D, respectively). That no slow tails are seen is consistent with the observation that the mutant channel does not inactivate. In addition, tail currents are similar in amplitude and time course at pH 7.4 and 6.4. From these data we conclude that an intact inactivation process is required for H⁺-induced current inhibition. This directly supports the notion that H⁺ ions inhibit hKv1.5 current by stabilizing channels in P/C-type inactivated states.

Figure 4.

Extracellular acidification does not inhibit Na⁺ current through the inactivation-deficient mutant hKv1.5-R487V. (A and B) Na⁺ currents from the same cell in response to the step voltage protocol shown above the current traces at pH 7.4 and pH 6.4. (C and D) Superimposed tail currents during the envelope of voltage steps shown above the current traces at pH 7.4. The depolarization to 40 mV was initially 1 ms in duration and the protocol was repeated every 10 s for increasing durations up to 500 ms.

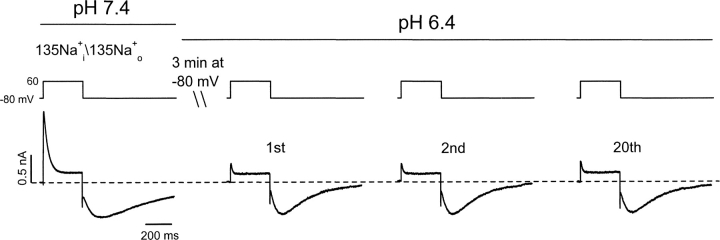
Inactivation of Kv1.5 Current Is Complete at the First Depolarization in Low pH

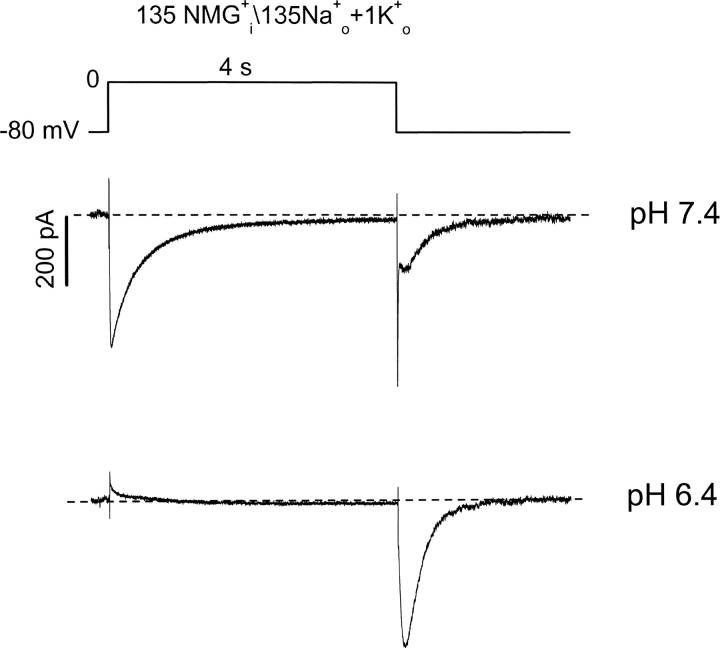
The data in Fig. 3 B showed that fast tails on repolarization were absent at pH 6.4, even after the shortest depolarization (1 ms). This absence of a fast deactivating K⁺ current tail suggests a very rapid entry into the inactivated state. The experiments in Figs. 5 and 6 show that, at low pH, inactivation is present the first time channels are activated, and that only a few open channels pass current. In symmetrical Na⁺, at pH 7.4, depolarizations to 60 mV evoke the typical transient current waveform and there is a slow tail on repolarization to −80 mV (Fig. 5, left). After a 3 min rest at −80 mV after changing the pH of the bath solution to pH 6.4, the first depolarization evokes a current just like that shown in Fig. 2 B. That is to say there is little outward current component, but a well-developed Na⁺ tail current can be seen. Note also, that as in Fig. 2 C, the Na⁺ tail current in pH 6.4 reaches a peak sooner and decays more rapidly than at pH 7.4. The waveform changes little over the next 20 pulses, indicating that a steady-state is reached at low pH in the first pulse, and that there is no cumulative effect. In a similar experiment with 1 mM K⁺ present in the bath solution to monitor K⁺ current through open channels (Fig. 6), there is a clear inward current through open channels at pH 7.4 during the depolarization to 0 mV. This is followed on repolarization by a very brief K⁺ tail through deactivating open channels, and then a slower Na⁺ tail through inactivated channels. After switching to pH 6.4, and allowing a 3-min rest, the first pulse shows that the open-channel K⁺ current is absent, as is the rapid K⁺ tail, whereas the Na⁺ tail current not only persists, but is in fact larger. The apparently instantaneous loss of the inward K⁺ current during the first depolarization at pH 6.4 illustrates the rapid nature of the conductance loss at low pH, but leaves open the question of whether there is resting inactivation and/or very fast open-state inactivation.

Figure 5.

Inactivation of Kv1.5 current is complete at the first depolarization in low pH. In symmetrical Na⁺ _i/Na⁺ _o solutions, control Na⁺ current was recorded by applying the voltage protocol shown above the current traces at pH 7.4. The pH of the bath solution was then changed to 6.4 while the cell was held at −80 mV for 3 min. Na⁺ currents at pH 6.4 were recorded again by applying the same voltage protocol every 10 s. The first depolarization elicited a response in which the outward current was largely eliminated but the tail current remained well developed. The waveform of the Na⁺ current remained unchanged over the next 20 pulses at pH 6.4 (n = 6).

Figure 6.

Extracellular acidification causes early and complete Kv1.5 channel inactivation. Kv1.5 channel current was elicited by depolarization to 0 mV for 4 s at pH 7.4. The inclusion of 1 mM K⁺ _o allowed an inactivating inward K⁺ current through the open state to be seen. Repolarization tail currents with fast (K⁺) and slow (Na⁺) components were also recorded. The pH of bath solution was then changed to 6.4 while the cell was held at −80 mV for 3 min. The current during the first depolarization of the same voltage protocol at pH 6.4 is shown in the bottom panel (n = 7).

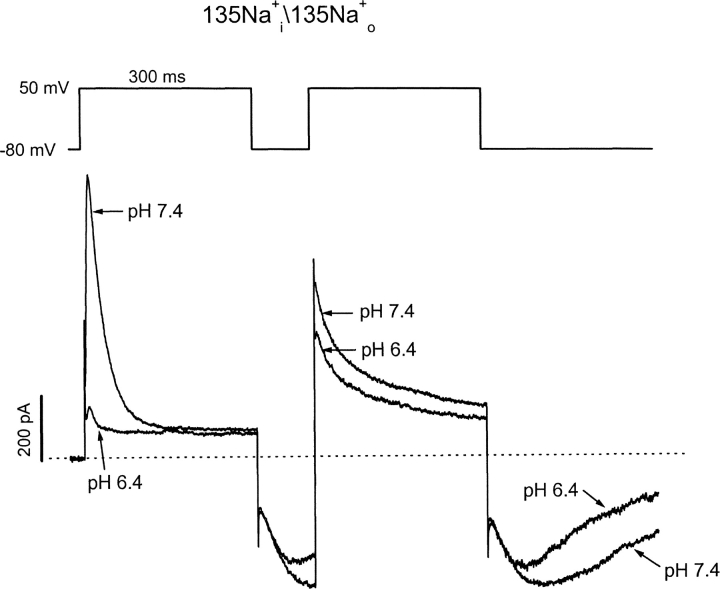
The experiment illustrated in Fig. 7 , where a two-pulse protocol was used to evoke currents in a symmetrical concentration (135 mM) of Na⁺, helps to distinguish between these two possibilities. At pH 7.4 the first pulse elicits a rapidly inactivating outward open-state Na⁺ current, which is followed by a Na⁺ tail current on repolarization. A second pulse applied at the peak of the tail current results in a very large, comparatively slowly relaxing outward Na⁺ current. The latter “supernormal” current is caused by rapid reactivation of closed-inactivated channels (see Scheme I in online supplemental material, available at http://www.jgp.org/cgi/content/full/jgp.20028760/DC1; Wang et al., 2000) and subsequent inactivation into the stable P/C-type inactivated state. At pH 6.4, this slowly relaxing outward current persists during the second step pulse, but is never seen during the first pulse. This suggests that inactivation from any closed state (i.e., at a holding potential of −80 mV) does not account for the conductance loss at pH 6.4.

Figure 7.

Slowly inactivating outward currents upon activation from closed inactivated states. In symmetrical Na⁺ _i/Na⁺ _o solutions, Kv1.5 channel current was elicited by depolarization to 50 mV for 300 ms at pH 7.4. After a brief 100-ms repolarization, a second test pulse to 50 mV was given near the peak of the slow inward tail current. The pH of the bath solution was then changed to 6.4 while the cell was held at −80 mV for 3 min, and the two-step voltage protocol was repeated (n = 7). Note the much slower inactivation of R-state “supernormal” current during the second step pulse at both pH 7.4 and 6.4.

DISCUSSION

Current inhibition by H⁺

External acidification has been reported previously to inhibit hKv1.5 current (Steidl and Yool, 1999; Jäger and Grissmer, 2001; Kehl et al., 2002), but the exact mechanism by which this occurs has remained uncertain. Steidl and Yool (1999) suggested that acidification of the external medium caused an acceleration of C-type inactivation, a use-dependent inhibition of the current, and a slowing of recovery from inactivation of rKv1.5 currents. They concluded that the proton-induced current decline was due to the accumulation of channels in the C-type inactivated state. Our results here confirm that lowered pH does indeed result in the accumulation of channels in the inactivated state, but we propose a rather different mechanism by which this occurs.

We have used the property of Na⁺ permeation through the inactivated state of hKv1.5 channels to interrogate the fate of channels at acid pH. Our initial experiments confirmed that Na⁺ currents through the channel responded to acid pH in the same manner as K⁺ currents (Fig. 1). The pH dependence of peak conductance and channel tail current was almost identical with pK _Hs of 6.8 and 6.9 for K⁺ and Na⁺ currents, respectively. Similarly, with either Na⁺ (Fig. 5) or K⁺ (Fig. 6) as the charge carrier, there was a very marked loss of open-state conductance as soon as channels were activated at low pH, confirming that H⁺ inhibition of Na⁺ currents through the open state is a good model for K⁺ fluxes. There is little doubt from the results of experiments assessing Na⁺ permeation of the inactivated state in Figs. 2, 3, and 5 that lowering the pH results in a decrease of the availability of the channels through an increased number of inactivated channels. Fig. 2 shows that the outward Na⁺ current was abolished, whereas the tail current, reflecting flux through inactivated channels, was unchanged in amplitude, although the tail peaked somewhat earlier and decayed more rapidly. Finally, the experiments with the noninactivating mutant hKv1.5-R487V (Fig. 4) indicated that channels that were unable to inactivate (and thus incidentally showed no slow Na⁺ tail currents), were unaffected by lowered pH. However, an examination of the current waveforms in Fig. 1, A and D, does not reveal an increased inactivation rate at acid pH in either the K⁺-conducting or the Na⁺-conducting conditions, though such an increase is sometimes evident with a longer depolarization (Lopez-Barneo et al., 1993; Claydon et al., 2002; Kehl et al., 2002). This suggests that another mechanism or mechanisms may contribute to the increased number of inactivated channels at pH 6.4.

The Relationship between Current Inhibition by H⁺ and P/C-type Inactivation

When the pH was changed from 7.4 to 6.4 while the channels were held at −80 mV, there was inhibition of either open-state Na⁺ or K⁺ current, whereas the slow Na⁺ tails were fully developed when the channel was first activated at low pH. This is clearly seen in data in Figs. 5 and 6. As a result, a hypothesis formulated early in this series of experiments was that the effect of reducing extracellular pH was to induce resting (i.e., closed-state) inactivation, thereby rendering channels unavailable even before the application of any depolarizing stimulus. This hypothesis was also motivated by the apparent immediacy of the effect of reducing extracellular pH on K⁺ currents (Fig. 9, Kehl et al., 2002). However, a number of lines of evidence and reasoning argue against this being the major mechanism of conductance loss under the present experimental conditions. A number of previous experiments (Kiss et al., 1999; Wang et al., 2000) have demonstrated that Na⁺-permeable states become occupied during inactivation and/or recovery from inactivation in Kv channels. Importantly, these latter studies have suggested the presence of a committed step during recovery from inactivation, such that Na⁺-permeable states are not fully accessible from resting closed-inactivated channel states (Wang et al., 2000). This is exemplified by data in Fig. 2 B. Here, at pH 6.4, outward Na⁺ currents are absent during the depolarizing pulse, whereas Na⁺ tail currents are comparable to those at pH 7.4. We adapted a previous model incorporating closed-state inactivation in Kv1.5 (Kurata et al., 2001) to include the transitions to Na⁺-permeable states that are occupied during recovery from inactivation (from Wang et al., 2000, Fig. 8 A). This adaptation of our previous model was used to test reopening of channels from resting closed-inactivated states when subjected to acid extracellular pH. If channels are permitted to activate from closed-inactivated states to the Na⁺-permeable states, then simulations with increased rates of closed-state inactivation (k_ci) predict a large outward current upon depolarization (Fig. 8 B), which decays slowly like the second-pulse current demonstrated in Fig. 7. However, slowly decaying outward currents were never observed during initial depolarizations at low pH (Figs. 2, 5, and 7), suggesting that channels activate from normal resting closed-states at both pH 7.4 and 6.4.

Figure 9.

Simulation of the development of Na⁺ currents at pH 7.4 or 6.4. Simulations were performed using the parameters described in Fig. 8 C for pH 7.4 (A) and pH 6.4 (B). In A and B, currents were simulated with depolarizing stimuli to 60 mV for 2, 4, 8, 15, 30, 60, 120, and 300 ms, followed by a repolarization to −80 mV. The simulations illustrate the more rapid development of the Na⁺ tail at pH 6.4, and also clearly illustrate the rapid rising phase and rapid decay of the Na⁺ tail (compare Fig. 3).

Additional evidence against increased numbers of channels residing in closed inactivated states at low pH comes from gating current measurements (Kehl et al., 2002). These studies have shown very similar gating current waveforms and a depolarizing shift of the on-gating charge voltage dependence at pH 6.4 compared with pH 7.4. In contrast to these actions, it is well known that channel inactivation causes both gating charge immobilization (Chen et al., 1997; Olcese et al., 1997) and a negative shift in the voltage dependence of charge availability (Olcese et al., 1997; Wang and Fedida, 2001). This suggests that channels are not C-type inactivated at rest in acid pH conditions, but still could be P-type inactivated.

Acceleration of the Open-inactivated Equilibrium by Low pH

These findings led us to focus our attention on the equilibrium between open and inactivated states (rates k_io and k_oi in Fig. 8 A). With the constraints established by the prior studies of Na⁺ conduction described above we next tested the idea that low pH somehow greatly accelerates inactivation from the open state, as we and others have discussed previously (Steidl and Yool, 1999; Claydon et al., 2002; Kehl et al., 2002). Some direct experimental evidence supports this idea. At pH 6.4, a small very rapidly decaying outward transient current is often apparent in symmetrical Na⁺ _o/Na⁺ _o when channels are activated on depolarization. Examples of these rapid transient currents, which are clearly neither capacity transients nor gating currents, can be seen in Figs. 2, 5, and 7, and suggest channels open very briefly before inactivating.

The experimental data presented in Fig. 7 offers many insights into the effects of pH on the gating mechanism of Kv1.5. The first striking observation is that at pH 6.4, depolarization of channels during the Na⁺ tail results in a significant outward current, which decays slowly. This result supports our previous conclusion (Kehl et al., 2002) that H⁺ ions are not occluding the pore. Furthermore, the similar rates of decay of the supernormal currents at pH 7.4 and 6.4 suggest that the transitions in the recovery pathway are not significantly affected by pH level. Most importantly, the outward Na⁺ current at pH 7.4 decays to the same level as the sustained outward current observed in pH 6.4, indicating that the steady-state outward current is also unaffected by pH level. This observation suggests that channels reach the same equilibrium upon depolarization, irrespective of the pH of the extracellular solution, but that low pH accelerates the time course for reaching this equilibrium. This can be envisioned as a reduction of the activation energy barrier which must be overcome in the transition from the open state to the inactivated state.

Interestingly, these observations are borne out in simulations of Na⁺ tail currents when the rate constants for transitions between the open state and inactivated state are altered. Specifically, if the rate of inactivation is selectively accelerated (shifting the O-I equilibrium toward the inactivated state), the resulting Na⁺ tail currents exhibit a slower rising phase and a slower decay than the simulated control currents (unpublished data). In addition, if the O-I transition is considered to be absorbing, acceleration of inactivation has no effect on the Na⁺ tail current waveform. However, if the O-I and I-O rate constants are increased (but the ratio of k_io and k_oi is left unchanged), our simulations replicate all of the features observed experimentally (see Fig. 8 C, where k_io and k_oi were both accelerated 50-fold to simulate currents at pH 6.4). This includes a very brief transient outward current, a sustained current equivalent to that observed under control conditions, a shorter latency to peak and a faster decay of the Na⁺ tail current waveform (Fig. 8 C). It should be noted that in order for these simulations to faithfully reproduce the currents observed experimentally, it is critical that there is a finite backward rate constant from the I to O state. However, this equilibrium clearly must strongly favor the I state, because rapidly deactivating Na⁺ tails are not detectable experimentally. In our simulations we fixed the equilibrium constant for inactivation from the open state at 39 (at equilibrium 97.5% of channels are inactivated); however, the acceleration of the kinetics of the Na⁺ tail is not strictly tied to the extent of the O-I equilibrium (equilibrium constants ranging from 20 to 100 were all able to duplicate the shorter latency to peak and faster decay of the slow Na⁺ tail).

In Fig. 9 we have simulated the effect of depolarization duration on the waveform of the Na⁺ tail currents at pH 7.4 and pH 6.4, in an attempt to replicate the experiment shown in Fig. 3. It can be seen that the model reproduces the balance between fast deactivating tails, their decay, and the gradual development of the slow Na⁺ tail at pH 7.4 (Fig. 9 A). At pH 6.4 the model reproduces the essential absence of a fast open-state to closed-state deactivation tail while illustrating the immediate steady-state amplitude of the slow Na⁺ tail through inactivated channels (Fig. 9 B). Although the transitions modeled in the recovery pathway are quite complex, we believe that the accelerated O-I equilibrium reproduces the experimental results by allowing a greater number of channels to recover via the deactivating O-C4 transition. This explains the more rapid decay of the slow Na⁺ tail at pH 6.4, and also accounts for its earlier and slightly smaller peak current amplitude, as fewer channels pass through the Na⁺-permeable R state. In essence, the rapid O-I equilibrium allows a larger fraction of channels to deactivate from the O state, rather than through the slow Na⁺-permeable states, and effectively increases the decay rate of the tail.

Conclusion

Based on our experimental and modeling studies we suggest that the reduction of hKv1.5 channel Na⁺ current on exposure to acid pH arises from the rapid entry of channels into the C-type inactivated state. We have shown that extracellular acidification reduces hKv1.5 channel conductance by accelerating the formation of the equilibrium between the open and inactivated states. A precedent exists for the action of pH to accelerate entry into P/C-type inactivated states in our understanding of the mechanism of the lack of open-state conduction in the W434F Shaker mutant. This is caused by extremely rapid entry into P/C type inactivated states upon activation, as evidenced by very brief open times (Yang et al., 1997).