Gain-of-function Mutations Reveal Expanded Intermediate States and a Sequential Action of Two Gates in MscL

Abstract

The tension-driven gating transition in the large mechanosensitive channel MscL proceeds through detectable states of intermediate conductance. Gain-of-function (GOF) mutants with polar or charged substitutions in the main hydrophobic gate display altered patterns of subconducting states, providing valuable information about gating intermediates. Here we present thermodynamic analysis of several GOF mutants to clarify the nature and position of low-conducting conformations in the transition pathway. Unlike wild-type (WT) MscL, which predominantly occupies the closed and fully open states with very brief substates, the mild V23T GOF mutant frequently visits a multitude of short-lived subconducting states. Severe mutants V23D and G22N open in sequence: closed (C) → low-conducting substate (S) → open (O), with the first subtransition occurring at lower tensions. Analyses of equilibrium state occupancies as functions of membrane tension show that the C→S subtransition in WT MscL is associated with only a minor conductance increment, but the largest in-plane expansion and free energy change. The GOF substitutions strongly affect the first subtransition by reducing area (ΔA) and energy (ΔE) changes between C and S states commensurably with the severity of mutation. GOF mutants also exhibited a considerably larger ΔE associated with the second (S→O) subtransition, but a ΔA similar to WT. The area changes indicate that closed conformations of GOF mutants are physically preexpanded. The tension dependencies of rate constants for channel closure (k _off) predict different positions of rate-limiting barriers on the energy-area profiles for WT and GOF MscL. The data support the two-gate mechanism in which the first subtransition (C→S) can be viewed as opening of the central (M1) gate, resulting in an expanded water-filled “leaky” conformation. Strong facilitation of this step by polar GOF substitutions suggests that separation of M1 helices associated with hydration of the pore in WT MscL is the major energetic barrier for opening. Mutants with a stabilized S1 gate demonstrate impeded transitions from low-conducting substates to the fully open state, whereas extensions of S1–M1 linkers result in a much higher probability of reverse O→S transitions. These data strongly suggest that the bulk of conductance gain in the second subtransition (S→O) occurs through the opening of the NH₂-terminal (S1) gate and the linkers are coupling elements between the M1 and S1 gates.

INTRODUCTION

Unified mainly by function, mechanosensitive ion channels form a diverse group of sensory receptors, comprising members of structurally unrelated channel families (for review see Sukharev and Corey, 2004). The multiplicity of mechanoreceptor types suggests that similar functions can be implemented with different sequences and structural designs, thus emphasizing the importance of unifying biophysical principles of gating by mechanical force.

Bacterial mechanosensitive channels are convenient model systems for the basic channel biophysics. They fulfill the role of turgor pressure regulators in small prokaryotic cells, which in the wild are subjected to a constantly changing environment. Three bacterial mechanosensitive channels have been identified in Escherichia coli: MscL, MscS, and MscK (Sukharev et al., 1994; Levina et al., 1999; Pivetti et al., 2003). Two of them, MscL and MscS, were isolated, reconstituted, and shown to be gated directly by tension in the lipid bilayer (Hase et al., 1995; Blount et al., 1996a; Okada et al., 2002; Sukharev, 2002). Successful efforts in crystallization of MscS from E. coli (Bass et al., 2002) and the MscL homologue from M. tuberculosis (Chang et al., 1998) (TbMscL) have opened rich opportunities for detailed structure-based studies of their gating mechanisms. Since then, MscL has been the best understood “simple” channel gated by membrane stretch (Blount, 2003; Perozo and Rees, 2003; Sukharev and Anishkin, 2004).

Identification of the main gate region in randomly generated gain-of-function mutants of MscL (Ou et al., 1998) corroborated extremely well with the crystal structure. The separation of the tightly packed M1 helices in the core of the complex was inferred to be the central step in the gating process (Chang et al., 1998; Yoshimura et al., 1999; Batiza et al., 1999; Sukharev et al., 2001a). The “iris” model of the MscL barrel expansion, which predicted tilting and outward movement of transmembrane helices (Sukharev et al., 2001b), has found substantial support in independent experimental (Betanzos et al., 2002; Perozo et al., 2002) and computational (Gullingsrud and Schulten, 2003) studies. The periplasmic loops were suggested to act as springs restraining barrel expansion (Ajouz et al., 2000; Park et al., 2004). The roles of other protein parts and the sequence of events in the channel opening process however remain largely hypothetical and call for more detailed analyses.

Single-channel currents provide a direct source of information about the gating process, where subconducting states may represent conformational intermediates between the fully closed and open states. The initial survey of MscL in liposome patches (Sukharev et al., 1999) has identified three prominent short-lived substates and estimated the tension dependencies of rate constants for each subtransition. The kinetics revealed that the major tension-dependent step in the process of opening is the subtransition from the closed state to the lower subconducting state. The thermodynamic treatment accounting for the (tension × expansion) term in the free energy of a conformational state suggested that the low substate must be characterized by a relatively large in-plane area (Sukharev et al., 1999; Chiang et al., 2004) and, despite low conductance, the conformation of the transmembrane barrel must resemble more the open than the closed state. Thus, the necessity of a structural element that partially occludes the pore in the expanded state evoked the hypothesis of a second gate (Sukharev et al., 2001a,b).

The isolation and functional analysis of easily opened gain-of-function (GOF) mutants (Ou et al., 1998; Yoshimura et al., 1999) revealed that some of them exhibit a prominent low-conducting substate. In most severe cases, the low substate was appreciably occupied even at zero tension, whereas the subsequent subtransition to the fully open state required higher tensions. This stable low substate was initially interpreted as partial opening of the main hydrophobic gate formed by M1 helices (Yoshimura et al., 1999). The question of whether the prominent low substate in GOF mutants is a result of partial opening of a single gate, or is an intermediate state with the main gate open, but the second gate still closed in the two-gate mechanism, becomes mechanistically important. If the latter is the case, then GOF mutations simply stabilize the low-conducting intermediate and separate the two parts of transition in time and on the tension scale, thus making each subtransition more tractable.

In the present work, we utilize the amplitude histogram method to determine equilibrium state occupancies in three GOF mutants of different severity. We take advantage of gating patterns in these mutants where the closed (C) to low substate (S) and low substate to open (O) subtransitions are separable, and analyze the entire gating process in the three-state framework (C↔S↔O). We demonstrate that hydrophilic substitutions in the pore constriction affect predominantly the first subtransition associated with the opening of the M1 gate and have a lesser effect on the second transition ascribed to the separation of the hypothetical S1 gate. This specific effect of gain-of-function mutations reveals the critical role of hydration in the opening of the M1 gate. The data permits us to reconstruct energy-area profiles for transitions in the GOF mutants and compare them to wild type (WT). We also take into consideration mutants with stabilized S1 gate or with extended S1–M1 linkers and find that these alterations affect primarily the second subtransition, thus providing more evidence to the two-gate mechanism of MscL and the proposed role of NH₂-terminal domains as the second gate.

MATERIALS AND METHODS

Strains and Cell Preparations

Severe gain-of-function mutants V23D and G22N (Ou et al., 1998) were gifts from Dr. Ching Kung (University of Wisconsin, Madison, WI). WT mscL (construct p5-2-2b; Blount et al., 1996a) was used as the template for generation of the V23T, F7H, and F10H mutants, using the previously described megaprimer technique (Yoshimura et al., 1999). The GG14 and GAG14 mutations that introduce one– and two–amino acid insertions into the S1–M1 linker were generated with the same technique. For functional patch-clamp analysis, WT and mutant channels were expressed in PB104 mscL ⁻ strain containing endogenous MscS channel. Giant E. coli spheroplasts were generated according to the standard technique by inducing filamentous forms in the presence of cephalexin (Martinac et al., 1987). To obtain a low number of active channels per patch, in most instances, spheroplasts were generated under noninducing conditions (no IPTG). In some experiments where the expression at the level of promoter “leakage” was low, the constructs were induced with 1 mM IPTG for 5 min before the plasting reaction was performed in the presence of EDTA and lysozyme.

Single-channel Recording and Pressure Protocols

All recordings were performed with borosilicate pipettes in excised inside-out patches, at room temperature. The symmetrical buffer contained (in mM) 200 KCl, 90 MgCl₂, 10 CaCl₂, 10 HEPES (pH 6.0). The membrane potential was −20 mV (pipette positive); recordings were low-pass filtered at either 10 or 30 kHz. Suction was delivered by a large (60 cc) screw-driven syringe and monitored with a PM 015D electronic manometer (WPI). After seal establishment and patch excision, negative pressure was ramped up at a rate of ∼60 mm Hg/s until endogenous MscS channels were fully activated. The pressure was then ramped more slowly until a desired degree of MscL activation was achieved and the following single-channel recordings were performed at a constant pressure. The pressure at which half of MscS channels were activated (p _1/2 ^MscS) was used as a tension calibration point, as reported previously (Chiang et al., 2004). According to previous measurements in spheroplasts (Cui and Adler, 1996) and liposomes (Sukharev, 2002), the tension midpoint for MscS activation (γ_1/2 ^MscS) is close to 5.5 dyne/cm. Pressures were converted to tensions using the formula: γ = (p/p _1/2 ^MscS) × 5.5 dyne/cm, which can be deduced from the law of Laplace for a spherical surface.

To record dose–response curves, the suction applied to the pipette was ramped up with the same rate as above, passing the entire MscS activation range until we observed first MscL currents. Then the pressure was increased in smaller increments of ∼10 mm Hg and kept constant for ∼10 s between the steps. Severe GOF MscL mutants were activated before MscS, consistent with previous observations (Yoshimura et al., 1999). With the lowest level of gene induction (no IPTG), we observed three to six WT MscLs per patch, two to three V23T channels, and usually one V23D or G22N channel.

Amplitude Histograms

The analysis of occupancies of different conducting states was performed by generating and fitting amplitude histograms. Following the baseline correction, which removes drift and some obvious MscS fluctuations, all-point probability density histograms were calculated. Segments of traces where more than one channel were simultaneously open were excluded. In this analysis of V23D and G22N mutants, only true single-channel traces were taken into consideration. All current values were normalized to the conductance of the fully open state and the range of analyzed amplitudes, which included the baseline noise and fluctuations around the fully open state, was set between −0.1 and 1.1. Histograms for all MscL records, WT or mutant, were fitted by a sum of 11 Gaussian functions, representing the closed, open, and nine intermediate levels using the HISTAN software, custom-written in Matlab. This number of Gaussians was chosen based on a previous analysis of WT MscL (Chiang et al., 2004), and kept constant to provide compatibility between datasets. Although the positions, occupancies, and widths of Gaussian peaks were free and independent adjustable parameters, it was possible to obtain reasonably accurate fits for all versions of the channel with essentially the same set of positions for peaks, which reflect common amplitudes of subconducting states (see results). Most of the analysis was focused on tension dependencies of occupancies of the fully closed and open states, and two low subconducting levels with relative amplitudes of 0.13 and 0.22. The fitting procedure was based on minimization of the geometrical mean of linear and logarithmic root mean standard deviations between the experimental histogram and reconstructed fit.

Before MscS opening and closure events were removed from MscL trace for the substate analysis, the conductances of the two channels were compared. MscL-to-MscS unitary current ratios were estimated from the median positions of Gaussian peaks for the closed state and fully open states obtained at several different tensions. The procedure was done for WT and repeated for all mutants.

Two-dimensional Amplitude Histograms

To present the average probabilities of various conducting states as a function of tension, 2D histograms (probability over the conductance-pressure plane) were generated from several independent traces. Standard one-dimensional histograms were first created for stretches of raw traces recorded at different constant pressures. The histograms were then stacked along the pressure scale, thus creating a 2D histogram of log probability with gaps between fixed pressure values at which recordings took place. The gaps were then filled using a spline interpolation procedure that created a smooth surface. For each pressure section, the sum of occupancies in all current bins was normalized to unity, thus transforming the amplitude histogram into the probability density distribution at a given tension. The current scale was then normalized such that the conductance of the fully open state is equal to one. The pressure scale was converted into tensions using p _1/2 ^MscS values as described above. 2D histograms generated for several individual traces were then averaged together to present the activation landscape for a mutant.

Dose–response Curves Measured with Mean Current

In some experiments the open probability (P_o) was calculated for each pressure step as the mean integral current divided by the maximum current that could be attained at saturating pressures. For multichannel patches, the maximal conductance (and the total number of channels) was estimated by extrapolating partial activation curves as reported previously (Chiang et al., 2004). The integral conductance G normalized to the maximal conductance G _max produces effective open probability P _o ^eff that includes contributions from all subconducting states.

Thermodynamic and Kinetic Analyses

The ability of a channel to expand in the plane of the membrane is the specific property that makes it responsive to external tension applied to the lipid bilayer. In the linear approximation, at equilibrium, the ratio of probabilities of any two states can be related by the Boltzmann equation:

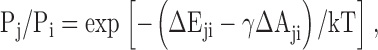(1)

where P _i and P _j are the state occupancies, ΔE _ji is the energy difference between two quasi-equilibrium states in an unstressed membrane, ΔA _ji is the in-plane protein area change upon the transition, γ is membrane tension, and kT is thermal energy (Howard and Hudspeth, 1988; Sachs, 1992; Sukharev et al., 1999). We assume that the distribution of channels among the states is always close to equilibrium since the recording time for an all-point histogram at every pressure step (∼10 s) was considerably longer than the typical dwell time of the channel in any of the states (1–100 ms), and MscL does not display any delay in equilibration or noticeable inactivation.

The rate constants for selected transitions in two mutants were determined using QuB program (Qin et al., 2000). The baseline-corrected single-channel fragments of traces were idealized in a two-state approximation using SKM, and then major rate constants were fitted using MIL. For WT MscL, which is characterized with a single rate-limiting step (Sukharev et al., 1999), the entire closed-to-open interval was counted as a single transition. For V23D mutant, only the S_0.13→O transition, which could be roughly approximated as an elementary step, was fitted. The rate constants for the forward and backward transitions were extracted at different tensions. The logarithmic slope of the backward rate constant (k _off) plotted as a function of tension was interpreted as ΔA _ob, the distance along the area axis between the bottom of the open state well and the top of the transition barrier separating it from low-conductance states.

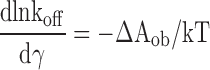This formalism is briefly described in Section 1 of the supplemental material.

Energy Estimations

The energetic effects of gain-of-function mutations were estimated in order to relate the energy-area profiles for gating transitions in different mutants. The differences in solvation energies for the native versus substitute residues and the contribution of electrostatic repulsion between introduced charges (in V23D) were taken into account. The procedural details of these estimations are presented in Section 2 of the supplemental material.

Online Supplemental Material

The online supplemental material is available at http://www.jgp.org/cgi/content/full/jgp.200409118/DC1. Section 1 describes the formalism used for treatment of the thermodynamic and kinetic data and determination of in-plane area differences between the conformational states and the positions of rate-limiting barriers. Section 2 explains methods used for energetic estimations of stabilizing and destabilizing effects of gain-of-function mutations on the closed and open states, where electrostatic and solvation energies were taken into account.

RESULTS

GOF Mutations Change Gating Patterns

The three mutations V23T, V23D, and G22N are hydrophilic substitutions in the pore constriction of MscL and all confer gain-of-function phenotypes of different magnitude. In in vivo assays, full expression of V23T driven by the p_lacUV promoter does not affect bacterial growth characteristics on plates, and the effect of growth retardation in liquid media was also insignificant. The V23D and G22N mutants displayed severe toxic phenotypes, completely abolishing growth after full induction with 1 mM IPTG (unpublished data), which is consistent with the data reported previously (Ou et al., 1998).

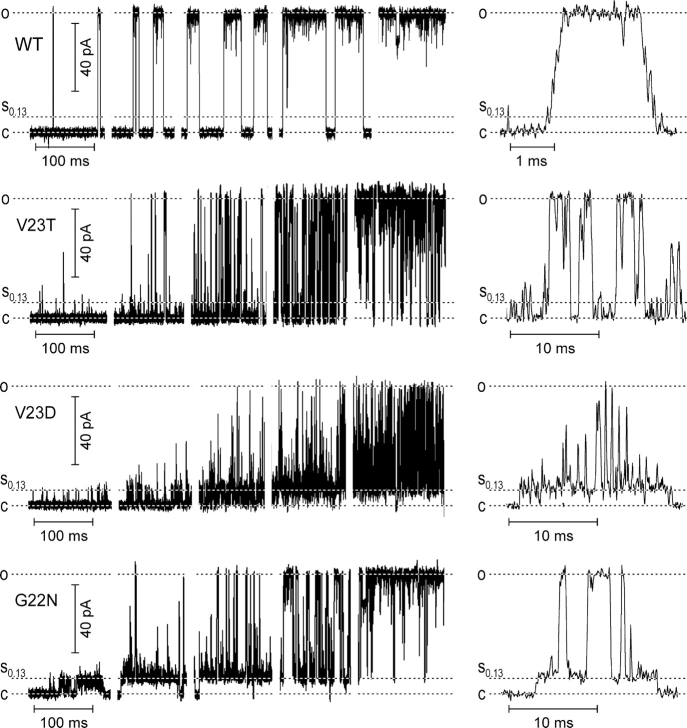
Fig. 1 shows fragments of typical single-channel traces recorded in WT MscL, mild V23T, and two severe gain-of-function mutants V23D and G22N. The traces originally recorded in a continuous manner with small pipette pressure increments are presented as sequences of 120 ms long fragments to illustrate typical gating patterns at five different pressures and open probabilities ranging from ∼10⁻² to ∼0.9. The right part of the figure shows expanded episodes with resolved characteristic transitions. WT MscL displays an almost binary character of behavior with high occupancies of fully closed and fully open states. Short sojourns to lower subconducting levels occur predominantly from the fully open level. The expanded fragment shows that in addition to the downward deflections from the open state, the channel also displays short stops on the way up or down, previously documented in liposome-reconstituted MscL (Sukharev et al., 1999). The dwell time in the lowest substate is not different from that of other short-lived substates.

Figure 1.

Typical gating patterns of WT MscL, mild GOF mutant V23T, and more severe V23D and G22N mutants. Recordings were done in inside-out patches at −20 mV (pipette positive). Low-pass filtering was at 30 kHz. At least three independent traces covering the range of Po from 0 to 0.9 were recorded for each mutant. Five selected episodes of gating at different pressures and Po illustrate preferential states and transitions. The fragments of traces in a “magnified” time scale are shown on the right. The occupancy of low-conducting substates increases with the severity of the mutation.

The mild V23T mutant displays a faster kinetics of the main transition. The downward deflections from the fully open level are deeper and more frequent. The channel visits intermediate conducting states more often, with a slightly higher probability of low levels at lower tensions. The expanded episode shows frequent excursions from the baseline to the low sublevels.

The more severe V23D mutant displays short openings to the low sublevel very early on tension. This low substate becomes 40–60% occupied in the middle of the stimulation range, when the channel starts displaying “spiky” transitions to intermediate and upper conducting states. When the open state becomes considerably populated, the channel practically never visits the resting closed state, returning always to one of the low-conducting levels. The amplitude of the upper conducting levels in many transitions is either unresolved or intrinsically not very well defined in this mutant. However, the maximal conductance is clearly limited by the upper 3.2 nS level similar to that of WT.

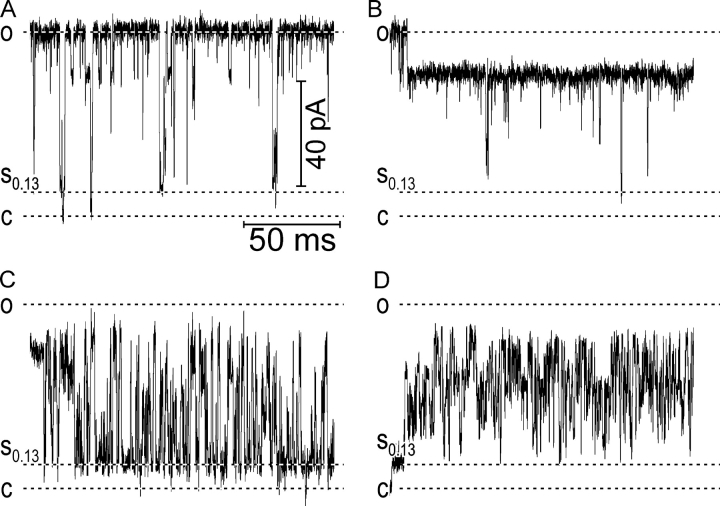
The transitions in the most severe G22N mutant are similar to that of V23D, however at low tensions, the channel even more stably populates the low-conducting level. At intermediate tensions, the channel displays the same spiky transitions to high-conductance states, however at higher tensions, it tends to reside more in the fully conducting state, resembling WT. It practically never visits the closed state at intermediate and higher tensions, always returning to the substate. Besides the stably occupied low-conducting state, which is kinetically distinct from other conducting states in this mutant, G22N also frequently displays unusual gating patterns. Fig. 2 shows four examples of different behaviors occurring at tensions that normally keep the channel at a high open probability (Po > 0.4). Fig. 2 A displays “normal” gating between the fully open state and a variety of subconductances, where the channel is rarely visiting the fully closed state. Long sojourns to the level of 0.78 relative conductance (Fig. 2 B) are also characteristic of the mutant. In every trace we observed various types of fast flickering behavior between the lower substate and either fully open level (Fig. 2 C) or another intermediate (D).

Figure 2.

Atypical gating patterns of G22N channels. (A) Extended fragment of a trace recorded at 8 dyne/cm illustrating “normal” gating pattern. The occupancy of intermediate levels is at least an order of magnitude higher than in WT. (B) A sojourn to the long-lived substate L0.78. (C) Flickering between two intermediate levels, with a higher probability of occupying the lower state. (D) Flickering between two intermediates with a higher occupancy of the upper level.

Positions of Prominent Substates

To assess the occupancies of the major conducting states, we analyzed amplitude histograms for WT and each mutant by uniformly fitting them with 11 Gaussian peaks of different amplitude and width (Fig. 3). The histograms represent fragments of traces recorded at tensions activating each channel to Po between 0.1 and 0.3. The number of peaks was initially chosen as the minimum required for accurate fitting of WT histograms (Chiang et al., 2004). Independent high-resolution recordings of MscL activities confirmed that the closed, open, and nine intermediate conductances is an adequate set of states to describe the amplitude distribution of this channel (Shapovalov and Lester, 2004). As the panels show, essentially the same set of Gaussian peak positions reflecting similar substate amplitudes provides good quality of histogram fitting for all versions of MscL. The occupancies of intermediate peaks are substantially higher for GOF mutants relative to that of WT. Some of these intermediate levels are not easily identifiable by eye on raw traces due to fast flickering kinetics, especially in V23D. The low subconducting state with the amplitudes of 0.13 experiences the most dramatic increase in probability as the severity of GOF mutation increases. It should be noted that while the amplitudes for prominent substates (S_0.13, S_0.22, S_0.33, and S_0.54) increased, the positions of their peaks remained approximately the same. Therefore, there was no compelling reason to introduce another set of substates when switching from one mutant to another. The following analysis is focused exclusively on the closed, open, and two prominent substates (S_0.13 and S_0.22), whose occupancies were reliably determined using this complex but accurate fitting procedure.

Figure 3.

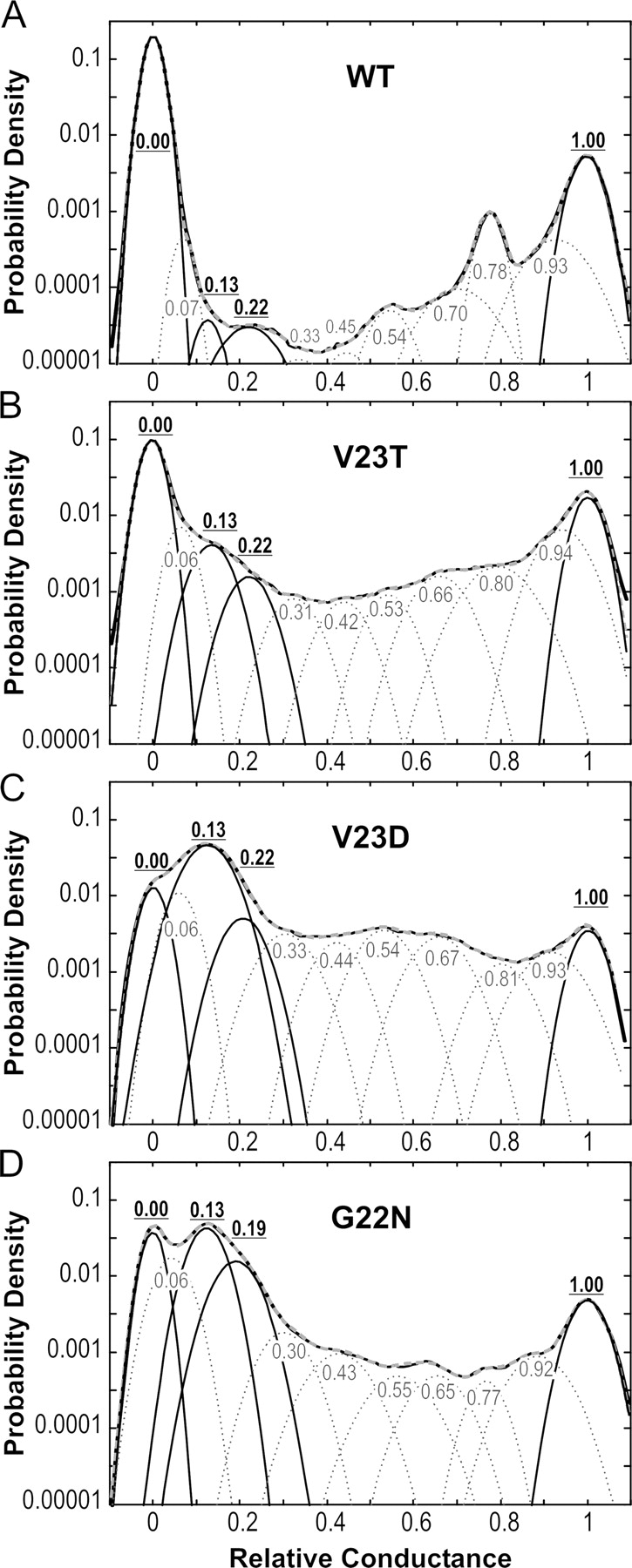
All-point amplitude histograms for WT and GOF mutants, each fit with 11 Gaussian distributions. The data for WT and the amplitude histogram fit are taken from Chiang et al. (2004), where the positions of obvious and implied subconducting states were first determined. Gaussians with essentially the same positions permitted accurate fitting of histograms for all mutants, their sums (gray dashed line) overlap with experimental histograms (black continuous line). The occupancies of the closed (0.00), fully open (1.00), and two lower substates with relative amplitudes of 0.13 and 0.22 were further used for thermodynamic analysis. The peaks for these states are presented as bold black lines. No statistically significant difference in fully open conductance (all in nS) was found between WT (3.11 ± 0.13), V32T (3.13 ± 0.14), V23D, (3.12 ± 0.14), and G22N (3.18 ± 0.10) when the histograms were first presented in absolute current units before normalization.

Note that the x-scale in each panel is normalized to the amplitude of the fully open state. Before the normalization, the absolute distances between the centers of peaks representing closed and fully open levels were compared with the amplitude of the small mechanosensitive channel MscS recorded in the same patch. No statistically significant variation of the unitary MscL conductance was found for any of the mutants as the ratio of full amplitudes, MscL versus MscS, was always ∼3.2 (see legend to Fig. 3 for details).

Fig. 4 represents 2D reconstructions of channel activation profiles based on several activation curves for WT MscL and the three mutants. Each surface indicates the probability density of occupying a specific conducting state by a channel as a function of membrane tension. The ridges on the left and on the right represent the baseline (closed state) and the fully open state, respectively. As seen from the upper panel, WT MscL is characterized by activation occurring quite late on tension. After only a few “anticipating” events, which slightly “bulge” from the baseline ridge, the channel switches straight to the fully open state. The smaller ridge on the right side represents the long-lived satellite state L_0.78 previously characterized not as intermediate, but alternative open state (Chiang et al., 2004). As the tension increases, a few intermediate states become visible, but with probabilities 10²–10³ times lower than that of the fully open state.

Figure 4.

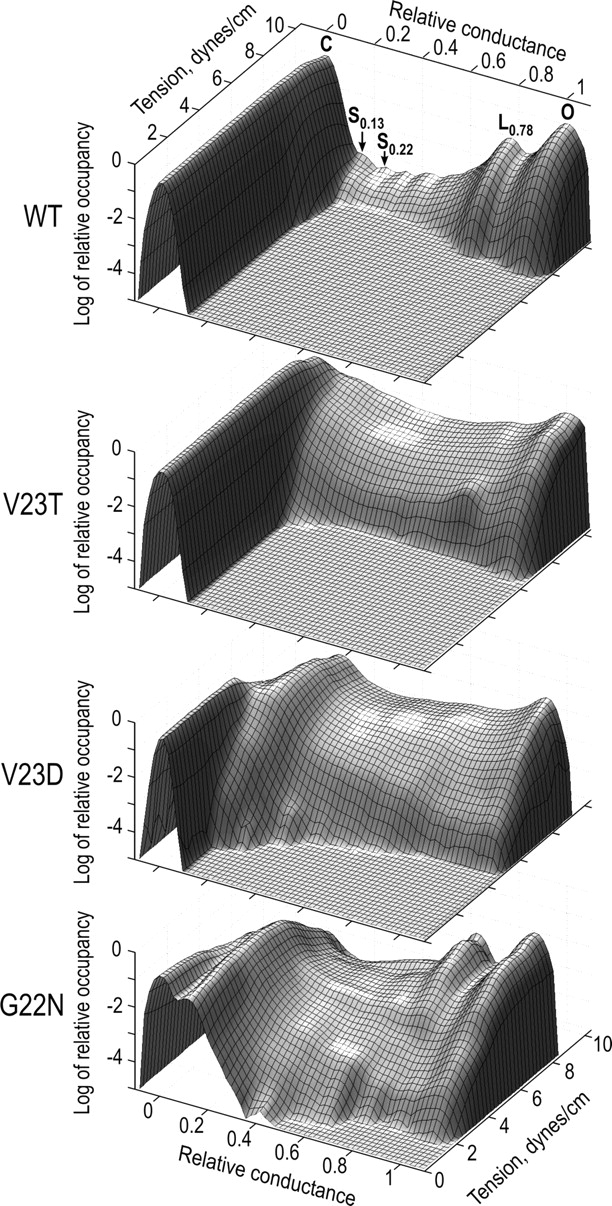
Two-dimensional amplitude histograms for WT MscL and GOF mutants. The x axis, as in a regular amplitude histogram, represents the relative conductance, the y axis represents tension, and the z axis is the density of probability of occupying the specific conducting level. The ridges on the left and on the right represent the baseline and the fully open state, respectively. Note that in G22N, the most severe mutant, the low substate (ridge next to the baseline) is occupied at zero tension. The number of independent traces taken for analysis: WT, n = 10; V23T, n = 4; V23D, n = 6; and G22N, n = 3.

V23T occupies more intermediate levels, but does not display prominent long-lived states. More severe V23D also shows high occupancy of intermediates, and early appearance of the low substate, which becomes substantially more occupied than the closed state at higher tensions as the ridge representing the baseline declines. G22N, the most severe mutant, shows a substantial occupancy of the low substate already at zero tension, it also reaches high-conducting intermediates and the fully open state relatively early on tension compared with other mutants. The total occupancy of intermediates appears to be lower than that in V23D, but the sharp ridge of long-lived substate at 0.78 is clearly visible, reflecting the abundance of this substate illustrated in Fig. 2 B.

Thermodynamic Analysis

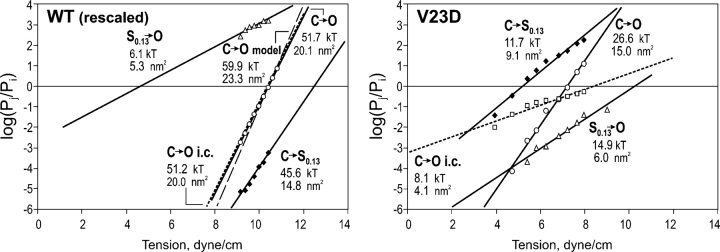
Fig. 5 shows ratios of occupancies of three individual conducting states, closed (C), low substate (S_0.13), and fully open (O) for WT and V23D MscL. Data points were obtained by fitting individual histograms, as shown in Fig. 3, recorded at different tensions. For WT MscL, the data are taken from the previous paper describing the positions and occupancies of substates and evaluation of gating parameters based on the analysis of nonuniform population responses (Chiang et al., 2004). The curves presented here are reconstructed with the parameters extracted from initial slopes of dose–response curves determined from the mean population current measured at each pressure step. The occupancy of the low-conducting substate S_0.13 and its position between the closed and open states on the ΔA scale were determined from the analysis of cumulative amplitude histograms based on 10 independent traces (see Fig. 4 in Chiang et al., 2004).

Figure 5.

Paired ratios of probabilities for the closed (C), low substate (S_0.13), and the fully open state (O) for WT and V23D MscL, shown as functions of tension. Boltzmann fitting (straight solid lines) gives thermodynamic parameters of energy and in-plane area changes between the two particular states. Squares and dotted lines represent dose–response curves determined with integral current. For the V23D mutant, the integral current curve has much lower slope than the dose–response determined from the ratio of O and C occupancies. The data for WT were rescaled to satisfy the total expansion of 20.4 nm², experimentally determined from initial slopes of dose–response curves (Chiang et al., 2004). The gray dashed line on the left panel represents the dose–response curve predicted from molecular models with parameters ΔA = 23.3 nm² and ΔE = 59 kT.

The right panel in Fig. 5 shows fitted curves and extracted parameters for the V23D mutant. The curve for the C→S_0.13 subtransition is shifted upwards compared with that of WT, signifying high occupancy of S_0.13. The entire curve for the second subtransition S_0.13→O moved downward, reflecting low occupancy of the fully open state compared with S_0.13. For both, the WT and the mutant, the slopes for the second subtransition are similar, corresponding to a 5–6 nm² expansion. Note that for V23D, the increase of integral current (open squares) shows a considerably lower slope, producing an apparent expansion of only 4.1 nm², which is much smaller than the total expansion predicted from the ratio of open and closed state occupancies (15.0 nm²) or the sum of expansions for the two subtransitions (15.1 nm²), which appear to be additive. In contrast, for WT, the integral current change follows the dose–response curve deduced from Po/Pc ratios. This is a clear consequence of differences between WT and V23D; the former has a single rate-limiting step for the entire C→O transition (Sukharev et al., 1999; Chiang et al., 2004), whereas the two subtransitions for the mutant are separated on the tension scale. Thus, the integral current can be used as measure of Po for channels with an apparent single transition (two-state) behavior, as WT MscL, but would be inappropriate for channels with prominent subtransitions. The figure illustrates that the procedure of log(P_j/P_i) fitting produces reliable slopes for individual subtransitions (i→j) in WT and mutant MscLs. While Fig. 5 shows only two examples, WT and V23D with one substate (S_0.13) included, the cumulative data for the closed, open, and two low-conducting intermediates for all mutants are given in Table I. The numbers illustrate that the two substates are positioned relatively close to each other on the energy and area scales, and their relative positions between the two “end” states vary depending on the mutation. The area and especially energy differences between the closed state and low-conducting intermediates remarkably decrease with the severity of the mutation.

TABLE I.

Energy and Area Differences between the Closed (C), Substates S_0.13 and S_0.22, and Fully Open State (O) Determined from the Slopes of their Occupancy Dependencies on Tension for WT MscL and the Three Mutants

	WTa (n = 10)		V23T (n = 9)		V23D (n = 6)		G22N (n = 3)
Substate	ΔE, kT	ΔA, nm2	ΔE, kT	ΔA, nm2	ΔE, kT	ΔA, nm2	ΔE, kT	ΔA, nm2
C	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
S0.13	45.6	14.8	27 ± 8	11 ± 3	12 ± 5	10 ± 2.5	0.9 ± 2.0	3.0 ± 0.2
S0..22	47.0	15.7	31 ± 10	12.5 ± 4	16.5 ± 5	11.0 ± 3	3.7 ± 1.4	3.9 ± 0.6
O	52 ± 13.0	20 ± 5	41 ± 14	18 ± 6	26 ± 4	15 ± 2	13 ± 3	12 ± 1.7

^aThe standard deviations are not shown because the ΔE and ΔA parameters for WT were determined from one unified dataset based on 10 independent traces.

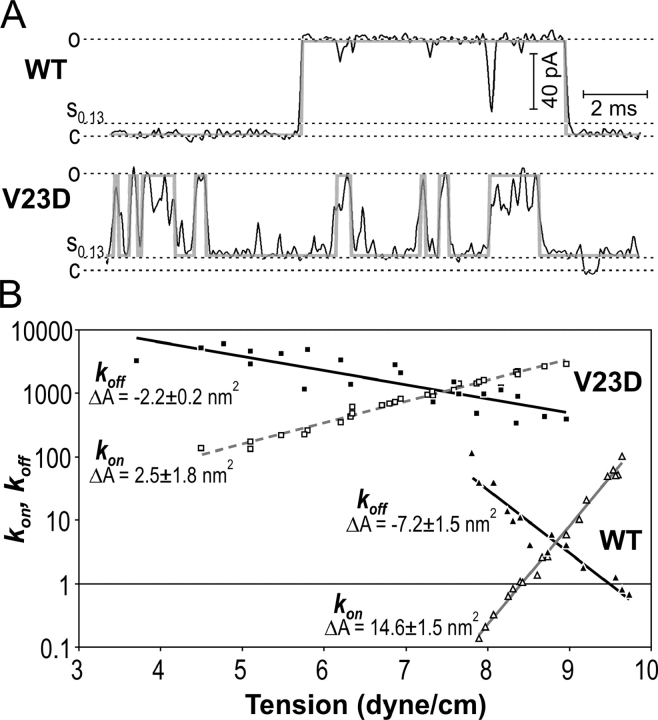
Kinetics of Closing Transitions

In addition to finding the positions of the energy wells for the subconducting states, we attempted to locate the main barriers that limit the rate of entering/exiting the fully open state for WT and V23D MscL. Using the QuB suite, we idealized the traces in the simplest two-state approximation, taking into account the full C→O transition for the WT and only the S_0.13→O transition for V23D, because in the latter case, the closed state is rarely visited at tensions allowing reliable assessment of the fully open state occupancy (Fig. 1 and Fig. 6 A). It is obvious that this crude approximation ignores low-amplitude spikes from the lower level, as well as brief downward deflections from the fully open state. The energetic closeness of short-lived high conducting states adjacent to the fully open state (Sukharev et al., 1999; Chiang et al., 2004) and their fast kinetics nevertheless suggest that grouping of these states with the open state may be a reasonable simplification allowing us to locate the dominant transition barrier. We focused our analysis primarily on the rate of downward transitions (k _off) from the fully open state to either low substate or fully closed state, as a function of tension. The linear free energy relationship (LFER) formalism, as applied to tension-gated channels (see Section 1 in supplemental material), predicts the slope of the log(k _off) dependency on tension (γ) to be proportional to the area difference between the bottom of the open-state well and the top of the main barrier. Fig. 6 B depicts k _off and (apparent) k _on as functions of tension. For V23D, k _on is shown conditionally as the low conductance level represents the composite state consisting of C, S_0.13, and S_0.22. At higher tensions, however, the channel gates primarily between the low substates and O state, essentially reducing the system to two states. The k _off values in both instances are real and represent the frequency of returns from the open state. The slope of k _off is higher for WT MscL and reflects the area change of −7.2 ± 1.5 nm² (n = 3) between the open state and the rate-limiting transition state, which places the barrier between the C and the low substates, close to S_0.13 (see discussion). The rate constants for V23D mutant are approximately two orders of magnitude higher than that for WT, indicating a transition barrier that must be at least 5 kT smaller. The lower slope suggests that the top of the rate-limiting barrier is only 2.1 nm² away from the fully open state, situated between the S_0.22 and O states.

Figure 6.

The kinetics of closing events in WT and V23D MscL channels. (A) Examples of simplified two-state idealization of traces using SKM protocol with level tolerances (standard deviations) for the closed and open states set at 2 and 5% of the unitary conductance, respectively. The original and idealized traces are shown in black and gray, respectively. For WT MscL, the complete C→O transition was fit, whereas only S→O subtransition was accounted for V23D. (B) Semilogarithmic plots of k _off and conditional k _on as functions of tension. The slopes of k _off in each case suggest the distance between the open state and the rate-limiting barrier on the ΔA reaction coordinate.

Effects of Histidine Substitutions in S1 Domains

A part of the homology model of E. coli MscL with the hypothetical bundle of the NH₂-terminal (S1) domains proposed to act as the second gate (Sukharev et al., 2001b) is shown in Fig. 7 A. The bundle is stabilized in part by apolar interactions between highly conserved internally located phenylalanines F7 and F10. Intersubunit disulfide cross-links shown to form easily in F7C and F10C mutants supported apposition of these residues in the native conformation (Sukharev et al., 2001a). Here we attempted a noncovalent stabilization of the S1 bundle to see its functional consequences. F7H or F10H substitutions were predicted to bring histidines from all five subunits into close proximity, creating a metal-binding site for Ni²⁺ or Cd²⁺. Binding of these metals was expected to stabilize association of S1 helices. In patch-clamp experiments, F7H and F10H MscL channels appeared to be “stiff,” activating at pressures exceeding the midpoint pressure for MscS (p _1/2 ^MscS) by 2–2.3 times. WT MscL usually activates at pressures of 1.6 × p _1/2 ^MscS. Episodes illustrating gating of F7H and F10H MscL in the presence of 0.1 mM Cd²⁺ are shown in Fig. 7 B. Similar patterns were routinely observed without special addition of Cd²⁺, i.e., in the presence of trace amounts of divalent metals in the media. At the onset of activation (270–320 mm Hg), channel openings were extremely short and mostly incomplete. At higher pressures (330–370 mm Hg), the channels visited the fully open state more frequently. F10H often displayed longer openings to the low substate. The amplitude histogram of F7H MscL obtained at Po of 0.02 (Fig. 7 C) depicts the distribution of occupancies for various substates. The areas under Gaussian peaks show that the combined occupancy of two low-conducting substates S_0.13 and S_0.22 is one order of magnitude higher than that of the fully open state. The low-conducting substates are preferred in these mutants apparently because stabilization of S1 bundle impedes transitions to the fully open state. As a result, gating patterns of F7H resemble that of V23D (Fig. 1), although the former are realized at much higher membrane tension. These data provide additional support to the hypothesis that separation of the S1 domains is the last event in the pathway to the open state.

Figure 7.

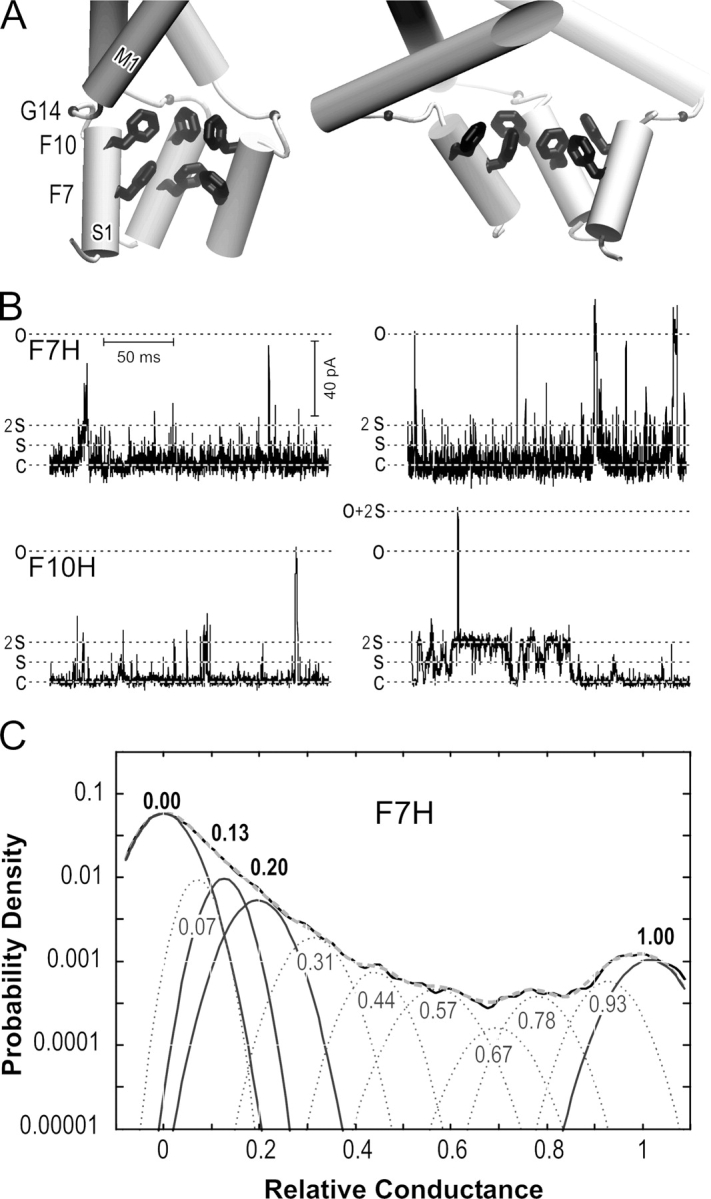
The putative structure of S1 gate and gating patterns of F7H and F10H MscL. (A) Hypothetical NH₂-terminal (S1) segments are represented as short amphipathic helices connected to M1 transmembrane helices via flexible linkers (three are shown). Highly conserved phenylalanines 7 and 10 inside the bundle and glycine 14 in the linker (small ball) are depicted. The bundle is shown in a relaxed conformation (left) and under stress (right) with extended linkers. Introduction of histidines in positions 7 or 10 is predicted to create a metal binding site stabilizing the bundle. (B) Representative traces of F7H and F10H MscL recorded in the presence of 100 μM Cd²⁺ near the onset of activation (300–330 mm Hg, left) and at a higher pressure (350–370 mm Hg, right). At least two active channels were present in each patch. (C) Amplitude histogram for F7H MscL. The occupancies are 0.73, 0.91, 0.7, and 0.16 for the closed, S_0.13, S_0.22, and fully open states, respectively.

S1–M1 Linker Extensions and the Second Subtransition

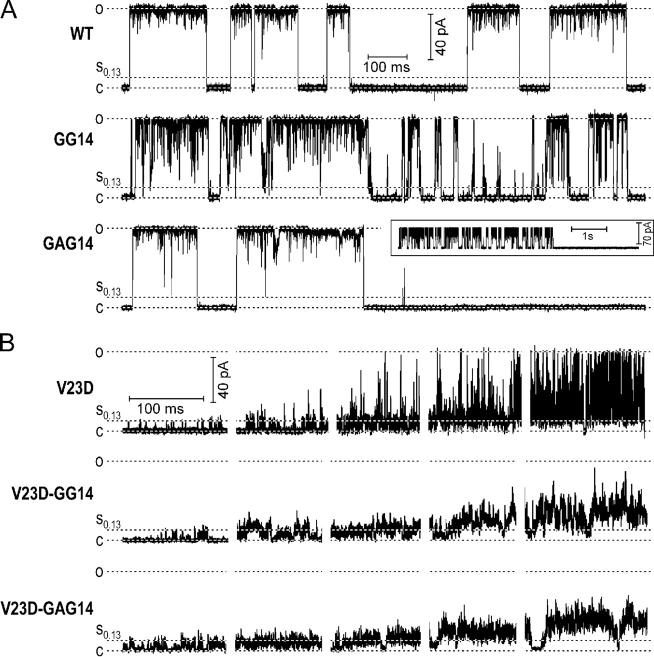
According to the previously proposed model of MscL gating (Sukharev et al., 2001a,b), expansion of transmembrane barrel strains the linkers connecting M1 helices with NH₂-terminal (S1) domains. The hypothetical S1 bundle (Fig. 7 A) was predicted to expand and then eventually disrupt under tension exerted by the linkers. The linker length was then suggested to be important for normal gating (Sukharev et al., 2001a). Fig. 8 shows how the gating patterns change after one– or two–amino acid insertions are introduced into the linker. Insertion of an extra glycine next to the “hinge” residue G14 (GG14 mutation) on the WT background increases the occupancy of short-lived subconducting states, especially those of low conductance. The probability of S_0.13 relative to the probability of fully open state is ∼1.5 × 10⁻³ for WT MscL, it increases 18 times (to 2.7 × 10⁻²) in GG14. When introduced on the V23D background, this mutation does not affect the low subconducting state, but practically abolishes transitions to the fully open state. A glycine-alanine insertion next to G14 (GAG14 mutation) on the GOF background has similar effect on the gating pattern with a more “smeared” amplitude of the low substates, and generally lower mean current at high tensions. With the extensions introduced on the GOF background, it was impossible to evoke openings of full amplitude at any attainable tension.

Figure 8.

Gating patterns of channels with extensions of S1–M1 linker introduced on WT and V23D backgrounds. The inset next to the GAG14 trace illustrates the typical use-dependent irreversible inactivation of the mutant. The extension mutants generated on V23D background never attain the fully open state.

The two–amino acid linker extension produced an unexpected phenotype when introduced on the WT background. Instead of a further increase in probability of intermediate states, the GAG14 mutation actually reduced their presence during periods of channel activity (relative probability of S_0.13 decreased eight times, to 2 × 10⁻⁴), but also introduced use-dependent inactivation. A small inset above the corresponding trace (Fig. 8 A) shows that after several seconds of continuous activity, the channel closes irreversibly, which was a typical outcome for all patches. It appears that the length of the S1–M1 linker is critical for the conformational stability of MscL with intact M1 gate, especially when the channel is driven into the open state by high membrane tension. The length of linkers seems to be less critical for the conformational stability of easily opened GOF mutants with more stable intermediates.

DISCUSSION

GOF mutations were first isolated in random mutagenesis trials as growth-suppressing MscL alleles (Ou et al., 1998). Most of the mutations grouped in the cytoplasmic half of the first transmembrane domain M1 shown to form the hydrophobic constriction of the pore (M1 gate). The toxicity of mutations and the leftward shifts in dose–response curve (early activation) correlated with the hydrophilicity of the substitute residue (Yoshimura et al., 1999). Some of the severe mutants (G22N and G22K) were shown to stably occupy low subconducting states, which split the entire transition into two subtransitions (Yoshimura et al., 1999). The analysis of GOF mutant gating presented above shows that with proper statistical tools similar subtransitions become separable in less severe mutants as well as in WT. Quantification of state occupancies and thermodynamic analysis show that GOF mutations affect the overall energetics of gating with the strongest impact specifically on the first subtransition.

The relative energy and area changes (Table I) combined with the positions of major rate-limiting barriers obtained from the kinetics (Fig. 6) allow partial reconstruction of free energy profiles for the transitions. Fig. 9 A shows the profiles for all four mutants calculated for zero-tension conditions and aligned by their open state areas. This type of alignment appears to be better than an alignment by the closed-state areas for two reasons. First, the conductance of fully open states for all four versions of MscL was indistinguishable, indicative of similar pore geometry and high likelihood of similar barrel dimensions. Second, charged or polar side chains packed in a narrow pore constriction are expected to influence strongly the conformation of the closed state, but less so the open state where the substitute residues are far separated.

Figure 9.

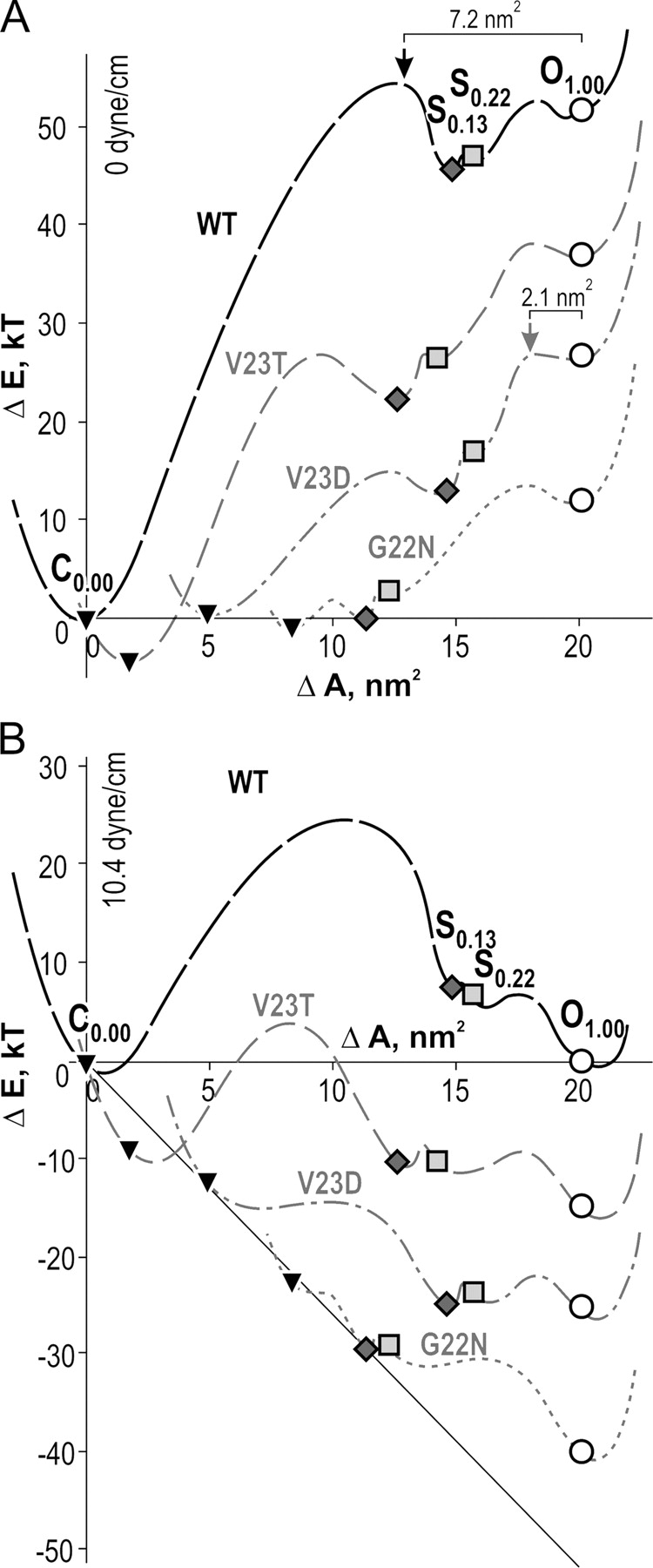
Energy-area profiles for WT MscL and the four mutants reconstructed with the positions of wells for the states presented in Table I. The absolute heights of the separating barriers are inferred. The distances between the curves on the energy axis were estimated from differences in hydration energies of the primary side chains and that of substitutes. The positions of energy barriers for WT and V23D mutants were determined from the kinetic analysis (Fig. 6). The profiles calculated for zero tension (A) and for tension of 10.4 dyne/cm (B). The symbols represent closed states (▾), S_0.13 (⋄), S_0.22 (□), and open states (○).

To illustrate the tendencies and directions in which mutations may affect the energies of each state, we separated the curves on the vertical (free energy) scale according to estimated energy differences between open-state conformations for different mutants. Each curve was shifted as a whole, keeping relative distances between the states constant. The down-shifts for the V23T and G22N mutants by −15 and −40 kT reflect more favorable hydration of polar and more exposed substitute side chains calculated from estimated water-exposed areas and atomic solvation parameters (see Section 2 in supplemental material). The shift of −25 kT for the charged V23D mutant includes both the hydration energy (−39 kT) and the positive contribution of coulombic repulsion between equivalent side chains in the pentamer (+14.0 kT). Because it is impossible to perform complete thermodynamic cycles and compare state occupancies for WT and mutants under equal conditions in the same patch (for instance, C_WT→O_WT→ O_V23D→C_V23D→C_WT), the procedure of energy assignment and curve separation is based on estimations only and given just to illustrate the tendencies.

The energy landscape for WT indicates that the major energy cost for opening is between C and S_0.13. The two states are separated by the major 46 kT gap, whereas only 2–3 kT separate S_0.13 from the fully open state. The total energy difference predicts that in the absence of tension, Po must be ∼10⁻²¹, qualifying MscL as a leak-proof and “safe” device that keeps the membrane permeability noncompromised at a low resting tension. Fig. 9 B shows the same profiles recalculated for 10.4 dyne/cm, which is the equipartitioning tension (γ_1/2) for WT MscL (Chiang et al., 2004). In the assumption that membrane tension produces a linear distortion of the entire profile, application of γ_1/2 not only equalizes the energies of the closed and fully open states, but also places S_0.13 and S_0.22 ∼10 kT above the open state. This defines their relative occupancy as ∼10⁻³, which is consistent with experimental observations (Fig. 3). The major expansion brought by the C→S_0.13 transition makes it the most tension-sensitive step in the gating of WT MscL. From the kinetic analysis of WT MscL (Fig. 6), we determined that the main rate-limiting barrier is positioned at ∼0.65 on the expansion scale just left of the substate S_0.13 and separated from the open state by 7.2 nm². Although we do not know its absolute height, the top of the barrier is apparently above the energy level for the S_0.13 state and remains dominant at all tensions in the studied range, as illustrated in Fig. 9 B. Under tensions near γ_1/2, the small barrier between S_0.22 and O states is largely reduced, thus the low substates in WT MscL are extremely short-lived as the latter steps S_0.13→S_0.22→…→O come immediately after the first subtransition.

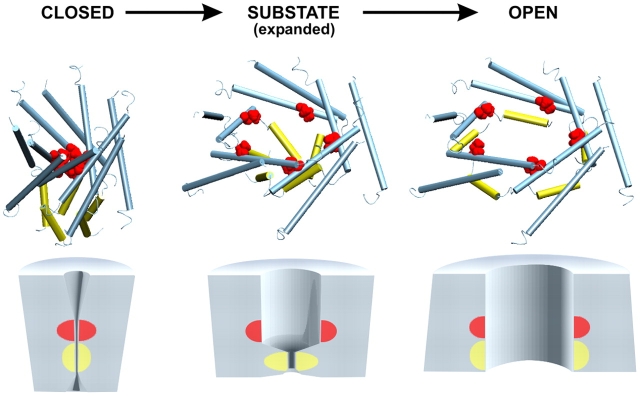
The helical models of the MscL barrel in the closed, expanded, and open conformations (Sukharev et al., 2001a) are illustrated in Fig. 10. The opening of the main gate at the intersection of M1 helices (formed by V23 and a few preceding residues) results in major expansion accompanied with pore hydration. The expanding barrel at the same time puts stress on S1–M1 linkers leading to separation of S1 domains and complete opening. The cylinders below approximate protein shapes and dimensions as the channel proceeds through sequential opening. The area increments of 17 and 6 nm² for the first and second subtransitions predicted by models are reasonably well supported by the results of thermodynamic analysis, indicating ΔA's of ∼15 and 5 nm² for the C→S_0.13 and S_0.13→O subtransitions in WT MscL (Table I).

Figure 10.

Structural models of the transmembrane barrel of MscL along the transition pathway. The transmembrane helices M1 and M2 forming pentameric assemblies are shown in blue, NH₂-terminal S1 helices in yellow, and the side chains of V23 are presented as space-filling model (red). The periplasmic loops and cytoplasmic domains are not shown. The cylinders below show approximate dimensions of the barrel. According to the atomic-scale models, the in-plane area of the closed conformation may be around 19 nm², increasing to 36 nm² in the substate and then to 42 nm² in the fully open state. The locations of the main (M1) and the cytoplasmic (S1) gates are shown in red and yellow, respectively.

The first major expansion of the transmembrane barrel (75% of the total area and correspondingly 87% of the outer diameter changes) is associated with a minor gain of conductance (13% of the total). Such a behavior can hardly be explained by a partial opening of a single gate. With the simplifying assumption that the pore cross section increases proportionally with the in-plane protein area, one may expect the conductance increase commensurate with expansion. A 75% protein area increase should then produce a substate conducting at 2.4 nS, five times higher than observed. Conversely, given that the conductance of S_0.13 is only 0.42 nS, the proportionality would predict expansion at the C→S_0.13 step of only ∼3 nm². The strong disparity between the area and conductance changes shows that the low substates are unlikely to be produced by partial opening of the single M1 gate, as was proposed previously (Yoshimura et al., 1999), and implies the second gate.

Although we classify the S_0.13 and S_0.22 substates as low (relative to the fully open state), yet their conductance is appreciable (0.4–0.7 nS), and, when combined with large in-plane area, it signifies that the pore interior in those substates is well hydrated. The substates are apparently sequential intermediates in the opening process, and the S_0.13→S_0.22 transition itself is associated with a small barrel expansion, however the exact nature of the twofold conductance increase remains unclear. One may speculate that at least in S_0.13 the S1 gate likely remains closed and the leakage takes place through gaps between S1–M1 linkers.

Before discussing why the behavior of the GOF mutants is particularly consistent with the two-gate model, we should restate that in the closed conformation, the hydrophobic core of the transmembrane barrel of WT MscL appears to be completely dehydrated according to EPR data (Perozo et al., 2002) and molecular dynamics (Gullingsrud and Schulten, 2003; unpublished data). The reduction of the free energy difference between the closed and low substates by GOF mutations clearly correlates with the hydrophilicity of the substituting side chain. The effects of single residue substitutions are magnified due to the presence of five identical mutation sites in the symmetrical homopentameric channel. The V23D mutation places five negative charges (assuming deprotonated state of aspartates) in the pore constriction instead of closely positioned aliphatic side chains (Fig. 10). Besides electrostatic repulsion pushing M1 helices apart, a strong hydration of the pore interior is also expected as a consequence of such substitution. The mild V23T mutant was generated by inference that it would have similar effect as V23D, but of lower magnitude, which appears to be the case. The most severe G22N mutation introduces a bulky and hydrophilic side chain in the tight contact between closely packed M1 helices, sterically pushing the helices apart. This mutation causes the largest effect, resulting in comparable occupancies of C and S_0.13 even at zero tension. However, full openings are still prohibited as 12–15 kT now separate S_0.13 from O. This characteristic increase in energy gap between the low substates and the open state in essentially all GOF mutants makes the substate stable at low and intermediate tensions. More tension is required to facilitate further transition to the open state. It is peculiar that a mechanosensitive channel found in the aortic endothelium behaves in a similar way, switching toward the upper substates as the tension increases (Yao et al., 2001).

The in-plane expansion (ΔA) associated with the first subtransition decreases with the severity of mutation, whereas ΔA associated with the second subtransition slightly increases meaning that the stable intermediate states in the GOF mutants are similar, but not exactly the same as the low substates in the WT. The alignment by the open state, as seen from Fig. 9, suggests that the initial closed-state areas of GOF proteins are considerably larger than that of WT MscL. This means that the GOF channel complexes reside in preexpanded closed conformations due to either partial hydration (V23T), electrostatic conflict of the pore constriction (V23D), or hydration on top of strong steric conflict in the interhelical contacts (G22N). The conformations of S1–M1 linkers and the role of the lower part of the hydrophobic gate (L19) in stabilization of preexpanded closed conformations in GOF mutants remain to be clarified. The G22N mutation clearly destabilizes not only the closed state, but also the fully open state, based on frequent observations of atypical gating patterns (Fig. 2) similar to those observed in Δ110–136 truncation mutant (Anishkin et al., 2003).

The kinetic analysis suggests that the nature of the barriers that limit the access to the fully open state in WT and GOF MscLs is different. For WT MscL, the position of the rate-limiting barrier on the area coordinate is just left of the substate S_0.13 (Fig. 9), meaning that the transition state just precedes the arrival to the low substate and is probably nonconductive. It is logical to associate the passage of the main barrier with the process of hydration of the largely hydrophobic pore, which is prerequisite for conduction. The domination of this barrier and probably all-or-nothing character of hydration of the entire pore (Beckstein et al., 2003) makes transitions in WT MscL highly cooperative. The easy hydration of the pore in GOF mutants lowers specifically this barrier, stabilizes the intermediate state, and shifts the rate-limiting step to the second subtransition, which involves separation of S1 domains. With a prehydrated state of the pore, the second subtransition becomes less cooperative, which is manifested as high occupancy of substates between S_0.13 and the fully open state. The question of when exactly on the transitional pathway the hydration of the pore occurs in each instance can be approached with molecular dynamic simulations (Beckstein et al., 2003; Gullingsrud and Schulten, 2003; Anishkin and Sukharev, 2004).

The structure of S1 gate and the mechanism of the second subtransition remain hypothetical, but the data presented here make the picture more consistent. Early deletion analysis indicated that although three NH₂-terminal residues of MscL are somewhat dispensable, a removal of 11 residues completely abolishes channel function (Blount et al., 1996b). Alterations of eight NH₂-terminal residues of MscL reported by Hase et al. (1997) systematically increased the pressure threshold and changed gating patterns. At the same time, analyzing a large library of MscL mutants, Maurer and Dougherty (2003) found that several randomly generated single-site mutations in the S1 domain did not compromise the function of the channel assayed in vivo, which questioned the earlier postulated role of S1 in the gating process (Sukharev et al., 2001a,b). Previous data showed that cysteines in positions 7 or 10 (F7C or F10C) spontaneously form intersubunit cross-links under ambient conditions, and this greatly impedes transitions to the fully open state (Sukharev et al., 2001a). We further tested the arrangement and the role of S1 domains using a noncovalent stabilization technique by creating metal-binding sites requiting apposition of several S1 domains. The experiments with the histidine mutants F7H or F10H presented above (Fig. 7) reassured us that the highly conserved phenylalanines in the NH₂-terminal domain of MscL are not easily mutable. Stabilization of interhelical interactions by an engineered metal binding site produced a profound effect on the tension sensitivity and relative occupancy of states. In both F10H and F7H mutants, the second subtransition (S→O) was impeded, consistent with the notion that the open conformation is achieved trough separation of S1 domains. In fact, the stabilization of S1–S1 association produced gating patterns similar to those observed in GOF mutants (compare traces of F7H and V23D), both characterized by mostly incomplete openings, which in GOF mutants were observed at much lower tensions. Therefore, either destabilization of the M1 gate or stabilization of the S1 gate brings the low-conducting intermediate to a similar relative position between the closed and open states on the energy-area profile, effectively increasing the fraction of energy spent on the S→O subtransition.

The opening of the S1 gate is clearly influenced by the length of the S1–M1 linker. The increased occupancy of short-lived low-conducting substates in the GG14 mutant (Fig. 8 A) is consistent with the reduction of stress that the linkers exert on the S1 domains and increased conformational freedom allowing S1s to recombine together, forming the transient intermediate. This effect is nonmonotonous with the length of the linker extension, as the two–amino acid insertion (GAG14) does not produce the same amount of substates, but makes the open conformation unstable (Fig. 8 B). It appears that while the separation of the S1 bundle is the last event in the opening process, recombination of these flexible domains may well be the first event on the way back to the closed state. If for some reason the S1 bundle formation cannot prime and guide the reformation of the closed state properly, then there would be a higher rate of misfolding specifically from the open state. The irreversible use-dependent inactivation of the GAG14 mutant (Fig. 8 A) suggests this scenario.

The same extensions introduced on the V23D background dramatically increase the probability of intermediate states, but at the same time completely abolish visits to the fully open state. This is consistent with a lower stress in extended linkers and a higher propensity of the S1 domains to recombine back into a bundle-like structure. The result also illustrates that in a mutant with unstable open state (open dwell time in V23D is indeed very short, Fig. 1 and Fig. 6 A), extension of linkers further lowers the probability of the fully open state. One– or two–amino acid extensions produce qualitatively similar effects on the GOF background. The comparison of gating patterns between WT and V23D (Fig. 1) as well as between GG14 and V23D-GG14 clearly shows that V23D mutation dramatically destabilizes the open state (increases the off rate), and in V23D-GG14 simply prevents its stable occupancy. Importantly, the in vivo osmotic survival screens (Maurer and Dougherty, 2003) indicated that V23D mutant is also of the “loss-of-function” type, suggesting that fast-flickering gating severely compromises the “safety valve” function of the channel. It appears that this mutation increases the reassociation rate of putative S1 domains, or conversely prevents their docking to the barrel wall as was proposed in structural models of the open state (Sukharev et al., 2001b). The successful docking of S1 domains may depend on the conformation of the S1–M1 linkers, but also on the angular position of M1 helix, which was predicted to change during the gating process (Yoshimura et al., 1999; Perozo et al., 2002; Bartlett et al., 2004). Further studies of helical rotations should clarify this important detail of the MscL gating mechanism.

In conclusion, the data presented above strongly support the two-gate mechanism of MscL. The opening of the main (M1) gate is associated with the major barrel expansion, whereas separation of the second (S1) gate pulled by S1–M1 linkers leads to the major gain in conductance. The energetics and kinetics of the rate-limiting first subtransition in WT MscL is largely defined by the process of hydration of the transmembrane pore interior. It is highly suggestive of a similar role of pore hydration in defining gating characteristics for other channels with hydrophobic gates.