The evolution of language

Abstract

The emergence of language was a defining moment in the evolution of modern humans. It was an innovation that changed radically the character of human society. Here, we provide an approach to language evolution based on evolutionary game theory. We explore the ways in which protolanguages can evolve in a nonlinguistic society and how specific signals can become associated with specific objects. We assume that early in the evolution of language, errors in signaling and perception would be common. We model the probability of misunderstanding a signal and show that this limits the number of objects that can be described by a protolanguage. This “error limit” is not overcome by employing more sounds but by combining a small set of more easily distinguishable sounds into words. The process of “word formation” enables a language to encode an essentially unlimited number of objects. Next, we analyze how words can be combined into sentences and specify the conditions for the evolution of very simple grammatical rules. We argue that grammar originated as a simplified rule system that evolved by natural selection to reduce mistakes in communication. Our theory provides a systematic approach for thinking about the origin and evolution of human language.

Language remains in the minds of many philosophers, linguists, and biologists a quintessentially human trait (1–3). Attempts to shed light on the evolution of human language have come from many areas including studies of primate social behavior (4–6), the diversity of existing human languages (7, 8), the development of language in children (9–11), and the genetic and anatomical correlates of language competence (12–16), as well as theoretical studies of cultural evolution (17–21) and of learning and lexicon formation (22). Studies of bees, birds, and mammals have shown that complex communication can evolve without the need for a human grammar or for large vocabularies of symbols (23, 24). All human languages are thought to possess the same general structure and permit an almost limitless production of information for communication (25). This limitlessness has been described as “making infinite use of finite means” (45). The lack of obvious formal similarities between human language and animal communication has led some to propose that human language is not a product of evolution but a side-effect of a large and complex brain evolved for nonlinguistic purposes (1, 26). Others suggest that language represents a mix of organic and cultural factors and, as such, can only be understood fully by investigating its cultural history (16, 27). One problem in the study of language evolution has been the tendency to identify contemporary features of human language and suggest scenarios in which these would be selectively advantageous. This approach ignores the fact that if language has evolved, it must have done so from a relatively simple precursor (28, 29). We are therefore required to provide an explanation that proposes an advantage for a very simple language in a population that is prelinguistic (30–32). This work can be seen as part of a recent program to understand language evolution based on mathematical and computational modeling (33–37).

The Evolution of Signal–Object Associations.

We assume that language evolved as a means of communicating information between individuals. In the basic “evolutionary language game,” we imagine a group of individuals (early hominids) that can produce a variety of sounds. Information shall be transferred about a number of “objects.” Suppose there are m sounds and n objects. The matrix P contains the entries p_ij, denoting the probability that for a speaker object i is associated with sound j. The matrix Q contains the entries q_ji, which denote the probability that for a listener sound j is associated with object i. P is called “active matrix,” whereas Q is called “passive matrix.” A similar formalism was used by Hurford (22).

Imagine two individuals, A and B, that use slightly different languages L (given by P and Q) and L′ (given by P′ and Q′). For individual A, p_ij denotes the probability of making sound j when seeing object i, whereas q_ji denotes the probability of inferring object i when hearing sound j. For individual B, these probabilities are given by p′_ij and q′_ji. Suppose A sees object i and signals, then B will infer object i with probability Σ_j=1^mp_ijq′_ji. A measure of A’s ability to convey information to B is given by summing this probability over all objects (n). The overall payoff for communication between A and B is taken as the average of A’s ability to convey information to B, and B’s ability to convey information to A. Thus,

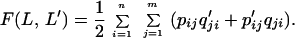1

In this equation, both L and L′ are treated once as listener and once as speaker, leading to the intrinsic symmetry of the language game: F(L,L′) = F(L′,L). Language L obtains from L′ the same payoff as L′ obtains from L. If two individuals use the same language, L, the payoff is F(L,L) = Σ_iⁿ₌₁Σ_j^m₌₁p_ijq_ji.

Hence, we assume that both speaker and listener receive a reward for mutual understanding. If for example only the listener receives a benefit, then the evolution of language requires cooperation.

In each round of the game, every individual communicates with every other individual, and the accumulated payoffs are summed up. The total payoff for each player represents the ability of this player to communicate information with other individuals of the community. Following the central assumption of evolutionary game theory (38), the payoff from the game is interpreted as fitness: individuals with a higher payoff have a higher survival chance and leave more offspring who learn the language of their parents by sampling their responses to individual objects.

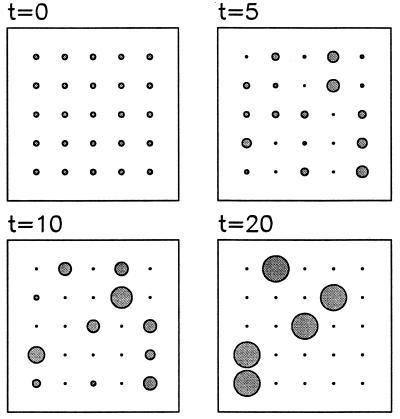
Fig. 1 shows a computer simulation of a group of 100 individuals. Initially, all individuals have different random entries in both active and passive matrices. After some rounds, specific sounds begin to associate with specific objects. Eventually each object is exactly associated with one signal. The simulation shows how a protolanguage can emerge in an originally prelinguistic society.

Figure 1.

Emergence of a protolanguage in an initially prelinguistic society. The population consists of 100 individuals. Each of them starts with a randomly chosen P and Q matrix. There are five objects and five signals (sounds). In one round of the game, every individual interacts with every other individual and the payoff of all interactions is evaluated according to Eq. 1. The total payoff of all individuals is calculated. For the next round, individuals produce offspring proportional to their payoff. Children learn the language of their parents by sampling their responses to each object. The figure shows the population average of the P matrix; the radius of the circle is proportional to the corresponding entry. Initially, all entries are about 0.25. After five generations some initial associations begin to form, which become stronger during subsequent rounds. At t = 20, each object is associated with one signal. Signal 1, however, is used for two objects, whereas signal 5 is not used at all. This solution is suboptimum but evolutionarily stable. Interestingly, errors during language acquisition increase the likelihood of reaching the optimum solution (M.A.N., J. Plotkin, and D.C.K., unpublished work).

For m = n, the evolutionary optimum is reached if each object is associated with one specific sound and vice versa. Evolution does not always lead to the optimum solution, but certain suboptimum solutions, in which the same signal is used for two (or more) objects, can be evolutionarily stable.

A Linguistic Error Limit.

Below, we discuss two essential extensions of the basic model. First, we include the possibility of errors in perception: early in the evolution of communication, signals are likely to have been noisy and can therefore be mistaken for each other (39). We denote the probability of interpreting sound i as sound j by u_ij. The payoff for L communicating with L′ is now given by

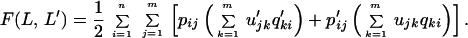2

The probabilities, u_ij, can be expressed in terms of similarities between sounds. We denote the similarity between sounds i and j by s_ij. We obtain u_ij = s_ij/Σ_k^m₌₁s_ik. As a simple example, we assume the similarity between two different sounds is constant and given by s_ij = ɛ, whereas s_ii = 1. In this case, the probability of correct understanding is u_ii = 1/[1 + (m − 1)ɛ]. The maximum payoff for a language with m sounds (when communicating with another individual who is using the same language) is given by F(m) = Σ_i^m₌₁u_ii, and therefore F(m) = m/[1 + (m − 1)ɛ]. The fitness, F, is an increasing function of m converging to a maximum value of 1/ɛ for large values of m. Without error, we would have F(m) = m. Thus, in the presence of error, the maximum capacity of information transfer is limited and equivalent to what could be achieved by 1/ɛ sounds without error.

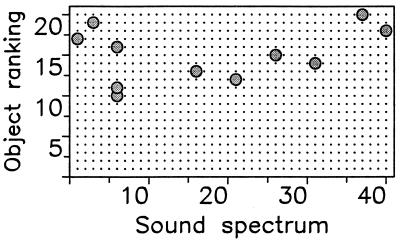
Next, we assume that objects can have different values, a_i. (For example when a leopard represents a higher risk than a python, the word “leopard” may be more valuable than “python.”) We have F(m) = [1 + (m − 1)ɛ]⁻¹Σ_i^m₌₁a_i, where the objects are ranked according to their value, a₁ > a₂ >… . This fitness function can adopt a maximum value for a certain number m and decline if the value of m becomes too big. In this case, natural selection will limit the number of sounds used in the language and consequently also limit the number of objects described. Fig. 2 shows a computer simulation of this extended evolutionary language game. The final outcome is a language that uses only a subset of all available sounds to describe the most valuable objects.

Figure 2.

Evolution of protolanguage in the context of misunderstanding. There are 20 objects and 40 sounds, but evolution leads to a language that uses only 9 sounds to describe 11 objects. Sounds are represented on a linear spectrum by numbers between 0 and 1. The similarity between two sounds, x_i and x_j, is given by s_ij = exp(−α|x_i − x_j|). For the computer simulation, m sounds are randomly chosen from a uniform distribution on (0,1). Objects have different values, a_i, chosen from a uniform distribution on (0,1). The payoff for language L against L′ is given by Eq. 2. In this simulation, we do not model individual players but simply evaluate whether or not a mutant language will be able to invade and replace the existing language. The simulation is started with a language L whose active matrix P has random elements p_ij sampled from a uniform distribution on (0,1) and normalized such that all rows have a sum of one. The passive matrix Q is derived from the active matrix: q_ji = p_ij/Σ_ip_ij. Then a mutant language L′ is produced. If F(L′,L) < F(L,L), then L′ cannot invade. Another mutant is generated. If F(L′,L′) > F(L′,L) > F(L,L), then L′ can invade and take over. The original language L is replaced by L′. The simulation searches for mutants that can replace L′. (It is also possible, though very rare, that F(L′,L) > F(L,L), but F(L′,L′) < F(L,L′). In this case, there would be a stable equilibrium between L and L′ and the simulation would stop.) The figure shows the final outcome after 100,000 different mutants, but the basic structure of the language is already present after 4,000 mutants. The x axis indicates the different sounds sorted according to their x_i value; the y axis indicates objects ranked according to their a_i value (20 being the most valuable). The 11 most valuable objects (y axis) are associated with nine different sounds (x axis). One sound is used for three different objects (including the two least valuable objects described by the language). The sounds seem ideally selected to minimize their similarity. Parameter values: α = 2, n = 20, m = 40; mutation process: all p_ij values between 0 and 1 are randomly changed within an interval ± 0.01; with probability 0.001, any p_ij is changed to 0 or 1; with probability 0.001, a whole column or a whole row of the P matrix is changed into 0. The mutation rules are designed to provide enough chance to gain or lose sounds or objects.

The principal result of the extended model, including misunderstanding, is that of a “linguistic error limit”: the number of distinguishable sounds in a protolanguage, and therefore the number of objects that can be accurately described by this language, is limited. Adding new sounds increases the number of objects that can be described but at the cost of an increased probability of making mistakes; the overall ability to transfer information does not improve. This obstacle in the evolution of language has interesting parallels with the error-threshold concept of molecular evolution (40). The origin of life has been described as a passage from limited to unlimited hereditary replicators, whereas the origin of language as a transition from limited to unlimited semantic representation (41).

Word Formation.

The way to overcome the error limit is by combining sounds into words. Words are strings of sounds. As before, we define the fitness of a language as the total amount of successful information transfer. The maximum fitness is obtained by summing over all probabilities of correct understanding of words. For a language with m sounds (phonemes) and a word-length l, the maximum payoff is given by F(m,l) = m^l[1 + (m − 1)ɛ]^−l, which converges to 1/ɛ^l for large values of m, thus allowing a much greater potential for communication. This equation assumes that understanding of a word is based on the correct understanding of each individual sound.

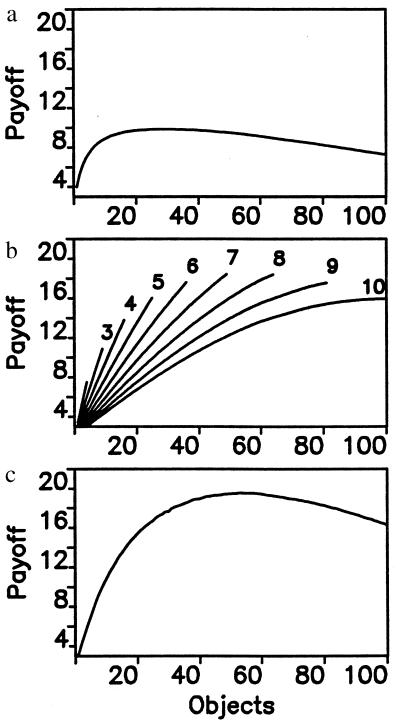
More realistically, we may assume that correct understanding of a word is based (to some extent) on matching the perceived string of phonemes to known words of the language. Consider a language with N words, w_i, which are strings of phonemes: w_i = (x_i1, x_i2… x_il). For m different phonemes there are m^l possible words. A particular language will contain a subset of these words, N ≤ m^l. We define the similarity between two words as the product of the similarities between individual phonemes in corresponding positions. The similarity between word w_i and w_j is S_ij = Π_k=1^ls_ij(k), where s_ij(k) denotes the similarity between the k–th phonemes of words w_i and w_j. The probability of correctly understanding word w_i is P_i = 1/Σ_j^ml₌₁S_ijσ_j, where σ_j = 1 if word w_j is part of the language, and σ_j = σ if word w_j is not part of the language. The parameter σ is a number between 0 and 1 and specifies the degree to which word recognition is based on correct understanding of every phoneme versus understanding of the whole word. If σ = 0, then each word is only compared with every other word that is a part of the language; correct understanding of a word consists in comparing the perceived word with all other words that are part of the lexicon. An implicit assumption here is that individuals have perfect knowledge of the whole lexicon. If σ = 1, then every word is compared with every other possible word that can be formed by combining the phonemes. Correct understanding of a word requires a correct identification of each individual phoneme. The listener does not need to have a list of the lexicon. A value of σ between 0 and 1 blends these two possibilities. In this case, recognition of a word is to some extent based on identification of each individual phoneme and to some extent on identification of the word selected from the list of all words that are contained in the language. The maximum payoff for such a language is given by F = Σ_i=1^NP_i (Fig. 3).

Figure 3.

Word formation can overcome the error limit. Suppose there are n = 100 objects with values a_i uniformly distributed between 0 and 1. (a) Without word formation, each object is described by one sound. The similarity between different sounds is ɛ. The maximum payoff of a language with m sounds is given by F = [1 + (m − 1)ɛ]⁻¹Σ_i=1^ma_i, where the a_i are ranked in descending order. In our example, ɛ = 0.2. The maximum payoff is obtained if the 28 most valuable objects are being described by individual sounds. All other objects are ignored. (b) As a simple example of word formation, we consider that each word consists of two sounds. The maximum payoff of a language with m sounds is F = [1 + (m − 1)ɛ]⁻²Σ_i=1^Ma_i, where M is the smaller of m² or n. In this model, correct identification of a word requires correct understanding of each individual sound. The figure shows the payoff curves for languages that have m = 2 to 10 different sounds. For each language, it is best to make use of the whole repertoire, that is, to use all m² combinations as words. The maximum payoff is achieved for m = 7, which leads to 49 words describing 49 objects. (c) A more sophisticated theory of word recognition assumes that correct understanding of a word is based on matching the perceived sequence of sounds to all combinations that are thought to be part of the lexicon of the language. For our example, we find that the maximum fitness is obtained for m = 11 sounds, when 52 of the 121 possible combinations are used as words. A smaller or higher number of sounds, m, leads to a lower maximum fitness. If longer words are being admitted, then both cases (b and c) lead to optimum solutions that describe a larger fraction of all objects.

Combining sounds into words leads to an essentially unlimited potential for different words. This step in language evolution can be seen as a transition from an analogue to a digital system. The repertoire is not increased by adding more sounds, but by combining a set of easily distinguishable sounds into words. In all existing human languages, only a small subset of the sounds producible by the vocal apparatus are employed to generate a large number of words. These words are then used to construct an unlimited number of sentences. The crucial difference between word and sentence formation is that the first consists essentially of memorizing all (relevant) words of a language, whereas the second is based on grammatical rules. We do not memorize a list of all possible sentences.

The Evolution of Basic Grammatical Rules.

The next step in language evolution is the emergence of a basic syntax or grammar. Recall that by combining sounds into words, the protolanguage achieves an almost limitless potential for generating words with the power of describing a large number of objects or actions. Grammar emerges in the attempt to convey more information by combining these words into phrases or sentences. Simply naming an object will be less valuable than naming it and describing its action. (A leopard can be stalking, in which case it is a serious risk, or merely sleeping and thereby posing a lesser risk.) There is an obvious advantage to describing both objects and actions. Suppose there are n objects and h actions; there are nh possible combinations, but only a fraction, φ, of them may be relevant (for example: leopard runs; monkey runs; but not banana runs). A “nongrammatical” approach would be to conceive N = φnh different words for all combinations. A “grammatical” approach would be to have n words for objects (i.e., nouns) and h words for actions (i.e., verbs). Let us compare the fitness of grammar and nongrammar.

Again, we will include errors, this time as a probability to mistake words, which can include acoustic misunderstanding and/or incorrect assignment of meaning. The maximum fitness of a nongrammatical language with N different words is F_ng = N/[1 + (N − 1)ξ]. The maximum fitness for a grammatical language is F_g = N/{[1 + (n − 1)ξ][1 + (h − 1)ξ]}. Here, ξ is the similarity between words. In the nongrammatical language, each event is described by one word, and correct communication requires that this word is distinguished from N − 1 other words. The grammatical language uses two words for every event: we can say that nouns describe objects and verbs describe actions. Each noun has to be distinguished from n − 1 other nouns, and each verb from h − 1 other verbs. Whether grammar wins in the evolutionary language game depends on the number of combinations of nouns and verbs that describe relevant events. F_g > F_ng leads to

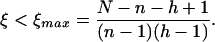3

If there is no possibility of mistakes (ξ = 0), then there is no difference between grammar and nongrammar. If there are too many mistakes (ξ > ξ_max), then grammar is disadvantageous. Between these two limits, there is a “grammar zone” (0 < ξ < ξ_max), where grammar has a higher fitness than nongrammar.

From Eq. 3, it follows that a necessary condition for grammar to win is

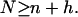4

The number of events must exceed (or equal) the sum of nouns and verbs that can be constructed to describe these events. In other words, a grammatical system is favored only if the number of relevant sentences (that individuals want to communicate to each other) exceeds the number of words that make up these sentences. Note that the main difference between grammar and nongrammar is not to use one or two words for each event, but the number (and types) of rules that need to be remembered for correct communication. Grammar can be seen as a simplified rule system that reduces the chances of mistakes in implementation and comprehension and is therefore favored by natural selection in a world where mistakes are possible.

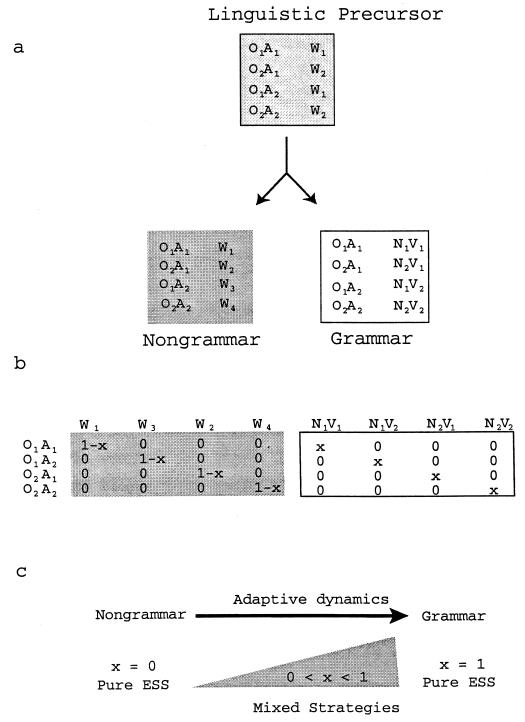
Thus far, we have specified only those conditions conducive for grammar to have a higher fitness than nongrammar. We can also formulate a model describing how grammar can evolve gradually by natural selection (see Fig. 4 and Appendix).

Figure 4.

Grammar can evolve by natural selection. (a) Imagine a simple protolanguage describing two objects, O₁ and O₂, by two words, W₁ and W₂. Suppose each object can occur with two actions, A₁ and A₂. Thus, there are four events, O₁A₁, O₂A₁, O₁A₂, and O₂A₂, that are described by two words. However, simply specifying the object may be less valuable than specifying the object and describing its action. Therefore, the language can be improved by distinguishing between all 4 events. This improvement can happen in two ways: (i) a nongrammatical approach is to specify four words, W₁–W₄, for these events; (ii) a grammatical approach is to have two words, N₁ and N₂ (nouns), for the objects and two words, V₁ and V₂ (verbs), for the actions. (b) The active matrix, P, for a range of mixed strategies that use the grammatical or the nongrammatical approach with probability x. The pure strategies are nongrammar (x = 0) and grammar (x = 1). (c) Both nongrammar and grammar are evolutionarily stable strategies (ESS), but every mixed strategy, x, is dominated by all mixed strategies, y, with y > x. The adaptive dynamics (42–44) flow from nongrammar to grammar.

The model can be extended in many ways. For example, events can consist of one action and several objects. Objects may be associated with properties, giving rise to adjectives. Events can have similar associations, giving rise to adverbs. The essential result is that a grammatical language that has words for each component of an event receives a higher payoff in the evolutionary language game than a nongrammatical language that has words (or a string of words) for the whole event. In this context, the grammar of human languages evolved to reflect the “grammar of the real world” (that is, the underlying logic of how objects relate to actions and other objects).

Conclusions.

In this paper, we have outlined simple mathematical models that provide new insights into how natural selection can guide three fundamental, early steps in the evolution of human language.

The question concerning why only humans evolved language is hard to answer. Interestingly, however, our models do not suggest that a protolanguage will evolve under all circumstances but outline several obstacles impeding its emergence. (i) In the simplest model (Fig. 1), signal–object associations form only when information transfer is beneficial to both speaker and listener. Otherwise, the evolution of communication requires cooperation between individuals. Thus, cooperation may represent an important prerequisite for the evolution of language. (ii) In the presence of errors, only a very limited communication system describing a small number of objects can evolve by natural selection (Fig. 2). We believe that this error limit is where most animal communication came to a stop. The obvious means to overcome this limit would be to use a larger variety of sounds, but this approach leads into a cul-de-sac. A completely different approach is to restrict the system to a subset of all possible sounds and to combine them into “words” (Fig. 3). (iii) Finally, although grammar can be an advantage for small systems (Fig. 4), it may become necessary only if the language refers to many events. Thus, the need for grammar arises only if communication about many different events is required: a language must have more relevant sentences than words. It is likely that for most animal communication systems, the inequality (4) is not fulfilled.

We view this paper as a contribution toward formalizing the laws that governed the evolution of the primordial human languages. There are, of course, many important and more complex properties of human language that we have not considered here and that should ultimately be part of an evolutionary theory of language. We argue, however, that any such theory has to address the basic questions of signal–object association, word formation, and the emergence of a simple syntax or grammar, for these are the atomic units that make up the edifice of human language.

Appendix

Consider two objects, O₁ and O₂, that can cooccur with two actions, A₁ and A₂. Thus, there are four events, O₁A₁, O₂A₁, O₁A₂, and O₂A₂. The nongrammatical approach is to describe each event with a separate word, W₁–W₄. The grammatical approach is to have separate words for objects, N₁ and N₂, and actions, V₁ and V₂. Consider mixed strategies that use the grammatical system with probability x. The active matrix, P, is given by

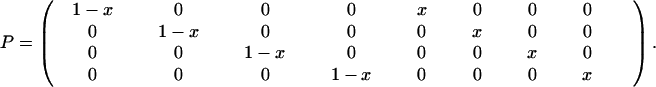The rows correspond to the four events: O₁A₁, O₂A₁, O₁A₂, and O₂A₂. The columns correspond to the eight signals: W₁, W₂, W₃, W₄, N₁V₁, N₂V₁, N₁V₂, and N₂V₂. The pure strategies, x = 0 and x = 1, describe nongrammar and grammar, respectively. The passive matrix, Q, is obtained by replacing all nonzero entries in P by 1 (and transforming this matrix). Note that mixed strategies, 0 < x < 1, have eight nonzero entries, whereas pure strategies have only four nonzero entries in both P and Q. Thus, mixed strategies have the possibility to understand both grammar and nongrammar, whereas the two pure strategies do not understand each other. Finally, we include the possibility of errors, either in implementation or comprehension. The error matrix is given by

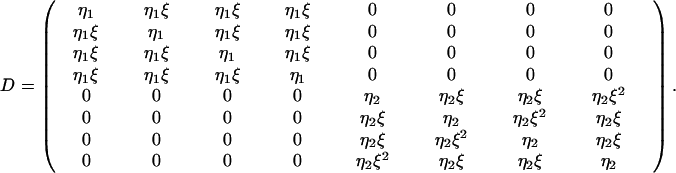Here, ξ is the similarity between words or the fraction of times a word is mistaken or misimplemented for another. We used η₁ = 1/(1 + 3ξ) and η₂ = 1/(1 + ξ)². We assume that the nongrammatical one-word sentences are not confused with the grammatical two-word sentences. The error matrix specifies the crucial difference between grammar and nongrammar.

The system can be completely understood in analytic terms. The payoff for language x communicating with language y is given (with Eq. 2) by: F (x,y) = (2 − x − y)f₁ + (x + y)f₂, where f₁ = 4/(1 + 3ξ) and f₂ = 4/(1 + ξ)². These equations hold for x and y between 0 and 1. Otherwise, we have F(x,0) = F(0,x) = (2 − x)f₁ and F(x,1) = F (1,x) = (1 + x)f₂. The payoffs for nongrammar and grammar are, respectively, F(0,0) = 2f₁ and F(1,1) = 2f₂. Because f₁ < f₂ and f₂ < 2f₁, we have the following interesting dynamics: both x = 0 and x = 1 are evolutionarily stable strategies that cannot invade any other strategy, but every mixed strategy, x, is invaded and replaced by every other strategy, y, if x < y < 1. Thus, the adaptive dynamics flow toward grammar. Alternatively, one can also assume that the pure strategies can understand each other, that is, the passive matrices of all strategies are the same; in this case, grammar (x = 1) is the only evolutionarily stable strategy and can beat every other strategy.