Extending the Fast Multipole Method for Charges inside a Dielectric Sphere in an Ionic Solvent: High Order Image Approximations for Reaction Fields

Abstract

As a sequel to our previous paper on extending the Fast Multipole Method (FMM) for charges inside a dielectric sphere [J. Comput. Phys. 223 (2007) 846-864], this paper further extends the FMM to the electrostatic calculation for charges inside a dielectric sphere immersed in an ionic solvent, a scenery with more relevance in biological applications. The key findings include two fourth-order multiple discrete image approximations in terms of u=λa to the reaction field induced by the ionic solvent, provided that u=λa < 1 where λ is the inverse Debye screening length of the ionic solvent and a is the radius of the dielectric sphere. A 10⁻⁴ relative accuracy in the reaction field of a source charge within the sphere can be achieved with only 3-4 point image charges. Together with the image charges, the FMM can be used to speed up the calculation of electrostatic interactions of charges in a dielectric sphere immersed in an ionic solvent.

1 Introduction

Solvent environment is well-known to provide a crucial contribution to the structure, dynamics and function of biological macromolecules. When modelling biological systems numerically, it has been a challenge, however, to account for this environment in a manner that is computationally efficient and physically accurate at the same time. Explicit representation of solvent molecules [1–3] offers a detailed and accurate description of a biological macromolecule, yet the large number of atoms needed limits the size of the simulated system. Alternatively, implicit solvent models [4,5] reduce the solute-solvent interactions to their mean-field characteristics, expressed as a function of the solute configuration alone, and thus yield significant computational savings. However, these implicit models also have fundamental limitations as the important atomic interaction at the solute-solvent interfaces is ignored. In order to take advantage of the efficiency of the implicit solvent models while also to account for ionic strength effect in the proximity of the solute, hybrid explicit/implicit solvent models [6–8] have emerged as promising tools for biomolecular simulations. For example, a popular hybrid approach, the solvent shell method [9–12], typically employs explicit solvent only for the first few solvation shells of the solute, with a surrounding dielectric continuum to model bulk effects beyond the shells.

This paper mainly addresses the fast and accurate calculation of electrostatic interactions in the hybrid solvent models with the spherical geometry, using a reaction field based approach. The spherical geometry has often been used because the reaction field of a spherical dielectric can be solved analytically, although this treatment may be inefficient for non-spherical solutes such as certain globular proteins and other elongated biopolymers like actin and DNA. For solutes of irregular shapes, using a non-spherical geometry to incorporate only a few layers of water adjacent to the solutes would make the simulated system much smaller, but how to efficiently obtain an accurate reaction field for such shapes remains a challenge. In particular, to employ solvation shells with irregular shapes, the Poisson's equation needs to be solved numerically at every simulation time step, which can become more computationally intensive than standard explicit solvent simulations (depending on the system size). Moreover, the proposed image approximations could be used together with other reaction field based methods. For instance, in the setting of periodic boundary conditions [13–15] to reduce artificial surface effect intrinsic to hybrid solvent models, a possible strategy is to place a different spherical cavity centered at each atom or group of atoms in the periodic box, or alternatively, to place a large spherical cavity to enclose the solute and a different spherical cavity centered at each atom outside this spherical cavity but within the periodic box [13,15].

For a pure water solvent, namely, with no ions present in the solvent, a variety of approaches exist for calculating the reaction field for charges inside a spherical cavity, including Kirkwood's classical series expansion [16], Friedman's image approximation [17], and Abagyan's modified image approximation (MIMEL) [18]. All these image approximation methods use just one image charge to represent the reaction field with limited accuracy. Recently, a high-order accurate image approximation using multiple image charges has been proposed [19], in which the resulting image charges can be incorporated into a fast multipole method (FMM) very straightforwardly to speed up the calculation of electrostatic interactions of charges inside a dielectric sphere.

In this paper, we shall focus on the ionic effect of an ionic solvent when the mobile ion concentration is given by the Debye-Hückel theory. For a solvent of weak ionic strength the linearized Poisson-Boltzmann equation [20–24] can be used to model the potential field in the solvent. In the case of a spherical cavity, analytical solution of the linearized Poisson-Boltzmann equation goes back to the work published by Kirkwood [16,25]. Utilizing Kirkwood's basic idea, Alper and Levy proposed a so-called generalized reaction field method for molecular dynamics simulations of liquid water [26]. Although they introduced one or two ions in the simulation, they did not include ionic strength effects in the reaction field.

Recently, in [27] we have developed a first- and a second-order image approximations (in terms of u=λa < 1) to an ionic solvent induced reaction field, where λ is the inverse Debye screening length and a is the radius of the spherical cavity. It is found that the resulting image approximations to the reaction field are similar to those obtained for a non-ionic, pure water solvent except for a couple of simple, ionic strength dependent correction potentials. In this paper, we will follow the same methodology [27] to develop fourth-order image approximations (in terms of u=λa < 1) to the reaction field induced by the ionic solvent for a charge inside a dielectric sphere. Moreover, we will discuss how the image approximations with the correction potential terms can be incorporated into existing fast methods for many-body problems such as the FMM to speed up the calculation of the electrostatic interactions for charges inside a dielectric sphere immersed in an ionic solvent.

The structure of the paper is as follows. In Section 2, we review the series solution to the ionic solvent induced reaction field due to a point charge inside a dielectric sphere. In Section 3, we present two fourth-order image approximations to this reaction field by a point charge at the conventional Kelvin image point and two line charges that extend along the radial direction from the Kelvin image point to infinity. Section 4 describes the general procedure to discretize the image line charges by discrete point charges, resulting in multiple discrete image approximations to the reaction field, while Section 5 describes how to apply such multiple discrete image approximations into the FMM for an O(N) calculation of electrostatic interactions of charges inside the dielectric sphere. Numerical results are then given in Section 6 to validate the convergence properties of the image approximations as well as the efficiency of the combination of the FMM and the high-order image approximations. Finally, a conclusion is given in Section 7.

2 Ionic solvent induced reaction field for a point charge

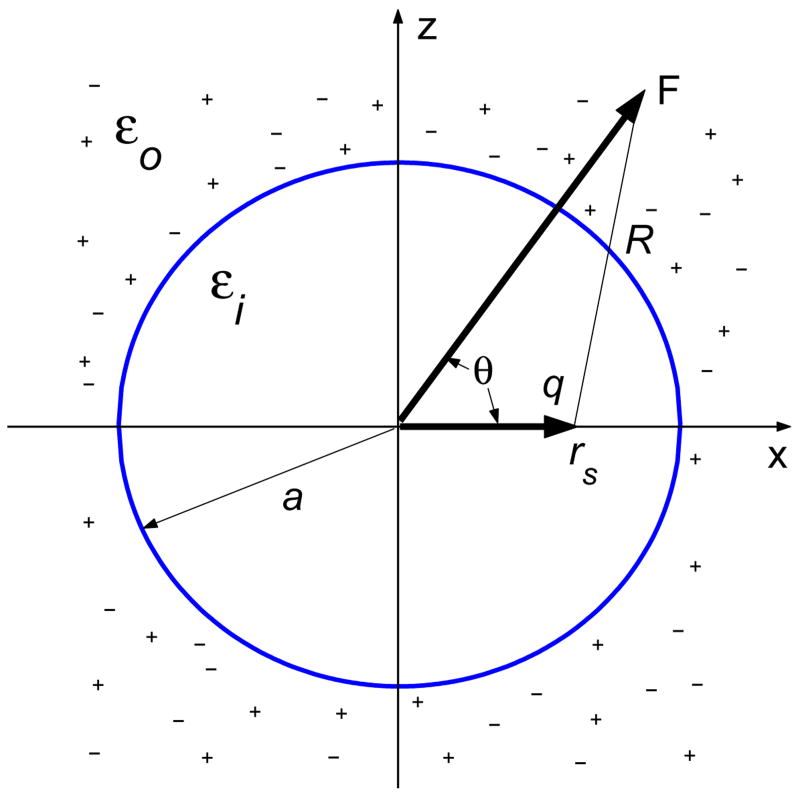
By the principle of linear superposition, we only need to consider the reaction field due to a single source charge q inside a spherical cavity centered at the origin. Without loss of generality, let us consider a dielectric sphere of radius a immersed in an ionic solvent. The sphere has a dielectric constant ε_i, and the surrounding ionic solvent is represented as a homogeneous dielectric continuum of a dielectric constant ε_o. The point charge q is located on the x-axis inside the sphere at a distance r_S < a from the center of the sphere, as shown in Fig. 1.

Fig. 1.

A point charge and a dielectric sphere immersed in an ionic solvent.

It is well-known that the total electrostatic potential Φ(r) at a point r inside the sphere is given by the solution to the Poisson's equation

$$\nabla ·({\epsilon }_{\text{i}}\nabla \Phi (\text{r}))=-q\delta (|\text{r}-{\text{r}}_s|),$$ (1)

where δ(r) is the Dirac delta function. Moreover, this potential can be expressed as Φ(r)=Φ_Cou(r)+Φ_RF(r), where Φ_Cou(r) is the Coulomb potential due to the source charge q alone, and Φ_RF(r) is the reaction potential due to the polarization of the outside dielectric medium.

Outside the sphere, on the other hand, by assuming that the mobile ion concentration in the ionic solvent is given by the Debye-Hückel theory, namely, the mobile charges follow a Boltzmann distribution in the mean field approximation, for a solvent of weak ionic strength, the linearized Poisson-Boltzmann equation [23,24]

$${\nabla }^2\Phi \left(\text{r}\right)-{\lambda }^2\Phi \left(\text{r}\right)=0$$ (2)

can be used to approximate the screened Coulomb potential in the solution. Here, λ is the inverse Debye screening length defined by

$${\lambda }^2=\frac{8\pi N_{\text{A}}{e}^2{\rho }_{\text{A}}}{1000{\epsilon }_{\text{o}}{k}_{\text{B}}T}{c}_s,$$ (3)

where N_A is Avogadro's number, ρ_A is the solvent density, e is the protonic charge (4.803×10⁻¹⁰esu), k_B is the Boltzmann constant, T is the absolute temperature, and c_s is the ionic concentration measured in molar units. From (3), we see that the inverse Debye screening length λ is proportional to the square root of the ionic concentration c_s. In particular, for 1:1 electrolytes (monovalent:monovalent salts like NaCl),

$$\lambda \approx 0.33\sqrt{c_{\text{s}}}{Å}^{-1}$$ (4)

at room temperature (25°), with ε_o=78.5 and Å=10⁻¹⁰m [28].

Using the classical electrostatic theory, the reaction field of the spherical dielectric can be solved analytically [27]. More precisely, with respect to a spherical coordinate system (r, θ, φ) with its origin at the center of the sphere (the pole is denoted by the x-axis in this paper), due to the azimuthal symmetry, the reaction field at an observation point r=(r, θ, φ) inside the sphere is

$${\Phi }_{\text{RF}}\left(\text{r}\right)=\sum _{n=0}^{\infty }{A}_n{r}^n{P}_n\left(cos\theta \right),$$ (5)

where P_n(x) are the Legendre polynomials and A_n are the expansion coefficients given by

$$\begin{array}{cc}{A}_n=\frac{q}{{\epsilon }_{\text{i}}a}\frac{1}{r_{\text{K}}^n}\frac{{\epsilon }_{\text{i}}\left(n+1\right)k_n\left(u\right)+{\epsilon }_{\text{o}}u{k}_n^{\prime }\left(u\right)}{{\epsilon }_{\text{i}}n{k}_n\left(u\right)-{\epsilon }_{\text{o}}u{k}_n^{\prime }\left(u\right)},& n\ge 0,\end{array}$$ (6)

where u=λa, r_K=a²/r_S with r_K=(r_K, 0, 0) denoting the conventional Kelvin image point, and k_n(r) are the modified spherical Hankel functions defined as [29,30]

$$\begin{array}{cc}{k}_n\left(r\right)=\frac{\pi }{2r}{e}^{-r}\sum _{k=0}^n\frac{\left(n+k\right)\text{!}}{k\text{!}\left(n-k\right)\text{!}}\frac{1}{{\left(2r\right)}^k},& n\ge 0.\end{array}$$ (7)

In particular, the first three modified spherical Hankel functions are

$$\begin{array}{l}{k}_0(r)=\frac{\pi }{2r}{e}^{-r},\\ k_1(r)=\frac{\pi }{2r}{e}^{-r}\hspace{0.17em}\left(1+\frac{1}{r}\right)\hspace{0.17em},\\ k_2(r)=\frac{\pi }{2r}{e}^{-r}\hspace{0.17em}\left(1+\frac{3}{r}+\frac{3}{r^2}\right).\end{array}$$

On the other hand, the potential outside the sphere is

$$\Phi \left(\text{r}\right)=\sum _{n=0}^{\infty }{B}_n{k}_n\left(\lambda r\right)P_n\left(cos\theta \right),$$ (8)

where B_n are the expansion coefficients given by

$$B_n=\frac{q}{{\epsilon }_{\text{i}}a}\hspace{0.17em}{\left(\frac{r_{\text{S}}}{a}\right)}^n\frac{{\epsilon }_{\text{i}}\left(2n+1\right)}{{\epsilon }_{\text{i}}n{k}_n\left(u\right)-{\epsilon }_{\text{o}}u{k}_n^{\prime }\left(u\right)}.$$ (9)

It has been shown in [27] that, when the ionic strength of the solvent, or equivalently the inverse Debye screening length λ, approaches zero, the above results can be identified with the corresponding results for the case of a dielectric sphere immersed in a pure water solvent [19].

3 Image line charge approximations to the reaction field

Let us now turn our attention to the problem of finding image charges outside the spherical region which should represent the reaction potential inside the sphere. For a pure water solvent, such image charges include a point charge at the conventional Kelvin image point and a continuous line charge extending along the radial direction from this Kelvin image point to infinity [31–33]. For an ionic solvent, as mentioned earlier, by assuming that the ionic strength of the solvent is weak enough so that the product of the inverse Debye screening length and the radius of the spherical cavity is less than one (u=λa < 1), we have developed a first- and a second-order image approximations (in terms of u=λa) to the ionic solvent induced reaction field [27]. Both approximations employ the same image point and line charges as those obtained for the pure water solvent, while the ionic strength effect is included in a couple of additional correction potentials.

It should be pointed out that the assumption of u=λa < 1 is physically justifiable. A general belief is that, the Debye-Hückel theory and thus the linearization of the Poisson-Boltzmann equation hold only for the case of dilute or moderate solutions (e.g., molar concentrations c_s < 1mM), but fail for cases of higher ionic concentrations (in particular when 1/λ reaches the atomic scale). The monograph by Fowler and Guggenheim [34] contains detailed discussions on when the Debye-Hückel theory applies. It also briefly mentions theories that were developed to work at higher ionic concentrations.

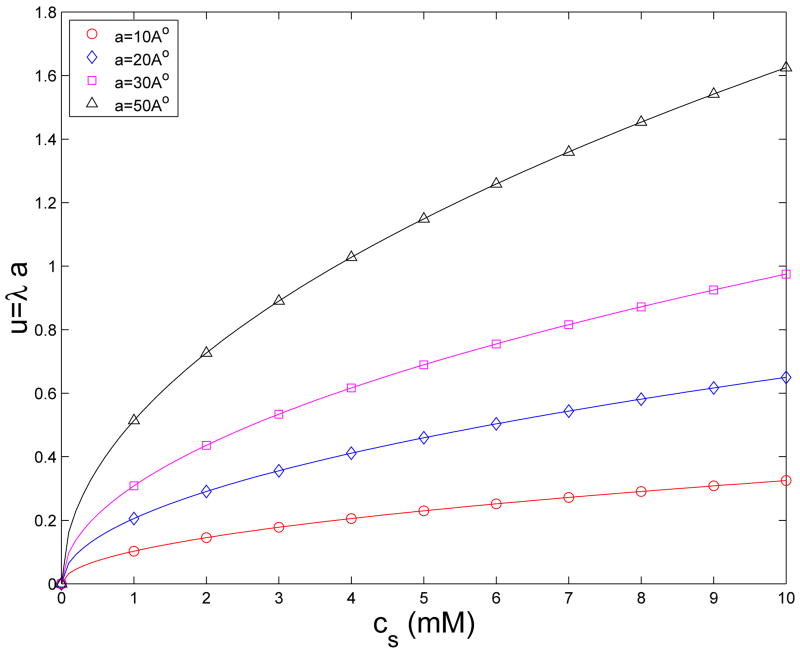
The condition that u=λa < 1 implies a maximum radius will be set for a specified inverse Debye screening length. Conversely, a fixed radius will limit the ionic strength for which the image approximations are valid. For dilute solutions, u=λa < 1 is true even for a very large simulated system. For 1mM NaCl salt, λ≈0.01Å⁻¹, we can use a < 100Å, which is more than enough for a relatively large protein. And for 10mM NaCl salt, λ≈0.03Å⁻¹, we can use a < 30Å. On the other hand, if a large system with a=50Å needs to be simulated, then the maximum ionic concentration that satisfies u=λa < 1 is about 4mM. Since physiological salt concentrations are normally in the mM range and lower, u=λa < 1 is therefore a reasonable assumption for most real biological systems. Figure 2 shows the scale of u=λa for physiological salts with c_s < 10mM for four different simulated systems with a=10Å, 20Å, 30Å, and 50Å, respectively.

Fig. 2.

Scale of u=λa for physiological salt concentrations.

3.1 Previous results: First- and second-order image approximations

Applying the asymptotic expansion of the modified spherical Hankel function for small r

$$\begin{array}{cc}{k}_n\left(r\right)=\pi \frac{\left(2n\right)\text{!}}{n\text{!}}\frac{1}{{\left(2r\right)}^{n+1}}+O\hspace{0.17em}\left(\frac{1}{r^n}\right)\hspace{0.17em},& n\ge 0,\end{array}$$ (10)

the first-order image approximation to the ionic solvent induced reaction field can be obtained as follows [27]

$${\Phi }_{\text{RF}}\left(\text{r}\right)=\frac{q_{\text{K}}}{{\epsilon }_i\left|\text{r}-{\text{r}}_{\text{K}}\right|}+{\int }_{r_{\text{K}}}^{\infty }\frac{q_{\text{L}0}\left(x\right)}{{\epsilon }_{\text{i}}\left|\text{r}-\text{x}\right|}\text{d}x+O\left(u\right),$$ (11)

with the image point charge q_K and the image line charge q_L0(x) defined by

$$\begin{array}{ccc}{q}_{\text{K}}=\gamma \frac{a}{r_{\text{S}}}q,& q_{\text{L}0}\hspace{0.17em}\left(x\right)=\frac{{\delta }_{0}q}{a}{\left(\frac{x}{r_{\text{K}}}\right)}^{-{\sigma }_0},& r_{\text{K}}\le x,\end{array}$$

respectively, where

$$\begin{array}{ccc}\gamma =\frac{{\epsilon }_{\text{i}}-{\epsilon }_{\text{o}}}{{\epsilon }_{\text{i}}+{\epsilon }_{\text{o}}},& {\sigma }_0=\frac{{\epsilon }_{\text{o}}}{{\epsilon }_{\text{i}}+{\epsilon }_{\text{o}}},& {\delta }_0=\frac{{\epsilon }_{\text{i}}\left({\epsilon }_{\text{i}}-{\epsilon }_{\text{o}}\right)}{{\left({\epsilon }_{\text{i}}+{\epsilon }_{\text{o}}\right)}^2}.\end{array}$$

Note that neither of the point charge q_K and the line charge q_L0(x) depends on the inverse Debye screening length λ, indicating that in essence the first-order image approximation to the ionic solvent induced reaction field totally ignores the ionic strength effect in the reaction potential. Hence, more accurate image approximations have to be developed to account for the ionic strength effect. To this end, by noticing that instead of the O(1/rⁿ) truncation error as described in (10), in fact we have

$$\begin{array}{cc}{k}_n\left(r\right)=\pi \frac{\left(2n\right)\text{!}}{n\text{!}}\frac{1}{{\left(2r\right)}^{n+1}}+O\hspace{0.17em}\left(\frac{1}{r^{n-1}}\right)\hspace{0.17em},& n\ge 1.\end{array}$$ (12)

The first-order image approximation thus can be improved by simply including a constant, position-independent correction potential, resulting in the following second-order image approximation to the ionic solvent induced reaction field [27]

$${\Phi }_{\text{RF}}\left(\text{r}\right)=\frac{q_{\text{K}}}{{\epsilon }_{\text{i}}\left|\text{r}-{\text{r}}_{\text{K}}\right|}+{\int }_{r_{\text{K}}}^{\infty }\frac{q_{\text{L}0}\left(x\right)}{{\epsilon }_{\text{i}}\left|\text{r}-\text{x}\right|}\text{d}x+{\Phi }_{\text{C}1}^{\prime }+O(u^2),$$ (13)

with the constant, position-independent correction potential ${\Phi }_{\text{C}1}^{\prime }$ defined by

$${\Phi }_{\text{C}1}^{\prime }=\frac{q}{{\epsilon }_{\text{i}}a}\hspace{0.17em}\left(C_0\left(u\right)-\gamma -\frac{{\delta }_0}{{\sigma }_0}\right)\hspace{0.17em},$$

where

$$C_0\left(u\right)=\frac{{\epsilon }_{\text{i}}-\left(1+u\right){\epsilon }_{\text{o}}}{\left(1+u\right){\epsilon }_{\text{o}}}.$$ (14)

Moreover, the accuracy of the second-order image approximation (13) can be further improved by including another position-dependent correction potential, yielding the improved second-order image approximation [27]

$${\Phi }_{\text{RF}}\left(\text{r}\right)=\frac{q_{\text{K}}}{{\epsilon }_{\text{i}}\left|\text{r}-{\text{r}}_{\text{K}}\right|}+{\int }_{r_{\text{K}}}^{\infty }\frac{q_{\text{L}0}\left(x\right)}{{\epsilon }_{\text{i}}\left|\text{r}-\text{x}\right|}\text{d}x+{\Phi }_{\text{C}1}^{\prime }+{\Phi }_{\text{C}2}^{\prime }(\text{r})+O(u^2),$$ (15)

with the position-dependent correction potential ${\Phi }_{\text{C}2}^{\prime }(\text{r})$ defined by

$${\Phi }_{\text{C}2}^{\prime }\left(\text{r}\right)=\frac{q}{{\epsilon }_{\text{i}}a}\hspace{0.17em}\left(C_1\left(u\right)-\gamma -\frac{{\delta }_0}{1+{\sigma }_0}\right)\hspace{0.17em}\left(\frac{r}{r_{\text{K}}}\right)\hspace{0.17em}cos\theta ,$$

where

$$C_1(u)=\frac{2(1+u){\epsilon }_{\text{i}}-(2+2u+u^2){\epsilon }_{\text{o}}}{(1+u){\epsilon }_{\text{i}}+(2+2u+u^2){\epsilon }_{\text{o}}}.$$ (16)

3.2 Fourth-order image approximations

To construct a fourth-order image approximation, first by using

$$e^{-r}=1-r+\frac{r^2}{2}-\frac{r^3}{6}+O(r^4),$$

and

$$\begin{array}{lll}\hfill \sum _{k=0}^n\frac{\left(n+k\right)\text{!}}{k\text{!}\left(n-k\right)\text{!}}\frac{1}{{\left(2r\right)}^k}\hspace{0.17em}=& \multicolumn{2}{c}{\frac{\left(2n\right)\text{!}}{n\text{!}}\frac{1}{{\left(2r\right)}^n}+\frac{\left(2n-1\right)\text{!}}{\left(n-1\right)\text{!}}\frac{1}{{\left(2r\right)}^{n-1}}+\frac{\left(2n-2\right)\text{!}}{2\left(n-2\right)\text{!}}\frac{1}{{\left(2r\right)}^{n-2}}}\\ & +\frac{\left(2n-3\right)\text{!}}{6\left(n-3\right)\text{!}}\frac{1}{{\left(2r\right)}^{n-3}}+O\hspace{0.17em}\left(\frac{1}{r^{n-4}}\right)\hspace{0.17em},\hfill & n\ge 3,\hfill \end{array}$$

we get the expansion of the modified spherical Hankel function k_n(r) in terms of 1/r for n ≥ 3

$$\begin{array}{cc}{k}_n\left(r\right)=\pi \frac{\left(2n-2\right)\text{!}}{\left(n-1\right)\text{!}}\hspace{0.17em}\left(\frac{2\left(2n-1\right)}{{\left(2r\right)}^{n+1}}-\frac{1}{4{\left(2r\right)}^{n-1}}\right)+O\hspace{0.17em}\left(\frac{1}{r^{n-3}}\right)\hspace{0.17em},& n\ge 3.\end{array}$$ (17)

Next, after expanding k₂(r) directly in terms of 1/r, it turns out that (17) is also true for n=2. Therefore, we have

$$\begin{array}{cc}{k}_n\left(r\right)=\pi \frac{\left(2n-2\right)\text{!}}{\left(n-1\right)\text{!}}\hspace{0.17em}\left(\frac{2\left(2n-1\right)}{{\left(2r\right)}^{n+1}}-\frac{1}{4{\left(2r\right)}^{n-1}}\right)+O\hspace{0.17em}\left(\frac{1}{r^{n-3}}\right)\hspace{0.17em},& n\ge 2.\end{array}$$ (18)

Correspondingly, the derivative of the modified spherical Hankel function can be expanded for small r as

$$\begin{array}{cc}{k}_n^{\prime }\left(r\right)=-\pi \frac{\left(2n-2\right)\text{!}}{\left(n-1\right)\text{!}}\hspace{0.17em}\left(\frac{4\left(2n-1\right)\left(n+1\right)}{{\left(2r\right)}^{n+2}}-\frac{n-1}{2{\left(2r\right)}^n}\right)+O\hspace{0.17em}\left(\frac{1}{r^{n-2}}\right)\hspace{0.17em},& n\ge 2.\end{array}$$

Consequently, we obtain

$$\begin{array}{cc}\frac{k_n\left(r\right)}{r{k}_n^{\prime }(r)}=-\frac{-(2+r^2)+4n}{(r^2-2)+(2-r^2)n+4n^2}+O(r^4),& n\ge 2.\end{array}$$

Inserting this approximation into (6) leads to

$$\begin{array}{cc}{A}_n=\frac{q}{{\epsilon }_{\text{i}}a}\frac{1}{r_{\text{K}}^n}\frac{a_1+a_{2}n+a_3{n}^2}{b_1+b_{2}n+b_3{n}^2}+O(u^4),& n\ge 2,\end{array}$$

where we denote

$$\begin{array}{c}{a}_1=-({\epsilon }_{\text{i}}+{\epsilon }_{\text{o}})u^2-2({\epsilon }_{\text{i}}-{\epsilon }_{\text{o}}),\hspace{0.17em}\hspace{0.17em}{a}_2=({\epsilon }_{\text{i}}-{\epsilon }_{\text{o}})(2-u^2),\hspace{0.17em}\hspace{0.17em}{a}_3=4({\epsilon }_{\text{i}}-{\epsilon }_{\text{o}}),\\ b_1=-{\epsilon }_{\text{o}}(2-u^2),\hspace{0.17em}\hspace{0.17em}{b}_2=-({\epsilon }_{\text{i}}+{\epsilon }_{\text{o}})u^2-2({\epsilon }_{\text{i}}-{\epsilon }_{\text{o}}),\hspace{0.17em}\hspace{0.17em}{b}_3=4({\epsilon }_{\text{i}}+{\epsilon }_{\text{o}}).\end{array}$$

After some algebraic manipulation, the expansion coefficients A_n are found to be

$$\begin{array}{cc}{A}_n=\frac{q}{{\epsilon }_{\text{i}}a}\frac{1}{r_{\text{K}}^n}\hspace{0.17em}\left(\gamma +\frac{{\alpha }_1+{\alpha }_{2}n}{{\beta }_1+{\beta }_{2}n+n^2}\right)+O(u^4),& n\ge 2,\end{array}$$

Where

$$\begin{array}{ll}{\alpha }_1=\gamma \hspace{0.17em}\left(\frac{a_1}{a_3}-\frac{b_1}{b_3}\right)\hspace{0.17em},& {\beta }_1=\frac{b_1}{b_3},\\ {\alpha }_2=\gamma \hspace{0.17em}\left(\frac{a_2}{a_3}-\frac{b_2}{b_3}\right)\hspace{0.17em},& {\beta }_2=\frac{b_2}{b_3}.\end{array}$$

Note that β₁ < 0 when 0 ≤ u < 1. Then, using partial fractions gives us

$$\begin{array}{cc}{A}_n=\frac{q}{{\epsilon }_{\text{i}}a}\frac{1}{r_{\text{K}}^n}\hspace{0.17em}\left(\gamma +\frac{{\delta }_1}{n+{\sigma }_1}+\frac{{\delta }_2}{n-{\sigma }_2}\right)+O(u^4),& n\ge 2,\end{array}$$ (19)

where

$$\begin{array}{ll}{\delta }_1=\frac{{\alpha }_2{\sigma }_1-{\alpha }_1}{{\sigma }_1+{\sigma }_2},& {\sigma }_1=\frac{\sqrt{{\beta }_2^2-4{\beta }_1}+{\beta }_2}{2},\\ {\delta }_2=\frac{{\alpha }_2{\sigma }_2+{\alpha }_1}{{\sigma }_1+{\sigma }_2},& {\sigma }_2=\frac{\sqrt{{\beta }_2^2-4{\beta }_1}-{\beta }_2}{2}.\end{array}$$

Moreover, it can be shown easily that both 0 < σ₁ < 1 and 0 < σ₂ < 1. Furthermore, we can prove that 1/2 < σ₁ when ε_i < ε_o/5, and σ₂ < 1/2 when ε_i < ε_o (and σ₂ > 1/2 if ε_i > ε_o, and σ₂=1/2 if ε_i=ε_o). Therefore, in hybrid explicit/implicit solvent models for biomolecular simulations where the typical dielectric constants are 1 to 4 for ε_i and 60 to 85 for ε_o, respectively, we always have 1/2 < σ₁ < 1 and 0 < σ₂ < 1/2.

On the other hand, for n ≤ 1, applying the exact expressions of k₀(r) and k₁(r), in fact we can arrive at

$$\begin{array}{cc}\frac{k_0\left(r\right)}{r{k}_0^{\prime }\left(r\right)}=-\frac{1}{1+r},& \frac{k_1\left(r\right)}{r{k}_1^{\prime }\left(r\right)}=-\frac{1+r}{2+2r+r^2},\end{array}$$

and accordingly,

$$\begin{array}{cc}{A}_0=C_0\left(u\right)\frac{q}{{\epsilon }_{\text{i}}a},& A_1=C_1\left(u\right)\frac{q}{{\epsilon }_{\text{i}}a}\frac{1}{r_{\text{K}}},\end{array}$$

with C₀(u) and C₁(u) being defined by (14) and (16), respectively.

Inserting now the approximation of A_n given by (19) into (5), the reaction field inside the sphere is taken as

$${\Phi }_{\text{RF}}\left(\text{r}\right)=A_0+A_{1}rcos\theta +S_1+S_2+S_3+O(u^4),$$ (20)

where the three series S₁, S₂ and S₃ are defined as

$$\begin{array}{l}{S}_1=\frac{\gamma q}{{\epsilon }_{\text{i}}a}\sum _{n=2}^{\infty }\hspace{0.17em}{\left(\frac{r}{r_{\text{K}}}\right)}^n\hspace{0.17em}{P}_n\left(cos\theta \right),\\ S_2=\frac{{\delta }_{1}q}{{\epsilon }_{\text{i}}a}\sum _{n=2}^{\infty }\frac{1}{n+{\sigma }_1}\hspace{0.17em}{\left(\frac{r}{r_{\text{K}}}\right)}^n\hspace{0.17em}{P}_n\left(cos\theta \right),\\ S_3=\frac{{\delta }_{2}q}{{\epsilon }_{\text{i}}a}\sum _{n=2}^{\infty }\frac{1}{n-{\sigma }_2}\hspace{0.17em}{\left(\frac{r}{r_{\text{K}}}\right)}^n\hspace{0.17em}{P}_n\left(cos\theta \right).\end{array}$$

To find an image representation of the first series S₁, we recall that the Coulomb potential Φ_S(r), the potential at r due to a point charge at r_S, can be expanded in terms of the Legendre polynomials of cos θ as follows [35].

$${\Phi }_{\text{S}}\left(\text{r}\right)=\frac{q}{{\epsilon }_{\text{i}}\left|\text{r}-{\text{r}}_{\text{S}}\right|}=\{\begin{array}{cc}\frac{q}{{\epsilon }_{\text{i}}r}{\sum _{n=0}^{\infty }\hspace{0.17em}\left(\frac{r_{\text{S}}}{r}\right)}^n\hspace{0.17em}{P}_n\left(cos\theta \right),& r_{\text{S}}\le r\le a,\\ \frac{q}{{\epsilon }_{\text{i}}{r}_{\text{S}}}{\sum _{n=0}^{\infty }\hspace{0.17em}\left(\frac{r}{r_{\text{S}}}\right)}^n\hspace{0.17em}{P}_n\left(cos\theta \right),& 0\le r\le r_{\text{S}}.\end{array}$$ (21)

Note that the first series S₁ can be written as

$$S_1=\frac{\gamma q}{{\epsilon }_{\text{i}}{r}_{\text{K}}}\frac{a}{r_{\text{S}}}{\sum _{n=0}^{\infty }\hspace{0.17em}\left(\frac{r}{r_{\text{K}}}\right)}^n\hspace{0.17em}{P}_n\left(cos\theta \right)-\frac{\gamma q}{{\epsilon }_{\text{i}}a}\hspace{0.17em}\left(1+\frac{r}{r_{\text{K}}}cos\theta \right)\hspace{0.17em},$$

where the first part is exactly the expansion given by (21) for a point charge of magnitude q_K outside the sphere at the conventional Kelvin image point r_K=(r_K, 0, 0), namely,

$$S_1=\frac{q_{\text{K}}}{{\epsilon }_{\text{i}}\left|\text{r}-{\text{r}}_{\text{K}}\right|}-\frac{\gamma q}{{\epsilon }_{\text{i}}a}\hspace{0.17em}\left(1+\frac{r}{r_{\text{K}}}cos\theta \right).$$ (22)

Next, to find an image representation for the second series S₂, we need the integral identity

$$\frac{1}{n+\sigma }=r_{\text{K}}^{n+\sigma }{\int }_{r_{\text{K}}}^{\infty }\frac{1}{x^{n+\sigma +1}}\hspace{0.17em}\text{d}x,$$ (23)

which is valid for all n ≥ 0 when σ > 0. Inserting (23) with σ=σ₁ into S₂ yields

$$S_2={\int }_{r_{\text{K}}}^{\infty }\hspace{0.17em}\left[\frac{q_{\text{L}1}\left(x\right)}{{\epsilon }_{\text{i}}x}\sum _{n=0}^{\infty }\hspace{0.17em}{\left(\frac{r}{x}\right)}^n\hspace{0.17em}{P}_n\left(cos\theta \right)\right]\hspace{0.17em}\text{d}x-\frac{{\delta }_{1}q}{{\epsilon }_{\text{i}}a}\hspace{0.17em}\left(\frac{1}{{\sigma }_1}+\frac{1}{1+{\sigma }_1}\frac{r}{r_{\text{K}}}cos\theta \right)\hspace{0.17em},$$

where

$$\begin{array}{cc}{q}_{\text{L}1}\left(x\right)=\frac{{\delta }_{1}q}{a}\hspace{0.17em}{\left(\frac{x}{r_{\text{K}}}\right)}^{-{\sigma }_1}\hspace{0.17em},& r_{\text{K}}\le x.\end{array}$$ (24)

Note that the integrand in the above integral again becomes the expansion given by (21) for a charge of magnitude q_L1(x) outside the sphere at the point x=(x, 0, 0). Therefore, q_L1(x) can be regarded as a continuous line charge that extends along the radial direction from the classical Kelvin image point r_K out to infinity. Thus, the second series S₂ becomes

$$S_2={\int }_{r_{\text{K}}}^{\infty }\frac{q_{\text{L}1}\left(x\right)}{{\epsilon }_{\text{i}}\left|\text{r}-\text{x}\right|}\text{d}x-\frac{{\delta }_{1}q}{{\epsilon }_{\text{i}}a}\hspace{0.17em}\left(\frac{1}{{\sigma }_1}+\frac{1}{1+{\sigma }_1}\frac{r}{r_{\text{K}}}cos\theta \right).$$ (25)

Last, to find an image representation for the third series S₃, we use a similar integral identity

$$\frac{1}{n-{\sigma }_2}=r_{\text{K}}^{n-{\sigma }_2}{\int }_{r_{\text{K}}}^{\infty }\frac{1}{x^{n-{\sigma }_2+1}}\hspace{0.17em}\text{d}x,$$ (26)

which is valid for all n ≥ 1 as 0 < σ₂ < 1. Inserting this into S₃ yields

$$S_3={\int }_{r_{\text{K}}}^{\infty }\frac{q_{\text{L}2}\left(x\right)}{{\epsilon }_{\text{i}}}\hspace{0.17em}\left[\sum _{n=0}^{\infty }\frac{1}{x}\hspace{0.17em}{\left(\frac{r}{x}\right)}^n\hspace{0.17em}{P}_n\left(cos\theta \right)-\left(\frac{1}{x}+\frac{r}{x^2}cos\theta \right)\right]\hspace{0.17em}\text{d}x,$$

where

$$\begin{array}{cc}{q}_{\text{L}2}\left(x\right)=\frac{{\delta }_{2}q}{a}\hspace{0.17em}{\left(\frac{x}{r_{\text{K}}}\right)}^{{\sigma }_2}\hspace{0.17em},& r_{\text{K}}\le x.\end{array}$$ (27)

Then applying the identity (Expansion (21) with r_S=x, q=1 and ε_i=1)

$$\begin{array}{cc}\frac{1}{\left|\text{r}-\text{x}\right|}=\sum _{n=0}^{\infty }\frac{1}{x}\hspace{0.17em}{\left(\frac{r}{x}\right)}^n\hspace{0.17em}{P}_n\left(cos\theta \right),& r<x,\end{array}$$

and noting that

$${\int }_{r_{\text{K}}}^{\infty }\frac{q_{\text{L}2}\left(x\right)}{{\epsilon }_{\text{i}}}\frac{r}{x^2}cos\theta \text{d}x=\frac{{\delta }_{2}q}{{\epsilon }_{\text{i}}a\left(1-{\sigma }_2\right)}\frac{r}{r_{\text{K}}}cos\theta ,$$

we obtain

$$S_3={\int }_{r_{\text{K}}}^{\infty }\frac{q_{\text{L}2}\left(x\right)}{{\epsilon }_{\text{i}}}\hspace{0.17em}\left(\frac{1}{\left|\text{r}-\text{x}\right|}-\frac{1}{x}\right)\hspace{0.17em}\text{d}x-\frac{{\delta }_{2}q}{{\epsilon }_{\text{i}}a\left(1-{\sigma }_2\right)}\frac{r}{r_{\text{K}}}cos\theta .$$ (28)

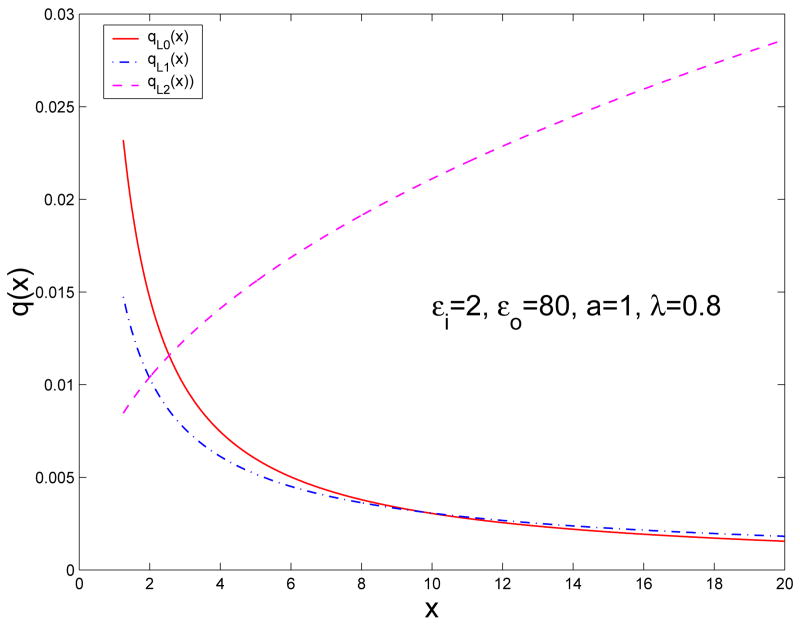
Likewise, q_L2(x) can be regarded as a continuous line charge (in fact, dipole moment) extending along the radial direction from the classical Kelvin image point r_K to infinity. Unlike q_L1(x) whose magnitude decays to zero faster than x^−1/2, however, q_L2(x) grows to infinity slower than x^1/2 in terms of its magnitude. Figure 3 shows the density distributions of the image line charges q_L0(x), q_L1(x) and q_L2(x) for a source charge q=−1 at r_S=0.8 on the x-axis in the case that ε_i=2, ε_o=80, a=1, and λ=0.8.

Fig. 3.

Density distributions of the image line charges q_L0(x), q_L1(x) and q_L2(x) for a source charge q=−1 at r_S=0.8 on the x-axis in the case that ε_i=2, ε_o=80, a=1, and λ=0.8.

Finally, after combining (22), (25) and (28), we obtain a fourth-order image approximation to the ionic solvent induced reaction potential as follows

$$\begin{array}{ll}\hfill {\Phi }_{\text{RF}}\left(\text{r}\right)\hspace{0.17em}=& \frac{q_{\text{K}}}{{\epsilon }_{\text{i}}\left|\text{r}-{\text{r}}_{\text{K}}\right|}+{\int }_{r_{\text{K}}}^{\infty }\frac{q_{\text{L}1}\left(x\right)}{{\epsilon }_{\text{i}}\left|\text{r}-\text{x}\right|}\text{d}x+{\int }_{r_{\text{K}}}^{\infty }\frac{q_{\text{L}2}\left(x\right)}{{\epsilon }_{\text{i}}}\hspace{0.17em}\left(\frac{1}{\left|\text{r}-\text{x}\right|}-\frac{1}{x}\right)\hspace{0.17em}\text{d}x\hfill \\ & +{\Phi }_{\text{C}1}+{\Phi }_{\text{C}2}\left(\text{r}\right)+O(u^4),\end{array}$$ (29)

where Φ_C1 is a constant, position-independent correction potential defined as

$${\Phi }_{\text{C}1}=\frac{q}{{\epsilon }_{\text{i}}a}\hspace{0.17em}\left(C_0\left(u\right)-\gamma -\frac{{\delta }_1}{{\sigma }_1}\right)\hspace{0.17em},$$ (30)

and on the other hand, Φ_C2(r) is a position-dependent correction potential given by

$${\Phi }_{\text{C}2}\left(\text{r}\right)=\frac{q}{{\epsilon }_{\text{i}}a}\hspace{0.17em}\left(C_1\left(u\right)-\gamma -\frac{{\delta }_1}{1+{\sigma }_1}-\frac{{\delta }_2}{1-{\sigma }_2}\right)\hspace{0.17em}\frac{r}{r_{\text{K}}}cos\theta .$$ (31)

To further improve the accuracy of the fourth-order image approximation, we can choose to calculate the third term in the series expansion (5) exactly. For n=2, from the exact expression of k₂(r), in fact we can arrive at

$$\frac{k_2\left(r\right)}{r{k}_2^{\prime }\left(r\right)}=-\frac{3+3r+r^2}{9+9r+4r^2+r^3}.$$

Substituting it into A₂ defined in (6), we now obtain

$$A_2=C_2\left(u\right)\frac{q}{{\epsilon }_{\text{i}}a}\frac{1}{r_{\text{K}}^2},$$

where

$$C_2(u)=\frac{3(3+3u+u^2){\epsilon }_{\text{i}}-(9+9u+4u^2+u^3){\epsilon }_{\text{o}}}{2(3+3u+u^2){\epsilon }_{\text{i}}+(9+9u+4u^2+u^3){\epsilon }_{\text{o}}}.$$ (32)

Now instead of (20), we express the reaction field inside the sphere as

$$\begin{array}{ll}\hfill {\Phi }_{\text{RF}}(\text{r})\hspace{0.17em}=& A_0+A_{1}rcos\theta +A_2{r}^2{P}_2(cos\theta )\hfill \\ & +\sum _{n=3}^{\infty }\frac{q}{{\epsilon }_{\text{i}}a}\frac{1}{r_{\text{K}}^n}\hspace{0.17em}\left(\gamma +\frac{{\delta }_1}{n+{\sigma }_1}+\frac{{\delta }_2}{n-{\sigma }_2}\right)\hspace{0.17em}{r}^n{P}_n(cos\theta )+(u^4).\hfill \end{array}$$ (33)

Note that the only difference between (20) and (33) is the way to calculate the third term. For this reason, the fourth-order image approximation defined by (29) can be improved by simply including a third correction potential, resulting in an improved fourth-order image approximation as follows.

$$\begin{array}{ll}\hfill {\Phi }_{\text{RF}}\left(\text{r}\right)\hspace{0.17em}=& \frac{q_{\text{K}}}{{\epsilon }_{\text{i}}\left|\text{r}-{\text{r}}_{\text{K}}\right|}+{\int }_{r_{\text{K}}}^{\infty }\frac{q_{\text{L}1}\left(x\right)}{{\epsilon }_{\text{i}}\left|\text{r}-\text{x}\right|}\text{d}x+{\int }_{r_{\text{K}}}^{\infty }\frac{q_{\text{L}2}\left(x\right)}{{\epsilon }_{\text{i}}}\hspace{0.17em}\left(\frac{1}{\left|\text{r}-\text{x}\right|}-\frac{1}{x}\right)\hspace{0.17em}\text{d}x\hfill \\ & +{\Phi }_{\text{C}1}+{\Phi }_{\text{C}2}\left(\text{r}\right)+{\Phi }_{\text{C}3}\left(\text{r}\right)+O(u^4),\hfill \end{array}$$ (34)

where the position-dependent correction potential Φ_C3(r) is defined as

$${\Phi }_{\text{C}3}\left(\text{r}\right)=\frac{q}{{\epsilon }_{\text{i}}a}\hspace{0.17em}\left(C_2\left(u\right)-\gamma -\frac{{\delta }_1}{2+{\sigma }_1}-\frac{{\delta }_2}{2-{\sigma }_2}\right)\hspace{0.17em}{\left(\frac{r}{r_{\text{K}}}\right)}^2\hspace{0.17em}{P}_2\left(cos\theta \right).$$ (35)

Here, P₂(cos θ)=(3 cos² θ − 1)/2.

As a special case, when u=λa=0, one can show that σ₁=σ₀ and δ₁=δ₀ so q_L1(x)=q_L0(x), and δ₂=0 so q_L2(x)=0. One can also verify that all three correction potentials become zero. This is not surprising since in this case the image approximation given by (29) or (34) should reduce to the image approximation for the case of a dielectric sphere immersed in a pure water solvent [19].

In addition, it should be mentioned that, although both correction potentials Φ_C2(r) and Φ_C3(r) are position-dependent, as demonstrated in Section 5, all correction terms to the reaction potentials at all observation points from all source charges still can be evaluated in O(N) operations. Here, N denotes the total number of charges in the simulated system. This means that, in principle, we can include as many terms as needed in the correction terms in order to get better/higher-order accuracy.

4 Discretization of the image line charges

Now let us show how to approximate each image line charge introduced in the previous section by a set of discrete image charges. The basic idea is to transform the underlying line integral for the potential for an image line charge onto the finite interval [−1, 1], and then apply appropriate Gauss or Gauss-Radau quadrature related to specific Jacobi polynomials. Without losing any generality, let us consider

$$I={\int }_{r_{\text{K}}}^{\infty }\hspace{0.17em}f\left(x\right)\hspace{0.17em}{\left(\frac{x}{r_{\text{K}}}\right)}^{-\sigma }\hspace{0.17em}\text{d}x,$$ (36)

Where σ > 0.

First, by introducing the change of variables r_K/x=((1−s)/2)^τ with τ > 0, we have

$$I=2^{-\tau \sigma }\tau {\int }_{-1}^1{\left(1-s\right)}^{\alpha }\hspace{0.17em}h\left(s,\tau \right)\text{d}s,$$ (37)

where α=τσ − 1 and

$$h\left(s,\tau \right)=\frac{2^{\tau }{r}_{\text{K}}}{{\left(1-s\right)}^{\tau }}\hspace{0.17em}\hspace{0.17em}f\hspace{0.17em}\left(\frac{2^{\tau }{r}_{\text{K}}}{{\left(1-s\right)}^{\tau }}\right).$$ (38)

Next, we shall employ a numerical quadrature to approximate the integral in (37). Note that s=−1 corresponds to the Kelvin image point x=r_K. Also α > −1 because σ > 0 and τ > 0. Therefore, we can choose either Gauss or Gauss-Radau quadrature based on Jacobi polynomials. More precisely, let s_m, ω_m, m=1, 2, …, M, be the Jacobi-Gauss or Jacobi-Gauss-Radau points and weights on the interval [−1, 1] with α=τσ − 1 and β=0 (s₁=−1 if Jacobi-Gauss-Radau quadrature is used.) Both s_m and ω_m can be obtained with the program ORTHPOL [36]. Then, the numerical quadrature for approximating the integral in (37) is

$$I\approx 2^{-\tau \sigma }\tau \sum _{m=1}^M{\omega }_{m}h\left(s_m,\tau \right)=2^{-\tau \sigma }\tau \sum _{m=1}^M{\omega }_m{x}_{m}f\left(x_m\right),$$ (39)

where for m=1, 2, …, M,

$$x_m=r_{\text{K}}\hspace{0.17em}{\left(\frac{2}{1-s_m}\right)}^{\tau }.$$ (40)

The parameter τ > 0 in the change of variables r_K/x=((1 − s)/2)^τ can be used as a parameter to control the accuracy of numerical approximations. In particular, when τ=1/σ we have α=0, and in this case the quadrature given by (39) simply reduces to the usual Gauss or Gauss-Radau quadrature.

4.1 Discretization of q_L1(x)

Note that

$${\int }_{r_{\text{K}}}^{\infty }\frac{q_{\text{L}1}\left(x\right)}{{\epsilon }_{\text{i}}\left|\text{r}-\text{x}\right|}\text{d}x={\int }_{r_{\text{K}}}^{\infty }\frac{{\delta }_{1}q}{{\epsilon }_{\text{i}}a\left|\text{r}-\text{x}\right|}\hspace{0.17em}{\left(\frac{x}{r_{\text{K}}}\right)}^{-{\sigma }_1}\hspace{0.17em}\text{d}x.$$

Recall that 0 < σ₁ < 1, and furthermore, when ε_i < ε_o/5, we have σ₁ > 1/2. Then using (39) with σ=σ₁ leads to

$${\int }_{r_{\text{K}}}^{\infty }\frac{q_{\text{L}1}\left(x\right)}{{\epsilon }_{\text{i}}\left|\text{r}-\text{x}\right|}\text{d}x\approx \sum _{m=1}^M\frac{q_m^{\text{L}1}}{{\epsilon }_{\text{i}}\left|\text{r}-{\text{x}}_m\right|},$$ (41)

Where for m=1, 2, …, M,

$$q_m^{\text{L}1}=2^{-\tau {\sigma }_1}\tau {\delta }_1{\omega }_m\frac{x_m}{a}q.$$ (42)

4.2 Discretization of q_L2(x)

Note that

$${\int }_{r_{\text{K}}}^{\infty }\frac{q_{\text{L}2}\left(x\right)}{{\epsilon }_{\text{i}}}\hspace{0.17em}\left(\frac{1}{\left|\text{r}-\text{x}\right|}-\frac{1}{x}\right)\hspace{0.17em}\text{d}x={\int }_{r_{\text{K}}}^{\infty }\frac{{\delta }_{2}q}{{\epsilon }_{\text{i}}a}\hspace{0.17em}\left(\frac{1}{\left|\text{r}-\text{x}\right|}-\frac{1}{x}\right)\hspace{0.17em}{\left(\frac{x}{r_{\text{K}}}\right)}^{{\sigma }_2}\hspace{0.17em}\text{d}x.$$ (43)

Recall that 0 < σ₂ < 1/2 when ε_i < ε_o. First it should be mentioned that the integrand decays faster than x^−3/2 so the integral converges, although the line charge q_L2(x) itself grows to infinity as x increases.

To use (39), we reformulate the right-hand side of (43) as

$${\int }_{r_{\text{K}}}^{\infty }\frac{{\delta }_{2}q}{{\epsilon }_{\text{i}}a}\hspace{0.17em}\left(\frac{1}{\left|\text{r}-\text{x}\right|}-\frac{1}{x}\right)\hspace{0.17em}\left(\frac{x}{r_{\text{K}}}\right)\hspace{0.17em}{\left(\frac{x}{r_{\text{K}}}\right)}^{-\left(1-{\sigma }_2\right)}\hspace{0.17em}\text{d}x.$$

Then applying (39) with σ=(1 − σ₂) > 1/2, we get

$${\int }_{r_{\text{K}}}^{\infty }\frac{q_{\text{L}2}\left(x\right)}{{\epsilon }_{\text{i}}}\hspace{0.17em}\left(\frac{1}{\left|\text{r}-\text{x}\right|}-\frac{1}{x}\right)\hspace{0.17em}\text{d}x\approx \sum _{m=1}^M\frac{q_m^{\text{L}2}}{{\epsilon }_{\text{i}}\left|\text{r}-{\text{x}}_m\right|}-\sum _{m=1}^M\frac{q_m^{\text{L}2}}{{\epsilon }_{\text{i}}{x}_m},$$ (44)

where for m=1, 2, …, M,

$$q_m^{\text{L}2}=2^{-\tau \left(1-{\sigma }_2\right)}\tau {\delta }_2{\omega }_m\hspace{0.17em}\left(\frac{x_m}{r_{\text{K}}}\right)\hspace{0.17em}\frac{x_m}{a}q.$$ (45)

Note that the second summation in the right-hand side of (44) is position-independent. Adding it to the position-independent correction potential Φ_C1 leaves us with a modified constant, position-independent correction potential

$${\overline{\Phi }}_{\text{C}1}={\Phi }_{\text{C}1}-\sum _{m=1}^M\frac{q_m^{\text{L}2}}{{\epsilon }_{\text{i}}{x}_m}.$$ (46)

4.3 Discretization of q_L1(x) and q_L2(x) by charges at the same locations

The discrete image charges defined in (42) and (45) are at different locations even when the same τ value is used in the change of variables. For computational efficiency, particularly when the image approximations are applied together with the FMM, one can choose to discretize q_L1(x) and q_L2(x) by point charges at the same locations, thus potentially cutting the number of discrete image charges in half. More specifically, one can choose a common parameter σ_c > 0 to rewrite the line charge q_L1(x) as

$$q_{\text{L}1}\left(x\right)=\frac{{\delta }_{1}q}{a}\hspace{0.17em}{\left(\frac{x}{r_{\text{K}}}\right)}^{{\sigma }_{\text{c}}-{\sigma }_1}\hspace{0.17em}{\left(\frac{x}{r_{\text{K}}}\right)}^{-{\sigma }_{\text{c}}},$$

and, at the same time, the right-hand side of (43) as

$${\int }_{r_{\text{K}}}^{\infty }\frac{{\delta }_{2}q}{{\epsilon }_{\text{i}}a}\hspace{0.17em}\left(\frac{1}{\left|\text{r}-\text{x}\right|}-\frac{1}{x}\right)\hspace{0.17em}{\left(\frac{x}{r_{\text{K}}}\right)}^{{\sigma }_{\text{c}}+{\sigma }_2}\hspace{0.17em}{\left(\frac{x}{r_{\text{K}}}\right)}^{-{\sigma }_{\text{c}}}\hspace{0.17em}\text{d}x.$$

Then using (39) with σ=σ_c leads to

$$q_m^{\text{L}1}=2^{-\tau {\sigma }_{\text{c}}}\tau {\delta }_1{\omega }_m\hspace{0.17em}{\left(\frac{x_m}{r_{\text{K}}}\right)}^{{\sigma }_{\text{c}}-{\sigma }_1}\frac{x_m}{a}q,$$ (47)

and

$$q_m^{\text{L}2}=2^{-\tau {\sigma }_{\text{c}}}\tau {\delta }_2{\omega }_m\hspace{0.17em}{\left(\frac{x_m}{r_{\text{K}}}\right)}^{{\sigma }_{\text{c}}+{\sigma }_2}\frac{x_m}{a}q.$$ (48)

The parameter σ_c > 0 is tunable for optimal computational efficiency. For example, depending on the value of u=λa, either of the two natural choices σ_c=σ₁ and σ_c=1 − σ₂ could perform better than the other.

In conclusion, in general we have the following fourth-order multiple discrete image approximations to the reaction potential inside the sphere in terms of the potentials of 2M + 1 point charges (or M + 1 point charges if a common parameter σ_c is utilized) and some correction potentials.

(a) A fourth-order multiple discrete image approximation:

$$\Phi \left(\text{r}\right)\approx \frac{1}{{\epsilon }_{\text{i}}}\hspace{0.17em}\left(\frac{q_{\text{K}}}{\left|\text{r}-{\text{r}}_{\text{K}}\right|}+\sum _{m=1}^M\frac{q_m^{\text{L}1}}{\left|\text{r}-{\text{x}}_m\right|}+\sum _{m=1}^M\frac{q_m^{\text{L}2}}{\left|\text{r}-{\text{x}}_m^{\prime }\right|}\right)+{\overline{\Phi }}_{\text{C}1}+{\Phi }_{\text{C}2}\left(\hspace{0.17em}\text{r}\right),$$ (49)

(b) An improved fourth-order multiple discrete image approximation:

$$\Phi \left(\text{r}\right)\approx \frac{1}{{\epsilon }_{\text{i}}}\hspace{0.17em}\left(\frac{q_{\text{K}}}{\left|\text{r}-{\text{r}}_{\text{K}}\right|}+\sum _{m=1}^M\frac{q_m^{\text{L}1}}{\left|\text{r}-{\text{x}}_m\right|}+\sum _{m=1}^M\frac{q_m^{\text{L}2}}{\left|\text{r}-{\text{x}}_m^{\prime }\right|}\right)+{\overline{\Phi }}_{\text{C}1}+{\Phi }_{\text{C}2}\left(\hspace{0.17em}\text{r}\right)+{\Phi }_{\text{C}3}\left(\text{r}\right).$$ (50)

5 Order N calculation of the image approximations

The main purpose for discrete image approximations to reaction fields is to apply existing fast methods for many-body problems directly in calculating the electrostatic interactions among N charges inside the spherical cavity in O(N logN) or even O(N) operations. Such fast algorithms include the O(N logN) hierarchical tree code- [37,38] or fast Fourier transform (FFT)-based algorithms [39,40], and the asymptotically optimal O(N) FMMs [41,42]. In particular, in this paper, we give a straightforward but far from optimal FMM-based O(N) implementation of the discrete image approximations.

For convenience, let ${\text{r}}_i^{\text{F}}=(x_i^{\text{F}},y_i^{\text{F}},z_i^{\text{F}}),\hspace{0.17em}i=1,2,\dots ,N$, be N observation points within the sphere, and ${\text{r}}_j^{\text{S}}\hspace{0.17em}=(x_j^{\text{S}},y_j^{\text{S}},z_j^{\text{S}}),\hspace{0.17em}j=1,2,\dots ,N$, be the locations of N source charges with charge strengths q₁, q₂, …, q_N. By the principle of linear superposition, the reaction field at an observation point ${\text{r}}_i^{\text{F}}$, in the case that the improved fourth-order multiple discrete image approximation (50) is employed, becomes

$$\begin{array}{ll}\hfill \Phi \left({\text{r}}_i^{\text{F}}\right)\hspace{0.17em}\approx & \frac{1}{{\epsilon }_{\text{i}}}\sum _{j=1}^N\hspace{0.17em}\left(\frac{q_{\text{K},j}}{\left|{\text{r}}_i^{\text{F}}-{\text{r}}_{\text{K},j}\right|}+\sum _{m=1}^M\frac{q_{m,j}^{\text{L}1}}{\left|{\text{r}}_i^{\text{F}}-{\text{x}}_{m,j}\right|}+\sum _{m=1}^M\frac{q_{m,j}^{\text{L}2}}{\left|{\text{r}}_i^{\text{F}}-{\text{x}}_{m,j}^{\prime }\right|}\right)\hfill \\ & +\sum _{j=1}^N{\overline{\Phi }}_{\text{C}1,j}+\sum _{j=1}^N{\Phi }_{\text{C}2,j}\left({\text{r}}_i^{\text{F}}\right)+\sum _{j=1}^N{\Phi }_{\text{C}3,j}\left({\text{r}}_i^{\text{F}}\right),\hfill \end{array}$$ (51)

where a quantity with a second subscript j designates the corresponding quantity associated with the source charge ${\text{r}}_j^{\text{S}}$, such as

$$\begin{array}{ccc}{q}_{\text{K},j}=\gamma \frac{a}{r_j^{\text{S}}}{q}_j,& r_{\text{K},j}=\frac{a^2}{r_j^{\text{S}}},& x_{m,j}=r_{\text{K},j}\hspace{0.17em}{\left(\frac{2}{1-s_m}\right)}^{\tau }.\end{array}$$

5.1 Order N calculation of the correction potentials

Obviously, the constant, position-independent correction potential

$$\sum _{j=1}^N{\overline{\Phi }}_{\text{C}1,j}=\sum _{j=1}^N\hspace{0.17em}\left[\frac{q_j}{{\epsilon }_{\text{i}}a}\hspace{0.17em}\left(C_0\left(u\right)-\gamma -\frac{{\delta }_1}{{\sigma }_1}\right)-\sum _{m=1}^M\frac{q_{m,j}^{\text{L}2}}{{\epsilon }_{\text{i}}{x}_{m,j}^{\prime }}\right]$$

can be evaluated in O(N) operations. The evaluation of the second correction potential in O(N) operations, however, needs special manipulation due to its position-dependence. Expressing the cosine of the angle θ between ${\text{r}}_i^{\text{F}}$ and ${\text{r}}_j^{\text{S}}$ in terms of their rectangular coordinates, we get

$$\sum _{j=1}^N{\Phi }_{\text{C}2,j}\left({\text{r}}_i^{\text{F}}\right)=\sum _{j=1}^N\frac{c_1{q}_j{r}_i^{\text{F}}}{r_{\text{K},j}}\hspace{0.17em}\left(\frac{x_i^{\text{F}}{x}_j^{\text{S}}+y_i^{\text{F}}{y}_j^{\text{S}}+z_i^{\text{F}}{z}_j^{\text{S}}}{r_i^{\text{F}}{r}_j^{\text{S}}}\right)\hspace{0.17em},$$ (52)

Where

$$c_1=\frac{1}{{\epsilon }_{\text{i}}a}\hspace{0.17em}\left(C_1\left(u\right)-\gamma -\frac{{\delta }_1}{1+{\sigma }_1}-\frac{{\delta }_2}{1-{\sigma }_2}\right).$$

Rearranging terms in (52) leads to

$$\sum _{j=1}^N{\Phi }_{\text{C}2,j}\left({\text{r}}_i^{\text{F}}\right)=d_1{x}_i^{\text{F}}+d_2{y}_i^{\text{F}}+d_3{z}_i^{\text{F}},$$

Where

$$\begin{array}{ccc}{d}_1=\frac{c_1}{a^2}\sum _{j=1}^N{q}_j{x}_j^{\text{S}},& d_2=\frac{c_1}{a^2}\sum _{j=1}^N{q}_j{y}_j^{\text{S}},& d_3=\frac{c_1}{a^2}\sum _{j=1}^N{q}_j{z}_j^{\text{S}}.\end{array}$$

Now it becomes clear that the second correction potential can be evaluated in O(N) operations. Analogously, the third correction potential can also be evaluated in O(N) operations. In fact, we have

$$\begin{array}{ll}\hfill \sum _{j=1}^N{\Phi }_{\text{C}3,j}\hspace{0.17em}\left({\text{r}}_i^{\text{F}}\right)\hspace{0.17em}=& e_1\hspace{0.17em}{\left(x_i^{\text{F}}\right)}^2+\hspace{0.17em}{e}_2\hspace{0.17em}{\left(y_i^{\text{F}}\right)}^2+e_3\hspace{0.17em}{\left(z_i^{\text{F}}\right)}^2\hfill \\ & +e_4{x}_i^{\text{F}}{y}_i^{\text{F}}+e_5{x}_i^{\text{F}}{z}_i^{\text{F}}+e_6{y}_i^{\text{F}}{z}_i^{\text{F}}+e_7\hspace{0.17em}{\left(r_i^{\text{F}}\right)}^2\hspace{0.17em},\hfill \end{array}$$

where

$$\begin{array}{ccc}{e}_1=\frac{3c_2}{2a^4}\sum _{j=1}^N{q}_j\hspace{0.17em}{\left(x_j^{\text{S}}\right)}^2,& e_2=\frac{3c_2}{2a^4}\sum _{j=1}^N{q}_j\hspace{0.17em}{\left(y_j^{\text{S}}\right)}^2,& e_3=\frac{3c_2}{2a^4}\sum _{j=1}^N{q}_j\hspace{0.17em}{\left(z_j^{\text{S}}\right)}^2,\\ e_4=\frac{3c_2}{a^4}\sum _{j=1}^N{q}_j{x}_j^{\text{S}}{y}_j^{\text{S}},& e_5=\frac{3c_2}{a^4}\sum _{j=1}^N{q}_j{x}_j^{\text{S}}{z}_j^{\text{S}},& e_6=\frac{3c_2}{a^4}\sum _{j=1}^N{q}_j{y}_j^{\text{S}}{z}_j^{\text{S}},\\ \multicolumn{3}{c}{e_7=-\frac{c_2}{2a^4}\sum _{j=1}^N{q}_j\hspace{0.17em}{\left(r_j^{\text{S}}\right)}^2\hspace{0.17em},}\end{array}$$

and

$$c_2=\frac{1}{{\epsilon }_{\text{i}}a}\hspace{0.17em}\left(C_2\left(u\right)-\gamma -\frac{{\delta }_1}{2+{\sigma }_2}-\frac{{\delta }_2}{2-{\sigma }_2}\right).$$

5.2 Order N calculation of the potentials of the image charges

The asymptotically optimal O(N) FMMs [41–44] are known to be very efficient in the evaluation of pairwise interactions in large ensembles of particles, such as expressions of the form

$$\begin{array}{cc}\Phi \left({\text{r}}_i\right)=\sum _{j=1,j\ne i}^N\frac{q_j}{|{\text{r}}_i-{\text{r}}_j|},& i=1,2,\dots ,N\end{array}$$

for the electrostatic potential, where r₁, r₂, …, r_N are points in R³ and q₁, q₂, …, q_N are the corresponding charge strengths. The large prefactor in O(N), however, makes the original FMM [41,42] less competitive (in three dimensions) for problems of current interest when compared to the tree code- or FFT-based methods. Later, a new version of FMM with an optimized prefactor was introduced for the Laplace equation [43]. Compared to the original FMM, a plane wave expansion-based diagonal translation operator is introduced, which dramatically reduces the prefactor in O(N) and thus makes the new version of FMM extremely efficient. For instance, in three dimensions a break-even point of N ≈ 500 for 3-digit accuracy has been numerically observed for the new version of FMM [43]. Further, an adaptive version of the new version of FMM for the Laplace equation in three dimensions is introduced [44] for applications with highly nonuniform charge distributions. The adaptive version still scales linearly in time and breaks even with the direct calculation at N ≈ 750 for 3-digit precision, N ≈ 1500 for 6-digit precision, and N ≈ 2500 for 9-digit precision, respectively [44]. However, the new version of FMM is more complicated than the original one in both programming and theory.

Recently, the new version of FMM was extended for screened Coulomb interactions in three dimensions [45]. By using this new version of FMM for the screened Coulomb interactions and a boundary integral equation approach to discretize the linearized Poisson-Boltzmann equation, an order N algorithm for the calculation of electrostatic interactions in biomolecular systems is developed [46]. Preliminary numerical experiments show that the overall break-even point becomes N ≈ 400 for 3-digit accuracy, and N ≈ 600 with 6-digit accuracy.

Using any FMM with O(N) computational complexity, the calculation of the potentials of the discrete image charges, namely,

$$\frac{1}{{\epsilon }_{\text{i}}}\sum _{j=1}^N\hspace{0.17em}\left(\frac{q_{\text{K},j}}{\left|{\text{r}}_i^{\text{F}}-{\text{r}}_{\text{K},j}\right|}+\sum _{m=1}^M\frac{q_{m,j}^{\text{L}1}}{\left|{\text{r}}_i^{\text{F}}-{\text{x}}_{m,j}\right|}+\sum _{m=1}^M\frac{q_{m,j}^{\text{L}2}}{\left|{\text{r}}_i^{\text{F}}-{\text{x}}_{m,j}^{\prime }\right|}\right)\hspace{0.17em},$$

for all observation points can be evaluated in O(N) operations in a straight-forward way. In the simplest implementation, such evaluation can be carried out with a single FMM run by including into the FMM cube all point image charges q_K,j at the conventional Kelvin image points r_K,j, all discrete image charges $q_{m,j}^{\text{L}1}$ at x_m,j, and all discrete image charges $q_{m,j}^{\text{L}2}$ at ${\text{x}}_{m,j}^{\prime }$, where all charges are taken as acting in a homogeneous medium of a dielectric constant ε_i In the case that the total potential is to be calculated, all original source charges are also included in the FMM cube.

In general, x_m and ${\text{x}}_m^{\prime }$ are different. To reduce the size of the FMM cube to achieve better computational efficiency, as described in Section 4.3, one can choose to approximate both line charges q_L1(x) and q_L2(x) by discrete image charges at the same locations. This way the discrete point charges for the two image line charges can be combined together, significantly reducing the FMM cube's size by a percentage of M/(1 + 2M).

Remark 1 (Local expansions of farther image charges)

The introduced discrete image charges outside the sphere will result in a large computational domain and the image charges are highly nonuniformly distributed, particularly because the image charges of those source charges close to the center of the sphere are far away from the spherical boundary. Therefore, direct application of the FMM by including all image charges in this large computational box is not efficient. Instead, a simple but more efficient way would be to calculate the local expansion due to the far field image charges directly inside the sphere. This way, we achieve not only a smaller FMM box but also a smaller number of total charges in the box.

More specifically, in practice we could introduce a bigger cut-off sphere of radius κa centered at the origin with κ > 1. The calculation of the potentials inside the original dielectric sphere due to those image charges inside this cut-off sphere is still carried out by the chosen fast method. For all image charges outside this cut-off sphere at (ρ_l, α_l, β_l), l=1, 2 …, L, with charge strengths ${\widehat{q}}_l,l=1,2,\dots ,q_L$, the calculation of the potential at r=(r, θ, φ) inside the dielectric sphere generated by these image charges can be described by a local expansion

$$\Phi \left(\text{r}\right)\approx \sum _{j=0}^p\sum _{k=-j}^j{\text{L}}_j^k\hspace{0.17em}·\hspace{0.17em}{\text{Y}}_j^k\left(\theta ,\phi \right)\hspace{0.17em}·\hspace{0.17em}{r}^j,$$ (53)

where ${\text{Y}}_j^k\left(\theta ,\phi \right)$ are the spherical harmonics, and ${\text{L}}_j^k$ are the local expansion coefficients given by

$${\text{L}}_j^k=\sum _{l=1}^L{\widehat{q}}_l\hspace{0.17em}·\hspace{0.17em}\frac{Y_j^{-k}\left({\alpha }_l,{\beta }_l\right)}{{\rho }_l^{j+1}}.$$ (54)

Furthermore, for any p ≥ 1,

$$\left|\Phi \left(\text{r}\right)-\sum _{j=0}^p\sum _{k=-j}^j{\text{L}}_j^k\hspace{0.17em}·\hspace{0.17em}{\text{Y}}_j^k\left(\theta ,\phi \right)\hspace{0.17em}·\hspace{0.17em}{r}^j\right|\le \left(\frac{{\sum }_{l=1}^L\left|{\widehat{q}}_l\right|}{\kappa a-r}\right)\hspace{0.17em}{\left(\frac{r}{\kappa a}\right)}^{p+1}.$$ (55)

6 Numerical results

For demonstration purpose, let us consider a unit dielectric sphere. The dielectric constants of the sphere and its surrounding medium are assumed to be ε_i=2 (normally 1, 2 or 4) and ε_o=80 (the dielectric constant of water), respectively. Unless otherwise specified, the results obtained by the direct series expansion with 400 terms are treated as the exact reaction fields to calculate the errors of the fourth-order image approximations.

6.1 Accuracy vs the ionic strength

Let us begin by verifying the convergence properties of the proposed image approximations. To this end, let us consider a single point charge located on the x-axis inside the sphere at a distance r_S=0.5 from the center of the sphere. Different σ values are used to approximate the underlying image line charges, but for simplicity, we always choose τ=1/σ and M=30 so that the same Gauss quadrature points and weights s_m and ω_m are involved. For each selected value of u=λa, we calculate the relative error of the image approximations in the reaction field, respectively, at 10, 000 observation points uniformly distributed (under the polar coordinates) within the unit disk that contains the x-axis. The maximum relative error ‖ E ‖ at the 10, 000 observation points for various u values and the corresponding order of convergence are shown in Table I. For sake of comparison, the results obtained using the first- and the second-order image approximations are also included. As can be observed, the results clearly demonstrate the O(u⁴) convergence property of the fourth-order image approximations.

Table I.

Convergence properties of the proposed image approximations.

	1st-order		2nd-order		4th-order		Impr. 4th-order
u	‖ E ‖	Order	‖ E ‖	Order	‖ E ‖	Order	‖ E ‖	Order
0.8	1.33E-2		3.45E-3		1.92E-4		2.13E-5
0.4	9.54E-3	0.48	1.29E-3	1.42	1.54E-5	3.64	1.42E-6	3.91
0.2	5.94E-3	0.68	4.02E-4	1.69	1.10E-6	3.80	9.14E-8	3.96
0.1	3.35E-3	0.82	1.12E-4	1.84	7.51E-8	3.88	6.03E-9	3.92
0.05	1.79E-3	0.91	2.97E-5	1.92	6.00E-9	3.64	4.97E-9

6.2 Accuracy vs the source location

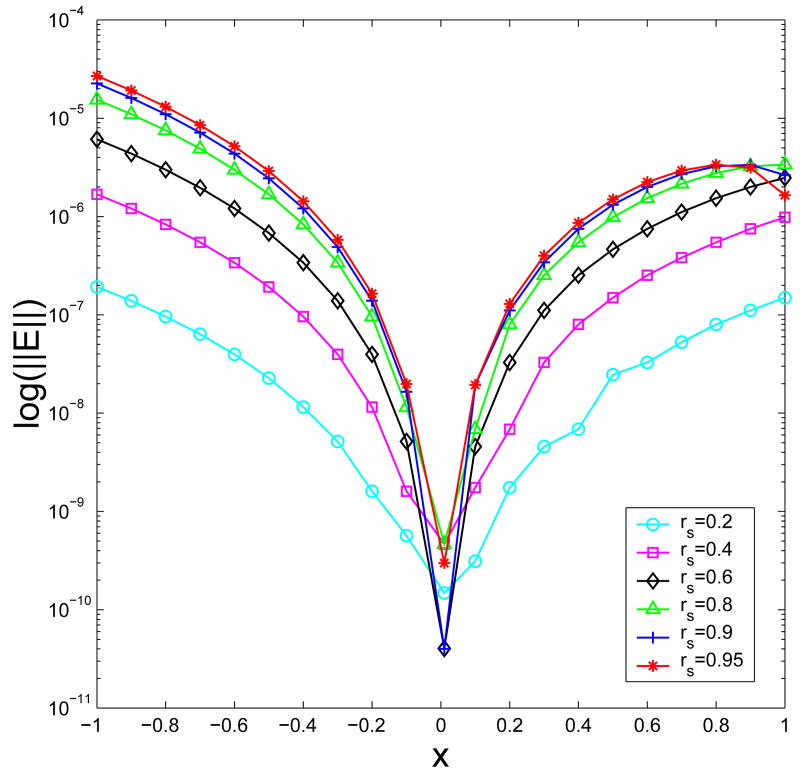
From now on, we shall confine ourselves to the improved fourth-order image approximation. Let us first investigate the dependence of its accuracy on the source location. To this end, in this test the inverse Debye screening length is set as λ=0.5, and the Gauss quadrature with M=30 is employed to approximate the underlying image line charges. For each selected source position, we calculate the relative error of the improved fourth-order image approximation in the reaction field, respectively, at 21 observation points equally spaced on the x-axis, from −1 to 1. The results are displayed in Fig. 4. As can be seen, the approximation error increases as the source charge moves to the spherical boundary while the observation point is fixed, or similarly as the observation point moves to the spherical boundary while the source location is fixed. In addition, for all cases where r_S ≤ 0.95, the relative error in the reaction potential is less than 10⁻⁴. It should be pointed out that, 400 terms in the series expansion could be insufficient to get accurate enough “exact reaction fields” at those observation points close to the spherical boundary, which explains the abnormal error behaviors near the spherical boundary.

Fig. 4.

The relative errors of the improved fourth-order image approximation in the reaction field at 21 observation points equally spaced on the x-axis, from −1 to 1, for six different source locations.

6.3 Direct series expansion vs the improved fourth-order image approximation

In the case that the source charge is close to the spherical boundary, the Kelvin image point r_K is close to the boundary as well. Therefore, when calculating the reaction field at an observation point also close to the spherical boundary, the convergence by the direct series expansion

$${\Phi }_{\text{RF}}\left(\text{r}\right)=\frac{q}{{\epsilon }_{\text{i}}a}\sum _{n=0}^{\infty }\frac{{\epsilon }_{\text{i}}\left(n+1\right)k_n\left(u\right)+{\epsilon }_{\text{o}}u{k}_n^{\prime }\left(u\right)}{{\epsilon }_{\text{i}}n{k}_n\left(u\right)-{\epsilon }_{\text{o}}u{k}_n^{\prime }\left(u\right)}\hspace{0.17em}{\left(\frac{r}{r_{\text{K}}}\right)}^n\hspace{0.17em}{P}_n\left(cos\theta \right)$$

shall be slow due to r/r_K ≈ 1, requiring a great number of terms to achieve high accuracy in the reaction field.

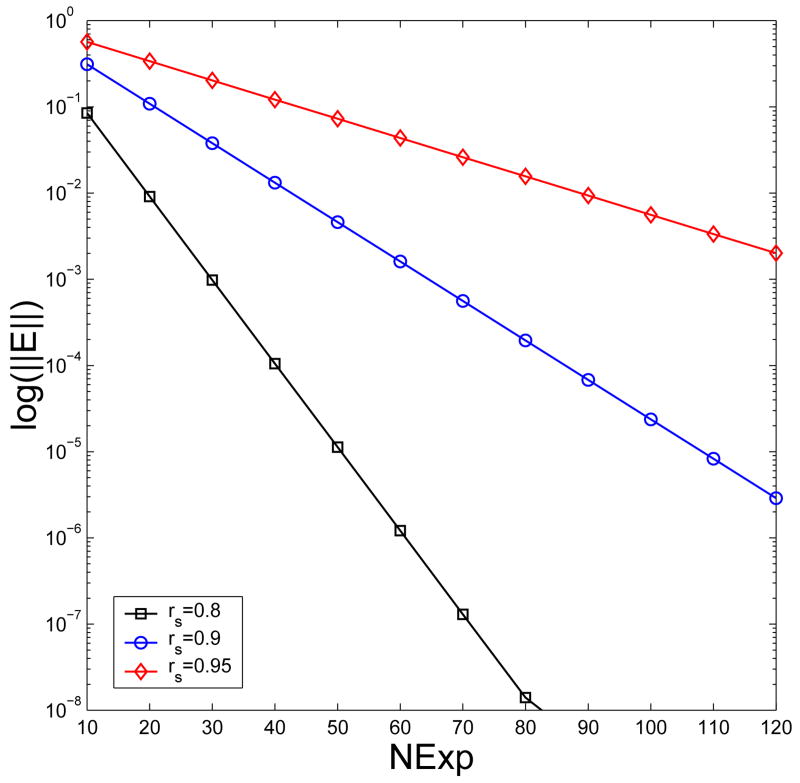
To compare the method of direct series expansion and the improved fourth-order multiple discrete image approximation, in this test the inverse Debye screening length is again fixed at λ=0.5, while the Gauss quadrature with M=3 and a common parameter σ_c=σ₁ is used to discretize the two line charges. Three different source locations with r_S=0.8, 0.9 and 0.95 are tested, respectively. For each selected source location, we approximate the reaction fields at the same 10,000 observation points as mentioned in Section 6.1 by the direct series expansion with various numbers of terms, compare the results to the exact ones obtained by the direct series expansion with 400 terms, calculate and plot in Fig. 5 the maximum relative errors. As indicated, more than 30, 65 and 130 terms have to be included for the approximation error to be less than 10⁻³ for the cases of r_S=0.8, 0.9 and 0.95, respectively. On the other hand, the corresponding errors of the improved fourth-order multiple discrete image approximation with a total of 4 point image charges (including the image charge at the Kelvin image point) are 6.50×10⁻⁴, 7.67×10⁻⁴, and 8.28×10⁻⁴, respectively, all less than 10⁻³ already! Therefore, to calculate reaction fields at points close to the spherical boundary due to source charges also close to the boundary, the improved fourth-order image approximation is clearly much more efficient than the method of direct series expansion.

Fig. 5.

The maximum relative errors of the method of direct series expansion in the reaction field at 10,000 observation points within the sphere for three different source locations, where NExp denotes the number of terms included in the expansion.

6.4 Accuracy vs the number of discrete image charges

One natural concern with the proposed multiple discrete image approximations is the final number of discrete image charges required to achieve certain order of degree of accuracy. For a desired accuracy, this number depends on the locations of both the source charge and the observation point. It should be small if compared to the number of terms needed to achieve the same degree of accuracy in the direct series expansion to make the image approximations useful in the practice.

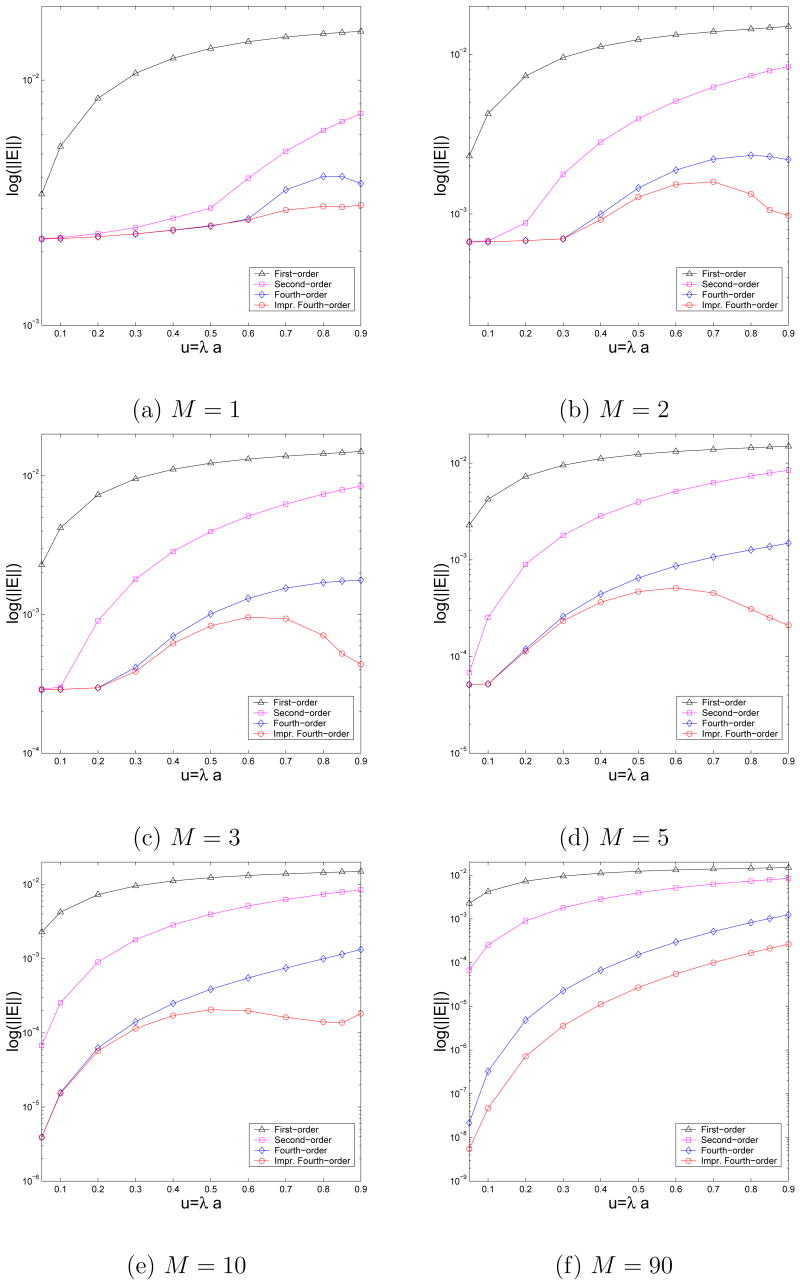
In this test, the source location is fixed at r_S=0.95, while the Gauss quadrature with a common parameter σ_c=σ₁ is used again to discretize the image line charges. For each selected value of u=λa ranging from 0.05 to 0.9, we approximate the reaction fields at the same 10,000 points within the sphere by the improved fourth-order image approximation with various numbers of discrete image charges. The maximum relative errors are plotted in Fig. 6. Once again, for sake of comparison, the corresponding error analysis results for the first-, the second-, and the original fourth-order image approximations are also included. As can be seen, for this particular choice of the parameter σ_c, three to four image charges including the image point charge at the Kelvin image point (M=2 or 3) are sufficient for the improved fourth-order multiple discrete image approximation to achieve a 10⁻⁴ relative accuracy.

Fig. 6.

Accuracy of the image approximations to the ionic solvent induced reaction field due to a source charge inside the unit sphere at distance r_S=0.95 from the center. The total number of discrete image charges is M + 1.

6.5 Computational complexity of FMM-accelerated image approximations

To investigate the computational complexity of the image approximations in conjunction with the FMM, the improved fourth-order image approximation described in Section 5 has been implemented simply by using the free software FastLap, a general FMM-accelerated solver for Laplace problems [47]. We assume that the observation points are distributed randomly but uniformly inside the whole sphere. The experiments are carried out on a Dell OptiPlex GX280 workstation with a CPU clock rate of 3GHz and a memory of 2GB.

In Table II, timing results of the FMM calculation of the reaction field are reported and compared to those obtained without the FMM acceleration. The expansion order and the partitioning level in the FMM calculation are set to be 2 and 9, respectively. The Gauss quadrature with M=2 and a common parameter σ_c=σ₁ is used to construct discrete image charges, so for each source charge, in total there are three discrete image charges. Also, u=λa=0.5. As can be seen, the timing scales as O(N²) without using the FMM, but linearly with the FMM. Note that in Table II, NP denotes the number of observation points, and NC the number of total discrete image charges included in the FMM cube, respectively.

Table II.

CPU time in seconds.

NP	NC	With FMM	No FMM
5,000	15,000	11.6	2.1
10,000	30,000	13.2	8.5
20,000	60,000	14.5	34.5
40,000	120,000	20.4	138.4

Remark 2

As shown in Table II, although the current implementation of the image approximations using the original FMM-based FastLap scales linearly in time, it breaks even at NC > 30, 000, which appears to be disappointing. One reason is that the original FMM, although asymptotically optimal O(N), has a very large prefactor in O(N). Another reason is that, although the original source charges are uniformly distributed inside the dielectric sphere, the distribution of the image charges are highly nonuniform outside the sphere, a case that FastLap is not designed for. Therefore, we believe much better computational efficiency such as a much smaller break-even point can be achieved if we (1) calculate the local expansion due to the far field image charges directly inside the dielectric sphere, as suggested in Remark 1, and (2) use the adaptive version of the new version of FMM [44] or even just the pre-corrected FFT [40] to calculate the potential due to the near field image charges. As a matter of fact, implementation of the two proposed techniques is under the way, and any significant progresses in this direction will be reported in future publications.

7 Conclusions

In this paper, we have presented two fourth-order discrete image approximations to the reaction field due to a point charge inside a dielectric sphere immersed in an ionic solvent for small values of u=λa (λ - the inverse Debye screening length of the ionic solvent, a - the radius of the dielectric sphere). Numerical results have demonstrated that only three to four discrete image charges are needed for the improved fourth-order image approximation to achieve a 10⁻⁴ relative accuracy in the reaction field. Furthermore, using the FMM, the image approximations presented in this paper require only O(N) work for calculating electrostatic interactions for N source charges in a dielectric sphere immersed in an ionic solvent.