The Tetrad-Pollen Model Fails to Explain the Bias in Mendel's Pea (Pisum sativum) Experiments

Abstract

For >40 years, geneticists and science historians have appealed to the tetrad-pollen model as an explanation of the bias toward expectation in Mendel's data, albeit without experimental support. Our experiments demonstrate that pollen sampling during self-pollination in pea conforms to the binomial distribution with no evidence of a tetrad-pollen effect.

THE bias toward expectation in Gregor Mendel's pea (Pisum sativum L.) experiments has generated controversy for more than a century. The first to notice the bias was Weldon (1902), who subjected Mendel's data to statistical analyses, including the recently developed chi-square test, and concluded that the data were exceptionally close to expectation. However, it was Fisher (1936) who instigated the modern controversy with his often-quoted conclusion that “the data of most, if not all, of the experiments have been falsified so as to agree closely with Mendel's expectation” (Fisher 1936, p. 132). Fisher was reluctant to ascribe the alleged data falsification to Mendel, attributing it instead to a supposed assistant. In 1965, the Mendel centenary year, a series of papers on the topic kindled an impassioned debate that has continued unabated, including recent publications in Genetics (Myers 2004; C. E. Novitski 2004; E. Novitski 2004; Hartl and Fairbanks 2007).

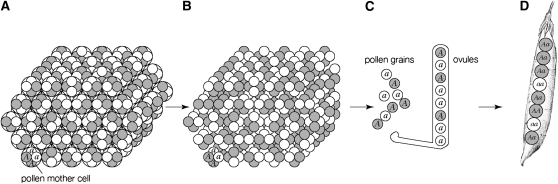
Among the most cited explanations of the bias that do not imply data falsification is the tetrad-pollen model. In flowering plants, meiosis take place in each pollen mother cell to produce a tetrad of four haploid nuclei. The plant ultimately produces four pollen grains from each tetrad. In a heterozygous plant, two of these pollen grains carry one allele and two carry the other allele, resulting in a perfect 1:1 ratio of alleles. According to the model, when anthers in heterozygous pea plants dehisce within the unopened flower, the four pollen grains derived from each tetrad remain spatially juxtaposed, resulting in a nonrandom spatial distribution of alleles, somewhat akin to a three-dimensional checkerboard. At dehiscence, the stigma samples pollen grains without replacement from a limited, nonrandomly distributed population. In such a situation, sampling of one allele increases the probability of sampling the other allele, resulting in distributions of pollen grains biased toward a 1:1 ratio when compared to the binomial distribution. The resulting F₂ segregation ratios then more closely approximate the expected 3:1 ratio than predicted by the binomial distribution (Figure 1).

Figure 1.—

Simplified depiction of the tetrad-pollen model. Cells (or nuclei) carrying a dominant allele (A) are shaded and those carrying a recessive allele (a) are open. (A) In the anthers of a heterozygous plant, each pollen mother cell contains a tetrad with a 2:2 distribution of alleles. (B) When pollen grains mature, their spatial distribution remains relatively uniform, essentially the same as in the pollen mother cells. (C) Pollen grains are sampled without replacement from a limited region, possibly, in some cases, from the same tetrad, biasing the distribution toward a 1:1 ratio. (D) The distribution of F₂ individuals within pods is biased more toward a 3:1 ratio than predicted by the binomial distribution.

Sturtevant (1965) and Beadle (1967) were the first to propose the tetrad-pollen model. Beadle concluded, “some years ago Professor Sturtevant and I explored this possibility to see if it was sufficient to account for the apparent bias. It works in the right direction but is not sufficient” (Beadle 1967, p. 337). Sturtevant (1965) published a similar conclusion regarding the insufficiency of the model but neither he nor Beadle provided the relevant calculations.

Thoday (1966) also appealed to the tetrad-pollen model to explain the bias in Mendel's data, stating, “unless therefore the number of pollen grains is vastly in excess of the number of ovules and the many tetrads are thoroughly randomised, we expect ratios that are better than Fisherian” (p. 122). Weiling (1971) claimed that “the variance of the ratios of A- and a-cells is not that of a binomial distribution,” and that as a consequence “the segregation ratios of the dominant and recessive plants should also have a smaller variance than that of the binomial distribution” (p. 76). Other authors have since highlighted these earlier references to the tetrad-pollen model (Campbell 1976; Olby 1985; Edwards 1986; Orel 1996; Seidenfeld 1998; Fairbanks and Rytting 2001; Franklin et al. 2008).

In spite of these multiple references to the tetrad-pollen model spanning a period of >40 years, the model remains entirely founded on hypothesis with no experimental evidence. However, as Fairbanks and Rytting (2001) pointed out, the tetrad-pollen model can be experimentally tested in the pea plant. All peas within a single pod result from the same set of pollen sampling events. Thus, if the tetrad-pollen model has an appreciable effect, it should be detectable as a significant deviation from the binomial distribution for phenotypes of F₂ seeds (or plants derived from them) within pods, with an excess of pods containing combinations with higher probabilities. This note presents the results of experiments designed to detect such a deviation.

We selected flower color as the phenotype for examination to exclude unconscious bias on the part of the experimenter. Plants with colored or white flowers are readily distinguished with no ambiguity, and a pleiotropic effect of presence or absence of anthocyanin pigmentation in the axils of the stipules is evident at multiple positions in the plant before flowering, permitting straightforward classification of plants that have not flowered. Moreover, because this phenotype must be examined in growing plants, the phenotypes of poorly developed seeds are not subject to experimenter bias because only those seeds that germinate and develop into whole plants are scored.

In our experiment, the paternal parent was the purple-flowered genotype Wt 10006 (kindly provided by W. K. Święcicki) and the maternal parent, the white-flowered variety “Green Arrow” (purchased locally). Parental plants were grown in the Brigham Young University greenhouses, and F₁ and F₂ plants were grown at the Brigham Young University Spanish Fork Experiment Farm under irrigation. F₂ seeds grouped by pods from F₁ plants were planted in hill plots and F₂ plants were scored for flower color, or for axillary pigmentation in plants that had not flowered. To ensure that each F₂ plant was scored separately, plants from each hill plot were fully unearthed and separated by the roots prior to scoring.

A total of 5204 F₂ plants from 973 pods were scored and the data were compiled as observed combinations of purple- and white-flowered plants from seeds grouped within pods (Table 1). Pearson's chi-square analysis, derived from logistic regression with a null hypothesis of a binomial distribution based on a 3:1 ratio, generated a chi-square value of 1003.58 with 973 degrees of freedom, and an associated probability of 0.2415, which is not significant. Interestingly, the summed data of the entire experiment were exceptionally close to a 3:1 ratio (3899:1305, χ² = 0.0164, 1 d.f., P = 0.8981). An earlier and smaller experiment with seed shape and seed color (similar to Mendel's dihybrid experiment) analyzed by logistic regression likewise displayed no evidence of a deviation from the binomial model (χ² = 208.5048, 216 d.f., P = 0.6181). These phenotypes may be subject to experimenter bias when classifying questionable individuals and excluding poorly developed seeds, as Mendel noted in his paper (Mendel 1866; Fairbanks and Rytting 2001). Nonetheless, the results of this experiment are consistent with those of the larger experiment with a more reliable phenotype.

TABLE 1.

Distribution of phenotypes partitioned by pods

Plants per pod	Purple flowered (pigmented axils)	White flowered (pigment-free axils)	Observed	Binomial expectation
1	0	1	6	6.25
1	1	0	19	18.75
2	0	2	5	3.13
2	1	1	16	18.75
2	2	0	29	28.13
3	0	3	2	1.64
3	1	2	19	14.77
3	2	1	39	44.30
3	3	0	45	44.30
4	0	4	1	0.50
4	1	3	4	6.05
4	2	2	33	27.21
4	3	1	49	54.42
4	4	0	42	40.82
5	0	5	1	0.18
5	1	4	3	2.67
5	2	3	17	16.00
5	3	2	43	47.99
5	4	1	79	71.98
5	5	0	39	43.19
6	0	6	0	0.05
6	1	5	0	0.91
6	2	4	4	6.79
6	3	3	32	27.16
6	4	2	56	61.11
6	5	1	64	73.33
6	6	0	50	36.66
7	0	7	0	0.01
7	1	6	0	0.19
7	2	5	3	1.72
7	3	4	9	8.59
7	4	3	23	25.78
7	5	2	41	46.41
7	6	1	58	46.41
7	7	0	15	19.89
8	0	8	0	0.00
8	1	7	0	0.03
8	2	6	0	0.35
8	3	5	1	2.10
8	4	4	6	7.87
8	5	3	26	18.90
8	6	2	30	28.34
8	7	1	17	24.30
8	8	0	11	9.11
9	0	9	0	0.00
9	1	8	0	0.00
9	2	7	0	0.04
9	3	6	0	0.25
9	4	5	2	1.13
9	5	4	6	3.39
9	6	3	7	6.77
9	7	2	7	8.71
9	8	1	6	6.53
9	9	0	1	2.18
10	0	10	0	0.00
10	1	9	0	0.00
10	2	8	0	0.00
10	3	7	0	0.02
10	4	6	0	0.11
10	5	5	0	0.41
10	6	4	1	1.02
10	7	3	4	1.75
10	8	2	1	1.97
10	9	1	1	1.31
10	10	0	0	0.39

According to the analyses of experimental results presented here, there is no evidence that the tetrad-pollen model explains any of the bias in Mendel's experiments.