Quantifying Evidence for Candidate Gene Polymorphisms: Bayesian Analysis Combining Sequence-Specific and Quantitative Trait Loci Colocation Information

Abstract

We calculate posterior probabilities for candidate genes as a function of genomic location. Posterior probabilities for quantitative trait loci (QTL) presence in a small interval are calculated using a Bayesian model-selection approach based on the Bayesian information criterion (BIC) and used to combine QTL colocation information with sequence-specific evidence, e.g., from differential expression and/or association studies. Our method takes into account uncertainty in estimation of number and locations of QTL and estimated map position. Posterior probabilities for QTL presence were calculated for simulated data with n = 100, 300, and 1200 QTL progeny and compared with interval mapping and composite-interval mapping. Candidate genes that mapped to QTL regions had substantially larger posterior probabilities. Among candidates with a given Bayes factor, those that map near a QTL are more promising for further investigation with association studies and functional testing or for use in marker-aided selection. The BIC is shown to correspond very closely to Bayes factors for linear models with a nearly noninformative Zellner prior for the simulated QTL data with n ≥ 100. It is shown how to modify the BIC to use a subjective prior for the QTL effects.

A quantitative trait locus (QTL) is a location or small region in the genome associated with variation in a quantitative (i.e., continuously variable) trait. QTL are mapped by statistical analysis of marker–trait associations within a QTL mapping family or pedigree. The accuracy of QTL-mapping location estimates is typically of the order of tens of centimorgans, considerably narrowing down the location of possible functional loci, but not enough for brute force sequencing to locate genes. Hence there is the need to combine QTL mapping with other evidence. In this article we combine evidence for candidate polymorphisms with QTL-mapping data, using the posterior probabilities for the candidate polymorphisms as priors for the QTL analysis.

Evidence for candidate polymorphisms can be obtained from various sources: e.g., from assays of differential expression between tissue types or between genotypes using microarrays, from homology with genes in other species where there is evidence for effects on the corresponding trait, from genes mapping to a QTL region in another species, from polymorphisms in genes coding for proteins in a biosynthetic pathway, from an association study, or from a combination of these sources.

Quantifying the evidence from all of these possible sources would be a large undertaking, with many evaluations particular to specific cases. To limit the scope of this article we assume candidate genes are given, and the evidence is quantified in the form of posterior probabilities and/or Bayes factors. Candidates could also be selected using QTL data (e.g., in a genome-scan approach), in which case the method of this article would not apply unless further independent QTL data were available to assess the QTL colocation.

Information from these sources often represents only weak or moderately strong evidence; e.g., ∼4000 candidate polymorphisms were differentially expressed for wood density (S. Cato, personal communication). Since prior odds for a random candidate gene are low (e.g., 1/3000 if there are 30,000 genes and 10 affecting the trait), further evidence is needed to justify the expense of functional testing, and to most effectively select candidates for testing, or for marker-aided selection applications.

In this article we quantify the additional evidence for a candidate gene from QTL colocation: this is based on the estimated map location of the candidate and QTL regions identified using independent data from a QTL-mapping pedigree. Our approach requires Bayesian posterior probabilities for a QTL to be present in a small genomic interval. To motivate the approach we first discuss possible alternative QTL-mapping approaches, both Bayesian and non-Bayesian.

Non-Bayesian QTL mapping:

A candidate gene is often considered to colocate with a QTL if the estimated candidate gene locus falls within a 95% confidence interval for QTL location. Various methods have been used to estimate confidence intervals for QTL location: the region around a peak where the interval-mapping LOD score (Lander and Botstein 1989) drops by less than a certain number, a method based on the sampling variation in estimated QTL location under bootstrap resampling (Visscher et al. 1996), and a method using the empirical formula of Darvasi and Soller (1997).

All of these methods have shortcomings. What LOD drop-off to use in a given situation is not clear and the graph of LOD scores may not even be unimodal due to artificial peaks in the likelihood ratio between markers. Bootstrap methods have been reported as giving different answers and inexact confidence-interval coverage (Bennewitz et al. 2002). Manichaikul et al. (2006) found that, when marker density is not high, bootstrap confidence intervals based on maximum-likelihood estimates of QTL location can be unstable due to the strong tendency of the maximum-likelihood estimate to occur at a marker, while Bayesian credible intervals exhibited stable coverage on the same simulated data. The Darvasi and Soller (1997) estimate (Equation 42 below) is based on the size of QTL effects. Unless power is high to detect the true size of effect, selection bias and sampling error in estimates of QTL effects will result in large errors in confidence-interval widths.

A more fundamental limitation of all the confidence-interval methods is that they condition on the existence of a single QTL in a region. For example, the interval-mapping LOD score is, up to an unknown constant, approximately the log-posterior distribution of QTL location assuming existence of a single QTL in a region (Sen and Churchill 2001); hence it cannot be used to infer the number of QTL. As we shall see, results can be misleading if there are two QTL when one is assumed or vice versa.

To limit the scope of this article we compare only the Darvasi and Soller confidence intervals with posterior probabilities from Bayesian model selection.

Bayesian QTL mapping:

The main advantage of the Bayesian approach in this context is that the required probabilities can be obtained directly, using a Bayesian model selection approach, where multiple models are considered according to their probabilities. In Bayesian model selection approaches (reviewed by Sillanpää and Corander 2002), inference is based on the total posterior probability of models satisfying a given property, and estimation is based on model averaging, averaging over estimates of effects from each model, weighted according to the posterior probability for models. Ball (2001) used a Bayesian model selection approach for QTL mapping where each model is a linear regression model for the trait as a function of a fixed set of markers, and approximate posterior probabilities for models were calculated using a modified Bayesian information criterion (BIC) (previously used by Broman 1997 and Broman and Speed 2002 to select a single model).

This approach can be used to infer the genetic architecture: for example, the posterior probability that there are two QTL on a chromosome is the sum of probabilities for models with two selected markers on that chromosome (Ball 2001; Yandell et al. 2002). Interactions (dominance and epistasis) can be allowed for simply by specifying the appropriate prior probabilities for interaction terms (Ball 2001; Bogdan et al. 2004).

The BIC is easily and rapidly calculated from standard regression model statistics, but is based on an asymptotic approximation. Alternatives include MCMC methods and analytical calculations. Posterior probabilities for individual models can be obtained in closed form if the Zellner priors are used (Smith and Kohn 1996; Sen and Churchill 2001). In fact, using the BIC is approximately equivalent to using the Bayes factors calculated using the Zellner prior with prior information equivalent to a single sample point [c = n in (18) below]. Hence closed-form calculations can be used as a check on the accuracy of the BIC approximation.

Interval mapping and composite-interval mapping likelihood-ratio statistics are for comparing a model with a single QTL vs. the null model, corresponding to a null hypotheses of no QTL anywhere. These methods test for the presence of a linked QTL but we need a test for a QTL at a specific location. To quantify the evidence for a polymorphism at locus x, we define a Bayes factor, B_Q(x), as the limiting case of the Bayes factor for testing the hypothesis of a QTL in a small interval (x, x + δx) vs. no QTL in the small interval. The possibility of QTL at other locations, possibly on the same chromosome, is allowed for in our null hypothesis. The Bayes factor, B_Q(x), is combined with prior probability and Bayes factor for a candidate gene to obtain an expression for the posterior probability for a candidate polymorphism at x to be functional. The posterior probability is then integrated over x to incorporate uncertainty in map position.

The rest of this article is structured as follows. The methods section contains five parts: (1) showing how to incorporate QTL colocation given posterior probabilities for QTL presence, (2) computing posterior probabilities for QTL presence using the Bayesian model-selection approach from Ball (2001), (3) introducing the Zellner priors and describing how closed-form calculations with these priors can be used to check on the accuracy of the BIC, (4) describing the data simulation, and (5) showing how to incorporate subjective prior information on the sizes of QTL effects into the BIC. In the results section a worked example is given on the basis of a published candidate gene in Eucalyptus spp. colocating with simulated QTL data: effects of QTL colocation are demonstrated for three simulated QTL data sets with different sample sizes, 12 chromosomes with 0 or 1 QTL or with two QTL in coupling or repulsion; and the BIC is compared to closed-form calculations of the log Bayes factors with Zellner priors on the coefficients.

METHODS

Incorporating QTL colocation information:

It follows from Bayes' theorem that the prior odds for a hypothesis are multiplied by the Bayes factor to give the posterior odds. Without QTL colocation information the posterior odds for a candidate gene are:

(1)

where p_c = Pr(H₁ | y_c) is the posterior probability for the candidate to represent a functional trait locus, and B_c is the Bayes factor representing the strength of evidence for H₁ over H₀ in the data for the candidate gene, denoted by y_c.

Now suppose we have independent data, denoted by y_q, from a QTL mapping pedigree. It follows easily from Bayes' theorem that, when analyzing multiple independent data sets, the posterior for the first data set can be used as the prior for the second data set, giving the same posterior as if the combined data were analyzed jointly. Thus we can use the posterior from the candidate gene data, y_c, as prior information for the analysis of the QTL data, y_q.

Note that, almost by definition, a candidate polymorphism at location x is a functional locus if, and only if, there is a QTL at x.

To combine candidate gene and QTL colocation evidence, we first consider the posterior for QTL in a small interval, I, in the absence of candidate gene information, then by comparing prior and posterior probabilities obtain the strength of evidence B_Q(I) for a QTL in I, and then combine this with evidence from the candidate gene data, giving posterior probabilities of H₁ for any given I containing the candidate.

Let p_Q(x) be defined by

(2)

where probabilities are posterior probabilities given y_q. Let π_Q(x) be defined similarly but with respect to the prior distribution. We refer to p_Q(x) as the probability intensity for QTL presence, i.e., the probability of finding a QTL in (x, x + dx) per unit change in x. Note that p_Q(x) is not the probability density for QTL location, and 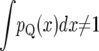: a probability density for QTL location entails the assumption that there is exactly 1 QTL within a region. Here the number of QTL is unknown, and we allow for the possibility of 0, 1, or multiple QTL.

Let π_Q(I), p_Q(I) be the prior and posterior probabilities for a QTL to be present in a small interval I. Ignoring y_c, the Bayes factor for a QTL to be located in I is given by

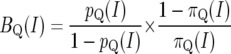(3)

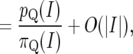(4)

where |I| denotes the width of the interval I. The approximation in (3) is good for small I since and 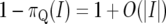. In the limit as 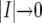, we obtain

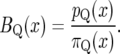(5)

To incorporate QTL colocation information, we replace the prior odds in (3) by the posterior odds from (1) and solve for the posterior odds, obtaining

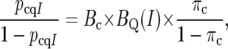(6)

where p_cqI = Pr(H₁ | y_c, y_q, cand ∈ I) is the posterior probability that the candidate represents a functional polymorphism, given the candidate is in I. Solving for p_cqI,

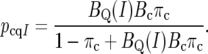(7)

To allow for uncertainty in the estimated map position we average over disjoint intervals, I, covering the region, R_C, of possible locations for the candidate gene, according to their posterior probabilities, and let the size of the intervals tend to zero. We obtain

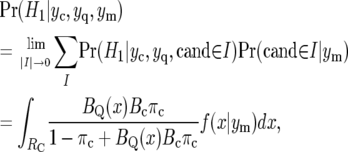(8)

where f(x | y_m) denotes the posterior density of map position x for the candidate gene, given linkage map data y_m. In practice, the standard error of estimated map position is usually on the order of several centimorgans, so the region of integration, R_C, need only be over a region of ∼20 cM (approximately three standard errors each side of the estimated location).

We have shown how to obtain the posterior probability for a candidate gene, given the posterior QTL intensity p_Q(x) and corresponding Bayes factor B_Q(x). Estimation of these functions is covered next.

Posterior probabilities for QTL:

We require probabilities for QTL to be located in any given genomic interval. These are obtained using Bayesian model selection (Ball 2001). Each model is a linear regression of the trait on a set of selected markers, representing a possible QTL configuration, with QTL at the selected marker loci. In reality QTL will lie between markers; however, a QTL between two markers is well represented by a combination of models with one or more markers selected. We use prior probabilities per marker proportional to the width of the vicinity of the marker. With this prior, the probability, over all models, that a marker is selected can be interpreted as the probability that a QTL is in the vicinity of the marker, i.e., closer to that marker than to any other.

Let X denote the model matrix of all marker covariates, and let 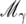be a model where γ is a indicator vector of zeros and ones with the ones indicating the subset of selected variables for a model. If the prior probability for the number of QTL is Poisson(λ_Q) per genome, and all genomic loci are equiprobable, then the prior probability for marker M_i is

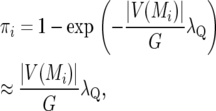(9)

and the prior for 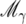is

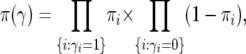(10)

where V(M_i) denotes the vicinity of marker M_i defined as the genomic interval of loci closer to M_i than any other marker, |V(M_i)| is the width of V(M_i), and G is the genome length. The approximation in (9) is accurate provided each marker interval is a small proportion of the genome.

Recall that the BIC for a linear model with p variables is given by

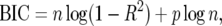(11)

where R² is the coefficient of determination for the model (Raftery 1995; Ball 2001).

Combining evidence from the BIC with prior probabilities for models, it follows that the posterior probability for model 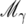is given by

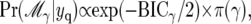(12)

where the constant of proportionality in (12) is chosen so that the total probability for all models adds up to 1 (Ball 2001).

The marginal posterior probability, g(M_i | y_c), for a QTL to be in the vicinity of a marker M_i is the sum of posterior probabilities of all possible models where M_i is selected:

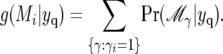(13)

This probability is shared between all points in V(M_i). If, as in interval mapping, we assume there is a single QTL locus within a region, we obtain a probability density for QTL presence over V(M_i). For simplicity, and to avoid this assumption, we assume a uniform distribution for QTL intensity over V(M_i). The probability intensity, p_Q(x), for QTL presence at genomic location x is then given by

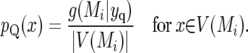(14)

For a genomic interval, I, the probability for a QTL to be located within I is given by integration:

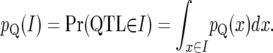(15)

Note that g(M_i | y_q) is the posterior probability of one or more QTL in V(M_i). If g(M_i | y_q) is large, there is a nonnegligible possibility of two or more QTL in V(M_i). Within V(M_i) there is only 1 marker, so the data are not expected to be informative on the number of QTL in excess of 1. Therefore, conditional on the existence of 1 QTL the posterior number of further QTL should follow the prior distribution with rate λ_i = −log(1 − π_i). We obtain

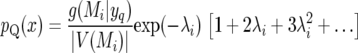(16)

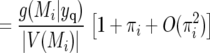(17)

These higher-order approximations can be used in place of (14) if desired.

Analytical calculations and Zellner priors:

Smith and Kohn (1996) use Zellner priors of the form

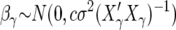(18)

for the selected coefficients {β_j:γ_j = 1}, point null priors for the unselected coefficients {β_j:γ_j = 0}, and an inverse gamma prior for σ², where X_γ is the matrix of columns of X corresponding to the selected coefficients. With these priors, marginal probabilities of the data, 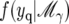, and hence the Bayes factors can be obtained in closed form. (See also Sen and Churchill 2001 for a generalization.)

The major influence on Bayes factors is the amount of information in the prior on the parameter(s) being tested. The parameter c in (18) should be chosen to match the variance of β_γ to prior expectations. In particular c = n in (18) is a prior with information equivalent to a single data point, i.e., a unit information prior.

With a unit information prior, marginal probabilities of the data, and hence Bayes factors, are given in terms of the BIC asymptotically to within a factor (1 + O(n^−1/2)) (Kass and Wasserman 1995). For a single model, M, the marginal probability of the data is

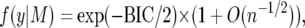(19)

and the Bayes factor, B₁₂, for comparing M₁, M₂ is

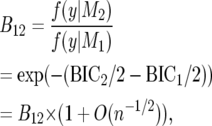(20)

where BIC₁, BIC₂ are the respective BIC values.

We use Bayes factors, with c = n in the Zellner prior, as a check on the accuracy of the BIC in the example below. An alternative, more computationally intensive, approach is to run an MCMC sampler for each of the linear models to estimate the marginal probabilities needed to calculate Bayes factors (see, e.g., Yi et al. 2003).

Data simulation:

To show comparisons with interval mapping (IM) (Lander and Botstein 1989) and composite-interval mapping (CIM) (Jansen and Stam 1994; Zeng 1993, 1994), data were simulated using QTL Cartographer version 1.17 (Basten et al. 1994, 2004). Data were simulated for a genome with 12 chromosomes of length 300 cM each for a total genome length of G = 3600 cM, with markers located every 20 cM. The number and size of QTL effects were simulated with an average number of 10 additive QTL, total QTL heritability 35% (by which we mean the total variance of QTL is 35% of the within-family variance), and QTL sizes distributed with the default Gamma(2, 2) distribution. Backcross QTL mapping families with n = 100, 300, and 1200 progeny were simulated and analyzed in separate runs with the same QTL and map configuration. Composite-interval mapping analyses (QTL Cartographer model 6) used the default values for window size (10 cM) and number of background markers (five). This means that for each test locus, five control markers are selected as covariates to control for possible QTL at other locations, and the control markers were selected from all genotyped markers except those within 10 cM of the test locus.

The QTL effects simulated by QTL Cartographer were all positive in sign, corresponding to QTL in coupling, where there are more than one QTL on a chromosome. To make the data slightly more interesting, the QTL on chromosome 4 was replaced with two midsized QTL in repulsion. The total QTL heritability was inadvertently increased slightly but we continue to work with the nominal value of 35%. Individual QTL locations, effects, and heritabilities are shown in Table 1. QTL locations are given by chromosome, marker number for the left flanking marker, and recombination distances r_L and r_R to the left and right flanking markers, respectively. The values b_i are the QTL effects. QTL Cartographer uses the parameterization where

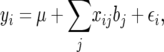(21)

and x_ij = 1 (resp. x_ij = 0) if the ith progeny has jth QTL genotypes QQ (resp. Qq). With this parameterization the ith QTL variance is .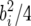

TABLE 1.

QTL heritabilities and map positions

i	Chromosome	Marker	rL	rR	bi	(%)
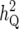1	3	9	0.1081	0.0724	1.3601	12.0
2	4	5	0.0747	0.1060	0.7221	3.4
3	4	7	0.0246	0.1475	−0.8634	4.8
4	5	6	0.0660	0.1139	0.6685	2.9
5	5	8	0.1012	0.0798	0.7715	3.8
6	6	12	0.0104	0.1577	0.8634	4.8
7	9	14	0.0021	0.1634	0.4485	1.3
8	10	2	0.1182	0.0610	0.3485	0.8
9	11	11	0.0621	0.1173	0.3993	1.0
10	12	15	0.1598	0.0074	0.4976	1.6

Priors for QTL effects:

We give adjustments to the BIC for subjective priors for QTL effects with lower variance. It is natural to specify the prior variance, 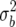, for the QTL effects as a multiple of the trait genetic variance, ,

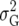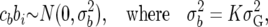(22)

where the constant c_b is chosen so that the QTL variance for a single QTL is E((c_bb_i)²) = 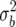. For the QTL Cartographer parameterization, the QTL variance is 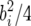so we use c_b = 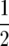. Use of c_b in this way avoids dependence on the parameterization. We refer to this prior as the independence prior, since the effects b_i are a priori, independent.

Recall that the QTL Cartographer parameterization uses effects 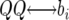, 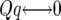for the ith QTL. For the following argument we use the parameterization

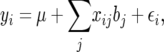(23)

where x_ij = 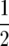(resp. x_ij = ) if the ith progeny has jth QTL genotypes QQ (resp. Qq). With this parameterization the ith QTL variance is still 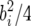, and for unlinked markers the columns of X are uncorrelated and hence approximately orthogonal for large sample sizes. The Zellner prior is unchanged, because the Zellner prior is invariant to linear transformations of the parameter (i.e., if we replace b by b* = Cb and X by X* = XC⁻¹, the transformed prior for b* is the Zellner prior with X replaced by X*).

Since we are considering a prior distribution, rather than a particular sample, we take expected values over possible samples, obtaining a choice of c with expected values of QTL variances agreeing with those of the independence prior (22). The expected values will approximate estimates based on averages over rows of X for large sample sizes. For unlinked QTL, we choose c in the Zellner prior (18) so that the Zellner prior has the same expected QTL genetic variances for each individual QTL as the independence prior with the desired value of K in (22). In the general case the Zellner prior will have the same total expected QTL variances, i.e., variance of the second term in (23), for each set of linked QTL as the independence prior with the chosen value of K.

For unlinked QTL the QTL variances in the Zellner prior can be simply computed from the diagonal elements of X′X. The QTL variances are the diagonal elements of c(X′X)⁻¹σ². For X corresponding to a set of unlinked QTL the columns of X are orthogonal, and the diagonals of (X′X)⁻¹ are the inverses of the diagonals of X′X. With the parameterization (23), the diagonals of X′X are n/4. It follows that

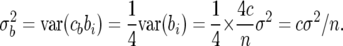(24)

For sets of mutually linked QTL the diagonals of (X′X)⁻¹ will be smaller than the inverses of the diagonals of X′X. For this case we give a more general derivation independent of the parameterization. The genetic variance due to QTL is the variance of the second term in (23),

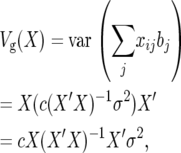(25)

which is an n × n variance–covariance matrix for samples. The genetic variance is either approximately the average diagonal element from a large sample or the expected value of any diagonal element.

First, consider the case of a single QTL. For a single QTL the matrix X has only 1 column, and i, j entry of X(X′X)⁻¹X′ is

(26)

i.e., the expected QTL variance is cσ²/n, which agrees with (24). This does not depend on any of the x_i so is the same for all QTL. Therefore, with k independent QTL loci, the total QTL genetic variance is k times this value; i.e.,

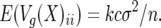(27)

In the general case we can choose the transformation C corresponding to the Gram–Schmidt orthogonalization procedure, reducing the columns of X to orthogonality. It follows that (27) also applies in the general case. Q.E.D.

The prior variance for any k QTL from the independence prior is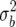 k = kK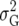. Equating this to the value for the Zellner prior gives

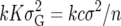(28)

so that

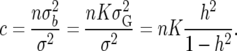(29)

Equation 29 assumes that all of the genetic variance is accounted for by QTL. If there is prior information on the proportion of variance from nonadditive, epistatic, and polygenic components this can be allowed for by choosing a smaller value of K in (22).

The marginal probability of the data for a linear model ℳ is given by

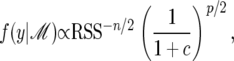(30)

where c is as in Equation 18, RSS denotes the residual sum of squares after fitting the model, n is the number of sample points, p is the number of explanatory variables in the model, and the proportionality constant is independent of the model matrix X (cf. Sen and Churchill 2001, Appendix C, where α there corresponds to 1/c here). Taking logs and multiplying by −2 gives the equivalent value for the BIC,

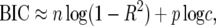(31)

where we have used log(RSS) = log(1 − R²) + log(var(y)) = log(1 − R²) + const., c ≈ 1 + c, and 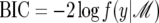up to an additive constant. The constant is chosen in (31) so that BIC = 0 for the null model with intercept alone (p = 0 and R² = 0). Posterior probabilities are unaffected by the choice of constant, because of the normalization of total probability to 1 when probabilities are calculated from (12).

To adjust the BIC for the prior for QTL effects corresponding to c in (18) replace p log n by p log c, or, equivalently, add p log(c/n) to the BIC criterion. Expressed in terms of K and h², this becomes

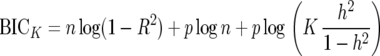(32)

Broman and Speed (2002) use the adjusted criterion

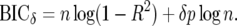(33)

Using (32) is equivalent to setting

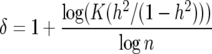(34)

in (33). For example, with K = 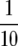, n = 1200, and h² = 0.35 we obtain

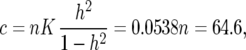(35)

and δ = 0.59.

RESULTS

Worked example:

Thumma et al. (2005) studied associations between SNPs and haplotypes in a candidate gene Cinnamoyl CoA reductase. Putative associations between an SNP marker, SNP21, and microfibril angle (MFA) in a Eucalyptus nitens association-mapping population and between markers SNP18 and SNP120 in the same gene and MFA in Eucalyptus families (used as validation populations) were reported.

On the basis of the reported sample sizes, allele frequencies, and percentage of variance explained, Bayes factors for the candidates were calculated using the method of Spiegelhalter and Smith for one-way ANOVA models (Spiegelhalter and Smith 1982; Ball 2007). Results are summarized in Table 2.

TABLE 2.

Statistics for markers with “significant” associations with MFA from Ball (2007)

Population	n	Marker	Frequency	% var	P	B
E. nitens association population	290	SNP21	0.31	4.6	0.00023	98.4
E. nitens family	287	SNP18	0.5	0.45	0.02	1.5
E. globulus family	148	SNP120	0.5	0.69	0.04	1.1

Reprinted with permission from Ball (2007), Table 8.8, p. 152.

To illustrate the QTL colocation calculations suppose the candidate SNP21 (with Bayes factor B_c = 98.4) is on chromosome 3 with map position 170 cM, estimated with a normal posterior distribution with standard error 10 cM, and the QTL data available are the simulated QTL data with n = 300 as described above.

We assume prior probability π_c = 1/50,000, corresponding to a prior expectation of 10 SNPs in 500,000 covering the genome, to be closest to one of 10 functional loci affecting the trait. Without using QTL information the posterior probability was 1.96 × 10⁻³ [solve p_c/(1 − p_c) = B_c × π_c/(1 − π_c) for p_c; cf. Ball 2007, Table 8.9].

Chromosome 3 had one probable QTL located near marker 10, which had a posterior probability of 0.923. Table 3 shows calculations of quantities needed to evaluate the posterior probabilities after allowing for QTL colocation.

TABLE 3.

Calculation of QTL colocation probabilities for candidate polymorphism SNP21, assumed to be located at 170 cM on chromosome 3, colocating with QTL from the simulated QTL mapping family with n = 300 progeny

	Marker Mi
	i = 8	i = 9	i = 10	i = 11
Position (cM)	140	160	180	200
|V(Mi)|	20	20	20	20
πQ(V(Mi))	0.06	0.06	0.06	0.06
g(Mi | yq)	0.003	0.089	0.923	0.004
BQ(x)	0.054	1.60	16.6	0.072
BQ(x)Bc	5.3	157.6	1634.8	6.71
100 × BQ(x)Bcπc/(1 − πc + BQ(x)Bcπc)	0.0106	0.3143	3.1662	0.0142

π_c = 1/50,000, B_c = 98.4.

Letting x ∈ V(M_i),

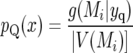(36)

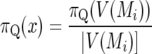(37)

since the within-vicinity probabilities are assumed to be uniform, so

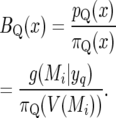(38)

For example, for marker 10 at 180 cM we have g(M_i | y_q) = 0.923 (Table 5, “Total(%)” entry for marker 10 with n = 300), so B_Q(x) = 0.923/0.0556 = 16.6.

TABLE 5.

Top 10 models for chromosome 3

		Marker
Model	k	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	R2	Postprob	Cumprob
n = 100
1	1	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	12.5	0.448	0.448
2	1	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	11.2	0.214	0.662
3	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0.0	0.094	0.756
4	1	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	7.7	0.030	0.786
5	2	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	1	17.8	0.028	0.814
6	2	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	1	17.4	0.022	0.836
7	2	0	0	0	0	0	0	0	0	1	0	0	0	0	0	1	0	15.9	0.019	0.855
8	2	0	0	0	0	0	0	0	1	1	0	0	0	0	0	0	0	15.6	0.015	0.870
9	2	0	0	0	1	0	0	0	0	0	1	0	0	0	0	0	0	15.2	0.013	0.883
10	2	0	0	0	0	0	0	0	0	0	1	0	0	0	0	1	0	14.9	0.010	0.893
Total (%)		0.4	0.7	1.2	2.5	1.5	0.5	0.5	2.6	31.2	55.0	3.9	0.5	0.7	0.6	3.6	6.3
n = 300
1	1	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	8.1	0.864	0.864
2	1	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	6.6	0.071	0.935
3	2	0	0	0	0	0	0	0	0	1	1	0	0	0	0	0	0	9.0	0.012	0.947
4	2	0	0	0	0	0	0	0	0	0	1	0	0	1	0	0	0	8.7	0.007	0.955
5	2	0	0	0	0	0	0	0	0	0	1	0	1	0	0	0	0	8.3	0.004	0.958
6	2	0	0	0	0	0	0	0	0	0	1	0	0	0	1	0	0	8.2	0.004	0.962
7	2	0	0	0	0	0	1	0	0	0	1	0	0	0	0	0	0	8.2	0.004	0.966
8	2	0	1	0	0	0	0	0	0	0	1	0	0	0	0	0	0	8.2	0.003	0.969
9	2	0	0	0	0	1	0	0	0	0	1	0	0	0	0	0	0	8.1	0.003	0.972
10	2	0	0	1	0	0	0	0	0	0	1	0	0	0	0	0	0	8.1	0.003	0.975
Total (%)		0.2	0.4	0.3	0.3	0.3	0.4	0.3	0.3	8.9	92.3	0.4	0.4	0.9	0.4	0.3	0.2
n = 1200
1	1	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	8.7	0.451	0.451
2	2	0	0	0	0	0	0	0	1	0	1	0	0	0	0	0	0	9.6	0.274	0.726
3	2	0	0	0	0	0	0	0	0	1	1	0	0	0	0	0	0	9.6	0.242	0.968
4	2	0	0	0	0	0	0	0	0	0	1	0	0	0	1	0	0	8.9	0.002	0.970
5	3	0	0	0	0	0	0	0	1	1	1	0	0	0	0	0	0	9.9	0.002	0.973
6	3	0	0	0	0	0	0	1	1	0	1	0	0	0	0	0	0	9.8	0.002	0.974
7	3	0	0	0	0	0	0	0	1	0	1	0	0	0	1	0	0	9.8	0.002	0.976
8	3	0	0	0	0	0	0	0	0	1	1	0	0	0	1	0	0	9.8	0.001	0.977
9	2	0	0	0	0	1	0	0	0	0	1	0	0	0	0	0	0	8.8	0.001	0.979
10	2	0	0	0	0	0	1	0	0	0	1	0	0	0	0	0	0	8.8	0.001	0.980
Total (%)		0.1	0.3	0.2	0.2	0.2	0.2	0.3	28.6	25.1	100.0	0.2	0.2	0.2	0.5	0.2	0.1

Postprob, posterior probability; Cumprob, cumulative sum of posterior probabilities.

It remains to integrate over the probability density for map location, which is the normal density with mean 170 cM and standard deviation 10 cM; i.e.,

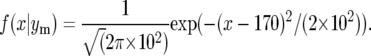(39)

Letting

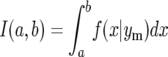(40)

the integral is given by

(41)

where the coefficients of I(a, b) terms in (41) are from the last row of Table 3.

Due to its colocation with the QTL on chromosome 3, the posterior probability for the candidate gene SNP21 has increased 8.5-fold to 0.017, which is still not high. Probabilities would increase further if the map location was known more precisely or the posterior probability for the QTL was higher. For example, if map position was known exactly to be 180 cM the posterior probability would rise to 0.032, representing a 16-fold increase in probability due to QTL colocation. Larger increases would require more accurate estimation of candidate map position and more accurate estimates of QTL position.

Note that in Thumma et al. (2005), the association was considered “validated” by associations in the E. nitens and E. globulus families (i.e., QTL data) with markers SNP18 and SNP128 (P = 0.02 and 0.04, respectively, in Table 2). This does not constitute validation at the level of resolution of an association study, but does represent evidence of colocation with a possible QTL. However, the Bayes factors of 1.5 and 1.1, respectively, are too small to make a significant difference.

Simulation results:

Except where otherwise stated all Bayesian analyses for the simulated data use a prior probability per marker based on an average number of 10 QTL per genome, and the standard BIC (equivalent to using c = n in the Zellner prior for QTL effects) is used to estimate posterior probabilities for models.

The posterior probability intensity for QTL presence, p_Q(x), is plotted against map position in Figure 1. Each chromosome is plotted in a separate graph. Shown with the heading for each graph are the QTL heritabilities (percentage of phenotypic variation) and marginal probabilities for model sizes 0, 1, and 2 (p₀, p₁, and p₂). Log-likelihood ratios for interval mapping and composite-interval mapping are shown for comparison. The interval-mapping curves are high for a much wider region about the QTL than p_Q(x) while the composite-interval-mapping curves are high for a slightly wider region about the QTL than p_Q(x) at this sample size. The curves are step functions because the posterior probability for models with the ith marker, M_i, selected is shared equally among genomic locations in V(M_i) (Equation 14).

Figure 1.—

Posterior probability density p_Q(x) for QTL presence. Data were simulated for 12 chromosomes with genome length G = 3600 cM, n = 1200 progeny, and 10 QTL with QTL heritabilities as shown. For each chromosome, marginal probabilities for models of size 0, 1, 2 QTL are p₀, p₁, p₂, respectively. QTL locations are denoted with an asterisk. Likelihood ratios for interval mapping (– – –) and composite interval mapping (· · ·) are shown for comparison.

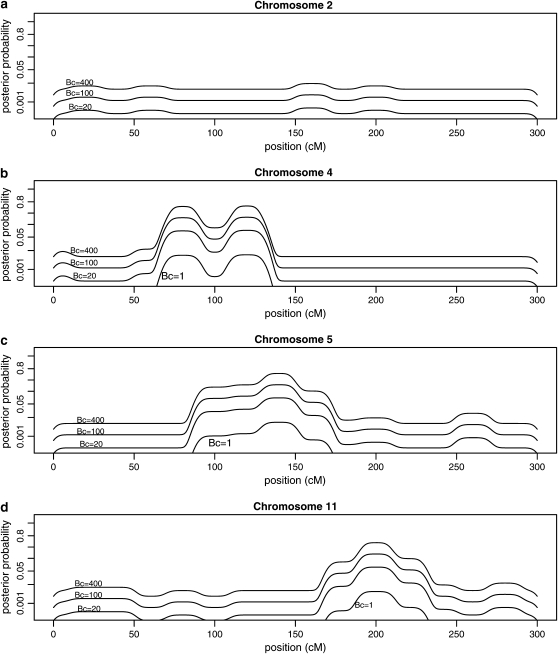
The probability, p₀, for model size 0 is <0.001 for chromosomes 3, 5, 6, 9, and 12, representing strong evidence for one or more QTL. These chromosomes had maximum log-likelihood-ratio (LR) statistics >20 except for chromosome 4 with two QTL in repulsion, where the QTL at 87 cM is not detected by interval mapping or composite-interval mapping (LR < 10), and the composite-interval mapping peak is broader and centered to the left of the peak in p_Q(x). The two QTL in repulsion are clearly separated with a low value of p_Q(x) for the intervening marker, and posterior probability for model size 2 was high (p₂ = 0.961), representing good evidence for two QTL. For chromosome 3, with one QTL, and chromosome 5 with two QTL in coupling, there was strong evidence for one or more QTL (p₀ < 0.001), but either one- or two-QTL models were compatible with the data: p₁ = 0.451, p₂ = 0.530 for chromosome 3, and p₁ = 0.562, p₂ = 0.412 for chromosome 5. For chromosome 3 the two-QTL model probability is dominated by QTL at the two flanking markers (Table 5). This represents either one or two QTL to within the resolution of the marker map.

For chromosome 11, with one QTL with 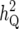= 1%, there was weak evidence for a QTL (p₀ = 0.12) or LR = 10 and17 for IM and CIM.

For chromosome 12, with one QTL with 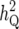= 1.6%, there was strong evidence for a QTL (p₀ < 0.001), but one “fake” QTL at the left-hand end was “detected” by IM and CIM with likelihood ratios >10. The posterior probability for model size 2, p₂ = 0.744, was approximately three times greater than p₁ = 0.229, representing weak evidence for two QTL.

For chromosomes 1, 2, 7, and 8, where there was no QTL, the posterior probability for model size 0 was not low (0.654–0.966), as would be expected where there are no QTL.

To show why we use p_Q(x) rather than confidence intervals, we illustrate the pitfalls in using a popular method for estimation of confidence intervals for QTL location. Table 4 shows estimated and actual heritabilities and confidence-interval widths calculated using the empirical formula of Darvasi and Soller (1997),

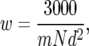(42)

where w is the confidence interval width for a QTL estimated from a progeny of size N. The QTL is assumed to have an allele substitution effect d, and m = 1 for a backcross, and m = 2 for an F₂. We have shown all distinguishable peaks down to LR_max = 4.5, not just those over a demanding threshold. Confidence interval widths are w, based on the true QTL effect sizes, and 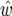based on QTL effect sizes estimated from the same data. Note there are some large differences between w and 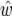due to the QTL effects being under- or overestimated. Note also for chromosome 5, where there are two QTL but only one detected, we have 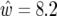, compared to w = 20.9 and w = 15.8 for each of the two QTL and together spanning a 62-cM region. This will happen whenever two QTL in coupling are detected as a single QTL. For chromosome 4, one of the QTL had an LR_max of only 5.0 and its heritability was underestimated by 10-fold. Together these confidence intervals span a region of 160 cM, compared with two regions of combined size 29 cM, when the true QTL effect sizes were used. This happened because the effects of the two QTL were underestimated, which happened because the two QTL were in repulsion. For chromosome 3, the estimated C.I. width was only ∼5 cM, which is less than our intermarker spacings. This suggests we could do better in this case by using the Darvasi and Soller formula or using virtual markers to subdivide the region. However, bearing in mind the results for chromosomes 4 and 5, caution is needed because we cannot rule out multiple QTL within the interval from 160 to 180 cM (the combined marker vicinities). If there were two QTL, e.g., at 167 and 173 cM with about half the variance each, their combined Darvasi and Soller confidence intervals would span a region of ≥20 cM. We conclude that we cannot rely on confidence intervals for QTL location, considering QTL location separately, but need to consider the joint probability distributions for QTL existence, QTL effects, and QTL location, as in our approach.

TABLE 4.

Heritabilities and confidence-interval widths for putative QTL from interval mapping

Chromosome	LRmax	x		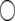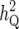(%)		w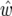
3	103.3	172.0	172.0	12.0	10.0	4.6	5.5
4	5.0	88.3	78.0	3.4	0.3	17.7	160.0
4	18.1	122.9	122.0	4.8	1.6	12.4	39.6
5		107.3		2.9		20.9
5	81.1		144.0		7.1		8.2
5		151.2		3.8		15.8
6	65.3	221.2	226.0	4.8	6.1	12.4	9.6
9	26.7	260.3	254.0	1.3	2.5	47.5	23.9
10	4.5	33.2	22.0	0.8	0.4	77.5	160.3
11	10.2	206.9	190.0	1.0	1.0	61.9	62.3
12	13.1		4.0	0.0	1.2		51.3
12	25.4	299.1	298.0	1.6	2.2	38.4	28.3

LR_max, the maximum log-likelihood for a peak; x and , the true QTL position and its estimate; 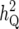(%) and 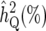, the QTL heritability as a percentage of phenotypic variance and its estimate; w and , QTL confidence interval widths based on the true and estimated QTL effects, calculated using the method of Darvasi and Soller (1997) (Equation 42). Cells are left blank where a QTL did not exist corresponding to a peak or where a there was no peak corresponding to a QTL.

Output from our method consists of a set of models with posterior probabilities and summary statistics, such as the marginal probability for each marker (total probability of all models with the marker selected), and marginal probabilities for model size (total probability of all models with the given size). These are shown for the top 10 markers for chromosomes 3 and 5 in Tables 5 and 6.

TABLE 6.

Top 10 models for chromosome 5

		Marker
Model	k	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	R2	Postprob	Cumprob
n = 100
1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0.0	0.488	0.488
2	1	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	8.2	0.202	0.690
3	1	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	6.3	0.073	0.764
4	1	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	5.3	0.043	0.807
5	1	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	5.2	0.042	0.849
6	1	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	4.7	0.033	0.882
7	1	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	4.2	0.025	0.906
8	1	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	3.2	0.015	0.921
9	2	0	0	0	0	0	0	1	0	0	0	1	0	0	0	0	0	11.8	0.009	0.930
10	2	0	0	0	0	0	0	1	0	0	1	0	0	0	0	0	0	11.5	0.008	0.937
Total (%)		0.3	0.6	0.4	0.5	0.6	3.2	24.0	3.6	4.9	8.9	5.7	0.8	0.5	2.0	0.4	0.2
n = 300
1	1	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	9.1	0.626	0.626
2	2	0	0	0	0	0	0	1	0	1	0	0	0	0	0	0	0	11.4	0.102	0.728
3	2	0	0	0	0	0	1	0	0	1	0	0	0	0	0	0	0	11.0	0.054	0.782
4	2	0	0	0	0	0	0	1	0	0	1	0	0	0	0	0	0	10.9	0.043	0.826
5	1	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	7.3	0.037	0.862
6	1	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	7.2	0.028	0.891
7	2	0	0	0	0	0	0	0	0	1	1	0	0	0	0	0	0	10.2	0.014	0.905
8	2	0	0	0	0	1	0	0	0	1	0	0	0	0	0	0	0	10.1	0.012	0.917
9	2	0	0	1	0	0	0	0	0	1	0	0	0	0	0	0	0	10.1	0.011	0.928
10	2	0	0	0	0	0	1	0	0	0	1	0	0	0	0	0	0	9.8	0.008	0.936
Total (%)		0.1	0.5	1.4	0.8	1.3	6.6	18.5	2.1	86.3	11.7	0.5	0.4	0.2	0.5	0.3	0.1
n = 1200
1	1	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	7.6	0.562	0.562
2	2	0	0	0	0	0	1	0	1	0	0	0	0	0	0	0	0	8.4	0.159	0.720
3	2	0	0	0	0	0	0	1	1	0	0	0	0	0	0	0	0	8.4	0.145	0.865
4	2	0	0	0	0	0	0	1	0	1	0	0	0	0	0	0	0	8.3	0.070	0.935
5	2	0	0	0	0	0	0	0	1	1	0	0	0	0	0	0	0	8.1	0.021	0.957
6	3	0	0	0	0	0	1	0	1	1	0	0	0	0	0	0	0	8.9	0.006	0.963
7	3	0	0	0	0	0	0	1	1	1	0	0	0	0	0	0	0	8.9	0.006	0.970
8	2	0	0	0	0	0	0	0	1	0	0	0	0	0	1	0	0	7.8	0.004	0.973
9	2	0	0	0	0	0	0	0	1	0	0	1	0	0	0	0	0	7.7	0.002	0.975
10	2	0	0	0	0	0	0	0	1	0	1	0	0	0	0	0	0	7.7	0.002	0.977
Total (%)		0.1	0.2	0.2	0.2	0.2	17.3	22.9	92.7	10.7	0.3	0.4	0.2	0.2	0.7	0.2	0.1

Postprob, posterior probability; Cumprob, cumulative sum of posterior probabilities.

Top 10 models for chromosome 3:

For chromosome 3, the top 10 models for each sample size are shown in Table 5. The first column is model number, in order of decreasing probability. The second column gives model size, k, while the next 16 columns show which markers are selected. The final 3 columns show the R² statistic, posterior probability per model, and cumulative sum of posterior probabilities for models. For example, for n = 300, model 1 with posterior probability 0.864 has marker 10 selected, model 2 with posterior probability 0.071 has marker 9 selected, and model 3 with posterior probability 0.01. Model 3 (model size k = 2) has higher R² than models 1 and 2 but lower posterior probability because of the penalty term in the BIC and because the prior probability per marker is <0.5.

For n = 1200, the top three models accounted for 97% of the probability, and marker 10 (at 180 cM) was selected in each of the top 10 models. In fact, marker 10 was selected in every model with nonnegligible probability, with a marginal probability of very close to 100%. Markers 8 and 9 had marginal probabilities of 28.6 and 25.1%, respectively. For n = 1200, the null model (not shown) had posterior probability <0.001, representing strong evidence for a QTL.

At smaller sample sizes there was, naturally, more variability. For n = 300, the top three models accounted for 95% of the posterior probability. Marker 9 and/or 10 was selected in the top three models. For n = 100, model 3, with model size k = 0 had posterior probability (p₀ = 0.09), representing weak to moderate evidence for a QTL, although markers 9 and 10 had the highest marginal probabilities (31.2 and 55.0%, respectively), with 4% probability for marker 11.

For n = 300, the highest-probability single model (model 1) with marker 10 selected had a posterior probability of 0.864. The same model had the highest posterior probability for n = 100 and 1200 but with lower posterior probability of 0.45. This has also resulted in less posterior variance of QTL location for n = 300, as is evident from the marginal probabilities for markers (Total % rows in Table 5). At first sight this seems counterintuitive, since as sample size increases the QTL location should be more accurately estimated, and the true model should be selected with probability asymptotically approaching 1. However, here we are not in the asymptotic situation—sample sizes are not large enough to select a single best model, nor is model 1 the true model, since the true QTL location is intermediate between markers 9 and 10. The probabilities 0.864 and 0.45 are intermediate probabilities, and the differences between them can easily occur by chance, e.g., as a result of fewer recombinations between the QTL and marker 10 for n = 300 than for the other two sample sizes.

Top 10 models for chromosome 5:

For chromosome 5, the top 10 models for each sample size are shown in Table 6. For n = 1200, the top 3 models accounted for 86% of the probability. As was the case for chromosome 3, the probability for model size 0 was <0.001, corresponding to strong evidence for one or more QTL on this chromosome, and models of size 1 and 2 shared the probability approximately equally. Unlike chromosome 3, the probability for models of size 2 was not concentrated at adjacent markers.

For n = 1200, markers 6–9 had marginal probabilities >1%, corresponding to a region of 80 cM for the double QTL. For n = 300 and 100 this region expanded to 120 cM.

Posterior probabilities for candidate gene polymorphisms:

Candidate gene polymorphisms were not simulated; rather, we consider hypothetical candidate gene polymorphisms with various values of B_c, at various genomic locations. To illustrate the method we plot the posterior probabilities for the candidates after incorporating QTL colocation information from the simulated QTL data, as a function of genomic location. Posterior probabilities for the candidate genes are calculated using Equation 8. A standard error of 3 cM (as would be obtained with a mapping population of size 100 and marker spacing of 20 cM) for estimated map location of candidate genes was assumed.

Figure 2 is a plot of posterior probabilities for candidate gene polymorphisms vs. estimated map position on chromosomes 2, 4, 5, and 11. There are separate curves corresponding to candidate polymorphisms with Bayes factors B_c = 20, B_c = 100, and B_c = 400. The posterior probability curves are “wavy,” because the integrand in (8) is the piecewise constant function B_Q(x)B_cπ_c/(1 − π_c + B_Q(x)B_cπ_c) multiplied by the density f(x | y_m) of map location, which has the effect of smoothing the piecewise constant function. If the map location was known exactly the curves would look similar to the step functions in Figure 1.

Figure 2.—

Posterior probabilities for candidate gene polymorphisms by estimated map position for n = 1200 QTL progeny. Values are shown for (a) chromosome 2, (b) chromosome 4, (c) chromosome 5, and (d) chromosome 11. Each line shows posterior probabilities as a function of estimated map position for a given Bayes factor B_c, for B_c = 1, 20, 100, 400, representing sequence-specific evidence for a candidate polymorphism. Results assume prior probability per candidate 1/3000 and standard deviation of 3 cM for map position estimates.

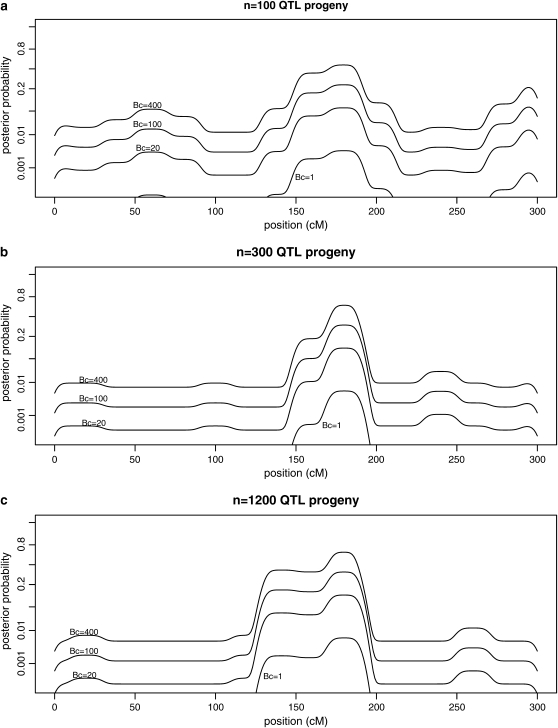
Figure 3 similarly shows posterior probabilities for candidate polymorphisms on chromosome 3 for various sample sizes.

Figure 3.—

Posterior probabilities for candidate gene polymorphisms by estimated map position for chromosome 3. Values are shown for (a) n = 100, (b) n = 300, and (c) n = 1200 QTL progeny. Each line shows posterior probabilities as a function of estimated map position for a given Bayes factor B_c, for B_c = 1, 20, 100, 400, representing sequence-specific evidence for a candidate polymorphism. Results assume prior probability per candidate 1/3000 and standard deviation of 3 cM for map position estimates.

Accuracy of the BIC:

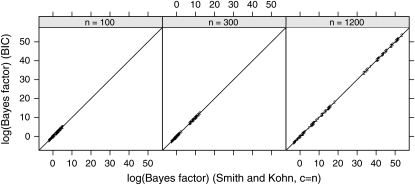
The Bayes factors corresponding to model probabilities estimated using the BIC are compared with the closed-form expressions for Bayes factors with the Zellner prior [Zellner 1986; c = n in (18)] in Figure 4 for n = 100, 300, and 1200. Differences, indicated by deviations from the diagonals, are almost imperceptible, indicating good agreement.

Figure 4.—

Accuracy of the BIC approximation. The logarithm of Bayes factors calculated from the BIC is plotted against the logarithm of Bayes factors calculated using the closed-form expression from Smith and Kohn (1996) with the Zellner prior [c = n in (18)] for n = 100, n = 300, and n = 1200 QTL progeny. Differences between the two Bayes factors are shown as deviations from the diagonal lines.

Subjective priors for QTL effects:

Figure 4 shows that the estimates of Bayes factors, and hence posterior probabilities based on the BIC, are very good approximations to the values with c = n in Equation 18. However, c = n in (18) corresponds to a prior variance of 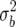= σ² for QTL that can be greater than the genetic variance. This is conservative, since QTL variances are generally only a fraction of the genetic variance, and the heritability is often approximately known.

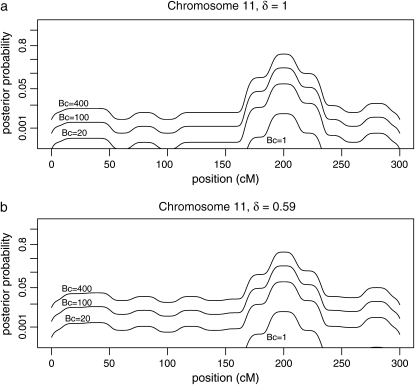
Posterior probabilities for QTL presence for two priors are shown for chromosome 11 in Figure 5. Probabilities are calculated with the default prior with K = 1.86 (δ = 1) and the subjective prior with K = 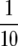(δ = 0.59), corresponding to an average QTL variance of 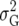/10.

Figure 5.—

Posterior probabilities for candidate gene polymorphisms by estimated map position for chromosome 11. Values are shown for (a) δ = 1, corresponding to a prior with c = n in (18) or a prior with QTL variance of 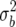= σ², with information equivalent to half a sample point, and (b) δ = 0.59, corresponding to 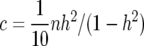in (18) or a prior with QTL variance of .

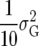The probabilities for QTL presence at long distances from QTL loci have increased approximately twofold, but are still less than the posterior odds from the candidate gene data alone.

DISCUSSION

We have shown how to calculate posterior probabilities for candidate gene polymorphisms by combining sequence-specific evidence for candidate genes with QTL colocation information. Our method takes into account uncertainty in number and locations of QTL on each chromosome and uncertainty in estimated map position. For candidate genes that map to QTL regions, this can result in substantially larger posterior probabilities. Where a number of candidate genes are available, among candidates with given Bayes factor B_c those that map near a QTL are most promising for functional testing.

QTL colocation is often specified as a candidate gene falling within a 95% confidence interval. Confidence intervals are formed by selecting a peak in the interval-mapping likelihood, assumed to represent a QTL. If QTL effects are known, or assumed (as in an experimental design situation) or estimated from independent data, unbiased confidence intervals can be obtained using the simple formula of Darvasi and Soller (1997). However, QTL effects are seldom estimated from independent data, and estimates for significant effects are subject to selection bias. For example, only 2 of 20 QTL-mapping experiments in forest trees, reviewed by Sewell and Neale (2000), used an independent verification population. Estimates of QTL effects free of selection bias can be obtained in the Bayesian model-selection approach (Ball 2001), but in this approach we do not need confidence intervals for QTL location, since we calculate posterior distributions. The confidence intervals for QTL location also assume the genetic architecture is known. We have seen that results can vary considerably if there are two QTL when one is assumed or if two QTL are in repulsion. Hence there is the need to jointly consider the number and locations of QTL, and size of their effects, as in our approach.

Bayes factors and posterior probabilities for QTL presence in a small interval were calculated on the basis of the output of QTL analysis using Bayesian model selection on the set of linear regression models with sets of selected markers as variables. As in Ball (2001), posterior probabilities for models were obtained using the BIC. Comparison with closed-form expressions for Bayes factors for comparing pairs of models with Zellner priors showed that the BIC approximation was very good for the sample sizes considered (n ≥ 100 QTL-mapping progeny).

Why not just use Bayes factors? In principle, the BIC is not needed—if using Zellner priors we could use the closed-form expressions for marginal probabilities of the data, and from these compute Bayes factors for pairs of models, and hence compute posterior probabilities directly without using the BIC. As we have seen, the adjusted BIC is essentially equivalent to probabilities from the Zellner prior for reasonably large QTL-mapping sample sizes. The BIC is used mainly for convenience and compatibility with existing software—it is easily computed from standard linear model software output, e.g., leaps and regsubsets in R and Splus, and is used in the bicreg S function (Raftery 1995; Raftery et al. 1997) for Bayesian model selection in linear models using the BIC. Moreover, the Zellner prior is not a natural subjective prior, with prior covariance between linked markers similar to the likelihood and with prior variance proportional to σ²—we do not necessarily recommend its use in any given situation.

The Bayes factor does not depend on the prior probability per marker but does depend on the prior distribution of the parameter(s) being tested. Broman and Speed (2002) introduced the extra penalty factor δ in the BIC and recommended δ = 2, 3, possibly allowing for asymptotics and, in the frequentist paradigm, multiple comparisons. We have seen here that when we allow for prior probabilities per marker, δ = 1 corresponds to a good generally useable, but conservative, default prior for QTL effects, with information approximately equivalent to one sample point. Where there is lower prior variance for QTL effects, higher Bayes factors and posterior probabilities will be obtained, so it is worth using this prior information if available.

We have shown how to modify the BIC to enable specification of a subjective prior for QTL effects with prior variance for QTL effects specified as a multiple of the within-family genetic variance, corresponding to δ < 1, e.g., δ = 0.59, corresponding to average QTL variances of one-tenth of the genetic variance for the simulated data set. Even lower values could be used if, for example, preliminary QTL studies have been carried out, so that remaining undetected QTL are likely to be small. However, comparison between δ = 1 and δ = 0.59 did not show a major difference—with the main apparent difference being larger posterior probabilities for candidates located farther from the QTL position: in this case the sensitivity to prior variance was not high. This is apparently paradoxical, because one would “like” posterior probabilities to be higher at the QTL and lower far from the QTL. However, using a more informative prior for the parameter being tested raises the Bayes factors for all loci, at least where the evidence from the QTL mapping is in favor of a QTL (B > 1). Nevertheless, the subjective prior is still recommended, as giving a more “correct” posterior where prior information is available.

In the worked example, an 8.5-fold increase in posterior odds for the candidate was obtained, due to QTL colocation. The posterior probability for a QTL in the vicinity of marker 10 was 0.923, which is already fairly high; increasing it to, e.g., 0.999 would yield only modest increases in posterior odds for the candidate. Larger increases are possible given more accurate candidate map locations and QTL locations. This would require both larger QTL-mapping sample sizes and more dense marker spacings. For example, if the marker spacing was 0.2 cM, the candidate was accurately mapped to marker 10, and the posterior probability for a QTL in the vicinity of marker 10 was 0.9, the posterior probability for the candidate would rise to 0.48, representing a 243-fold increase in probability due to QTL colocation.

In spite of a Bayes factor of 98.4 and a further 8.5-fold increase in odds due to QTL colocation, the posterior probabilities for the candidate were still not high. This is because we have used low prior probabilities. Thumma et al. (2005) tested 25 SNP markers within the candidate gene and gave P-values adjusted for the number of tests. For this to be relevant amounts to a tacit prior assumption that at least one real effect is present within the gene with high probability. (Here, as is common in other examples, the frequentist analysis also uses prior information, albeit poorly quantified and nontransparently.) However, we see no reason why the gene should directly affect the trait in question (MFA); hence we have used low prior odds appropriate for a random candidate. The number of loci tested, or that might be tested, affects the P-values, but does not govern the posterior probabilities—hence our assertion: QTL and association mapping are model-selection problems, not multiple-testing problems.

The posterior probabilities for QTL presence were compared to interval mapping and composite-interval mapping. The composite-interval mapping curves were qualitatively similar to the posterior probabilities, in that, where evidence for a QTL was strong, the composite-interval mapping curves were high in a region similar to or slightly wider than the region with high posterior probability for a QTL, while interval-mapping curves were high for a substantially wider region. This is not surprising since our approach tests for a QTL within a small region vs. the null hypothesis of no QTL in that region, but for possible QTL anywhere else, while interval mapping tests for a QTL at a location vs. no QTL anywhere. Composite-interval mapping attempts to allow for possible QTL elsewhere by conditioning on a set of auxiliary marker genotypes. If there is an auxiliary marker between the location being tested and another QTL, then the effect of the other QTL will be absorbed by the auxiliary marker. (Conditional on the auxiliary marker genotype, the genotypes for the marker being tested are independent of the QTL genotype.) Where there are two or more reasonably close QTL on a chromosome, composite-interval mapping may not choose a suitable auxiliary marker. For example, the two QTL on chromosome 4 in our simulated data were not resolved by composite-interval mapping. The effectiveness, or otherwise, of composite-interval mapping hinges on the choice of auxiliary markers to condition on—auxiliary markers can absorb the effect of the QTL being tested as well as other QTL, and estimating coefficients for the auxiliary markers can add error, as well as reduce residual variation. The optimal choice of number and location of auxiliary markers depends on unknown locations and magnitudes of QTL effects; hence mixed results for CIM are reported by Broman and Speed (2002). Bayesian model selection does, optimally, in a coherent mathematical framework, based on interpretable prior distributions, what composite-interval mapping attempts to do in an ad hoc way with arbitrary choices.

In our simulated data, chromosome 4 had two QTL in repulsion. For n = 1200 QTL progeny, these were strongly detected and well separated by the Bayesian model-selection method but not by composite-interval mapping or interval mapping. It is important to detect QTL pairs in repulsion—QTL in repulsion represent an important source of latent variation, particularly for traits of undomesticated species that have been subject to stabilizing selection, which could be exploited by future selection or QTL mapping. We note that the QTL effects simulated by QTL Cartographer (Basten et al. 1994, 2004) were all positive in sign, whereas in many cases there would be a number of QTL pairs in repulsion. This means that many QTL Cartographer-based simulations may be optimistic.

As in QTL Cartographer, the within-family variation was assumed to be fully accounted for by QTL. In practice, nonadditive, epistatic, and polygenic components may reduce the proportion of genetic variance due to QTL. Prior information on these terms can be allowed for if known; otherwise the prior variance for QTL effects will be slightly larger. This is conservative, since Bayes factors reduce when there is weaker prior information for the size of effects being tested.

In our method, probabilities p_Q(x) are piecewise constant in the vicinity of the nearest marker. This is not a major problem; however, if desired, the probabilities (14, 15) can be smoothed by applying a kernel smoother and renormalizing, so that the probability integral for each chromosome or linkage group is unchanged. Or, missing marker data can be estimated by multiple imputation (Ball 2001). This was intended for markers where marker genotypes were missing for some individuals, but can also be used for “virtual markers” with all data missing (cf. Sen and Churchill 2001). One or more virtual markers can be placed between each pair of actual markers, to obtain intermediate probabilities and hence smooth the graph of posterior probabilities. This is potentially useful if most of the posterior probability for a QTL is concentrated around a single marker. There is, however, a limit to the benefit of adding virtual markers—a single QTL located between two markers is well represented by one QTL at each of two adjacent flanking markers with posterior probabilities for each marker reflecting the relative proximity of the QTL to each of the flanking markers. To distinguish between these two possible genetic architectures requires more actual markers.

Sen and Churchill (2001) use closed-form expressions for marginal probabilities for linear models to estimate a joint posterior probability density for QTL locations for a set of QTL. In their Figure 2 and Appendix D they note the log posterior densities for QTL location and the LOD scores calculated using the EM algorithm were very similar. This is surprising, since we have seen that the interval-mapping likelihood ratios give excessively wide intervals around QTL. In fact, it is an error to estimate QTL location from probabilities of models with a fixed number of QTL. Their log posterior density and LOD scores are similar because, when restricting to a fixed number of QTL, the BIC is the same as the log likelihood or LOD score up to a constant, and the sample sizes are such that the BIC gives good approximations to marginal probabilities for models. Their posterior density for QTL location is not the same as p_Q(x), since they assume a fixed number of QTL per chromosome. We have seen that the number of QTL on a linkage group may not be unequivocally determined (e.g., Figure 1, chromosomes 5 and 12); hence there is the need to incorporate model uncertainty in both the number and the locations of QTL. When considering models of different size we often see that models of size 2 (e.g., Table 2, n = 1200) dominate models of size 1 except for the model with only the marker closest to the QTL selected, resulting in a sharper drop-off in p_Q(x) than the LOD score. In other words, when testing for a QTL at a given location one has to allow for possible QTL at other locations, which entails models of size 2 or more.

There are various possible experimental strategies for gene discovery combining, for example, information from association studies and QTL-mapping studies. Depending on sample size and size of QTL effects, most QTL-mapping studies have a resolution of tens of centimorgans for QTL location (Tables 5 and 6 and discussion). Preliminary results for genome scans (Ball 2007) suggest that not only is QTL-mapping information useful, but prior to association studies it is more efficient to do an even larger QTL-mapping study than most QTL-mapping studies (e.g., with n = 3000 QTL-mapping progeny for small QTL effects). For candidate genes, graphs of posterior probability for different sample sizes (cf. Figure 4) could be used to find the optimal design; however, in the absence of a theoretical power calculation, many replicate simulations are needed.