Quantitative Trait Loci for the Circadian Clock in Neurospora crassa

Abstract

Neurospora crassa has been a model organism for the study of circadian clocks for the past four decades. Among natural accessions of Neurospora crassa, there is significant variation in clock phenotypes. In an attempt to investigate natural allelic variants contributing to quantitative variation, we used a quantitative trait loci mapping approach to analyze three independent mapping populations whose progenitors were collected from geographically isolated locations. Two circadian clock phenotypes, free-running period and entrained phase, were evaluated in the 188 F₁ progeny of each mapping population. To identify the clock QTL, we applied two QTL mapping analyses: composite interval mapping (CIM) and Bayesian multiple QTL analysis (BMQ). When controlling false positive rates ≤0.05, BMQ appears to be the more sensitive of the two approaches. BMQ confirmed most of the QTL from CIM (18 QTL) and identified 23 additional QTL. While 13 QTL colocalize with previously identified clock genes, we identified 30 QTL that were not linked with any previously characterized clock genes. These are candidate regions where clock genes may be located and are expected to lead to new insights in clock regulation.

BIOLOGICAL rhythms with an ∼24-hr period have been found in all forms of life from bacteria to humans (Feldman and Hoyle 1973; Young and Kay 2001; Stanewsky 2003; Bell-Pedersen et al. 2005; Lakin-Thomas 2006; Schibler 2006). The availability of powerful genetic analysis tools and the easily assayable clock phenotype in Neurospora crassa has made the system one of the most successful model organisms for dissecting the circadian clock using a forward genetics approach (Feldman and Hoyle 1973; Loros and Dunlap 2001; Dunlap and Loros 2004). Mutant screens for clock genes have focused on mutants with altered period or arrhythmic phenotypes caused by a single mutation inherited through Mendelian segregation (Feldman and Hoyle 1973). The most interesting gene discovered in these mutant screenings is frequency (frq). Different mutant alleles of frq could cause a long period, a short period, or an arrhythmic phenotype (Feldman and Hoyle 1973; Loros and Dunlap 2001; Dunlap and Loros 2004). This finding led to the proposal that a single gene could function as a “state variable” for the circadian oscillator (Aronson et al. 1994).

Cloning and characterizing the frq gene significantly advanced our molecular understanding of eukaryotic circadian oscillators (Dunlap and Loros 2006; Liu and Bell-Pedersen 2006). Despite extensive molecular characterization of frq and other known clock genes in N. crassa, there is still no comprehensive understanding of the Neurospora circadian clock. Furthermore, with advances in our understanding of the molecular structure of Neurospora clocks, it is apparent that the circadian clock is more tightly linked to other cellular machinery than speculated previously (Bell-Pedersen et al. 2001). For example frq-less oscillators (FLO) coupled to other oscillators in the cell have been proposed (Lakin-Thomas 2006). Currently, we know very little about the genetic basis of these loosely defined oscillators (Dunlap and Loros 2006).

The conventional forward genetics approach is limited in two ways: it cannot uncover genetic loci with subtle clock phenotypes or those associated with essential cellular functions (Mackay 2001a; He et al. 2005). Furthermore, most of the genetic screening done previously was focused on identifying period determinants. Thus, just a handful of genetic loci have been characterized that are responsible for other clock properties such as entrained phase or temperature compensation. Here, we explore an alternative strategy for detecting novel genetic loci affecting the N. crassa circadian clock.

Within natural populations there reside important clues to genetic variation, which are vital in unraveling the mysteries of gene function (Alonso-Blanco and Koornneef 2000). Identifying the molecular components and characterizing the molecular mechanisms of the natural variations will provide us novel insights into molecular mechanisms of complex circadian traits. Quantitative genetics techniques have been utilized successfully over the past decade to describe how alleles genetically interact with each other to modulate the circadian traits as well as to isolate new loci in the same pathway (Shimomura et al. 2001). Quantitative genetics is an extension of fundamental Mendelian principles to polygenic traits (phenotypes encoded by multiple loci). Much of the phenotypic variation seen in natural populations is due to multiple loci contributing to phenotypic variation (Alonso-Blanco and Koornneef 2000). Each quantitative trait locus has a relatively small effect on the phenotype. The combination of genomic sequence, new molecular marker technologies, and sophisticated mapping algorithms has made it possible to utilize natural variation in combination with QTL analysis to dissect complex traits down to a single sequence polymorphism (Lander and Schork 1994; Doerge 2002). For circadian clock phenotypes, clock QTL have been identified in multiple organisms including Arabidopsis and in mice (Swarup et al. 1999; Suzuki et al. 2001; Michael et al. 2003; Edwards et al. 2005, 2006; Darrah et al. 2006).

There have been no reports on QTL analysis for Neurospora circadian clock phenotypes. This may have been due to technical barriers. The most common assay to measure the Neurospora clock has been the race tube assay. As a result of circadian clock-controlled asexual development, Neurospora produces orange spores. These dense orange colored spores create a “banding” phenotype in a long glass tube or “race tube” (Loros and Dunlap 2001). This easily detected clock phenotype made the Neurospora circadian rhythm an attractive system for genetic studies. All laboratory Neurospora strains used in clock studies contain a useful mutation band, bd (Sargent and Woodward 1969; Belden et al. 2007). This mutation allows a robust conidial banding pattern even in the high CO₂ environment of the race tube culture. In the wild-type strains without the bd mutation, the rhythmic asexual development of Neurospora in a race tube is suppressed, which has been a major obstacle in clock study (Sargent and Kaltenborn 1972). However, modified race assays have recently been developed that allow study of Neurospora circadian clocks in natural accessions without the bd mutation in their genetic background (Park and Lee 2004; Belden et al. 2007).

The Neurospora system provides a unique opportunity to extend quantitative genetics to molecular genomics due to its sequenced haploid genome (Galagan et al. 2003). Haploid organisms provide multiple advantages in quantitative studies: (1) they can be maintained clonally to allow large numbers of individuals to be assayed (thereby reducing error from environmental effects; (2) genetic dominance does not contribute to the genetic variation; (3) a permanent segregating population is available after the first generation; and (4) as in the case of Neurospora, the sexual cycle is short (Davis and Perkins 2002). For these reasons, Neurospora can serve as a valuable model organism for elucidating fundamental questions of quantitative genetics for complex behaviors such as the circadian clock. In previous studies, we found significant natural variation in clock phenotypes and known clock genes among 143 natural accessions of N. crassa (Michael et al. 2007). By crossing these natural accessions, we successfully produced linkage maps for three line-cross populations (Kim et al. 2007).

In this report, we describe the QTL analysis of the two clock phenotypes, period and entrained phase, using natural populations. In an effort to find natural genetic variations affecting the clock phenotype efficiently, we employed two QTL analyses, composite interval mapping (CIM) and Bayesian multiple QTL (BMQ) analysis in three independent mapping populations derived from the natural accessions that were collected from geographically isolated areas. We expected that QTL analyses using multiple populations would provide us additional insight into natural variation of clock phenotypes. We predicted that we would find certain clock QTL in more than one population. We hypothesized that these common QTL might play an important role for ecological adaptation. We also expected that analyzing multiple populations would give us meaningful insight into how many QTL are involved in period, phase, and both phenotypes. Our results include identification of (1) common QTL that are detected in more than one population, (2) population-specific QTL, and (3) QTL that contribute to both period and phase phenotypes.

MATERIALS AND METHODS

Strains and growth conditions:

Natural accessions, FGSC 3223, FGSC 4724, FGSC 4720, FGSC 4715, FGSC 4825, and FGSC 2223, were obtained from the Fungal Genetics Stock Center (www.fgsc.net). F₁ progenies from three crosses were obtained as previously described (Davis 2000). Detailed information on the parental strains in their estimated geographical origin and circadian properties is summarized in Table 1. The germination rate of the cross varied significantly between batches of spores. For example, we compared the 16 small batches of ascospores of the same cross (N2 progeny) for their germination rate over a period of a month. The germination rates ranged from 15 to 66%. Strains used in this study were cultured as previously described (Lee et al. 2003). The overt clock phenotypes including period and phase were measured utilizing the inverted race tube assay (Park and Lee 2004).

TABLE 1.

N. crassa accessions used as parental strains in crosses

Cross	Straina	Mating type	Geographical origin	Periodb	Phasec
N2	3223 (♀)	mat A	Louisiana	21.3 ± 0.20	0.6 ± 0.18
N2	4724 (♂)	mat a	Penang, Malaysia	21.0 ± 0.17	0.5 ± 0.24
N4	4720 (♀)	mat A	India	21.4 ± 0.42	23.2 ± 0.44
N4	4715 (♂)	mat a	Haiti	21.7 ± 0.14	23.5 ± 0.26
N6	4825 (♀)	mat A	Tiassale, Ivory Coast	22.2 ± 0.10	2.5 ± 0.25
N6	2223 (♂)	mat a	Iowa	21.3 ± 0.10	1.4 ± 0.19

^a♀ and ♂ represent female or male parent, respectively, of each F₁ progeny. Strain number is Fungal Genetic Stock Center (FGSC) number.

^bPeriod value under free-running condition, in hours.

^cPhase value under 12-hr light:12-hr dark cycles, in ZT hours.

Assessing phenotype:

Race tubes were incubated in constant light (LL) for 12 hr at room temperature. After confirming normal mycelial growth in the race tube, tubes were transferred to an I-36L Percival Scientific (Perry, IA) growth chamber and incubated an additional 12 hr under LL. For all experiments, temperature was set at 25°. After the 24-hr LL treatment, the light was off for the rest of the experiment for the period measurement. The growing front was marked at the light-to-dark transition and on the last day of the experiment. In the race tube experiment for the phase phenotype, the light condition was a light 12-hr:dark 12-hr (LD) cycle. The growing front of the culture in the race tube was marked every 24 hr at the time when the light-to-dark transition occurred. The fluence rate was 250 μE/m²/sec in LL. Light sources were white fluorescent bulbs and incandescent bulbs (Osram Sylvania, Danvers, MA). In both period and phase experiments, tubes were randomly positioned within the chamber to reduce the possibility of positional effects. In each experiment, three replicates of each progeny were assayed. We repeated the experiment to generate data from at least three biological replicates for each strain; sometimes, we were not able to attain data from all three replicates in one experiment.

Period analysis:

For the analysis of period phenotype, individual period estimates of F₁ progenies of each population were produced after 4–5 days of consecutive conidial banding, using the fast Fourier transform nonlinear least-squares (FFTNLS) program (Plautz et al. 1997; Edwards et al. 2005).

Phase analysis:

The reference time for phase of each individual genotype/progeny was the band center. Thus, the phase of each individual progeny was determined on the basis of the time elapsed to reach the band center within a day. Band center was visually determined by the spore density. The time when cultures were transferred to the dark cycle is, by definition, CT12 (dusk). Thus, in these experiments, the time in band center of each individual was calculated by the following formula: zeitgeber (ZT) phase = (growth to band center/overall growth) × 24 + 12. For example, if conidial band occurs at 180 mm and total growth after light-dark transition is 280 mm, ZT phase = 24 × (180/280) + 12 = 27.43. By convention, ZT is always expressed as <24 ZT hr. For example, ZT phase 27.43 is expressed as ZT 3.43 (27.43 – 24) instead of ZT 27.43.

Genotyping and genetic map construction:

The genotyping method and linkage group analysis was done as described previously (Cho et al. 2000; Schuelke 2000; Yu et al. 2006). We also utilized the physical map information at the Broad Institute database (http://www.broad.mit.edu/annotation/genome/neurospora/maps/Index.html).

Statistical analysis:

QTL analysis was carried out on the mean value of free-running period and entrained phase in N2, N4, and N6 populations (Table 2). Markers with significant segregation distortion (χ² test, P = 0.05) were disregarded. CIM and BMQ were used to identify putative clock QTL.

TABLE 2.

Phenotypic variation in period length and phase in N2, N4, and N6 populations

						% of progenies that show transgressive segregation
Phenotype	Cross	Meana	SD	Rangeb	Heritabilityc	Total (%)	(−) sided (%)	(+) sidee (%)
Period	N2	21.4	0.62	4.60	0.62	47	31	69
	N4	21.7	0.98	5.80	0.87	43	46	54
	N6	21.7	0.57	4.10	0.85	20	54	46
Phase	N2	0.5	0.75	4.67	0.84	54	49	51
	N4	0.5	0.92	6.11	0.87	80	7	93
	N6	1.9	1.05	4.14	0.74	44	49	51

^aPeriod is in hours and phase is in ZT hours.

^bRange for period is highest phenotype to lowest phenotype.

^cVariance associated with the genotype effect by two-way ANOVA and its significance.

^dPercentage of progeny that show transgressive phenotypic segregation of lower phenotypic value than mean value of parental phenotypes in each mapping population.

^ePercentage of progeny that show transgressive phenotypic segregation of higher phenotypic value than mean value of parental phenotypes in each mapping population.

CIM analysis:

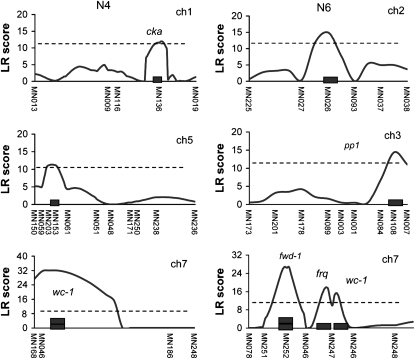
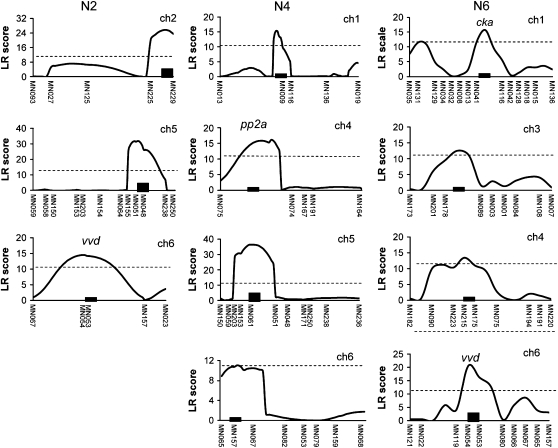
CIM analysis using the QTL Cartographer v.2.5 (Basten et al. 2006) was conducted with a walking speed of 0.5 and a window size of 3 cM under a forward and backward regression model (probability into, 0.01; probability out, 0.1). To determine experimental type 1 error, 1000 permutations were performed for period and phase phenotypes in three (N2, N4, and N6) populations (Churchill and Doerge 1994). We defined the confidence interval as the physical genome region above the threshold defined by these 1000 permutations. This functional confidence interval region was on average 10 cM or ∼200–300 kbp around the genetic positions with the maximum likelihood-ratio (LR) score. We searched for candidate clock QTL genes in the genome region within confidence interval regions. LR critical values ranged from 11 to 12 (P = 0.05) in all analyses. Additive effect estimates and percentages of variance explained by the QTL were generated with Eqtl, testing hypothesis 10, and using model 6 from Zmapqtl. LR profiles for two circadian properties including free-running period and entrained phase in the three populations of our study are displayed in Figures 3 and 4 and Table 3.

Figure 3.—

The graphical description of composite interval mapping (CIM) analysis in period length under free-running condition in N4 (A) and N6 (B) populations. The x-axis represents the marker position within the linkage map. The y-axis represents the likelihood ratio (LR) score of each genetic position denoted by centimorgans. The dotted line stands for the threshold level determined by 1000 permutation tests. QTL names (indicated by arrows with dotted line) and candidate genes in the corresponding QTL are shown around the peak position of the QTL (refer to Table 3).

Figure 4.—

Graphical description of composite interval mapping (CIM) analysis in the phase under the 12:12 LD cycle in N2 (A), N4 (B), and N6 (C) populations. The x-axis represents the marker position within the linkage map. The y-axis represents the likelihood ratio (LR) score of each genetic position. The dotted line stands for the threshold level determined by 1000 permutations. QTL names (indicated by arrows with dotted line) and candidate genes in the corresponding QTL are shown around the peak position of the QTL (refer to Table 3).

TABLE 3.

Summary of the additive QTL in circadian properties that are segregated in three different populations formed by N. crassa natural accessions using Bayesian QTL analysis

Cross	Trait	QTL identification no.	Marker	Chra	PPTb	LRc	Additive genetic varianced	Origin of allelic effecte	Candidate genef (NCU)
N2	Phase	N2BPha2-1	MN125	2	0.30	7.10	0.31	3223	NA
N2	Phase	N2CBPha2	MN229	2	0.72	25.30	0.46	4724	NA
N2	Phase	N2BPha3	MN173	3	0.19	5.50	0.25	3223	NA
N2	Phase	N2BPha4	MN182	4	0.17	5.90	0.26	3223	pp2a (ncu06630.2)
N2	Phase	N2CBPha5-1	MN051	5	0.78	31.50	0.48	4724	NA
N2	Phase	N2CBPha6	MN054	6	0.46	14.70	0.36	3223	vvd (ncu03967.2)
N2	Phase	N2BPha7-2	MN247	7	0.17	4.20	0.22	4724	NA
N4	Period	N4CBPer1-1	MN008	1	0.16	4.8	0.28	4715	NA
N4	Period	N4CBPer1-3	MN129	1	0.19	4.3	0.29	4715	prd-4 (ncu02814.2)
N4	Period	N4CBPer1-2	MN042	1	0.30	12	0.41	4720	ckII catalytic subunit (ncu03124.2)
N4	Period	N4BPer2	MN094	2	0.44	9.4	0.38	4715	NA
N4	Period	N4BPer3	MN003	3	0.25	8.2	0.31	4715	NA
N4	Period	N4BPer4	MN162	4	0.44	6.9	0.34	4720	NA
N4	Period	N4CBPer5	MN153	5	0.58	11.3	0.45	4720	NA
N4	Period	N4CBPer7	MN046	7	0.95	32.1	0.66	4720	wc-1 (ncu02356.2)
N4	Phase	N4CBPha1-1	MN008	1	0.42	15.5	0.35	4715	NA
N4	Phase	N4BPha1-3	MN019	1	0.28	4.5	0.25	4715	NA
N4	Phase	N4BPha1-2	MN129	1	0.22	3	0.26	4715	prd-4 (ncu02814.2)
N4	Phase	N4BPha4-1	MN074	4	0.22	1.1	0.32	4715	NA
N4	Phase	N4CBPha4-2	MN090	4	0.57	16.3	0.39	4715	pp2a (ncu06630.2)
N4	Phase	N4CBPha5	MN061	5	0.90	36.58	0.59	4715	NA
N4	Phase	N4CBPha6	MN157	6	0.40	12.1	0.34	4715	NA
N6	Period	N6CBPer2	MN026	2	0.34	14.5	0.30	2223	NA
N6	Period	N6CBPer3	MN108	3	0.28	14.4	0.22	4825	NA
N6	Period	N6BPer4-1	MN075	4	0.20	0.6	0.22	4825	NA
N6	Period	N6BPer4-2	MN220	4	0.23	9.1	0.23	4825	NA
N6	Period	N6BPer5-2	MN061	5	0.17	3.9	0.21	4825	NA
N6	Period	N6CPer-7-3	MN046	7	0.00	15.2	na	2223	wc-1 (ncu02356.2)
N6	Period	N6CPer-7-2	MN046	7	0.10	17.75	na	2223	frq (ncu02265.2)
N6	Period	N6CBPer-7-1	MN168	7	0.95	29.6	0.35	4825	fwd-1 (ncu045450.2)
N6	Phase	N6BPha1-1	MN018	1	0.56	5.4	0.39	2223	NA
N6	Phase	N6CBPha1-2	MN131	1	0.79	10.2	0.37	4825	prd-4 (ncu02814.2)
N6	Phase	N6CBPha1-3	MN041	1	0.55	21.5	0.38	2223	ckII catalytic subunit (ncu03124.2)
N6	Phase	N6BPha2-2	MN027	2	0.28	1.6	0.25	2223	NA
N6	Phase	N6BPha2-1	MN038	2	0.84	10.9	0.51	4825	NA
N6	Phase	N6BPha3-1	MN084	3	0.30	8.9	0.37	2223	NA
N6	Phase	N6BPha3-2	MN089	3	0.39	11.7	0.34	2223	NA
N6	Phase	N6CBPha4	MN215	4	0.53	17.3	0.47	4825	NA
N6	Phase	N6BPha5-2	MN153	5	0.43	0.1	0.40	2223	NA
N6	Phase	N6BPha5	MN155	5	0.36	4.4	0.49	4825	NA
N6	Phase	N6BPha5-1	MN083	5	0.37	2.8	0.35	2223	NA
N6	Phase	N6CBPha6	MN054	6	0.96	21.9	0.79	4825	vvd (ncu03967.2)
N6	Phase	N6CBPha6-1	MN067	6	0.69	10.4	0.41	2223	NA

^aChromosome number.

^bPosterior probability threshold.

^cLikelihood ratio.

^dEstimation of additive genetic variance value originates from Bayesian multiple QTL analysis.

^eAccession number used in the Fungal Genetics Stock Center (www.fgsc.net).

^fThe range of each candidate gene is ±200–300 kbp at the genetic locus where LR score or PPT is maximized. NA, not available, which means no previously characterized clock gene is available. For cases in which a candidate gene is available, the corresponding NCU number is recorded in parentheses (Broad Institute, at http://www.broad.mit.edu/annotation/genome/neurospora/Home.html).

BMQ analysis:

The BMQ approach uses a hierarchical modeling scheme in which at the “top” level, each marker has a probability of being categorized into one of three classes: linked to a QTL with a positive effect on (i.e., increases) the value of the phenotype (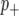), linked to a QTL with a negative effect on the phenotype (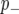), and not linked to a QTL (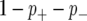) (Zhang et al. 2005). At the “bottom” level, the actual effects of QTL are defined in the usual way using a linear model. The advantage of this hierarchical classification approach is that, with an appropriate choice of prior for marker class hyperparameters (Zhang et al. 2005), we can implement an efficient stochastic search in low-dimensional model subspaces. This avoids the tendency to over-shrink estimates of QTL effects observed with other multi-QTL Bayesian approaches (Yi et al. 2003; Ter Braak et al. 2005).

Following a previous report (Zhang et al. 2005), we used a “spike and slab” prior (George and Mcculloch 1993) which incorporates the assumption that most markers will not be linked to a QTL. Thus, in our Bayesian classification framework, the probability that a marker is linked to a QTL is reflected by the posterior probability distribution associated with the marker classes 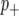and 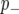. We implemented the Gibbs sampler described in Zhang et al. (2005) to generate samples from these posterior distributions. Marginal posteriors for both the additive effect (β) and probabilities of categorization (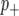, 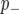) were estimated by sampling 5000 iterations after an initial burn in of 5000.

We considered the cumulative probability >0.5 that the marker is in the 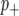(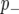) class to determine whether a marker is linked to a QTL (hereafter we refer to this as the posterior probability threshold (PPT). This is a univariate version of the heat map summary provided in Zhang et al. (2005) and reflects the probability that a marker has a >50% chance of being linked to a QTL.

QTL names were formulated in order of the name of the mapping population: the QTL method used (“C” for CIM-specific QTL and “B” for BMQ-specific QTL, BC for the QTL detected both by CIM and BMQ), the trait targeted (for example, “per” for period and “pha” for phase), chromosome number, and numeric numbers to differentiate QTL within a chromosome. For example, N6CBper7-1 refers to the first QTL located on chromosome VII, a period phenotype in N6 that was detected both by CIM and by BMQ methods.

RESULTS

Period and phase analyses:

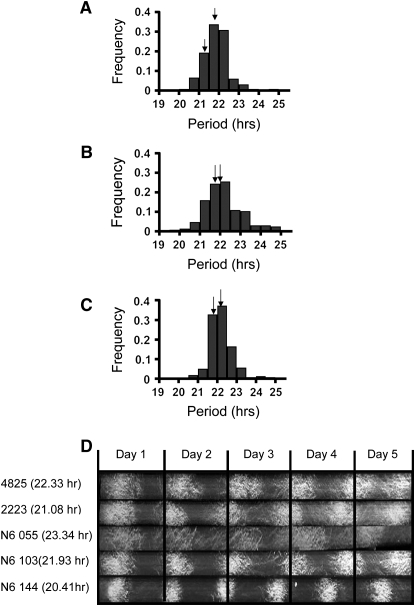
We generated three F₁ progeny derived from mapping parents described in Table 1 to map QTL for two circadian phenotypes, free-running period and light-entrained phase. Each mapping population was composed of 188 progeny derived from a cross between two N. crassa natural accessions (Table 2). Continuous patterns of the distribution of both circadian phenotypes in F₁ progenies were observed in all three crosses, indicating that inheritance of the circadian properties in N. crassa is polygenic (Figures 1 and 2), which is consistent with results of previous studies in other systems (Hofstetter et al. 1995, 1999; Mayeda and Hofstetter 1999; Swarup et al. 1999; Toth and Williams 1999; Kopp 2001; Suzuki et al. 2001; Salathia et al. 2002; Kernek et al. 2004; Edwards et al. 2005, 2006; Welch et al. 2005; Darrah et al. 2006). The mean period lengths of our mapping populations were 21.4 hr, 21.7 hr, and 21.7 in N2, N4, and N6 populations, respectively (Table 2). The period of the parental lines of each population was approximately similar to the mean values of the periods in the F₁ progeny (Figure 1 and Table 2). The ranges of the period length in N2, N4, and N6 were 4.55, 5.79, and 4.12 hr, respectively. The broad sense of heritability (H²) of the N. crassa clock phenotype was high in all populations, 0.62, 0.87, and 0.85, which suggests phenotypic variation in the segregating populations was due to mostly genetic effects.

Figure 1.—

The circadian period variation in F₁ populations. Phenotypic distributions of F₁ progenies of N2 (A), N4 (B), and N6 (C) populations. The x-axis represents circadian period and the y-axis represents frequency of period in the corresponding F₁ progenies. Arrows indicate the periods of the parents for each cross. (D) Race tube images of conidial banding patterns under constant darkness (free-running condition). Two N6 parents (FGSC 4825 and FGSC 2223) and three representative progeny (N6 055, N6 103, and N6 144) with different free-running periods are shown. The vertical black lines represent the growing front in a 24-hr period. The number in parentheses is the average period of the strain.

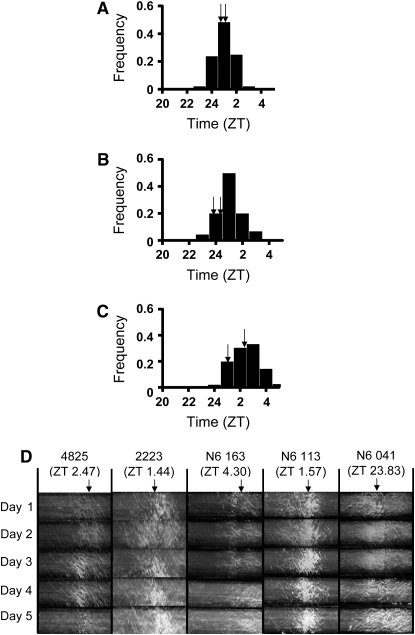
Figure 2.—

The entrained phase variation under 12:12 light/dark condition in F₁ populations. The phenotypic distribution of F₁ progeny of N2 (A), N4 (B), and N6 (C) populations are shown. The x-axis represents the entrained phase in ZT (see materials and methods) and the y-axis represents the frequency of the periods of the corresponding F₁ progeny. ZT 24 is the same as ZT 0. ZT 0 is when light is on (dawn) and ZT 12 is when light is off (dusk). Arrows indicate the phases of the parents for each cross. (D). Race tube images of conidial banding pattern under 12:12 LD cycles for 5 days. N6 parents (FGSC 4825 and FGSC 2223) and three representative progeny (N6 163, N6 113, and N6 041) with different phases are shown. The number in parentheses is the average phase of the strain for 5 days. The arrow indicates the average phase value of each strain.

Traditionally, the phase phenotype has been expressed in subjective hours, or zeitgeber (ZT) hours (see materials and methods). In contrast to period, the means of the phase values among progenies in different populations were different; the mean phase value in N2 and N4 was 0.5 ZT hr, whereas, in N6 it was 1.6 ZT hr (Figure 2 and Table 2). The phase of the parental lines of N2 and N6 populations was close to the mean of the phase of the progenies. However, in the N4 population, 93% of N4 progeny were distributed toward the right side (+ side) of the mean value of parental strains in the phase phenotype (Figure 2 and Table 2). The ranges of phase distribution in N2, N4, and N6 were 4.7, 6.1, and 4.1 ZT hr, respectively. As observed in period value, relatively high heritability in phase was also observed in each population; the heritabilities of N2, N4, and N6 were 0.84, 0.87, and 0.74, respectively. There was no correlation between period and phase under entrained environment within a population in all three populations (supplemental Figure 1 at http://www.genetics.org/supplemental/).

Comparison of CIM and BMQ methods for clock QTL analyses:

In an effort to pinpoint the clock QTL and identify genetic elements responsible for subtle phenotypic variation in the N. crassa clock efficiently, two independent QTL analysis methods (CIM and BMQ, see materials and methods) were used.

In the BMQ approach, we considered a cumulative probability >0.5 PPT to determine whether a marker was linked to a QTL (materials and methods). To assess the appropriate PPT cutoff when determining whether a marker was linked to a QTL, we simulated QTL data using marker data from population N6. We defined “neutral markers” as markers that are not linked to QTL (Zhang et al. 2005). In our simulation study we estimated the PPT level expected to minimize the number of false positives.

The results of the simulations are summarized in supplemental Figure 2 at http://www.genetics.org/supplemental/. When there is no QTL, i.e., additive effects = 0, no neutral marker had a PPT >0.01 (or <−0.01). When three QTL of equal effect spaced throughout the genome are simulated, the PPT for neutral markers can be larger but the bulk of the truly neutral markers still have a PPT <0.05. In fact, even as the effects of the simulated true QTL are decreased to an additive effect of 0.25 (heritability of 0.13), only one neutral marker had a PPT >0.05, showing PPT = 0.16 (supplemental Figure 2 at http://www.genetics.org/supplemental/).

Missing genotype data can increase the type 1 error rates for neutral loci when there are QTL present as seen in supplemental Figure 2 at http://www.genetics.org/supplemental/, where the distribution of the PPT across neutral markers has greater outliers with smaller additive effects. We therefore used PPT = 0.17 as a cutoff for deciding whether markers were linked to QTL to minimize false positive rates.

We also performed a simulation experiment with three predefined QTL (supplemental Figure 3 at http://www.genetics.org/supplemental/). Note that neutral markers surrounding the marker in strongest linkage disequilibrium with a QTL also have a reasonably high PPT but that the highest PPT occurs at the marker where the true QTL is positioned (supplemental Figure 3 at http://www.genetics.org/supplemental/). For a set of consecutive markers with PPT ≥0.17, we therefore determined the marker with the greatest PPT to be linked to a QTL.

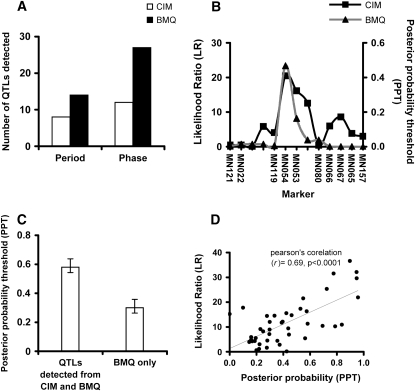
We detected twice the number of QTL from BMQ compared to that from CIM (Figure 5A). BMQ identified all QTL that were found in CIM in both phenotypes of our study (Table 3, Figure 5B) except two QTL (N6CPer7-2 and N6Cper7-3, Table 3). The peak positions on the marker loci linked to significant QTL were highly consistent in the two methods (Figure 5B). The ranges of the PPT were variable, spanning from 0.17 to 0.96 (supplemental Figure 4 at http://www.genetics.org/supplemental/), in which the median value is 0.43; the average PPT for QTL detected by both methods is significantly higher than the average PPT for QTL that were detected only by BMQ (0.58 vs. 0.30, Figure 5C). The LR score in CIM showed a highly significant positive correlation with PPT in BMQ (Pearson's correlation coefficient = 0.69 P < 0.0001, Figure 5D). Hereafter, we ascribe all QTL with PPT values except for those two QTL (N6CPer7-2 and N6Cper7-3) undetectable by BMQ.

Figure 5.—

Summary of Bayesian QTL analysis (BMQ). The distribution of the PPT from BMQ analysis for period and phase are shown. (A) Comparison of number of QTL using CIM (open bar) and BMQ methods (solid bar). (B) Graphical description of CIM (line with solid squares) and BMQ (line with solid triangles) analysis. The x-axis represents the marker position in the linkage map. The primary y-axis on the left is the LR score for CIM analysis and the secondary y-axis is the PPT score for the BMQ approach. (C) The average PPT (y-axis) in between QTL mapped by BMQ and CIM simultaneously and QTL mapped by BMQ specifically (x-axis). Error bars represent standard error around the mean. (D) Scatter plot analysis between the LR score by CIM and by BMQ for each QTL locus. In D, the variable plotted on the x-axis represents the PPT of a QTL detected by BMQ analysis and the y-axis is the LR score of the corresponding locus measured by CIM.

Clock QTL:

From two statistical methods, we detected 43 QTL from three populations that affect the two circadian clock properties, period and phase (Table 3). We detected a similar number of QTL in two clock phenotypes per population; eight QTL in period and nine QTL in phase per population (Table 3 and supplemental Figure 5 at http://www.genetics.org/supplemental/) except the period phenotype in N2 where we did not detect any significant QTL with either CIM or BMQ analyses.

We searched for candidate QTL genes around the detected clock QTL regions to see whether previously characterized clock genes were localized with the clock QTL. We defined the confidence interval region for the clock QTL by performing a permutation test (see materials and methods). We also developed wc-1- and vvd-specific SSR markers as positive controls. This strategy was based on the idea that one of the QTL may colocalize with these two key genes (wc-1 in period, vvd in phase) in N. crassa clock regulation. Two QTL in period (N6Cper7-3 and N4CBper7, Table 3 and Figure 3) and two QTL in phase (N2CBpha6 and N6CBpha6, Table 3 and Figure 4) colocalized with those clock gene-specific markers. In period QTL, in addition to wc-1, we found several QTL that were linked to previously characterized genes involved in period determination; the key clock gene frq and the genes involved in frq phosphorylation and degradation. Candidate period QTL genes and phase QTL genes are listed in Table 3. Although, these genes were known to influence phase of the N. crassa clock, the specific roles of these candidate genes for phase determination have not been clearly studied except for vvd (Heintzen et al. 2001; Elvin et al. 2005). These results suggest that our QTL studies were concordant with previous clock studies and give insight into the mechanism of N. crassa regulation, especially in phase regulation. Nine (of 16 QTL in period) and 16 QTL (of 26 QTL in phase) were characterized as unknown clock loci, which suggests there is a lot more to understand about the N. crassa circadian clock. Several QTL, especially in phase phenotype, with high significance level are still uncharacterized, including N2Bpha5-1 (PPT = 0.78, LR = 35.5), N2Bpha2 (PPT = 0.72, LR = 25.3) and N4Bpha5 (PPT = 0.90, LR = 35.8). The colocalized candidate genes with QTL are also summarized in Table 3.

We wanted to estimate how many clock QTL were identified more than once in different populations. Obviously, we could increase the chance of identifying all potential clock QTL by increasing the number of mapping populations. However, for practical reasons, we chose to characterize three independent line-cross populations. To avoid the overestimation of the number of clock QTL, we excluded the common QTL identified in different populations. We found that there were no significant chromosome rearrangements among N. crassa natural isolates that we studied (Kim et al. 2007). Thus, we defined the common QTL as a QTL linked to the same SSR marker in more than one population for the same phenotype regardless of their relative genetic positions. Three QTL of 16 QTL for the period phenotype and 8 QTL of 27 QTL for the phase phenotype are common QTL (supplemental Figure 6 at http://www.genetics.org/supplemental/). Thus, our data suggest that at least 13 different QTL contribute to the period phenotype, and 19 different QTL contribute to the phase phenotype, respectively.

Last, we wanted to know how closely the period- and entrained-phase phenotypes were genetically interrelated. To answer that question, we investigated how many QTL were contributing both to period and phase phenotypes. Since we could not detect any period QTL in N2, we excluded the comparison between the phase and period QTL in N2 populations. Three QTL in N4 and two QTL in N6 contribute to both in period and phase variations, respectively (Table 3 and supplemental Figure 6 at http://www.genetics.org/supplemental/). We also found seven QTL that contribute to both period and phase variations when we consider all three populations (Table 3 and supplemental Figure 7 at http://www.genetics.org/supplemental/). This suggests that there are common genetic elements contributing to both period and phase phenotypes.

DISCUSSION

Our study showed that fungal F₁ populations can be employed as mapping populations for a QTL study of circadian clock phenotypes. From the three independent F₁ populations in our study (N2, N4, and N6), a wide range of phenotypic transgressive segregation was observed in both free-running period and light-entrained phase clock phenotypes. Since those phenotypes show high heritability consistently in the line-cross populations (average H² = 0.79, standard deviation = 0.12) and the genome structure of two parental strains is so divergent (minimum pairwise dissimilarity = 0.91, supplemental Figure 8 at http://www.genetics.org/supplemental/), the phenotypic transgressive segregations of the phenotypes that are observed in those populations are presumably attributable to segregation of the accumulated genetic variations between the parental strains.

Haploid organisms have an important advantage in constructing a mapping population; due to the haploid nature of the genome, one generation (F₁) is enough to make a breeding population similar to that of the recombinant inbred line (RIL), where it takes at least 8–9 generations of selfing in plant species or ∼20 generations of full-sib mating for outbreeding animals. The size of the mapping population is the critical consideration when using an F₁ population for QTL analysis. Because there are so few meiotic events in an F₁ population compared to RIL lines, a small number of progeny can cause errors in estimating genetic distance and order. Hackett and Broadfoot (2003) performed simulation studies to give a reasonable guess for the mapping population size. They investigated locus ordering performance in genetic linkage map construction of a double-haploid (DH) population under the conditions where effects of missing values, typing errors, and distorted segregation are allowed (Hackett and Broadfoot 2003). With 150 DH progeny, they concluded that a locus order spacing of 10 cM is relatively insensitive to missing values as high as 20% and typing errors ∼3%. In agreement with their result, the order of mapped loci in our study is quite consistent with the physical map (Kim et al. 2007). Furthermore, significant QTL associated with period and phase variation were detected in a 10-cM resolution (Table 3).

The statistical power to detect meaningful QTL can be determined by many factors including the size of the mapping population, the genome organization of the target organism, the experimental designs for the mapping population, the types of molecular markers, the qualities of phenotyping and genotyping analysis, and method of statistical analysis (Zeng 1994; Zeng et al. 1999, 2005). Thus, it is important to find a sensitive statistical method to detect meaningful QTL from the available experimental data. To do this, we compared the result of the QTL analysis with the two different statistical methods, CIM (Zeng 1994) and BMQ (Zhang et al. 2005). We detected twice the number of QTL using BMQ analysis compared to CIM (20 QTL from CIM vs. 41 QTL from BMQ) (Table 3, Figure 5A). The QTL identified by both methods showed a highly significant positive correlation in their significance levels estimated by both methods (Figure 5D).

CIM has been used extensively in QTL studies (Zeng 1994; Jordan et al. 2006; Leips et al. 2006). While CIM incorporates additional markers into the regression analysis that can, in theory, account for the effects of other QTL, the method is potentially sensitive to model selection criteria (i.e., which markers are included as covariates) and can have reduced power when conditioning on linked markers (Zeng 1993, 1994). The Bayesian approach utilized in this study directly fits a multi-QTL model using a hierarchical variable-selection approach that avoids many of the difficulties associated with model selection in likelihood-based approaches (Kao et al. 1999; Liao 1999; Zhang et al. 2005). By directly modeling how multiple QTL contribute to phenotype variation, BMQ is expected to identify true QTL, particularly those with more subtle effects. In our analysis, 22 additional clock QTL were detected by BMQ.

Numerous studies have demonstrated that QTL analysis is a powerful way to identify loci where segregating alleles are contributing to natural variation (Abiola et al. 2003). However, the method does have a major limitation: QTL detected in one cross are limited to the different alleles fixed in a parental strain (Mackay 2001b). Regardless of the amount of divergence between parents, those QTL detected in the cross may therefore be only one snapshot of the total variation possible (Mackay 2001a). To overcome this problem, we increased the number of populations and derived each population by crossing different accessions adapted to different geographical regions to widen our search for genetic loci that can potentially contribute to circadian clock traits (Xie et al. 1998; Mackay 2001b).

Our study found 43 QTL affecting the two N. crassa circadian clock phenotypes (period length and the entrain phase). As expected, QTL of both phenotypes in our study showed population-specific patterns, suggesting that those divergent mapping parents have accumulated genetic variation at independent loci. Thus, similar trait values in circadian properties among mapping parents observed in Table 1 originate from different genetic variation at different loci accumulated as a result of distinct evolutionary histories. Besides the population-specific QTL, common QTL affecting period (3 QTL) or phase (8 QTL) variation were detected from our mapping populations. Cloning and characterizing those common QTL may reveal the molecular nature of clock variation in nature.

From QTL affecting period length, some QTL colocalized with previously characterized clock genes, which includes the catalytic subunit (cka) (N4CBper1-2) of casein kinase II (ckII), frq (N6Cper7-2), and fwd-1 (N6CBper7-1) (Table 3). This result suggests that our QTL study agrees with a previous clock study in period, where progressive phosphorylation of FRQ (by cka) and FRQ degradation (by fwd-1) are suggested as major determinants of period length of the N. crassa circadian clock (Liu and Bell-Pedersen 2006).

A total of 27 QTL affecting phase variation were detected from all three populations (N2, N4, and N6). As observed in period QTL, QTL affecting phase determinant underlie numerous known clock genes including ckba (N6CBpha1-3), prd-4 (N4Bpha1-2 and N6Bpha1-2), pp2a (N2Bpha4 and N4Bpha4-2), and vvd (N2Bpha6 and N6Bpha6) (Table 3). Currently, the roles of these candidate genes are undefined except for vvd which influences light-dependent entrainment of the N. crassa circadian clock (Heintzen et al. 2001). Thus, characterizations of the role of these candidate genes in phase determination will provide valuable insight into the regulation of this phenotype. The resolution of our current QTL map is still too big to pinpoint candidate genes. Additional studies are required to narrow down the identified clock QTL to gene level.

One of the interesting findings in our study was the phase QTL linked to the marker MN129, which was detected both in N4 and N6 populations. Those QTL were closely linked to prd-4 as a candidate gene. One of the known roles in prd-4 in circadian clock oscillation is enhancing FRQ phosphorylation in response to DNA-damaging agents, resulting in resetting the N. crassa clock (Pregueiro et al. 2006). Interestingly, the prd-4 mutant failed to show an appropriate circadian phase shift in response to a light pulse (Okamura 2004; Pregueiro et al. 2006). It is tempting to propose that prd-4 plays a role in phase determination in a light/dark cycling environment. In general, light information is one of the important environmental signals for fungi. However, light also could be a DNA-damaging agent. The prd-4 might play a role in determining the phase in such a way as to avoid adversary photo-oxidative damage/stress in light phase, which may function as a DNA-damaging agent (Okamura 2004).

From the correlation analysis between period and phase, we found no evidence that there is a significant correlation between period and phase in the three populations of our study (Pearson's correlation, P-value for N2 = 0.61, P-value for N4 = 0.64, P-value for N6 = 0.68, supplemental Figure 1 at http://www.genetics.org/supplemental/). Consistent with this result, we found few common QTL between the two phenotypes within a population (supplemental Figure 7 at http://www.genetics.org/supplemental/). However, when we consider the three populations, seven QTL overlapped between period and phase phenotypes (supplemental Figure 7 at http://www.genetics.org/supplemental/). This suggests at least some pleiotropic effects for the regulation of phase and period. More in-depth study of those common QTL may provide an important clue to how phase and period are functionally associated. The fact that 30 QTL of 43 (70%) are not linked to any previously characterized clock genes strongly suggests that our current understanding of N. crassa circadian clock regulation is not complete. Further characterization of these 30 genomic regions will aid our understanding of N. crassa circadian clock regulation.