Synaptic depression creates a switch that controls the frequency of an oscillatory circuit

Abstract

Synaptic depression is a form of short-term plasticity exhibited by many synapses. Nonetheless, the functional significance of synaptic depression in oscillatory networks is not well understood. We show that, in a recurrent inhibitory network that includes an intrinsic oscillator, synaptic depression can give rise to two distinct modes of network operation. When the maximal conductance of the depressing synapse is small, the oscillation period is determined by the oscillator component. Increasing the maximal conductance beyond a threshold value activates a positive-feedback mechanism that greatly enhances the synaptic strength. In this mode, the oscillation period is determined by the strength and dynamics of the depressing synapse. Because of the regenerative nature of the feedback mechanism, the circuit can be switched from one mode of operation to another by a very small change in the maximal conductance of the depressing synapse. Our model was inspired by experimental work on the pyloric network of the lobster. The pyloric network produces a simple motor rhythm generated by a pacemaker neuron that receives feedback inhibition from a depressing synapse. In some preparations, elimination of the synapse had no effect on the period of the rhythm, whereas in other preparations, there was a significant decrease in the period. We propose that the pyloric network can operate in either of the two modes suggested by the model, depending on the maximal conductance of the depressing synapse.

Many synapses show a variety of forms of short-term plasticity such as facilitation and depression (1). Nonetheless, in most cases the contributions of these processes to network dynamics are obscure. Recent work has suggested that synaptic depression may be critical for visual processing in the cortex (2–4) and has stimulated a great deal of interest in the possible computational consequences of short-term synaptic depression elsewhere.

The pyloric network of the crustacean stomatogastric nervous system is an ideal model system for studying the role of synaptic depression in rhythmically active networks. In this network, a bursting rhythm is generated by three neurons, the anterior burster (AB) neuron and the two pyloric dilator (PD) neurons. These three neurons are commonly referred to as the pacemaker group. Other neurons in the circuit are rhythmically active because of their connections, via inhibitory and electrical synapses, to the pacemaker group. The lateral pyloric (LP) neuron makes a graded inhibitory synapse to the PD neurons. The LP–PD synapse is the sole feedback to the pacemaker group. It is therefore ideally positioned for regulating the period of the pyloric rhythm.

We have previously described the kinetics of synaptic depression at the LP–PD synapse in the stomatogastric ganglion of the lobster Panulirus interruptus (5). We found that the recovery from depression is slow relative to the period of the pyloric rhythm. Consequently, these data indicate that during normal function of the pyloric rhythm, this synapse is always partially depressed and that changes in the pyloric rhythm can alter the strength of the synapse as it depresses more, or recovers more from depression (5).

In this paper we take advantage of the unique functional position of the LP–PD synapse to elucidate a possible role for synaptic depression. We construct a computational model that demonstrates a novel mechanism, a “switch” that controls the period of an oscillator. This switch depends on the kinetics and extent of depression in the synapse that feeds back to the oscillator. We show that in some parameter regimes, the switch is “turned off” and the oscillation is not affected by the depressing synapse. In other parameter regimes, the switch is “turned on,” and the strength and dynamics of the synapse control the period of oscillation. We also demonstrate that these two operational modes are compatible with two distinct effects of the LP–PD synapse on the pyloric rhythm, which we display experimentally by functional elimination of the LP–PD synapse.

METHODS

Physiology.

Maintenance of animals and physiological methods were identical to those described (5). Where indicated in the text, the LP neuron was functionally removed by a 10 nA DC hyperpolarizing current injection. In the experiment shown in Fig. 1C, action potentials were blocked by bath application of 10⁻⁶ M tetrodotoxin.

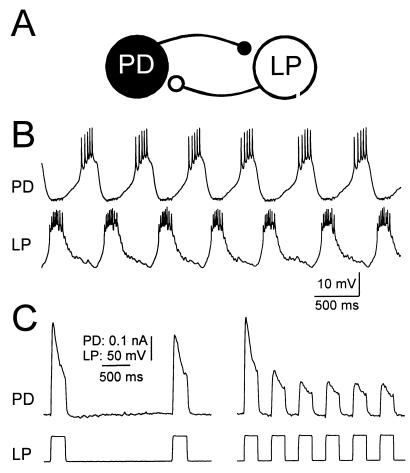
Figure 1.

The PD and LP neurons of the pyloric network make reciprocally inhibitory synapses. (A) Schematic diagram of PD and LP neurons and their connectivity. (B) Simultaneous intracellular recordings of LP and PD in normal saline shows alternating activity. (C) Voltage step depolarizations of the LP neuron in tetrodotoxin produces a graded IPSC in the PD neuron. During each voltage pulse, the IPSC depresses; it recovers between pulses. The recovery from depression is a direct function of the time interval between pulses. The LP neuron was voltage clamped with a holding potential of −60 mV. The PD neuron was voltage clamped at a constant potential of −35 mV and the synaptic currents were measured. B and C are recordings from the same experimental preparation.

Model.

We modeled the depressing synapse as an inactivating ionic current with activation and depression (inactivation) states depending on the presynaptic potential. Our model was built to fit the experimental measurements of the LP–PD synaptic current in response to sequences of depolarizing pulses and realistic waveforms injected into LP in voltage-clamp mode (6). This model depends on two time courses: one describing depression when the presynaptic cell is depolarized and the second describing recovery when the presynaptic cell is hyperpolarized. In contrast, in earlier models of synaptic depression (2), only recovery from depression is modeled as a continuous variable with a time constant. In those models, the synaptic decay is expressed as a sequence of discrete events depending on the occurrence of action potentials in the presynaptic neuron. The model presented in the current work consists of two cells, LP and PD, each obeying the current balance equation −CdV/dt = I_leak + I_Ca + I_Syn, where g_leak = 0.3, E_leak = −65, g_Ca = (PD = 1.6, LP = 2), E_Ca = 120 (all conductances in mS/cm², potentials in mV). I_Ca has first-order kinetics with instantaneous activation m_∞(V) and slow inactivation h described with the differential equation dh/dt = [h_∞(V) − h]/τ_h, where τ_h is 350 msec for both cells. The steady-state functions m_∞ and h_∞ are given by (1 + exp[(V − V_1/2)/k)]⁻¹, where the parameters (in mV) for both cells are m_∞:V_1/2 = −61, k = −4.2; h_∞: V_1/2 = −88, k = 8.5. The synaptic current I_Syn is described by 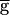_Syn × m_Syn,∞(V_pre) × h_Syn × (V_post − E_Syn), where E_Syn = −80. The synaptic transfer function m_Syn,∞ is given by (1 + exp[(V − V_1/2)/k)]⁻¹, where the parameters (in mV) for PD–LP are V_1/2 = −30, k = −3, 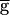_Syn = 0.5, and h_Syn ≡ 1. For LP–PD, V_1/2 = −50, k = −2, and h_Syn is described by dh_Syn/dt = (h_Syn,∞(V_LP) − h)/τ_Syn(V_LP). h_Syn,∞ = (1 + exp[(V − V_1/2)/k])⁻¹ and τ_Syn = τ_hi + (τ_lo − τ_hi) × (1 + exp[(V − V_1/2)/k])⁻¹ with V_1/2 = −71 mV, k = 1 mV, τ_lo = 3,500 msec, and τ_hi = 500 msec.

RESULTS

Synaptic Depression in the LP–PD Graded Synapse.

The PD neurons make reciprocally inhibitory connections with the LP neuron (Fig. 1A), which fires out of phase bursts with the pacemaker neurons (Fig. 1B). The synapse from the LP neuron to the PD neurons is graded and persists when action potentials are blocked by tetrodotoxin. Fig. 1C shows the graded inhibitory postsynaptic currents (gIPSCs) in the PD neuron that result from depolarization of the LP neuron with a square wave. Synaptic depression of this synapse is seen as the decrease in the peak amplitude of the gIPSC during a single sustained depolarization and as the decrease in the peak amplitude of successive gIPSCs when repeated pulses are given. Because the recovery from depression of the graded synapse between the LP and PD neurons is slow relative to the cycle period of a rhythmically active pyloric network (5), during an ongoing pyloric rhythm, the LP–PD synapse is always partially depressed.

The Role of the LP–PD Synapse in Controlling Pyloric Period.

The strong inhibitory postsynaptic potential (IPSP) from the LP neuron to the PD neurons suggests that LP neuron activity plays an important role in controlling the frequency of the pyloric rhythm, as is occasionally observed (7, 8). In other cases, even strong steady-state activation of the LP neuron produces relatively little or no change in the pyloric frequency (9). These two qualitatively different effects of the LP neuron on the rhythm frequency are illustrated in Fig. 2A, which shows recordings from two different preparations. In these traces, the intracellular recording of the PD neuron is used as a monitor of the pyloric rhythm. In each preparation, the rhythm was compared when the LP neuron was firing in the normal pyloric rhythm (Top traces), functionally removed from the circuit by injecting a constant hyperpolarizing current (Middle traces), or hyperpolarized briefly and released from hyperpolarization (Bottom traces). In both experiments, release of the LP neuron from a brief hyperpolarization resulted in a large inhibition of the PD neuron and a transient prolongation of the rhythm period. In Fig. 2A Left, the steady-state functional removal of the LP–PD synapse did not change the steady-state pyloric cycle period (compare PD period in the Top and Middle traces of Fig. 2A Left). In contrast, in Fig. 2A Right, the steady-state removal of the LP synapse resulted in a 15% decrease in the pyloric period.

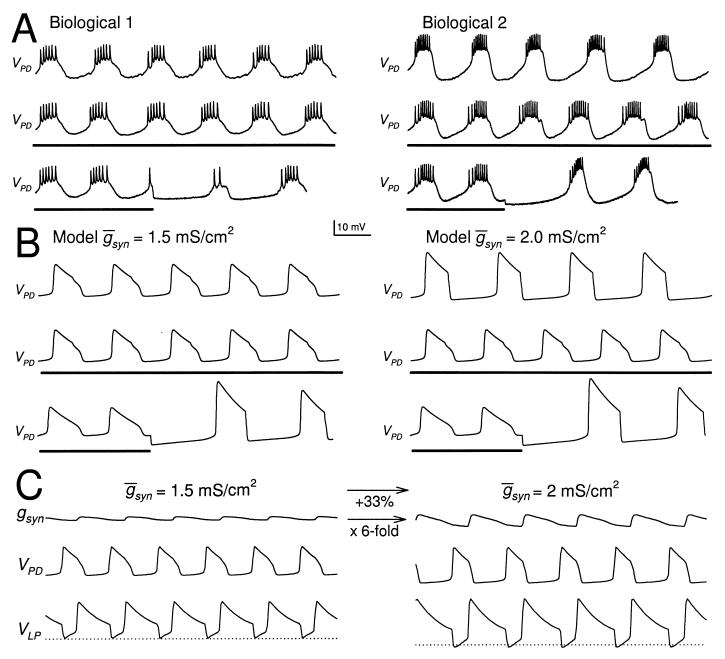
Figure 2.

The LP neuron affects the period of the PD neuron oscillation only in some preparations. (A) The PD neuron activity in two different biological preparations (Biological 1 and 2). In each preparation, the PD neuron activity is shown when the LP neuron was present (Top), continually hyperpolarized (Middle), or briefly hyperpolarized and released from hyperpolarization (Bottom). The thick horizontal bars indicate −10 nA DC current injection in the LP neuron. In both preparations, release of the LP neuron from a brief hyperpolarization resulted in a large IPSP and delay of the next PD neuron burst, indicating the presence of a strong LP–PD synapse. In Biological 1, the period of the PD neuron oscillation was not affected by the continual hyperpolarization of the LP neuron. In Biological 2, the period of oscillation increased by 15% as a result of the continual hyperpolarization of the LP neuron. (B) The same phenomenon is shown in the model of the network. Left traces show the model PD neuron membrane potential when the maximal conductance 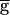_syn of the LP–PD synapse was 1.5 mS/cm². Right traces show the same when 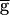_syn=2 mS/cm². Time scale indicated by the horizontal bar is 500 msec for Biological 1 and the model traces and 750 msec for Biological 2. (C) Model traces of the LP–PD synaptic conductance g_Syn and the membrane potentials of the PD and LP neurons for B. When 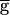_syn was increased from 1.5 to 2 mS/cm², the amplitude of g_Syn increased 6-fold. The amplitude of the PD and LP membrane potentials also increased, and the rhythm slowed. Dotted line denotes −71 mV, the midpoint of the steady-state depression curve h_Syn,∞.

These data show that in both experiments, the LP–PD synapse was strong enough to potentially slow the rhythm, as shown by the Bottom traces of Fig. 2A. Nevertheless, only in one of the two preparations did the LP–PD synapse actually slow the rhythm in steady-state conditions. It is virtually impossible to measure the size of the gIPSP in an ongoing rhythm. Therefore, in this paper we use computational tools to understand whether, how, and under what conditions the dynamics of the depressing synapse determine the network activity.

A Computational Model Demonstrates Two Modes of Network Operation.

To explore the role of the depression of the LP–PD synapse in this circuit, we constructed a simplified computational model of the network (see Methods). Two runs of the model, differing only in the maximal conductance of the synapse from LP–PD (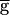_Syn), are shown in Fig. 2B. In both cases, just as in the experimental traces, the rhythm was compared when the LP neuron was firing in alternation with the PD neuron (Top), functionally removed from the circuit by injecting a constant hyperpolarizing current (Middle), or hyperpolarized briefly and released from hyperpolarization (Bottom). In both cases, release of the LP neuron from a brief hyperpolarization resulted in a large inhibition of the PD neuron and a transient prolongation of the rhythm period. In the model traces labeled 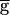_Syn = 1.5 mS/cm², hyperpolarizing the model LP neuron produced no changes in the steady-state period or amplitude of the PD neuron oscillation. In contrast, in the model traces labeled 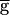_Syn = 2 mS/cm², hyperpolarizing the model LP neuron produced a significant decrease in the steady-state period and a significant decrease in the amplitude of the PD neuron oscillation. Fig. 2C shows the amplitude of the actual conductance g_Syn and voltage traces of the model LP and PD neurons for the two parameter sets shown in Fig. 2B. Note that a 33% increase in 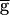_Syn results in a 6-fold increase in g_syn during ongoing network dynamics.

Fig. 3A shows the period of the rhythm as function of 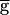_Syn when the LP–PD synapse does not have depression (▵) and when it is depressing (●). In the absence of synaptic depression, the period increases with 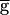_Syn until the oscillation is abolished. With synaptic depression, when 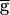_Syn is below some threshold value, the period is insensitive to changes in 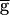_Syn. We refer to this parameter regime as the pacemaker-dominated regime. The period sharply increases when 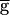_Syn is above that threshold value. This is the synapse-dominated regime. As 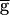_Syn is increased across the threshold value, the rhythm switches from the pacemaker-dominated regime to the synapse-dominated regime. We therefore refer to this threshold value as the switch point. Although the numerical simulations do not conclusively demonstrate a discontinuity in the oscillation period at the switch point (Fig. 3A, ●), the slope of the period plotted versus 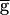_Syn is clearly different in the regions below and above this point.

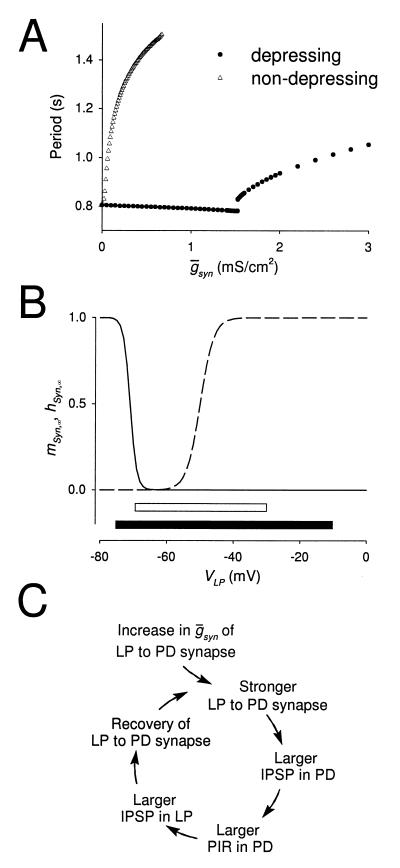
Figure 3.

The frequency of the pyloric rhythm may be regulated by a switch mechanism. (A) The model oscillation period plotted against 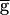_Syn, when this synapse is not depressing (h_Syn ≡ 1; ▵) and when it is depressing (●). When the synapse is depressing, the rhythm period changes discontinuously at 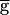_syn = 1.54 mS/cm² (the switch value) from 780 to 820 msec. (B) Steady-state activation (m_Syn,∞; dashed line) and depression (h_Syn,∞; solid line) curves for the LP–PD synapse plotted as function of V_LP. Shown below the curves are the range of the V_LP values during oscillations in the pacemaker-dominated (open bar) and the synapse-dominated (filled bar) regimes. (C) Schematic diagram shows the cellular and synaptic events that trigger a regenerative loop when 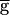_syn is increased beyond the switch value (top arrow).

The two model examples shown in Fig. 2 A and B were for values below and above the switch, and therefore removing the LP neuron from the circuit produced either no or substantial changes in steady-state period. We speculate that the biological preparation in Fig. 2A Left was in a parameter range below the switch point, whereas the preparation in the Right traces was in a parameter range above the switch point.

Fig. 3B shows the steady-state activation (m_Syn,∞) and depression (h_Syn,∞) curves for the LP–PD synapse as a function of the LP neuron membrane potential. Plotted below the curves are the range of the V_LP values during oscillations in the pacemaker-dominated (open bar) and the synapse-dominated (filled bar) regimes. In the synapse-dominated regime, V_LP oscillations had a larger amplitude and a lower minimum value. The larger minimum value resulted in more recovery of the synaptic depression variable h_Syn.

The Cellular Mechanisms Underlying the Two Modes of Oscillation.

The switch mechanism arises from the interaction between the kinetics of synaptic depression and the other voltage and time-dependent processes in the network. We first describe the sequence of events that takes place when 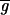_Syn is in the synapse-dominated regime. This sequence is shown schematically in Fig. 3C. A small increase in 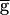_Syn produces a small increase in the actual conductance g_Syn. The increased synaptic conductance produces a larger IPSP in the PD neuron. This triggers a larger postinhibitory rebound in the PD neuron, with a concomitant larger membrane potential excursion. Because the PD–LP synapse is graded, the larger PD neuron membrane potential evokes a larger IPSP in the LP neuron. The larger IPSP in the LP neuron allows the LP–PD synapse to recover more fully from its depression. On the next cycle, this process continues, producing an additional amplification with each cycle until a new steady-state value is produced. Thus, the cycle in Fig. 3C describes a regenerative process that gives rise to the increase of the actual conductance g_Syn. This regenerative process depends crucially on the LP neuron becoming strongly inhibited in each cycle so that the actual conductance g_Syn recovers from depression.

In the pacemaker-dominated regime, the LP neuron does not reach low enough membrane potentials to allow the LP–PD synapse to recover from depression. As a result, the regenerative process discussed above does not occur. It is only for large enough g_Syn that the larger postinhibitory rebound in the PD neuron inhibits the LP neuron sufficiently and allows for recovery from depression. The 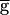_Syn value that is just enough to engage the regenerative process is the switch point. Once the regenerative process is engaged, the actual conductance g_Syn is greatly amplified, and the synapse starts to be significant enough to slow down the rhythm.

What Stops the Regenerative Loop?

In the oscillations within the synapse-dominated regime, the maximum value of the actual conductance g_Syn remains much smaller than the maximal 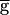_Syn (data not shown). Therefore, the question remains that, at any value of 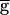_Syn, what stops the regenerative process? Any of the events displayed in the cycle shown in Fig. 3C could potentially do so. First, the strength of the LP–PD synapse may reach a maximal level. Indeed, the conductance of the LP–PD synapse is limited to 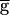_Syn. However, for 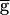_Syn above and near the switch value, the peak value of g_Syn remains an order of magnitude smaller than 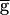_Syn (data not shown), indicating that the process is not limited by the inability of g_syn to increase further. Second, in principle, the LP–PD synapse could recover fully from depression when the LP neuron is inhibited by the PD neuron, and this could contribute to limiting the regenerative loop. However, the interval durations required to obtain 100% recovery of the synapse are much longer than the calculated periods.

The more likely candidates are the maximal amplitude of the postinhibitory rebound of the PD neuron, and the maximal conductance of the PD–LP synapse. The maximum possible amplitude of the postinhibitory rebound in the PD model neuron is set by the ratio of the leak and calcium conductances. At some iteration in the loop, the PD neuron rebound reaches this maximal level even if the LP neuron evoked IPSP in PD is larger than that in the previous iteration. Moreover, the dependence of the PD–LP synapse on the presynaptic voltage is sigmoidal, which means that above some presynaptic voltage, the synapse is saturated and does not become stronger. Hence, at some iteration in the loop, the PD–LP IPSP in LP stops increasing, even if the postinhibitory rebound in the PD neuron is still incrementing. Depending on the parameters of the model, one or the other of these two saturating variables limits the time interval during which the PD neuron can inhibit the LP neuron and stops the regenerative process.

Bistability in the Network.

In some parameter ranges, synaptic depression can produce bistability of the two regimes. To produce the bistability demonstrated in Fig. 4, the time constant of recovery from depression of the LP–PD synapse was halved from 3,500 to 1,750 msec. Two sets of simulations were run in sequence. In the first set (the “upward sweep”), 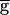_Syn (in mS/cm²) was increased from 0 to 2.0. In the second set (the “downward sweep”), 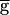_Syn was decreased from 2.0 to 0. From run to run, the value of 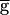_Syn was changed, but within each run, 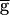_Syn was at a fixed value. In the upward sweep, the period of the oscillation was constant (0.8 sec) when 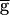_Syn was increased from 0 to 0.9, jumped to 1.2 sec when 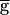_Syn was at 0.9, and then gradually increased to 1.4 sec when 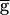_Syn was increased to 2.0. In the downward sweep, the period gradually decreased from 1.4 sec to 1.2 sec when 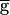_Syn was decreased from 2.0 to 0.9, following the same path as in the upward sweep. In contrast to the upward sweep, the period continued to decrease gradually when 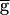_Syn was further decreased, until it reached a value of 0.93 sec when 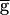_Syn reached 0.4. At this value, the period jumped down to 0.8 sec, and remained at that value as 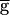_Syn was decreased to 0. A similar result was obtained if the time constant of depression (not recovery) was doubled from 500 to 1,000 msec.

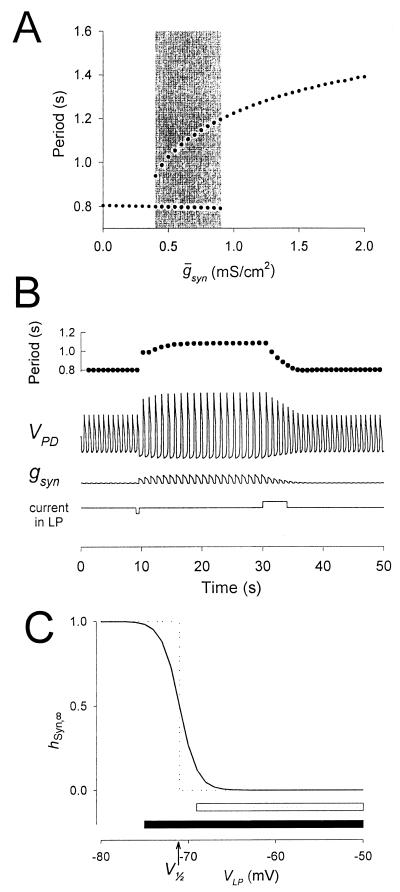
Figure 4.

The switch mechanism can produce bistability in the network oscillations. Same model parameters as in Fig. 3A, but the time constant for recovery from depression of the LP–PD synapse is halved (see Methods). (A) Hysteresis seen in the model oscillation period plotted against maximal conductance (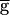_syn) of the LP–PD synapse. This plot shows the period of oscillation for 84 simulation runs. From run to run, 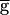_syn was incrementally increased (from 0 to 2, in steps of 0.05; all units in mS/cm²). For each run, the period after the transient was measured. The end point of each simulation run was used as the initial point in the next run. The shaded area highlights the region of bistability. (B) Bistability shown in the model time traces of the LP–PD synaptic conductance (g_syn) and the membrane potential of the PD neuron for 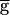_syn = 0.6 mS/cm² (within the shaded region in A). Also shown is the cycle-to-cycle period of oscillation. From t = 9 to 9.5 sec, a negative current (−0.1 μA/cm²) was injected in the LP neuron. This transient current switched the rhythm from a fast period (800 msec) to a slow period (1,090 msec), and the amplitude of the PD neuron membrane potential excursions also increased. From t = 30 to 34 sec, a positive current (+0.1 μA/cm²) was injected in the LP neuron. This transient current switched the rhythm back to the initial fast oscillation. (C) Synaptic depression curve h_Syn,∞ for the LP–PD synapse as shown in Fig. 3B (solid line) and as a step function (dotted line) centered at V_1/2. Shown below the curves are the range of the V_LP values during oscillations in the pacemaker-dominated (open bar) and the synapse-dominated (filled bar) regimes.

The shaded region in Fig. 4A shows the range of bistability extending from 0.4, the jump point in the downward sweep of 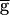_Syn, to 0.9, the jump point in the upward sweep 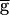_Syn. This range is determined by the rates of depression and recovery from depression. Fig. 4B demonstrates the bistability in the period and amplitude of the oscillations for a fixed value of 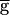_Syn = 0.6. The simulation starts from a case where the synapse from LP–PD is significantly depressed and the period of oscillation is fast. When a brief hyperpolarizing current pulse was given to the LP neuron, the switch mechanism was activated and the LP–PD synapse became greatly amplified. The resulting change in the amplitude and period of the oscillation was sustained after the pulse was terminated. A depolarizing pulse to the LP neuron (this one was several cycles long) returned the network to its initial state. These simulations demonstrate that when synaptic depression is incorporated in a recurrent network, a short synaptic input can produce a long-lasting alteration in the period of the network oscillation.

We now give a heuristic explanation for the bistability behavior of the model. There are at least two sets of parameters in the model that, if varied, produce bistability in the system. One set consists of the two parameters mentioned above, the time constant of decay and the time constant of recovery of the depressing synapse. Additionally, the parameters that set the shape of the steady-state depression curve h_Syn,∞ of the LP–PD synapse are crucial. All of these parameters directly affect the amount of recovery h_Syn and therefore the actual strength g_Syn of the depressing synapse. Even though the two factors are obviously closely related, the emergence of bistability may be more easily explained by considering the shape of h_Syn,∞.

To understand how bistability emerges in the model, we consider a hypothetical case in which the depression curve h_Syn,∞ is a step function that changes from 0 to 1 at some voltage V_1/2 (Fig. 4C, dotted line). Two qualitatively different cases are possible. In the first case, the oscillations of LP lie entirely to the right of V_1/2, in the voltage range where h_Syn,∞ is 0. In this case, no matter how large 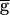_Syn is, the actual synaptic conductance g_Syn is always 0. Hence, the pacemaker-dominated regime exists for all values of 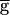_Syn. In the second case, the oscillations cross the point where h_Syn,∞ changes from 0 to 1. Hence, during the time window that V_LP dips below V_1/2, the synapse recovers from depression and the value of g_Syn will be nonzero. The extent of recovery depends on the length of the recovery-time constant relative to the duration of this time window. In this case, there is a value of the maximal synaptic conductance beyond which the oscillations are dominated by the dynamics of the synapse. Therefore, there is a range of maximal synaptic conductances where these two cases coexist. This is the range of bistability. This hypothetical case is an approximation of the general case where the steady-state depression curve is not a step function. In the general case, however, g_Syn is never 0, and the pacemaker-dominated regime does not exist for all values of 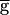_Syn.

DISCUSSION

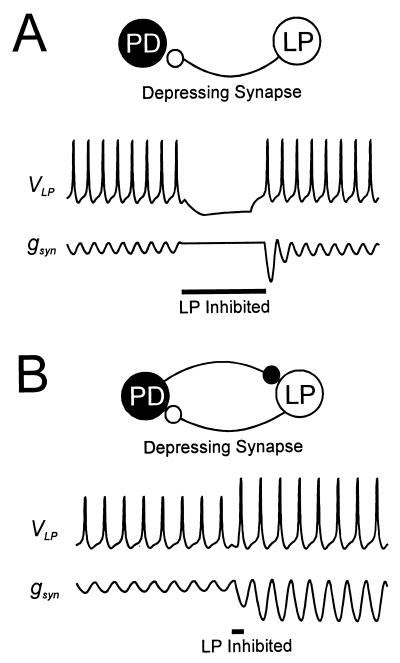
Neuronal oscillators are now thought to be important components of both sensory and motor networks (10, 11), and synaptic depression is common in many cortical and other synapses (1, 12). The results in this paper illustrate that a relatively simple process such as synaptic depression can have significant and unexpected actions when it is found in networks of oscillatory neurons with recurrent feedback connections. Before this work, our understanding of the functional consequences of synaptic depression in an oscillating network can be represented as shown in Fig. 5A. In this model, the synapse from the LP neuron to the PD neuron shows depression that comes to some steady-state value at a given network frequency. If the LP neuron is inhibited, the synapse will recover from depression, so that in the first cycle after that interruption the synapse will be large, until the synaptic strength settles back to steady state. In contrast, we show here that synaptic depression in a feedback network can produce an amplification mechanism in which inhibition of the LP neuron can result in a stronger synapse and a long-lasting change in period (Fig. 5B). This process demonstrates a novel mechanism through which synaptic dynamics can act to produce nonlinear effects and even bistability in networks.

Figure 5.

The switch mechanism provides a novel view of synaptic depression. (A) Traditional view of synaptic depression: hyperpolarization of the presynaptic LP neuron results in a transient increase in the strength of the depressed synapse. (B) A novel view of synaptic depression: through a switch mechanism, the interaction between synaptic dynamics and network mechanisms allows a depressed synapse to become lastingly strong.

Our results show that the dynamics of depression and its recovery can interact with the kinetics of other cellular processes to build interesting switches, or other nonlinear effects. In the specific case demonstrated here, we find that the control of an oscillator by its major feedback element is bimodal: synaptic depression makes the period of the oscillator almost completely insensitive to feedback over a large range of synaptic strengths, but when that range is exceeded, the effect of the feedback element is switched on. This argues that modulation of synaptic strength below the switch value may be relatively ineffective, but a modulator that alters the kinetics of depression or its recovery could significantly change the position of the switch or the extent of bistability and hysteresis in an oscillatory network.

ABBREVIATIONS

AB

anterior burster

PD

pyloric dilator

IPSP

inhibitory postsynaptic potential