Macaque inferior temporal neurons are selective for disparity-defined three-dimensional shapes

Abstract

Real-world objects are three-dimensional (3D). Yet, it is unknown whether the neurons of the inferior temporal cortex, which is critical for object recognition, are selective for the 3D shape of objects. We tested for such selectivity by comparing responses to stereo-defined curved 3D shapes derived from identical pairs of monocular images. More than one-third of macaque inferior temporal neurons were selective for 3D shape. In the vast majority of those neurons, this selectivity depended on the global binocular disparity gradient and not on the local disparity. Thus, inferior temporal cortex processes not only two-dimensional but also 3D shape information.

The inferior temporal (IT) cortex is part of the ventral visual stream, which is known to be critical for object recognition (1–5). Although objects in the world are three-dimensional (3D), single-cell studies in macaque monkeys have thus far shown only that IT neurons are selective for attributes such as two-dimensional (2D) form, color, and texture (6–10). Very little is known about the selectivity of IT neurons for the 3D structure of objects. Both Gross et al. and Tanaka et al. (6, 8) noted that under monocular viewing conditions, a number of IT neurons responded to 3D objects but not to the corresponding 2D images. However, the animals were anesthetized and paralyzed in these studies, and depth cues, in particular stereoscopic cues, were not manipulated. In fact, Tanaka et al. speculated that some IT neurons might require particular disparity values for their activation. In a similar vein, Perrett et al. (11) reported that IT neurons responded equally to binocular and monocular presentations of real faces. These monocular presentations still contained several depth cues. Hence, previous IT studies, which have been interpreted as suggesting that IT contributes little to depth processing, in particular depth from stereo (12), did not manipulate depth cues systematically.

The relative horizontal positions of the two retinal images of an object (binocular disparity) are among the most powerful depth cues (13–15). In the primate visual cortex, disparity-sensitive neurons are present both in striate cortex (16–17) and in a number of extrastriate visual areas (18–20). This sensitivity indicates only that these neurons can signal position in depth. In the present study, we explicitly manipulated the 3D structure of shapes defined only by binocular disparity. We recorded the activity of single IT neurons in awake fixating rhesus monkeys, while we presented different 3D shapes derived from a single pair of monocular images and found that IT neurons are selective for the 3D structure of shapes.

MATERIALS AND METHODS

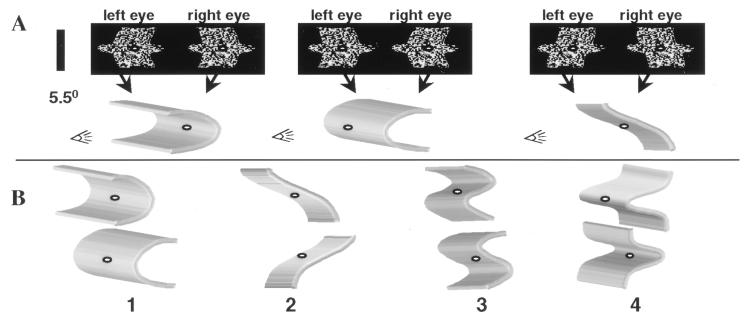
The stimulus set consisted of 64 curved 3D shapes, which were filled with a random dot texture (density 50%, dot size 7.5 arcmin, maximal stimulus diameter 5.5 deg). These shapes had one of eight different depth profiles that were defined by disparity gradients along the vertical axis (Fig. 1). By using disparity gradients along the vertical axis, we avoided introducing texture density gradients (21). The 64 3D shapes were derived from eight different 2D shapes. The dots of each of the eight 2D shapes were horizontally displaced according to one of eight depth profiles (Fig. 1A). These displacements were equal but of opposite sign in the monocular images. Both the shapes’ borders and their inner surfaces were curved in depth, which maximizes the amount of disparity information in the stimuli. The eight depth profiles are grouped into four pairs (Fig. 1B). The members of a given pair use the same two monocular images (Fig. 1A). By interchanging the images presented to the right and left eyes, one creates two 3D shapes that differ only in the sign of their binocular disparity. Yet, the percepts of the members of a pair differ quite dramatically, because concave surfaces become convex (Fig. 1A).

Figure 1.

(A) Monocular images presented to left eye and right eye (Upper) and schematic illustrations of the perceived 3D structure (Lower). Left and Center illustrate a pair of 3D shapes having the same two monocular images. Exchanging the monocular images results in concave surfaces being perceived as convex and vice versa (compare Left and Center). On the Right are shown the monocular images of another 3D shape, derived from the same 2D shape as the two other 3D shapes. (B) Illustration of the eight different depth profiles that are grouped into four pairs (1–4). The profiles of the first three pairs are derived from a sine function, whereas a Gaussian function defines the depth profile of the last pair. Note that in the stimuli used in the experiment, depth was defined by binocular disparity only. Shading and perspective are used merely to illustrate the perceived depth of the stimuli. Moreover, the schematic illustration of the depth profiles does not show the actual borders of the stimulus.

The stimuli were presented dichoptically by means of a double pair of ferroelectric liquid crystal shutters (optical rise/fall time, 35 μs; Displaytech, Boulder, CO), which were placed in front of the monkeys’ eyes. The shutters closed and opened alternately at a rate of 60 Hz each, synchronized with the vertical retrace of the monitor (Barco Medical Workstation Display, Kortrijk, Belgium). Stimulus luminance and contrast (measured behind the shutters operating at 60 Hz) were 0.8 cd/m² (mesopic) and 1 (ΔI/I), respectively. There was no detectable crosstalk between the monocular images. A white fixation target (diameter 24 arcmin) was superimposed on the red stimuli. The fixation distance was 86 cm, and disparity ranged from 1 deg crossed to 1 deg uncrossed. The amplitude of the disparity gradients was chosen to be large but easily fusible to the human observer. They ranged from 1.3 deg for pairs 1 and 4 in Fig. 1B to 0.8 deg for pair 3 in Fig. 1B. In each recording session, three different random-dot textures were generated de novo and were used to fill each of the shapes. Presentation of shapes with different textures was interleaved.

Two male rhesus monkeys participated in the experiments. Both monkeys were emmetropic and showed excellent stereopsis, as demonstrated by means of stereo Visual Evoked Potentials (22). Horizontal and vertical movements of the right eye were recorded with the scleral search-coil technique (23) at a sampling rate of 200 Hz. The animals were trained to fixate a small (0.4 deg) central target. After a fixation interval of 1,000 ms, the stimulus was presented centrally for 800 ms. Only trials in which the monkey had maintained fixation for the entire duration of the trial were rewarded with juice and included in the analysis. The fixation window measured 1.2 deg on a side.

Standard extracellular single-cell recordings were made with tungsten microelectrodes. Recording positions were verified as being in area TE, the anterior part of IT, by combining structural MRI of the brain and computed tomography (CT) with the guiding tube in situ. We measured the distance between the tip of the guiding tube and the temporal bone on the CT images (slice thickness, 1 mm). This was compared with the magnetic resonance images indicating the distance between the temporal bone and different parts of the IT cortex and to the transitions between white and gray matter noted during the recording sessions. Thus, we could ascertain that the recording positions were located in the ventral bank of the superior temporal sulcus and the lateral convexity of the temporal gyrus. Surgical procedures and animal treatment were in accordance with the guidelines established by the National Institutes of Health for the care and use of laboratory animals.

We searched for responsive TE neurons using a subset of 32 3D shapes. These consisted of one member of each of the 32 stimulus pairs, using only the four depth profiles shown in the upper row of Fig. 1B. A responsive neuron was then tested in detail by presenting two pairs of 3D shapes derived from the same 2D shape (Fig. 1A). One of the pairs included the 3D shape to which the neuron responded most strongly in the search test. To determine whether response differences between members of a pair were caused by binocular disparity, monocular images were also presented to the left or right eye alone. In these monocular presentations, the shutters in front of the tested eye were opened at 60 Hz, while the shutters in front of the other eye remained closed. The image sequence displayed was the same as in the dichoptic presentations. Additionally, we tested the neurons with a binocular presentation of the two monocular images superimposed into a single image (binocular superposition condition). All conditions were presented in an interleaved fashion for at least six trials (median number of trials, 10).

Net neural responses were computed trialwise by subtracting the number of spikes counted in a 400-ms interval immediately preceding stimulus onset from the number of spikes in a 400-ms interval starting 100 ms after stimulus onset. ANOVA was used to test the significance of the 3D shape selectivity. To compare the responses to the members of a pair of 3D shapes, we used a post hoc least significant difference test.

Because vergence eye movements may confound the measurement of responses to stereo stimuli, the horizontal position of the right eye was used to detect horizontal vergence movements. Because vergence movements are coordinated eye movements, they should be detectable in eye movement recordings of one eye. This was confirmed by measuring horizontal movements of the right eye elicited by the presentation of a small target at 1 deg crossed or uncrossed disparity. The mean latency of these vergence eye movements was 160 ms, reaching an amplitude of −0.5 and +0.5 deg for near and far targets, respectively, after 430 ms. The match between the amplitude of the vergence eye movements and the disparity of the stimuli strongly suggest that the monkey fused the images of the fixation point. It could be argued that microsaccades during fixation might compensate vergence movements, especially the faster ones elicited by a larger target (24). We compared the dynamics of these two types of eye movements and found them to be very different. Microsaccades during fixation, on average, last only 15 ms with speeds of 15 deg/sec. On the other hand, convergence movements elicited by a 14 deg random dot stereogram presented at +1 and −1 deg last 300 ms with speeds of only 1.5 deg/sec. Thus, recording of a single eye suffices to detect vergence eye movements.

Means and variances of horizontal eye position were calculated trialwise in the same 400-ms intervals as those used for the neuronal responses. For every trial, we computed the difference in mean eye position and in eye position variance between pre- and poststimulus presentation. These differences were averaged over trials. In principle, significant differences in mean eye position could be produced either by eye movements or by a small drift in the eye position signal. A significant poststimulus increase in the variance of the eye position, however, can be the result only of a horizontal eye movement.

RESULTS

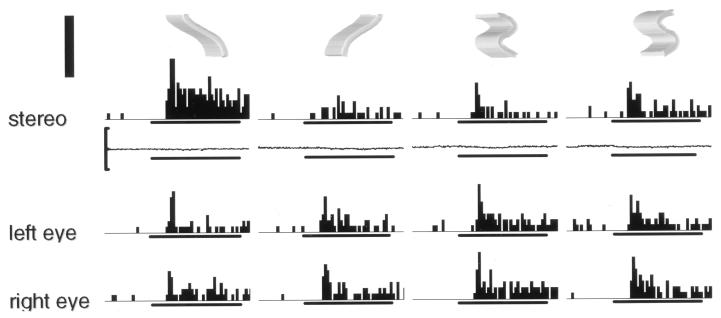
An example of one of the 135 responsive TE neurons is shown in Fig. 2. This neuron responded selectively to the presentation of a 3D shape for which the upper part is tilted toward the observer. This selectivity was significant when statistically comparing responses to the four 3D shapes tested (ANOVA, F(3, 20) = 21.3, P < 0.001). The selectivity is even more apparent when comparing the responses to the two members of the pair of 3D shapes: interchanging the monocular images between the eyes alters the response substantially (post hoc paired comparison, P < 0.001). This marked difference in responses to the two members of the 3D shape pair could not be accounted for by the small differences in the weak monocular responses (compare bottom rows with upper one in Fig. 2). Moreover, the eye movement traces did not differ significantly between stimulus conditions. For the neuron illustrated in Fig. 2, the mean deviation of the eye position between pre- and poststimulus onset intervals was 1.4 and 1.1 arcmin for the preferred and unpreferred shape, and the increases in eye position variance between the two intervals equaled 0.5 and 2.1 arcmin². Therefore, the differences in the neuronal responses cannot result from these nonsignificant differences in eye position.

Figure 2.

Selectivity of a TE neuron for disparity-defined 3D shape. The top row shows profiles of the two pairs of 3D stimuli with which the neuron was tested. The second row shows the peristimulus-time histograms of the neuronal responses to the dichoptic presentation (stereo), together with the mean horizontal eye position in these conditions. The two bottom rows are the responses to monocular presentation of the images to the left eye and to the right eye. The horizontal bars below each histogram and below the eye movement traces indicate the duration of stimulus presentation (800 ms); the vertical calibration along the eye position traces indicates ±1 deg, and the thick vertical bar (top left corner), 80 spikes/sec. Notice the large difference between the stereo responses to the two left-sided 3D shapes. This difference cannot be accounted for by the difference between the sums of the monocular responses.

Forty-four percent of the neurons (59/135) showed significant differences between the responses to the members of a pair of 3D shapes. To decide whether the 3D shape selectivity reflects a selectivity for the monocular images, we computed a stereo difference index, defined as (difference in response in the stereo condition − difference in response in the sum of the monocular presentations)/(difference in response in the stereo condition + difference in response in the sum of the monocular presentations). Positive values of the index indicate that the difference in the stereo conditions exceeds the monocular differences. A value exceeding 1 indicates that shape selectivity is reversed in the monocular conditions. 3D shape selectivity was judged to arise from binocular mechanisms if the stereo difference index was larger than 0.5, i.e., when the difference in response between the dichoptic presentations was at least three times larger than the difference between the sum of the responses to the two monocular presentations. It should be stressed that this index does not compare monocular response strengths to binocular ones, but rather evaluates whether differences between binocular responses can be accounted for by the pattern of monocular responses. The differential response in the stereo condition could be accounted for by a difference in the monocular responses in only three neurons. The remaining 56 neurons were considered 3D-shape selective neurons. Their median stereo difference index equaled 1.17, indicating that, on average, the sum of the responses to the monocular presentations of the preferred 3D shape was even weaker than that for the nonpreferred shape.

To obtain a worst-case estimate of possible differences in eye movements between conditions, we took the largest absolute difference and the largest increase in variance amongst conditions. Averaged over all 3D-shape selective neurons, the maximal absolute difference in the mean eye position equaled 2.5 arcmin (SD = 1.5 arcmin), and the maximal increase in variance was 1 arcmin² (SD = 2 arcmin²). This increase in variance reached significance (ANOVA, P < 0.05) in only 5 of the 56 neurons. For these five neurons, the average eye deviation equaled 2.5 arcmin, and in only one of these five was the interaction between eye deviation and stimulus significant. Because in the overwhelming majority of neurons no significant deviations of the right eye were detected during stimulus presentation, we can conclude that the selectivity for 3D shape cannot be explained by differences in eye movements. Hence, these results show that a sizeable proportion of TE neurons is highly selective for the retinal disparity of curved shapes. It may well be, however, that the exact proportion of selective TE neurons depends on the type of search stimuli used.

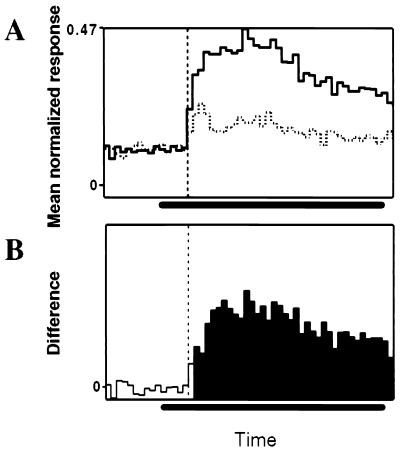
To quantify the degree of 3D shape selectivity, we computed a selectivity index for each neuron, defined as (response to the preferred 3D shape − response to other member of the pair)/(response to preferred 3D shape). For the neurons considered to be 3D shape selective, the median selectivity index was 0.73 (first quartile, 0.60; third quartile, 0.95; n = 56), meaning that the response to the preferred depth profile was on average a factor of 3.7 larger than the response to the other member of that pair. Not only did these neurons exhibit a substantial selectivity, but their selectivity appeared very early after response onset. We computed population peristimulus-time histograms (PSTHs) for the preferred and nonpreferred 3D shape (Fig. 3A). Before averaging, the PSTHs of each neuron were normalized to the highest bin count in either PSTH. The shape selectivity was already statistically significant at 20 ms after response onset (Fig. 3B) and 130 ms after stimulus onset (paired t test, P < 0.002). This early onset of the 3D shape selectivity virtually excludes the possibility that it would arise from vergence eye movements. Indeed, vergence eye movements in monkeys have a latency of at least 60 ms (24, 25), and the latency of the response onset in our sample of TE neurons was 110 ms. Thus, any effect of vergence on the neuronal responses in area TE cannot occur before 170 ms after stimulus onset.

Figure 3.

(A) Population peristimulus-time histogram of 3D-shape selective neurons (n = 56). The solid line represents the population response to the preferred 3D shape and the dotted line, the population response to the nonpreferred 3D shape (bin width, 20 ms). The vertical dashed line indicates the onset of the population response, and the horizontal bar indicates the duration of stimulus presentation. (B) Difference between the normalized responses to preferred and unpreferred 3D shape plotted as a function of time. Open bins indicate nonsignificant differences in normalized response, filled bins, significant differences.

An additional 8% (11/135) of the responsive neurons showed significant differences in responses to members of different pairs but not to members of the same pair (ANOVA comparing the net responses for the four 3D shapes). For 45% (5/11) of these neurons, the shape selectivity could be attributed neither to differences in the responses to the monocular presentations nor to differences in the 2D shape of the superimposed monocular images (comparison to binocular superposition condition). Note that within one pair of 3D shapes, the binocular superposition of the images results in identical 2D shapes for the two members of the pair.

The two members of a pair of 3D stimuli always differed, at least partially, in local disparity. Thus, differences in response to these stimuli could be caused by a tuning for local disparities instead of selectivity for the global 3D shape per se, i.e., the changes in disparity along the vertical axis. For instance, a neuron merely tuned for far disparities would also respond much more strongly to the convex than to the concave stimulus illustrated in Fig. 1A. To determine whether the selectivity for the 3D stimuli could be explained by a mere tuning for local disparities, we presented the preferred and unpreferred 3D shape at five different positions in depth. These positions were chosen so that the disparities within the two types of stimuli overlapped completely (Fig. 4). If a tuning for local disparity underlies the 3D shape selectivity, the responses to the preferred and nonpreferred shape should be similar when the latter is also presented at a position in depth to which the neuron is tuned. As in the first test, the maximal crossed or uncrossed disparity was limited to 1 deg. Therefore, on average, the amplitude of the disparity gradient in this test was reduced by a factor of two. We analyzed the net responses in this test using a two-way ANOVA with position and 3D shape as factors. Only neurons with a significant (P < 0.05) main effect of 3D shape and/or a significant interaction between shape and position in depth (n = 22) were analyzed for changes in 3D selectivity with position in depth.

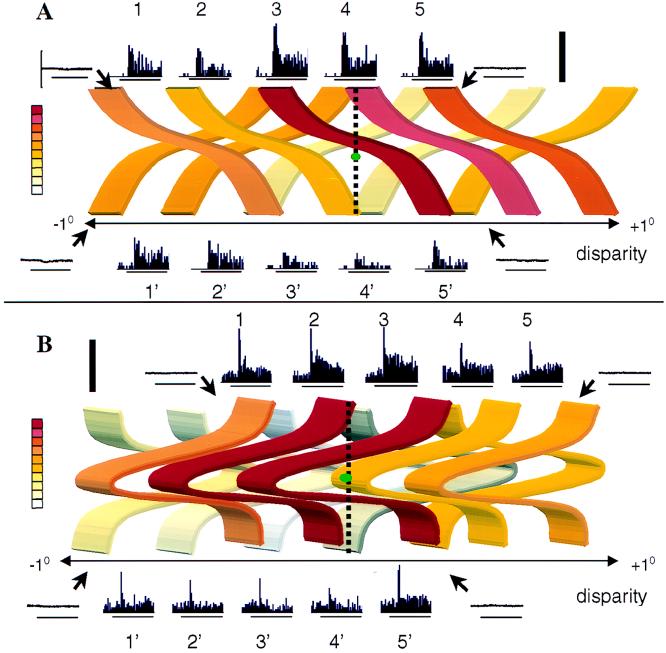
Figure 4.

Neuronal responses in position-in-depth test. (A) Responses of the same neuron as in Fig. 2. (B) Responses of another TE neuron, tested with Gaussian depth profiles. The depth profiles of the stimuli are shown as positioned in depth, and the colors represent the net average firing rate of the neuron: red, 30 spikes/sec; white, 0 spikes/sec. The plane of fixation is indicated by the vertical dotted line (near disparities are to the left, far disparities to the right); the green dot represents the fixation point. The peristimulus-time histograms of the responses to the preferred 3D shape at five positions in depth (positions 1–5) are illustrated on top of the depth profiles, whereas the responses to the nonpreferred stimulus (positions 1′–5′) are shown below. Horizontal bars indicate the duration of stimulus presentation (800 ms), and the thick vertical bar indicates 70 and 100 spikes/sec in A and B, respectively. Eye movement traces are shown for the extreme stimulus presentations (positions 1, 1′, 5, and 5′). The vertical calibration along the eye position trace indicates ±1 deg.

Fig. 4A shows the result of this position-in-depth test for the same neuron as illustrated in Fig. 2. The results of the position test nicely confirm the 3D shape selectivity observed in the standard test, despite the reduction in disparity amplitude (compare positions 3 and 3′ in Fig. 4 to Fig. 2). The response to the preferred shape at position 3 was significantly higher than that to the overlapping nonpreferred shape at any of the positions 1′–5′ (post hoc paired comparison tests P < 0.001). This finding argues strongly against tuning for local disparities as the basis of the shape selectivity, but rather suggests that the global 3D structure of the shape is critical. This conclusion was confirmed by testing flat shapes, i.e., without a disparity gradient, at seven different positions in depth, equally distributed between + and −1 deg disparity. The neuron was not tuned for position in depth of the flat surface (F(6, 56) = 2.04, not significant). Fig. 4B shows a second cell for which the shape selectivity also could not be explained by tuning for a local disparity. Again, the neuron’s response to the preferred shape at position 3 is significantly higher than to the nonpreferred shapes at any position in depth. In contrast to the cell in Fig. 4A, however, selectivity is highest for near disparities (positions 1–4), rather than for far ones. Based on the position-in-depth test, 20 of the 22 neurons tested (91%) were selective for the global 3D structure. This was confirmed by directly testing the local disparity tuning in 15 of the 20 global 3D-shape selective neurons. Four of these neurons did not respond to the flat shape at any of the seven depths tested, and in five others, the response was not significantly affected by the disparity of the flat shape. The remaining six neurons were broadly tuned for disparity (median width at half height, 1.1 deg, which is more than half of the total disparity range in our test).

Again, differences in eye movements between conditions cannot explain the shape selectivity for the two neurons of Fig. 4. For the extreme near and far positions, the maximal deviation in eye position was 4 and 2 arcmin, respectively, and the maximal increase in variance of eye position was 2.7 and 0.5 arcmin². These changes were nonsignificant. For the global 3D-shape selective neurons, the maximal deviation in eye position averaged 2.5 arcmin (SD = 1 arcmin), and the maximal increase in eye position variance averaged 1.9 arcmin² (SD = 2 arcmin²). For only 2 of these 20 neurons was the maximal increase in variance significant. For these two neurons, the average eye deviation equaled 1.5 arcmin, and there was no significant interaction between eye deviation and stimulus condition.

The position-in-depth test also allows us to determine the degree to which the 3D shape selectivity is invariant with respect to changes in the average depth of the shape. We found that for the majority of the global 3D-shape selective neurons (19 of 20 neurons), the shape selectivity depended on the average disparity of the shape. Only one neuron preserved its 3D shape selectivity at each of the five positions in depth (post hoc paired comparison, P < 0.01 for all positions). As shown in Fig. 4, some neurons showed 3D shape selectivity only at positions around the fixation plane (n = 7), while others were shape selective predominantly at near (n = 6) or far (n = 6) positions. Thus, the selectivity was usually restricted to a limited number of depths, although the response to the nonpreferred shape never significantly exceeded the response to the preferred shape at corresponding positions in depth. Of course, this holds only for those neurons responding to global aspects of the 3D shape. The two neurons tuned to a local disparity did show a reversal in shape preference.

DISCUSSION

The present study investigated the selectivity of TE neurons for the 3D structure of shapes. We found that a population of TE neurons was highly selective for disparity-defined 3D shapes, and that this selectivity generally resulted from differences in the global 3D shape, not from differences in local disparities. In the present experiments, we used only large disparity gradients and low-luminance stimuli. However, in subsequent experiments, we were able to show that TE neurons remain 3D shape selective for even small gradient amplitudes and higher luminances.

Because the stimuli we used can evoke eye movements, which can potentially influence the responses of TE neurons, we took great care to exclude the possibility that the selectivity we found merely resulted from differences in eye movements. We recorded the position of the right eye during every test. Given the large difference in dynamics of microsaccades and vergence eye movements, it is extremely unlikely that this measurement would fail to detect vergence eye movements. The poststimulus changes in eye position were nonsignificant in the overwhelming majority of the two tests applied to the 3D-shape selective neurons. Therefore, the eye movement recordings demonstrate that, with the exception of a single test, there were no significant vergence eye movements during stimulus presentation. Moreover, the onset of significant 3D shape selectivity in the population peristimulus-time histograms at 130 ms after stimulus presentation by itself rules out any significant contribution of eye movements to the observed 3D shape selectivity.

It should be noted that our results present no conflict with the selectivity of TE neurons for different views of the same 3D object (26). In many modeling studies of object recognition, 3D objects are represented by a set of 2D views (27). Object views, however, can be represented in two or three dimensions, and in fact our results demonstrate that TE neurons are sensitive for differences in the depth profile of a particular view of an object or object part.

Disparity-selective neurons have been found in early visual areas (16–18), as well as in areas of the dorsal pathway (19–20). Little is known, however, about the processing of disparity in the ventral visual stream. Only unpublished data (quoted in ref. 28) are available for area V4, which is an intermediate area in the visual processing hierarchy and projects to IT. These data suggest that V4 contains local disparity-tuned neurons, which could provide disparity information to anterior IT. Thus, our results provide the first evidence for disparity selectivity in a sizeable proportion of TE neurons. Furthermore, the overwhelming majority of these TE neurons are selective not merely for local disparity but also for disparity gradients.

It has been suggested that the 3D structure of objects is processed in the parietal areas, where it is closely related to the manipulation of objects (29–30). However, in these studies, only the orientation of a planar surface in 3D space was tested with monocular controls (30). Here, we explicitly manipulated the 3D structure of shapes having the same orientation in space and derived from identical pairs of monocular images. We have demonstrated that neurons in the temporal area TE are selective for disparity-defined 3D shapes and that this selectivity arises from processing of the global 3D structure of the shape. The seemingly parallel processing of 3D shape in parietal and temporal areas is likely to be related to two distinct processes, object manipulation and object recognition. To what extent these two cortical regions process different aspects of the 3D structure of shapes remains to be investigated.

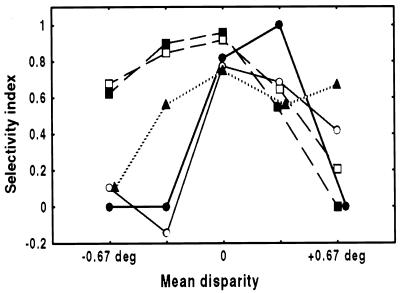
Figure 5.

Selectivity for 3D shape depends on the average depth of the shape. The selectivity index is plotted as a function of the mean disparity for five TE neurons. To prevent spuriously large indices, the index was set to zero for responses smaller than three spikes/sec (which generally did not differ significantly from zero). Solid lines are two examples of neurons where 3D selectivity predominates in the plane of fixation, dashed lines are neurons where selectivity predominates at near disparities, and the dotted line represents an example of a neuron that is selective at far disparities. Open circles and open squares are the neurons shown in Fig. 4 A and B, respectively.

ABBREVIATIONS

IT

inferior temporal cortex

3D

three-dimensional

2D

two-dimensional