Electrostatic effects in unfolded staphylococcal nuclease

Abstract

Structure-based calculations of pK _a values and electrostatic free energies of proteins assume that electrostatic effects in the unfolded state are negligible. In light of experimental evidence showing that this assumption is invalid for many proteins, and with increasing awareness that the unfolded state is more structured and compact than previously thought, a detailed examination of electrostatic effects in unfolded proteins is warranted. Here we address this issue with structure-based calculations of electrostatic interactions in unfolded staphylococcal nuclease. The approach involves the generation of ensembles of structures representing the unfolded state, and calculation of Coulomb energies to Boltzmann weight the unfolded state ensembles. Four different structural models of the unfolded state were tested. Experimental proton binding data measured with a variant of nuclease that is unfolded under native conditions were used to establish the validity of the calculations. These calculations suggest that weak Coulomb interactions are an unavoidable property of unfolded proteins. At neutral pH, the interactions are too weak to organize the unfolded state; however, at extreme pH values, where the protein has a significant net charge, the combined action of a large number of weak repulsive interactions can lead to the expansion of the unfolded state. The calculated pK _a values of ionizable groups in the unfolded state are similar but not identical to the values in small peptides in water. These studies suggest that the accuracy of structure-based calculations of electrostatic contributions to stability cannot be improved unless electrostatic effects in the unfolded state are calculated explicitly.

The stability of most single-domain proteins can be described in terms of a thermodynamic equilibrium between two states, the folded native (N) state and the disordered unfolded (U) state. While our understanding of the structure and properties of the N state has continued to accrue, our knowledge of the U state has lagged behind, owing primarily to the paucity of detailed structural information. Interest in the U state has increased following the recognition that the structural basis of protein stability cannot be understood without understanding both the folded and the unfolded states (Tanford 1968). It has also been spurred by the discovery of possible organization in the U state (Gillespie and Shortle 1997; Pappu et al. 2000; Shortle and Ackerman 2001; Shi et al. 2002; Fitzkee and Rose 2005; Anil et al. 2006) and by the recognition of a biological role for intrinsically disordered proteins and protein aggregates (Dunker et al. 2001; Chiti and Dobson 2006). As interest in the U state has developed, computational models of unfolded proteins have matured. These models have already been useful to address several interesting questions about the elusive ensemble of disordered conformations (Fitzkee and Rose 2004; Jha et al. 2005; Tran et al. 2005; Tran and Pappu 2006), but they have not been used previously to examine the physical character of electrostatic effects in unfolded proteins.

The role of Coulomb interactions in the U state is of special interest because Coulomb forces can be significant over distances comparable to the dimensions of unfolded proteins. Coulomb interactions may induce or destroy structure in the U state (Cho et al. 2004; Cho and Raleigh 2005). Alternatively, pre-existing structure in the U state stabilized by nonelectrostatic forces, such as hydrogen bonding and the hydrophobic effect, may result in significant electrostatic effects in the U state, which could alter electrostatic contributions to protein stability (Tan et al. 1995; Pace et al. 2000). These two possibilities cannot be easily distinguished experimentally.

Because electrostatic interactions perturb the pK _a values of ionizable residues, it is possible to characterize electrostatic interactions in unfolded proteins from their proton (H⁺) binding behavior (Whitten and García-Moreno E. 2000; Lee et al. 2002). Early experiments showed that the pK _a values of ionizable groups in proteins denatured with GdmCl are similar to those of model compounds in water. This was interpreted as evidence for the absence of significant electrostatic effects in the U state (Nozaki and Tanford 1967; Roxby and Tanford 1971), which in turn led to the common practice in structure-based electrostatics calculations of assuming that ionizable groups in unfolded proteins have the same pK _a values as in model compounds (e.g., Ala-X-Ala peptides, where X represents one of the ionizable groups) (Matthew et al. 1985; Bashford and Karplus 1990; Yang et al. 1993; Antosiewicz et al. 1994). This is tantamount to assuming the total absence of electrostatic effects in the U state. The assumption is valid in the very high ionic strengths in the original measurements of pK _a values in GdmCl but not at lower ionic strengths. Recent studies have shown that the pK _a values of ionizable groups in unfolded proteins in water can be different from those of model compounds. This is clear evidence that electrostatic effects can be significant in unfolded proteins.

Two approaches have commonly been used to identify shifts in pK _a values in the U state. The first is to exploit the thermodynamic linkage between stability and H⁺ titration properties of proteins (Wyman Jr. 1964; Tanford 1968, 1970; Schellman 1975). Studies of this type demonstrate that protein stability measured as a function of pH cannot always be reconciled with the stability calculated under the assumption that the ionization properties of the U state are well represented by the pK _a values of model compounds in water (Oliveberg et al. 1995; Swint-Kruse and Robertson 1995; Tan et al. 1995; Kuhlman et al. 1999; Whitten and García-Moreno E. 2000). Such studies do not measure pK _a values in the U state directly, but it is possible to infer that the pK _a values of acidic groups in the U state are depressed by 0.3–0.4 units on average (Oliveberg et al. 1995; Tan et al. 1995). A second approach to studying the pK _a values of ionizable groups in the U state is to measure them directly using nuclear magnetic resonance spectroscopy. When pK _a values of carboxylic groups in the unfolded drkN SH3 domain were measured in this way, they were indeed found to be shifted, but by less than 0.4 units (Tollinger et al. 2002, 2003). Small shifts less than 0.4 have also been documented in disordered peptide fragments extracted from native proteins (Kuhlman et al. 1999; Pujato et al. 2005).

Significant Coulomb interactions in the U state can be explained in terms of persistent structure that brings charges closer than they would be in a random coil. It is also possible that they are simply a reflection of the high effective concentration of charge imposed by the random-flight properties of the unstructured polypeptide chain. If this were the case, compaction or residual structure would not need to be invoked to explain the presence of strong electrostatic effects in the U state; the perturbation of pK _a values would be a consequence of the many weak and random Coulomb interactions present in the disordered chain. This is precisely what three different types of computational models have suggested: (1) Calculations with an artificially expanded protein have shown that compaction is not necessary for Coulomb interactions to perturb pK _a values (Elcock 1999); (2) a Gaussian-chain model that assumes the distance between pairs of ionizable residues is well represented by a distribution derived for a random coil is also able to reproduce many of these effects (Zhou 2002a,b, 2003); and (3) the shifts in pK _a values in the U state can also be reproduced by a model in which charges are placed randomly on an expanded low-dielectric sphere (Kundrotas and Karshikoff 2002, 2004).

These three different models suggest that a random cloud of ionizable residues is sufficient to explain the significant Coulomb effects observed in the U state. However, none of the models include an accurate representation of the protein structure; therefore, none of them is useful to examine the possible role of electrostatics as an organizing force that could modulate the structure or dimensions of the U state. These models are also not useful to examine the magnitude of electrostatic effects in partially ordered U states; all three would fail to reproduce the pK _a values of ionizable groups in U states containing persistent structure stabilized by Coulomb interactions.

This is the problem that is addressed by the present study. Our computational approach combines a rigorous treatment of electrostatic interactions with four different structural representations of the U state ensemble state of a protein. The four different models that were used are already known to reproduce certain statistical properties of unfolded proteins accurately. None of them explicitly includes any type of electrostatic effects. The models differ in the amount of disorder allowed in the U state (Fitzkee and Rose 2004; Jha et al. 2005; Tran et al. 2005; Tran and Pappu 2006). In the present work, each of these four models was used to generate the U state ensemble of a protein. Electrostatic energies were calculated for each structure in each U state ensemble using a simple Coulomb potential that has been shown to reproduce Coulomb effects in proteins (Linderstrøm-Lang 1924; Lee et al. 2002). More rigorous calculations of electrostatic energies were also performed with the finite difference solution of the linearized Poisson-Boltzmann equation to demonstrate that the simple Coulomb potential was appropriate for our purposes (Antosiewicz et al. 1994). The electrostatic energies were used to Boltzmann-weight the ensembles, and a mean-field approximation was then used to calculate the pK _a values of ionizable groups (Roxby and Tanford 1971).

The present calculations focus on the electrostatic properties of staphylococcal nuclease (SNase). This protein was selected because the H⁺ titration of its U state in water has been measured using the T62P variant. T62 is located in the middle of the first helix (Fig. 1). The T62P variant is highly destabilized, it exists in the U state in water over a wide range of pH, and it can be refolded with osmolytes into an N state indistinguishable from the folded wild type (Baskakov and Bolen 1998). This variant is a useful model for the U state of SNase in water because it exhibits all the physical attributes of chemically denatured SNase but avoids the complications related to the presence of denaturants. By comparing the H⁺ titration behavior of the T62P variant measured with direct potentiometric methods in 0.1 M KCl (Lee 2001) with the calculated behavior, we were able to test the validity of the structure-based calculations with the unfolded ensemble.

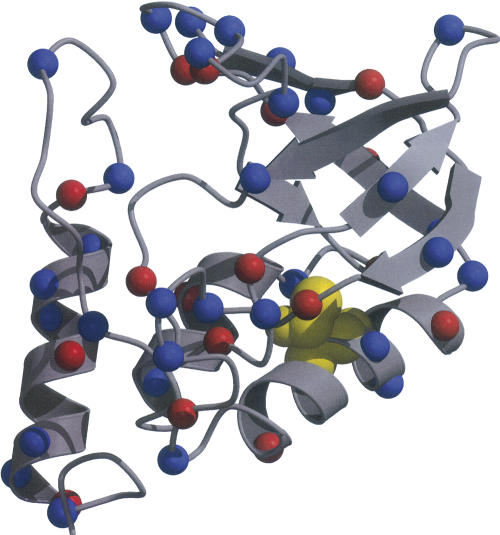
Figure 1.

Structure of native SNase with red and blue spheres to identify the C_α atoms of acidic and basic residues, respectively. Thr 62 is shown in yellow CPK spheres (Kraulis 1991; Merritt and Bacon 1997).

After calibration against experimental data, the calculations were used to address four fundamental questions about electrostatic effects in the U state: (1) What is the magnitude of Coulomb interactions in unfolded proteins? (2) What are the electrostatic consequences of organization in the U state, and, conversely, can Coulomb interactions organize the U state? (3) Is it appropriate to assume that ionizable groups in the U state titrate with the pK _a values of model compounds in water? (4) If the pK _a values of simple model compounds in water (e.g., peptides or blocked amino acids) are not appropriate to describe the pK _a values of ionizable groups in the U state, are structural models of the U state necessary to correct for electrostatic effects in the U state, or are simpler, more abstract models sufficient?

Results and Discussion

Generating U state ensembles

Four different structural ensembles representing the U state of SNase were used in this study: (1) In the rigid segment (RS) ensemble, SNase was held in its native conformation except for φ, ψ torsions at 12 residues. To construct this ensemble, these 12 residues sampled sterically allowable conformations, as described previously (Fitzkee and Rose 2004). (2) In the coil library (CL) ensemble, backbone conformations were chosen randomly from a database of non-helix, non-strand conformations in folded proteins (Jha et al. 2005), and side chain conformations were generated using a graph-theoretic approach described previously (Canutescu et al. 2003). (3) In the excluded-volume limit (EV) ensemble, independent structures were generated by sampling sterically allowable φ, ψ values, as outlined previously (Tran and Pappu 2006). (4) In the EV limit ensemble with hydrogen bond satisfaction (EV/HBS), all atomic overlap was avoided and all hydrogen bonds were satisfied, either internally with protein or externally with solvent (Fitzkee and Rose 2005; Fleming and Rose 2005). In both the EV and EV/HBS ensembles, side chain conformations were chosen from a library of rotamers (Lovell et al. 2000).

Two other models were also studied to serve as reference: (1) In the extended model, all backbone and side chain torsion angles were set to maximally extended values. Presumably the distance between charges is maximal in this model, thus it sets a physical limit to how weak Coulomb interactions could be. (2) In the exploded model, atoms were expanded isotropically about the geometric center until the radius of gyration (R_G) of 37.2 Å of unfolded SNase (Kohn et al. 2004) was obtained. This model is qualitatively similar to that of Elcock, except that energy minimization was not performed and realistic bond lengths were not conserved (Elcock 1999).

Each of the four statistical ensembles consisted of 10,000 structures. Electrostatic energies were calculated for each structure in each ensemble with a simple Coulomb formalism or with the more rigorous solution of the linearized Poisson-Boltzmann equation by the method of finite differences. The structures in the ensemble were Boltzmann-weighted by electrostatic energies to account for electrostatic contributions to the U state.

Comparison of calculated and measured proton binding behavior

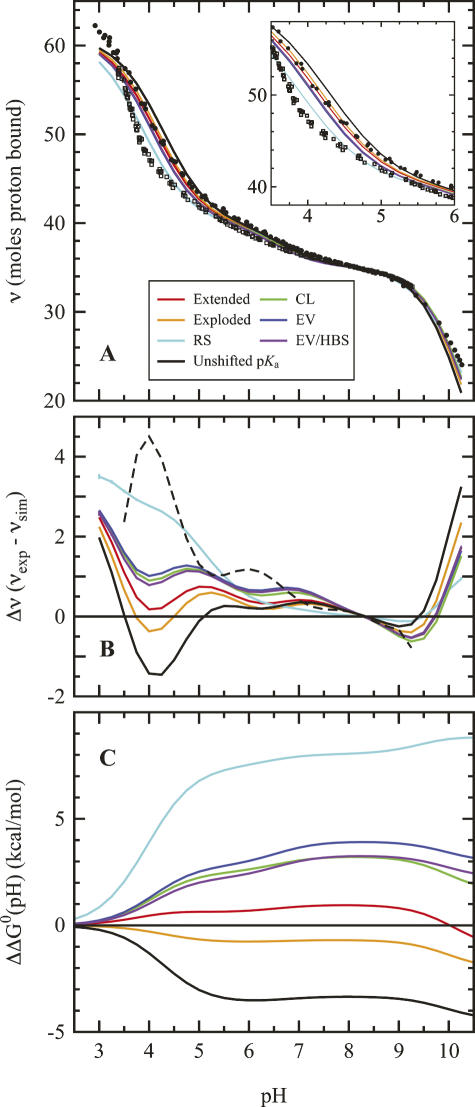
The electrostatic properties of proteins are reflected in their H⁺ binding properties. This is illustrated by the differences between the H⁺ titration curve of the unfolded T62P protein in 0.1 M KCl, shown as solid circles in Figure 2A, and the titration curve of the WT native state under identical conditions, shown as open squares. At pH values below pH 8, the U state binds more H⁺ than the N state because the pK _a values of histidines and carboxylic residues in the N state are depressed relative to the values in the U state represented by the T62P protein. Analysis of the titration curve of T62P as a sum of H⁺ binding isotherms showed that the curve can be reproduced approximately by assuming all residues of the same type titrate with identical pK _a values shifted by 0.1–0.2 units from the set of model compound values in water listed in the Materials and Methods section, which are used in many structure-based calculations. The pK _a values of acidic residues are depressed and those of basic residues are elevated, suggesting that in the U state of this protein the net Coulomb interactions are attractive.

Figure 2.

Comparison of measured and calculated H⁺ binding energetics to the unfolded T62P variant of SNase. Solid curve represent the H⁺ binding of T62P SNase, calculated with the RS (cyan), CL (green), EV limit (blue), and EV/HBS (violet) ensembles. Calculations with the extended and exploded structures are in red and orange, respectively. Calculations using the set of pK _a values of model compounds described in the Materials and Methods section are shown in black. (A) H⁺ binding curves over the experimentally relevant region. Solid circles represent the measured H⁺ titration curve of unfolded T62P nuclease in 0.1 M KCl, and open squares are titration measurements for the folded wild-type SNase in 0.1 M KCl. The inset shows a close-up of the acid titration region; even in these plots the CL, EV, and EV/HBS ensembles nearly overlay. (B) Computed difference between the experimental and calculated H⁺ binding curves, superimposed arbitrarily at pH 8.5. The broken line shows the difference between the N and U states in SNase. The standard error of the mean of five independent H⁺ binding calculations is maximal at pH 4.5, where it is ≈ 0.4 H⁺. (C) Free energies obtained by numerical integration (Equation 1) of H⁺ binding curves starting from pH = 0 (i.e., 1 M H⁺ reference state). The data describe the differences between H⁺ binding curves calculated from pK _a values of the unfolded ensemble, and the set of pK _a values obtained by analysis of the experimental H⁺ binding curve. Standard error of the mean is ≈1.2 kcal/mol for each data point.

The H⁺ titration curve of T62P suggests that net Coulomb interactions in the U state are weak even in a highly charged protein such as SNase, but it does not provide a structural explanation for this observation. To establish how the structure of the U state ensemble governs its electrostatic behavior, the H⁺ binding behavior of the U state ensembles generated with four different models were compared directly with the experimental curve of T62P. Solid colored lines in Figure 2 show the calculated titration curves for each ensemble. Differences between experimental and calculated curves are plotted in Figure 2B, and the Gibbs free energy represented by these differences are shown in Figure 2C.

The experimental H⁺ binding data with T62P were useful to validate calculations on the U state of SNase. Our ensemble calculations reproduce the experimental titration curve of T62P over a wide range of pH. With the exception of the RS ensemble, the calculated and experimental curves agree to within one H⁺. The disagreement between all models and the experimental data at low pH (<3.5) is not relevant. It reflects the fact that the quality of the experimental data deteriorates as water becomes a better H⁺ buffer than protein at low pH (Oliveberg et al. 1995; Whitten and García-Moreno E. 2000). The discrepancy between the measured H⁺ binding data and the set calculated with the RS ensemble reflects the unrealistic amount of native secondary structure retained in this ensemble. The other ensembles reproduce the experimental behavior equally well; no ensemble is clearly better than the others. Surprisingly, the static, maximally extended representation and the exploded representation of the U state perform better than all of the more realistic ensembles, which tend to overestimate the shifts in pK _a values. Also included in Figure 2 are curves calculated with the set of model compounds used in the calculations. These curves underestimate the shifts in pK _a values. Note that the differences between the measured and the calculated H⁺ binding curves are determined partly by the set of model compound pK _a values that are used as reference (Thurlkill et al. 2006).

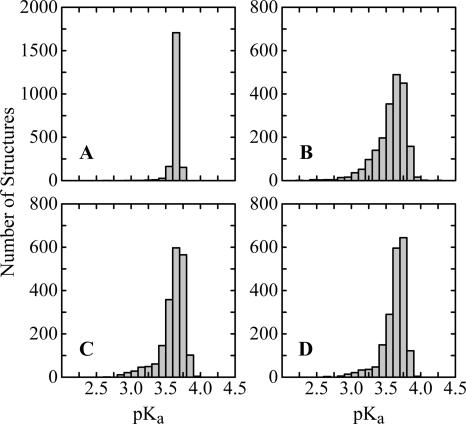
None of the ensembles used in the calculations sample the vast conformational diversity of the U state exhaustively. However, sampling is sufficient to ensure convergence in the predicted electrostatic behavior. This is implied by the close agreement between calculated and experimental data, especially across such structurally diverse ensembles. Additionally, the H⁺ binding curves presented here are actually the average from five sets of independent calculations, and the standard deviation of this average was generally very low (<0.4 H⁺). The standard deviation of pK _a values was even smaller (<0.01). Histograms of pK _a values show more significant perturbations for some structures, indicating the presence of strong electrostatic interactions in some of the structures in the ensemble (Fig. 3). This is evidence that structural states in which Coulomb interactions are strong are sampled in each ensemble. In the case of Asp 83 illustrated by Figure 3, the calculated pK _a values below four indicate that this Asp is sampling favorable electrostatic environment in most structures in the ensembles. Other residues occasionally sample states where electrostatic interactions are less favorable (data not shown). Apparently these states contribute only marginally to the Boltzmann-weighted ensemble. Finally, the conclusions were unaffected even when the most compact 10% of each ensemble was used in the calculations (R_G ≈ 36–38 Å). These observations suggest that the sampling is sufficient for the purpose of these calculations.

Figure 3.

Histograms of calculated pK _a values of Asp 83. (A) RS ensemble; (B) CL ensemble; (C) EV ensemble; (D) EV/HBS ensemble. The histograms illustrate that conformations with significant interactions, while sampled, do not contribute significantly to the Boltzmann-weighted ensemble average. Note the different scale for the ES ensemble histogram. These histograms were representative of those observed for other titratable residues.

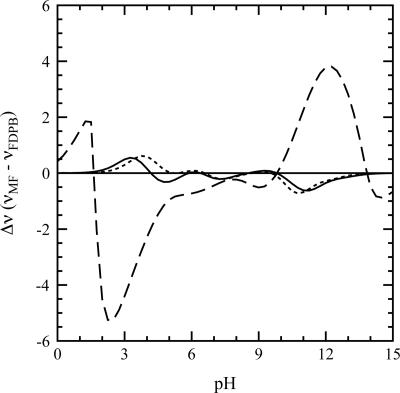
The agreement between the calculations and the experiments has several implications about electrostatics of the U state. It implies that electrostatic effects in the U state are governed by Coulomb interactions and that hydration effects and charge-dipole energies, which are ignored in our calculations, and which are known to be important determinants of pK _a values in folded proteins, are insignificant in the unstructured and extensively hydrated U state. The agreement between calculations and experiments also implies that the mean-field approximation used in the calculations to describe coupling between H⁺ binding sites is adequate (Bashford and Karplus 1991). The validity of these two statements was further corroborated by the agreement between the calculations based on a simple Coulomb potential and the ones performed with the more sophisticated finite-difference Poisson-Boltzmann method on a subset of the EV ensemble (Fig. 4).

Figure 4.

Impact of the mean-field approximation on H⁺ binding in the EV/HBS ensemble. The curves depict the difference between the mean-field and FDPB electrostatic treatment at 0.0 M (long dashes), 0.1 M (solid line), and 1.0 M (short dashes) ionic strength. Although significant systematic errors arise at low salt concentrations, the mean-field approximation is valid for the ionic strength used here (0.1 M). See Materials and Methods for more details.

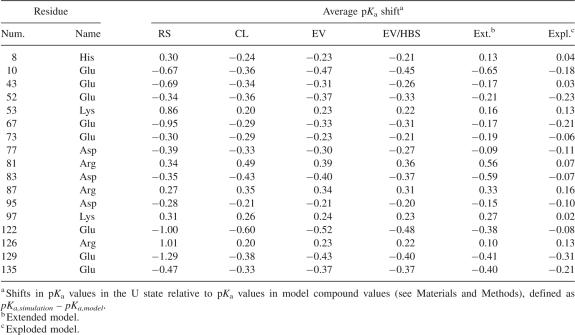
pKa values in the U state of SNase

The pK _a values of the 61 titratable groups in SNase were calculated and averaged over all structures in each U state ensemble. Table 1 lists residues where the pK _a values were shifted by more than 0.2 units in most of the different ensembles (the complete list of shifts in pK _a values is provided as Supplemental material). For most residues the shifts in pK _a values were small. The pK _a values of acidic residues were depressed and those of basic residues were elevated, suggesting that net Coulomb interactions in the U state of SNase are stabilizing. The RS ensemble typically yielded larger shifts (e.g., Glu 129) owing to the presence of residual, native Coulomb interactions between residues in the same rigid segment. Only 17 (∼28%) residues consistently had pK _a shifts less than 0.2. No experimental pK _a values are available for unfolded SNase, but our results are consistent with the depression of pK _a values of carboxylic groups by 0.1–0.4 observed experimentally in other proteins in the U state (Oliveberg et al. 1995; Tan et al. 1995; Tollinger et al. 2003). Our calculations produce similar shifts: In the RS ensemble the pK _a values of carboxylic groups are depressed on average by 0.37 pK _a units, and in the CL, EV, and EV/HBS ensembles they were depressed by 0.21, 0.22, and 0.20 pK _a units, respectively. Note that the shifts in pK _a values calculated with the U state ensembles are highly correlated with those calculated with the Gaussian chain model (Zhou 2002b). As expected, the correlation between pK _a shifts is higher for the more random EV and EV/HBS ensembles (R = 0.97 and R = 0.96, respectively), than for the CL (R = 0.92) and RS ensembles (R = 0.74).

Table 1.

Selected pK_a shifts calculated with U state models

The shifts observed in U state pK _a values relative to those of model compounds reflect weak Coulomb interactions. The Boltzmann-weighted electrostatic free energy of the RS ensemble at pH 7 is favorable by 5.7 kcal/mol. This value is lower for all other models, and the minimum value, 2.4 kcal/mol, is observed in the EV/HBS ensemble. These are small energies, and the pK _a shifts are similarly small. The calculated shifts in pK _a values in the U state also show that favorable Coulomb interactions in this state are small compared with other factors in folding. Even in the highly organized RS model, the shifts in pK _a values are consistent with weak Coulomb interactions. However, there are cases where Coulomb interactions in the U state ensemble appear to be significant. For example, the shifts in pK _a values of equal magnitude and opposite sign for residues Arg 81–Asp 83 and Asp 95–Lys 97 indicate a persistent favorable Coulomb interaction between these pairs of residues in all U state ensembles. The removal of either one of these groups by mutagenesis has no significant impact on the stability of the protein (Meeker et al. 1996). This is explained by the present calculations, which suggest that the Coulomb interaction between these pairs of neighboring residues does not stabilize the N state because the interaction persists in the U states. This is an example of how detailed knowledge of electrostatic effects in the U state is necessary to explain the contributions to stability by interactions observed in the crystal structure representing the N state.

Although the differences in the pK _a values of model compounds in water and in the U state ensemble are small, these small differences can represent a significant effect when they are present in many ionizable groups. The free energy stored in the sum of the shifts in pK _a values was calculated using pH 0 (i.e., 1 M H⁺) as a reference state and the following functional form (Wyman Jr. 1964):

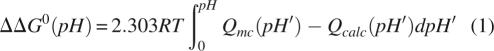where Q_mc is the number of moles of H⁺ bound per mole of protein, calculated with the pK _a values obtained by analysis of the experimental H⁺ binding curve; Q_calc is the number of bound H⁺ calculated for the U state with the structural ensembles. The curves calculated with this expression are plotted in Figure 2C. Each curve describes how the shifts in pK _a values are reflected in stability. The plot may be interpreted in the following way: If the U state were best represented by the RS ensemble, the pH dependence of stability calculated using model compound pK _a values could be in error by up to 8 kcal/mol at pH 7. The difference is smaller if the U state is represented by the more realistic CL or EV limit ensembles, but at pH 7 the calculation with these ensembles could be off by 3–4 kcal/mol if pH 0 were chosen as a reference. The errors would be even larger if the pK _a values of model compounds in water were used as reference instead of the pK _a values obtained by analysis of the experimental H⁺ binding curve. This implies that even though Coulomb interactions in the U state are weak according to the calculations with ensembles, use of model compound pK _a values to represent the U state can lead to inaccurate calculations of the pH dependence of stability (Fitch et al. 2006).

The pH dependence of stability calculated with the pK _a values of model compounds in water, using as reference the set of pK _a values obtained from the experimental H⁺ titration curve, is also shown in Figure 2C (black curve). This curve shows that the assumption that pK _a values in the U state are not shifted is also incorrect. Many small shifts in pK _a values distributed over a large number of residues can lead to significant errors (Fitch et al. 2006). This underscores the need for explicit treatment of electrostatic effects in the U state to enhance the accuracy of structure-based calculations of the pH dependence of stability of proteins. It also underscores the need for further experimental measurements of pK _a values in model compounds in water. This is necessary to examine how neighboring amino acids can affect the pK _a value of an ionizable group in a small peptide.

Role of Coulomb interactions as an organizing force in the U state

Previous calculations, such as those with the Gaussian chain model, assume the distances between charges in the U state are well characterized by a Gaussian chain. On the other hand, our calculations make no assumptions whatsoever about the spatial distribution of charges in the U state. In our model, these distances were calculated directly in each structure in each of the four different U state ensembles; therefore, we are able to probe the structural origins of the shifts in pK _a values.

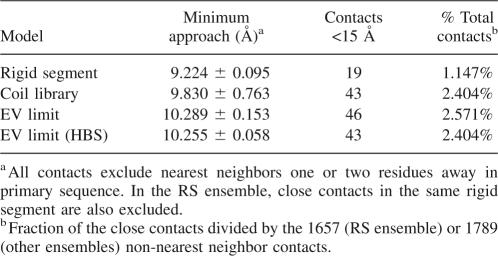
The suggestion that specific Coulomb interactions can prevail in the U state (Cho and Raleigh 2005) was tested by evaluating contributions to the pK _a values by ion pairs and by medium- and long-range Coulomb interactions. This involved calculation of the Boltzmann-weighted average distance of closest approach between all titratable atoms. Table 2 presents a summary of these distance calculations for all ionizable residues separated by more than two residues in primary sequence. In no ensemble were average distances shorter than 9 Å observed. Furthermore, the number of contacts smaller than the Debye length (∼15 Å at 0.1 M ionic strength) was small. Although ion pairs were found in some individual structures in each ensemble, the significance of these interactions was minor owing to the vast number of U state conformations sampled. According to our calculations, the shifts in pK _a values in the U state are governed by nonspecific, long-range interactions. The agreement of all ensembles on this point, even the RS ensemble, supports the idea that Coulomb interactions are too weak to drive specific organization in the U state ensemble, even though they may be influenced by other local organizing forces. In unfolded SNase, the existence of long-range ion pairs appears to be highly unlikely.

Table 2.

Close contacts between charges in the U state ensembles

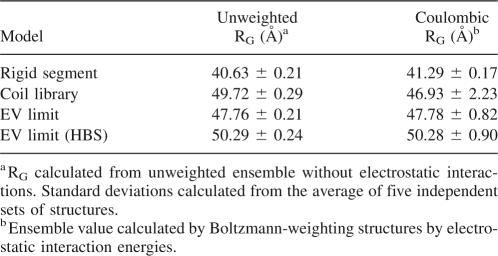
Another way to explain the impact of Coulomb interactions on the average structure of the U state is to determine whether Coulomb interactions are sufficiently strong to expand or condense this state. Although medium- and long-range Coulomb interactions between individual pairs of charges in the U state are individually weak, the sheer number of such interactions could exert an influence on the dimensions of the U state ensemble. If this were the case, this would imply that electrostatic effects could bias the conformational search during folding. A natural metric to consider for this purpose is the R_G, a measure of the dimensions of the U state ensemble (Flory 1953). Table 3 shows the R_G calculated for each of the U state models, with and without Coulomb interactions at pH 7. These calculations show unequivocally that Coulomb interactions do not exert an influence on the dimensions of the U state at neutral pH, thereby ruling them out as a means of preorganizing the U state. The CL ensemble is the one exception; the calculations detected a slight compaction of this ensemble as a result of electrostatics in the U state. Two factors indicate this is not significant: First, the standard deviation from the CL calculations is large and the difference in compaction is probably not statistically meaningful. Second, under the assumptions of Flory-Huggins theory, there is no entropic difference between confinement in a 50 Å sphere versus that in a 45 Å sphere (Flory 1953; Dill 1985). It is therefore unlikely that electrostatic forces can compact the unfolded chain at physiological pH, and even if marginal compaction does occur, it is not sufficient to preorganize the folding reaction.

Table 3.

U state compaction with and without electrostatics

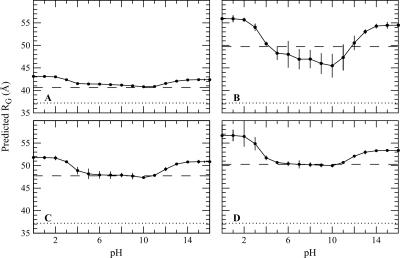
The behavior is different at extremes of pH, where proteins have high net charge. An expansion of the ensemble can be expected under those conditions. This was tested by calculating the pH sensitivity of the Boltzmann-weighted R_G. The dependence of R_G of SNase on pH is shown in Figure 5. Although the different ensembles respond differently to changes in pH, they all share the expected features: The R_G for all ensembles increases at low and high pH values, consistent with expansion of the U state under these conditions. The origins of the notable difference between the behavior of the CL ensemble and of the other ensembles are not obvious. In contrast, the insensitivity of the RS ensemble to changes in pH can be interpreted structurally: In the RS ensemble, the segments of native structure impose a physical limit to how much the ensemble can expand.

Figure 5.

pH sensitivity of the radius of gyration (R_G) calculated with (A) RS ensemble; (B) CL ensemble; (C) EV ensemble; (D) EV/HBS ensembles. The solid lines are only meant to guide the eye. The broken line in each panel represents R_G when electrostatic effects and their pH sensitivity are ignored. The experimentally determined R_G for chemically denatured SNase is shown as a dotted line (Kohn et al. 2004).

The effect of pH on R_G predicted by the calculations is reminiscent of the behavior of the molten-globule state. The molten globule of many proteins can be obtained by exposing the acid-U state to high salt concentration (Ohgushi and Wada 1983). It can also be formed at extremely low pH values, where all titratable groups are protonated and where Coulomb interactions are screened either by site-specific binding or through the ionic strength effect governed by the high concentrations of Cl⁻ resulting from the HCl used to achieve low pH (Goto and Fink 1990; Goto et al. 1990). Our calculations reproduce this behavior qualitatively (data not shown), but because in our calculations the U state is modeled, and not the transition from N to U, the effects are much less pronounced. Our predictions of the effects of pH on R_G apply to a state that is already unfolded, not to the expansion of the N state as it is unfolds at low pH. The present calculations suggest that the chemically denatured state of SNase should be somewhat larger at pH 2 than at neutral pH. To test these predictions it will be necessary to measure the R_G of the U state at several pH values in a nonionic denaturant, such as urea.

The behavior predicted by the ensemble calculations is reasonable for two reasons. First, it makes intuitive sense. Despite being highly solvated, the peptide chain will probably expand somewhat when it has a net charge of +40e (at low pH) or −21e (at high pH). Second, it suggests a structural explanation of the pH sensitivity of m-values obtained by analysis of chemical denaturation titrations by the linear extrapolation method. Under conditions where a molten-globule intermediate is not formed, the m-value typically increases at low pH (Whitten et al. 2001). This has been rationalized in terms of the expansion of the U state that is observed in our calculations (Pace et al. 2000). Although the experimentally measured R_G for SNase is smaller than the value calculated with the ensembles (Kohn et al. 2004), the change in R_G with pH may prove to be a useful experimental probe of the U state.

Conclusions

Our calculations show that weak Coulomb interactions are unavoidable in unfolded proteins. Even when the U state is modeled as an artificial, static, fully extended structure, charges are not completely screened from each other in 100 mM ionic strength. These weak Coulomb interactions can lead to small shifts in the pK _a values of ionizable groups in the U state relative to the values of model compounds in water. In the U state of SNase, the pK _a values are shifted on average by 0.2–0.3 pK _a units. This is fully consistent with experimental observations in other proteins and with previous predictions for SNase. Therefore, the pK _a values measured in model compounds in water should not be expected to represent those in the U state of proteins. Although the shifts in the pK _a value of individual groups are small, small shifts in many ionizable groups can lead to a significant effect. For this same reason, more measurements of pK _a values in model compounds (i.e., small peptides in water) will be needed to describe how the canonical values are affected by the chemical nature of the host peptide.

The structural calculations suggest that it will be necessary to treat electrostatic effects of the U state explicitly to improve the accuracy of structure-based calculations of pH effects on protein stability. In the case of unfolded SNase there is excellent agreement between the pK _a values calculated by our structural model and those calculated with the Gaussian chain model of Zhou (2002b) or the statistical model of Kundrotas and Karshikoff (2002^{, 2004}), presumably because the U state of SNase is highly unstructured. We anticipate that our calculations will allow more realistic predictions in cases where the U state has persistent local structure (Cho and Raleigh 2005). Calculations in other proteins will be necessary to determine whether structure-based calculations such as the ones presented in this paper will be necessary for this purpose, or if simpler calculations, for example, the Gaussian chain model or the fully extended model, will be sufficient.

The long- and medium-range Coulomb interactions that govern electrostatic effects in the U state are too weak to influence the structure of the U state ensemble at neutral pH. However, at the extremes of the pH range, repulsive interactions can expand the U state. Calculations and experiments in other proteins will be necessary to assess whether the behavior of SNase in this respect is representative of all proteins.

Finally, electrostatic effects in the U state are not useful to gauge the merits of different structural models of the U state. Here, we have compared computed H⁺ binding curves with those experimentally measured in an unfolded variant of SNase. The H⁺ binding behavior of the RS ensemble is distinguishable from that of the other ensembles, but even this highly organized ensemble exhibits small perturbations in pK _a values on average, and it possesses approximately the same electrostatic properties as the other ensembles. The other ensembles—L, EV, and EV/HBS—are practically indistinguishable from each other in terms of H⁺ binding properties, and these ensembles are all consistent with the experimental data. Our calculations cannot probe the merits of these ensembles in structural terms. This is likely to be a limitation of electrostatic measurements in general: Because Coulomb interactions in the U state are so weak, making fine structural distinctions between different models of the U state will be extremely difficult. On the other hand, the data suggest that the calculated effects of pH on R_G will be useful to assess the relative merits of different structural models of the U state.

Materials and Methods

U state ensembles

Four different ensembles were generated to model the U state. All ensembles contained 10,000 structures. The RS ensemble was constructed as described previously (Fitzkee and Rose 2004). Using the native structure in PDB ID 1STN (Hynes and Fox 1991), the structure was treated in terms of independent, rigid segment with flexible torsions at only the following residues: 11, 20, 29, 38, 50, 60, 68, 75, 86, 95, 109, and 120. Because this structure does not contain residues 1–5 or 142–149, the titratable residues Ala 1 (NT), Lys 5, Glu 142, Asp 143, Asp 146, and Gln 149 (CT) were added to the structure at infinite separation for electrostatics calculations. The CL ensemble was implemented as described by Jha et al. (2005) with nearest neighbor effects included. Independent structures containing the entire peptide backbone were generated using software downloaded from the authors' Web site (http://unfolded.uchicago.edu/), and side chains were added using the SCWRL3 program (Canutescu et al. 2003).

The EV limit ensemble was computed based on work by Pappu and coworkers (Tran et al. 2005), with several modifications to improve performance in generating structures. First, instead of Boltzmann-weighting with a soft-sphere potential, the validity of each structure was determined based on hard-sphere steric overlap. Structural snapshots were taken after every 223 successful moves, and autocorrelation analysis of internal coordinates confirmed that snapshots were conformationally independent. Side chain moves were selected from a rotamer library by Lovell et al. (2000). These changes resulted in an ensemble of structures that was similar to calculations by Tran et al. (2005) by all metrics tested. For example, Tran et al. (2005) calculate the R_G of SNase to be 50.6 ± 0.7 Å (Tran et al. 2005), and our calculations yield an R_G of 47.8 ± 0.2 (Table 3). The EV/HBS ensemble was generated independently, using an additional constraint of enforcing hydrogen bond satisfaction. Briefly, the backbone must either hydrogen bond to the protein itself or to water molecules positioned at sterically accessible locations near the carbonyl and amino groups in the peptide bond (Fitzkee and Rose 2005; Fleming and Rose 2005; Fleming et al. 2005).

In addition to these four ensembles, calculations were also performed on two static structures. The first of these was an extended chain. Backbone torsions were assigned φ, ψ values of −120°, 120°, except for Pro residues, which were assigned to have backbone torsions of −70°, 120° because of steric constraints. Side chains in this model were extended to avoid steric overlap. The second of the static structures expanded the folded protein isotropically from its geometric center. This “exploded” model started with 1STN and scaled the vectors between all atoms and the center of the protein by a factor 2.55 to yield a structure with a R_G of 37.4 Å. This value closely matches the R_G of chemically denatured SNase (Kohn et al. 2004). Once again, titratable groups not found in the crystal structure were added at infinite separation, as described above. Bond lengths and other geometric parameters, as well as hard sphere radii for all but the CL ensemble, were taken from the LINUS molecular simulation package (Srinivasan et al. 2004).

Boltzmann-weighting of ensembles with Coulomb energies

The polypeptide in the U state is highly disorganized. For this reason it was assumed that the titratable groups in the U state ensembles are fully hydrated and that contributions by the self-energy to the pK _a values could be ignored. The free energy of pairwise interactions between charges q_i and q_j, ΔG^o_ij,_elect, was calculated with Coulomb's law with the dielectric constant ε equal to that of water, 78.4. It is expressed in units of kcal/mol,

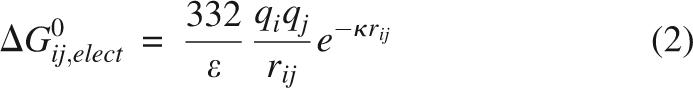where r_ij is the distance between the charged atoms (Å) and κ is the Debye-Hückel parameter, proportional to the ionic strength. ε = 78.4 was used for these calculations because this dielectric constant is the one that best describes pairwise Coulomb interactions on the surface of SNase in the N state (Lee et al. 2002). Because this dielectric constant reproduces the magnitude of Coulomb interactions in the fully folded form of SNase, there was no physical basis for using lower values of ε to describe interactions in the U state, where charged groups are presumably even better solvated and where there is no well-defined dielectric cavity. All simulations were performed at 0.1 M ionic strength. In Glu, Asp, His, and Arg, the charge was placed in the most water-accessible atom (Lee and Richards 1971). A mean-field approximation was used to calculate the fractional protonation state of each ionizable group (Tanford and Roxby 1972). The pK _a shift values were calculated iteratively using the following relation,

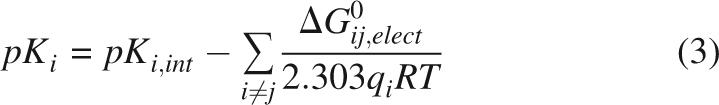where pK_{i, int} is the pK _a of model compounds in water for a given residue i, R is the gas constant, and T is the temperature, fixed at 298 K for all simulations. The pK_{i, int} values used were Asp, 4.0; Glu, 4.5; His, 6.6; Tyr, 10.0; Lys, 10.4; Arg, 12.0; N terminus 7.0, C terminus, 3.6 (Matthew et al. 1985). This mean-field approximation is exact when Coulomb interactions between titratable sites are weak, which is the case in these calculations (Bashford and Karplus 1991).

After electrostatic energies were calculated, bulk properties of the U state were determined by averaging. Net H⁺ binding behavior was calculated directly from the mean-field electrostatic calculations. pK _a values were calculated as the pH where a residue was half protonated. The values were averaged without Boltzmann-weighting. It was found that Boltzmann-weighting of pK _a values had no effect on the reported values and that the weighted values closely reproduced the H⁺ binding curves taken directly from the Boltzmann-averaged electrostatic calculations. For all other observable properties, such as contact distance, total H⁺ bound, or R_G, a standard Boltzmann-weighted average was calculated, weighting by the total electrostatic free energy of each structure. For example, for R_G, this calculation was,

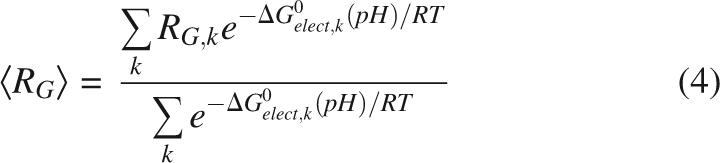where R_G,k is the R_G for structure k and ΔG ⁰ _elect,_k(pH) is the corresponding electrostatic energy for that structure, a function of pH.

To test how the conclusions of our calculations depended on the various simplifying approximations used to calculate electrostatic free energies, a more rigorous calculation was applied to a subset of the EV ensemble for comparison. In these calculations the electrostatic energies and pK _a values were calculated with the methods based on the finite-difference solution of the linearized Poisson-Boltzmann equation using the UHBD program (Antosiewicz et al. 1994). The model-compound pK _a values listed above were used. In addition to the Coulomb term, a self-energy term was included to account for hydration effects and for interactions between titratable charges and polar atoms. The protein was assigned a dielectric constant of 20 because this value is known to maximize the agreement between measured and calculated electrostatic energies (Antosiewicz et al. 1994). The clustering method of Gilson was used to calculate the H⁺ binding properties of the unfolded chains (Gilson 1993). With this more exact method it took ∼100 times longer to compute H⁺ binding behavior than with the simple Coulomb potential. The results were indistinguishable from those obtained with Equations 2 and 3. Although the finite-difference algorithm was only used in a limited set of calculations, this was enough to establish that our conclusions were not sensitive to the choice of ε = 78.4 used in equation 2, which was used for most of our calculations. If anything, the structural models overestimate the shifts in pK _a values, suggesting that interactions between charges are even weaker than calculated.

Convergence in Monte Carlo simulations

For all of the ensemble-weighted observables (e.g., pK _a values, distances, R_G), convergence was confirmed by subdividing the set of structures into five sets of ∼2000 structures per set. The observable values were averaged and the standard error of the mean was calculated. This error, calculated from five independent trials, is reported throughout this work as the uncertainty of observations, and is not intended to represent statistical uncertainty of the observable. Because the standard error was small (for H⁺ binding, typically <0.1%), convergence of the electrostatic properties was assumed. Convergence was not as good for the Boltzmann-weighted R_G (see Table 3 and Figure 5), but it was still within reasonable limits (∼1%).

Experimental H⁺ titration curves

The continuous, direct potentiometric titrations of T62P SNase in 0.1 M KCl used for this study were measured by Dr. K. Lee (Lee et al. 2002) with methods described elsewhere (Whitten and García-Moreno E. 2000). We have demonstrated previously that the accuracy and precision of the H⁺ titration curves measured with the setup used for these experiments is sufficient to allow the resolution of the titration curves of individual ionizable groups from difference titration curves (Garcia-Moreno et al. 1997; Dwyer et al. 2000; Fitch et al. 2002). The titration curves in Figure 2A represent the superposition of several independent experiments. The set of pK _a values that describe the experimental titration curve of T62P SNase was extracted by nonlinear least-squares fit: Asp, 3.89; Glu, 4.35; His, 6.66; Tyr, 9.88, N terminus, 6.67. To compare calculated H⁺ binding with experimental data, ninth-order polynomial fits were made of experimental data points. Residuals on these fits are different in different regions of the titration curve, but they were always small, typically <0.2 H⁺. The difference in H⁺ binding (Δν) was calculated by shifting the experimental data such that Δν was equal to 0 at pH 8.5. This shift was necessary because the protein was never fully titrated at low pH, and pH 8.5 is a reasonable value because very few residues will titrate in this region.

Electronic supplementary material

A complete table of all calculated pK _a values for SNase is available in the online supplementary material.