Ion Channel Selectivity through Stepwise Changes in Binding Affinity

Abstract

Voltage-gated Ca²⁺ channels select Ca²⁺ over competing, more abundant ions by means of a high affinity binding site in the pore. The maximum off rate from this site is ∼1,000× slower than observed Ca²⁺ current. Various theories that explain how high Ca²⁺ current can pass through such a sticky pore all assume that flux occurs from a condition in which the pore's affinity for Ca²⁺ transiently decreases because of ion interactions. Here, we use rate theory calculations to demonstrate a different mechanism that requires no transient changes in affinity to quantitatively reproduce observed Ca²⁺ channel behavior. The model pore has a single high affinity Ca²⁺ binding site flanked by a low affinity site on either side; ions permeate in single file without repulsive interactions. The low affinity sites provide steps of potential energy that speed the exit of a Ca²⁺ ion off the selectivity site, just as potential energy steps accelerate other chemical reactions. The steps could be provided by weak binding in the nonselective vestibules that appear to be a general feature of ion channels, by specific protein structures in a long pore, or by stepwise rehydration of a permeating ion. The previous ion-interaction models and this stepwise permeation model demonstrate two general mechanisms, which might well work together, to simultaneously generate high flux and high selectivity in single file pores.

introduction

Ca²⁺ channels choose Ca²⁺ over Na⁺ at a ratio of 1,000:1 (Hess et al., 1986) because of an intrapore, high affinity Ca²⁺ binding site (K _d = 0.7 μM Ca²⁺). In the absence of Ca²⁺, Na⁺ and other monovalent ions pass freely through Ca²⁺ channels, but they are blocked when external Ca²⁺ concentration rises above 1 μm (Kostyuk et al., 1983; Almers et al., 1984). Block depends on membrane voltage (Lansman et al., 1986; Fukushima and Hagiwara, 1985; Lux et al., 1990), as required of a site within the pore (Woodhull, 1973), and on the direction of ion movement (Kuo and Hess, 1993a , 1993b ), as required of a site within a multi-ion pore (Hille and Schwarz, 1978). The maximum off rate from a micromolar binding site in free solution is ∼10³ ions per second, yet picoampere currents (over 10⁶ Ca²⁺ ions per second) pass through Ca²⁺ channels. This is a specific example of a general problem of channel permeation: how high flux can occur through a channel that selects its preferred ion with an intrapore binding site. This cannot happen in a rigid pore with just a single binding site because, as affinity for an ion increases, the ion's exit rate decreases in exact proportion to the increased occupancy of the site (Bezanilla and Armstrong, 1972). The gross discrepancy between flux and binding in Ca²⁺ channels makes them a valuable system for exploring this problem. Several theories of Ca²⁺ channel permeation have been proposed and they share an essential feature: when Ca²⁺ ions bind to the channel, the pore's affinity for Ca²⁺ diminishes, thereby promoting high Ca²⁺ flux. Here, we describe a model that generates high flux without such changes in affinity, thereby demonstrating a second general mechanism.

The most widely known Ca²⁺ channel model proposes a pair of high affinity intrapore binding sites through which ions move in single file (Hess and Tsien, 1984; Almers and McCleskey, 1984). Previously, single file models had successfully described permeation in K⁺ channels (Hille and Schwarz, 1978), gramicidin channels (Andersen and Procopio, 1980), and Na⁺ channels (Begenisich, 1987). In such models, ions hop sequentially from one site to the other following two rules: (a) an ion cannot bind to a site already occupied by another; (b) an ion cannot pass over a site without binding to it (Hille, 1992). The same rules govern movement of ions through semiconductor crystals (Shockley et al., 1952). Thus, such models explore whether this simple physical precedent can explain the relatively complex selectivity and permeation of ion channel proteins.

Although high fluxes are impossible with just a single high affinity binding site, they can occur when there are two sites because, when both are occupied, the adjacent ions can repel each other. Specifically, Ca²⁺ affinity diminishes 20,000-fold when two ions are in the model pore compared with when one ion is present (Hess and Tsien, 1984; Almers and McCleskey, 1984). Electrostatic repulsion between Ca²⁺ ions ∼10 Å apart is sufficient to generate this change in affinity, but it is not the only mechanism possible. Competition for binding moieties between two Ca²⁺ ions in a multiply occupied channel has been suggested as an alternate mechanism (Armstrong and Neyton, 1991; Yang et al., 1993), as has long-lived conformational changes triggered by Ca²⁺ binding in a single ion pore (Lux et al., 1990; Mironov, 1992).

Two observations indicate that the pore of the Ca²⁺ channel contains only a single high affinity binding site, rather than the two suggested by the traditional model. (a) Single point mutations of critical glutamate residues simply shift the pore's affinity for Ca²⁺, whereas micromolar binding should still be present if there were two independent sites with the same affinity (Yang et al., 1993; Kim et al., 1993; Ellinor et al., 1995). (b) As judged from the voltage dependence of Ca²⁺ block, Ca²⁺ binds to the same pore location whether it arrives from the outside or the inside solution (Kuo and Hess, 1993a ; but a different voltage dependence was found by Rosenberg and Chen, 1991). These experiments prompted us to quantitatively evaluate a model, mentioned briefly in Almers and McCleskey (1984), that uses only one high affinity intrapore site and needs no ion–ion interactions or transient decreases in Ca²⁺ affinity. Using rate theory calculations for single file pores, we test the ability of this mechanism to fit published data regarding: (a) selectivity of Ca²⁺ over monovalent ions, (b) selectivity of Ca²⁺ over Ba²⁺, (c) sigmoidal current–voltage (I-V)¹ curves, and (d) block by Cd²⁺.

methods

Calculations were done using rate theory models written in Visual Basic 2.0 in which two different kinds of ions move through pores in single file via either two or three binding sites. In such models, the rate that an ion moves from one site to another equals the product of the rate constant for the transition and the probability that the site is occupied by that ion. The rate constant (r) diminishes exponentially as the energy of transition (G) increases relative to the average kinetic energy of an atom (kT): r = νe ^−(G/kT), where k is the Boltzmann constant, T is the temperature, and ν, the fastest possible reaction rate, is taken to be the atomic vibration frequency (5.8 × 10¹² s⁻¹ = kT/h, where h is Plank's constant). G is the sum of the chemical and electrical potential energies that affect the ion movement: G = G _b − G _s + zδV_m, where G_b is the energy of the barrier to be overcome, G_s is the energy of the present binding site, z is the ion's charge, and δ is the fraction of the membrane voltage (V_m) traversed by the ion in passing from the site to the barrier. If desired, rate constants can be adjusted with a “repulsion factor” to reflect negative interaction between ions that occupy adjacent sites. (We used the factor only to reproduce earlier repulsion-dependent models and raised the factor to an exponent of the product of the valences of the adjacent ions, as appropriate for electrostatic repulsion (see Almers and McCleskey, 1984).)

The energies of barriers and binding sites are all adjustable parameters, but critical ones are determined (or at least constrained) by known data. Outer barriers limit entry to the pore, so they must respect the diffusion limit. A typical diffusion limit for a small ion is 10⁹ M⁻¹ s⁻¹ (Hille, 1992); this corresponds to an energy barrier of 8.7 kT (= ln[10⁹/5.8 × 10¹²]). The energies of some binding sites can be obtained from apparent dissociation constants (K _d) by G = −kT  ln (K _d).

The concentration of Ca²⁺ that causes half block of monovalent ion current provides a close approximation of the energy of the highest affinity Ca²⁺ binding site in the pore since block is caused by entry of a single Ca²⁺ into the pore; for example, a half-blocking concentration of 1 μM suggests a binding energy of −14 kT (= ln10⁻⁶). The concentration of Ca²⁺ that causes half-maximal Ca²⁺ current provides an approximation of the energy of the lowest affinity site since saturation of current reflects filling of the pore; half saturation at 10 mM suggests a binding energy of −4.5 kT (= ln10⁻²). The locations of sites and barriers within the electric field can also be free parameters, but we just arranged them symmetrically.

The barrier and site energies determine the individual rate constants and these, together, determine the probabilities that sites are occupied by the different ions. Each site has three possible states: unoccupied or occupied by one of the two ions. Therefore, the two-site pore can exist in 9 (3²) possible states and the three-site pore can exist in 27 (3³). The probabilities of occupancy of the different states of the pore were calculated through their steady state kinetic equations, in which the rates of creation and loss of the state are equal. For example, the steady state of a two-site channel having ion B in the left site and ion A in the right is described by dP _BA/dt = 0 = r ₁ P _0A + r ₂ P _B0 − r ₋₁ P _BA − r ₋₂ P _BA, where r ₁ and r ₋₁ are rate constants for entry and exit, respectively, of ion B to the left site, r₂ and r₋₂ are rate constants for entry and exit of ion A to the right site, and P _BA, P _0A, and P _B0 are the probabilities that the channel exists in these three states (0 indicates an unoccupied site). Together with the conservation equation (the sum of all probabilities equals 1), there are 9 and 27 independent kinetic equations for the two- and three-site pores, respectively. These equations were solved for the state probabilities in 9 × 9 and 27 × 27 matrices by Gauss elimination. Numbering the states in base 3 greatly eased bookkeeping and troubleshooting for this operation.

Current for each ion was calculated as the net flux (rate constant × state probability) over the second energy barrier times the ion's charge. Calculation of currents carried by extracellular Na⁺ and Ca²⁺ through a single site pore used the formula for a weighted rectangular hyperbola, as would be appropriate for competitive binding at a single site enzyme (Hille, 1992):

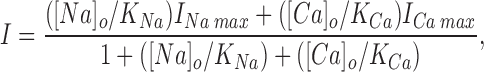where I _max is the maximum current of the indicated ion and K is the ion's dissociation constant from the site.

results

Choosing Ca²⁺ over Na⁺

From a physiological perspective, the selectivity of Ca²⁺ over Na⁺ is the most important feature of the Ca²⁺ channel pore; it allows the channel to preferentially pass Ca²⁺ despite the 100-fold concentration advantage held by Na⁺. The two essential features of this selectivity are: (a) Na⁺ (and other inorganic monovalents) pass freely through the channel when Ca²⁺ is absent, but their currents are blocked by micromolar Ca²⁺; (b) high Ca²⁺ flux occurs at millimolar Ca²⁺ and there is no inward Na⁺ flux at these concentrations. These properties are evident in the data points in Fig. 1 B (scaled and replotted from Almers et al., 1984), which show combined Na⁺ and Ca²⁺ current through Ca²⁺ channels over a 1,000,000-fold range of extracellular [Ca²⁺]. There is a broad minimum between 10⁻⁶ and 10⁻³ M Ca²⁺; Na⁺ carries the current below and Ca²⁺ carries it above this range. In practice, fitting this data is the primary challenge of the modeling; once successful, the same model easily fits a variety of other Ca²⁺ channel data.

Figure 1.

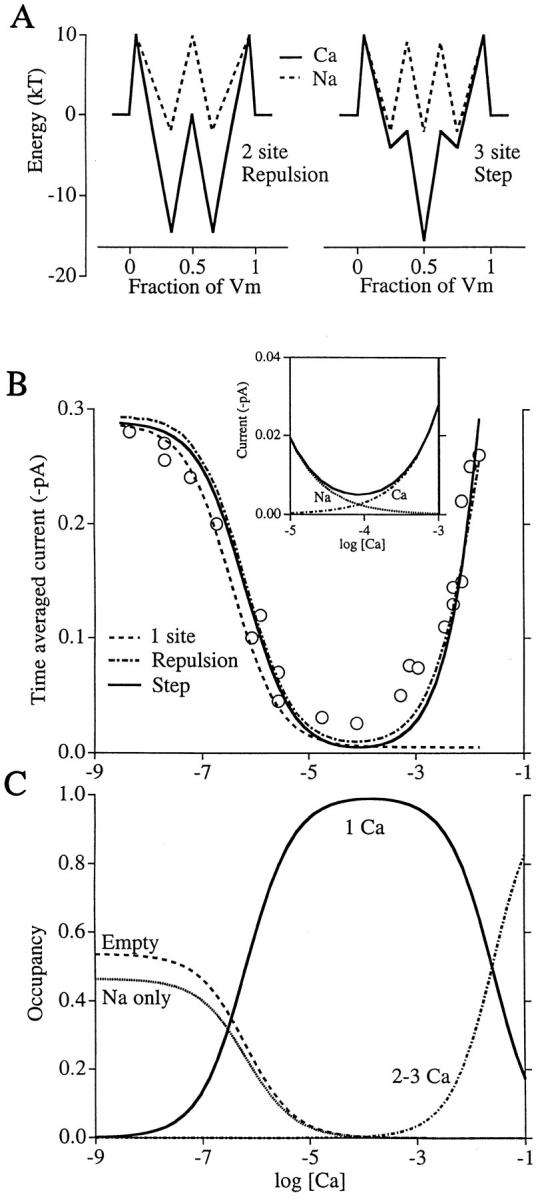
Ca²⁺ blocks and permeates in two distinct Ca²⁺ channel models. (A) Chemical potential energies experienced by Ca²⁺ (solid line) or Na⁺ (dashed line) in passing through the repulsion model pore (left, from Almers and McCleskey, 1984) or the step model (right). Axes: potential energy (divided by kT, the average kinetic energy per atom) versus fractional distance across the membrane electric field. In the repulsion model, off rates are increased 20,000-fold when two Ca²⁺ ions simultaneously occupy the pore; in the step model, off rates are unaffected by occupancy. Exact values of parameters are below. (B) Fits to scaled data points (from Almers et al., 1984) describing whole cell Na⁺ and Ca²⁺ currents through skeletal muscle L-type Ca²⁺ channels as a function of log extracellular [Ca²⁺]. The three curves describe average current for single channels predicted by the repulsion model (broken line), step model (solid line), and a single-site model (dashed line). (To offset it from the step model curve, 0.005 pA has been added to the repulsion curve.) [Ca²⁺]_i = 0, [Na⁺]_i = [Na⁺]_o = 32 mM, and V_m = −20 mV for data and calculations. Inset shows current carried by Na⁺ and Ca²⁺ in the step model in the region where the pore switches from Na⁺ to Ca²⁺ permeability. (C) Probability that the repulsion model pore exists in the indicated states. (Empty) No ion in the pore; (Na only) only Na⁺ occupies the pore; (1 Ca) Ca²⁺ occupies the high affinity site and no other site; (2-3 Ca) two or three Ca²⁺ ions occupy the pore. Parameters for Ca²⁺ in the repulsion model: outer barriers, 10.3; middle barrier, 0; wells, −14.5. Parameters for Ca²⁺ in the step model: outer barriers, 10; inner barriers, −2; outer wells, −4; central well, −15.5. Na⁺ in the repulsion model: barriers, 10; wells, −2. Na⁺ in the step model: outer barriers, 10; inner barriers, 9.2; wells, −2. Barriers and wells are arranged symmetrically within the membrane field with the outer barriers set at 0.05 V_m. Repulsion factors are 11.89 (repulsion model) and 1 (step model). Single-site model: K _dCa = 0.3 μM (chosen to provide a small offset; 0.7 μM gives data that exactly aligns with the other models), K _dNa = 135 mM, I_Namax = 1.5 pA, I_Camax = 0.32 fA (10³ Ca²⁺/s, the maximum off rate for a 1 μM K _d binding site).

Both the traditional, two-site repulsion-dependent model (Fig. 1 A, left) and the new model (Fig. 1 A, right) fit the data in Fig. 1 B (broken and solid curves). However, a pore with only a single high affinity binding site exhibits appropriate block of Na⁺ current by micromolar Ca²⁺, but no significant Ca²⁺ flux as [Ca²⁺] rises further (Fig. 1 B, dashed curve). As discussed above, high Ca²⁺ flux occurs in the repulsion model because off rates increase when both sites are simultaneously occupied by Ca²⁺ ions. In contrast, off rates are unaffected by multiple occupancy in the other model. This new model has a single high affinity site, two flanking low affinity sites, and allows no repulsion between ions. We will call this the “step model” because the low affinity sites essentially provide stairsteps of potential energy that speed exit from the pore (see discussion). The inset shows the contributions of the individual ions to the total current in the step model in the vicinity of 10⁻⁴ M Ca²⁺.

Fig. 1 C  plots the probability that the step model pore is occupied in various ways as Ca²⁺ concentration changes. Block of Na⁺ current occurs as occupancy of the high affinity site by Ca²⁺ (one Ca curve) increases when Ca²⁺ rises to the micromolar range. Ca²⁺ flux occurs at still higher Ca²⁺ concentrations as the probability increases that two or three Ca²⁺ ions simultaneously occupy the pore. Most directly, inward Ca²⁺ flux parallels the occupancy of the internal low affinity site. This occurs as the external Ca²⁺ concentration becomes significant compared with the site's dissociation constant, which is 18 mM Ca²⁺. Although the occupancy plots for the step model are qualitatively similar to those for the repulsion model (Almers and McCleskey, 1984), the effects of multiple Ca²⁺ occupancy are different. An ion at one site of the step model does not affect an ion at another site through remote forces.

Choosing Ca²⁺ over Ba²⁺

Ca²⁺ channels generally pass greater Ba²⁺ currents than Ca²⁺, but they choose Ca²⁺ when both ions are present. The key features of Ca²⁺/Ba²⁺ permeation are: (a) pure Ba²⁺ currents are larger and saturate at higher concentrations than pure Ca²⁺ currents (Hess et al., 1986); (b) Ba²⁺ blocks monovalent currents at ∼50× higher concentration than does Ca²⁺ (Kostyuk et al., 1983); (c) Ca²⁺ blocks Ba²⁺ current, and does so more strongly than would occur through simple competition for a single site. The powerful block of Ba²⁺ current by Ca²⁺ can manifest itself as an “anomalous mole fraction effect” in which current carried by mixtures of Ca²⁺ and Ba²⁺ having constant total divalent ion concentration exhibit a minimum at low [Ca²⁺] (Hess and Tsien, 1984; Almers and McCleskey, 1984; Friel and Tsien, 1989; but Yue and Marban, 1990, saw no Ca²⁺/Ba²⁺ anomalous mole fraction effect).

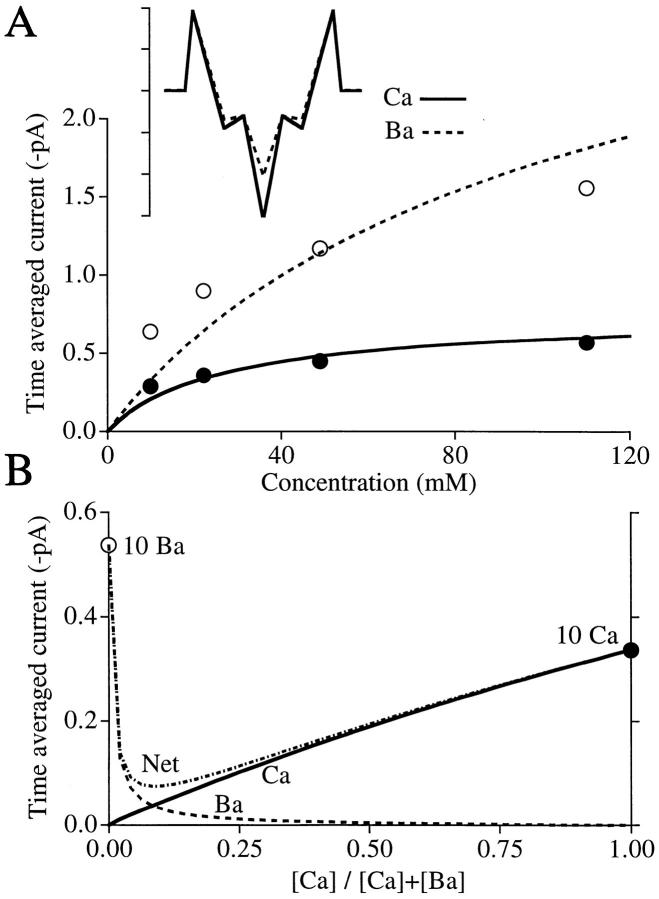
The data points in Fig. 2 A (replotted from Hess et al., 1984) give unitary Ca²⁺ (•) and Ba²⁺ (○) current amplitudes from cardiac Ca²⁺ channels as a function of divalent ion concentration. Being actual single channel amplitudes (rather than the scaled whole cell currents of Fig. 1 B), these data test whether the step model can quantitatively fit observed single channel flux. The Ca²⁺ (solid curve) and Ba²⁺ (dashed curve) currents calculated from the model (inset) reproduce the key features of the data—Ba²⁺ current has higher amplitude and higher half-saturation than Ca²⁺ current. The energies for Ca²⁺ in the model were adjusted to give a good fit to this cardiac Ca²⁺ channel data and they differ only slightly from those used to fit skeletal muscle data in Fig. 1. The Ba²⁺ and Ca²⁺ models differ only in the energy of the binding sites. Ba²⁺ energies for the high and low affinity sites correspond to Ba²⁺ concentrations that cause half-block of monovalent currents (35 μM, Kostyuk et al., 1983) and half-saturation of Ba²⁺ current (28 mM, Hess et al., 1986), respectively.

Figure 2.

Ca²⁺ and Ba²⁺ permeation in the step model. (A) Fits to data (from Hess et al., 1986) describing unitary currents for single cardiac L-type Ca²⁺ channels as a function of [Ca²⁺]_out or [Ba²⁺]_out at V_m = 0 mV. [Ca²⁺]_in = [Ba²⁺]_in = [Na⁺]_out = 0. [Na⁺]_in = 140 mM. (inset) Energy profiles for Ca²⁺ and Ba²⁺; exact parameters below. (B) Anomalous mole fraction behavior. Ca²⁺ current is roughly proportional to [Ca²⁺], but Ba²⁺ current is lost upon addition of a few millimoles Ca²⁺. Consequently, net current passes through a minimum. Sum of extracellular [Ca²⁺] and [Ba²⁺] = 10 mM throughout; intracellular concentrations = 0. V_m = 0 mV. Parameters for Ca²⁺ in the model: outer barriers, 9.6; inner barriers, −3; outer wells, −4.5; central well, −15.5. Ba²⁺: barriers same as Ca²⁺; outer wells, −3.5; central well, −10.3. Na⁺ (not shown): same as in Fig. 1.

Fig. 2 B shows the predicted anomalous mole fraction behavior when the total divalent ion concentration is 10 mM. Net current passes through a minimum as the Ca²⁺:Ba²⁺ ratio changes because Ca²⁺ is so effective at blocking Ba²⁺ current. For example, there is virtually no current carried by 5 mM Ba²⁺ when 5 mM Ca²⁺ is present. Fig. 1 B shows a similar, but far more dramatic, U shape because the difference in affinities between Ca²⁺ and Na⁺ is far greater than between Ca²⁺ and Ba²⁺. (As seen experimentally [Friel and Tsien, 1989], the mole fraction curve no longer passes through a minimum at high divalent ion concentrations [data not shown]. In this respect, a nearly saturated multi-site pore behaves like a single site pore; presumably, this is because only a single site at a time is unoccupied in the near-saturated pore.)

Sigmoid I-V Curves

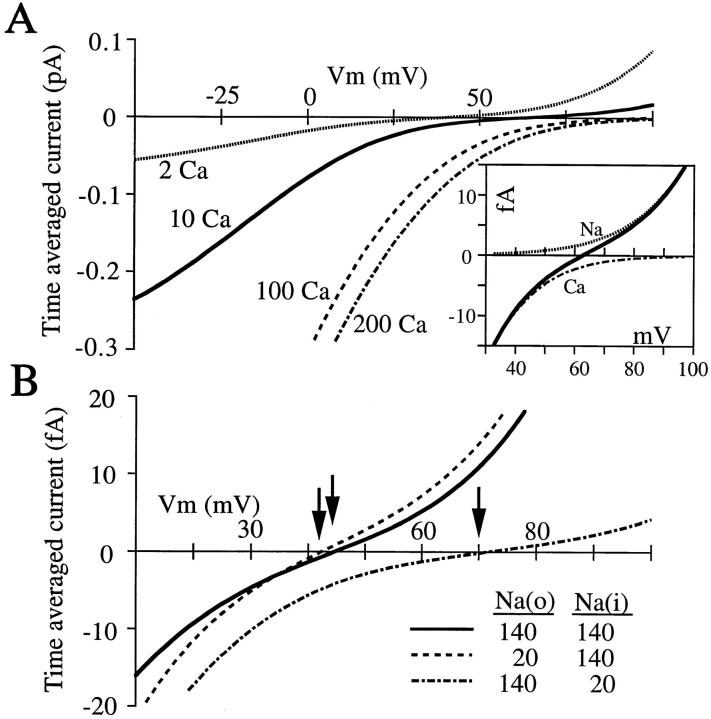
The current–voltage curve of Ca²⁺ channels exposed to physiological ionic concentrations has a rich array of features that further illustrate the role of Ca²⁺ block in selectivity against monovalent ions: (a) current reverses at positive potentials, but not nearly as positive as the equilibrium potential for Ca²⁺ (Fenwick et al., 1982; Lee and Tsien, 1984); (b) the outward current is carried by intracellular monovalent cations (Lee and Tsien, 1984; Hess et al., 1986), and these are far more permeant than extracellular monovalents (Yamashita et al., 1990); (c) despite their impermeability, extracellular monovalents at physiological concentrations block currents carried by divalent ions (Polo-Parada and Korn, 1997); (d) the I-V curve is sigmoid in the vicinity of the reversal potential (Fenwick et al., 1982; Lee and Tsien, 1984). The step model generates each of these features (Fig. 3).

Figure 3.

Effects of Ca²⁺ and Na⁺ on I-V curves of the step model. (A) I-V curves with the indicated (millimolar) concentrations of extracellular Ca²⁺. Current becomes more sigmoid near the reversal potentials as Ca²⁺ rises. (inset) Current carried by Na⁺ and Ca²⁺ near the reversal potential when [Ca²⁺]_out = 10 mM. For all curves, [Ca²⁺]_in = 0, [Na⁺]_in = [Na⁺]_out = 140 mM. Energies as in Fig. 1 A, right. (B) I-V curves with the indicated internal and external [Na⁺] ([Ca²⁺]_out = 3 mM; [Ca²⁺]_in = 0). Reversal potentials: 43.5 mV with symmetrical Na⁺; 41.5 mV with low external Na⁺; 72 mV with low internal Na⁺.

In the absence of Ca²⁺, the single Ca²⁺ channel I-V curve is linear and reverses at 0 mV (Rosenberg and Chen, 1991); the model does the same (not shown). As extracellular Ca²⁺ concentration increases, the reversal potential becomes more positive and the curve becomes more and more sigmoid near the reversal potential (Fig. 3 A). Sigmoidicity, a region of low conductance, occurs when the pore is more likely occupied by just a single Ca²⁺ ion (occupancy plot not shown). When sufficiently positive voltages force the final Ca²⁺ ion outward from the pore, monovalent cations pass freely outward. Thus, sigmoidicity in the I-V curve reflects block of the pore by single Ca²⁺ ions.

Fig. 3 A (inset) shows how much of the net current is carried by each of the individual ions near the reversal potential when [Ca²⁺]_out is 10 mM (0 [Ca²⁺]_in). Although Na⁺ is at the same concentration (140 mM) inside and out, it only carries outward current; clearly, internal Na⁺ is more permeant than external in the model. This point was demonstrated in elegant experiments showing that internal Na⁺ affects the reversal potential of Ca²⁺ channels far more than external Na⁺ (Yamashita et al., 1990). In the step model, a change in Na⁺ concentration that causes a 2-mV shift if made extracellularly causes a 27-mV shift if made intracellularly (Fig. 3 B). With respect to monovalent cations, Ca²⁺ channels are outward rectifiers because of the presence of an extracellular blocking ion, Ca²⁺. Intracellular Na⁺ is more permeant than extracellular because of the difference in Ca²⁺ concentration inside and out. As shown previously by Hille and Schwarz (1978), such asymmetry requires neither an asymmetric energy profile nor ionic repulsion.

Block of inward Ca²⁺ current by 140 mM extracellular Na⁺ is reproduced (compare solid and dashed curves, Fig. 3 B). As was suggested by Polo-Parada and Korn (1997), this block is caused by competition between Na⁺ and Ca²⁺ at the external, low affinity binding site.

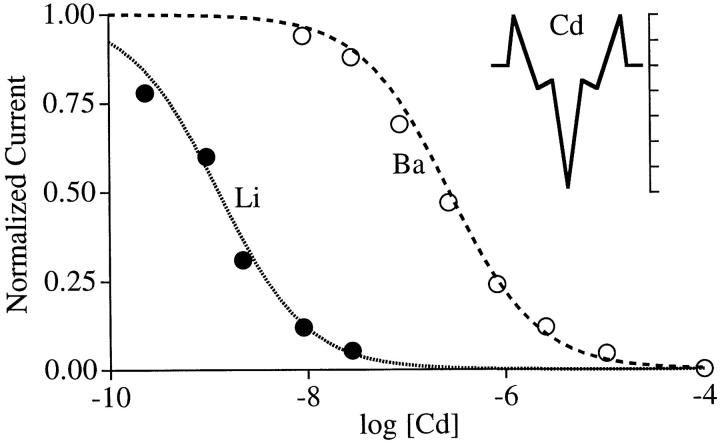
Block by Cadmium

Cd²⁺ is one of several polyvalent cations that block Ca²⁺ channels at very low concentrations (Hess et al., 1986). The data points in Fig. 4, replotted from Ellinor et al. (1995), show that Cd²⁺ blocks monovalent ion currents at ∼200-fold lower concentrations than divalent ion currents. The data is fit by assuming that Cd²⁺ binds to the selectivity site far more strongly than does Ca²⁺ (−24 kT for Cd²⁺ [Fig. 4, inset] vs. −15.5 kT for Ca²⁺). The difference in blocking concentrations for Li⁺ and Ba²⁺ currents is due to their differences in binding to this site (−10.3 kT for Ba²⁺ and −5 kT for Li⁺).

Figure 4.

Block of monovalent and divalent currents by Cd²⁺. Data points from Ellinor et al. (1995) are normalized inward whole cell currents carried by Li⁺ or Ba²⁺ at the indicated extracellular [Cd²⁺]. [Ba²⁺]_out = 40 mM; [Li⁺]_out = [Li⁺]_in = 100 mM. V_m = −20 mV for data and calculations. Calculated Ba²⁺ and Li⁺ currents normalized to their values at 10⁻¹⁰ and 10⁻¹² M Cd²⁺, respectively. (inset) Energy profile for Cd²⁺ (5 kT per tick). Cd²⁺ energies are the same as for Ca²⁺ in Fig. 2, except the central well, which was set at −24 kT (absolute K _d = 40 pM) to give a good fit to the data. Ba²⁺ energies same as in Fig. 2. Li⁺ energies: outer barriers, 9; inner barriers, 7; wells, −5.

discussion

This paper asks how a million Ca²⁺ ions can pass through a Ca²⁺ channel in a second when its pore contains a binding site having a maximum off rate of a thousand per second. This is a specific example of a general problem: how channels pass high flux if they select their preferred ion with a binding site. All previous models assumed that one Ca²⁺ ion diminishes the affinity of the pore for others and that Ca²⁺ flux ensued from this low affinity state. The suggested mechanisms for this negative interaction between ions are electrostatic repulsion (Hess and Tsien, 1984; Almers and McCleskey, 1984), competition for binding moieties (Armstrong and Neyton, 1991; Yang et al., 1993; Ellinor et al., 1995), and Ca²⁺-induced conformational changes (Mironov, 1992; Lux et al., 1990). The step model described here does not allow one ion to alter another's binding to other sites, yet it fits the wide variety of Ca²⁺ channel permeation data; most importantly, submicromolar Ca²⁺ blocks current carried by monovalent ions and Ca²⁺ above a millimolar generates picoampere, saturable Ca²⁺ flux. The calculations demonstrate that ion–ion interactions are not required to generate high flux in pores that tightly bind their preferred ion. Kiss et al. (1998) demonstrates that the same principle fits data from K⁺ channels. Below, we describe the mechanism that underlies the model, evidence that supports its plausibility, and alternate interpretations of it.

Mechanism

The model has a simple mathematical explanation and a physical mechanism that is part of everyday experience. Fig. 5 shows the potential energies of Ca²⁺ in a single-site pore (A), the repulsion model (B), and the step model (C). The energy of the strongest binding site in each model (arrow 1) determines block of foreign ions by micromolar Ca²⁺. The energy of the highest barrier to exit the pore (arrow 2) limits Ca²⁺ flux. In a single-site pore, the rate-limiting exit barrier increases as the selecting binding well deepens. This pictorially represents why an increase in selectivity is expected to decrease flux.

Figure 5.

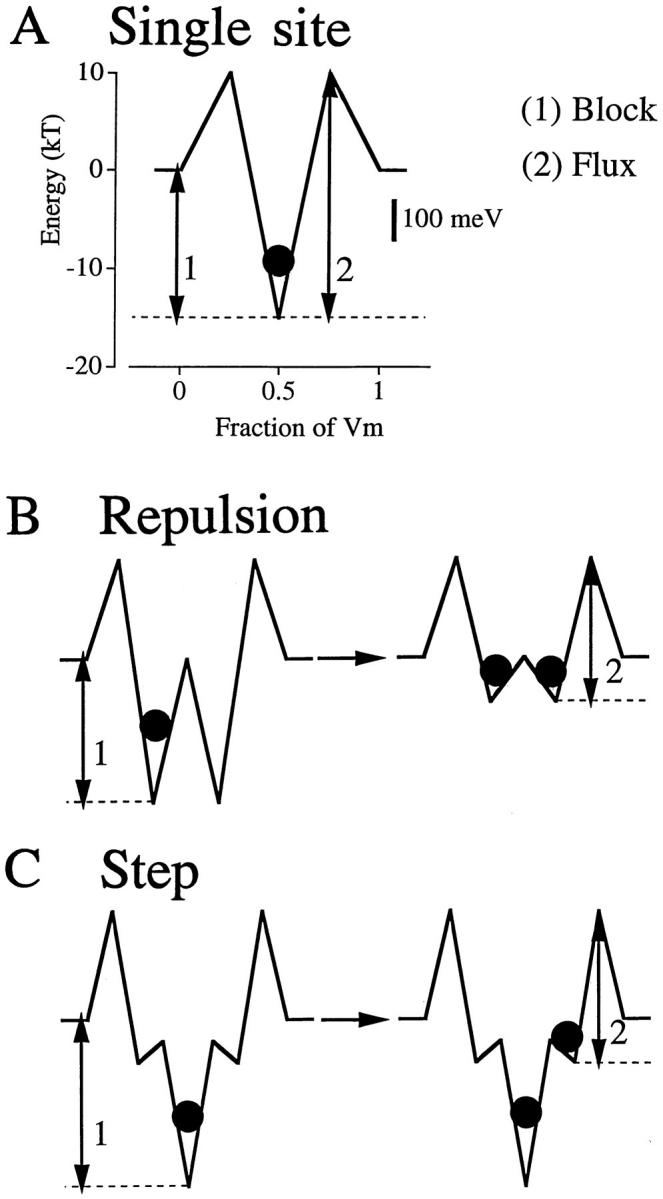
Ca²⁺ energies in three models. The potential energies that determine Ca²⁺ block (1) and limit Ca²⁺ flux (2) are interlinked in a one-site pore (A); since both energies increase together, strong binding and high flux cannot both occur. In contrast, the block and flux energies in the repulsion model (B) and the step model (C) can be independently manipulated. In the repulsion model, multiple Ca²⁺ occupancy (•) forces a change to a low affinity, high flux state due to the negative interaction between the ions. Low affinity sites are built into the step model, making ion–ion interactions unnecessary for high flux. The energy of the low affinity (escape) site in both successful models is ∼100 millielectronvolts (scale bar in A).

The repulsion and step models provide two ways of separating the energies that control binding and flux. In the repulsion model (Fig. 5 B), double occupancy (right) of the pore diminishes affinity of the binding sites. Dissociation constants for Ca²⁺ change from 0.5 μM to 10 mM when the pore goes from singly occupied to doubly occupied. Whether the mechanism is electrostatic repulsion, competition, or conformational changes, Ca²⁺ flux occurs from this state of shallow binding wells.

In the step model (Fig. 5 C), flux occurs from low affinity sites that are built into the energy profile; therefore, there is no need for multiple occupancy to alter binding affinities. The essence of the mathematics is trivial: because the energies that control binding and flux are similar in the two viable models, binding and flux are similar. The physical mechanisms of permeation differ, but with the arrows having roughly similar length in the two models, the calculations come out approximately the same. In both the repulsion and step models, exit from the pore occurs from a site of ∼−4 kT. This is ∼100 millielectronvolts (Fig. 5 A, scale bar), the energy imparted to a single charge by the 100-mV driving force typical of biological membranes. Regardless of the permeation mechanism, it seems that the final site before escape from a pore must have an energy no more negative than such a “biological” magnitude.

The step used in the model more or less cuts the exit barrier into two halves. The physical mechanism that causes the profound increase in flux with just a twofold change in barrier height is analogous to stairsteps. Imagine a wall, a gravitational potential energy barrier, 2 m high. Flux of people over it is exceedingly low because only the most talented can leap 2 m. Now, place a 1-m step in front of it. Most of us can easily step up that meter, and then the next, so flux over the wall increases dramatically. The increase in flux is disproportional to the change in limiting barrier height because the number of people that can hurdle a gravitational barrier decreases nonlinearly with increasing height. Similarly, the number of atoms with sufficient kinetic energy to surpass a chemical potential energy barrier decreases exponentially with increasing height. Once it has reached the intermediate step, an atom faces the next barrier with no memory of the energy expended in reaching there because atoms thermally reequilibrate at the atomic vibration frequency (kT/h = 5.8 × 10¹² s⁻¹). Therefore, steps of chemical potential energy speed reaction rates much as stairsteps of gravitational potential energy speed traffic over obstacles.

Although remote interactions between ions do not occur in the step model, multiple occupancy by Ca²⁺ is required for significant Ca²⁺ flux. The rate constant for exit of Ca²⁺ from one of the low affinity sites in Fig. 1 over the exit barrier to the outside is 5 × 10⁶ per second (=[kT/h]exp − [14]). If ions went directly from the high affinity site to the exterior, the rate constant would be 50 per second (=[kT/h]exp − [25.5]). As large as this difference is, it is insignificant if the pore is singly occupied. With just a single ion in the pore, the probability of occupying one of the low affinity sites is 10⁻⁵ that of occupying the high affinity site (P_low/P_high = exp − [G_low − G_high]). This exactly negates the advantage in rate constant since flux equals the product of the occupancy probability and the rate constant. Significant flux occurs only when there is high occupancy of the escape site by Ca²⁺. This occurs when extracellular [Ca²⁺] becomes significant compared with the site's dissociation constant (18 mM). Ca²⁺ flux is entirely driven by Ca²⁺ concentration and its effect on occupancy of the pore.

Plausibility

Ca²⁺ channels clearly have only a single high affinity binding site within their pore (Yang et al., 1993; Kim et al., 1993; Ellinor et al., 1995). This selectivity site appears to be flanked by other binding sites because: (a) extracellular monovalent ions inhibit exit of Ca²⁺ from the high affinity site to the outside and intracellular ions inhibit exit to the inside (Kuo and Hess, 1993b ); (b) extracellular Na⁺ diminishes inward Ca²⁺ and Ba²⁺ current, suggesting that the ions compete for a low affinity entry site that is on the outside of the selectivity site (Polo-Parada and Korn, 1997); (c) in the presence of extracellular Ca²⁺, monovalent ions are far more permeant from the inside than the outside (Yamashita et al., 1990), suggesting an internal entry site at which monovalents compete favorably with Ca²⁺ because of the low intracellular Ca²⁺ concentration. These findings suggest that the Ca²⁺ channel is a multi-site pore that has a single high affinity site that is flanked by others of lower affinity. This image of the Ca²⁺ channel pore has potential energy steps built into it. Any such step of potential energy must contribute to generating high Ca²⁺ flux.

Although our calculations show that appropriately designed potential energy steps are sufficient to fit critical Ca²⁺ channel data, the steps need not be the only factor. Ion–ion interactions are physically reasonable because both electrostatic repulsion and competition for binding moieties are plausible when identical ions simultaneously occupy a pore. The ionic repulsion model and the step model both quantitatively fit the same Ca²⁺ channel data; at most, this demonstrates that these mechanisms make sense, not that they are real. The reality of Ca²⁺ channel permeation might involve a combination of the mechanisms that have been theoretically explored in isolation, or, perhaps, some mechanism that has been overlooked.

Steps Might Not Be Sites

The literal interpretation of an energy diagram is that each well corresponds to a discrete binding site that should be evident in the three-dimensional structure of the protein's pore. Surely, this must be the case with the high affinity site, which consists of a cage of four glutamates (Yang et al., 1993; Kim et al., 1993). However, physical interpretation of the low affinity sites is ambiguous. It may be that the Ca²⁺ ion can experience steps of potential energy without explicit binding sites built into the protein. For example, ion channels appear generally to have wide entrance vestibules that may be on either side of a narrow, short pore (Miller, 1996). Weak ion binding within the vestibule might be able to provide the same favorable energy steps provided by discrete sites in a long pore. Indeed, placement of the model's low affinity sites at the very edge of the electric field, the location of the vestibules, gives qualitatively similar results as those shown. If one literally interprets the steps as sites in the vestibules, the model suggests that a vestibule serves as an energy “plateau” from which Ca²⁺ can rapidly enter the pore over a low energy barrier. However, literal interpretation is dangerous; the low affinity sites are just a mathematical artifice for showing that steps of potential energy, no matter what their cause, can speed flux.

A different interpretation of the low affinity sites is suggested by a previous case in which stairsteps of potential energy were invoked in the ion transport literature. Eigen and Winkler (1971) and Chock et al. (1977) asked how entry of ions to binding sites on carriers could be diffusion limited when the ions had to undergo complete dehydration, which is normally an exceedingly slow process. The paradox is solved through stepwise replacement of water molecules by coordinating ligands on the carrier; in essence, the carrier catalyzes dehydration of the ion, step by step. This same phenomenon must occur with channels, where entry is generally diffusion limited (e.g., Lansman et al., 1986) despite the need for nearly complete dehydration (Hille, 1971).

Might stepwise rehydration of an exiting ion also occur? This seems probable, not just possible. A Ca²⁺ ion coordinates to seven or eight electronegative oxygen ligands at a time (Falke et al., 1994). Outside the pore, water molecules provide this coordination. At the selectivity site, negative carboxyl oxygens on four glutamates contribute to coordination, thereby forming a stronger bond (Yang et al., 1993; Kim et al., 1993). Unless the Ca²⁺ ion bursts from the glutamate cage immediately into water, there must be intermediate lower affinity states in which the glutamates are replaced by less negative moieties. One possibility would be stepwise replacement of the four carboxyls by water molecules, a mechanism consistent with the proposed flexibility of the glutamate residues (Yang et al., 1993; Ellinor et al., 1995). Any such event would provide a step of potential energy in the Ca²⁺ ion's travel, even though it need not be a discrete binding site in the channel structure. In this manner, stepwise rehydration might provide a path for rapid exit from a pore just as stepwise dehydration surely provides the path for rapid entry. By showing that even a single energy step can be sufficient, our calculations suggest the feasibility of this simple mechanism of permeation.

Abbreviation used in this paper

I-V

current–voltage