Ligand-insensitive State of Cardiac ATP-sensitive K⁺ Channels

Abstract

The mechanism by which ATP-sensitive K⁺ (K_ATP) channels open in the presence of inhibitory concentrations of ATP remains unknown. Herein, using a four-state kinetic model, we found that the nucleotide diphosphate UDP directed cardiac K_ATP channels to operate within intraburst transitions. These transitions are not targeted by ATP, nor the structurally unrelated sulfonylurea glyburide, which inhibit channel opening by acting on interburst transitions. Therefore, the channel remained insensitive to ATP and glyburide in the presence of UDP. “Rundown” of channel activity decreased the efficacy with which UDP could direct and maintain the channel to operate within intraburst transitions. Under this condition, the channel was sensitive to inhibition by ATP and glyburide despite the presence of UDP. This behavior of the K_ATP channel could be accounted for by an allosteric model of ligand-channel interaction. Thus, the response of cardiac K_ATP channels towards inhibitory ligands is determined by the relative lifetime the channel spends in a ligand-sensitive versus -insensitive state. Interconversion between these two conformational states represents a novel basis for K_ATP channel opening in the presence of inhibitory concentrations of ATP in a cardiac cell.

introduction

ATP-sensitive K⁺ (K_ATP) channels transduce cellular metabolic events into membrane potential changes (Ashcroft and Ashcroft, 1990; Lazdunski, 1994; Seino et al., 1996; Bryan and Aguilar-Bryan, 1997), which in heart muscle leads to shortening of action potential duration during ischemia (Nichols and Lederer, 1991; Findlay, 1994; Terzic et al., 1995). The defining property of K_ATP channels is their inhibition by intracellular ATP (Noma, 1983). In cardiomyocytes, however, the ATP concentration (∼5–10 mM) exceeds by >100-fold the IC₅₀ value for K_ATP channel closure. Thus, a change of two orders of magnitude in the ATP concentration would be required for channels to open, which does not occur even under extreme cellular hypoxia (Weiss and Hiltbrand, 1985; Decking et al., 1995, 1997), suggesting that additional modulators of K_ATP channel opening are important.

In this regard, intracellular nucleotide diphosphates are of particular importance since they favor opening of K_ATP channels even within a cytosolic environment of high ATP concentration (Ashcroft and Ashcroft, 1990; Nichols and Lederer, 1991; Weiss and Venkatesh, 1993; Findlay, 1994; Terzic et al., 1994d ; Elvir-Mairena et al., 1996). However, the mechanism of this action of nucleotide diphosphates remains controversial. A conventional assumption has been that nucleotide diphosphates competitively antagonize ATP at an inhibitory binding site on the channel protein (Dunne and Petersen, 1986; Kakei et al., 1986; Misler et al., 1986; Findlay, 1987; Bokvist et al., 1991; Nichols and Lederer, 1991; Ueda et al., 1997). However, this mechanism cannot fully explain K_ATP channel opening since altered concentrations of cytosolic ATP and/or nucleotide diphosphates are not readily detectable, nor do they correlate with changes in K_ATP channel function. Moreover, nucleotide diphosphates, such as ADP or UDP, induce channel opening in the absence of ATP (Findlay, 1988; Lederer and Nichols, 1989; Tung and Kurachi, 1991; Allard and Lazdunski, 1992; Forestier and Vivaudou, 1993; Terzic et al., 1994a ) and can lose their ability to antagonize ATP-dependent channel inhibition under certain operative conditions of the channel (Deutsch and Weiss, 1993; Terzic et al., 1994a ). Such nonuniform regulation of K_ATP channel opening by nucleotide diphosphates has also been observed with other inhibitory ligands including sulfonylurea drugs (Venkatesh et al., 1991; Brady et al., 1996b , 1998) and diadenosine polyphosphates (Jovanovic et al., 1996, 1997). These findings suggest that an operative condition-dependent response of K_ATP channels is a fundamental property of the channel, which may be the basis for channel opening in the presence of inhibitory ligands.

To determine whether nucleotide diphosphates induce an alteration in channel behavior that could account for the observed response of K_ATP channels towards inhibitory ligands, we investigated the action of UDP on transitional states of the cardiac K_ATP channel. Based on a kinetic model of channel behavior, we demonstrate that UDP drives the channel into a state that is insensitive towards inhibitory ligands. Interconversion between ligand-sensitive and -insensitive states could be interpreted using an allosteric model that predicted the outcome of the interaction between an inhibitory ligand and the K_ATP channel in the presence of a nucleotide diphosphate. Transition of the channel into a ligand-insensitive channel state provides a means for K_ATP channel opening even in the presence of high concentrations of inhibitory ligands within a cardiomyocyte.

materials and methods

Isolated Cardiomyocytes

Ventricular myocytes were isolated by enzymatic dissociation (Alekseev et al., 1996a ). Solutions were prepared based on a “low Ca²⁺ medium” containing (mM): 100 NaCl, 10 KCl, 1.2 KH₂PO₄, 5 MgSO₄, 20 glucose, 50 taurine, 10 HEPES, pH 7.2–7.3. Guinea pigs were anesthetized with pentobarbital (1 ml/100 mg body weight i.p.). After cardiotomy, the heart was retrogradely perfused (at 37°C) with: medium 199 (Sigma Chemical Co., St. Louis, MO) for 2–3 min, followed by Ca²⁺ EGTA-buffered low Ca²⁺ medium (pCa 7) for 80 s, and finally low Ca²⁺ medium containing pronase E (8 mg/100 ml; Serva Biochemicals, Heidelberg, Germany), proteinase K (1.7 mg/100 ml; Boehringer Mannheim Biochemicals, Indianapolis, IN), bovine serum albumin (0.1 g/100 ml, fraction V; Sigma Chemical Co.), and 200 μM CaCl₂. Ventricles were separated from atria and cut into small fragments (6–10 mm³) in the low Ca²⁺ medium enriched with 200 μM CaCl₂. Single cells were then isolated by stirring the tissue (at 37°C) in a solution containing pronase E and proteinase K supplemented with collagenase (5 mg/10 ml; Worthington Biochemical Corp., Freehold, NJ). After 10 min, the first aliquot was removed, filtered through a nylon sieve, centrifuged (at 300– 400 rpm, 1 min), and washed twice. Remaining tissue fragments were reexposed to collagenase, and isolation continued for two to three such cycles. Isolated cardiomyocytes were stored in low Ca²⁺ medium with 200 μM CaCl₂. Rod-shaped cardiomyocytes with clear striations and a smooth surface were used for electrophysiological recordings. Experiments were performed with the approval of the Institutional Animal Care and Use Committee (Mayo Clinic).

Single-Channel Recording

Fire-polished pipettes, coated with Sylgard (resistance ∼5 MΩ), were filled with “pipette solution” containing (mM): 140 KCl, 1 CaCl₂, 1 MgCl₂, 5 HEPES-KOH, pH 7.3. Cardiac cells were superfused with “internal solution” containing (mM): 140 KCl, 1 MgCl₂, 5 EGTA, 5 HEPES-KOH, pH 7.3, in the absence or presence of nucleotides (UDP or ATP) and/or glyburide (Sigma Chemical Co.), and recordings made at room temperature (20– 22°C) as described (Terzic et al., 1994c  ; Terzic and Kurachi, 1996). Glyburide was dissolved in dimethylsulfoxide as concentrated stock solution, and the final concentration of dimethylsulfoxide was <0.1%, which did not affect K_ATP channels. UDP (Boehringer Mannheim Biochemicals) and ATP (potassium salt; Sigma Chemical Co.) were dissolved in internal solution before use. Single-channel recordings in the inside-out configuration were monitored online on a high-gain digital storage oscilloscope (VC-6025; Hitachi Ltd., Tokyo, Japan) and stored on tape using a PCM converter system (VR-10; Instrutech Corp., Great Neck, NY). Data were reproduced, low-pass filtered at 4 kHz (−3 dB) by a Bessel filter (902; Frequency Devices Inc., Haverhill, MA), sampled at 80-μs rate, and further analyzed using “BioQuest” software (Alekseev et al., 1997a , 1997b ).

Analysis of Channel Activity

The threshold for judging the open state of K_ATP channels was set at half single channel amplitude. The degree of channel activity was assessed by digitizing segments of current records, expressed as nP _o, where n represents the number of channels in the patch and P _o the probability of each channel to be open.

Kinetic schemes for cardiac K_ATP channels are commonly represented by one open and two closed states (Kakei and Noma, 1984). Herein, in prolonged records of single channel activity (under symmetrical K⁺ concentration and negative membrane potential), distribution of total dwell time could be best fit by three exponents, thus requiring consideration of an additional closed state as proposed for more detailed schemes of K_ATP channel behavior (Gillis et al., 1989; Furukawa et al., 1993). Accordingly, channel kinetic analysis was performed based upon a four-state kinetic scheme with three forward and three backward rate constants:

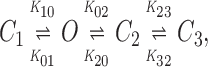1

where transitions between the open (O) and the first closed (C₁) state represent transitions within a burst (intraburst kinetics), whereas transitions between the open (O) and the second (C₂) and third (C₃) closed states define interburst kinetics.

Rate constants (see Scheme 1) were calculated based on parameters obtained from the fit of separated distributions of intraburst and interburst closed times, since relative areas under exponents that correspond to interburst transitions were negligible compared with intraburst events. A critical time (t _cutoff) was used to define the maximal duration of an event that could still be interpreted as closure within a burst of channel activity and was used to construct distributions of open and closed events within and between bursts. The value for t _cutoff  ≥ 3.5 ms was determined based upon the relationship (Gillis et al., 1989):

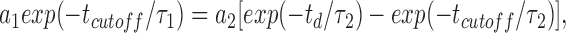where τ₁ is the time constant of closed intervals within a burst; τ₂ is the time constant of closed intervals between bursts; a ₁ and a ₂ are areas of exponential fits corresponding to τ₁ and τ₂, respectively; and t _d is the “dead time;” i.e., time of underestimated events that equals the double sampling rate (∼100 μs). Fitting closed and open time distributions by the sum of exponents was carried out using minimization of the χ² criterion with the Nelder-Meed method of deformed polyhedron (Alekseev et al., 1996b ).

Characteristic open time (τ_o) was interpreted as:

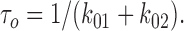2

Characteristic intraburst closed time (τ_c,1), corresponding to gaps within burst, was interpreted as the lifetime in the C₁ state:

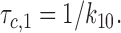3

Similarly, the first characteristic interburst closed time (τ_c,2) was interpreted as the lifetime in the C₂ state:

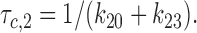4

Finally, the second characteristic interburst closed time (τ_c,3) can be approximated as (see Sakmann and Trube, 1984; Gillis et al., 1989):

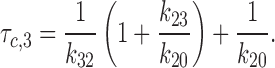5

In addition, the number of intraburst closures per burst was expressed as:

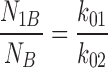6

where N _IB is the number of events within a burst, and N _B is the number of bursts or ofgaps between bursts, distribution of which was defined by τ_c,2 and τ_c,3, with representative relative areas under each exponent, a ₂ and a ₃ (a ₂ + a ₃ = 1), respectively. Therefore:

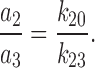7

Eqs. 2–7 were then solved for each of the three forward and three backward rates of transition (see Scheme 1):

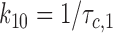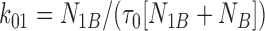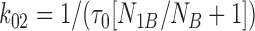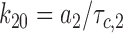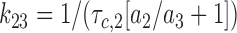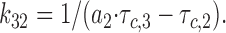8

Calculated rates of transition were used as a quantitative tool to describe the effect of nucleotides and sulfonylurea drugs on K_ATP channel kinetics.

Results are expressed as mean ± SEM; n refers to the number of myocytes used in each analysis.

results

UDP Directs Cardiac K_ATP Channel Activity Towards Intraburst Transitions

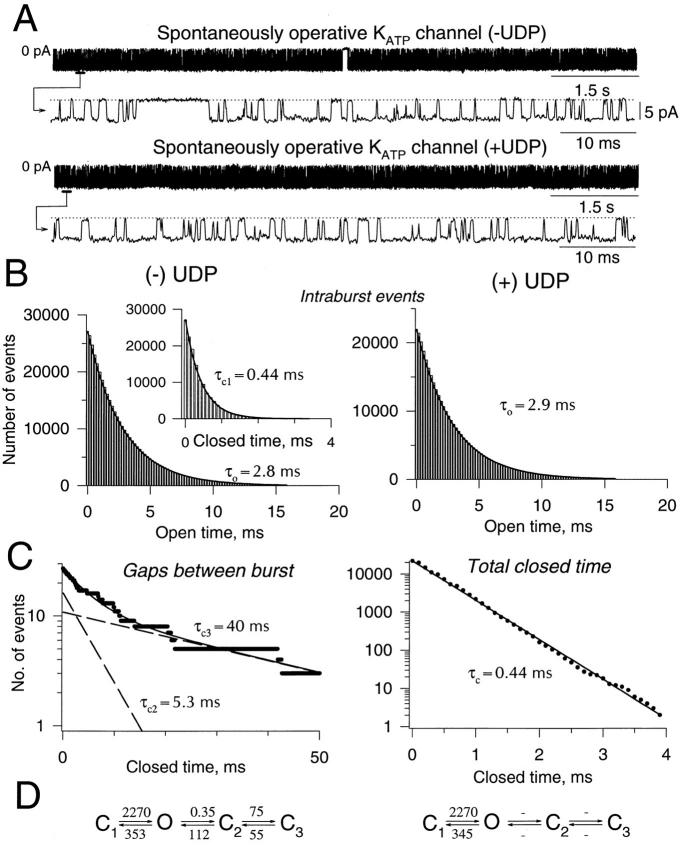
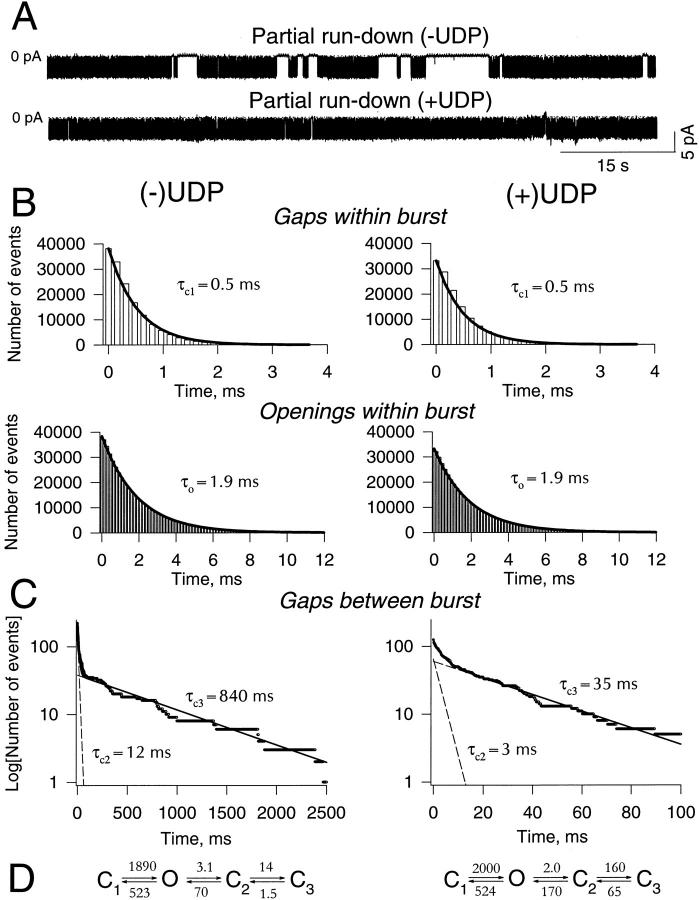
The single channel behavior of cardiac K_ATP channels is characterized by clustering of channel openings in groups (bursts) separated by prolonged closures (gaps between bursts; Fig. 1 A). Within a burst, distributions of closed and open times were fitted by corresponding single exponents (characteristic times τ_c,1 = 0.48 ± 0.03 ms and τ_o = 2.21 ± 0.18 ms, respectively; n = 5; Fig. 1 B, left). Between bursts, distribution of gaps required at least two exponents (Fig. 1 C, left). Thus, in addition to the open and closed channel states that define intraburst (C₁ ↔ O) transitions, two closed states were required to describe interburst (↔ C₂ ↔ C₃) K_ATP channel behavior (Fig. 1 D, left).

Figure 1.

UDP induces loss of interburst transition. (A) Single K_ATP channel records (80 s in duration) in the absence (top) and presence (bottom) of 1 mM UDP. Records under both conditions are presented on compressed and extended time scales. Zero-current level is indicated by 0 pA in the compressed, and by a dotted line in the extended time record. (B, left) In the absence of UDP, open and closed (inset) time distributions of intraburst events were fitted by single exponents (solid lines) with characteristic times τ_o andτ_c,1. (right) Distribution of openings within a burst in the presence of 1 mM of UDP. (C, left) In the absence of UDP, distribution of gaps between bursts was fitted by the sum of two exponents (solid line) with characteristic times τ_c,2 andτ_c,3. Dashed lines correspond to individual exponents. (right) In the presence of UDP, there were no interburst events, and the distribution of closed times could be fitted by a single exponent with a characteristic time, τ_c, essentially identical to the mean closed time for intraburst events (τ_c,1) obtained in the absence of UDP. Kinetic scheme constructed based on calculated rates of transitions (in s⁻¹) using Eq. 8 in the absence (left) and presence (right) of 1 mM UDP. Holding potential was −60 mV.

The nucleotide diphosphate UDP (1 mM) eliminated gaps between bursts, promoting the channel to operate within a sustained burst (Fig. 1 A; Table I). UDP did not change the distribution of open times (Table I) that could be fitted by a single exponent (characteristic time τ_o = 2.36 ± 0.22 ms; n = 4; Fig. 1 B, right), not statistically different from the value obtained in the absence of UDP (P < 0.05; see above). However, since UDP eliminated gaps between bursts, the total distribution of closed times became a single exponent (Fig. 1 C, right) with a characteristic time τ_c,1 = 0.48 ± 0.04 ms (n = 4). This value was identical to the parameter defining closures within bursts of channel activity in the absence of UDP (P < 0.05; see above). In terms of the four-state linear scheme of K_ATP channel activity, UDP reduced channel operation to one closed and one open state with a rate of transition (Fig. 1 D, right), identical to the rate of intraburst transition measured in the absence of UDP (Fig. 1 D, left). Thus, UDP directed the K_ATP channel to operate exclusively within intraburst transitions (Fig. 1 D, right).

Table I.

Parameters of Open and Closed Time Distributions of K_ATP Channel Activity Obtained under Different Experimental Conditions

		Sustained channel activity																Partial rundown
		−UDP		+UDP		−ATP		+ATP		−Glyburide		+Glyburide		−UDP		+UDP+ATP		−UDP		+UDP
Number of events within burst (NIB)		27115		23094		18022		3825		13022		11255		9113		9471		38094		33183
Number of events between burst (NB)		27		2		23		255		14		31		14		4		224		125
Gaps within a burst (τc,1), ms		0.44		0.44		0.49		0.53		0.53		0.54		0.5		0.5		0.53		0.50
Gaps between bursts, fast (τc,2), ms		5.34		—		9.4		12.1		9.8		21		12		—		11.9		3.05
Gaps between burst, slow (t𝔠,3), ms		39.3		—		230		700		544		1500		383		—		842		35.4
Relative area of τc,2 (a  2)		0.6		—		0.66		0.27		0.77		0.58		0.74		—		0.83		0.52
Relative area of τc,3 (a  3)		0.4		—		0.34		0.73		0.23		0.42		0.26		—		0.17		0.48
Open time (τo), ms		2.83		2.9		2.3		2.2		2.1		2.1		2.3		2.4		1.9		1.9

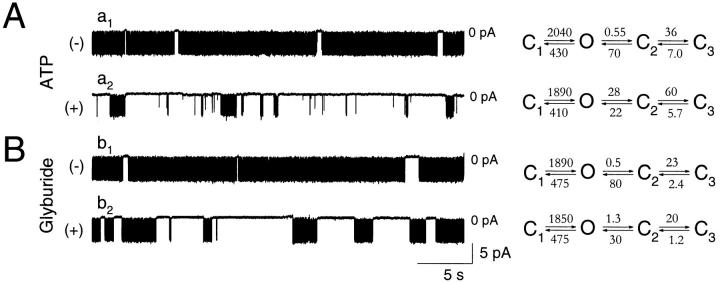
ATP and Glyburide Affect K_ATP Channel Behavior Outside Intraburst Transitions

In the absence of ligands, K_ATP channel activity displayed intraburst and interburst transitions (Fig. 2, a₁ and b₁). ATP (100 μM; Fig. 2 A, a₂) or glyburide (1 μM; Fig. 2 B, b₂) blocked K_ATP channel activity without affecting single channel amplitude (n = 48). Neither ATP (n = 5) nor glyburide (n = 4) significantly changed mean closed (τ_c,1) and mean open (τ_o) times that define intraburst kinetics (Table I). However, both inhibitory ligands did prolong the fast (τ_c,2) and slow (τ_c,3) characteristic times that define the distribution of gaps between bursts (Table I) and increased the number of prolonged channel closures (Table I; relative areas a ₁ and a ₂). This was associated with a significant change in transition rates defining interburst, without a change in rates (k ₁₀ and k ₀₁) defining intraburst (C₁ ↔ O; Fig. 2) transitions. Specifically, ATP (100 μM) promoted escape of the channel from intraburst transitions to the C₂ closed state by increasing the k ₀₂ rate from 0.55 to 28 s⁻¹, and delayed initiation of a burst by decreasing the backward k ₂₀ rate from 70 to 22 s⁻¹ (Fig. 2 A). Similarly, but to a lesser extent than ATP, glyburide (1 μM) increased by threefold the k ₀₂ rate, and decreased by over twofold the backward k ₂₀ rate (Fig. 2 B). Consequently, the mean duration of a burst (2,210 ms, n _burst = 23 and 2,380 ms, n _burst = 14 in the absence of ATP and glyburide, respectively) was reduced by each of the inhibitory ligands (56 ms, n _burst = 255 and 850 ms, n _burst = 31 in the presence of ATP and glyburide, respectively).

Figure 2.

Inhibitory ligands act on K_ATP channels outside intraburst transition. Portions of original single channel records in the absence (a₁ and b₁) and presence (a₂) of 100 μM ATP or 1 μM glyburide (b₂). Corresponding kinetic schemes with calculated rates of transitions (in s⁻¹, Eq. 8) are provided for each record in the absence and presence of ATP (A) and in the absence and presence of glyburide (B). Holding potential was −60 mV throughout.

In agreement with experimental data, calculated mean burst duration, using rates defining intraburst transitions and the rate leading away from these transitions (Sakmann and Trube, 1984):

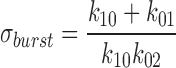8

was 2,200 vs. 44 ms in the absence and presence of ATP, and 2,500 vs. 960 ms in the absence and presence of glyburide.

Since the lifetime the channel spends in a specific state is defined by the reciprocal of the sum of transition rates that lead away from this state:

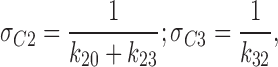9

the lifetime the K_ATP channel spent in C₂ or C₃, in the presence of ATP (100 μM), was 12.2 and 175 ms, respectively. Although these values were within the range of values obtained in the absence of ATP (σ_C2 = 9.1 ± 1.4 ms, and σ_C3 = 207 ± 84 ms; n = 4), ATP by accelerating k ₂₃ and by reducing k ₂₀ rates (Fig. 2 A) promoted the channel to operate within C₂ ↔ C₃ closed states, away from intraburst transitions. Thereby, ATP significantly increased the combined lifetime the K_ATP channel spent within interburst transitions (Sakmann and Trube, 1984):

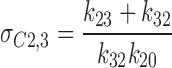10

from 87.8 ms in the absence to 524 ms in the presence of ATP (Fig. 2 A).

Glyburide (1 μM) reduced the lifetime in either the C₂ (from 9.7 to 20 ms) or the C₃ (from 417 to 833 ms) closed states (Fig. 2 B). The mean lifetime (σ_C2,3) the channel spent within C₂ ↔ C₃ closed states increased from 132 ms in the absence to 589 ms in the presence of glyburide (Fig. 2 B). Thus, ATP and glyburide, despite apparent differences in the mechanism of channel inhibition, act outside the intraburst C₁ ↔ O transition, shorten burst duration, and prolong the time the K_ATP channel remains within C₂ and C₃ closed states.

UDP Prevents Ligand Inhibition of K_ATP Channels by Favoring Intraburst Activity

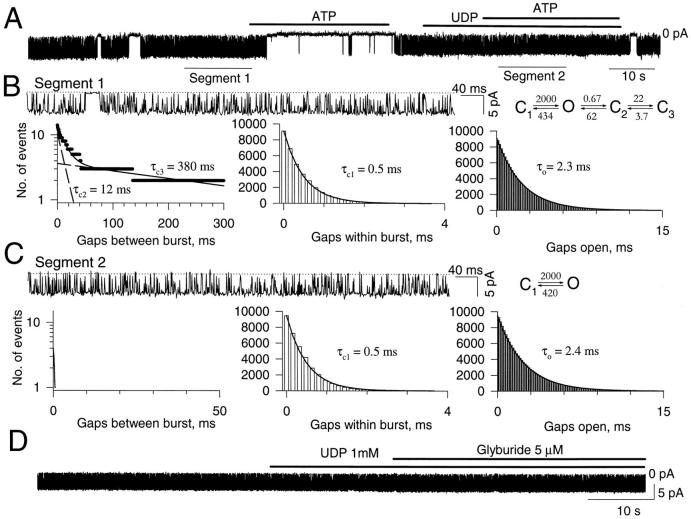
In the absence of UDP, K_ATP channel activity exhibited intraburst and interburst transitions (Fig. 3, A and B, Table I) and was sensitive to the inhibitory action of ATP (200 μM). Washout of ATP restored channel activity, which was directed towards intraburst transition by 1 mM UDP (Fig. 3, A and C). Intraburst forward and backward rates of transition were similar before (2,000 and 434 s⁻¹), and after (2,000 and 420 s⁻¹) addition of UDP and ATP. However, UDP eliminated gaps between bursts in all patches so tested (n = 4), which induced an apparent insensitivity of the K_ATP channel towards ATP (Fig. 3 A).

Figure 3.

Loss of interburst events induced by UDP associated with loss of ATP or glyburide sensitivity of K_ATP channels. (A) Single-channel record of K_ATP channel activity inhibited by ATP (200 μM) in the absence but not in the presence of UDP (1 mM). (B) Single-channel record of segment 1 (in A) presented on an extended time scale with distributions for gaps between burst (left), gaps within burst (middle), and open gaps (right). Corresponding kinetic scheme with rates of transitions (s⁻¹, Eq. 8) is provided. (C) Single-channel record of segment 2 (in A), obtained in the presence of UDP (1 mM) and ATP (200 μM) and presented on an extended time scale with distributions for gaps between burst (left), gaps within burst (middle), and open gaps (right). In the presence of both UDP and ATP, essentially no gaps between bursts were visible, while no effect on intraburst kinetics was observed. A corresponding kinetic scheme, without interburst transitions and with calculated rates of intraburst transitions (s⁻¹), is provided. (D) Single-channel record of K_ATP channel activity depicting UDP-induced antagonism of glyburide-mediated channel inhibition. Holding potential was −60 mV throughout.

The effect of UDP was also tested in the presence of glyburide, a nonnucleotide inhibitory ligand of the channel. As in the case of ATP (Fig. 3 A), maintenance of channel activity within intraburst transitions by UDP also prevented glyburide (3 μM) to block K_ATP channel activity (Fig. 3 D; n = 6). Thus, regardless of the structure of the inhibitory ligand, UDP could apparently shield the K_ATP channel from ATP or glyburide by “trapping” the channel within ligand-insensitive transitions.

UDP Is Not the Sole Determinant of Sensitivity to Inhibitory Ligands

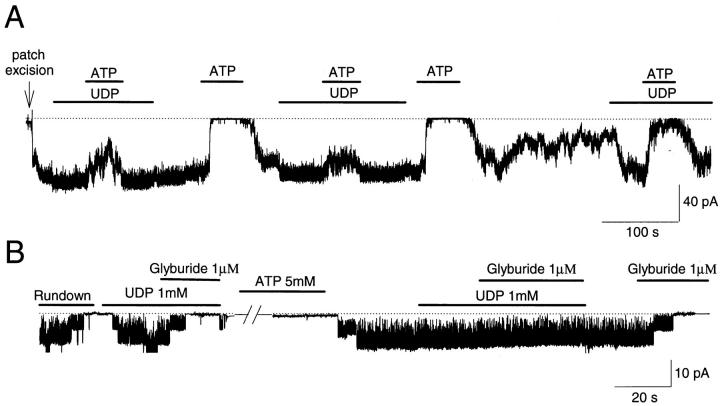
The efficacy with which UDP antagonizes ATP- and glyburide-inhibitory gating has been reported to vary with the operative condition of the K_ATP channel (Terzic et al., 1994a ; Brady at al., 1998). As shown in Fig. 4 A, sustained spontaneous K_ATP channel activity was only partially sensitive to ATP (300 μM) in the presence of UDP (2 mM), yet fully sensitive in the absence of UDP (n = 10). With channel “rundown,” UDP restored channel activity but could no longer antagonize ATP (Fig. 4 A, see also Terzic et al., 1994a ). Similarly, after rundown, UDP induced channel opening that was inhibited by glyburide (1 μM; Fig. 4 B; n = 5). However, restoration of spontaneous channel activity, by pretreatment with MgATP (5 mM), was associated with return of UDP- induced antagonism of glyburide inhibition (Fig. 4 B, see also Brady et al., 1998). Thus, channel rundown appears to decrease the efficacy with which UDP antagonizes the action of inhibitory ligands.

Figure 4.

Dual responsive behavior of K_ATP channels, in the presence of UDP, towards ATP and glyburide. (A) After patch excision, K_ATP channel activity was vigorous and sustained at maximal level by UDP (2 mM), under which condition ATP (300 μM) produced only partial channel inhibition. Removal of UDP was associated with channel inhibition by ATP. Such effect was reproducible. With time after patch excision, K_ATP channel activity was observed to rundown. Under partial rundown, UDP enhanced channel activity, but only partially antagonized ATP- induced channel inhibition. The dotted line corresponds to the zero-current level. (B) Conversion of rundown to spontaneous K_ATP channel activity by Mg-ATP switches on the UDP-induced antagonism of glyburide-dependent channel block. A 10-min long pretreatment of rundown K_ATP channels with 5 mM Mg-ATP restored spontaneous channel activity and with it the UDP-induced antagonism of glyburide-dependent channel block lost in rundown channels. In the absence of UDP, channel activity was readily inhibited by glyburide. The dotted line with original trace corresponds to the zero-current level. nP _o values, corresponding to the trace record, were calculated over 1.02-s-long intervals. Holding potential was −60 mV throughout.

Rundown Prevents UDP from Holding K_ATP Channels within Intraburst Transitions

Progression of rundown of K_ATP channel activity was associated with an increased number of prolonged closures (Fig. 5 A, top). Intraburst channel properties (τ_c,1 and τ₀, Fig. 5 B, Table I) were unchanged with rundown, but both fast and slow time components defining gaps between burst (τ_c,2 and τ_c,3) were prolonged (Fig. 5 C, Table I). As the process of rundown accelerated, the k ₀₂ rate responsible for exit of the channel from a burst (from 0.52 ± 0.07 s⁻¹, n = 4, under sustained activity to 3.1 s⁻¹ during rundown; Fig. 5), mean burst duration of partial rundown channels was shorter when compared with sustained channel activity (τ_burst = 440 ms; n _burst = 224 vs. τ_burst = 2,456 ± 315 ms; n = 4). Furthermore, K_ATP channels under partial rundown spent a significantly longer time in the C₃ state (Eq. 10) when compared with channels under sustained channel activity (670 ms vs. 207 ± 84 ms; n = 4), although the apparent lifetime in the C₂ state (12 ms vs. 9.1 ± 1.4 ms, n = 4; Eq. 10) was similar under both conditions. Thus, channel rundown directed K_ATP channels away from intraburst and towards interburst transitions.

Figure 5.

Rundown prevents UDP from locking K_ATP channels within intraburst transitions. (A) Single K_ATP channel records during partial rundown in the absence (top) and presence (bottom) of 1 mM UDP. Zero-current level indicated by 0 pA. (B) Intraburst kinetic properties. UDP (right) did not affect distributions of closed (top) and open (bottom) times within bursts of channel activity. Both distributions were well-fitted by single exponents, with τ_c,1 and τ_o representing characteristic closed and open times, respectively. (C) Distribution of gaps between bursts in the absence (left) and presence (right) of UDP. Under both conditions, distributions needed to be fitted by the sum of two exponents with characteristic times τ_c,2 andτ_c,3. Solid lines correspond to the sum of both exponents drawn by fitting, whereas dashed lines correspond to individual exponents. Holding potential was −60 mV. (D) Kinetic scheme constructed based on calculated rates of transitions (in s⁻¹, Eq. 8) in the absence (left) and presence (right) of 1 mM UDP.

To determine the efficacy with which UDP acts on K_ATP channels driven towards the C₃ state as rundown progresses, UDP (1 mM) was applied to partially rundown channels (Fig. 5 A, bottom). UDP increased channel activity and reduced the number of channel closures (Fig. 5 A, bottom). Similar to its effect on sustained K_ATP channel activity, UDP did not affect intraburst kinetics; i.e., UDP did not significantly change rates defining the C₁ ↔ O transition (k ₁₀ and k ₀₁) of partially rundown channels (Fig. 5, A and B). However, in contrast to sustained K_ATP channel activity (Fig. 1), UDP did not eliminate interburst events in rundown channels, the distribution of which remained biexponential (Fig. 5 C). Also, in contrast to its effect on sustained channel activity where UDP eliminated the O ↔ C₂ transition (from 0.35 to ∼0 s⁻¹; Fig. 1, Table I), UDP only decreased the transition rate (k ₀₂) associated with burst closure of partially rundown channels (i.e., the O ↔ C₂ transition changed from 3.1 to 2.0 s⁻¹; Fig. 5 D). Under this condition, the K_ATP channel could still transit between intraburst and interburst states despite the presence of UDP (Fig. 5, A and C). Mean burst duration (Eq. 9) of partially rundown channels increased in the presence of UDP from τ_burst = 440 ms (n _burst = 224) to τ_burst = 684 ms (n _burst = 125), similar to calculated values of τ_burst (412 and 631 ms in the absence and presence of UDP, respectively; Eq. 9). Acting on partially rundown channels, UDP apparently reduced the lifetime the channel spent within interburst transitions (3 and 15 ms for C₂ and C₃, respectively; Fig. 5 A; Eq. 10). Thus, under such conditions, although UDP still directed partially rundown channels towards intraburst ligand-insensitive transitions, the nucleotide diphosphate could not maintain the channel within a ligand-insensitive state.

Allosteric Model of Ligand/Channel Interaction

It has been reported that UDP shifts to the right the concentration–response curve to ATP (Terzic et al., 1994a ), whereas it completely eliminates the sensitivity of the K_ATP channel to glyburide (Brady et al., 1998). Based on the kinetic model, it was not possible to quantitatively predict the different response of K_ATP channels to inhibitory ligands. Therefore, an allosteric model of ligand/protein interaction (Monod et al., 1965), previously applied to analyze ligand regulation of ion channels (Karlin, 1967; Hosoya et al., 1997; Tibbs et al., 1997), was used. The features of such allosteric models are that (a) the allosteric protein (i.e., the channel complex) interconverts within two distinct conformational states: ligand-sensitive (S) and -insensitive (I); (b) the channel complex possesses two sets of binding sites (n and m), one for the inhibitor (A), and the second for the activator (B); (c) each set of binding sites is equivalent within a state, but exhibits different microscopic dissociation constants (K_A,S or K_B,S in S and K_A,I or K_B,I in I) between states; and (d) binding of an inhibitor or an activator shifts, in opposite directions, the equilibrium between the two conformational states and thus increases the fraction of total protein (channel complex) in the state with higher affinity for a particular ligand and decreases the apparent (macroscopic) affinity towards the other ligand.

The equilibrium constant (L) in the absence of a ligand was expressed by the ratio between the channel lifetime in ligand-insensitive (i.e., mean burst duration; Eq. 9) and -sensitive (i.e., lifetime spent in C₂ plus C₃; Eq. 11) states:

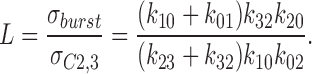11

From our experimental data (i.e., Figs. 1 and 2), calculation of L revealed a value in the range of 150–200 under spontaneous channel activity. This indicates that under sustained spontaneous channel activity the equilibrium between ligand-sensitive and -insensitive states is significantly shifted towards ligand-insensitive states, which corresponds to a prolonged burst of channel activity.

Channel inhibition is a function of the fraction of the protein in the S state:

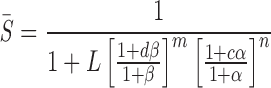12

where d = K_B,S /K_B,I, β = [B]/K_B,S, c = K_A,S/K_A,I, and α = [A]/K_A,S. For A, the allosteric inhibitor (e.g., glyburide or ATP), c < 1. For B, the allosteric activator (i.e., UDP), d > 1.

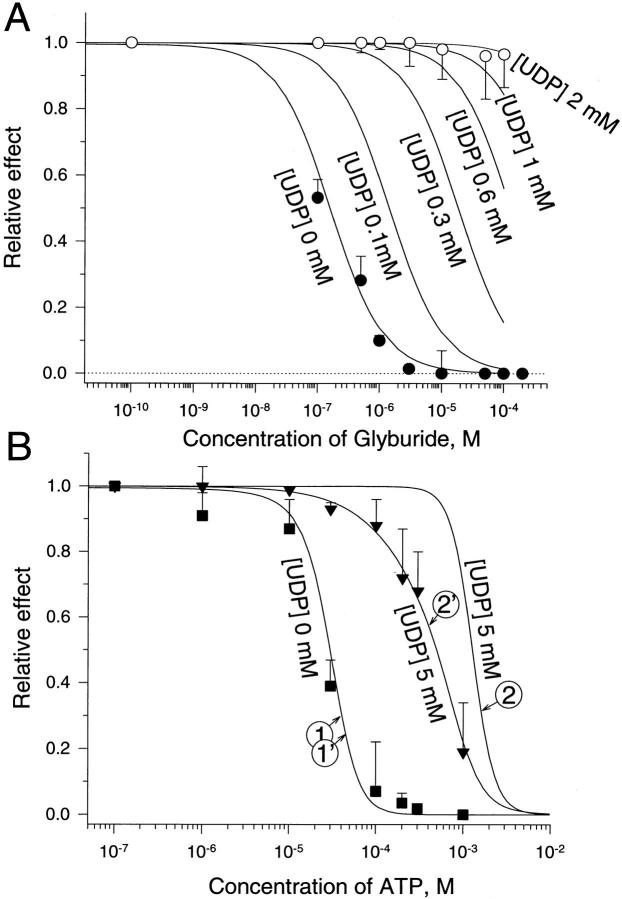
In the absence of UDP, the concentration dependence of K_ATP channel inhibition by glyburide (A; Fig. 6 A, •) was well fitted by the 1-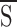 function (Eq. 13) using the following parameters: L = 200; K_A,S = 1 nM, K_A,I = 1 mM, n = 1 (Fig. 6 A, solid line). In the presence of 1 mM UDP, the observed loss of sensitivity of the K_ATP channel towards the sulfonylurea (Fig. 6 A, ○) was well described by the allosteric model (L = 200; K_A,S = 1 nM, K_A,I = 1 mM, n = 1; K_B,S = 3.5 mM, K_B,I = 0.1 mM, m = 4). The model predicts that at millimolar concentrations of the activator (UDP) the effect of glyburide on K_ATP channel activity will be fully antagonized even at tens of micromoles of the inhibitor (Fig. 6 A, solid line).

Figure 6.

Use of an allosteric model to predict the effect of glyburide or ATP on K_ATP channel opening in the absence and presence of UDP. (A) Concentration dependence of glyburide-induced K_ATP channel inhibition in the absence (•) and presence (○) of 1 mM UDP. Data points are from five to nine patches. Relative effect of glyburide was calculated in each patch as a ratio between slopes of cumulative nP _o measured in the presence over the value obtained in the absence of glyburide (see Brady et al., 1998). Solid curves were constructed using Eq. 13 at various concentrations of UDP (see text for values of parameters). (B) Concentration dependence of ATP-induced K_ATP channel inhibition in the absence (▪) and presence (▾) of 5 mM UDP. Data points are from 4 to 10 patches. Relative effect of ATP was calculated in each patch as a ratio between nP _o values measured in the presence over the value obtained in the absence of ATP (see Terzic et al., 1994a ). Curves 1 and 1′ (at 0 mM UDP), 2 and 2′ (at 5 mM UDP) were constructed using Eqs. 13 and 14, respectively. See text for values of parameters.

In the absence of UDP, the concentration dependence of K_ATP channel inhibition by ATP (A; Fig. 6 B, ▪) was also well fitted by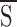 the 1- function (Eq. 13) using the following parameters: L = 200; K_A,S = 8.5 μM, K_A,I = 70 mM, n = 3.6 (Fig. 6 B, curve 1). However, in the presence of UDP (5 mM; K_B,S = 3.5 mM, K_B,I = 0.1 mM, m = 4), the allosteric model predicted a rightward shift but failed to precisely fit (Fig. 6 B, curve 2) the experimentally obtained data defining the concentration response of ATP-induced K_ATP channel inhibition under this condition (Fig. 6 B, ▾). Since varying the number of binding sites, cooperativity, and/or dissociation constants for ATP did not improve the fit, we further developed the model taking into account the existence of an additional presumed binding site for ATP not affected by nucleotide diphosphate regulation (Tucker et al., 1997; Ueda et al., 1997). Therefore, we added to the 1-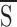 function (Eq. 13) an additional allosteric regulation-independent inhibitory process to account for both mechanisms of ATP inhibitory action:

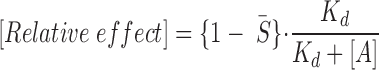13

where K _d is the dissociation constant to this additional ATP binding site. In this adjusted model, K _d = 610 μM could fully account for the ATP-induced channel inhibition in the absence (Fig. 6 B, curve 1′) and presence (Fig. 6 B, curve 2′) of UDP. The prediction based on the developed model can be interpreted to mean that UDP antagonized ATP-induced K_ATP channel inhibition through one set of ATP-binding sites, thus reducing channel inhibition to the other set of ATP-binding sites.

Despite the lack of reliable means to quantify the rundown process, the allosteric model could, in principle, also be used to describe the effects of ligands under rundown of K_ATP channel activity. Based on our experimental data (Fig. 5), rundown shifted the equilibrium constant (L) from 150–200 under spontaneous channel activity to 10–20 under partial rundown, and to even lower values with further progression of rundown. This was associated with a prolongation of the lifetime the channel spent in C₂ and C₃ closed states. In contrast to spontaneous channel activity, where UDP increased L → ∞•(by k ₀₂ → 0), under partial rundown UDP elevated L only up to 70–90 (i.e., Fig. 5). However, such a change in L was not sufficient to restore the experimentally obtained channel sensitivity towards ATP and glyburide (Terzic et al., 1994a ; Brady et al., 1998). This could indicate that besides the effect on L, rundown could also alter other parameters of channel/ ligand interaction. For instance, rundown could decrease the affinity of ligands for the I state, which would promote the effect of inhibitors (Thuringer and Escande, 1989; Deutsch and Weiss, 1993). Thus, the use of the allosteric model could explain the nonuniform responsive behavior of K_ATP channels to inhibitory ligands in the presence of UDP depending on the operative condition of the channel.

discussion

The present study demonstrates that cardiac K_ATP channels can be directed to operate within ligand-insensitive conformational states. The switch into ligand-insensitive behavior was induced by the nucleotide diphosphate, UDP. Interconversion between ligand-sensitive and -insensitive states represents a novel mechanism of K_ATP channel regulation. The property of a nucleotide diphosphate to direct cardiac K_ATP channels towards a state that is insensitive towards inhibitory ligands could provide a mechanistic basis for channel opening in the presence of inhibitory concentrations of ATP within an intact cell.

Ligand–Channel Interaction and Kinetic Model

To distinguish between conformational transitions that define K_ATP channel activity, we applied a linear kinetic model used previously (Sakmann and Trube, 1984; Gillis et al., 1989; Nichols et al., 1991; Furukawa et al., 1993; Takano and Noma, 1993). This entropic model does not describe all conformations through which a channel transits, but it does allow description of end points of sequential conformational transitions accessible to direct measurement. Although this simplified model was developed for inward K_ATP channel current as recorded under present experimental conditions (with symmetrical K⁺ solutions and at a holding potential of −60 mV), intraburst and interburst transitions can also be distinguished for outward K_ATP channel currents despite more complex intraburst kinetics (Zilberter et al., 1988; Larsson et al., 1993; Alekseev et al., 1997b ). Herein, we found that the inhibitory ligands, ATP and glyburide, inhibited K_ATP channel activity by acting upon conformational states that define interburst behavior without affecting intraburst channel transitions. This is in agreement with previous studies that have also shown that inhibitory ligands target specific rates of channel kinetics (Gillis et al., 1989; Qin et al., 1989; Nichols et al., 1991; Takano and Noma, 1993; Benz and Kohlhardt, 1994; Smith et al., 1994). We further found that UDP could keep the channel within a burst, preventing interburst transitions. Therefore, the observed effect of UDP to antagonize channel inhibition by ATP and glyburide could be attributed to the limitation of channel behavior within ligand-insensitive intraburst conformational transitions. Such a mechanism could explain the altered responsiveness of cardiac K_ATP channels towards ATP and sulfonylureas observed in the presence of nucleotide diphosphates (Nichols and Lederer, 1991; Venkatesh et al., 1991; Virag et al., 1993; Findlay, 1994; Terzic et al., 1994a ; Brady et al., 1998). Based on the kinetic model used, the present study provides evidence that the response of the cardiac K_ATP channel depends not only on the concentration of an inhibitor, but also on the lifetime the channel spends within ligand-sensitive states. This concept may not be limited to UDP. Indeed, it has been shown that other agents, such as potassium channel openers (Fan et al., 1990; Terzic et al., 1994b ), intracellular protons (Vivaudou and Forestier, 1995; Alekseev et al., 1997a ), cytoskeleton disrupters (Brady et al., 1996a ), or channel trypsinization (Deutsch and Weiss, 1994), which also promote the K_ATP channel to operate within a burst, decrease the sensitivity of the channel towards inhibitory ligands. Furthermore, combined application of ADP and the opener diazoxide potentiated the ability of these agents to antagonize ATP inhibition of K_ATP channels by prolonging the lifetime the channel spends within a burst (Larsson et al., 1993). Conversely, ATP and related nucleotides that direct the K_ATP channel to operate within interburst transitions were shown to enhance the sensitivity of K_ATP channels towards sulfonylureas (Virag et al., 1993; Schwanstecher et al., 1994).

Application of an Allosteric Model to the Regulation of K_ATP Channels

The dual nature of K_ATP channel behavior, in terms of ligand-sensitive and -insensitive states, drew parallelism with interconversion of an allosteric protein between two significant conformational states with different affinities to ligands (Monod et al., 1965; Karlin, 1967). This allosteric model predicted the observed change in the ATP- and glyburide-dependent inhibitory gating of the channel induced by a UDP-mediated shift in the equilibrium towards the ligand-insensitive state of the K_ATP channel. The difference in the microscopic affinities for the two conformational states (10⁶ for glyburide and ∼10⁴ for ATP) predicted by the present allosteric model is consistent with the existence of ligand-insensitive and -sensitive states of the channel. In fact, the allosteric model predicted that at millimolar concentrations of UDP the cardiac K_ATP channel loses its sensitivity towards glyburide. This is in accord with previous studies that have established that under spontaneous K_ATP channel activity, nucleotide diphosphates, such as UDP or ADP, antagonize sulfonylurea-induced channel inhibition (Venkatesh et al., 1991; Virag et al., 1993; Brady et al., 1998). Although it is difficult to compare microscopic with apparent dissociation constants, high and low affinities for sulfonylurea binding have been previously reported (Fosset et al., 1988; Aguilar-Bryan et al., 1992). Thus, due to the negligible affinity of glyburide towards the ligand-insensitive (I) state, UDP by shifting the equilibrium of the K_ATP channel towards this particular state could effectively antagonize the effect of the sulfonylurea. In the case of ATP, for which the model predicts an additional, nucleotide diphosphate-independent, ATP-inhibitory channel gating, UDP could produce only a rightward shift in the concentration response curve of ATP-induced channel inhibition, as previously experimentally observed with UDP (Terzic et al., 1994a ) or other nucleotide diphosphates such as ADP (Findlay, 1988; Lederer and Nichols, 1989). In contrast to UDP, channel rundown shifted the equilibrium towards the ligand-sensitive state of the K_ATP channel. This increased sensitivity of the channel towards inhibitory ligands is in accord with experimental findings that have shown that rundown enhances the inhibitory action of ATP on cardiac K_ATP channel activity (Thuringer and Escande, 1989; Deutsch and Weiss, 1993). Since rundown is believed to be associated with changes in the phosphorylation status of the K_ATP channel or associated proteins (Trube and Hescheler, 1984; Findlay and Dunne, 1986; Findlay, 1987; Ohno-Shosaku et al., 1987; Takano et al., 1990; Furukawa et al., 1996; Hilgemann and Ball, 1996), the equilibrium between the S and I channel states may be dependent upon a phosphorylation process. Treatment of rundown membrane patches with Mg-ATP (but not with ATP alone or with nonhydrolyzable ATP analogs), through presumed “rephosphorylation” of channel proteins, restored spontaneous cardiac K_ATP channel activity, and with it the efficacy of UDP to antagonize ATP- and glyburide-induced channel inhibition (see also Terzic et al., 1994a ; Brady et al., 1998).

Relevance to the Molecular Structure of K_ATP Channels

Results predicted by the allosteric model applied herein to the native cardiac K_ATP channel are in agreement with the reported structure and stoichiometry of the recombinant K_ATP channel complex (Inagaki et al., 1995, 1996; Isomoto et al., 1996; Clement et al., 1997; Tucker et al., 1997). This channel is a heteromultimer that combines four Kir6.2 and four SUR subunits into an octamer (Clement et al., 1997; Inagaki et al., 1997). It has been suggested that ATP binds to both the pore-forming Kir6.2 (Tucker et al., 1997) and the regulatory SUR (Bernardi et al., 1992; Ueda et al., 1997) subunits. In view of this, the requirement of two sets of binding sites for ATP could be interpreted to indicate two separate ATP-binding sites on each subunit of the channel complex. The allosteric model further predicts four binding sites for UDP on the K_ATP channel complex. This apparently correlates with the previously observed binding of a nucleotide diphosphate to only one of the channel subunits, the SUR subunit (Bernardi et al., 1992; Nichols et al., 1996; Gribble et al., 1997; Trapp et al., 1997; Tucker et al., 1997; Ueda et al., 1997). The binding of sulfonylureas to the K_ATP channel is also presumed to occur on the SUR subunit (Aguilar-Bryan et al., 1995; Inagaki et al., 1995, 1996; Clement et al., 1997). However, in terms of the allosteric model and in contrast to nucleotides, K_ATP channel regulation by glyburide was characterized by lack of cooperativity (see also Venkatesh et al., 1991).

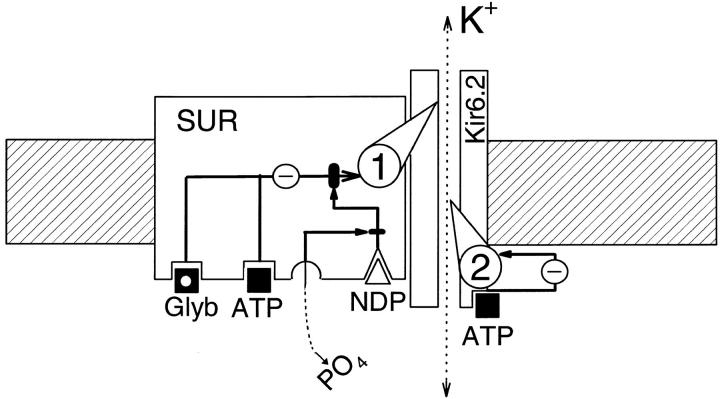
Intraburst kinetics that define ligand-insensitive transitions are apparently associated with conformational fluctuation of Kir6.2 itself (Alekseev et al., 1997b ; Tucker et al., 1997), whereas interburst kinetics are modulated by association of Kir6.2 with the SUR subunit (Inagaki et al., 1996). In view of the proposed structure of the K_ATP channel complex (Inagaki et al., 1995, 1996, 1997; Clement et al., 1997; Tucker et al., 1997), the kinetic and allosteric properties of channel behavior may provide the basis for a mechanistic model of the UDP- induced changes in the ATP- and glyburide-dependent regulation of K_ATP channel gating (Fig. 7). Such a model implies the existence of two inhibitory gating pathways. The first, mediated through binding of inhibitory ligands to the SUR subunit, appears to be sensitive to UDP regulation. The second, mediated through binding of ATP to Kir6.2, appears to be insensitive to UDP regulation. Disruption of the first inhibitory gating pathway by UDP switches the channel into sulfonylurea- insensitive behavior and decreases the channel sensitivity towards ATP (Fig. 7). Phosphorylation(s) of the channel protein can apparently restore the ability of UDP to disrupt the first inhibitory pathway lost after rundown of channel activity.

Figure 7.

Scheme of UDP-induced change in ATP- and glyburide-dependent inhibitory channel gating. This mechanistic model, which takes into account the proposed structure of the K_ATP channel (Inagaki et al., 1995, 1996, 1997; Clement et al., 1997; Tucker et al., 1997), as well as the kinetic and allosteric properties of channel behavior, suggests the existence of two inhibitory gating mechanisms of K_ATP channels labeled 1 and 2. The gating mechanism number 1 transduces inhibitory signals from glyburide (Glyb) and ATP-binding sites on the SUR channel subunit. This inhibitory gating can be intercepted after binding of a nucleotide-diphosphate (NDP) to the SUR subunit. Presumed dephosphorylation of the channel affects nucleotide diphosphate–dependent regulation of channel gating. The gating mechanism number 2 transduces inhibitory signals from the ATP-binding site on the Kir6.2 channel subunit, which appears to be insensitive to nucleotide-diphosphate regulation.

Concluding Remarks

Although the present study used UDP as a nucleotide diphosphate, the observed effect on K_ATP channel behavior may also be attributable to other nucleotide diphosphates, such as ADP. In contrast to UDP, the presence of the adenine moiety could make the interpretation of the effect of ADP more complex due to possible competitive interaction of ADP with an ATP-binding site (Ueda et al., 1997). Despite this, similar effects of ADP (MgADP) in modulating the K_ATP channel inhibitory gating and postrundown channel behavior have previously been demonstrated (Dunne and Petersen, 1986; Tung and Kurachi, 1991; Venkatesh et al., 1991; Weiss and Venkatesh, 1993; Findlay, 1988, 1994; Elvir-Mairena et al., 1996), as well as the ability of MgADP to prolong burst duration (Larsson et al., 1993).

The property of cardiac K_ATP channels to interconvert between ligand-sensitive and -insensitive states, described herein, resembles other ion channels that also show differential sensitivity towards ligands depending on their operative state, including “use-dependent” blockade of Na⁺ and Ca²⁺ channels (Lee and Tsien, 1983; Hill et al., 1989; Ragsdale at al., 1994; Nuss et al., 1995). Entry of the K_ATP channel into a ligand-insensitive state by a nucleotide diphosphate could provide a basis for cardiac K_ATP channel opening during hypoxia or ischemia despite rather constant levels of ATP within the cell.