Local Control Models of Cardiac Excitation–Contraction Coupling

Abstract

In cardiac muscle, release of activator calcium from the sarcoplasmic reticulum occurs by calcium- induced calcium release through ryanodine receptors (RyRs), which are clustered in a dense, regular, two-dimensional lattice array at the diad junction. We simulated numerically the stochastic dynamics of RyRs and L-type sarcolemmal calcium channels interacting via calcium nano-domains in the junctional cleft. Four putative RyR gating schemes based on single-channel measurements in lipid bilayers all failed to give stable excitation–contraction coupling, due either to insufficiently strong inactivation to terminate locally regenerative calcium-induced calcium release or insufficient cooperativity to discriminate against RyR activation by background calcium. If the ryanodine receptor was represented, instead, by a phenomenological four-state gating scheme, with channel opening resulting from simultaneous binding of two Ca²⁺ ions, and either calcium-dependent or activation-linked inactivation, the simulations gave a good semiquantitative accounting for the macroscopic features of excitation–contraction coupling. It was possible to restore stability to a model based on a bilayer-derived gating scheme, by introducing allosteric interactions between nearest-neighbor RyRs so as to stabilize the inactivated state and produce cooperativity among calcium binding sites on different RyRs. Such allosteric coupling between RyRs may be a function of the foot process and lattice array, explaining their conservation during evolution.

introduction

The intracellular signal that triggers the contraction of cardiac muscle is a transient rise in intracellular free calcium. The majority of this calcium (50–95%, depending upon species and conditions) is released from the sarcoplasmic reticulum (SR).¹ This calcium is released by a process of calcium-induced calcium release (CICR) (Endo et al., 1970; Fabiato, 1985) via release channels, which have been shown to be type-2 ryanodine receptors (RyR2). It is generally believed that the major stimulus for CICR is calcium entering the cell via sarcolemmal dihydropyridine–sensitive L-type calcium channels. The rate and amount of calcium release from the SR is tightly controlled by the magnitude and duration of the L-type calcium current (See Ríos and Stern, 1997, for a review of the evidence). This graded control is paradoxical because the released calcium, which is roughly 10× larger in amount than the trigger, would be expected to stimulate further CICR, leading to a regenerative, nearly all-or-none release. Several years ago (Stern, 1992), we proposed that this paradox of control might be explained if the stimulus for release of calcium by RyRs were actually the local nanodomains of [Ca²⁺] generated by nearby L-type channels, rather than the global cytosolic [Ca²⁺]. According to this local control hypothesis, the graded control of macroscopic SR calcium release would actually be achieved by graded statistical recruitment of individual, autonomous, stochastic release events.

Recent ultrastructural studies (Franzini-Armstrong, C., F. Protasi, and V. Ramesh, manuscript in preparation) show that, depending on species, from a few tens to ∼200 RyRs are clustered in a two dimensional crystal-lattice array on the surface of SR release terminals, apposed, across the 15-nm cleft of the diad junction, to clusters of sarcolemmal dihydropyridine receptors (DHPRs). RyR2 is a homotetramer of a polypeptide of roughly 5,000 amino acids. The transmembrane calcium-sensitive channel is formed by the COOH-terminal ∼600 amino acids (Tunwell et al., 1996; Bhat et al., 1997a), while the remainder of the molecule forms a 30-nm quatrefoil “foot process” that spans the diadic cleft, and is required for interaction of the channel with a variety of modulators (Bhat et al., 1997b). The DHPRs in cardiac muscle, whose number varies in different studies from 10–100% of the number of RyRs (Wibo et al., 1991; Bers and Stiffel, 1993; Sun et al., 1995), are localized at the junctions, but are randomly positioned relative to the ryanodine receptor lattice (Franzini-Armstrong, C., F. Protasi, and V. Ramesh, manuscript in preparation). This contrasts with the regular arrangement of DHPR tetrads found in skeletal muscle.

We carried out numerical simulations of this system of channels, interacting stochastically via calcium diffusing in the diadic cleft. These simulations have revealed a new paradox. Local control succeeds if the gating of the RyR is represented by a simple, phenomenological, four-state scheme. However, published schemes derived from actual gating statistics of single RyR2 channels incorporated into lipid bilayers give rise to unacceptable instabilities when used in the local control model. These instabilities are traceable to two deficiencies in bilayer-derived gating schemes. The absence of strong inactivation prevents termination of locally regenerative release by clustered RyRs. Activation by binding of a single Ca²⁺ ion, in some bilayer-derived schemes, does not provide adequate discrimination against activation by global (rather than microdomain) Ca²⁺. This suggests that the gating of RyR2 in situ may differ significantly from its behavior in bilayers. One possible explanation of this difference would be the existence of allosteric interactions between the large foot processes of adjacent RyRs, which appear anatomically to be in contact. We show by simulation that RyR–RyR allosteric interaction energies can be chosen in such a way as to remedy both the inactivation and the cooperativity deficiencies of RyR2 gating schemes. Such interactions may be one of the important functions of the foot process, which has been highly conserved in evolution.

methods

Simulation

Monte Carlo simulations were carried out using a modification of an algorithm previously reported (Stern et al., 1997). In brief, the set of channels at each diad was treated as a single stochastic system whose state (“macrostate”) is defined by specifying the Markov state of each of the individual channels. State transitions of individual channels are considered to take place instantaneously so that a macrostate transition corresponds to a transition of exactly one channel. The transition rates of the individual channels were determined from their gating schemes as a function of the local [Ca²⁺] at the position of each channel. The dwell time and destination of each transition were selected by use of appropriately distributed random numbers, while the local [Ca²⁺] was determined concomitantly by solving the partial differential equations governing diffusion and binding reactions in the diadic cleft. The aggregate calcium fluxes produced by 1,000–10,000 such diads were taken as input to a conventional lumped-compartment model of global cytosolic and SR calcium dynamics. This model (a set of ordinary differential equations) was solved to update the values of [Ca²⁺]_cytosolic and [Ca²⁺]_SR. These were used, in turn, to determine unitary currents of the channels and to set boundary conditions at the edges of the diadic clefts. The global model consisted of seven differential equations governing the following dynamical variables: [Ca²⁺]_cyto, SR lumenal calcium (in rapid equilibrium with calsequestrin), and calcium bound to five types of buffer sites, representing calcium-sensing dye (fluo-3), troponin, calmodulin, SR membrane sites, and low affinity sarcolemmal sites. The SR calcium pump was modeled as a steady uptake, represented by a Hill function of [Ca²⁺]_cyto, balanced (in the resting state) by a leak proportional to lumenal [Ca²⁺]. Compartmental volumes and the kinetic parameters of all buffers and pumps were taken from the literature (Table I) and were not treated as adjustable parameters of the model. The details of the cytosolic calcium removal model have very little effect on the short term simulations presented in this paper.

Table I.

Global Ca²⁺ Parameters

Variable		Description/units		Value
B2T		Total calmodulin Ca sites, mM		0.024*
B3T		Total troponin Ca sites, mM		0.07*
B4T		Total SR surface Ca sites, mM		0.047*
B5T		Total SL low-affinity Ca sites, mM		1.124*
BT		Total dye (fluo-3), mM		0.1
CA0		Starting cytosolic [Ca2+], mM		0.0001
CAIREST		Resting intracellular [Ca2+], mM		0.0001
CAO		Extracellular [Ca2+], mM		1.0
CAOREST		Resting extracellular [Ca2+], mM		1.0
CASR0		Starting SR calcium content, mmol/liter cytosol		0.15‡
CASRR		Resting SR calcium content, mmol/liter cytosol		0.15‡
CSQT		[Calsequestrin sites], mM in SR lumen		3.9‡
ETA		Na/Ca voltage splitting parameter		0.35§
K2OFF		Calmodulin Ca off rate, ms−1		0.038*
K2ON		Calmodulin Ca on rate, mM−1 ms−1		100.0*
K3OFF		Troponin Ca off rate, ms−1		0.02*
K3ON		Troponin Ca on rate, mM−1 ms−1		39.0*
K4OFF		SR surface site Ca off rate, ms−1		0.1*
K4ON		SR surface site Ca on rate, mM−1 ms−1		115.0*
K5OFF		SL surface site Ca off rate, ms−1		1.0*
K5ON		SL surface site Ca on rate, mM−1 ms−1		115.0*
KCA		Na/Ca exchanger K d for Ca, mM		1.38§
KDCSQ		K d of calsequestrin sites, mM		0.638‡
KNA		Na/Ca K d Na, mM		87.5§
KOFF		Dye (fluo-3) Ca off rate, ms−1		0.09*
KON		Dye (fluo-3) Ca on rate, mM−1 ms−1		80.0*
KPUMP		SR Ca pump affinity, mM		0.0003‡
KPUMPR		Resting SR Ca pump affinity, mM		0.0003‡
KSAT		Na/Ca saturation parameter		0.1§
NAI		Cytosolic [Na+], mM		10.0
NAIREST		Resting intracellular [Na+], mM		10.0
NAO		Extracellular [Na+], mM		140.0
NAOREST		Resting extracellular [Na+], mM		140.0
NP		SR Ca pump cooperativity		2.0‡
RNC		Na/Ca exchanger rate parameter, ms−1		0.2‡
SRVF		(Cytosol volume)/(SR volume)		17.6‡
VFAC		Relative volume density of diads		1.0‖
VMAX		SR Ca pump maximum rate, mM ms−1/cytosolic volume		0.0002‡
VMAXR		Resting SR Ca pump vmax, mM ms−1/cytosolic volume		0.0002‡
VREST		Resting potential, mV		−70.0

^* Smith et al., 1998;  

^‡ Bers, 1998;  

^§  Luo and Rudy, 1994;  

^‖ VFAC is proportional to the volume density of diads, scaled so that VFAC = 1 corresponds to the density of ryanodine receptors estimated by Bers (1999).  

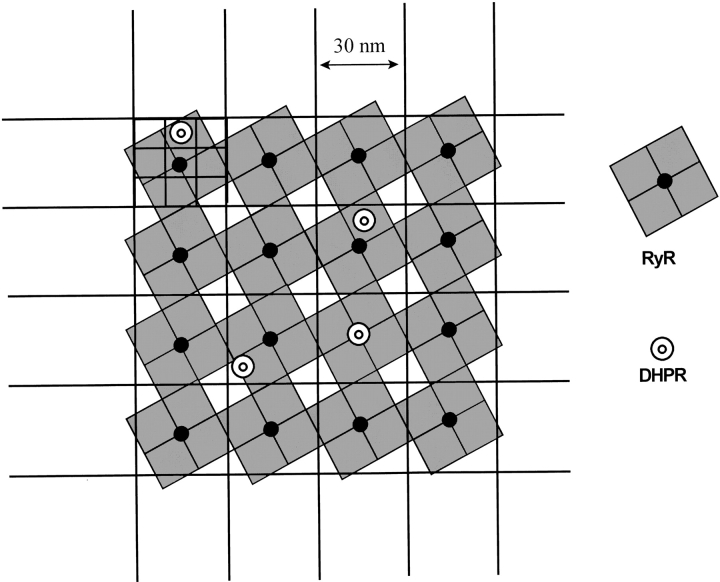
The extreme computational demands of such a simulation required the use of approximations to the reaction–diffusion equations in the diadic cleft. Because of the large aspect ratio of the cleft (diameter 100–400 nm, height 15 nm), diffusion was treated in two dimensions only, and the equations were discretized on a 10-nm mesh. This coarse approximation can be justified because the locations of the exit pore(s) and calcium sensing site(s) of the ryanodine receptor, as well as the diffusion paths of Ca²⁺ through the space occupied by the RyR foot processes, are not known with any greater precision. L-type channels were located at random on the mesh, while RyRs were located regularly at 30-nm center-to-center spacing (Fig. 1). Effective values of the cleft height and calcium diffusion coefficient were used to approximate the effects of surface charge, viscosity and tortuosity, as estimated by Soeller and Cannell (1997). Diads containing up to 121 RyRs were simulated; most of the results shown here were computed for 25-RyR diads containing an average of five randomly located DHPRs that display the qualitative features and save computation time.

Figure 1.

Schematic of the geometry used in approximate solution of the diffusion equations in the diadic cleft. The diad was treated as two dimensional, and the equations were discretized on a mesh of 10-nm squares (outlined in top left cell). Dihydropyridine receptors were located randomly on mesh squares, whereas ryanodine receptor Ca²⁺ sensing and releasing sites were located on central squares of 3 × 3 blocks; i.e., on a regular square lattice of 30-nm spacing. The approximate positions of the quatrefoil foot processes of the ryanodine receptors are indicated by the tilted squares.

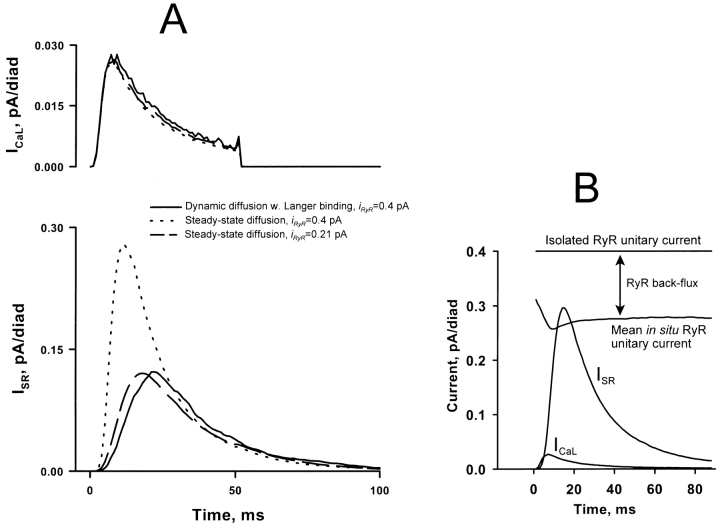
Even with these approximations, computation times of hours were required for the full simulation. For this reason, many of the results shown were computed using the approximation that calcium diffusion in the cleft is at steady-state during the dwell time in any given macrostate, which accelerates the computation by about two orders of magnitude. The accuracy of this approximation depends on the density of fixed calcium binding sites in the diadic cleft. In the absence of such sites, it agrees with the full simulation to within a few percent. In the presence of low affinity fixed Ca²⁺ binding sites at the density estimated by Post and Langer (1992), errors of 30–50% may occur with the steady state approximation, but the qualitative features of the results appear to be correct, and most of the quantitative results can be recovered by use of effective values of channel parameters that are well within the large experimental uncertainties (Fig. 2). The fixed buffer sites in the cleft do not appear explicitly in the steady state diffusion approximation since these sites are nonmobile and therefore have no effect on the steady state distribution of [Ca²⁺], although they control the rate at which the steady state profile is established after a change in the sources.

Figure 2.

(A) Simulated L-type currents (above) and SR release currents (below) generated by the full dynamic diffusion model (solid line) or the steady state approximation (dotted line, see text). In the presence of fixed calcium binding sites, the amplitude of the release flux is only half that predicted by the steady state approximation. Most of the discrepancy can be compensated by assuming a reduced “effective” value for the RyR unitary current when using the steady state approximation. (B) Back-flux of calcium from the diadic cleft into the SR lumen through RyRs, taken into account in the dynamic-diffusion simulations, contributes to the reduction in the effective value of the RyR unitary current. For this computation, it was assumed that the net unitary current through the open RyR is proportional to the SR transmembrane gradient of [Ca²⁺], rather than SR lumenal [Ca²⁺] as in the steady state simulations, thereby taking account of the possible (unidirectional) flux of Ca²⁺ from cleft to lumen. The horizontal line shows the 0.4-pA unitary current assumed for the RyR in isolation, as in lipid bilayers. The mean in situ unitary current was defined as the ensemble-average SR release current divided by the open probability of the RyRs. The in situ current is less than that in isolation because calcium can reflux from the cleft to the SR, either through the channel through which it entered the cleft, or through neighboring RyRs. The latter effect makes the effective unitary current time dependent, because of the varying number of open RyRs available for back flux. Note that the net flux through the RyR can never be negative (since most of the calcium in the cleft originates in the SR), but it can be reduced by a component of unidirectional back flux.

L-Type Channel

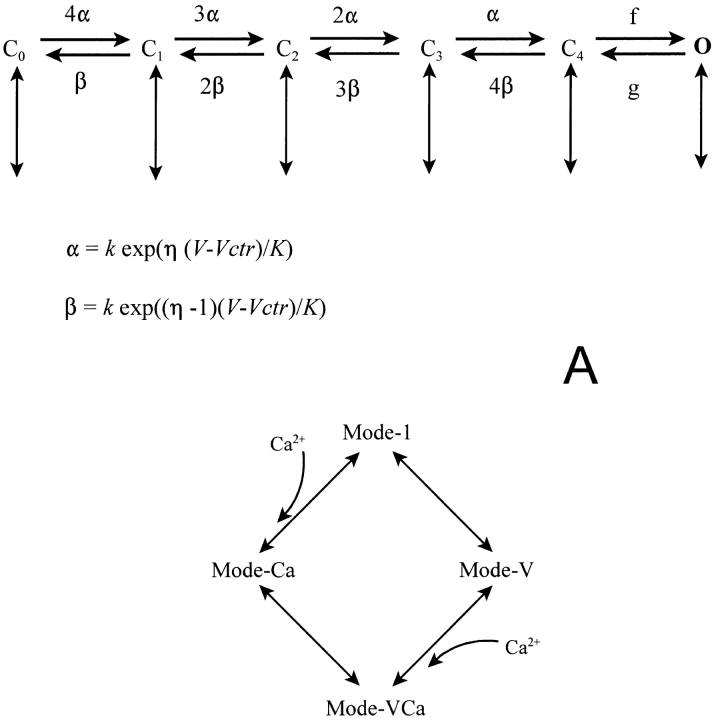
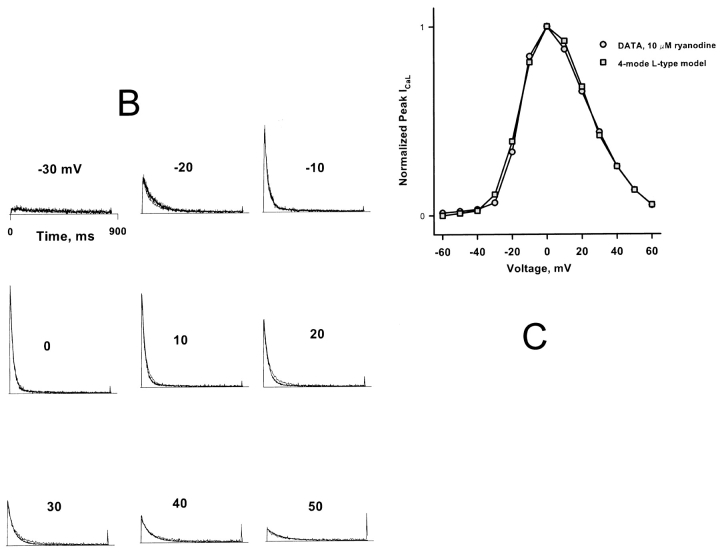
There is no consensus on the gating scheme of the L-type sarcolemmal calcium channel. In these simulations, it was modeled using a novel 24-state gating scheme that we developed as an improvement of the scheme recently proposed by Jafri et al. (1998). The new scheme combines the scheme of Imredy and Yue (1994) for calcium-dependent inactivation with that proposed by Shirokov et al. (1993) to explain gating charge movement and voltage-dependent inactivation. This scheme (shown in Fig. 3 A) consists of four-gating modes (normal, calcium-inactivated, voltage inactivated, and both calcium and voltage inactivated). This model is in the process of being validated and parametrized using measured whole cell and single channel calcium currents. For the purposes of this paper, it may be thought of as an empirical source of DHPR openings that act as input to the CICR process. Fig. 3, B and C, shows representative L-type calcium currents measured from a rat cardiac myocyte in the presence of 10 μM ryanodine. The parameters of the L-type gating model were adjusted manually to fit these data, as shown, and these parameter values were used for most of the simulations shown in the rest of the paper without any further adjustment. They should not be considered necessarily optimal or unique.

Figure 3.

(A) Structure of the scheme of L-type channel gating. The scheme consists of four modes. Each mode (above) consists of a cascade of five closed states connected by movement of four gating charges (horizontal transitions). Openings occur from the rightmost closed state. Each mode has its own center potential and barrier symmetry constants (V_ctr and η). Inactivation is due to mode switching (vertical transitions) to modes with bound calcium, left-shifted V_ctr, or both (below). “Voltage-dependent” inactivation is actually due to voltage-independent transitions to left-shifted modes, which are strongly favored in the rightward charge states because of the requirements of microscopic reversibility, as suggested by Shirokov et al. (1993). (B and C) Measured L-type currents from a cardiac myocyte in the presence of 10 μM ryanodine are superimposed on simulations with SR release disabled, in the time (B) or voltage (C) domain. Simulated and measured currents were normalized so as to make the peak value of both equal to 1 at 0 mV. The L-type model parameters (Table II) were adjusted “by hand” to achieve the fit.

RyR Gating Schemes

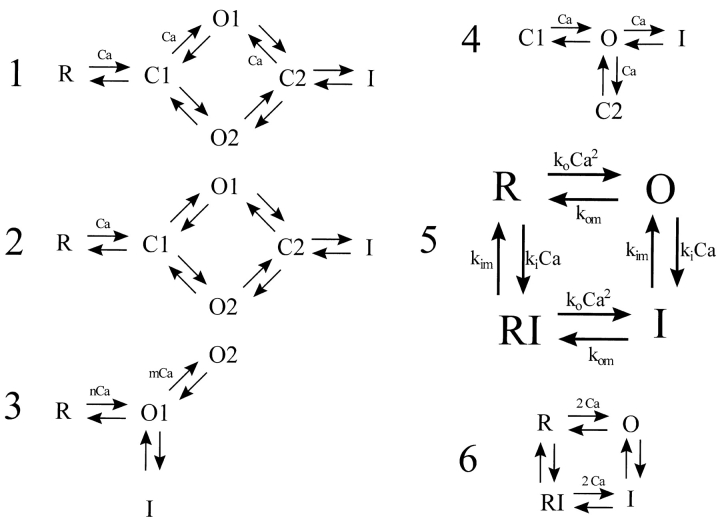
Simulations were carried out using six different gating schemes for RyR2, shown in Fig. 4. Two of these are phenomenological schemes representing, in simplest form, the combination of activation by binding of two calcium ions and either calcium-dependent or fateful inactivation. The other four are published gating schemes based on single-channel observations of purified RyRs in lipid bilayers.

Figure 4.

RyR gating schemes tested in the simulations. Schemes 1–4 are published schemes deduced from isolated RyR currents measured in lipid bilayers; none of these schemes gave stable local control of SR release. Scheme 5 is the phenomenological scheme used in most of the simulations presented in this paper; it is similar to a scheme proposed by Fabiato (1985), and to the scheme governing individual RyR subunits in the adaptation model of Cheng et al. (1995). Scheme 6 is a phenomenological scheme in which transitions to inactivated states are state-dependent rather than calcium-dependent as in Scheme 5. This scheme was also capable of giving stable EC coupling. Scheme 1, Villalba et al. (1998); Scheme 2, Zahradnikova and Zahradnik (1996); Scheme 3, Keizer and Levine (1996); Scheme 4, Scheifer et al. (1995).

Measurement of SR Release Flux

SR release flux was measured by the recently developed Oregon green/EGTA method, which has been described in detail by Song et al. (1998). In brief, adult rat ventricular cardiac myocytes were enzymatically isolated and studied under whole cell patch-pipette voltage clamp. The fast, low affinity fluorescent calcium indicator Oregon green 488 BAPTA 5N (1 mM) and EGTA (4 mM) were dialyzed into the cell from the pipette. As we have shown previously, this combination gives a fluorescence signal dominated by a term directly proportional to SR release flux. Myocytes were imaged in the line scan mode of an inverted confocal microscope (LSM-410; Carl Zeiss, Inc.), with the scan line oriented longitudinally. This method makes it possible to see the localized SR release at the Z line of each sarcomere. Whole cell calcium release rate was estimated by averaging over the length of the scan line.

results

Local Control Produces Graded Release of SR Calcium

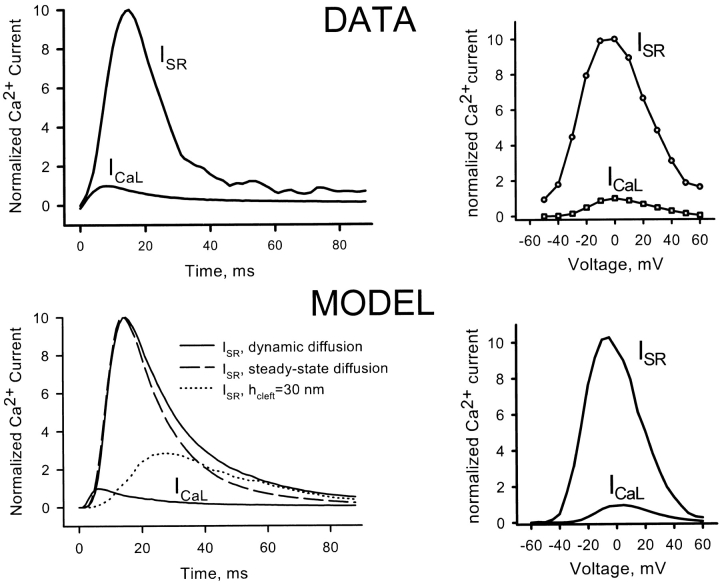
Fig. 5 shows representative measurements of calcium release flux from the SR of a rat cardiac myocyte, compared with simulations using the phenomenological RyR gating Scheme 5 in Fig. 4. Fig. 5 (left) shows the time course of SR release flux during a single voltage clamp depolarization to 0 mV from a holding potential of −70 mV. The figure demonstrates that the local control model can simulate the observed time course of release, particularly the fact that release declines during sustained depolarization. The fact that release in this model is dependent on local geometry is illustrated by the much smaller dotted curve, which shows the release flux that would be computed assuming a diadic cleft height of 30 nm instead of the correct 15 nm. Fig. 5 (right) shows the peak release flux as a function of the voltage of the clamp pulse. I_Ca, the macroscopic current of the L-type channels, shows the bell-shaped voltage dependence typical of voltage-controlled ion channels, while the SR flux recapitulates (approximately, see below) the voltage dependence of I_Ca, but at an absolute magnitude 10-fold larger. The simulation reproduces these features well. This demonstrates the central point of the local control hypothesis: the complicated stochastic interactions of calcium-coupled channels can produce high amplification with stable, graded control by trigger calcium.

Figure 5.

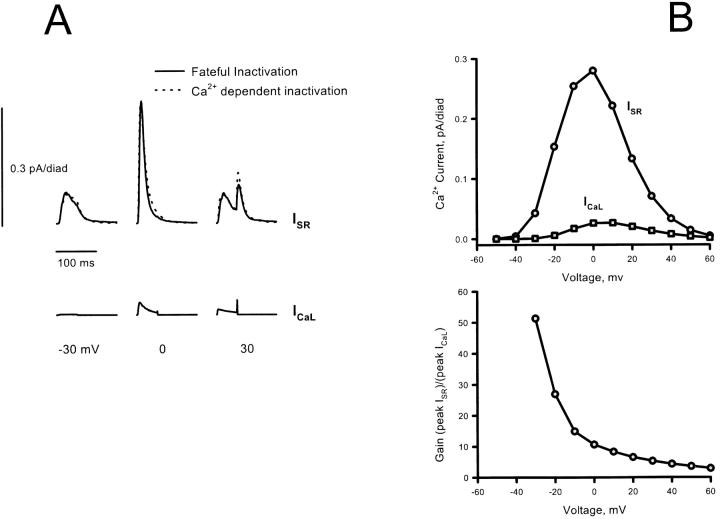
L-type calcium current and SR calcium release as a function of time at 0 mV (left) and peak current as a function of voltage (right), measured in a rat myocyte (above) and simulated (below). All currents were normalized to the peak I _CaL at 0 mV. The time-dependent simulation was done using either the full dynamic-diffusion algorithm or the steady state approximation with k _o and k _i (see also Table III) adjusted to match the magnitude and timing of peak release. The graded dependence of I _SR on I _CaL across the range of voltages is successfully reproduced by the local control model. The dotted line at bottom left shows the markedly different result of the simulation if the assumed height of the diadic cleft is doubled. The strong dependence on geometry is the hallmark of local control.

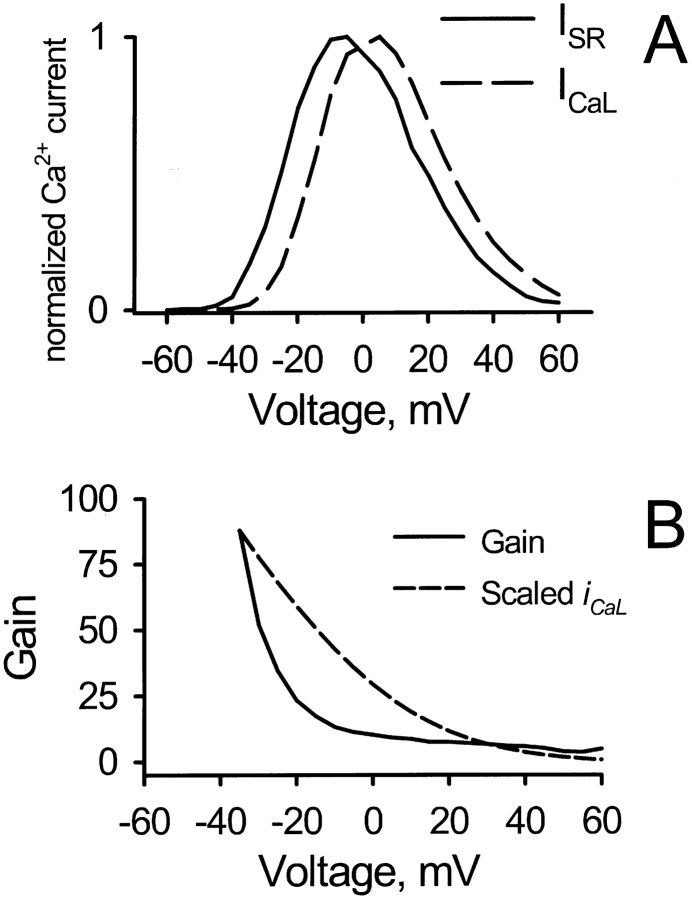
As shown in Fig. 6, if the bell shaped I_CaL vs. V and I_SR vs. V curves are normalized to their respective peaks, there is a small difference between their positions. When these curves are then divided to give a plot of the gain of excitation–contraction (EC) coupling (peak I_SR divided by peak I_CaL), the resulting gain diminishes with voltage. This was one of the original predictions of the local control theory, which has been confirmed in several laboratories (Wier et al., 1994; Cannell et al., 1995; Janczewski et al., 1995; Santana et al., 1996). It stems from the fact that local activation of the RyR depends on the unitary current of the triggering L-type channel(s) rather than on the macroscopic ensemble-average current. As pointed out previously (Cannell et al., 1995; Santana et al., 1996), the decline of gain at positive voltages is a manifestation of the cooperativity of RyR activation by calcium, because the diminution of L-type unitary current as the calcium reversal potential is approached reduces I_SR disproportionately in comparison to its linear effect on macroscopic I_CaL. As argued by those authors, a quadratic dependence of RyR activation on local calcium should result in a macroscopic gain that is roughly proportional to the L-type unitary current. The decline of gain with voltage in the simulations is steeper than that of the L-type current over the midrange of voltages (Fig. 6 B), even though activation of the RyR was assumed to require two Ca²⁺ ions. This “elbow” in the voltage-gain relation results from the depletion of SR calcium (by release to the cytosol) during the depolarization, as indicated by the fact that it is prevented if SR depletion is minimized by reducing the number of diads per unit cytosolic volume, or reducing the number of available L-type channels (not shown). Such an elbow has been observed experimentally in intact cardiac myocytes (see Fig. 3 in Wier et al., 1994). It was not seen when I_CaL (and therefore I_SR and SR depletion) was reduced by a factor of 20 with nifedipine in order to study calcium sparks (Cannell et al., 1995).

Figure 6.

(A) If the trigger and release currents from the simulation are normalized to their respective maximum values, it is seen that the current–voltage relations are centered at somewhat different voltages. (B) When release is then divided by trigger to get the gain function of EC coupling, the resulting gain decreases with voltage, because the efficacy of the L-type current to trigger release from the RyR depends on the unitary current of the L-type channel, which decreases as the calcium reversal potential is approached. This effect, one of the basic predictions of local control theory, has been confirmed experimentally by several laboratories. Although activation of the RyR requires only two Ca²⁺ ions in this model, the gain declines more rapidly than the L-type unitary current (scaled to match the gain curve at −35 mV) in the midrange of voltages, as a consequence of partial depletion of SR calcium during the depolarization. This “elbow” effect has been observed in whole-cell calcium recordings, but not when the majority of the L-type current (and therefore SR release) has been blocked with nifedipine in order to count calcium sparks (see text).

SR Calcium Release Is Locally Regenerative

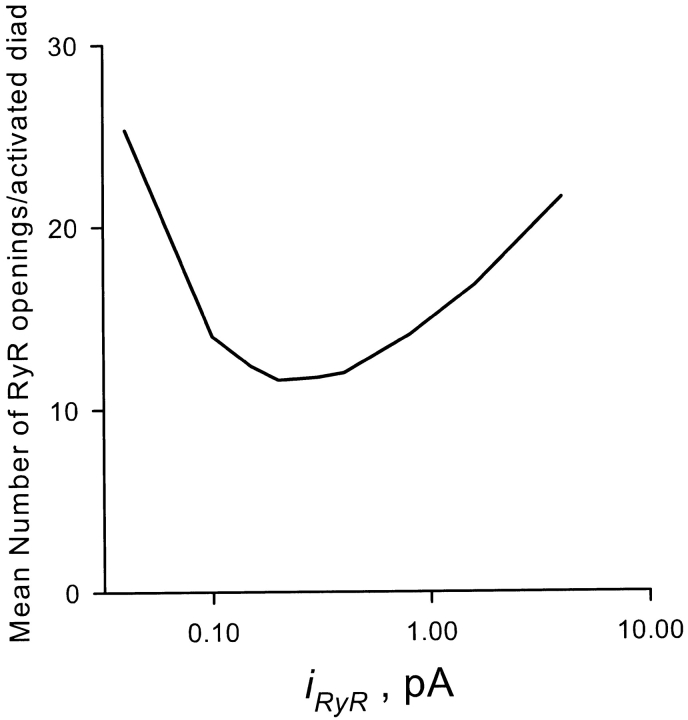
The number of RyRs that contribute to SR calcium release at a single diad is not known. As an index of that number, we computed the mean number of RyR openings per diad during a clamp pulse to 0 mV for 50 ms, averaged over those diads at which at least one RyR opening occurred. Neither the unitary current i _RyR of the RyR nor its calcium sensitivity in situ is well known. We therefore varied the RyR permeability over two orders of magnitude, adjusting the sensitivity k _o in each case to give the observed macroscopic gain of 10 at 0 mV and standard SR loading, to determine whether there could be a regime in which an L-type channel communicates with a single RyR without regenerative local recruitment of other RyRs. As shown in Fig. 7, the mean number of RyR openings per diad has a U-shaped dependence on i _RyR, with a nadir of ∼11 (achieved, coincidentally, near the estimated physiologic i _RyR of 0.4 pA; Mejia-Alvarez et al., 1999). This shows that, at least in the context of this model, RyR activation is always locally regenerative. This result can be understood qualitatively as follows. If i _RyR were small, the RyR sensitivity would have to be high, since many RyRs would need to be recruited to achieve the macroscopic gain of 10. If i _RyR were high, on the other hand, the sensitivity must be low, as a result of which the coupling from DHPR to RyR frequently fails. The release in this case is made up of rare diadic release events, each of which is highly regenerative. The fact that the DHPR-RyR communication fails before RyR–RyR recruitment is basically a consequence of geometry: if the DHPRs are located randomly at the junction, they cannot, on average, be much closer to RyR sensing sites than the latter are to the release pores of neighboring RyRs. If DHPRs were located in registry with RyRs, and if the calcium-sensing site of the latter were located on the “top” of the foot process, within a few nanometers of the DHPR, then nonregenerative 1:1 communication would be possible, as originally envisioned in the model of Györke and Palade (1993).

Figure 7.

The unitary current of the RyR, and its calcium sensitivity k _o, neither of which is known precisely in vivo, were varied over two orders of magnitude, keeping the gain of EC coupling at 0 mV equal to the experimental value of 10. The mean number of RyR openings in those diads in which at least one opening occurred is plotted on the abscissa; it is a measure of the degree of local regenerative recruitment of RyRs by CICR. This number was never <11, indicating that, for this model, there is no regime in which EC coupling operates with the observed gain without local regeneration.

Local and Global Stability

Before discussing simulations using empirically determined RyR gating schemes, we define two different concepts of stability. Local stability refers to the fact that there must be some mechanism to terminate the regenerative release at an individual diad. Global stability refers to the fact that the resting state of the myocyte must be stable against regenerative build up of global calcium, and the cell must eventually relax to this resting state after stimulation. The average diadic release rate triggered by global cytosolic calcium must, therefore, be less than the removal rate (SR pump + Na/Ca exchange) in the vicinity of the resting state. These two concepts of stability are distinct, though related. If there were no calcium removal, [Ca²⁺]_cyto would eventually build up to cause global regenerative release, no matter how well behaved the RyRs. On the other hand, it is evident that a cell cannot return to the resting state unless local release terminates. Both forms of stability are adversely affected by the clustering of RyRs. Clustered RyRs will have a more regenerative local release, which will be more difficult to terminate. Release triggered by background calcium will also be enhanced by clustering, since if a single RyR in the cluster opens in response to background calcium, this will trigger opening of most of the other RyRs in the cluster.

There are three mechanisms that contribute to the termination of local release: (a) depletion of SR calcium, (b) inactivation of RyRs, and (c) stochastic attrition. The last refers to the fact that for a finite-size cluster of RyRs, gating stochastically, there is always a nonzero probability that all RyRs will be closed at the same time, and this event will interrupt the positive feedback and extinguish the activity of the cluster, as long as there are no further DHPR openings to re-ignite it. SR depletion cannot be the principal mechanism of local release termination, since release terminates after voltage steps to very negative or positive voltage, which release very little of the SR calcium stores, and release in calcium sparks (Cheng et al., 1993) also terminates despite the fact that there is no global SR depletion. Conversely, greatly prolonged sparks occur in the presence of ryanodine (Cheng et al., 1993), indicating the absence of local SR depletion. Inactivation and stochastic attrition must, together, be capable of terminating release at a single diad.

The contribution of stochastic attrition may be roughly estimated from a simple, analytical model. Consider a “cluster” of n identical channels, each of which has only two states, open and closed. Start with each channel in equilibrium, with an open probability P _o and an opening duration τ_o. The channels are assumed to gate independently, except that, if all close at once, the cluster is considered to be extinct. So long as the cluster is “alive,” the number of open channels, n _o, will be binomially distributed, except that n _o = 0 is excluded. The probability that a cluster becomes extinct during a time interval dt is given by

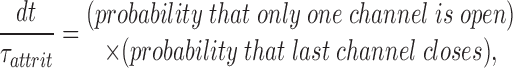where τ_attrit is defined to be the time constant for extinction of clusters by stochastic attrition. Using this relationship together with the binomial distribution, it is straightforward to determine the attrition time constant:

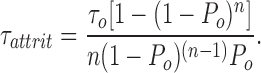1

This time constant varies roughly exponentially with the product nP _o, the expected number of open channels. Some numerical values are instructive. For a cluster of 25 channels with a mean opening duration of 10 ms and P _o = 10%, τ_attrit is ∼46 ms. For 75 channels with a 50% open probability, it becomes 160 billion years, ∼10× the age of the universe! This makes it clear that stochastic attrition alone cannot be relied upon to terminate local release robustly if the number of RyRs in a diad is as large as present ultrastructural data indicate. There must also be an inactivation process that is capable of substantially reducing P _o. For an opening duration of 10 ms, one finds numerically that to extinguish clusters with a time constant of 50 ms requires nP _o < 2.6. Therefore, for RyR clusters of the size found in cardiac muscle, local stability requires an inactivation process that, while it need not be completely absorbing, can reduce the RyR open probability to a few percent or less. It needs to be kept in mind, however, that stochastic attrition is not an alternative to inactivation, but an intrinsic feature of multichannel local control models, which always contributes to the cluster extinction process regardless of what other mechanisms are present.

Fateful Inactivation of RyR Gives Stable EC Coupling

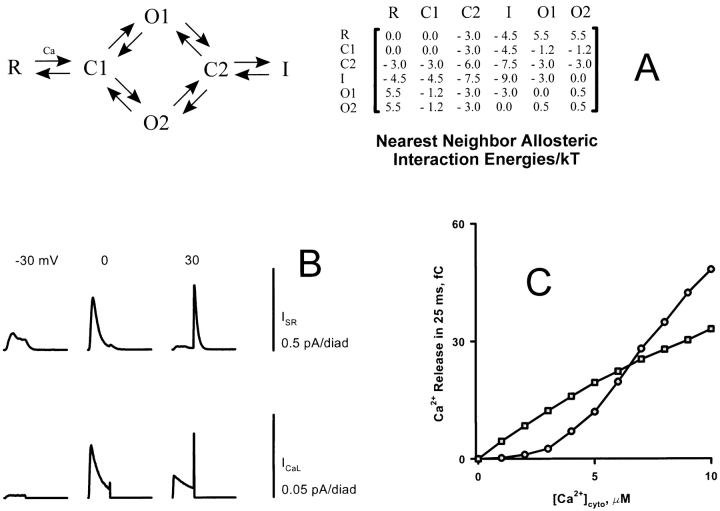
Since the stability of local control EC coupling depends critically on the inactivation process of the RyR, it is reasonable to ask whether the calcium-dependent inactivation mechanism employed in the phenomenological gating of Fig. 4, Scheme 5, is essential to the success of the model. The answer is no; as shown in Fig. 8, qualitatively comparable results can be obtained with Fig. 4, Scheme 6, in which inactivation is fatefully linked to activation, but not explicitly dependent on calcium (as suggested by Pizarro et al., 1997). In this scheme, unlike Scheme 5, the activation and inactivation “gates” are not independent. The inactivation and repriming rate constants (vertical transitions) are different in the calcium-free and -activated states of the channel (subject to the constraint of microscopic reversibility, which requires that the products around the loop of forward and reverse rates be equal). By proper choice of these rate constants, it can be arranged that, on exposure to Ca²⁺ the channel first activates and then inactivates, while on removal of Ca²⁺, channels predominantly deactivate before repriming, avoiding another passage through the open state. This arrangement requires some tuning to secure sufficiently rapid decay of release both on depolarization and repolarization.

Figure 8.

Simulation results in the time (A) and voltage (B) domains using RyR gating Scheme 6 (see Fig. 4), in which inactivation is fatefully linked to activation. In A, the simulations using Scheme 5 (see Fig. 4; calcium-dependent inactivation) are also plotted (dotted lines) for comparison. The fateful inactivation scheme successfully reproduces the major features of local EC coupling.

Bilayer-derived RyR Gating Schemes Give Unstable EC Coupling

We now turn to consideration of models based on the empirically derived RyR gating Schemes 1–4 in Fig. 4. Each of these schemes proves to have one or more deficiencies that preclude local and global stability. We can consider, first, Scheme 3 proposed by Keizer and Levine (1996). This scheme was developed to explain the “adaptation” of the RyR observed by Györke and Fill (1993). When used in an ensemble-average sense, where [Ca²⁺] is taken to be a global value imposed by the researcher, this scheme gives a reasonable description of RyR adaptation as seen in bilayers with Cs⁺ as current carrier. It is clear, however, that it cannot be considered as a description of microscopic events in a local control model, because it has a calcium-dependent transition between two open states. As shown in Fig. 4, once the channel reaches state O1, it will be exposed to the microdomain of high [Ca²⁺] created by its own permeating calcium. This will immediately induce a transition to O2, precluding any opportunity for inactivation or adaptation. The rate and extent of inactivation will be minimal in a local control setting, preventing termination of local release, as was confirmed by carrying out the simulation with this gating scheme (not shown).

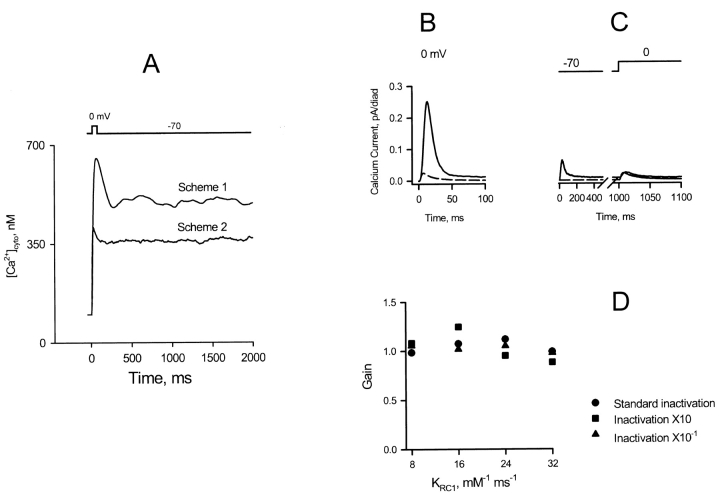
The remaining three schemes of Fig. 4 share certain features. All have a slow inactivation process, which is calcium dependent only in Scheme 4. Each also has the possibility of opening the channel after binding only a single calcium ion, although only Scheme 2 of Zahradnikova and Zahradnik (1996) has only one calcium binding site. Each of these schemes was put forward with a set of rate constants determined by measurements in lipid bilayers, in the absence of Mg²⁺ and ATP. To incorporate these schemes into the local control simulation, it is necessary to decide how (if) these constants should be modified to describe the channel in the intracellular milieu. Fig. 4, Scheme 1, for example, has an open state reachable after binding two Ca²⁺, as well as one reachable with only a single calcium. Clearly, by completely rearranging the rate constants, it would be possible to make this scheme behave somewhat similarly to the phenomenological Scheme 6. But Scheme 1 was determined by very careful fitting to a series of data on transient activation after flash photolysis of caged calcium, taking into account the transient overshoot of [Ca²⁺] after the flash. It makes little sense to discard this information. We therefore explored parameter values according to the following strategy. Since all lipid bilayer schemes studied in the absence of Mg²⁺ and ATP gave activation rates that were much too high for local control, we reduced the rates of calcium binding by about two orders of magnitude to account for the effect of Mg²⁺ competition; the exact factor used was determined by requiring the gain (ratio of peak release current to peak I_CaL) to be 10 for a depolarization to 0 mV. This criterion was relatively independent of the values of rate constants related to adaptation/inactivation. When the resulting models failed to show adequate stability, we examined the effect of increasing the kinetic rates of adaptation/inactivation steps by a factor of ∼20, consistent with the observations of Valdivia et al. (1995). This also failed, whereupon we examined the effect of increasing only the forward rates of inactivating steps, thereby stabilizing the inactivated/adapted states. This strategy was limited by the onset of an unacceptable degree of inactivation in the resting ([Ca²⁺] = 100 nM) condition, and moved the steady state activation curve rightward so that the steady state P _o approached unity only at [Ca²⁺] values over 100 mM. Even with these adjustments, all three schemes gave models that manifested local instability (failure of release termination after activation) or global instability (spontaneous activation by background [Ca²⁺]). Because of these instabilities, [Ca²⁺]_cyto fails to relax to the resting value following repolarization, as shown in Fig. 9 A (Schemes 1 and 2). The process of parameter exploration is illustrated for Scheme 2 in B–D. Initially, the bilayer-derived rate constants were kept, except that the rate of calcium binding to the activating site (K _RC1) was decreased from 1,000 to 16 mM⁻¹ ms⁻¹, consistent with a competitive effect of Mg²⁺, giving an apparent gain of 10 for a depolarization to 0 mV, starting with all channels in the resting state (Fig. 9 B). The apparent success of this parameter set is illusory, as shown in Fig. 9 C, where the depolarization is preceded by a 1-s conditioning run-in at the holding potential. Exposure to background calcium triggers a spontaneous SR release, which continues indefinitely, partially inactivating the channels so that, in the true resting state, the gain at 0 mV is reduced to only ∼1. As shown in Fig. 9 D, variation of the activating rate constant (K _RC1) over a fourfold range and of the inactivating rate constants (for K _O1C2, K _O2C2, and K _C2I, refer to Fig. 4, Scheme 2) over a 100-fold range was powerless to recover the normal gain in the true resting state of the model. Extensive parameter variations of this kind failed to identify a satisfactory parameter set for Schemes 1 or 2. The authors of Fig. 4, Scheme 4, did not specify a complete set of kinetic constants for the scheme, but it suffers from the same generic problems as the first two: slow and incomplete inactivation (73% at pCa 3) and activation by only a single Ca²⁺ ion.

Figure 9.

Instability of EC coupling simulated using RyR gating Schemes 1 and 2 (see Fig. 4). (A) The calcium binding rate of the RyR, which may be affected in vivo by Mg²⁺ competition, was adjusted to give the observed gain of 10 at the initial peak of release, keeping all other rate constants equal to their published values, and starting the simulation with all channels in the resting state R. After the stimulus, global cytosolic [Ca²⁺] does not relax to the resting value because local release fails to terminate reliably, and new release events are stimulated by background calcium. (B) SR release flux (solid line) and sarcolemmal calcium current (dashed line) for Scheme 2, showing an apparent gain of 10 when all channels start in state R. (C) When the depolarization is preceded by a 1-s conditioning run-in period at −70 mV with channels exposed to global [Ca²⁺]_cyto, there is a spontaneous release of SR calcium. The resulting RyR inactivation and SR calcium depletion greatly reduces SR release in response to the depolarization, reducing the gain to about 1 in the true resting (i.e., conditioned) state. (D) Varying the activating and inactivating rate constants (K _RC1, K _O1C2, K _O2C2 and K _C2I) over a wide range failed to prevent global instability and restore the gain for a cell in the true resting state.

The global stability problem that arises if the RyR can be activated by a single calcium ion can be demonstrated in a relatively model-independent way. The time-averaged local [Ca²⁺] at a distance r from an L-type channel with an open probability P _o, passing a unitary calcium current i _CaL, considered as a point source, is given by

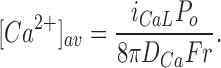2

The openings of the L-type channel are brief and sparse, with P _o probably not in excess of 5% (Rose et al., 1992). Using this value, and assuming a unitary current of 0.1 pA and an (effective) calcium diffusion coefficient of 0.15 × 10⁻⁵ cm² s⁻¹, the time-average local [Ca²⁺] at a distance of 10 nm from the L-type channel is only 1.4 μM, which is comparable to the global [Ca²⁺]_cyto reached during a forceful beat, and only 14× resting [Ca²⁺]_cyto. A RyR that opens as the first power of local [Ca²⁺] cannot, therefore, discriminate against activation by global background calcium, because the average release flux will be proportional to the average [Ca²⁺], which has a major contribution from nonlocal background calcium. This implies that globally stable local EC coupling cannot be achieved by any RyR that can be activated by a single Ca²⁺ ion, assuming that the position of DHPRs is random in relation to the RyR lattice so that the average distance from DHPR pore to RyR sensing site is ∼10 nm.

The previous argument tacitly assumed that an RyR with only a single calcium binding site would have a time-averaged open probability roughly proportional to the time-averaged local [Ca²⁺]. It might be argued that this is not necessarily so: there could be schemes in which the occupancy of the single binding site is proportional to the local [Ca²⁺], but the mean RyR P _o during repeated exposure to brief pulses of high [Ca²⁺] is larger, as a result of nonlinear steps downstream from the calcium binding reaction. The difficulty with this argument becomes apparent if one tries to construct such a model. For a single RyR in isolation, the binding site occupancy translates into the probability that the Markovian channel is found in certain states. But how is one to make the open probability depend nonlinearly on this probability when the master equations governing Markov transitions are linear? For the case of a channel with a microreversible (i.e., thermodynamically passive) gating scheme exposed to a steady calcium level, we can be quite rigorous about this. The equilibrium law of mass action requires that the P _o be a rational function of degree 1; i.e., a Michaelis-Menten function. The question, then, is whether there could be a gating scheme in which the non–steady state effects of exposure to a train of brief, very high pulses of [Ca²⁺] could “pump” the channel into a higher P _o than predicted by linear extrapolation from the resting state. The experimental constraints on this problem are actually very strong. In a resting cardiac myocyte, calcium sparks occur at a rate of 100 s⁻¹ (Cheng et al., 1993). If the spark corresponds to a release of 4 pA for 10 ms, and if the RyR unitary current is 0.4 pA, then resting spark release amounts to an average of only ∼10 open RyRs per cell. If there are, conservatively, 10⁵ RyRs per myocyte, the resting P _o at [Ca²⁺] = 100 nM is 10⁻⁴. Is it possible that a one-calcium gating scheme with this resting P _o could, in response to a 200-μs pulse of [Ca²⁺] = 100 μM, open with a probability of, say, 0.1? This is a special case of a problem that has been solved previously in connection with thermodynamic constraints on RyR adaptation (Stern, 1996). Using the methods in that paper, we found that it is impossible, assuming that the Markov scheme follows the kinetic law of mass action. We can therefore be fairly confident that the difficulty in obtaining global stability in simulations with single-calcium RyR gating schemes is generic.

Local Control Can Be Stabilized by RyR–RyR Allosteric Interactions

The fact that many RyR gating schemes derived from lipid bilayer data fail to support stable EC coupling in simulations suggests that RyR gating in situ may differ from that in bilayers. Two features are required to achieve local and global stability: “strong” inactivation and cooperative activation by more than one Ca²⁺ ion. A possible clue as to how these features might arise comes from the ultrastructure and molecular biology of the RyR. In all striated muscles from crustaceans to man, including those that are activated purely by CICR (e.g., crayfish skeletal, mammalian cardiac) RyRs are found in dense two-dimensional crystalline arrays, although the details of the crystal lattice have varied somewhat (Loesser et al., 1992). Moreover, the amino acid sequence of the foot process has been strongly conserved. Tunwell et al. (1996) found 98.6% amino acid identity between rabbit and human RyR2. We have identified a sequence of 200 amino acids located in the foot region that is 100% identical between mouse and human RyR2, despite the presence of 82 synonymous mutations at the DNA level (data not shown). Since only ∼29% of random mutations are synonymous (Nei, 1987), the probability that all would be synonymous in the absence of selection is only 0.29⁸² (8.2 × 10⁻⁴⁵). This implies that the foot has an important (though unknown) function even though the COOH-terminal region of the molecule suffices to form a calcium-sensitive channel (Bhat et al., 1997a). Could the difference between in situ and in vitro gating of the RyR be due to allosteric interactions between the foot processes of nearest-neighbor RyRs, which appear ultrastructurally to be in contact? To test this possibility, we modified the simulation algorithm to make the transition rates of each RyR dependent on the states of its (up to) four nearest neighbors. To satisfy the constraint of microscopic reversibility, the interactions were specified in the form of free energies of interaction between neighboring RyRs, depending (symmetrically) on the states of each. To determine the transition rate K _ij of a given RyR from state i to state j, the sum of the allosteric contact energies with its neighbors (in their present states) were added up in the initial and final states of the transition, and the exponential of the difference, divided by kT was multiplied into the affinity k _ji/k _ij of the transition. This still leaves one kinetic degree of freedom to determine how the effects of the free energy change are to be partitioned between the forward and backward rate constants. The transition rate therefore has the form

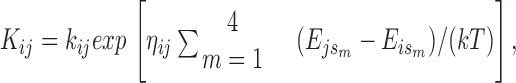3

where k _ij is the transition rate of the RyR in isolation, E _js = E _sj is the allosteric interaction energy between a RyR in state j and a neighbor in state s (zero if the neighbor is absent from the array), and η_ij = 1 − η_ji is a “splitting coefficient.” From the point of view of reaction rate theory, η may be considered to be the weighting factor that would be required to express the allosteric interaction energy of the transition state as a weighted average of the allosteric energies of the initial (“reactant”) and final (“product”) states. This makes it reasonable that η should lie between 0 and 1, but this is not required. In principle, each source of allosteric energy could have its own value of η for each transition, but, to avoid excessive proliferation of parameters, we assumed that a single value applies to all allosteric contributions affecting the rate of a given transition. By default, η = 0.5 was assumed, except for the case of a diffusion-limited calcium binding reaction, for which η = 0 is logical, since a change in the free energies cannot increase the on-rate and would decrease it only if it engendered a sufficient conformational change in the molecule to restrict access to the binding site, or a sufficient reduction in the magnitude of the binding energy to prevent capture of the ion.

For the allosteric model, we used gating Scheme 2 of Zahradnikova and Zahradnikov (1996; see Fig. 4), since it can be considered a “worst case,” having slow inactivation and only a single calcium binding site. In this model, RyRs interact both allosterically and by CICR— a process difficult to analyze intuitively. The strategy we used to choose the allosteric interaction energies had two parts. To produce local stability, the forward rates of inactivating transitions need to be increased, which requires stabilizing the inactivated state(s) relative to the noninactivated. A simple counting argument shows that adding an allosteric energy E _ij that is equal to −E/4 if one of the states i and j is an inactivated state and −E/2 if both are, will contribute −E to the free energy change associated with any inactivating transition of a channel that has four nearest neighbors. To produce global stability is somewhat more subtle, because it requires creating, de novo, cooperativity of RyR activation by calcium. Since, in Scheme 2, each RyR has only a single Ca²⁺ binding site, it is necessary to create positive cooperativity between binding sites on different RyRs. The strategy here is to add a large, positive allosteric contact energy between a RyR in an open state and one in the resting state. Initially, all RyRs in the diad are in the resting state R. Binding of calcium to one of these RyRs will move it to state C₁, from which it could open if the channel were in isolation. But, to move this RyR to states O₁ or O₂ when it is surrounded by resting channels would cause a large increase in allosteric energy, so this transition is effectively prevented by an energy barrier. If more of its neighbors acquire bound calcium, moving them out of state R, the energy barrier is decreased so that the RyR can open, effectively responding to the binding of several Ca²⁺ ions by the array as a whole. The important insight here is that, for this strategy to work, the underlying single-RyR gating scheme must have a closed state with bound calcium, so that binding of multiple Ca²⁺ ions by the array can occur before any channel opens. If binding of the first Ca²⁺ is tantamount to opening of the channel, then this event, however rare, will supply the local calcium to permit opening of nearby channels so that the whole array is effectively triggered by a single Ca²⁺.

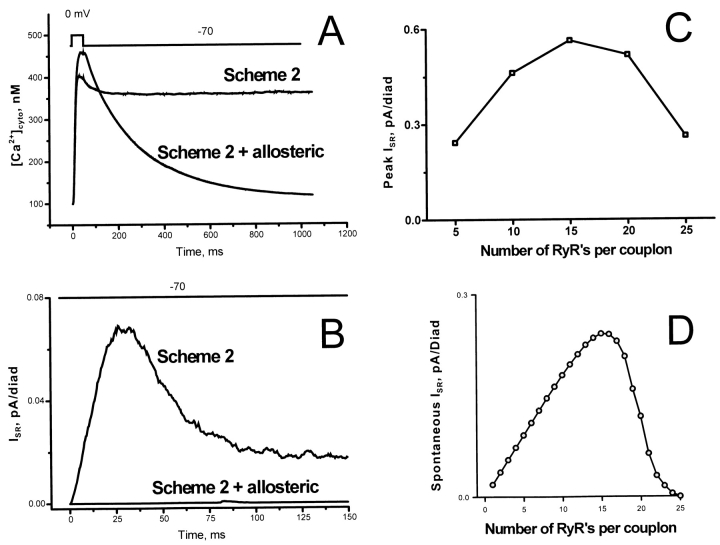
Once one RyR opens, a complicated interplay of allosteric and CICR interactions ensues, including some unexpected effects. For example, the energy barrier that prevented opening of a RyR surrounded by resting neighbors will, during the relaxation phase, prevent calcium from dissociating from RyRs that are in contact with one that is still open. We started with allosteric energies chosen by the two strategies described in the preceding paragraph, which succeeded in creating cooperativity of activation and strong inactivation. We then made adjustments, guided by admittedly incomplete intuition, until the performance of the model was satisfactory. The final matrix of allosteric interaction energies is shown in Fig. 10 A; they are not necessarily either unique or optimal. It should be noted that in this model we made no changes in the bilayer-derived parameters other than the introduction of the allosteric interactions. In Fig. 10 B, we show typical time courses of SR release in response to 50-ms depolarizations to the voltages shown. While the responses are not exactly the same as those of the phenomenological model, they serve to demonstrate that Fig. 4, Scheme 2, when augmented by the allosteric couplings, produces locally stable release. Fig. 10 C shows the rate of release stimulated by global cytosolic Ca²⁺, for Scheme 2 with and without allosteric couplings. The presence of the allosteric couplings converts the first order dependence of release flux on global [Ca²⁺]_cyto into a cooperative response. This markedly reduces the rate of release triggered by global [Ca²⁺]_cyto in the physiologic range, as required for global stability. Fig. 11, A and B, shows explicitly that the dynamics of [Ca²⁺]_cyto after repolarization, and the spontaneous release rate when exposed to resting [Ca²⁺]_cyto have been stabilized by the allosteric interactions. These allosteric interactions are basically inhibitory in character, as demonstrated in Fig. 11, C and D, which shows the effect of reducing the number of RyRs by leaving random vacancies in the RyR lattice. When the lattice is more than ∼60% filled, increasing the number of RyRs actually decreases the absolute release rate, because the effect of allosteric inhibitions more than compensates for the increased number of RyRs carrying the release flux. It is striking that even a few vacancies per diad markedly increase background calcium release, impairing global stability (Fig. 11 D).

Figure 10.

(A) Nearest neighbor allosteric interaction energies, as a function of the states of the interacting channels, for the model using Scheme 2 (from Fig. 4, shown at top left) augmented by allosteric interactions. (B) SR release currents produced by depolarizations to different voltages, showing a pattern similar to those produced by the phenomenological Schemes 5 and 6 (see Fig. 4), with termination of release upon repolarization. (C) “Spontaneous” release triggered by exposure to a constant global calcium level for Scheme 2 with and without the allosteric interactions. The interactions cause the activation of the diad to depend cooperatively on calcium, even though each RyR has only a single Ca²⁺ binding site. This suppresses release at physiologic levels of global [Ca²⁺], conferring global stability on the model.

Figure 11.

(A) Global cytosolic [Ca²⁺] for the model using Scheme 2 (see Fig. 4) with and without allosteric interactions is shown. With Na/Ca release disabled, there is no relaxation of global [Ca²⁺] after a stimulus; normal relaxation is produced when allosteric interactions between RyRs are included. (B) Global instability of the model using Scheme 2 is revealed by major calcium release when the diads are exposed to resting global background [Ca²⁺] (100 nM) in the absence of depolarization. Inclusion of allosteric interactions eliminates this background sensitivity by requiring cooperative activation by Ca²⁺ bound to different RyRs. (C) The effect of the allosteric interactions is basically inhibitory. As a result, if the number of RyRs per diad is reduced by leaving vacancies in the RyR lattice, there is a paradoxical increase in the rate of SR calcium release, until the number of RyR remaining is no longer sufficient to support the release. (D) The allosteric suppression of spontaneous release triggered by background calcium (C) is very sensitive to completeness of the RyR lattice. Introduction of small numbers of vacancies per diad unmasks the unstable release characteristic of Scheme 2 RyR activation by a single bound Ca²⁺. The effect of reducing the number of RyRs by introducing vacancies in the lattice is much larger than the effect of simply reducing the size of a complete array, which has only a slight effect on global stability.

discussion

In contrast to the situation in skeletal muscle, it is well established that mammalian cardiac excitation–contraction coupling is mediated by calcium-induced calcium release. This creates the paradox of control: why does the calcium released from the SR not feed back to trigger more release, causing an explosive chain reaction that would release all of the calcium in the SR? Previously (Stern, 1992), we analyzed some highly simplified and idealized models of stochastic CICR, with the conclusion that local control might be able to explain graded coupling. Since that time, a considerable amount of evidence has arisen in support of local control (see Ríos and Stern, 1997, for a review), but we have yet to see a single local calcium release event triggered by an identified L-type channel opening. However, considerably more information has become available about the ultrastructure of the diad junction and the gating of L-type channels and RyRs, and computer power has increased to the point where it is now practical to make use of this information in simulations.

Ideally, such simulations should be used to rule out erroneous mechanisms, prove the uniqueness of correct models, and identify the numerical values of their parameters. In practice, it is impossible to explore completely the multidimensional parameter space of these models, so the goal must be approached in stages. First, we ask whether local control, in a realistic setting of diad geometry, number, and location of channels, could explain the paradoxical gradedness of cardiac EC coupling. This question is answered in the affirmative by the demonstration that a phenomenological local control model with numerous, regularly spaced RyRs and multiple randomly located DHPRs at each diad junction can display graded control of SR calcium release flux by a sarcolemmal calcium current only one tenth as large. In the second stage, we ask whether one or more of the proposed RyR gating schemes based on lipid bilayer data are compatible with local control. It is difficult to answer this question with complete rigor, because of the large parameter space of these schemes. The approach that we have taken is to begin with the parameters obtained in lipid bilayers and make a trial series of parameter modifications consistent with known effects of the intracellular milieu; e.g., competition of Mg²⁺ at Ca²⁺ binding sites and acceleration of adaptation/inactivation kinetics. Based on these explorations, we have drawn inferences about how and why RyR gating schemes fail in the local control model, and what properties a successful RyR must possess. We have tried to back these inferences with relatively model-independent arguments. The third stage would involve detailed fitting of models to large amounts of whole-cell EC coupling data, identifying parameter values and establishing what experiments would discriminate between competing models. This stage goes beyond the scope of this paper, although the results obtained so far offer some tantalizing hints.

The somewhat surprising result of our stage-2 explorations is that none of the published bilayer-derived gating schemes gives a successful local control model, even when plausible modifications are made to adjust for the effects of the intracellular milieu. While it is difficult to exclude rigorously the possibility that some alternative set of parameters might solve the problem, it appears from our explorations that this could not be done without sacrificing crucial features of the gating behavior seen in bilayers; e.g., turning an adaptive inactivation into an irreversible one. All the schemes failed by lack of sufficient stability. Based on our explorations, this failure appears to result from the absence of two critical features: cooperative activation by more than one calcium ion and a “sufficiently” rapid and complete inactivation mechanism. The isolated RyR in bilayer is a very artificial system, and there are many reasons why it might not demonstrate physiological gating behavior, including the absence of other proteins associated with the RyR at the junction (e.g., triadin, junctin, calsequestrin). However, the most intriguing possibility is that the missing factor is the densely packed regular array of other RyRs that has been so well conserved through hundreds of millions of years of evolution. Recently, it has been reported that pairs (and, on occasion, groups of three, four, or even five) of skeletal muscle RyRs in lipid bilayers can gate synchronously when the associated protein FKBP-12 is present (Marx et al., 1998). Similar behavior is sometimes observed with RyR2 (A.R. Marks, private communication). This positive cooperativity was seen even when barium, rather than calcium, was the permeant ion, indicating that it is probably not mediated by the CICR mechanism. Our simulations show that cooperative allosteric interactions between nearest neighbor RyRs, interacting with CICR, can lead to stable local control of SR calcium release by a RyR whose gating scheme in isolation lacks the properties required for stability.

Limitations of the Allosteric Gating Model

Our construction of a stable gating scheme using allosteric interaction energies should be considered only as a proof of principle. In particular, our use of gating Scheme 2 from Fig. 4 as a starting point should not be construed as an endorsement of that gating scheme— we chose it only because it displays the pathologies of both inactivation and cooperativity in a simple form, and because it has a calcium-bound closed state, needed for our construction of RyR–RyR cooperativity. Our particular choice of allosteric energies should also not be considered either unique or optimal. They were obtained by starting with a certain strategy and then “tinkering” to get improved activation and inactivation behavior. The resulting model may deviate significantly from observations in many areas that we did not examine carefully, such as repriming dynamics. Our choice of allosteric interactions, while it produces positive cooperativity between RyRs, does not give rise to the perfect synchronization of opening and closing of coupled RyRs observed by Marx et al. (1998). Bers and Fill (1998) have suggested that such synchronization among all the RyRs in a cardiac diad might be a mechanism to generate calcium sparks, as an alternative to stochastic CICR, which also produces spontaneous multi-channel release events consistent with observed sparks (results not shown). It is not likely that allosteric interactions are required for the production of sparks since removal of FKBP12, the immunophyllin that is associated with the native RyR and is required for synchronized gating (Marx et al., 1998), does not abolish sparks (McCall et al., 1996), but may actually increase their frequency and duration and induce global calcium oscillations (Xiao et al., 1997). This observation finds a natural place in our allosteric coupling scheme, which is fundamentally inhibitory in character, as shown in Fig. 11. In fact, for the model based on RyR gating Scheme 2, even partial relief of the allosteric inhibitions (Fig. 11 D) unmasks a much greater degree of instability than is observed in intact cardiac myocytes deprived of FKBP12 by either knockout or the drug FK506. In interpreting such findings, it is important to bear in mind that FKBP has major effects on the gating properties of RyRs even in isolation, perhaps by mediating coordination between monomers in the tetramer (Kaftan et al., 1996).

There are, moreover, fundamental reasons to doubt that allosteric coupling alone, unaided by CICR, could produce acceptable synchronous gating of all the RyRs at a diad. Marx et al. (1998) reported that all the components of the dwell time distribution of synchronously gating pairs of RyR1 (two open times and two closed times) were unchanged from those of single channels. As pointed out by Bers and Fill (1998), this is quite surprising on energetic grounds. One way to model such an array is to assume that the coupling gangs together the molecular degrees of freedom involved in gating so that the only available states of the array are those in which all channels are in the same state. If that were the case, then an array of n channels would have all the state and, presumably, transition-state, energies n-fold larger than a single channel. For the large n found in the cardiac diad, these increased energies, which appear as negative exponentials, would produce an overwhelming slowing of the gating process, as well as reduce the occupancy of the less probable states in the gating scheme to negligible values. Another way to model a synchronized array, more in keeping with our approach in the simulations, is to assume that the gating of individual channels in the array remains well defined, but is modulated by allosteric interaction energies that are additive over all the points of RyR–RyR contact in the array. The fact that Marx et al. (1998) did not observe intermediate states (one channel open, one closed) in coupled channel pairs implies that occupancy of such states is suppressed by a positive allosteric energy, large compared with kT, at a contact between open and closed channels. In order for all the RyRs at a diad to go from closed to open, it would be necessary to pass, however briefly, through such intermediate states, which would have an allosteric energy proportional to the perimeter of contact between open and closed channels. This perimeter must, at some point in the process, be as large as the minimum diameter of the diad, 10 or more RyRs for large diads (Franzini-Armstrong, C., F. Protasi, and V. Ramesh, manuscript in preparation). This would represent an enormous energy barrier, which would, again, greatly slow the synchronous gating.

We are led to the conclusion that coupled gating, unaided by CICR or other exogenous sources of energy, should be greatly slowed compared with single channel gating. These arguments fall short of rigorous proof, because we have assumed that the states and transitions states of individual channels remain well defined in the array, and that allosteric interactions can be treated as an additive perturbation generated at the interface between nearest-neighbor RyRs. One could, instead, achieve coupled gating without change in the dwell times by assuming that ganging together n channels has a catalytic effect that reduces the transition state energies of individual channels by a factor of 1/n. Such a long range mechanical interaction in a lattice of huge macromolecules would be, at the least, ad hoc, although it might not be physically impossible. This argument shows that synchronous gating of many channels, with unchanged dwell times, is not a natural consequence of the interaction of multiple RyRs. It is therefore likely, as indicated by Bers and Fill (1998), that allosteric interactions collaborate with local CICR to produce the observed macroscopic and microscopic phenomena of cardiac EC coupling. Whether this collaboration is of the form modeled here is a matter presently beyond the resolution of direct measurement. In light of the observations by Marx et al. (1998), it is also likely that allosteric interactions would contribute substantially to the quantitative behavior and robustness of gating schemes (e.g., Fig. 4, Scheme 6) that are not intrinsically unstable, but require “tuning” to give acceptable behavior.

Although the possible role of allosteric interactions in cardiac EC coupling is the most novel phenomenon to emerge from the modeling, it should be put in perspective. To achieve stable local control, two characteristics are required: “strong” RyR inactivation and cooperative RyR activation by more than one Ca²⁺ ion. Inactivation could be produced by any interaction of the RyR with its native environment that stabilizes the inactivated state—it is not necessary to invoke state-dependent allosteric interactions with neighboring RyRs for this purpose. In contrast, the creation of cooperative activation, starting from a gating scheme that permits RyR opening in response to a single Ca²⁺, does require the exchange of information between RyRs. However, it is not entirely certain that the cooperativity problem is a real one. While published gating schemes based on bilayer data all permit single-Ca²⁺ activation, some studies have shown the steady state open probability of a single RyR2 depending on [Ca²⁺] with a Hill coefficient of >2 (Laver et al., 1995; Sitsapesan and Williams, 1994; Copello et al., 1997), suggesting that intramolecular cooperativity might be adequate to achieve global stability.

In any case, it is unlikely that any of the currently proposed RyR gating schemes captures all of the features of importance for physiologic EC coupling. One complicating factor that we have not considered here is the possibility that SR lumenal calcium may directly influence gating kinetics. Another (possibly related to the first) is that increasing the SR calcium load of a rat myocyte modestly above normal provokes periodic calcium oscillations, whereas “latch up” of the cell in a stable state of high [Ca²⁺]_cyto and high RyR open probability is never observed, even when egress of calcium from the cell is prevented. None of the models described above reproduces this global behavior accurately. It is possible that “adaptation” or other modulation of RyR gating by sustained elevation of [Ca²⁺] in the submicromolar range plays an important role in determining global stability. Further simulation and experimentation will be required to determine how this and other physiologic constraints translate into required properties of the RyR at the molecular level.

Table II.

L-Type Channel Parameters

Variable		Description/units		Value
BPERM		L-type permeation constant (effective Cao activity coeff.)		0.341*
CA1		L-type permeation constant (equivalent channel mouth [Ca2+])		0.001*
ETAM01		L-type mode-normal mode-V energy splitting factor		0.84‡
ETAM02		L-type mode-normal mode-Ca energy splitting factor		0.3‡
ETAM13		L-type mode-Ca mode-VCa energy splitting factor		0.3‡
ETAM23		L-type mode-Ca mode-VCa energy splitting factor		0.84*
ETAV0		L-type voltage sensor barrier symmetry, normal mode		0.5‡
ETAV1		L-type voltage sensor barrier symmetry, V-inact. mode		0.5‡
ETAV2		L-type voltage sensor barrier symmetry, mode-Ca		0.5‡
ETAV3		L-type voltage sensor barrier symmetry, mode V-Ca		0.5‡
F0		L-type transition rate into open state, ms−1		0.3*
F1		L-type transition rate into open state, mode-V, ms−1		0§
F2		L-type transition rate into open state, mode-Ca, ms−1		0.03*
F3		L-type transition rate into open state, mode-VCa, ms−1		0§
G0		L-type transition rate into closed state, mode-normal, ms−1		2.0*
G1		L-type transition rate into closed state, mode-V, ms−1		100.0§
G2		L-type transition rate into closed state, ms−1, mode-Ca		20.0*
G3		L-type transition rate into closed state, ms−1, mode-V-Ca		100.0§
KC0		L-type voltage sensor transition rate, normal mode, ms−1		0.2‡
KC1		L-type voltage sensor transition rate, mode-V, ms−1		0.1‡
KC2		L-type voltage sensor transition rate, mode-Ca, ms−1		0.2‡
KC3		L-type voltage sensor transition rate, mode-VCa, ms−1		0.1‡
KIV		L-type V-inactivation rate constant, ms−1		0.005‡
KIVCA		L-type V-inactivation rate constant from mode-Ca, ms−1		0.005‡
KIVM		L-type repriming rate constant, mode-V → normal, ms−1		0.000561‡
KK		L-type voltage sensor steepness, mV		10.0‡
KVIOFF		L-type Ca off-rate in VCa-inactivated mode, ms−1		0.0001‡
KVION		L-type Ca binding rate in V-inactivated mode, mM−1 ms−1		0.2‡
KVIOON		L-type Ca binding rate in mode-V open state, mM−1 ms−1		0§
KVOFF		L-type Ca off-rate in mode-Ca, ms−1		0.0001‡
KVON		L-type Ca binding rate in normal mode, mM−1 ms−1		0.2‡
KVOON		L-type Ca binding rate in mode-N open state, mM−1 ms−1		9.0‡
VCTR0		L-type voltage sensor center voltage, normal mode, mV		−24.0‡
VCTR1		L-type voltage sensor center voltage, mode-V mV		−104.0‡
VCTR2		L-type voltage sensor center voltage, mode-Ca, mV		−34.0‡
VCTR3		L-type voltage sensor center voltage, mode-VCa, mV		−114.0‡
UIV		L-type unitary current at 0 mV, pA		0.1‡

^*  Jafri et al., 1998;  

^‡ Values estimated from Shirokov et al., 1993, and Imredy and Yue, 1994, and adjusted manually to give a good fit to the data in Fig. 3 while preserving semiquantitative agreement with charge movement results of Shirokov et al. (1993). Transition rates between modes are specified for the preopen state of the voltage sensor C₄; intermode transition rates in other voltage-sensor states are determined by detailed balancing.  

^§ Mode-V and mode-VCa of the L-type channel are assumed not to open.  

Table III.

Ryanodine Receptor and Diffusion Parameters

Variable		Description/units		Value
KI		RyR Ca-dependent inactivation rate, mM−1 ms−1		0.5*
KIM		RyR repriming rate, ms−1		0.005*
KO		RyR Ca-activation rate, mM−2 ms−1		35.0*
KOM		RyR deactivation rate, ms−1		0.06*
UIC		RyR unitary current at CASR=CASRR, pA		0.4‡
DCA		Effective Ca2+ diffusion coefficient in cleft, m2 ms−1		0.15§
DB		Dye diffusion coefficient, m2 ms−1		0.02‖
HJ		Effective cleft height corrected for surface charge, m		0.0297925¶

^*Default values of the four parameters of the phenomenological RyR gating scheme were chosen “by hand” to give the observed gain of 10 at 0 mV, the observed time to peak of SR release (15 ms at 0 mV), and plausible macroscopic inactivation and repriming behavior.  

^‡ Mejia-Alvarez et al., 1998.  

^§ Soeller and Cannel, 1997.  

^‖  Harkins et al., 1993.  

^¶ The full three-dimensional electrodiffusion problem was solved for the case of steady state diffusion from a point source at the center of a cylindrical diad, using the Galerkin finite-element method as implemented in the program PDEase (Macsyma Corp.) with parameters from Soeller and Cannel (1997). An effective value of cleft height and a two-dimensional (2D) resistive boundary condition at the edge of the cleft were then determined so as to give the best simultaneous least-squares fit by the analytical solutions of the 2D cylindrical free-calcium diffusion problem for diad radii of 50, 100, 200, and 250 nm. These values were then used in the numerical 2D diffusion computation in the Monte Carlo simulations.  

Abbreviations used in this paper

CICR

calcium-induced calcium release

DHPR

dihydropyridine receptor

EC

excitation–contraction

RyR

ryanodine receptor

SR

sarcoplasmic reticulum